A Natural Gradient Algorithm for Stochastic Distribution Systems
Abstract
:1. Introduction
2. Model Description
- (1)
- The inverse function of y = f(u, ω) with respect to ω exists and is denoted by ω = f−1(y, u), which is at least C2 with respect to all variables (y, u).
- (2)
- The output PDF p(y; u) is at least C2 with respect to all variables (y, u).
Definition 1
Definition 2 ([5,6,24])
3. Natural Gradient Algorithm
Lemma 1 ([15])
Proposition 1
Proof
Theorem 1
Proof
- (1)
- Initialize u0.
- (2)
- At the sample time k − 1, formulate ∇J(uk−1) and use Equation (1) to give the inverse of the Fisher metric Gk−1.
- (3)
- (4)
- If J(uk) < δ, where δ is a positive constant, which is determined by the precision needed, escape. Additionally, at the sample time k, the output PDF p(y; uk) is the final one. If not, turn to Step 5.
- (5)
- Increase k by one and go back to Step 2.
4. Convergence of the Algorithm
Lemma 2
Proof
Lemma 3
Proof
Theorem 2
Proof
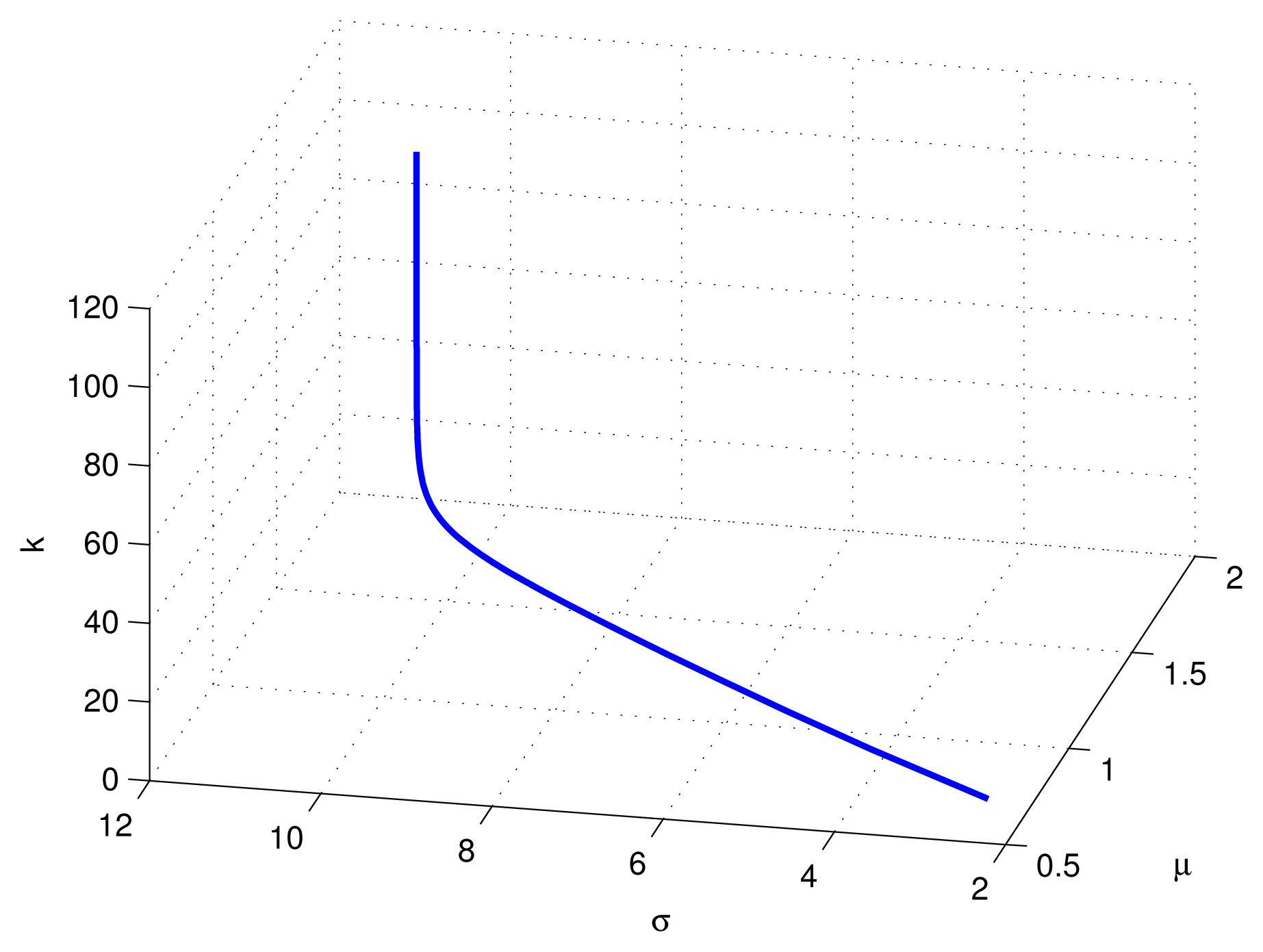
5. Simulations
6. Conclusions
- (1)
- By the statistical characterizations of the stochastic distribution control systems, we formulate the controller design in the frame of information geometry. By virtue of the natural gradient algorithm, a steepest descent algorithm is proposed.
- (2)
- The convergence of the obtained algorithm is proven.
- (3)
- An example is discussed in detail to demonstrate our algorithm.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rao, C.R. Infromation and accuracy attainable in the estimation of statistical parameters. Bull. Calcutta. Math. Soc 1945, 37, 81–91. [Google Scholar]
- Efron, B. Defining the curvature of a statistical problem. Ann. Stat 1975, 3, 1189–1242. [Google Scholar]
- Efron, B. The geometry of exponential families. Ann. Stat 1978, 6, 362–376. [Google Scholar]
- Chentsov, N.N. Statistical Decision Rules and Optimal Inference; AMS: Providence, RI, USA, 1982. [Google Scholar]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Amari, S. Differential Geometrical Methods in Statistics; Springer-Verlag: Berlin/Heidelberg, Germany,, 1990. [Google Scholar]
- Amari, S. Information geometry of the EM and em algorithm for neural networks. Neural Netw 1995, 8, 1379–1408. [Google Scholar]
- Amari, S.; Kurata, K.; Nagaoka, H. Information geometry of Boltzmann machines. IEEE Trans. Neural Netw 1992, 3, 260–271. [Google Scholar]
- Amari, S. Differential geometry of a parametric family of invertible linear systems-Riemannian metric, dual affine connections, and divergence. Math. Syst. Theory 1987, 20, 53–83. [Google Scholar]
- Zhang, Z.; Sun, H.; Zhong, F. Natural gradient-projection algorithm for distribution control. Optim. Control Appl. Methods 2009, 30, 495–504. [Google Scholar]
- Zhong, F.; Sun, H.; Zhang, Z. An Information geometry algorithm for distribution control. Bull. Braz. Math. Soc 2008, 39, 1–10. [Google Scholar]
- Zhang, Z.; Sun, H.; Peng, L. Natural gradient algorithm for stochastic distribution systems with output feedback. Differ. Geom. Appl 2013, 31, 682–690. [Google Scholar]
- Peng, L.; Sun, H.; Sun, D.; Yi, J. The geometric structures and instability of entropic dynamical models. Adv. Math 2011, 227, 459–471. [Google Scholar]
- Peng, L.; Sun, H.; Xu, G. Information geometric characterization of the complexity of fractional Brownian motions. J. Math. Phys 2012, 53, 123305. [Google Scholar]
- Amari, S. Natural gradient works efficiently in learning. Neural Comput 1998, 10, 251–276. [Google Scholar]
- Amari, S. Natural gradient learning for over- and under-complete bases in ICA. Neural Comput 1999, 11, 1875–1883. [Google Scholar]
- Park, H.; Amari, S.; Fukumizu, K. Adaptive natural gradient learning algorithms for various stochastic model. Neural Netw 2000, 13, 755–764. [Google Scholar]
- Guo, L.; Wang, H. Stochastic Distribution Control System Design: A Convex Optimization Approach; Springer: London, UK, 2010. [Google Scholar]
- Wang, H. Control of Conditional output probability density functions for general nonlinear and non-Gaussian dynamic stochastic systems. IEE Proc. Control Theory Appl 2003, 150, 55–60. [Google Scholar]
- Guo, L.; Wang, H. Minimum entropy filtering for multivariate stochastic systems with non-Gaussian noises. IEEE Trans. Autom. Control 2006, 51, 695–670. [Google Scholar]
- Wang, A.; Afshar, P.; Wang, H. Complex stochastic systems modelling and control via iterative machine learning. Neurocomputing 2008, 71, 2685–2692. [Google Scholar]
- Dodson, C.T.J.; Wang, H. Iterative approximation of statistical distributions and relation to information geometry. Stat. Inference Stoch. Process 2001, 4, 307–318. [Google Scholar]
- Wang, A.; Wang, H.; Guo, L. Recent Advances on Stochastic Distribution Control: Probability Density Function Control. Proceedings of the CCDC 2009: Chinese Control and Decision Conference, Guilin, China, 17–19 June 2009. [CrossRef]
- Sun, H.; Peng, L.; Zhang, Z. Information geometry and its applications. Adv. Math. (China) 2011, 40, 257–269. (In Chinese) [Google Scholar]




© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, Z.; Sun, H.; Peng, L.; Jiu, L. A Natural Gradient Algorithm for Stochastic Distribution Systems. Entropy 2014, 16, 4338-4352. https://doi.org/10.3390/e16084338
Zhang Z, Sun H, Peng L, Jiu L. A Natural Gradient Algorithm for Stochastic Distribution Systems. Entropy. 2014; 16(8):4338-4352. https://doi.org/10.3390/e16084338
Chicago/Turabian StyleZhang, Zhenning, Huafei Sun, Linyu Peng, and Lin Jiu. 2014. "A Natural Gradient Algorithm for Stochastic Distribution Systems" Entropy 16, no. 8: 4338-4352. https://doi.org/10.3390/e16084338
APA StyleZhang, Z., Sun, H., Peng, L., & Jiu, L. (2014). A Natural Gradient Algorithm for Stochastic Distribution Systems. Entropy, 16(8), 4338-4352. https://doi.org/10.3390/e16084338




