As was mentioned in the Introduction, there are many interesting physical problems for which a detailed description of the system at the all-atom (AA) level is not necessary to obtain the relevant information. In these cases a simpler model might be used, where a given high-resolution, computationally expensive model is replaced with a simpler one.
2.1. The Mapping Function and the Potential of Mean Force
In a multiscale approach, one first needs to define the relationship between the two levels of resolution. This is typically done via mapping functions which determine the CG Cartesian coordinates of each site as a linear combination of coordinates for the atoms that are involved in the site (that could be via a center-of-mass or a center-of-geometry mapping or some other geometric construction). This means the CG coordinates R are constructed from the atomistic coordinates r via
where M is an n × N matrix (n and N being the number of particles in the atomistic and CG system, respectively). In the (canonical) sampling of the atomistic and CG systems with respective interaction potentials VAA(r) and VCG(R) the corresponding configuration functions PAA(r) and PCG(R) are given by
and
with ZAA = ∫ exp[−βV AA(r)]dr and ZCG = ∫ exp[−βVCG(R)]dR being the respective partition functions and β = 1/kBT. If one analyses the atomistically sampled system in CG coordinates one can determine the probability distribution of sampling atomistic coordinates that map to a given CG coordinate r)
(Here, we follow the notation used by Noid and collaborators, e.g., in References [
99,
100]). The angular brackets indicate canonical sampling of the atomistic system (
i.e., according to
PAA(
r)). One can formulate the aim of many systematic coarse graining approaches in the following way: To sample the part of phase space which is sampled by the atomistic system with the same probability distribution. Following this, one possible definition of consistency between atomistic and CG level of resolution is that the two models are consistent if the canonical configurational distribution sampled by the CG model
PCG(
R) is equal to the probability distribution
PAA(
R) obtained after mapping the atomistic system to CG coordinates. In a canonical ensemble, independent degrees of freedom
q are Boltzmann distributed and the Boltzmann inverse of
P(
q)
is a many-dimensional potential of mean force (PMF), which, when used for example as an interaction potential in a CG simulation, reproduces the distribution P(q). This means that Boltzmann inversion of PAA(R) defines, uniquely up to an additive constant, a high-dimensional CG potential
which will result in a sampling of CG configurations consistent with the atomistic reference simulation. This high-dimensional, many-body CG potential contains both energetic and entropic contributions from the configurational sampling in the high-resolution model and the mapping between high-resolution and CG model (
Equation (4)). Therefore, the resulting CG model is state point dependent and not necessarily readily transferable. While it is conceptually easy to formulate the PMF as a solution of the systematic coarse graining task, it is practically unfeasible. In most cases the PMF cannot be easily determined, and even if it were possible, the resulting high-dimensional potentials are computationally prohibitive. In addition,
is a function of
R,
i.e., this PMF as is can in principle only be applied to a system which is identical in size to the atomistic reference system; if this limitation cannot be overcome, e.g., by breaking it down to short-range interactions, it would defeat the purpose of coarse graining. Therefore, one has to decompose the PMF into simpler independent terms and approximate it by simpler interaction functions, ideally ones that resemble interaction functions typically used in molecular mechanics forcefields,
i.e., short range bonded contributions and pair potentials or similar. Conceptually, one can decompose the PMF into a series of many-body terms up to an
N-body term, where
N is the number of particles on the system. However, this itself does not solve the problem since these multi-body interactions are again computationally unfeasible.
In
Equation (7) one approximates the series by an effective pair interaction which also contains contributions from the higher order terms in
Equation (7) (some approaches also include three-body terms for systems where this is necessary [
101]). There are many approaches to this task of determining effective CG interactions, and all the resulting CG models are (only) approximations to
.
2.2. Multi-Scale Coarse-Graining
Probably the most painful limitation in the use of the many-body PMF is the fact that, in general, it cannot be decomposed into a sum of local contributions depending on the interactions between two to a few particles. A simple strategy would therefore be to decide a simple functional form of the potential, e.g., a sum of pairwise, radial interactions, which depend on a set of parameters; the values of the latter are then chosen so that the CG potential is as close as possible to the true PMF. This approach was pioneered by Ercolessi and Adams in 1994 [
102] and Tschöp and coworkers in 1998 [
103]. Later, Izvekov and Voth [
104,
105] made use of the force-matching concept of Ercolessi and Adams in the development of the Multi-Scale Coarse-Graining (MS-CG) method. These approaches have been successfully applied to a multitude of biomolecular and other soft matter systems, in particular to biomolecules [
90–
95].
The central idea of Force Matching is to use a variational (
i.e., non-iterative) approach for constructing the CG potential based on the atomistic reference simulation (the recorded forces from the atomistic simulation). The numerical implementation of this variational principle works in such a way that the exact many-body PMF (
Equation (6)) is represented by a linear combination of basis functions that are functions of the CG site coordinates [
14,
15]. For a given configuration of the CG coordinates, in fact, the average of the total atomistic force
fα acting on a CG site
α is equal to the derivative of the many-body PMF:
where the subscript R on the averages indicates that the sampling is constrained to those configurations of the AA system having the CG sites in a fixed configuration. The CG force field depends on M parameters g1, ···, gM, that can be prefactors of analytical functions, tabulated values of the interaction potentials, or coefficients of splines used to describe these potentials. These parameters have to be optimized so that the CG force field reproduces the forces in the atomistic system (after mapping) as close as possible. To this end, one minimizes the difference between the average AA force 〈fΑ〉R and the force Fα due to the CG potential by minimizing the following quadratic function:
Equation (9) can be rephrased in terms of generalized scalar products of elements in a multi-dimensional vector space; these elements are the 3
N-dimensional force-fields
f and
F acting on the CG sites, with the scalar product and the corresponding norm given by:
Given the definitions in
Equation (10), it can be shown that minimizing the function
χ2 in the MS-CG method is equivalent to minimizing the ‘distance’ between the many-body PMF and the CG potential:
The force-matching strategy thus
projects the true many-body PMF onto the basis of functions that are used to define the CG force-field; a thorough formal explanation of this interpretation can be found in Reference [
14,
15].
It should be noted, however, that the CG force field is still an approximation to the high dimensional PMF within the limitations of the types of CG forces chosen (for example pair forces that can be derived either from analytical or from numerical tabulated potentials). This also implies that a CG model obtained from force matching does not by construction reproduce the pair correlation functions in the system, and the reproduction of local structural properties such as pair distributions may (or may not) be imperfect depending on the importance of cross-correlations between degrees of freedom. An exact reproduction of the underlying atomistic problem by matching mean forces therefore potentially requires the introduction of higher order (e.g., three-body) interactions. Noid and coworkers have extended the force matching method and demonstrated that the CG force field can be directly determined from structural correlation functions obtained from the atomistic system instead of the forces [
99]. Their theoretical approach also allows an assessment of the correlations between different interactions that are neglected by straightforward Boltzmann inversion and allows the quantification of the importance of many-body correlations in CG models. In a recent study, Rudzinski and Noid explore these aspects in detail [
106]. They demonstrate how the balance between accurately reproducing individual correlation functions (such as pair correlation functions or angle distributions) and also reproducing cross correlations between the respective degrees of freedom is affected by the mapping scheme and the coarse graining method (or more accurately its targets, namely the mean forces versus the individual correlation functions).
2.3. Boltzmann-Inversion Based Methods
In contrast to the Force Matching or Multi-scale coarse graining scheme, other structure-based methods provide CG interactions that reproduce pre-defined target structure properties—often a set of radial distribution functions [
77–
89]. This means that the many-body PMF (
Equations (6) and
(7)) is replaced as a target by a set of simpler structural correlation functions. If the interactions in the CG model are statistically independent or only weakly coupled then direct Boltzmann inversion determines each term in the potential immediately from the corresponding distribution function [
77,
107–
109]; for non-bonded interactions in dense systems, though, this is typically not the case. This means that the individual distribution functions and their corresponding potentials of mean force, e.g., a radial distribution function of a simple liquid
gtarget(
r) and its Boltzmann inverse, the pair PMF,
, cannot be directly used as an interaction function since they correspond not only to the interaction potential but also to the correlated contributions from the surroundings. These multi-body effects of the environment need to be removed from the PMF in order to generate an effective pair potential that reproduces the target structure, for example the pair correlation function in the liquid. It can be shown that such a pair potential is unique up to an arbitrary constant [
110] and exists [
96,
111–
113]. There are several numerical methods to generate this pair potential (tabulated interaction function).
Iterative Boltzmann inversion (IBI) [
81,
114,
115] is a natural extension of the Boltzmann inversion method. Here, a numerical CG potential is iteratively refined until the target structure is reproduced within a predefined error. Each step in the iteration procedure is a CG simulation with potential
which yields an RDF
gi(
r) that differs from the target
gtarget(
r). The potential is then modified by a correction term Δ
V (
r) according to
Sometimes the potential correction ΔVi(r) is multiplied by a prefactor 0 < λ ≤ 1 to avoid overshooting in the numerical procedure. The iterative procedure is often initiated with the pair potential of mean force
, but that is not mandatory. Different starting potentials can be useful, in particular for more complex mixed systems where the iterative procedure may be unstable because intermediate CG models lead to phase separation. This is for example observed in the case of hydrophobic molecules in aqueous solution where both above-mentioned precautions have found to be useful to prevent strong oscillations or even instability of the IBI procedure.
IBI is by no means the only numerical method that solves the above task. Another numerical scheme is the so called inverse Monte Carlo (or more recently renamed Newton inversion) method [
78,
79,
83,
84] which, according to Henderson’s theorem, should lead to the same numerical solution for the pair potential corresponding to a given pair correlation function. While in IBI the potential update Δ
Vi is ad hoc, in IMC it is computed using rigorous statistical mechanical arguments (for details see Reference [
78]). In the case of multicomponent systems, where several pair potentials need to be updated, IMC accounts for correlations between observables,
i.e., the updates for the different potentials are interdependent. In contrast, for IBI each potential is updated independently, which might lead to oscillations and convergence problems in the iteration procedure. The disadvantage of IMC on the other hand is a high computational cost and problems with numerical stability; for a detailed comparison see Reference [
116]. Related to IMC, there are several other recent developments, e.g., a molecular renormalization group approach [
85–
87] or an approach that relies on relative entropies [
96–
98] (which will be discussed in more detail below). While the above structure-based methods by construction reproduce
exactly, within the error of the numerical procedure, the local pair structures and thus are well-suited to the reinsertion of atomistic coordinates, it can be expected
a priori that they will not be equally well suited to the reproduction of thermodynamic properties (pressure, phase behavior,
etc.) of the reference system; in this respect, water provides a prototypical case and a reference for testing. Note also that CG models based on pair correlation functions do not necessarily reproduce higher-order (e.g., three-body) structural correlations [
116] since the pair correlation functions as structural targets are just an approximation to the total conformational distribution function obtained from the atomistic sampling,
PAA(
R) (
Equation (4)). This means that if higher order correlations are a crucial part of the many-body PMF, models based on pair structures may fail to represent these, and it may even be possible that models which are limited to pair potentials may fail to reproduce these correlations irrespective of the parametrization methodology. One example where this is studied in detail is liquid water [
101,
116–
119]. Recently Noid and coworkers have analyzed these aspects using concepts from liquid state theory [
100,
120].
One more note concerning Henderson’s theorem: even though there is in principle one
exact solution for the effective pair potential that reproduces a given pair correlation function, different potentials might give a reasonably close representation of the structure,
i.e., the above inverse problem is mathematically ill-posed [
116,
121].This effect becomes even more pronounced in complex systems where several interaction functions corresponding to several RDFs need to be numerically determined. This can to some extent be turned into an advantage since it allows one to impose thermodynamic constraints in the parametrization procedure. This will result in interaction functions which do
not exactly reproduce the target structure but give a very close representation while at the same time producing the desired thermodynamic behavior. One example of this is pressure correction terms [
81,
117]. Here, an additional linear pressure correction is applied during the iterative Boltzmann inversion procedure with
where rcut is the radial cutoff distance of the non-bonded interaction and the constant A is determined via the virial expression for the pressure to
V is the volume of the system,
Pi the pressure of the CG model in the
i-th iteration, and
Ptarget the target pressure. The price to pay for this adjustment, however, is the loss of the perfect compressibility match. This phenomenon is of course a direct consequence of the state point dependency of coarse grained interactions. Further details on this topic can be found in Reference [
117]. Recently, different functional forms of pressure correction terms and the influence of the cutoff length have been explored by Fu
et al. [
122].
It is to be expected that there will be more development in this direction (using other types of thermodynamic constraints) since in particular for complex soft matter system the balancing of structural and thermodynamic behavior in CG models is an ongoing field of research [
88,
89].
The IBI method is in its original form designed and best suited for systems with uniform density distributions. Recently, Jochum
et al. have shown how it can be generalized for non-bonded potentials for inhomogeneous systems [
123]. For a system with a slab geometry (such as systems of solvent slabs in vacuum or phase-separated systems consisting of two liquid slabs in contact with each other), the method is analogous to IBI but the iterative update of the interaction potential consists of two terms, one based on the radial distribution function calculated in a slab geometry and one that accounts for the slab and interfacial widths. These latter geometric features are very sensitive to the thermodynamic properties (surface tension) of the interface. Therefore the two update terms allow for a balance between the local liquid structure and the thermodynamic properties of the liquid/vapor or liquid/liquid interface. In addition to water/vapor and methanol/vapor interfaces, the method has also been successfully applied to a solute-solvent system of a single benzene molecule at the vacuum-water interface,
i.e., it is possible to account to some extent for the partitioning behavior of a solute between bulk and interface, an aspect that makes this method promising in the context of designing transferable CG models for phase separation processes (see below).
Last but not least, one should mention the particular case of Boltzmann-inversion based approaches for mixed systems where (at least) one component is very dilute (from now on termed solute), e.g., biomolecules in aqueous solution. In this case, iterative Boltzmann inversion and similar methods are problematic. While one can easily compute the solvent-solvent and the solute-solvent radial distribution functions, and therefore determine the corresponding CG potentials with for example IBI, this is not so straightforward for the interactions between the low concentration component (solute). (Note that for simplicity only solutes that are represented by a single CG bead will be discussed here.) In these cases, obtaining the PMF through brute force sampling of a radial distribution function is not advisable. One should rather compute the solute-solute pair PMF (between two solute particles) with an advanced sampling method such as umbrella sampling or thermodynamic integration (using distance constraints) [
124,
125].
When solvent degrees of freedom are not explicitly present in the CG system, this solute-solute PMF can be used directly as an effective solute-solute non-bonded interaction since the environmental (solvent) effects within the PMF are not explicitly represented through solvent degrees of freedom in the CG model. For many types of solutes the solute-solute PMF has been used as an interaction potential in implicit solvent models [
126,
127]. One prominent example is the use of the solute-solute pair PMF for implicit solvent models of aqueous electrolyte solutions,
i.e., implicit solvent ion models [
37,
79,
85,
128,
129].
The case is somewhat different if some sort of explicit solvent representation, for example in the form of a CG water model, is present in the CG system. In this case, effective solute-solute non-bonded pair interactions are needed from which the solvent contributions are removed in the same way they are removed by IBI in other systems. However, due to the sampling problem of the PMF between dilute components, an iterative procedure is prohibitive for solute-solute interactions. To solve this problem, an approximate method has been developed by Villa
et al. [
38,
130]. Here, the CG solvent-solvent and solute-solvent interactions are first determined, for example through normal IBI. Now the pair PMF between the solutes
is computed (from atomistic umbrella sampling or thermodynamic integration) and used as a target, in other words the resulting CG model is parameterized to reproduce the solute-solute association strength observed in the atomistic system. In order to remove the solvent contribution from
, a subtraction procedure is employed. One conducts a separate PMF calculation (again with umbrella sampling or thermodynamic integration), this time in a CG system, where the (previously determined) CG solvent-solvent and solute-solvent interactions are present but no direct interaction between the solute particles is turned on. The resulting PMF
only consists of the environmental contributions (in the CG environment). By subtracting
from the target PMF one obtains the missing direct pair interaction
which by construction reproduces the target PMF. Note that this subtraction procedure is not necessarily limited to CG solvent-solvent or solute-solvent interactions determined by IBI. In principle other types of CG solvent-solvent or solute-solvent interactions could also be used to determine
If one then applies
Equation (14), one obtains an effective solute-solute interaction
VCG(
r) which reproduces the atomistically observed solute-solute association strength (
i.e.,
) in the particular CG solvent that was chosen.
2.4. Relative Entropy
Aiming at reproducing different properties or objective functions of the reference, atomistic system, IBI and Force Matching have manifestly different algorithms and produce qualitatively different results. Recently a different coarse-graining strategy has been developed, namely the Relative Entropy method [
131–
133], which relies on a quantitative measure of the loss of information that follows from the description of a system in terms of different interaction potentials and/or different resolution. Remarkably, it is possible to demonstrate that the information function employed in this strategy connects Relative Entropy, IBI and Force Matching together. The functional form of this measure function is given by the relative entropy, or Kullback–Leibler distance:
In
Equation (15),
ν labels a given microstate or atomistic configuration, ℘
AA(
ν) is the probability of sampling a configuration
ν in the fully atomistic system, and ℘
CG(
ν) is the probability of sampling the same (atomistic) configuration in the system with coarse-grained interactions, but still described by a high-resolution structure. This latter probability is degenerate with respect to the atomistic-potential configurations, as many of them correspond to the same coarse-grained configuration
![Entropy 16 04199f12]()
. It is therefore advantageous to write the probability to sample a given atomistic configuration in the CG system in terms of the function that maps the fine-grained configurations onto the coarse-grained ones:
Here,
is the probability of sampling the CG configuration
![Entropy 16 04199f12]()
in the low-resolution system and Ω(
![Entropy 16 04199f12]()
) = ∑
ν δ(
M(
ν) −
![Entropy 16 04199f12]()
) is a measure of the degeneracy of the configuration
![Entropy 16 04199f12]()
in the atomistic system. It should be noted that this last quantity depends only on the mapping function
M and not on the coarse-grained interactions; this term can therefore be separated out in the definition of the relative entropy to obtain:
The quantity
φ(
ν) can be interpreted as the amount of information in the configuration
ν which discriminates between the atomistic and the coarse-grained probability. The definition in
Equation (17) is particularly appealing because it shows that the relative entropy can be computed as the sum of operator averages. In the special, but quite common case of systems in thermal equilibrium, the probability distributions ℘ are simply given by the Boltzmann weights, and the relative entropy reduces to the form:
with AAA (resp. AAA) being the free energy of the atomistic (resp. CG) system. For a given choice of the mapping function M, the optimal coarse-grained potential is obtained by minimizing the relative entropy functional with respect to the parameters in terms of which the aforementioned potential is defined: common choices for non-bonded, two-body interactions are the coefficients of a Lennard-Jones potential or the nodes of a spline.
As anticipated at the beginning of this section, IBI and Force Matching can be connected using the concept of relative entropy. In fact, a straightforward minimization of
Srel making use of two-body coarse-grained potentials can be shown to be equivalent to the IBI algorithm; on the other hand, the Force Matching scheme is retrieved if the average of the function |∇
φ|
2 is minimized instead of the average of
φ [
134]: the squared gradient of the
φ function with respect to the Cartesian coordinates, in fact, is proportional to the squared difference of the forces obtained from the AA and the CG descriptions, so that:
In conclusion, it therefore appears evident that different coarse-graining schemes are obtained through the minimization of different functionals of the same information function φ, which represents the unifying element between various approaches.
2.5. Transferability of Coarse-Grained Models
From the preceding sections we have seen that there are different approaches to the systematical parameterization of CG models which by construction will not be equally well suited to the reproduction of thermodynamic and structural properties of the system. It is not
a priori clear whether structure-based potentials reproduce macroscopic thermodynamic properties and, vice versa, if thermodynamics-based potentials reproduce microscopic structural properties. However, the interplay of structure and thermodynamics is crucial for the investigation of structure formation processes, in particular for biomolecular aggregation in aqueous solution where partitioning and phase separation play a decisive role. All CG models (in fact also all classical atomistic forcefields) are state-point dependent and cannot necessarily be—without reparametrization—transferred to different thermodynamic conditions or a different chemical environment compared to the one where they had been derived. This means “transferability” can refer to a change in temperature, density, concentration, system composition, phase,
etc., but also a change in chemical environment, e.g., the change of length or sequence of an amino acid chain. Structure-motivated CG models which approximate the high dimensional PMF obtained from an atomistic reference are by construction heavily state point dependent, and several studies have addressed questions regarding their ability to reproduce thermodynamic properties. One system that has been of particular interest in this context is liquid water [
112,
117,
135]. The reason is on the one hand of course its immense importance in all questions regarding biomolecular systems. In addition, it is of particular methodological interest because for single bead models of water it is known that three-body correlations play a decisive role and the potential compromise between reproducing pair- or higher order structural correlations is particularly relevant for the properties of the model [
101,
116,
117]. Different studies have been carried out that compare structure-motivated and thermodynamics-based CG models [
121,
136,
137]. While CG models where the parametrization targets had been solvation and partitioning properties are particularly well suited to reproduce processes where for example hydrophilicity/hydrophobicity arguments play a decisive role, they do not per se reproduce the structure of the system [
121,
136]. Related to their ability to reproduce the thermodynamic properties of certain chemical units, these models exhibit considerable transferability and can often be applied to a variety of molecular systems and a range of thermodynamic conditions. Motivated by these observations, intensive research is currently being carried out to derive CG potentials that are both thermodynamically as well as structurally consistent with the underlying higher-resolution description, thus ensuring for example a certain state point transferability [
38,
88,
89,
94,
138].
One possibility to improve transferability in this context is to exploit—similar to the case of the pressure correction described above—the fact that the derivation of a CG model based on the reproduction of structural properties (potentials of mean force) is an ill-posed problem which allows a reproduction of the original target property within a given error while at the same time including certain thermodynamic target properties during parametrization. One approach developed by Ganguly
et al. for multicomponent systems that follows this idea combines the IBI method with Kirkwood–Buff integrals as additional targets which are related to the activity coefficients of the components [
139]. With this approach transferability over a certain concentration range can be achieved.
Yet another non-structure-based method that produces CG pair potentials with remarkable state point transferability is the conditional reversible work method by Brini
et al. [
140–
142]. Here, several calculations of pair potentials of mean force on the atomistic level are used to assess and correctly account for the indirect contribution by the environment to the effective CG pair forces. The observed transferability of this method can be ascribed to the fact that the method relies on direct pairwise interactions in the atomistic reference system. In other words, the method does
not rely on reproducing a structural property such as a pair PMF or multi-body PMF,
i.e., on properties that are extremely dependent on the precise thermodynamic state of the reference system.
It has been mentioned before that effective pair potentials account for multi-body effects, for example, three body interactions. For this reason, they are only to a limited extent additive, which limits the transferability of the potentials [
38,
143]. Understanding the physical nature of non-additivity in the system of interest can help to make a CG model transferable. In principle, there are various possibilities to approach the question of transferability of effective pair potentials: (
i) One applies a model derived at/optimized for a given state point unaltered to a range of state points nearby; in that case, one has to carefully investigate the range in which this is permitted [
144–
146]; (
ii) One creates a new set of potentials for each state point one wants to investigate [
144]; (
iii) One specifically designs a single CG model with the aim of transferability (for example specific density dependent potentials [
94,
147,
148], CG models that are designed to be applicable for a range of mixture compositions [
71,
138], or CG models that are capable of capturing a liquid crystalline phase transition [
88,
89]); (
iv) One uses a model derived at one state point and (analytically) modifies it to be applicable to different conditions (one example being the rescaling of potentials in order to apply them to a different temperature [
149]).
The approach of using a model at a specific state point and then testing its transferability over a reasonably wide range of different physical conditions has traditionally been applied in the case of classical polymer melts. In this field, structure-based models have been very successfully applied, and decent temperature [
77,
150–
152] and pressure transferability [
153] have been found. In fact in the first papers by Tschöp
et al. [
77,
103] the temperature transferability already allowed the semi-quantitative prediction of shifts in Vogel Fulcher temperature for different polycarbonate modifications. This observation appears to hold for classical isotropic polymer melt systems where the behavior is largely dominated by the correct representation of the chain conformations and the excluded volume of the chain. As soon as more specific chemical interactions play a role, the case of transferability becomes more delicate.
In the following, we discuss three examples which illustrate that understanding the physical basis behind the limitations in transferability can help to design transferable models.
Binary mixtures have in general been widely used as model systems to explore various aspects of the transferability of CG models [
37,
38,
71,
128,
129,
138,
143,
147,
148]. The transferability to different concentrations of liquid mixtures or solutions is of vital importance for simulation of processes such as (bio)molecular aggregation which are characterized by spatially varying structure and fluctuating concentrations.
Following the above-described method to apply Boltzmann-inversion derived methods in dilute solute solvent systems, a CG model for mixed systems of benzene in water had been derived [
38]. This means that the CG benzene-benzene potential had been parameterized on the basis of the benzene-benzene PMF of two benzene molecules in aqueous solution,
i.e., at “infinite” dilution. Benzene-water mixtures of different composition have been studied with this CG model and analyzed using the Kirkwood-Buff theory of solutions [
154]. Kirkwood-Buff theory provides a link between local structural information and thermodynamic properties of the solution. This CG model, parametrized at infinite dilution of benzene, reproduces the Kirkwood-Buff integrals of mixtures at various concentrations obtained with the detailed-atomistic model. It reproduces the changes in the benzene chemical potential and the activity coefficients of the mixtures over a range of mixture compositions (up to concentrations where benzene and water demix in the atomistic reference simulation). A possible explanation is that hydrophobic interactions between benzene solutes are short-ranged, and the multi-body correlations involved in hydrophobic association can be described by pairwise additive effective potentials (category (
i) of the above list). The observed transferability of the potential supports the idea that hydrophobic interactions between small molecules are pairwise additive. Villa
et al. also found that a different CG model for benzene-benzene interactions that had been derived for pure benzene (via IBI) is neither suited to describe benzene-benzene interactions in aqueous solution at different concentrations nor a phase-separated benzene/water system with a bulk benzene layer [
38].
To reproduce the actual phase separation process as well as the behavior of the mixed (or dilute) systems is much more complicated (yet it is of vital importance in the parameterization of bottom-up CG models that are able to reproduce biological partitioning and self aggregation phenomena). Here, a combination of a wise choice of one or possibly several reference state points is promising, in particular combining the reference of infinite dilution with the phase separated one. For the latter, application of the IBI extension by Jochum
et al. for inhomogeneous systems with an interface/phase boundary can be utilized [
123].
In this context it should also be mentioned that similar transferability problems exist in other areas, for example in the simulations of solids (e.g., with embedded atom potentials). As soon as one encounters surfaces or interfaces the local environment of an atom differs substantially from the bulk (crystalline) phase, which was used to parameterize the interaction potentials. Consequently the transferability of the potentials will affect the ability to model processes such as crack formation or the relocation of grain boundaries [
155,
156].
In the second example, the situation is different. Here, the transferability of CG (in this case implicit-solvent) ion models in aqueous solution had been investigated. Due to long-range electrostatic interactions, the ions affect the behavior of water increasingly strongly with increasing ion concentration. More specifically, the presence of many ions reduces the orientational fluctuations of the water molecules and thus the dielectric permittivity of the solvent. Therefore, effective ion-ion potentials parametrized at infinite dilution are not directly transferable to higher salt concentrations. Hess
et al. developed a reduced-resolution (in this case implicit-solvent) potential for aqueous electrolyte solutions where an ion-concentration-dependent Coulomb term was added to the (ion-specific) pair interaction. Thus, by using a concentration-dependent dielectric permittivity for water, part of the multi-body effects in the system were accounted for in the ion-ion pairwise interaction in the implicit solvent model [
128,
129]. This approach reproduced the NaCl solution osmotic properties and the ion coordination up to a concentration of 2.8 M (mol/L). While in the case of the CG model of benzene/water mixtures [
38] the short-range hydrophobic interactions parameterized at infinite dilution were directly transferable to higher benzene concentrations, the ion-ion interactions determined at infinite dilution had to be split into a short-range ion-specific and a long-range electrostatic part. The interactions were then made transferable by keeping the short-ranged part constant and analytically modifying the long-ranged electrostatic part (category (
iv) of the above list). Shen
et al. have further investigated the structure and osmotic properties of electrolyte solutions over a wide range of concentrations [
37]. Using a concentration-dependent dielectric constant one also obtains very good structural properties of the electrolyte solution at low and intermediate salt concentrations while for larger salt concentrations multi-body ion-ion correlations limit straightforward transferability. Guided by this structural analysis, the transferability of the implicit-solvent model could also be improved for high ion concentrations. One obtains transferable implicit-solvent effective pair potentials which are both structurally and thermodynamically consistent with an explicit solvent reference model.
The third example again stresses the immense importance of a good reference state point. It also shows how the reference choice can be guided by understanding the underlying physics.
One highly relevant case of a transferability problem is the ability of a CG model to correctly describe a phase transition while being (reasonably) faithful at both phases below and above, a prominent example being liquid crystalline systems. For such systems, coarse graining can gain access to large system sizes with local disorder, domains etc., and a bottom-up, non-generic CG model has the power to include molecular flexibility and other chemistry specific details. This means that the model should on the one hand faithfully represent the structure in the LC ordered state and on the other hand reproduce the LC/isotropic phase transition.
For an azobenzene-based liquid crystalline compound (8AB8) it was found that state point transferability could be achieved by choosing as an appropriate state point for the reference simulation the supercooled liquid just below the smectic-isotropic phase transition. This reference state is characterized by a high degree of local nematic order while being overall isotropic. The primary idea behind this choice of reference state is the observation that—in the spirit of arguments from classical density functional theories of liquids [
157]—the short ranged correlations in the ordered phase are not very different from the local correlations present in a disordered phase at suitable thermodynamic state (density, temperature,
etc.) (as one approaches the transition from the high-temperature side). If one captures these local correlations and builds them into the (structure-based) potentials, then these potentials should be able to describe phases on both sides of the transition. For 8AB8, indeed an excellent structural correspondence with the atomistic reference in the smectic state has been found. With the resulting CG model it is possible to switch between the atomistic and the CG levels (and vice versa) in a seamless manner maintaining values of all the relevant order parameters which describe the LC ordered state (see
Figure 1). At the same time, this CG model shows remarkable state point transferability and reproduces the LC-isotropic phase transition upon heating and cooling [
39]. Such a CG LC model—since it is on the one hand sufficiently coarse grained to study a variety of processes in the LC phase while being at the same time still very closely related to an underlying chemically realistic atomistic description, e.g., allowing for realistic molecular flexibility—is able to give new insights into for example microscopic dynamics in LC phases [
40]
3. Adaptive Resolution Simulations
In the introduction we defined a class of systems for which the focus of the researcher’s interest is on a (possibly small) subregion of the simulated system: this is the case, for example, of the hydrogen bond network at the surface of a solvated molecule in water. The bulk of water molecules has to be simulated in order to sustain the thermodynamical properties of the subsystem of interest—the interfacial water—and to provide the correct exchange of molecules. Nonetheless, the fine-grained detail of molecules far from the interface is not relevant; it would be therefore desirable to replace the atomistic, expensive interactions of hydrogen and oxygen atoms with a coarser model.
We can then introduce a geometrical separation between an “inside” and an “outside”, i.e., an all-atom and a coarse-grained region, and assign different types of representations and interactions to the molecules according to their position in the simulation domain.
This idea has a long and successful history: to investigate crack propagation in hard matter, for example, several authors [
158–
162] made use of a hybrid description of the system, where a “high resolution” description is employed only for the area in the proximity of the crack, and the material far from the crack is treated with a simpler model. Another important example of hybrid resolution simulation is provided by Quantum Mechanics/Molecular Mechanics (QM/MM) methods [
163–
167]. In this case the structure of the system is described at the same (atomistic) level everywhere; however, the interactions are obtained from a classical force-field in the bulk of the system, but in a small region
ab initio methods -such as Density Functional Theory, DFT- are employed to calculate the forces. Many different “flavors” of this approach have been developed; in all of them, though, one of the crucial aspects is how to interface the two domains where interactions are different, and in most of the established methods the identity or resolution of the particle is not allowed to change. In general, one has to answer the two following questions:
- (1)
how should two atoms/molecules in different domains interact?
- (2)
how should the properties of an atom/molecule change in crossing the interface?
The last question is of particular importance for all systems whose components can diffuse on large length scales (at last of the order of the molecules’ size) in the simulation time. It appears natural to introduce a
transition region (often called hybrid region, or healing region) that allows for a smooth interpolation from a given representation of the molecule’s structure/interaction to another; a schematic representation of this setup is provided in
Figure 2. The choice of the specific way this interpolation is implemented depends, as we mentioned earlier, on the properties that have to be preserved in the CG region.
Irrespective of the chosen method to interface the two regions of the system, however, it is natural to expect that the equilibrium state that will be reached in the absence of external driving forces will not be the desired one. A further crucial point is then to find the simplest way to impose the desired thermodynamics.
The central, strong requirement that has to be satisfied is that molecules should be free to diffuse from any region of the simulation box to any other. Additionally, in a hybrid resolution model thermal equilibrium should be preserved, i.e., the temperature of the system has to be constant during the simulation. Another possible constraint is to impose a uniform density across the box, irrespective of the specific resolution; nonetheless, we’ll see that there are cases where this is neither strictly necessary nor desirable.
These are the fundamental constraints that can be imposed on the system as a whole. Other, more specific ones can be introduced on the properties of the CG region as well as the transition region, which will “drive” us towards a specific formulation of a double-resolution simulation method.
3.1. The Adaptive Resolution Simulation Scheme
The Adaptive Resolution Scheme (AdResS) represents the first effective and computationally efficient method to simulate a system where two different models, e.g., an all-atom one and a coarse-grained one, are simultaneously employed in different subregions of the simulation domain, interfaced in such a way to allow molecules to freely diffuse from one region to the other.
The basic constraint that was enforced in the original version of this scheme is that Newton’s 3rd law has to be exactly satisfied everywhere in the simulation domain. This requirement rules out any form of potential energy interpolation: it can in fact be formally demonstrated [
168] that no method exists to smoothly “blend” the interaction between two molecules from a given potential energy to another without generating forces that cannot be recast in a form that satisfies Newton’s Third Law. In order to preserve the latter, then, a
force-interpolation scheme is required, such that the force that a given molecule receives due to the interaction with a second one is antisymmetric under exchange of the molecules’ labels:
A second, less strict requirement is that CG molecules possess CG degrees of freedom only; this determines the specific way the force mixing is performed: a molecule in the CG region loses completely its atomistic detail (thus retaining, for example, the center of mass coordinates only), and interacts with a molecule in the AA or even the transition region only via its CG degrees of freedom. Formally, this constraint imposes that the atomistic forces vanish when at least one of the two interacting molecules is in the CG domain.
These two constraints are sufficient to define the force-field interpolation; the force acting between molecules α and β is given by:
In
Equation (21) λ(
x) is any smooth function that goes from 1 in the AA region to 0 in the CG region.
Rα (resp.
Rβ) is the CoM coordinate of molecule
α (resp.
β).
and
are, respectively, the atomistic and the coarse-grained forces acting on molecule
α due to the interaction with molecule
β.
The CG force is computed between the coarse grained centers of the molecules and then redistributed to the atoms weighted by the ratio of the atom’s mass to the mass of molecule [
169]; in the transition region this operation is required by the fact that molecules interact at both the AA and the CG level. AA degrees of freedom thus
have to be explicitly integrated, at least into the hybrid region. In the CG region, on the other hand, it is in principle not necessary to conserve the atomistic detail of the molecules, so that the CG force could be applied directly to the CoM coordinate; a molecule’s internal structure can thus be removed when it enters the CG region, and reintroduced (e.g., taking it from a reservoir/repertoire of equilibrated atomistic molecules) as soon as it approaches the hybrid region. In all AdResS versions implemented so far, though, the atomistic DoFs are retained for simplicity of implementation [
24]; the CoM of the molecule is nonetheless decoupled from the internal atomistic structure, and it evolves only subject to the CG force.
It was previously mentioned that no energy interpolation is possible, that is compatible with the requirement of having Newton’s 3rd law preserved everywhere in the system [
168]; as a consequence, a force interpolation had to be chosen. It is evident, then, that the AdResS scheme cannot be formulated in terms of a Hamiltonian, thus making it impossible to perform microcanonical,
i.e., energy-conserving simulations. The force-field used in this adaptive resolution simulation framework is not conservative in the transition region, and when crossing it a molecule receives a surplus of energy that has to be removed in order to prevent the system from artificially heating up. This excess energy can be removed with a
local thermostat, such as Langevin thermostat: in this way, the temperature of the system is kept constant everywhere. The equilibrium state of the system is then
dynamical: the thermostat takes care of absorbing the extra heat produced in the transition region by non-conservative forces, and the system samples equilibrium configurations according to Boltzmann’s distribution [
24–
32].
The pressure difference between an AA system and a low-resolution model typically resulting from coarse graining procedures determines the onset of a non-uniform density profile. For example, a one-site CG model of water obtained with IBI can have a pressure ~6000 times the atomistic reference value [
117]. Therefore, the densities in the two subregions will change in order to equate the pressures. A possible solution to this density imbalance is to parametrize the CG potential to the target pressure. In the IBI framework this can be achieved by introducing a “pressure correction” [
81]. This approach can provide a CG potential that has the target pressure, but this would also result in a modified compressibility [
117].
Another option to preserve a uniform density across the simulation domain without modifying the CG potential is to introduce an external force which counterbalances the high pressure of the CG model. This
thermodynamic force can be obtained with an iterative procedure via the following expression [
169–
171]:
where ρ* is the reference molecular density, κT is the system’s isothermal compressibility and ρi(r) is the molecular density profile as a function of the position in the direction perpendicular to the CG-AA interface. The thermodynamic force is initialized to zero,
, while the initial density profile is the one calculated from an AdResS simulation with fth = 0. As can be easily seen, the iterative procedure converges once the density profile is flat (∇ρ(r) = 0).
This approach guarantees a flat density profile without having to modify the CG potential: because of its very definition, the thermodynamic force only acts on those molecules that cross the hybrid region, leaving the others unaffected. It can also be shown [
24,
169] that the integral of the thermodynamic force across the interface,
i.e., the work due to this force performed by a molecule while crossing the hybrid region, is proportional to the local pressure profile, the proportionality factor being the reference density
ρ*.
In summary, the thermodynamic force allows us to couple a system at atomistic resolution to a coarse-grained counterpart whose pressure, for given values of density and temperature, is significantly different. The global properties of the force, whose direct effect is restricted to the hybrid region, only depend on the pressure difference between the two coupled subsystems; the detailed profile of the force, on the other hand, can be obtained via a system-specific iterative procedure. This method not only allows one to preserve the desired structure of the system in the CG region; in principle, in fact, an arbitrary CG force-field, with pressure
and structure completely different from the target atomistic ones, can be used. Consequently, the AA region behaves as an open system [
169] that exchanges energy and molecules with a reservoir: the molecule number fluctuations, the pressure and all other thermodynamically relevant quantities are the same as if the AA region were simply ‘cut’ from a large all-atom simulations. It is relevant to stress here that because of the thermodynamic force this condition can be established
irrespective of the specific model used in the CG region.
3.2. Applications
The possibility of treating a system with a reduced number of degrees of freedom except where it is strictly necessary was explored, making use of the AdResS method, in several applications [
24–
30,
172]. From the numerical/computational point of view it clearly represents an advantage, since a much smaller number of force calculations are required in the coarse-grained region: this is particularly true for parallel MD codes such as GROMACS [
173], where a dynamical decomposition of the simulation box allows one to subdivide the box with a finer grid in the AA and hybrid region, while a smaller number of processors is assigned to the CG region. For example, for a water system with an AA region covering 1
/6 of the total simulation box, simulated with GROMACS on a 16-cores processor, the speed-up is about a factor three. This factor is nonetheless small compared to what can be achieved with other simulation packages, such as ESPRESSO++ [
174]: in fact, water simulation in GROMACS is extremely optimized, and any hacking of the standard code can introduce a bottleneck.
A major strength of the AdResS method is the fact that it introduces a decoupling between a given region of the system and the rest while keeping the thermodynamic properties of both regions under control: as a consequence, it is possible to conceive numerical experiments in which the spatial extension of correlations in the system is investigated. More specifically, one can study the structural properties of the high-resolution region as a function of its size, in order to determine their dependency on the interaction with molecules in the bulk region. This kind of experiments is different from the study of finite-size effects: in the latter, in fact, the system has the same resolution and interaction type everywhere, and the change of a property with the box size depends on the asymptotic approach to the thermodynamic limit. In the AdResS setup, on the other hand, finite-size effect can be neglected for sufficiently large boxes, thus allowing one to characterize the response of the system’s properties in a small subregion when atomistic interactions with the bulk are switched off, but the thermodynamics is the same as in a fully-atomistic simulation. An example of this applications is provided by the work in Reference [
175]: here a molecule with both hydrophilic and hydrophobic interactions was solvated in water and put at the center of the high-resolution region, while the water molecules far from the surface were treated at the coarse-grained level. The ordering degree of the hydrogen bond network on the molecule’s surface was measured as a function of the size of the all-atom region: the results showed a dependency of the ordering for water molecules close to the surface of the repulsive solute, while no relevant effect was observed for the attractive case.
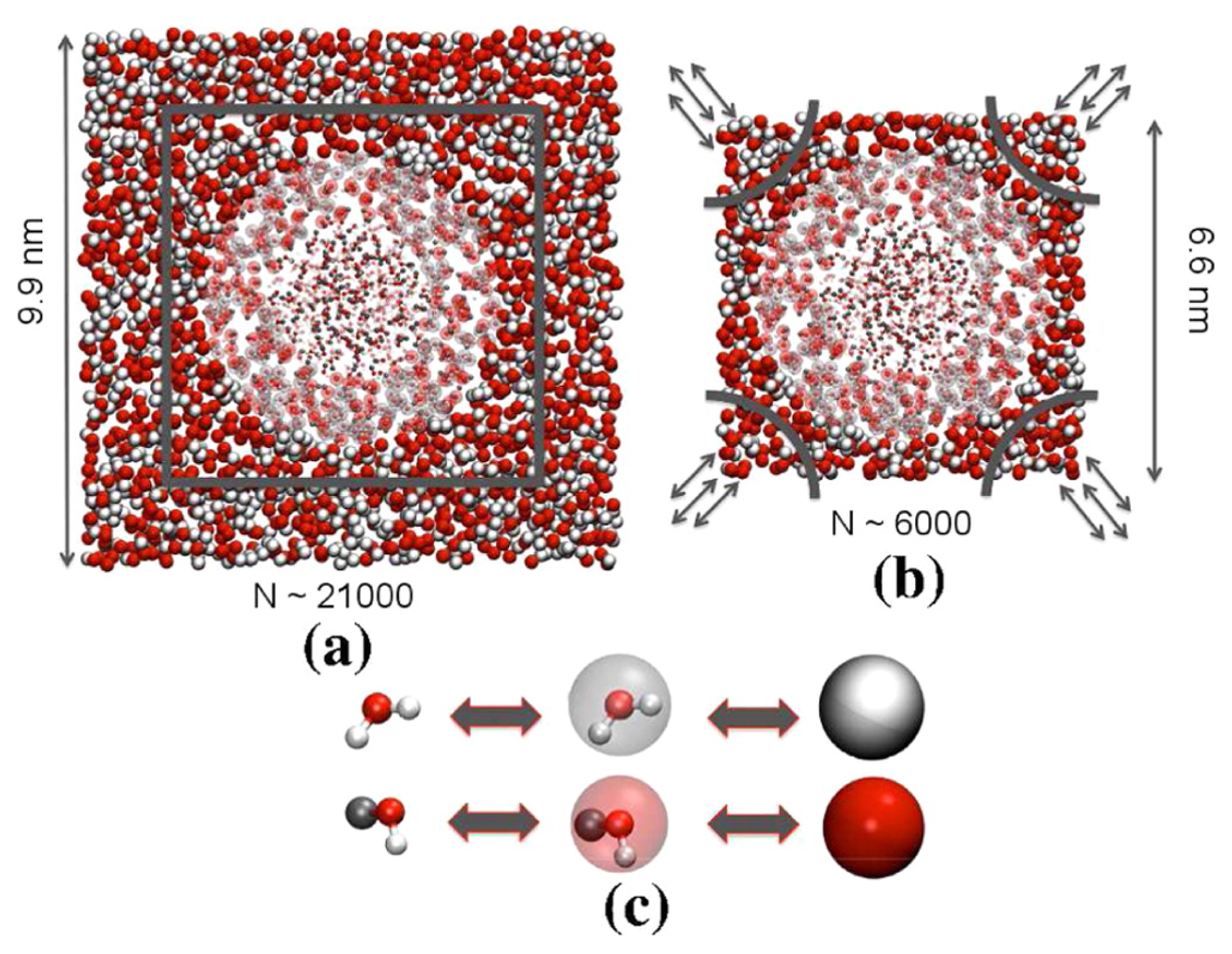
The same strategy has been applied to investigate the extent of spatial correlations in a quantum fluid, namely low-temperature para-hydrogen [
30,
176]. The latter is the spin-zero singlet state of molecular hydrogen. Because of the spherical symmetry of the global wave function, para-hydrogen in the solid and gas phase can be modeled as a classical, point-like particle interacting via a simple radial potential, such as Lennard-Jones or the more accurate Silvera-Goldman potential [
177,
178]. The same classical potential has been shown to correctly reproduce the experimental results both in the solid and the gas phase [
178]. In the fluid phase, however, nuclear delocalization effects become important, and a quantum mechanical treatment of the problem is necessary. This can be achieved through the path integral formalism [
179,
180], which allows for the explicit inclusion of nuclear quantum effects in a “classical” description; unfortunately, this also implies a significant increase in the number of degrees of freedom that have to be simulated, since each molecule becomes a collection of
P beads connected by springs. The possibility to simulate a quantum system in a classical framework such as classical MD makes it possible to couple quantum a classical descriptions with the AdResS scheme. In particular, a low-temperature para-hydrogen system was simulated making use of the explicit path integral representation only in a small spherical subregion of the domain, while the molecules in the outer region were treated at the purely classical level,
i.e., point-like particles interacting through a coarse-grained potential [
30]; in
Figure 3 a snapshot of the simulated system is provided. This study showed that a few molecules in a small (~0.6 nm radius) region of the system are sufficient to reproduce the quantum pair correlation function obtained from a full path integral simulation, but treating the molecules in the outer region at the CG level; this result opens the way to simulate large systems of low-temperature para-hydrogen taking advantage of a double resolution without disrupting the thermodynamical and structural properties of the small, purely quantum region, thus saving computational time in the CG region.
More recently the AdResS scheme has been successfully employed to perform simulations of biologically relevant systems such as methanol-water mixtures [
181] and triglycine in aqueous urea [
171], and to study the coil-globule transition of a PNIPAm molecule in aqueous methanol [
182]. In all these cases a crucial necessity is to correctly reproduce the solvation free energies of the system, a condition that is verified only when the particle number fluctuations are compatible with those observed in the Grand Canonical ensemble. The large system sizes necessary to fulfill this requirement in a standard, all atom simulation often make the latter unfeasible; the employment of dual-resolution simulation methods, possibly coupled to a Monte Carlo scheme [
182] to enforce fluctuations in the total number of molecules, see
Figure 4, allows one to keep the computational cost low and obtain results that would otherwise require a significantly longer time.
3.4. The Hamiltonian Adaptive Resolution Scheme
As was discussed in the previous section, the force-based AdResS method was developed on the basis of a central requirement, namely that Newton’s 3rd law has to be exactly satisfied everywhere. A consequence of this constraint is that no Hamiltonian formulation is possible [
168]: if a position-dependent interpolation of the potential energies is done, in fact, the resulting forces include a term proportional to the derivatives of the switching function
λ that cannot be recast in a form that satisfies Newton’s Third Law. The only method developed in the past that allows one to explicitly conserve the energy in an adaptive resolution simulation is that proposed by Heyden and Truhlar, [
184,
185], where a sum of the Lagrangians of all possible groupings of atomistic and coarse-grained molecules is done. Due to its combinatoric nature, this approach is extremely difficult to implement efficiently; moreover, the resulting Lagrangian includes a position-dependent kinetic energy term for which a specific, non-symplectic integrator is required.
In the H-AdResS method [
33], which we now describe, the aforementioned constraints are relaxed in order to develop an energy-based, Hamiltonian adaptive resolution simulation scheme. As will be clear in a few lines, the particular choice of energy “mixing” gives rise to forces that do not comply with the first constraint; nevertheless, the physical interpretation of these terms is immediate and naturally points towards the solution -though approximate- of the Newton’s Third Law breakdown.
The core idea of the energy-based approach is to weight the total energy of each molecule with a position-dependent function:
where
![Entropy 16 04199f13]()
is the (all-atom) kinetic energy of the molecules,
Vint is the interaction internal to the molecules, and:
The switching function
λ goes from 0 (purely CG) to 1 (purely AA). The force acting on atom
i in molecule
α is obtained through differentiation of the Hamiltonian in
Equation (23):
The forces
and
are defined as:
The redistribution of the CG force on the atomistic degrees of freedom follows the same rules as applied in the case of the force-based AdResS method. It’s worth noting that in this energy-based scheme the atomistic degrees of freedom are retained and integrated everywhere in the system, a necessary requirement in order to perform a microcanonical simulation making use of a Hamiltonian.
We now detail the various components of the force,
Equation (24). The first term,
is due to the interactions
internal to the molecule; as such, it automatically satisfies Newton’s Third Law. The second term is a sum of pairwise forces obtained from all-atom and coarse-grained Hamiltonians, weighted by a function that is symmetric under molecule label exchange, that is
α ↔
β; this force also complies with Newton’s Law. Up to this point we modified only one aspect of the original AdResS scheme, that is, the force weights are not given by the product of the two molecules’ switching function, rather by the average; consequently, the molecules in the coarse-grained region are also allowed to interact through their atomistic degrees of freedom.
The third term of the forces in
Equation (24) is the part that breaks down Newton’s Third Law: in fact, it cannot be written as a sum of terms antisymmetric under molecule label exchange. This force, which is nonzero
only in the hybrid region, is proportional to the difference between the potential energies of a given molecule in the AA and the CG representation; if a systematic difference exists between the AA and the CG potentials, the effect of this term is to push molecules into one of the two bulk regions. The hybrid region thus behaves as an
active membrane, inducing a density imbalance and a non-flat pressure profile. One is then naturally led to ask how strong is the drift term
; if it is negligible in some cases; which these cases are; and if there is a general way at least to minimize its effect without giving up the Hamiltonian character of these forces. We shall now address these questions.
The optimal case in which this term is minimized is when the CG potential perfectly reproduces the many-body PMF. If this is true, in fact, the drift term vanishes on average:
This can be numerically verified with a simple toy model, for which a pairwise CG potential represents an excellent approximation to the PMF. Such a model is provided by a low-density fluid of purely repulsive tetrahedral molecules [
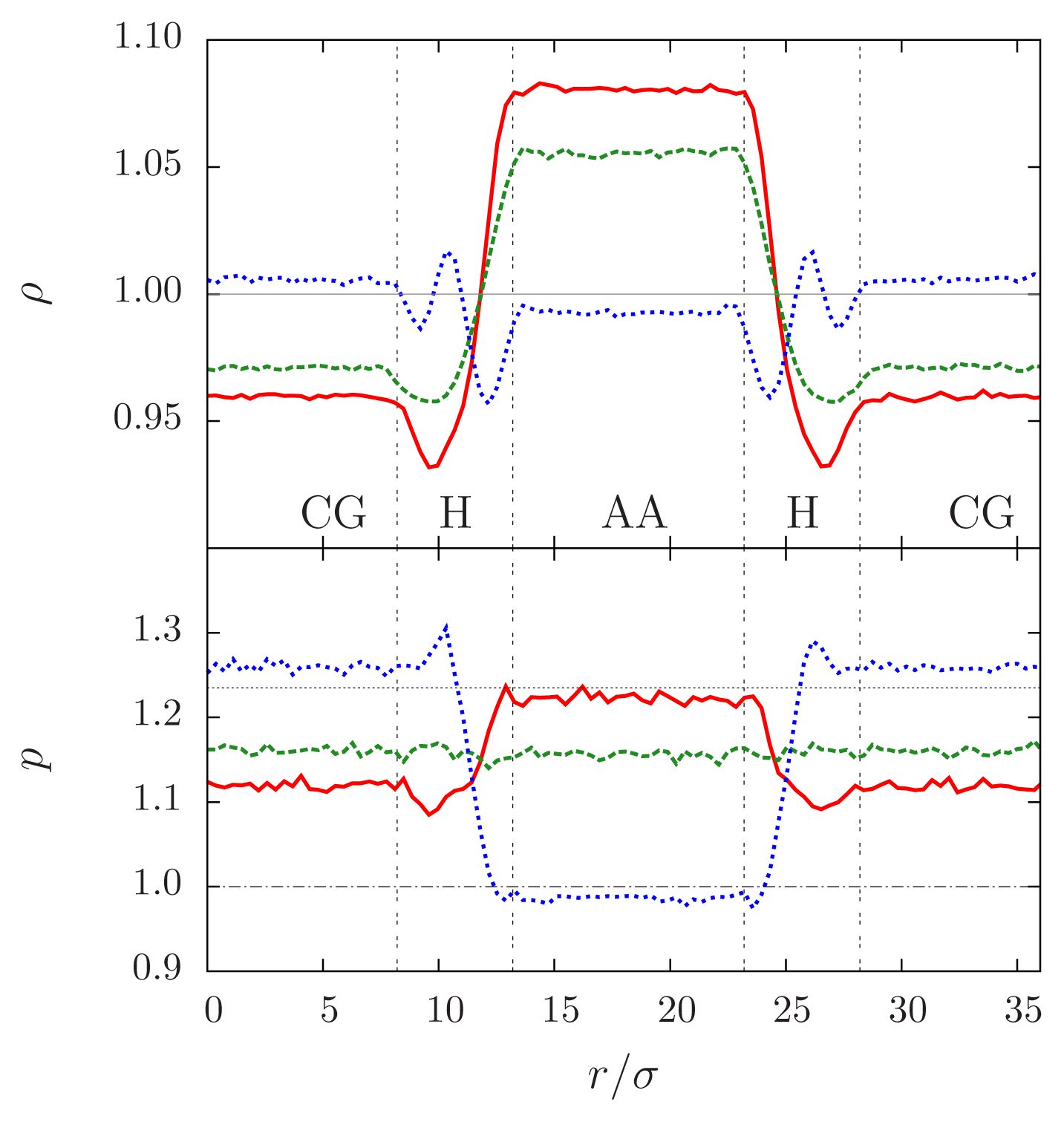
24], whose CG potential has been obtained from IBI. This model was used in an energy-conserving H-AdResS simulation, and the resulting density profile is plotted in
Figure 5. The molecular density attains the same value in both the AA and CG regions; in the hybrid region a small depletion is present, because the free energy of the mixed potential is different from the free energy of the “pure” (
i.e., purely AA or purely CG) potentials. The same behavior has been systematically observed in AdResS simulations [
24].
Needless to say, this particular case is very fortunate: as we discussed in the previous sections, the CG potentials almost never reproduce the many-body potential of mean force [
117,
186]. The difference between an atomistic model and its coarse-grained representation therefore results in a thermodynamic imbalance, that is, both pressure and density of the two bulk (AA and CG) regions are different [
13]. The solution to this problem is again to introduce a compensation term in the Hamiltonian, as was done in the AdResS scheme with the thermodynamic force. More specifically, we modify the Hamiltonian as follows:
where ΔH(λ) is a function to be defined. It’s worth noting that this term preserves the conservative nature of the Hamiltonian.
In order to determine the specific form of ΔH we impose that the drift force cancels on average:
or equivalently:
where the subscript in the average indicates that the latter has to be performed constraining the CG site of molecule α in the position Rα.
In principle,
Equation (28) provides us with the way to compute the compensating function—or, more precisely, its derivative; nonetheless, an approximation to Δ
H might be sufficient. A way to do this is the following:
where λ′ ≡ λ(Rα) is the same for all molecules. The approximate function ΔH is obtained by integration:
Most interestingly, we see from
Equation (30) that the compensation needed to cancel
is related to the
Helmholtz free energy difference between AA and CG system [
187]. Therefore, it is possible to calculate the compensating function needed to restore, on average, Newton’s Third Law by performing a Kirkwood thermodynamic integration.
The “Helmholtz free energy compensation” thus cancels the active effect of the hybrid region, restoring a flat pressure profile. Nonetheless, coarse-grained models have, in general, a substantially different pressure with respect to their atomistic reference [
117], thus inducing a further density imbalance (usually larger than the one due to the different Helmholtz free energy). In order to restore a flat density profile a second term has then to be added to the compensating function, that counterbalances the pressure difference.
The right way to introduce the pressure into the compensating function is to balance, rather than Helmholtz free energy, the Gibbs free energy difference per particle, that is, the chemical potential Δμ = ΔG/N:
Figure 6 shows the density and pressure profiles for the three possible cases we discussed: the previously mentioned system of tetrahedral molecules was coupled to a coarse-grained fluid of purely repulsive point-like molecules; the pressure of this fluid has a larger pressure then the reference all-atom one for the same temperature and density. In the plot, the red lines correspond to the case in which no free energy compensation is introduced: the density is higher in the AA region, due to the molecules in the CG region that “push” with a higher pressure. The profile of the pressure is also not flat: the Helmholtz free energy of two systems differs, therefore an active force exists in the hybrid region. When the Helmholtz free energy compensation is applied we have the situation shown by the green lines: the density is still higher in the AA region, but the pressure profile is now flat: the forces that break Newton’s Third Law in the hybrid region are cancelled on average, and the density imbalance decreases. Finally, when the Gibbs free energy compensation is applied the densities of the AA and CG regions attain the same value, but for a small deviation due to the fluctuations present in the hybrid region (that the compensation function Δ
H, computed in a homogeneous system, cannot remove). The pressure, on the other hand, is different: in fact, in each region it reaches the value that corresponds to the reference state of density and temperature. Analogous results are obtained in a thermostatted simulation of a water box, as shown in
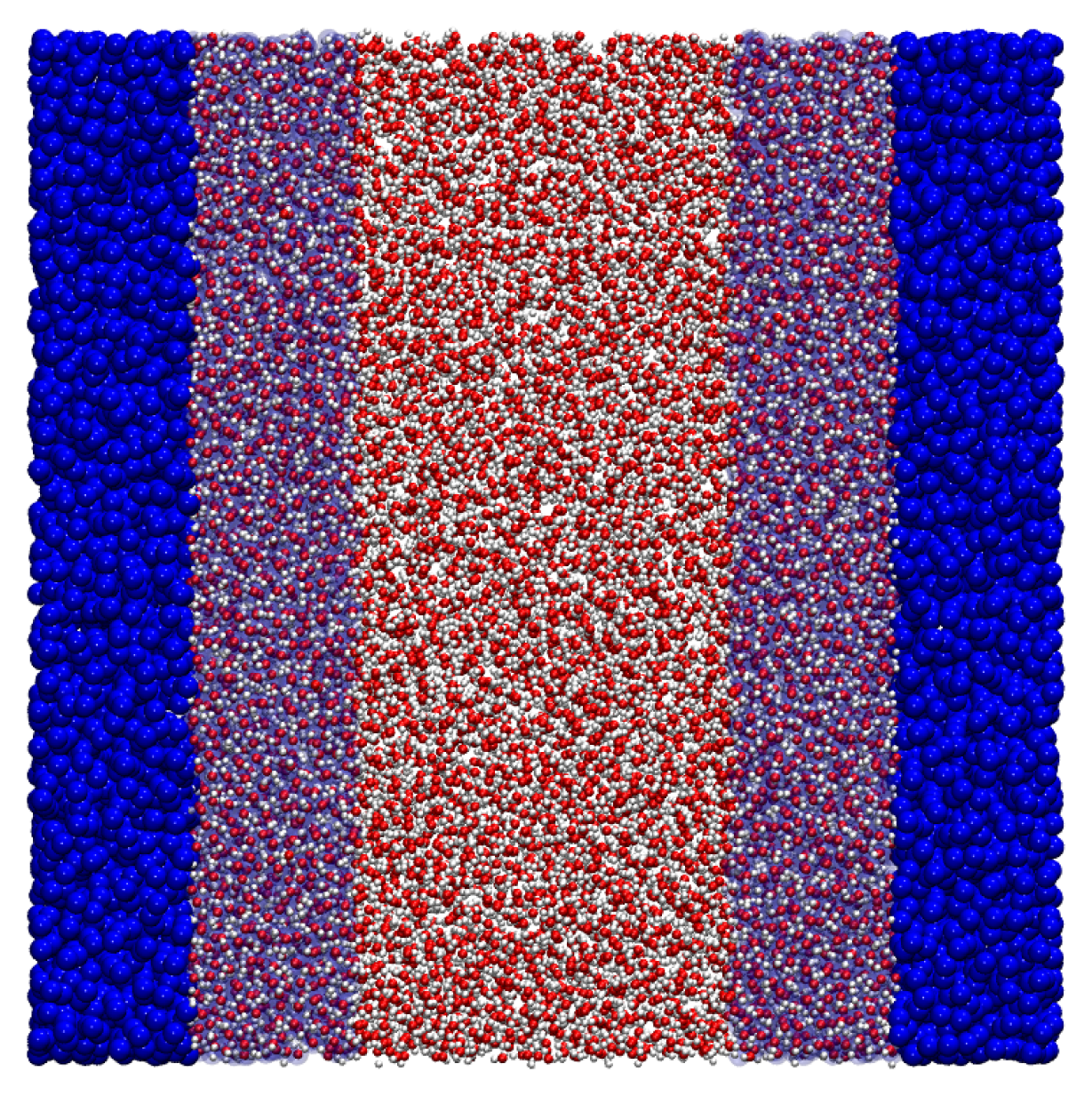
Figure 7: here the system is composed of a slab of water molecules described at atomistic resolution, coupled to a CG bulk where particles interact via a purely repulsive WCA potential. As in the previous case, the CG interaction was parametrized to induce an increase of the density in the atomistic region, as can be seen in
Figure 8 (upper panel). The Free Energy Compensation restores the correct density profile, and guarantees that in the AA region the pairwise correlations,
i.e., the radial distribution functions, are the same that one would measure in a fully atomistic simulation, as shown in
Figure 8 (bottom panel). We notice that Gibbs free energy compensation, even though it equates the densities in the bulk regions, is not sufficient to remove small fluctuations (of the order of ~3%) in the hybrid region: these deviations from the reference value are due to the fact that the compensation Δ
H is computed in a homogeneous system, where all molecules have the same value of λ—that is, a regular Kirkwood thermodynamic integration Hamiltonian. The molecules in the hybrid region, on the other hand, interact with other molecules having different λ values. The resulting fluctuations are expected to decrease with increasing size of the hybrid region, in which case the environment of a given molecule approaches the condition of homogeneous λ. Another strategy to flatten the density profile is clearly provided by the iterative approach of the thermodynamic force (
Equation (22)), a few iterations of which would be sufficient to modify the Δ
H function by the small amount necessary to remove the fluctuations.
The Free Energy Compensation (FEC) strategy, defined by
Equation (26), can be extended to multi-component systems. To illustrate this idea we consider a molecular liquid composed by two types of molecules,
A and
B, indexed with
a and
b, respectively. The corresponding H-AdResS Hamiltonian for this system reads:
with λa = λ(Ra) and λb = λ(Rb). The intermolecular potential energy terms are given by the following expressions:
where V [XY ] is the non-bonded interaction between a molecule of type X and a molecule of type Y, with X, Y = A, B, and the indices i, j labeling the atoms.
In analogy with one-component systems we introduce a FEC term for each species to compensate for the free energy difference between the AA and the CG regions:
An Ansatz for the compensation term of a given species k = a, b can be obtained from TI as follows:
where the
Nk,
and
pk are, respectively, the number of molecules, the reference partial density and the partial virial pressure of species
k. We stress that all the quantities in
Equation (34) can be computed in a single TI of the mixture from AA to CG at the concentration of interest, irrespective of the number of species. All the cross-interactions between different types of molecules are automatically included in the free energy contribution of each species. Additionally, the Free Energy Compensation Δ
Hk(
λ) is an
intensive quantity and does not depend on the specific geometry of the H-AdResS setup. It is therefore possible to perform the TI in a relatively small system, provided that it is statistically representative,
i.e., finite size effects are negligible.
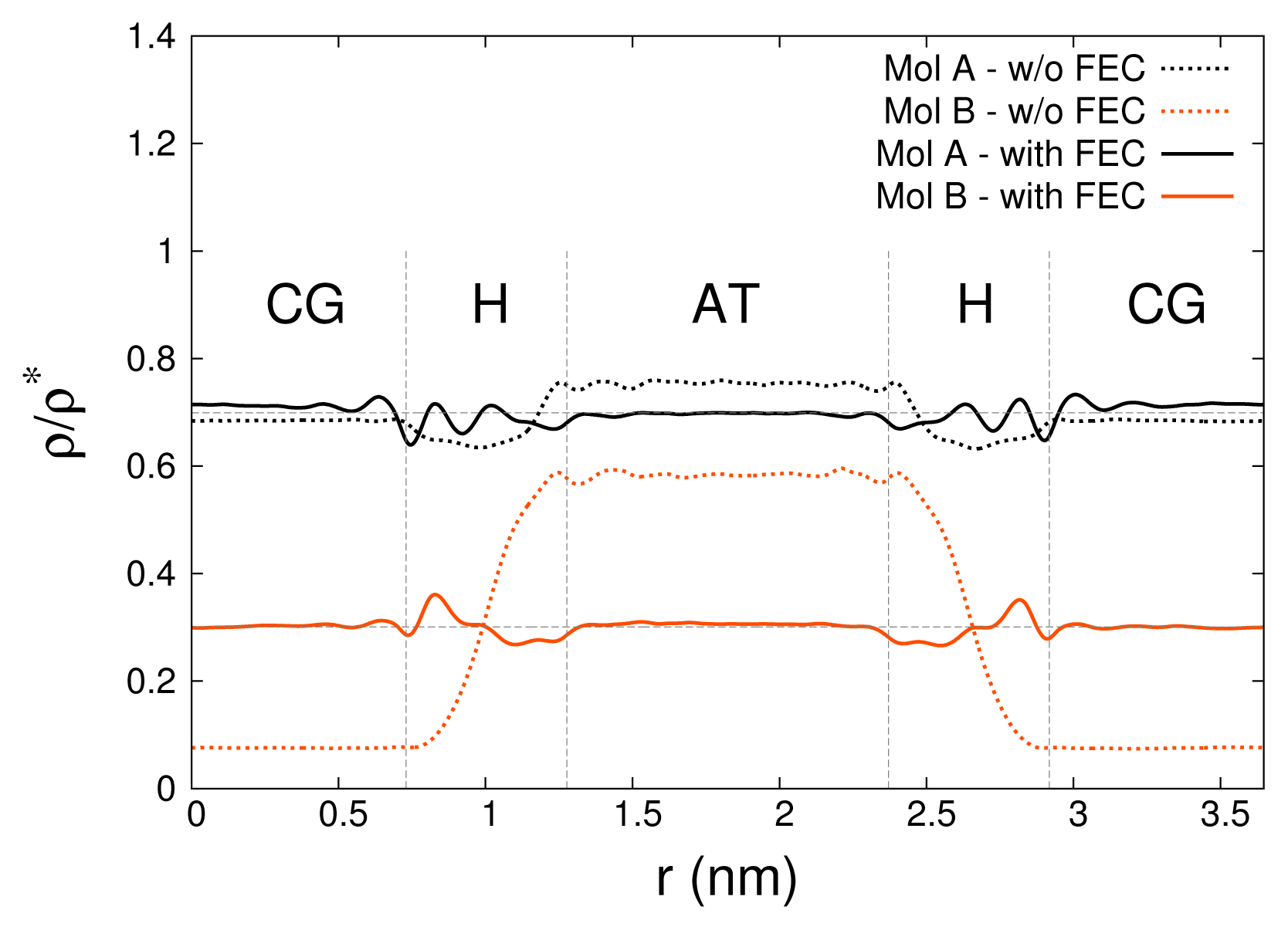
The effectiveness of this strategy has been proven by the Monte Carlo simulations of binary mixtures performed in Reference [
34]. Here we report one of these simulations, specifically the mixture of 70% A-type molecules and 30% B-type molecules, both made of four identical atoms; the A–A and B–B interactions are identical WCA potentials, while the A–B interaction is a Lennard-Jones potential. In the CG region both molecules are represented as spherical particles with identical, purely repulsive WCA A–A, B–B and A–B interactions, resulting in a particularly large thermodynamic mismatch between AA and CG domains. This can be directly observed in the snapshot of the simulation reported in
Figure 9 (top) as well as in the density profiles (dotted lines in
Figure 10): the chemical potential imbalance between the two resolutions leads to a large accumulation of B-molecules in the AA zone. As a consequence, neither the total density nor the relative concentrations in the AA zone obtained using the uncompensated adaptive resolution Hamiltonian in
Equation (31) correspond to the reference atomistic system.
According to
Equation (34), a thermodynamic integration was performed to determine the thermodynamic mismatch between the AA and the CG zone. The Helmholtz and Gibbs free energy differences per molecule between the CG and AA models as a function of the coupling parameter
λ, computed for both species
simultaneously in a single TI, are shown in
Figure 11. In spite of the same interaction between molecules of the same type (
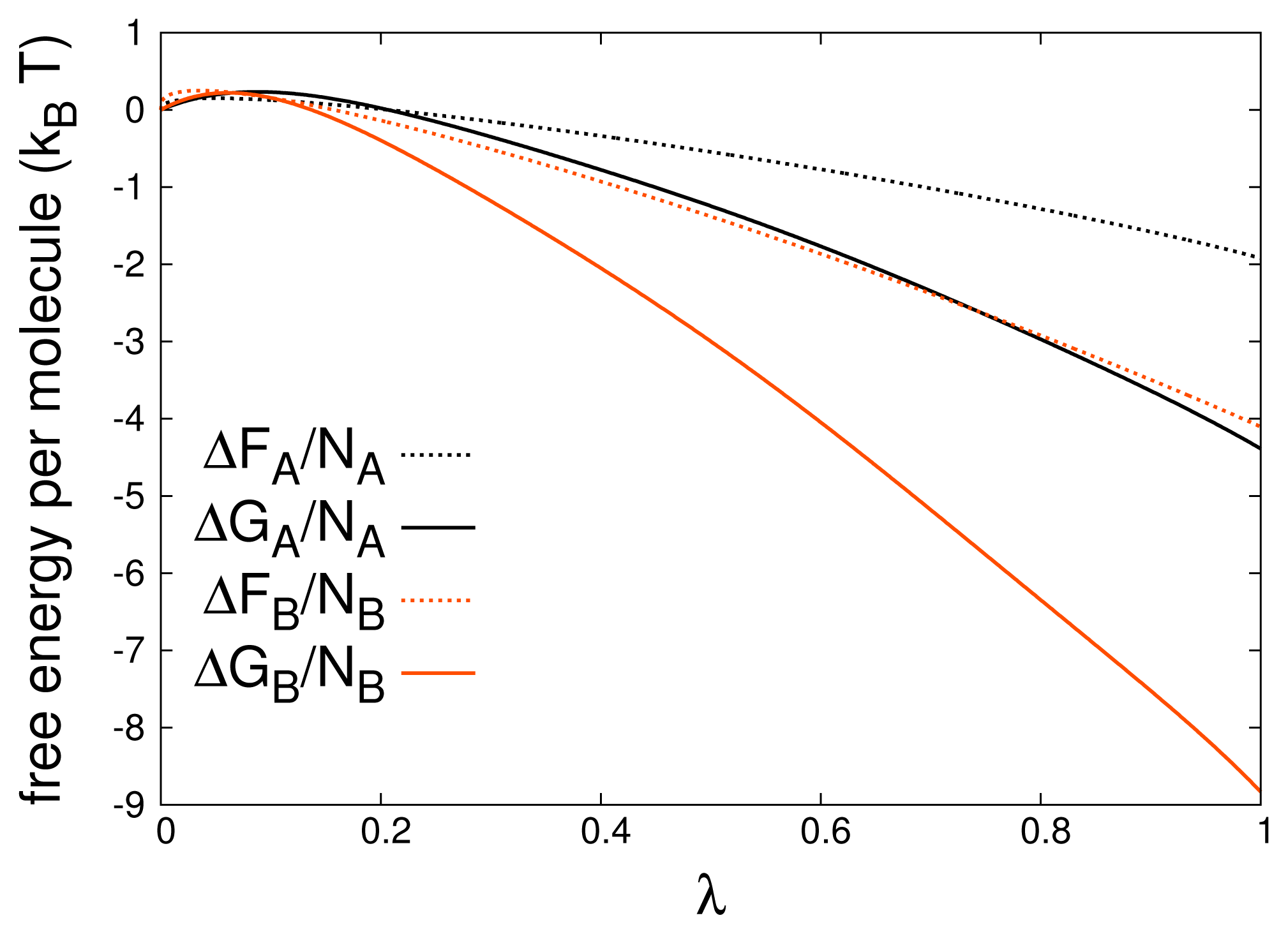
V [
AA] ≡
V [
BB]), the uneven relative concentration of the two species determines a much larger free energy difference between the AA and CG models for the B-type. In fact, the latter shows a Gibbs free energy difference per particle |Δ
GB/NB|> 2 |Δ
GA/NA|. This is mainly due to the fact that the interaction between A and B types is attractive only in the AA representation, thus determining a lower chemical potential for the minority type (B) in the AA region. In addition, in both cases the sign of Δ
G favors the densification of particles in the AA region, as can be seen in
Figure 10. To counterbalance the mismatch in chemical potentials a FEC was introduced in the H-AdResS Hamiltonian according to
Equation (33), using the free energy functions shown in
Figure 11. The resulting density profiles (solid lines in
Figure 10) demonstrate the success of the procedure.
In this section we discussed the H-AdResS method, which allows for a seamless coupling of two models of the same system with different resolution within a Hamiltonian framework. In order to define an energy-based mixing rule for the two models, the requirement to preserve Newton’s Third Law everywhere in the system had to be relaxed. Nonetheless, the “undesired” term that appears in the forces due to the differentiation of the switching function λ is non-zero only in the hybrid region, and its particular form naturally indicates how to introduce, in a physically sound manner, a compensation function that cancels the average effect of the drift force without disrupting the Hamiltonian character of the model. The computational cost of the H-AdResS simulations is comparable to that of the AdResS method, the only difference being the need to calculate the drift force
in the hybrid region: nonetheless, the number of molecules that are affected by this force is typically small (both the AA and the CG regions are expected to be much larger than the hybrid region), and the quantities involved, namely interaction energies and molecules’ CoM coordinates, are normally computed in a MD simulation.
In spite of its simple formulation and relatively small difference with respect to the force-based method, H-AdResS represents a major step forward in terms of understanding and practical advantages. In fact, the existence of a Hamiltonian allows one to precisely formulate a statistical physics theory of double-resolution systems, providing a deep insight into the properties of a given all-atom model, its coarse-grained counterpart and the relation between them. In particular, the free energy compensations provide a simple and effective way to modulate the thermodynamic balance of AA and CG regions, thus leaving to the user the choice of the environment for the AA region most appropriate for the specific problem under examination. Last but not least, this scheme broadens the spectrum of physical ensembles that can be simulated to the microcanonical ensemble, and allows the use use of simulations techniques—e.g., Monte Carlo—that were not accessible in the force-based AdResS framework, with the a priori guarantee that real equilibrium configurations are sampled.
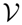 . It is therefore advantageous to write the probability to sample a given atomistic configuration in the CG system in terms of the function that maps the fine-grained configurations onto the coarse-grained ones:
. It is therefore advantageous to write the probability to sample a given atomistic configuration in the CG system in terms of the function that maps the fine-grained configurations onto the coarse-grained ones: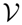 in the low-resolution system and Ω(
in the low-resolution system and Ω(
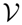 ) = ∑ν δ(M(ν) −
) = ∑ν δ(M(ν) −
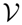 ) is a measure of the degeneracy of the configuration
) is a measure of the degeneracy of the configuration
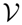 in the atomistic system. It should be noted that this last quantity depends only on the mapping function M and not on the coarse-grained interactions; this term can therefore be separated out in the definition of the relative entropy to obtain:
in the atomistic system. It should be noted that this last quantity depends only on the mapping function M and not on the coarse-grained interactions; this term can therefore be separated out in the definition of the relative entropy to obtain: is the (all-atom) kinetic energy of the molecules, Vint is the interaction internal to the molecules, and:
is the (all-atom) kinetic energy of the molecules, Vint is the interaction internal to the molecules, and: