Hybrid Quantum-Classical Protocol for Storage and Retrieval of Discrete-Valued Information
Abstract
: In this paper we present a hybrid (i.e., quantum-classical) adaptive protocol for the storage and retrieval of discrete-valued information. The purpose of this paper is to introduce a procedure that exhibits how to store and retrieve unanticipated information values by using a quantum property, that of using different vector space bases for preparation and measurement of quantum states. This simple idea leads to an interesting old wish in Artificial Intelligence: the development of computer systems that can incorporate new knowledge on a real-time basis just by hardware manipulation.1. Introduction
Theoretical computer science is a branch of modern mathematics that, in its canonical form, does not take into account the physical properties of those devices used for information processing. This characteristic could be perceived as a drawback because the behavior of any physical device used for computation must ultimately be predicted by the laws of physics. Consequently, several research approaches have concentrated on thinking of computation in a physical context (e.g., [1–11]), being the rationale behind this approach that the concepts of information and computation can and must be built upon physical principles. Quantum computation, one of the most recent joint ventures between physics and computer science, is a promising branch of science and technology devoted to the development of algorithms and experimental devices that allow us to exploit the quantum effects of physical systems, in order to perform simulations and calculations. Quantum computing promises great advances in the solution of some problems for which we know no efficient algorithms under the classical computer models and systems we currently have (e.g., [12–16].)
Among the theoretical discoveries and promising conjectures that have positioned quantum computation as a key element in modern science, we find: (1) the development of novel and powerful methods of computation that may allow us to significantly increase our processing power for solving certain hard problems [12–15,17–23]; (2) the simulation of complex physical systems [5,24,25]; and (3) an increased interest of several applied scientific communities to cross-fertilize their own fields with techniques and ideas from this discipline (e.g., image processing and computational geometry [26–36], pattern recognition [37–40], quantum games [41], and warfare [42]). A detailed summary of scientific and technological applications of quantum computers can be found in [43,44].
The use of vector spaces for the description of quantum systems is a departure point to understand the power of quantum computation and quantum information [12,45]. We have become interested in studying how to use the representation of vectors in several bases together with the projection of such vectors into disjoint subspaces for information processing purposes. In physical terms, we want to analyze how information can be stored and extracted by using several vector bases for multiple qubit state preparation and measurement. Our motivation comes from the following statements:
- (1)
The preparation and measurement of quantum states are essential activities in quantum information processing. In this context, quantum state preparation depends on the characteristics of the information we want to store. Information retrieval from quantum states depends on what we want to learn from the quantum system, i.e., which physical properties of the quantum states used to store information we are prepared to measure.
- (2)
The potential use of quantum mechanical systems in disciplines like machine learning and artificial intelligence is an exciting research field with open opportunities for scientists, engineers and society at large (an example of the flourish of this emergent blend of physics and computation can be found in [46].) In those two disciplines, the priority and importance of certain pieces of information is largely related to the context such pieces are released into. Also, it is usually the case in machine learning and artificial intelligence that new and unanticipated information values have to be processed. Examples of concrete problems in which processing unanticipated data is relevant are:
Natural language processing. Languages are living and vibrant entities. The cultural heritage of human language allows us not only to accurately describe our past and the world we live in, but also to create words in order to draft descriptions of new realities. Those new realities are highly diverse and depend on many factors. For example, slang used in a rough area in Mexico City makes little sense in terms of the formal use of the Spanish language; however, this slang makes perfect sense when analyzed in terms of creativity, local state of affairs, and the problems and challenges people from that area live on a daily basis.
A key challenge for natural language processing is to make computers able to understand both formal and vernacular uses of human language. Vernacular language is very difficult to tackle because it is usually ambiguous and also because new words are frequently created on-the-go, i.e., just a spontaneous result of human creativity [47]. In order to make computers capable of processing vernacular expressions, we need to be able to store (and process, later on) new information and its context.
Robotics. Robot navigation in arbitrary environments. Robots are very useful machines when working on either dangerous activities or boring chores. In many dangerous situations, like exploring an explosive environment, identifying humans in natural disasters or performing specific activities in unstable nuclear sites, robots must be able to adapt themselves to the environment they are immersed into if they are to remain useful. In other words, robots must be able to learn quickly and, to do so, they need information storage hardware and software capable of incorporating new data into their information processing system.
A concrete example would be to identify survivors trapped in collapsed buildings after an earthquake. In this situation, a robot needs to quickly learn many new situations. In this case, a system capable of incorporating unanticipated data would be useful to rescue trapped humans [48].
Finance. Understanding the behavior and the nature of financial markets, like the stock market, remains a challenging task for contemporary scientists, mathematicians and engineers. In fact, our understanding of most complex systems is rather limited due to the lack of consistent and comprehensive mathematical models. Moreover, computer simulators of financial systems need to be constantly improved as new correlations and causal relationships are found during the analysis of such financial systems.
In all cases, having a protocol that incorporates new information in real time would be beneficial to the users. In addition to our protocol, using techniques and computational devices produced with quantum technology could provide key advantages, like computational speed-up, to researchers working on those areas mentioned above.
The qualitative notion of storing and reading unanticipated information in terms of the context such information belongs to has led us to the development of a hybrid (quantum-classical) adaptive protocol for information storage and retrieval. The protocol is hybrid because we use both quantum and classical computational resources. Moreover, the protocol is adaptive in the sense that it is possible to store and retrieve information values that were not expected by the users of this protocol. We have designed our protocol having in mind a readership composed not only of scientists working on quantum computation and quantum information, but also a wider audience composed of applied computer scientists as well as computer and software engineers interested in learning about new quantum-mechanical tools and strategies that may be useful in their field of expertise. Hence, in this paper we focus on new ways of using quantum systems for computational purposes, not on computational complexity issues.
In the following section we present the hybrid adaptive protocol we have designed, followed by pour conclusions. Moreover, in Appendix A, we present our protocol in practice, i.e., as an example, we run our protocol with concrete data. A full introduction to the mathematical structure of quantum mechanics amenable to computer scientists and computer/software engineers can be found in several sources, among them [12,19,23,49–51].
2. Hybrid Quantum-Classical Protocol
Initially, our protocol is expected to store and retrieve values from a set composed of 2n different input values. Moreover, as unexpected data may reach us, we may need to store and retrieve more input values in real time. Our strategy includes the use of several vector bases to store additional input values in quantum data registers |Φ⟩. Those vector bases consist of rotations of the computational basis of the Hilbert space . We use a classical list L to remember which rotation angles, i.e., which vector bases, have been used.
Let us begin by providing a list of components and corresponding initial conditions for our storage and retrieval algorithms. As a second step, we present two algorithms, one for information storage and another for information retrieval. In the following, we assume that the computer we work with is a hybrid machine, partly classical and partly quantum.
The components and initial conditions of our protocol are:
is an ordered set (e.g., a list) that originally contains 2n different classical data to be stored in our hybrid protocol. The original 2n elements of A are known in advance by protocol users (for example, these data could be some color values used in a digital image processing system.)
As unexpected information becomes available to protocol users, it will be added to A (details to be provided in the storage algorithm that follows.) Please note that the elements of A are ordered in terms of index i, i.e., the actual value of ai is independent from the order provided by index i.
The canonical basis of :
B will be used to build the quantum data registers that will be employed to store the contents of A.R = {θ1, θ2,…, θr} = {θβ|β ∈ {1, 2, 3,…, r}} is a set of allowed rotation angles for basis vectors from B. These angles shall be used to store unanticipated data in our protocol.
Please note that we could either have a predefined list of angles or, alternatively, a dynamically generated list. The choice depends of the technology used to implement our protocol and/or on the preferences of protocol users. Our protocol would be invariant with respect to that choice.
m quantum data registers |Φ⟩γ, where γ ∈ {0, 1,…, m − 1}, being each register of size p and initialized as , i.e.,
A table (i.e., a classical data structure with several fields) L composed of the following fields: [data index (i.e., index i)|angle value|quantum data register (i.e., index γ)]. Initial conditions are: data index runs from 0 to 2n − 1 (i.e., the number of classical data originally stored in A), angle value is 0 (as B suffices to store 2n values) and quantum data register index runs from 0 to 2n − 1.
p ancilla qubits |ζ⟩η, η ∈ {0, 1, 2,…, p − 1}. Ancilla qubits |ζ⟩η will be used as intermediaries to store the binary representation of input values into the quantum data registers.
The following operators (also expressed in matrix form):The Ĉnot operator
Rotation about y axis operator [12]:A decimal to binary converter function F : A → {0, 1}p defined by
where (f0f1 … fp−1)2 = (ai)10We now introduce , the Rotated Ĉnot operator. Let us start by defining the following qudits:
After some calculations, it can be seen that the set Bθ={|100⟩θ,|01⟩θ, |10⟩θ, |11⟩θ} is an orthonormal basis of . Let us now introduce the operator :where |ij⟩θ⟨ij| is shorthand for |ij⟩θθ⟨ij|, i.e., |ij⟩θ⟨ij| = |ij⟩θθ⟨ij|.Let us now define a rotated basis Bθ for Hilbert space using the rotation operator :
After some calculations, it can be seen that behaves as expected for qubits initialized using basis Bθ:
2.1. Information Storage Algorithm
The purpose of this algorithm is to store input values by preparing quantum data registers in one of several possible vector bases. The algorithm allows new and unanticipated input values to be stored in a quantum data register by applying the rotation operator (Equation (4)) to the canonical vector basis B (Equation (1)), for a certain angle value θβ.
For each quantum register composed of p qubits, it can be easily seen that we have 2p fully distinguishable p-qubit states and, therefore, one out of 2p possible data values can be stored in the quantum register, each of those data values with retrieval probability equal to 1. For example, given the computational basis {|0⟩, |1⟩} of a 2-dimensional Hilbert space and a quantum register |Φ⟩ composed of p qubits, then we have 2p fully distinguishable states for |Φ⟩: |000…00⟩,…, |111…11⟩ and, consequently, we can store any value ai from the set . Now, let us suppose that a new and unexpected value, not contained in the original set A, has reached our system and we need to store it in |Φ⟩. Then, by performing a rotation of θβ degrees on the canonical basis, our protocol changes the basis for the Hilbert space in which the p-qubit quantum data register lives and uses the new basis to store the unexpected value. Following the example presented above, a new Hilbert space basis for the quantum register |Φ⟩ could be |+ + + … + +⟩,…, |− − − … − −⟩, where and . The angle θβ is stored in the indexed list L.
2.2. Information Retrieval Algorithm
We now proceed to introduce a method to recover the information that has been stored on quantum data registers |Φ⟩γ.
Information Retrieval Algorithm
- (1)
For a given quantum data register |Φ⟩γ, we find the rotation angle θβ with which information was stored on |Φ⟩γ simply by querying table L using index γ. We then use angle θβ to build a measurement basis of the form:
where that is, is a basis built by rotating the computational basis B (Equation (1)) by angle θβ, recovered from list L.- (2)
Build an observable using the measurement basis
where , for k ∈ {0, 1,…, 2p − 1}- (3)
Perform a measurement on |Φ⟩γ using Ô. Since we are performing a measurement on a fully distinguishable state of the basis , it is always possible to perfectly retrieve any input value ai stored on |Φ⟩γ.
3. Conclusions
Motivated by the potential of incorporating unanticipated data on applied areas of computer science like artificial intelligence and machine learning, we have presented a hybrid (i.e., quantum-classical) adaptive protocol that shows how to store and retrieve unanticipated information values by manipulating the vector space representation of qubits for preparation and measurement of quantum states. In addition to the description of algorithms, in which we have used standard quantum gates together with the Rotated Ĉnot operator (a generalization of the ), we present a concise and detailed example of our protocol in Appendix A.
The information stored in our hybrid protocol is classical, that is, fully distinguishable under quantum state measurement. Consequently, next steps in our research include generalizing our protocol with the purpose of processing quantum states in superposition as well as entangled quantum states.
Acknowledgments
The study is sponsored by the Salman Bin Abdulaziz University via the Deanship for Scientific Research International partnership Programme. Additionally, SVA gratefully acknowledges the support of SNI-CONACyT (SNI number 41594) and Tecnológico de Monterrey. All authors thank the anonymous reviewers of our manuscript for their insightful criticisms which greatly improved our work.
Author Contributions
Abdullah M. Iliyasu and Salvador E. Venegas-Andraca contributed to the conception and design of the study and the discussion of the results. Fei Yan and Ahmed Sayed were involved in the discussion of results. All authors have written, read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
A. The Protocol in practice
Part 1. Storing information
To illustrate how the protocol works, let us start by providing the following initial conditions:
- -
A = {a0, a1, a2, a3} with a0 =2, a1 = 1, a2 = 4, a3 = 3
- -
R = {θ1, θ2, θ3} with
- -
The canonical basis of
- -
m quantum data registers , with m = 8 and p = 4.
- -
Table L = [NIL|NIL|NIL].
- -
4 ancilla qubits |ζ⟩η, η ∈ {0, 1, 2, 3, 4}.
Let us now suppose that our protocol is fed with the following input data, in this precise order: 1, 2, 3, 4, 6:
Step 1
d = 1. d ∈ A as d = a1.
F (d == a1) = 0001, i.e., f0 = 1, f1 = 0, f2 = 0, f3 = 0.
|ζ⟩0 = |1⟩, |ζ⟩1 = |0⟩, |ζ⟩2 = |0⟩, |ζ⟩3 = |0⟩
|ψ⟩0,0 = |1⟩, |ψ⟩0,1 = |0⟩, |ψ⟩0,2 = |0⟩, |ψ⟩0,3 = |0⟩
|Φ⟩0 = |0001⟩

Step 2
d = 2. d ∈ A as d = a0.
F (d == a0) = 0010, i.e., f0 = 0, f1 = 1, f2 = 0, f3 = 0.
|ζ⟩0 = |0⟩, |ζ⟩1 = |1⟩, |ζ⟩2 = |0⟩, |ζ⟩3 = |0⟩
|ψ⟩1,0 = |0⟩, |ψ⟩1,1 = |1⟩, |ψ⟩1,2 = |0⟩, |ψ⟩1,3 = |0⟩
|Φ⟩1 = |0010⟩

Step 3
d = 3. d ∈ A as d = a3.
F (d == a3) = 0011, i.e., f0 = 1, f1 = 1, f2 = 0, f3 = 0.
|ζ⟩0 = |1⟩, |ζ⟩1 = |1⟩, |ζ⟩2 = |0⟩, |ζ⟩3 = |0⟩
|ψ⟩2,0 = |1⟩, |ψ⟩2,1 = |1⟩, |ψ⟩2,2 = |0⟩, |ψ⟩2,3 = |0⟩
|Φ⟩2 = |0011⟩

Step 4
d = 4. d ∈ A as d = a2.
F (d == a3) = 0100, i.e., f0 = 0, f1 = 0, f2 = 1, f3 = 0.
|ζ⟩0 = |0⟩, |ζ⟩1 = |0⟩, |ζ⟩2 = |1⟩, |ζ⟩3 = |0⟩
|ψ⟩3,0 = |0⟩, |ψ⟩3,1 = |0⟩, |ψ⟩3,2 = |1⟩, |ψ⟩3,3 = |0⟩
|Φ⟩3 = |0011⟩
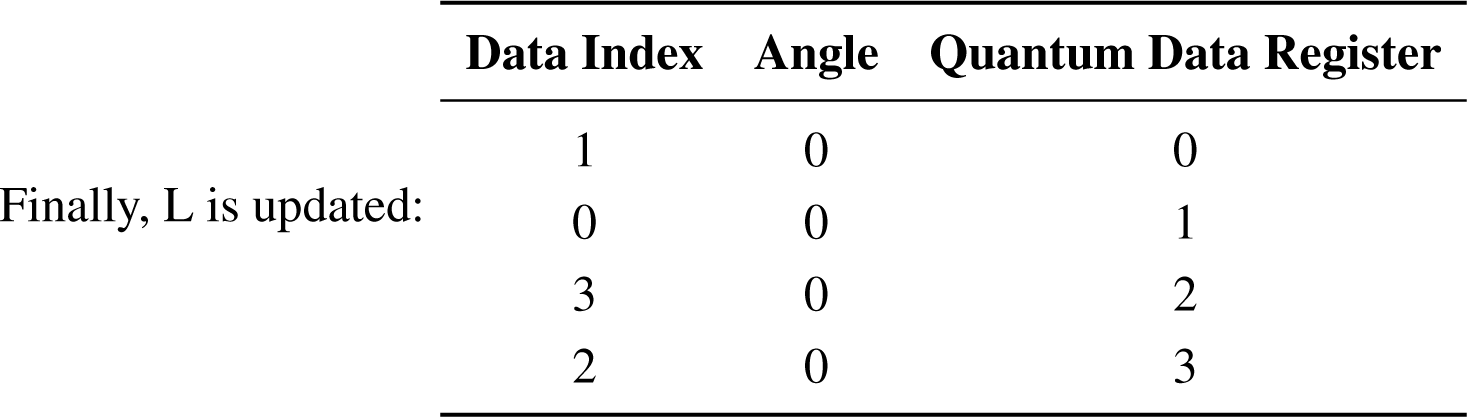
Step 5
d = 6. d ∉ A, so let us make a4 = 6. Now, A = {a0, a1a2, a3, a4}
F (d == a4) = 0110, i.e., f0 = 0, f1 = 0, f2 = 1, f3 = 0.
#(A) = 5, n = 2, 2n = 4 then Quo = 1 and Res = 1
Since Res ≠ 0 then θ = θ1, i.e.,
Then,
Then,
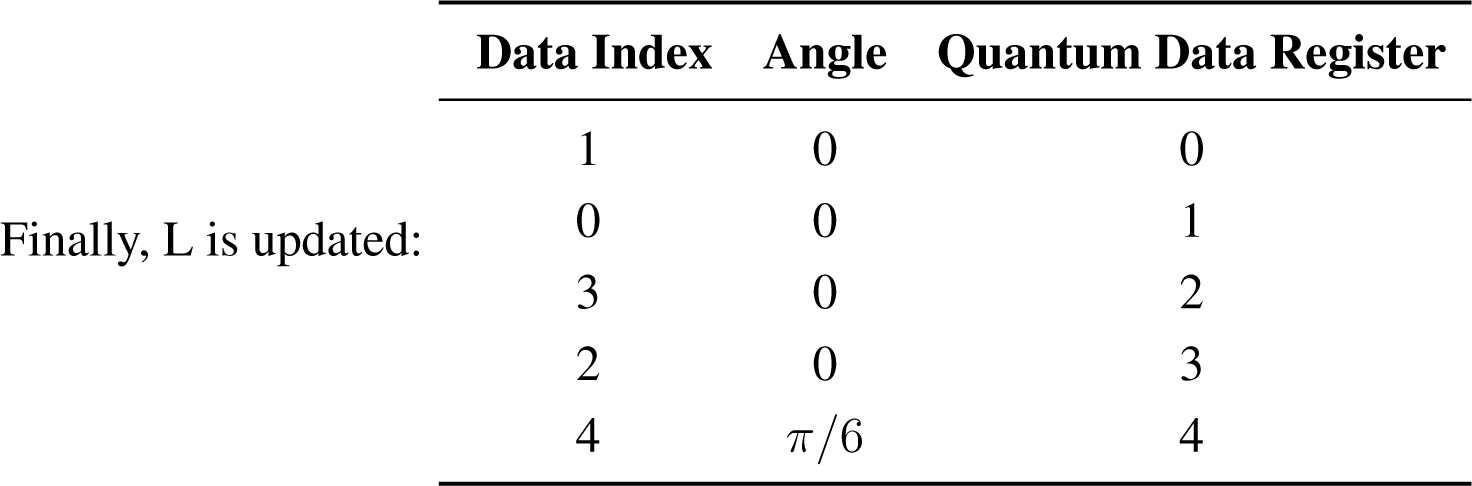
Part 2. Retrieving information
Our algorithm for retrieving information has the following data as input:
Quantum data registers:
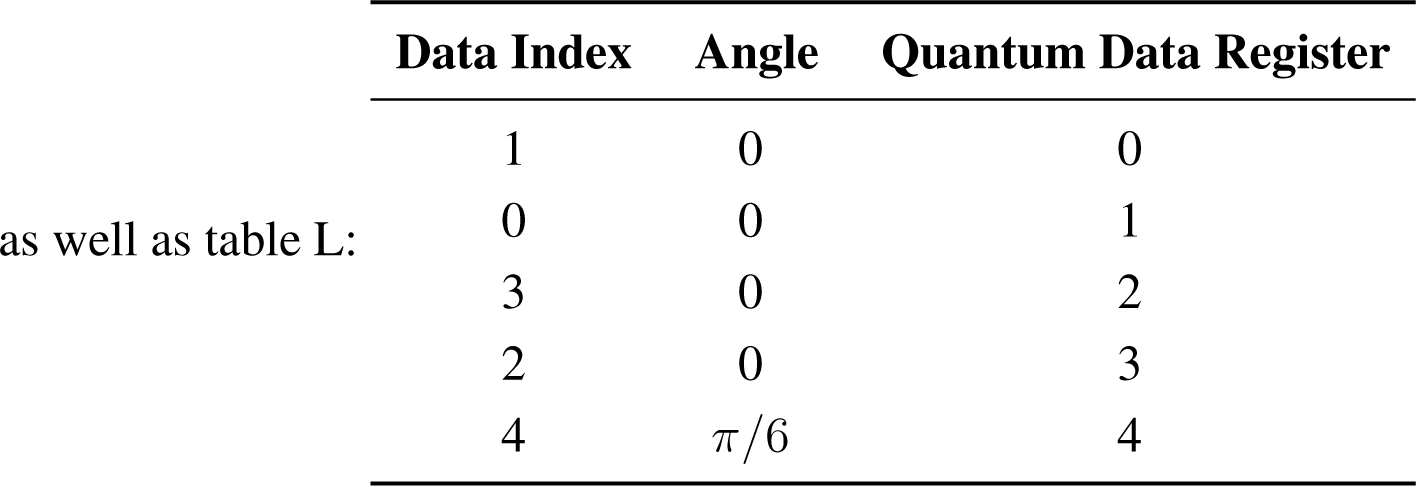
Measurement 1
We start by querying the smallest value of parameter γ from table L: γ = 0
After some calculations, it can be seen that the probability of getting measurement outcome s1 is equal to one, i.e., P (s1) = 1 and, consequently, P (sk) = 0 ∀k ∈ {0, 1,… 15} − {1}. Moreover, postmeasurement state |Φ⟩pm = |0001⟩.
Measurement 2
Next value of parameter γ from table L: is γ = 1
After some calculations, it can be seen that the probability of getting measurement outcome s2 is equal to one, i.e., P (s2) = 1 and, consequently, P (sk) = 0 ∀k ∈ {0, 1,…15} − {2}. Moreover, postmeasurement state |Φ⟩pm = |0010⟩.
Measurement 3
Next value of parameter γ from table L: is γ = 2
After some calculations, it can be seen that the probability of getting measurement outcome s3 is equal to one, i.e., P (s3) = 1 and, consequently, P (sk) = 0 ∀k ∈ {0, 1,… 15} − {3}. Moreover, postmeasurement state |Φ⟩pm = |0011⟩.
Measurement 4
Next value of parameter γ from table L: is γ = 3
After some calculations, it can be seen that the probability of getting measurement outcome s4 is equal to one, i.e., P (s4) = 1 and, consequently, P (sk) = 0 ∀k ∈ {0, 1,… 15} − {4}. Moreover, postmeasurement state |Φ⟩pm = |0100⟩.
Measurement 5
Next value of parameter γ from table L: is γ = 4
After some calculations, it can be seen that the probability of getting measurement outcome s6 is equal to one, i.e., P (s6) = 1 and, consequently, P (sk) = 0 ∀k ∈ {0, 1,… 15} − {6}. Moreover, postmeasurement state |Φ⟩pm = |0100⟩π/6.
References
- Benioff, P.A. The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. J. Stat. Phys 1980, 22, 563–591. [Google Scholar]
- Benioff, P.A. Quantum mechanical Hamiltonian models of discrete processes that erase their own histories: Application to Turing machines. Int. J. Theor. Phys 1982, 21, 177–201. [Google Scholar]
- Benioff, P.A. Quantum mechanical Hamiltonian models of Turing machines. J. Stat. Phys 1982, 3, 515–546. [Google Scholar]
- Benioff, P.A. Quantum mechanical models of Turing machines that dissipate no energy. Phys. Rev. Lett 1982, 48, 1581–1585. [Google Scholar]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys 1982, 21, 467–488. [Google Scholar]
- Feynman, R.P. Quantum mechanical computers. Found. Phys 1986, 16, 507–531. [Google Scholar]
- Feynman, R.P. Feynman Lectures on Computation; Penguin Books: London, UK, 1999. [Google Scholar]
- Deutsch, D. Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. Lond. Ser. A 1985, 400, 97–117. [Google Scholar]
- Deutsch, D.; Ekert, A.; Lupacchini, R. Machines, logic and quantum physics. Bull. Symb. Logic 2000, 6, 265–283. [Google Scholar]
- Margolus, N. Looking at nature as a computer. Int. J. Theor. Phys 2003, 42, 309–327. [Google Scholar]
- Mariantoni, M.; Wang, H.; Yamamoto, T.; Neeley, M.; Bialczak, R.C.; Chen, Y.; Lenander, M.; Erik Lucero, E.; O’Connell, A.D.; Sank, D.; et al. Implementing the Quantum von Neumann Architecture with Superconducting Circuits. Science 2011, 334, 61–65. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search, Proceedings of the 28th Annual ACM Symposium on the Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219.
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete algorithms on a quantum computer. SIAM J. Comput 1997, 26, 1484–1509. [Google Scholar]
- Childs, A.M.; Cleve, R.; Deotto, E.; Farhi, E.; Gutmann, S.; Spielman, D. Exponential algorithmic speedup by quantum walk, Proceedings of the 35th ACM Symposium on The Theory of Computation (STOC’03) ACM, San Diego, CA, USA, 09–11 June 2003; pp. 59–68.
- Childs, A.M. Universal computation by quantum walk. Phys. Rev. Lett 2009, 102. 180501. [Google Scholar]
- Kitaev, A.Y.; Shen, A.H.; Vyalyi, M.N. Classical and Quantum Computation; American Mathematical Society: New York, NY, USA, 2002. [Google Scholar]
- Lanzagorta, M.; Ullman, J. Quantum Computer Science; Morgan and Claypool Publishers: San Diego, CA, USA, 2009. [Google Scholar]
- Bergou, J.A.; Hillery, M. Introduction to the Theory of Quantum Information Processing; Springer: New York, NY, USA, 2013. [Google Scholar]
- Jordan, S. Fast quantum algorithm for numerical gradient estimation. Phys. Rev. Lett 2005, 95, 050501. [Google Scholar]
- Childs, A.; van Dam, W. Quantum algorithms for algebraic problems. Rev. Mod. Phys 2010, 82, 1–51. [Google Scholar]
- Gruska, J. Quantum Computing; McGraw-Hill Publishing Co: New York, NY, USA, 1999. [Google Scholar]
- Venegas-Andraca, S.E. Quantum Walks for Computer Scientists; Morgan and Claypool: San Diego, CA, USA, 2008. [Google Scholar]
- Harris, S.; Kendon, V.M. Quantum-assisted biomolecular modelling. Phil. Trans. R. Soc. A 2010, 368, 3581–3592. [Google Scholar]
- Brown, K.L.; Munro, W.J.; Kendon, V.M. Using Quantum Computers for Quantum Simulation. Entropy 2010, 12, 2268–2307. [Google Scholar]
- Venegas-Andraca, S.E.; Bose, S. Quantum computation and image processing: New trends in artificial intelligence, Proceedings of the 18th International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 9–15 August 2003; pp. 1563–1564.
- Venegas-Andraca, S.E.; Bose, S. Storing, processing and retrieving an image using quantum mechanics, Proceedings of the SPIE Conference Quantum Information and Computation, Orlando, FL, USA, 21–22 April 2003; pp. 137–147.
- Venegas-Andraca, S.E.; Ball, J.L. Processing images in entangled quantum systems. Quant. Inf. Process 2010, 9, 1–11. [Google Scholar]
- Le, P.Q.; Doyng, F.; Hirota, K. A flexible representation of quantum images for polynomial preparation, image compression, and processing operations. Quant. Inf. Process 2010, 10, 63–84. [Google Scholar]
- Iliyasu, A.M. Towards Realising Secure and Efficient Image and Video Processing Applications on Quantum Computers 2013, 15(8), 2874–2974.
- Le, P.Q.; Iliyasu, A.M.; Dong, F.; Hirota, K. Efficient color transformations on quantum images. J. Adv. Comput. Intell. Intell. Inf 2011, 15, 698–706. [Google Scholar]
- Le, P.Q.; Iliyasu, A.M.; Doyng, F.; Hirota, K. Strategies for designing geometric transformations on quantum images. Theor. Comput. Sci 2011, 412, 1046–1418. [Google Scholar]
- Sun, B.; Le, P.Q.; Iliyasu, A.M.; Yan, F.; García, J.A.; Dong, F.; Hirota, K. A multi-channel representation for images on quantum computers using the rgbα color space, Proceedings of the IEEE 7th International Symposium on Intelligent Signal Processing, Floriana, Malta, 19–21 September 2011; pp. 160–165.
- Iliyasu, A.M.; Le, P.Q.; Dong, F.; Hirota, K. A framework for representing and producing movies on quantum computers. Int. J. Quant. Inf 2011, 9, 1459–1497. [Google Scholar]
- Iliyasu, A.M.; Le, P.Q.; Dong, F.; Hirota, K. Watermarking and authentication of quantum images based on restricted geometric transformations. Inf. Sci 2012, 186, 126–149. [Google Scholar]
- Lanzagorta, M.; Uhlmann, J. Quantum algorithmic methods for computational geometry. Math. Struct. Comput. Sci 2010, 20, 1117–1125. [Google Scholar]
- Trugenberger, C. Quantum pattern recognition. Quant. Inf. Process 2002, 1, 471–493. [Google Scholar]
- Trugenberger, C. Phase transitions in quantum pattern recognition. Phys. Rev. Lett 2002, 89, 277903. [Google Scholar]
- Horn, D.; Gottlieb, A. Algorithm for data clustering in pattern recognition problems based on quantum mechanics. Phys. Rev. Lett 2002, 88, 18702. [Google Scholar]
- Trugenberger, C. Probabilistic quantum memories. Phys. Rev. Lett 2001, 87, 067901. [Google Scholar]
- Abal, G.; Donangelo, R.; Fort, H. Conditional strategies in iterated quantum games. Physica A 2008, 387, 5326–5332. [Google Scholar]
- Lanzagorta, M. Quantum Radar; Morgan and Claypool: San Diego, CA, USA, 2011. [Google Scholar]
- ERA-Pilot. Quantum Information Processing and Communication Strategic Report Version 1.5, 2007. Available online: http://www.qist-europe.net/ (accessed on 19 June 2014).
- QIST 2004, Advanced Research and Development Activity (2004); A Quantum Information Science and Technology Roadmap: USA; Available online: http://qist.lanl.gov/ (accessed on 19 June 2014).
- Wootters, W.K.; Fields, B.C. Optimal State-Determination by Mutually Unbiased Measurements. Ann. Phys 2008, 191, 363–381. [Google Scholar]
- Quantum Artificial Intelligence Laboratory, Available online: https://www.nas.nasa.gov/quantum/ (accessed on 19 June 2014).
- Crowston, K.; Liu, X.; Allen, E. Machine learning and rule-based automated coding of qualitative data. Proceedings of the 73rd ASIS&T Annual Meeting on Navigating Streams in an Information Ecosystem, Pittsburgh, PA, USA, 22–27 October 2010; American Society for Information Science: Silver Springs, MD, USA, 2010. [Google Scholar]
- Huo, R.; Agapiou, A.; Bocos-Bintintan, V.; Brown, L.J.; Burns, C.; Creaser, C.S.; Devenport, N.A.; Gao-Lau, B.; Guallar-Hoyas, C.; Hildebrand, L.; et al. The trapped human experiment. J. Breath Res 2011, 5, 046006. [Google Scholar]
- Mermin, N.D. From cbits to qbits: Teaching computer scientists quantum mechanics. Am. J. Phys 2003, 71, 23–30. [Google Scholar]
- Mermin, N.D. Quantum Computer Science: An Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Rieffel, E.; Polak, W. An introduction to quantum computing for non-physicists. ACM Comput. Surv 2000, 32, 300–335. [Google Scholar]
 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Iliyasu, A.M.; Venegas-Andraca, S.E.; Yan, F.; Sayed, A. Hybrid Quantum-Classical Protocol for Storage and Retrieval of Discrete-Valued Information. Entropy 2014, 16, 3537-3551. https://doi.org/10.3390/e16063537
Iliyasu AM, Venegas-Andraca SE, Yan F, Sayed A. Hybrid Quantum-Classical Protocol for Storage and Retrieval of Discrete-Valued Information. Entropy. 2014; 16(6):3537-3551. https://doi.org/10.3390/e16063537
Chicago/Turabian StyleIliyasu, Abdullah M., Salvador E. Venegas-Andraca, Fei Yan, and Ahmed Sayed. 2014. "Hybrid Quantum-Classical Protocol for Storage and Retrieval of Discrete-Valued Information" Entropy 16, no. 6: 3537-3551. https://doi.org/10.3390/e16063537
APA StyleIliyasu, A. M., Venegas-Andraca, S. E., Yan, F., & Sayed, A. (2014). Hybrid Quantum-Classical Protocol for Storage and Retrieval of Discrete-Valued Information. Entropy, 16(6), 3537-3551. https://doi.org/10.3390/e16063537





