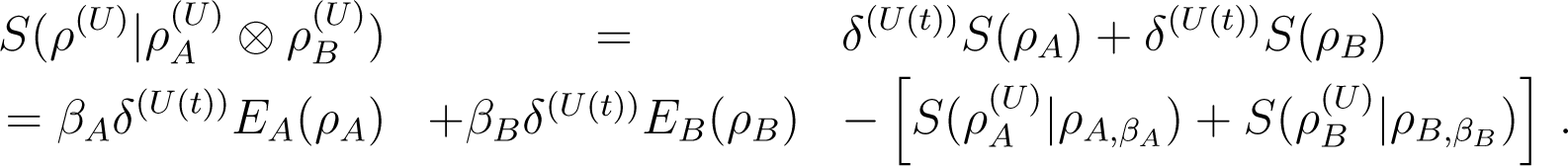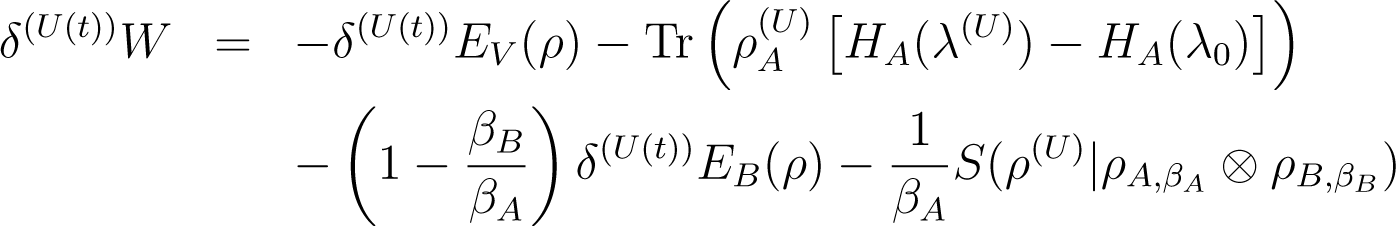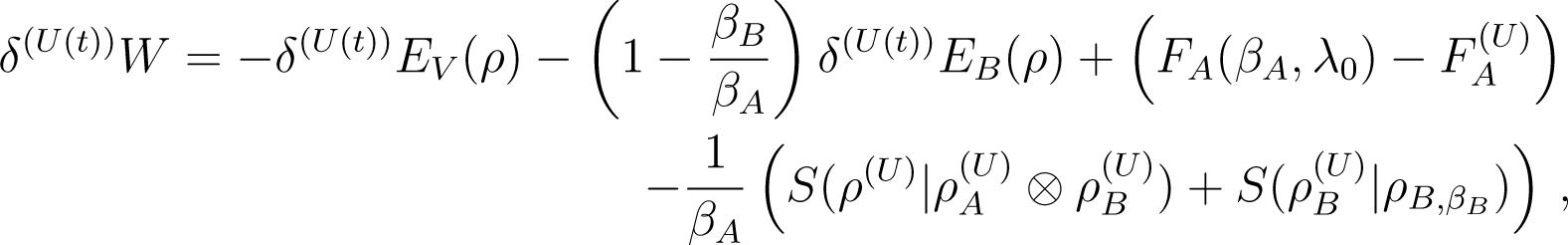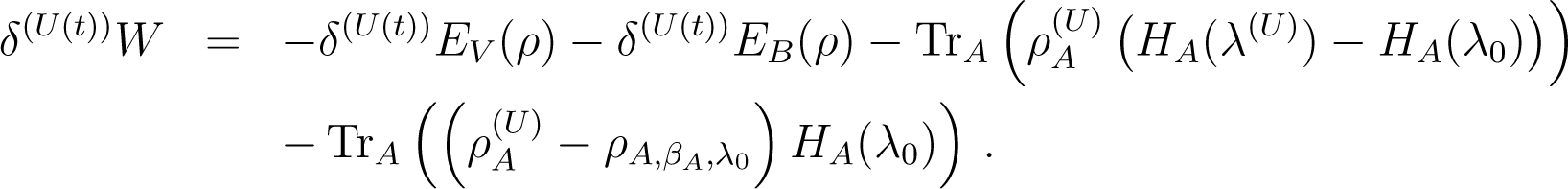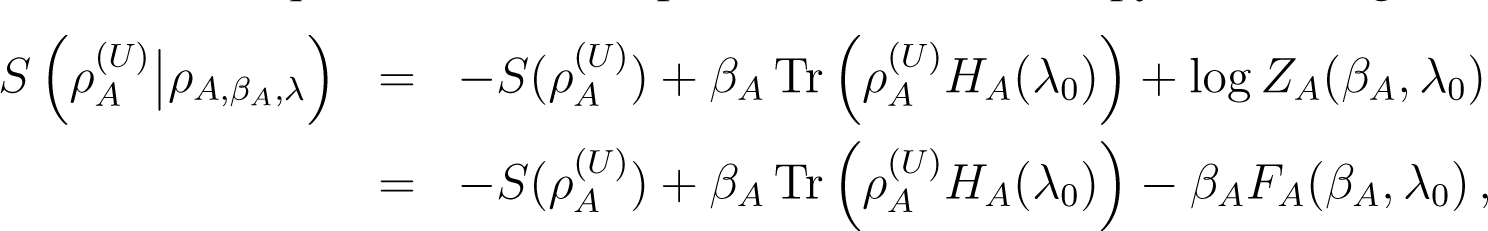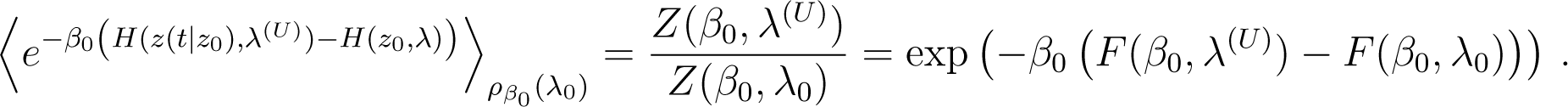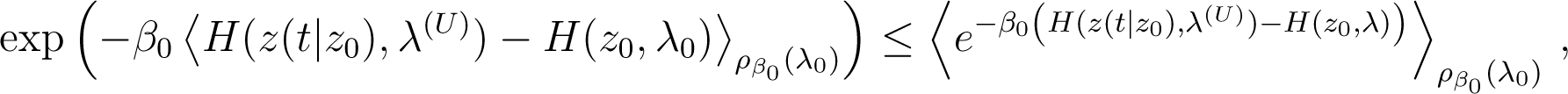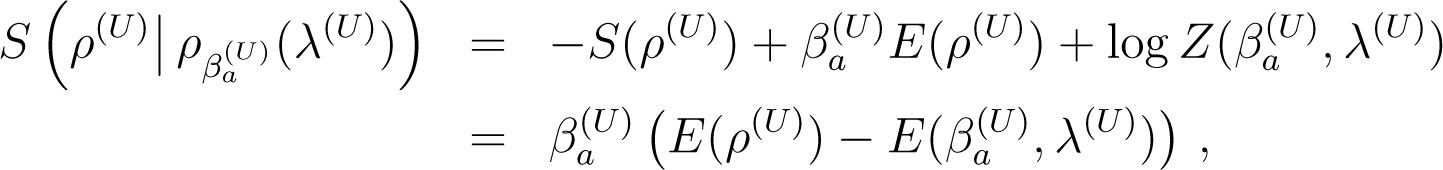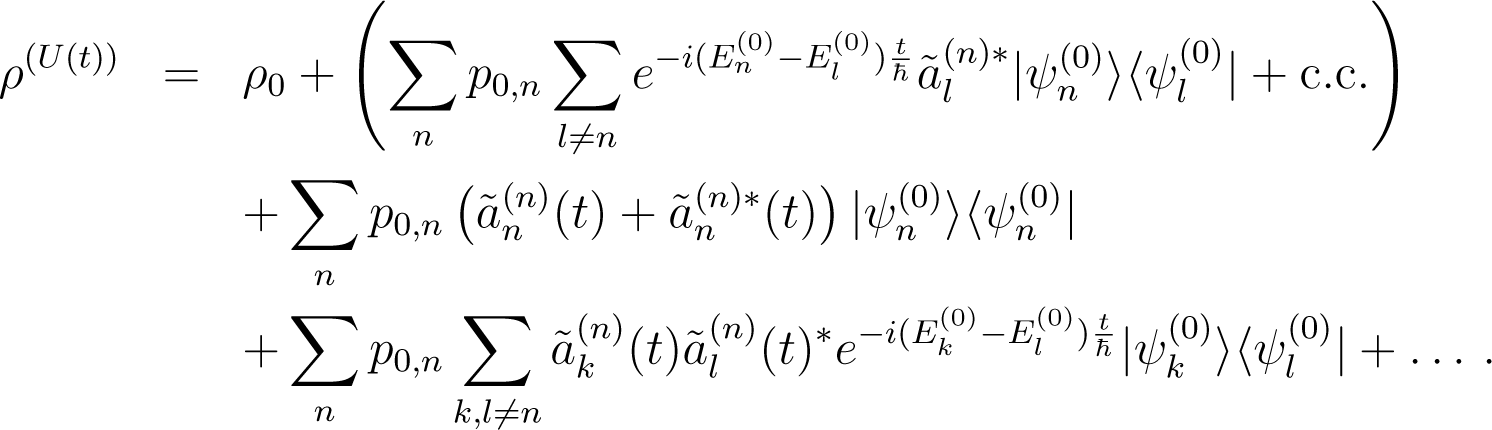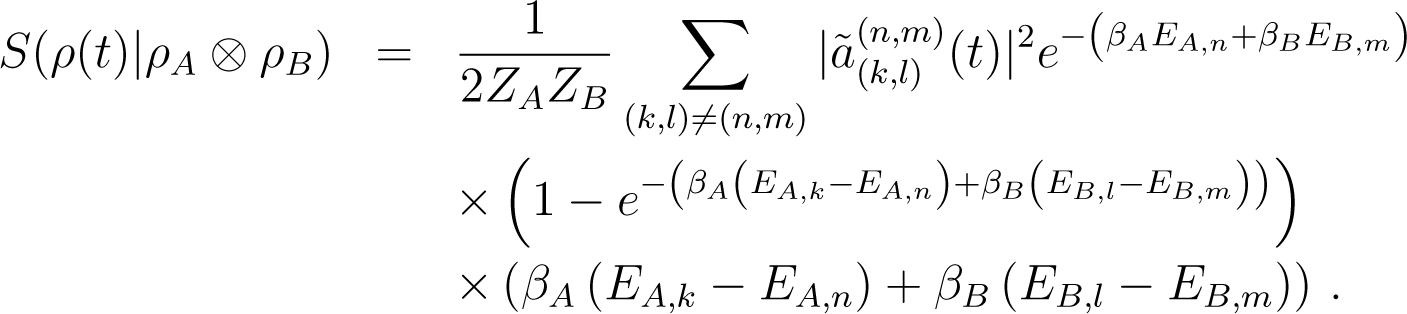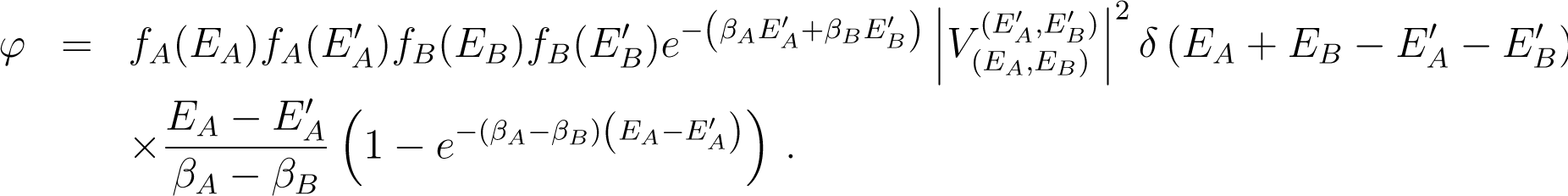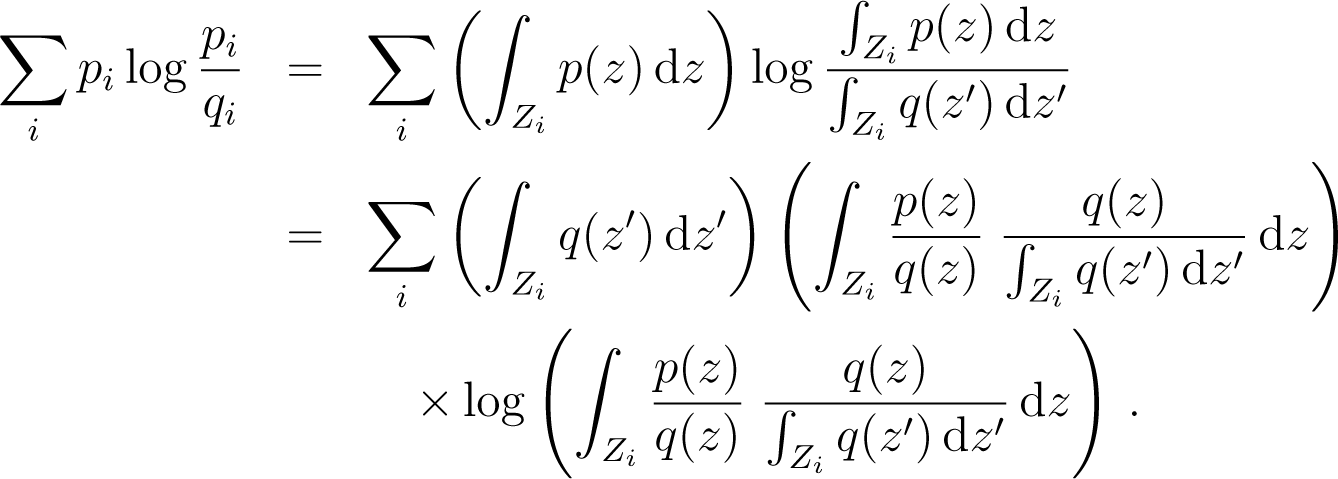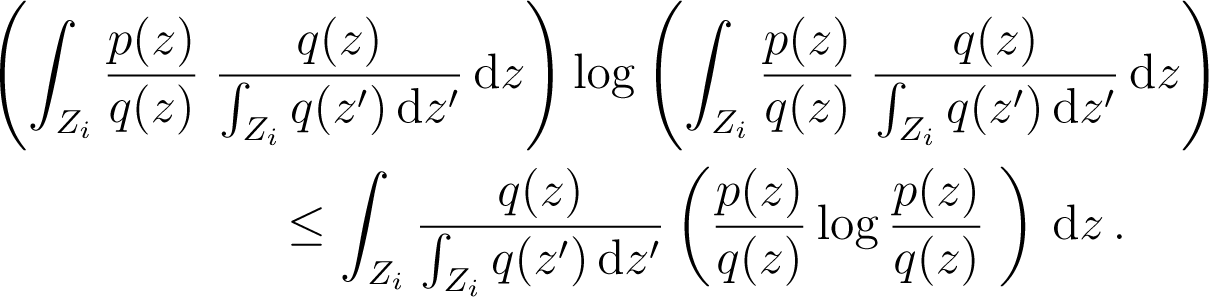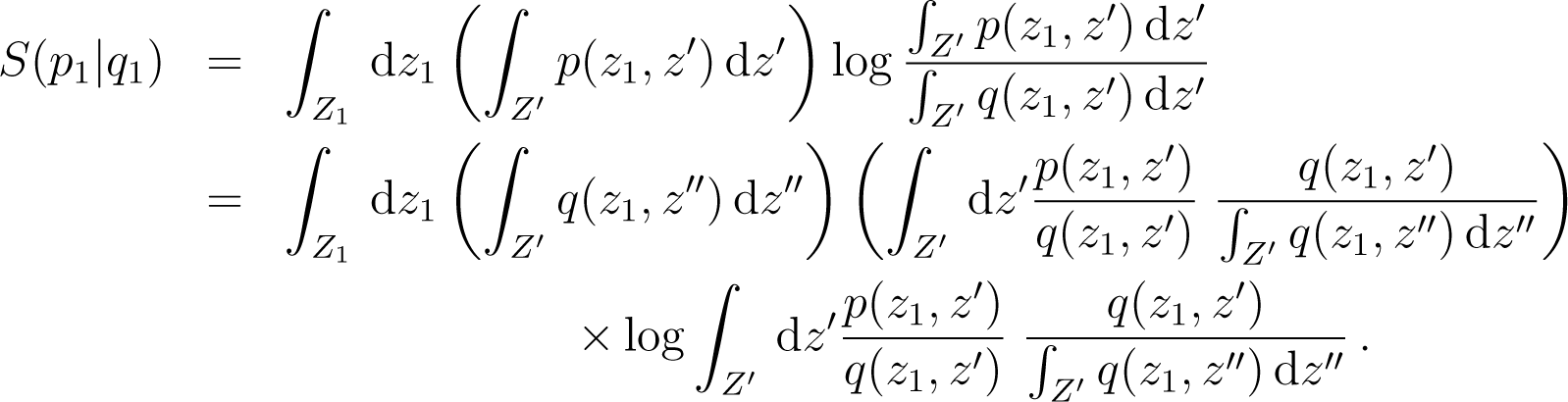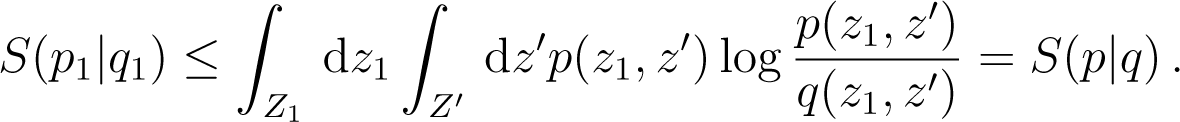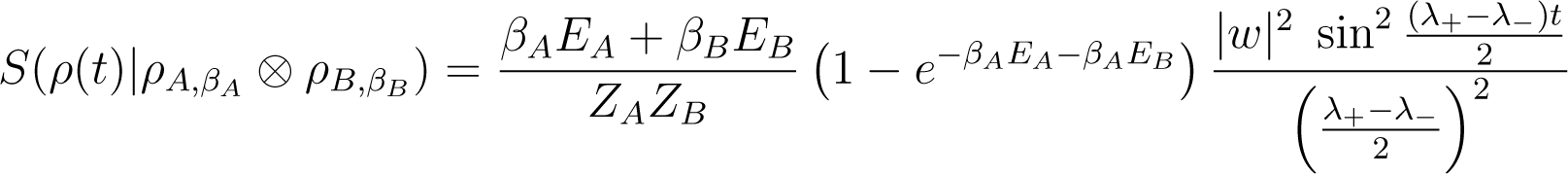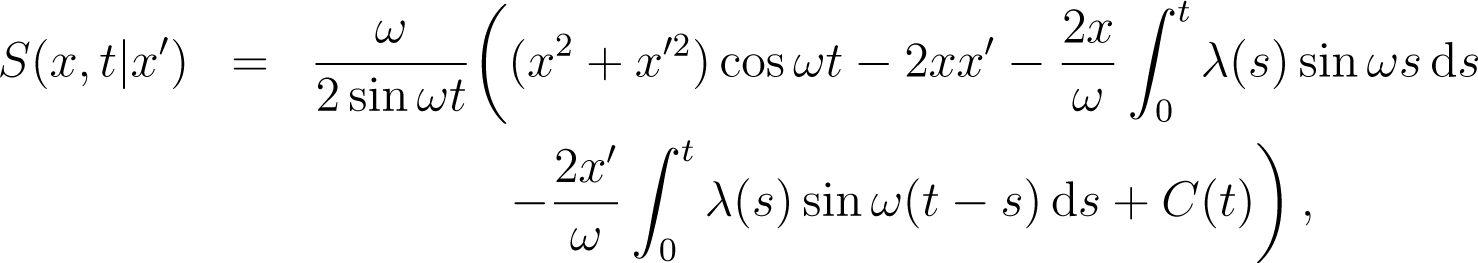Relative Entropy, Interaction Energy and the Nature of Dissipation

Abstract

Many thermodynamic relations involve inequalities, with equality if a process does not involve dissipation. In this article we provide equalities in which the dissipative contribution is shown to involve the relative entropy (a.k.a. Kullback-Leibler divergence). The processes considered are general time evolutions both in classical and quantum mechanics, and the initial state is sometimes thermal, sometimes partially so. By calculating a transport coefficient we show that indeed—at least in this case—the source of dissipation in that coefficient is the relative entropy.

1. Introduction

The distinction between heat and work, between the uncontrollable flow of energy of molecular processes and the controllable flow of energy usable by an agent, underlies all of thermodynamics, and is implicitly incorporated in the equation dE = đW + đQ. This distinction is defined by human subjectivity and by the human technological ability to extract work from the flow of energy of microscopic processes.

On the other hand, assuming that the evolution is given by the fundamental laws of dynamics, classical or quantum, one must represent the evolution of a system at a fundamental microscopic level by the action of a unitary operator on a quantum state (density operator) in quantum situations or by the action of a symplectic operator on a classical state (probability distribution) in classical situations. The state of the system evolves according to the Heisenberg equation of motion or according to the Liouville equation respectively. An immediate consequence is that the entropy of the exact microscopic state of a system that is isolated or is coupled only to an external source of work stays constant during the evolution. In particular, the microscopic state cannot tend to an equilibrium state. Thus, the information content of the exact microscopic state stays constant during the evolution. The problem is that in practice it is impossible both to define the microscopic state and to follow its exact evolution. The definition of the state and the representation of the exact evolution using unitary or symplectic dynamics are thus untenable idealizations. Nevertheless, and this constitutes a paradox, these idealizations cannot be ignored or dismissed, because it is precisely the difference between the exact evolution and its standard approximations which explains and can be used to predict dissipative effects, both of energy and information.

In thermodynamics, in kinetic theories or in stochastic dynamics, the exact microscopic state of a system is replaced by an approximate or “coarse-grained” state and the corresponding exact evolution is replaced by an evolution of the corresponding coarse-grained state (or, in standard thermodynamics by a quasi-static or formal evolution). There are two main reasons for using these approximate states and evolutions:

(1)

As discussed, it is impossible—even in principle—to specify the exact state of a large system and follow its evolution. An attempt at extremely high precision would modify the system, even in a classical context (related to Maxwell’s demon). And it is even worse for quantum systems. Moreover, this would be useless.

(2)

Only slow variables (on the time scales of microscopic processes) can be measured with confidence and stability. As a result, an observer can only describe the system as a state of minimal information (or maximal entropy) compatible with the observed slow variables [1,2].

The coarse-grained state is thus a statistical data structure which summarizes at a given moment the knowledge of the observer. The evolution of this coarse-grained state merely reflects the evolution of the knowledge of the observer about the system. The observer cannot follow the microscopic processes, but only the slow variables which can be measured and used, and as a consequence there is a loss of information about the details of the microscopic processes; in the traditional language of thermodynamics, entropy increases or is produced. The observer, reflecting a particular state of knowledge (or more precisely, a lack of knowledge), describes the state of the system as a state of minimal information (or maximal entropy) compatible with observation. Thus, entropy is not a kind of substance flowing from one part of a system to another part or mysteriously produced internally by the physical system, as is often suggested by many texts of thermodynamics or statistical physics: it is only the observer’s partial inability to relate the exact microscopic theory to a reduced macroscopic description in order to use the system as a source of useful work or information. This is what is measured as an increase of entropy or by entropy production. The macroscopic state is the result of a statistical inference (specifically, maximum entropy) for the given, observed, macroscopic variables (which are the slow variables of the system [1,2]. This point of view on the nature of entropy was emphasized by Jaynes, who observed [3,4], “The expression ‘irreversible process’ represents a semantic confusion…”

The difference between the exact evolution of the microscopic ideal state and the evolution of its coarse-grained approximation is what is called “dissipation,” both of information content and of energy or other “useful” variables. Standard thermodynamics uses the maximal coarse graining of equilibrium, and the idealized evolution is not modeled explicitly, so dissipation can be taken into account only by inequalities. For more detailed coarse-graining (as in hydrodynamics, Boltzmann’s equation, kinetic theories or stochastic thermodynamics) one can obtain an estimate for the dissipative effects, for example, by the calculation of transport coefficients.

In this article, our main purpose is to prove that the relative entropy term between the initial and final states measures dissipation. In our approach, “dissipation” is defined as the difference between the maximal work that the physicist thinks could be extracted from a system when using the thermodynamic or quasi-static theory to make predictions, and the work that is actually extracted because the system is evolving according to the exact dynamics, classical or quantum, independently of what the physicist thinks (see also our use of relative entropy in [5] and [6], where the context was more limited [7]). Moreover, in the present context we find that the relative entropy terms are proportional to the square of the interaction energy. In all standard theories, dissipative effects are measured by the transport coefficients of energy or momentum or concentration of chemical species. Thus, we need prove that the relative entropy allows the calculation of transport coefficients. Indeed, we show below that the relative entropy terms provide the calculation of the thermal conductivity between two general quantum systems, initially at thermal equilibrium at different temperatures. This is a kind of Fourier law, except that we do not suppose a linear regime, so that the temperature dependence is more complicated than simple linearity. Moreover, our exact calculation of the transport coefficient shows that it is indeed proportional to the square of the interaction energy, which confirms that for vanishingly small interaction energy no transfer occurs in finite time. In other words, no power or finite rate of information flow can be extracted from a system if one does not have at the same time dissipative effects.

In the following material, we first consider a system comprised of two components, A and B. We make no specific hypotheses on the size of the systems, and we do not introduce thermal reservoirs. Thus, the identities we derive are in effect exact tautologies. In Sections 3 to 5, we present several identities. We here mention two examples: (1) a derivation of the Brillouin-Landauer estimate of the energy necessary to change the information content of a system; (2) an estimate of the work that can be extracted from a two-part system in interaction with an external source of work in terms of non-equilibrium free energies and relative entropy of the state before and after the evolution. Similar identities were also obtained recently by Esposito et al. [8], Reeb and Wolf [9], and Takara et al. [10] Continuing, we study the effect of an external agent on an (otherwise) isolated system; again we obtain an identity relating the work to the difference of internal (not the free) energies along with the usual dissipative terms. Then, we derive the relation between the relative entropy and the heat conductivity in a quantum system. Finally, we define a general notion of coarse-graining or reduced description, which includes the usual notions. In some of our examples one or both systems are initially at thermal equilibrium, but only the initial temperatures appear explicitly in the definition of the non-equilibrium free energies. The latter are no longer state functions because they depend explicitly on the initial temperature and not on the actual effective temperature. No coarse graining by an effective final or intermediate thermal state is used, and neither system is a reservoir.

2. Notations and Basic Identities

2.1. States and Entropy

Many results will be valid both in classical and quantum contexts. We denote by ρ either a probability distribution function over a classical phase space, or a density matrix in the quantum case. We denote by Tr either the integral on the phase space, or the trace operation. Thus ρ is a positive quantity and satisfies Tr ρ = 1. The entropy of ρ is

$$S\left(\rho \right)=-\mathrm{Tr}\rho \log \rho .$$

(1)

It is defined up to a multiplicative constant. (Classically ρ should be divided by a dimensional constant to render it dimensionless.)

The relative entropy (see [11]) is defined by

$$S\left(\rho |{\rho }^{\prime }\right)=\mathrm{Tr}\left(\rho \left(\log \rho -\log {\rho }^{\prime }\right)\right),$$

(2)

where ρ and ρ′ are states.

One has

$$S\left(\rho |{\rho }^{\prime }\right)\ge 0,$$

(3)

and S(ρ|ρ′) does not depend on the units in phase space. Moreover S(ρ|ρ′) = 0 if and only if ρ = ρ′.

Writing S(ρ|ρ′) as − Tr ρ log ρ′ − (− Tr ρ log ρ), suggests the following interpretation: Suppose the true state is ρ, but the observer thinks that the state is ρ′. S(ρ|ρ′) is then the true average of the missing information minus the estimate of the missing information.

2.2. The Basic Identity

If we add and subtract S(ρ′) in the second member of Equation (2), we obtain the basic identity

$$S\left(\rho |\rho \prime \right)=S\left(\rho \prime \right)-S\left(\rho \right)-\mathrm{Tr}\left(\left(\rho -\rho \prime \right)\log \rho \prime \right).$$

(4)

Most of our results follow from this identity.

When ρ′ is a thermal state at (inverse) temperature β [12],

$${\rho }^{\prime }={\rho }_{\beta }=\frac{e^{-\beta H}}{Z\left(\beta ,H\right)},$$

(5)

where

$$Z\left(\beta ,H\right)=\mathrm{Tr}{e}^{-\beta H}$$

(6)

is the partition function. With ρ′ = ρ_β, the identity (4) reduces to

$$S\left(\rho |{\rho }_{\beta }\right)=S\left({\rho }_{\beta }\right)-S\left(\rho \right)+\beta \mathrm{Tr}\left(\left(\rho -{\rho }_{\beta }\right)H\right).$$

(7)

Here H is a given function or operator.

Defining the free energy of state ρ by

$$F\left(\rho ,H\right)=\mathrm{Tr}\left(\rho H\right)-\frac{1}{\beta }S\left(\rho \right),$$

(8)

we obtain

$$S\left(\rho |{\rho }_{\beta }\right)=\beta \left(F\left(\rho ,H\right)-F\left({\rho }_{\beta },H\right)\right),$$

(9)

and F (ρ_β, H) is the equilibrium free energy related to the partition function by

$$Z\left(\beta ,H\right)=\exp \left(-\beta F\left({\rho }_{\beta },H\right)\right).$$

(10)

Equation (9) is important for applications, because its right hand side can be related to energy dissipation (up to the factor β), which gives a clear physical meaning to the relative entropy (see Section 3).

2.3. Evolution Operators and Entropy

We assume that the system (classical or quantum) evolves under the action of an arbitrary operator U (symplectic or unitary). If ρ is a state, we denote by ρ^(U) the new state after the evolution U.

Entropy is conserved by the evolution

$$S\left({\rho }^{\left(U\right)}\right)=S\left(\rho \right).$$

(11)

For example, in the quantum case, we have ρ^(U) = Uρ U^†, where U is the propagator: $i\frac{dU}{dt}=\left[H,U\right]$, U|_t=0 = 1, with H a possibly time-dependent Hamiltonian.

If ϕ(ρ) is a functional of ρ which evolves with U, and ϕ(ρ^(U)) is the functional after evolution of ρ, we denote the variation of ϕ(ρ) after the evolution U in the following way

$${\delta }^{\left(U\right)}\left(\varphi \left(\rho \right)\right)=\varphi \left({\rho }^{\left(U\right)}\right)-\varphi \left(\rho \right).$$

(12)

Remark 1: Many of our results are valid for a general evolution U which is not symplectic or unitary, for example stochastic evolution.

3. Two Systems in Interaction

A basic procedure in thermodynamics is to consider the evolution and properties of an otherwise isolated two-part system. Although it is often the case that the overall system conserves energy, for the subsystems more general behavior is often seen.

3.1. Hypotheses

We assume that the system is formed of two parts, A and B, in interaction. At time-0, the state is a product state

$${\rho }_0={\rho }_{A,0}\otimes {\rho }_{B,0}.$$

(13)

After the evolution U, the state is ρ^(U) and we denote by ${\rho }_A^{(U)}$ and ${\rho }_B^{\left(U\right)}$ its marginals,

$${\rho }_A^{\left(U\right)}={\mathrm{Tr}}_B{\rho }^{\left(U\right)}\text{and}{\rho }_B^{\left(U\right)}={\mathrm{Tr}}_A{\rho }^{\left(U\right)},$$

(14)

which are then states on A and B respectively. We also assume that there is a quantity H that is conserved by the evolution and H has the form

$$H=H_A+H_B+V_{AB},$$

(15)

where H_A and H_B are quantities depending only on A and B respectively and V_AB is an interaction term. Then, if we denote

$$E\left(\rho \right)=\mathrm{Tr}\left(\rho H\right)=E_A\left(\rho \right)+E_B\left(\rho \right)+E_V\left(\rho \right)$$

(16)

$$E_A\left(\rho \right)=\mathrm{Tr}\left(\rho H_A\right)=\mathrm{Tr}\left({\rho }_A{H}_A\right)$$

(17)

$$E_B\left(\rho \right)=\mathrm{Tr}\left(\rho H_B\right)=\mathrm{Tr}\left({\rho }_B{H}_B\right)$$

(18)

$$E_V\left(\rho \right)=\mathrm{Tr}\left(\rho V_{AB}\right),$$

(19)

our hypothesis is that

$${\delta }^{\left(U\left(t\right)\right)}E\left(\rho \right)\equiv E\left({\rho }^{\left(U\right)}\right)-E\left({\rho }_0\right)=0.$$

(20)

In particular this is the case if U is time-evolution with Hamiltonian H.

Remark 2: For this situation, certain results are also valid without the assumption that the evolution U preserves the energy H.

If ρ is a state corresponding to a system formed of two parts, A and B, and ρ_A and ρ_B are its marginals (as in Equation (14)), then the relative entropy S (ρ|ρ_A ⊗ ρ_B) is the same as the mutual information of the associated distributions. It can be interpreted as the amount of information in ρ that comes from the fact that A and B are in interaction (see [11]). This quantity will appear in many of our relations below (e.g., Equation (28)) as part of the dissipation.

3.2. Relation between a State and Its Marginals

Assuming Equation (13) (that the initial state is a product state), one has the identity

$${\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)+{\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right)=S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right).$$

(21)

Indeed, using the conservation of the entropy of ρ during the evolution U,

This is because one evidently has $-\mathrm{Tr}\left({\rho }^{\left(U\right)}\log {\rho }_A^{\left(U\right)}\right)=-\mathrm{Tr}\left({\rho }_A^{\left(U\right)}\log {\rho }_A^{\left(U\right)}\right)$. Note that Equation (21) requires that U preserve the entropy. One has also the well-known inequality

$$S\left({\rho }^{\left(U\right)}\right)\le S\left({\rho }_A^{\left(U\right)}\right)+S\left({\rho }_B^{\left(U\right)}\right),$$

(22)

which is a particular case of

$$S\left(\rho \right)\le S\left({\rho }_A\right)+S\left({\rho }_B\right)$$

(23)

for any state ρ.

Note that the stronger result, Equation (21), is obtained by retaining the relative entropy term in this equation. The same remark will apply in most of the following results.

3.3. The Case Where A is Initially in a Thermal State

At time 0 we take ρ_A,0 to be thermal with temperature β_A,

$${\rho }_{A,0}={\rho }_{A,{\beta }_A}=\frac{e^{-{\beta }_A{H}_A}}{Z_A\left({\beta }_A\right)},$$

(24)

where Z_A(β_A) = Z_A(β_A, H_A) is the partition function, (6). From Equation (7) with $\rho \to {\rho }_A^{\left(U\right)}$ and ${\rho }_{\beta }\to {\rho }_{A,{\beta }_A}$, we deduce (note that this requires that H_A be independent of time)

$${\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)-{\beta }_A{\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)=-S\left({\rho }_A^{(U)}|{\rho }_{A,{\beta }_A}\right),$$

(25)

and as a consequence

$${\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)-{\beta }_A{\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)\le 0.$$

(26)

The last two equations do not require that U be a unitary evolution conserving the entropy, nor that it conserve the energy.

Remark 3: This inequality can be found in [13] as an unnumbered equation. Its consequences were not deduced in that reference.

Remark4: Note that it is the initial temperature that appears in Equations (25) and (26). Moreover, ${\rho }_A^{(U)}$ is not in general an equilibrium state.

Suppose that B starts in an arbitrary initial state ρ_B,0, while A begins in the thermal state ${\rho }_{A,{\beta }_A}$. Combining Equations (21) and (25), we obtain

$${\beta }_A{\delta }^{\left(U\left(t\right)\right)}{E}_A\left(\rho \right)+{\delta }^{{}^{\left(U\left(t\right)\right)}}S\left({\rho }_B\right)=S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right)+S\left({\rho }_A^{\left(U\right)}|{\rho }_{A,{\beta }_A}\right).$$

(27)

The last equation requires that U preserve entropy, since that feature is used in the derivation of Equation (21). It also remains valid if the Hamiltonian of B, H_B, depends on an external parameter varying with time, so that B receives work from an external agent. This is because the entropy-preserving property only depends on U being unitary (or symplectic). On the other hand, H_A should be time independent (see the parenthetical remark before Equation (25)). Then if U conserves energy

$${\beta }_A\left({\delta }^{\left(U\left(t\right)\right)}{E}_B\left(\rho \right)+{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)\right)={\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right)-\left[S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right)+S\left({\rho }_A^{\left(U\right)}|{\rho }_{A,{\beta }_A}\right)\right].$$

(28)

These relations imply the following inequalities:

(1)

If U preserves entropy, even if H_B depends on an external parameter varying with time

$${\beta }_A{\delta }^{\left(U\left(t\right)\right)}{E}_A\left(\rho \right)\ge -{\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right).$$

(29)

(2)

If U conserves entropy and the total energy, one has

$${\beta }_A\left({\delta }^{\left(U\left(t\right)\right)}{E}_B\left(\rho \right)+{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)\right)\le {\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right),$$

(30)

with the following interpretations. Suppose U conserves the entropy; then we couple a system B (initially in an arbitrary state ρ_B,0) to system A (initially in thermal equilibrium) and that we want to lower the entropy of B so that δ^(U(t)) S(ρ_B) ≤ 0. Then, the energy of A must increase by at least

$${\delta }^{\left(U\left(t\right)\right)}{E}_A\left(\rho \right)\ge \frac{1}{{\beta }_A}\left|{\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right)\right|$$

(31)

even if B receives work from an external source (so that H_B depends on an external parameter). Moreover, if the total energy is conserved, the sum of the energy of B and the coupling energy must decrease by at least:

$${\delta }^{\left(U\left(t\right)\right)}{E}_B\left(\rho \right)+{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)\le \frac{1}{{\beta }_A}{\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right)<0.$$

(32)

Thus lowering the entropy of a system B, coupled to a system initially at equilibrium, costs transfers of energy from B to A or to the interaction energy; thus the sum of B’s energy and the interaction energy must decrease, but B’s energy alone need not decrease. This is a result analogous to those of Brillouin [14] and Landauer [15] (reprinted in Leff and Rex [16]), even if system B receives work from an external source. But note again that only the temperature β_A appears. This is the initial temperature at the beginning of the evolution U, so that system A is not necessarily a thermal bath, because its temperature may vary during the evolution U.

3.4. The Case of Equality in Equation (31)

It is important to study the case where the previous inequalities are changed into equalities, because this occurs if and only if strong conditions are verified: expressing these conditions is one of the advantages of our approach.

Equation (31) was derived under the hypothesis δ^(U) S(ρ_B) < 0. Then by Equation (27) one has $S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right)=S\left({\rho }_A^{\left(U\right)}|{\rho }_{A,{\beta }_A}\right)=0$. This implies ${\rho }_A^{\left(U\right)}={\rho }_{A,{\beta }_A}$ and ${\rho }^{\left(U\right)}={\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}$. Because ${\rho }_A^{\left(U\right)}={\rho }_{A,{\beta }_A},{\delta }^{\left(U\right)}{E}_A\left({\rho }_A\right)=0$, so by Equation (31), δ^(U) S(ρ_B) = 0. But we could also derive δ^(U) S(ρ_B) = 0 from Equation (21), because δ^(U(t)) S(ρ_A) = 0 and $S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right)=0$.

3.5. Both Systems A and B are at Equilibrium

Assume that A and B are initially at thermal equilibrium at different temperatures. Then, one has

(1)

For a general evolution

$${\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)-{\beta }_A{\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)=-S\left({\rho }_A^{\left(U\right)}|{\rho }_{A,{\beta }_A}\right),$$

(33)

$${\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right)-{\beta }_B{\delta }^{\left(U\left(t\right)\right)}{E}_B\left({\rho }_B\right)=-S\left({\rho }_B^{(U)}|{\rho }_{B,{\beta }_B}\right).$$

(34)

(1)

If U conserves entropy

$${\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)+{\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right)=S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right).$$

(35)

(1)

If U conserves energy

$${\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)+{\delta }^{\left(U\left(t\right)\right)}{E}_B\left({\rho }_B\right)+{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)=0.$$

(36)

Then, we conclude

(A)

If U conserves entropy: Combining Equations (33), (34), and (35) yields

$${\beta }_A{\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)+{\beta }_B{\delta }^{\left(U\left(t\right)\right)}{E}_B\left({\rho }_B\right)=S\left({\rho }^{\left(U\right)}|{\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}\right),$$

(37)

It is easy to check directly that

$$S\left({\rho }^{\left(U\right)}|{\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}\right)=S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right)+S\left({\rho }_A^{\left(U\right)}|{\rho }_{A,{\beta }_A}\right)+S\left({\rho }_B^{\left(U\right)}|{\rho }_{B,{\beta }_B}\right).$$

Thus

(38)

This last identity implies the Clausius-like inequality

$$0\le {\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)+{\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right)\le {\beta }_A{\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)+{\beta }_B{\delta }^{\left(U\left(t\right)\right)}{E}_B\left({\rho }_B\right).$$

(39)

(B)

For a general evolution U: Combining Equations (33) and (34)

$${\delta }^{(U(t))}{E}_A({\rho }_A)+{\delta }^{(U(t))}{E}_B({\rho }_B)=T_A[{\delta }^{(U(t))}S({\rho }_A)+S({\rho }_A^{(U)}|{\rho }_{A,{\beta }_A})]+T_B[{\delta }^{(U(t))}S({\rho }_B)+S({\rho }_B^{(U)}|{\rho }_{B,{\beta }_B})],$$

(40)

and thus

$${\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)+{\delta }^{\left(U\left(t\right)\right)}{E}_B\left({\rho }_B\right)\ge T_A{\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)+T_B{\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right).$$

(41)

This may be viewed as an inequality for free energies of A and B at the respective temperatures T_A and T_B. Note again that during the time evolution neither A nor B need remain in thermal states.

3.6. Case of Equality in (39) (2nd) and (41)

(A)

U conserves entropy. Equality in Equation (39) implies immediately that ${\rho }_A^{\left(U\right)}={\rho }_{A,{\beta }_A}$ and ${\rho }_B^{\left(U\right)}={\rho }_{B,{\beta }_B}$, in which case the energy of A and the energy of B have not changed and δ^(U(t)) S(ρ_A) = δ^(U(t)) S(ρ_B) = 0. From the first equality in Equation (38) one has

$${\rho }^{\left(U\right)}={\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}={\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B},$$

(42)

and one deduces that the state ρ has not changed.

(B)

General evolution U. If one has equality in Equation (41), it follows from Equation (40) the same results as above: the state ρ has not changed.

3.7. Interaction Energy and Relative Entropy

It is often assumed that the interaction energy between the parts of the complete system can be neglected but, obviously, if this were exactly true the subsystems would evolve independently. Of course, an interaction can be small but nevertheless have significant impact when it persists for long times. However, there are cases where even for short times the interaction cannot be neglected. Assume then that U conserves entropy and energy. Divide Equations (33) and (34) by β_B and add; then use the conservation of energy Equation (36) to eliminate δ^(U) E_B(ρ) and deduce after some calculations

$$-{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)=\left(1-\frac{{\beta }_A}{{\beta }_B}\right){\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)+T_{B}S\left({\rho }^{\left(U\right)}|{\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}\right),$$

(43)

so that

$$-{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)\ge \left(1-\frac{{\beta }_A}{{\beta }_B}\right){\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right).$$

(44)

In case of equality in Equation (44), one deduces that ${\rho }^{\left(U\right)}={\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}$ so that the state has not changed and δ^(U) E_A(ρ_A) = δ^(U) E_V (ρ) = 0. Moreover if δ^(U) E_A(ρ_A) is positive and T_A is larger than T_B, the interaction energy V is necessarily not zero and δ^(U) E_V (ρ) is negative.

Finally, if one could neglect the interaction energy, Equation (44) implies that energy flows from the hot to the cold system.

3.8. The Case β_A = β_B

Again assume that U conserves both entropy and energy. From Equation (43) and the conservation of energy, one deduces

$$-{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)={\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)+{\delta }^{\left(U\left(t\right)\right)}{E}_B\left({\rho }_B\right)=\frac{1}{\beta }S\left({\rho }^{\left(U\right)}|{\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}\right),$$

(45)

so that δ^(U) E_V (ρ) ≤ 0. Thus when A and B are initially at thermal equilibrium at the same temperature, the sum of the energies of A and B can only increase at the expense of the interaction energy [17].

4. Two Systems in Interaction With a Work Source

The problem of converting heat into work, first treated by Carnot, was at the origin of classical thermodynamics. Here, to address this issue, we explicitly introduce a work source interacting with two systems A and B, before focusing in Section 5 on the interaction of one system with a work source.

4.1. Hypotheses

We consider two systems A and B in interaction, with system A coupled to a work source. We represent the action of the work source by parameters, collectively denoted by λ, so that H_A = H_A(λ). Thus we assume that H_B and V are independent of λ. The action of the work source is given by an evolution of the parameters λ(t) imposed by an external agent. The total system A+B has a unitary or symplectic evolution U(t) depending explicitly on time-t. Clearly, U(t) conserves entropy but does not conserve energy, and instead one has the identity

$${\delta }^{\left(U\left(t\right)\right)}{E}_A\left(\rho \right)+{\delta }^{\left(U\left(t\right)\right)}{E}_B\left(\rho \right)+{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)+{\delta }^{\left(U\left(t\right)\right)}W=0,$$

(46)

with the following notation

$${\delta }^{\left(U\left(t\right)\right)}{E}_B\left(\rho \right)=\mathrm{Tr}\left(\left({\rho }^{\left(U\right)}-{\rho }_0\right)H_B\right)$$

(47)

$${\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)=\mathrm{Tr}\left(\left({\rho }^{\left(U\right)}-{\rho }_0\right)H_V\right)$$

(48)

$${\delta }^{\left(U\left(t\right)\right)}{E}_A\left(\rho \right)=\mathrm{Tr}\left({\rho }^{\left(U\right)}{H}_A\left({\lambda }^{\left(U\right)}\right)-{\rho }_0{H}_A\left({\lambda }_0\right)\right).$$

(49)

Here, λ₀ is the initial value of the parameter λ and λ^(U) is its final value at the end of the evolution U, this being an abbreviation for U(t), t being the final time. Note that Equation (49) extends the definition given near Equation (12). Such an extension is needed because we now allow changes in the Hamiltonian, represented by the additional variable λ. Equation (46) defines the work δ^(U)W, which is taken to be positive if the source receives work from the system A + B. (Note that this is opposite to the usual convention which was implicit in the opening paragraph of this paper.)

We assume that initially A and B are in independent thermal states, but A depends on the work source parameter λ. The complete initial state at time 0 is thus

$${\rho }_0={\rho }_{A,{\beta }_{A,}{\lambda }_0}\otimes {\rho }_{B,{\beta }_B},$$

(50)

with

$${\rho }_{A,{\beta }_{A,}{\lambda }_0}=\frac{e^{-{\beta }_A{H}_A\left({\lambda }_0\right)}}{Z_A\left({\beta }_A,{\lambda }_0\right)},$$

(51)

$$Z_A\left({\beta }_A,{\lambda }_0\right)=\mathrm{Tr}\left(e^{-{\beta }_A{H}_A\left({\lambda }_0\right)}\right),$$

(52)

and

$$Z_A\left({\beta }_A,{\lambda }_0\right)=\exp \left(-{\beta }_A{F}_A\left({\beta }_A,{\lambda }_0\right)\right).$$

(53)

Here, F_A(β_A, λ₀) denotes the equilibrium free energy for A. For a general state ρ of a system with energy H we define the non equilibrium free energy of the state ρ at temperature T to be

$$F\left(\beta ,\rho \right)=\mathrm{Tr}\left(\rho H\right)-\frac{1}{\beta }S\left(\rho \right).$$

(54)

In particular, for subsystem A one can define the non equilibrium free energy of the state ${\rho }_A^{(U)}$ at temperature β_A to be

$$F_A^{\left(U\right)}\left({\beta }_A\right)=F_A\left({\beta }_A,{\rho }_A^{\left(U\right)}\right)=\mathrm{Tr}\left({\rho }_A^{\left(U\right)}{H}_A\left({\lambda }^{\left(U\right)}\right)\right)-\frac{1}{{\beta }_A}S\left({\rho }_A^{\left(U\right)}\right).$$

(55)

In both of the above formulas temperature is not necessarily related to the state ρ.

4.2. Identities for the Work

We next establish the following two relations

(56)

and

(57)

with $F_A^{\left(U\right)}$ the non equilibrium free energy of ${\rho }_A^{(U)}$ calculated at the initial temperature T_A, namely Equation (55), $F_A^{\left(U\right)}={\mathrm{Tr}}_A({\rho }_A^{\left(U\right)}{H}_A\left({\lambda }^{\left(U\right)}\right)-T_{A}S\left({\rho }_A^{\left(U\right)}\right)$. We will comment on these relations in Par. 4.3 Remark 5: Here the free energy of Equation (55) is not a state function, because it is calculated at the initial temperature of A. Note our notation: When we write F_A(β_A, λ₀) this is the equilibrium free energy of the thermal state of A at temperature β_A and external parameter λ₀. When we write $F_A^{\left(U\right)}$ we mean the non-equilibrium free energy, as defined above.

Proof of Equation (56): One again starts from the fundamental identities Equations (7) and (25)

$${\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right)-{\beta }_B{\delta }^{\left(U\left(t\right)\right)}{E}_B\left(\rho \right)=-S\left({\rho }_B^{\left(U\right)}|{\rho }_{B,{\beta }_B}\right),$$

(58)

$${\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)-{\beta }_A{\mathrm{Tr}}_A\left(\left({\rho }_A^{\left(U\right)}-{\rho }_{A,{\beta }_A,{\lambda }_0}\right)H_A\left({\lambda }_0\right)\right)=-S\left({\rho }_A^{\left(U\right)}|{\rho }_{A,{\beta }_A,{\lambda }_0}\right),$$

(59)

and

$${\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)+{\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_B\right)=S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right).$$

(60)

Note that Equation (59) is just Equation (7) with the substitutions $\rho \to {\rho }_A^{\left(U\right)}$ and ${\rho }_B\to {\rho }_{A,{\beta }_A,{\lambda }_0}$. Therefore it contains the initial H_A(λ₀) (referring to ${\rho }_B\to {\rho }_{A,{\beta }_A,{\lambda }_0}$), not the final one. Equation (60) is likewise a rewriting of Equation (35).

Now add Equations (58) and (59) and subtract Equation (60), using the fact that

$$S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right)+S\left({\rho }_A^{\left(U\right)}|{\rho }_{A,0}\right)+S\left({\rho }_B^{\left(U\right)}|{\rho }_{B,0}\right)=S\left({\rho }^{\left(U\right)}|{\rho }_{A,0}\otimes {\rho }_{B,0}\right)$$

(61)

(this is the same as our unnumbered equation between Equations (37) and (38)) we obtain

$$-{\beta }_B{\delta }^{\left(U\left(t\right)\right)}{E}_B\left(\rho \right)-{\beta }_A{\mathrm{Tr}}_A\left(\left({\rho }_A^{\left(U\right)}-{\rho }_{A,{\beta }_A,{\lambda }_0}\right)H_A\left({\lambda }_0\right)\right)=-S\left({\rho }^{(U)}|{\rho }_{A,0}\otimes {\rho }_{B,0}\right).$$

(62)

Conservation of energy Equation (46) gives

(63)

We eliminate the second trace in the right hand side of Equation (63) using Equation (62), multiply by T_A to obtain Equation (56).

Proof of Equation (57): In Equation (56), we replace the relative entropy term, using

(64)

and use the definition of $F_A^{\left(U\right)}$ of Equation (55)

$$-\frac{1}{{\beta }_A}S-\left({\rho }_A^{\left(U\right)}|{\rho }_{A,{\beta }_A,{\mathrm{\lambda }}_0}\right)\text{Tr}\left({\rho }_A^{\left(U\right)}\left(H_A\left({\lambda }^{\left(U\right)}\right)-H_A\left({\lambda }_0\right)\right)\right)=F_A\left({\beta }_A,{\lambda }_0\right)-F_A^{\left(U\right)}.$$

(65)

4.3. Inequalities for the Work

From the identities of Equations (56) and (57), we deduce immediately corresponding inequalities

$${\delta }^{\left(U\left(t\right)\right)}W\le -{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)-{\mathrm{Tr}}_A\left({\rho }_A^{\left(U\right)}\left(H_A\left({\lambda }^{\left(U\right)}\right)-H_A\left({\lambda }_0\right)\right)\right)-\left(1-\frac{{\beta }_B}{{\beta }_A}\right){\delta }^{\left(U\left(t\right)\right)}{E}_B\left(\rho \right)$$

(66)

and

$${\delta }^{\left(U\left(t\right)\right)}W\le -{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)-\left(1-\frac{{\beta }_B}{{\beta }_A}\right){\delta }^{\left(U\left(t\right)\right)}{E}_B\left(\rho \right)+\left(F_A\left({\beta }_A,{\lambda }_0\right)-F_A^{\left(U\right)}\right).$$

(67)

The interpretation of inequality (67) is straightforward. If one can neglect the interaction energy, and if T_A = T_B, one gets an analogue of the familiar thermodynamic inequality giving an upper bound between the work received by the work source and the variation of the free energy of A,

$${\delta }^{\left(U\left(t\right)\right)}W\le F_A\left({\beta }_A,{\lambda }_0\right)-F_A^{\left(U\right)}.$$

(68)

Note that this relation is not restricted to cycles, nor to exchanges with thermal baths (which would stay in their initial thermal states).

Remark 6: Equation (57) contains much more information than inequalities Equations (67) and (68), since it expresses the difference between the maximum work that can be delivered by system A and the work effectively extracted from A, which is the energy dissipated in the process. It is expressed in terms of relative entropies, and it will be shown in Section 6 that it can be explicitly estimated, which yields a calculation of transport coefficients from first principles.

4.4. The Case of Equalities in Equations (66) and (67)

If one has equality in Equation (66), the relative entropy of Equation (56) must be equal to 0,

$$S\left({\rho }^{\left(U\right)}|{\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}\right)=0,$$

(69)

so ${\rho }^{\left(U\right)}={\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}$ and the final state has come back to its initial value. If we have equality in Equation (67), both relative entropies of Equation (57) are equal to 0. In this case ${\rho }_B^{\left(U\right)}$ has come back to its initial value ${\rho }_{B,{\beta }_B}$ and δ^(U)E_B(ρ) = 0. Then, one has

$${\delta }^{\left(U\left(t\right)\right)}W=-{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)+F_A\left({\beta }_A,{\lambda }_0\right)-F_A^{\left(U\right)}.$$

(70)

4.5. Case Where A is not Initially in Thermal Equilibrium

We shall now assume that the initial state is

$${\rho }_0={\rho }_{A,0}\otimes {\rho }_{B,{\beta }_0},$$

(71)

ρ_A,0 being a general state.

The following identity also holds:

$$-{\delta }^{(U(t))}W={\delta }^{(U(t))}{F}_A({\beta }_B,{\rho }_A)+{\delta }^{(U(t))}{E}_V(\rho )+T_B(S({\rho }_A^{(U)}|{\rho }_A^{(U)}\otimes {\rho }_B^{(U)})+S({\rho }_B^{(U)}|{\rho }_{B,{\beta }_B})).$$

(72)

This equation, true for any initial state ρ_A, can be found in [8,18]. Note the temperature of B appearing in the non equilibrium free energy of A

$$F_A\left({\beta }_B,{\rho }_A\right)=E_A\left({\rho }_A\right)-T_{B}S\left({\rho }_A\right).$$

(73)

If no work is performed, Equation (72) reduces to Equation (28) upon exchanging the labels A and B. Proof: Using S(ρ^(U)) = S(ρ₀) and the definition of the thermal state, one has

$$S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right)+S\left({\rho }_B^{\left(U\right)}|{\rho }_{B,{\beta }_B}\right)=-S\left({\rho }_{A,0}\right)-S\left({\rho }_{B,{\beta }_B}\right)+S\left({\rho }_A^{\left(U\right)}\right)+{\beta }_B{E}_B\left({\rho }_B^{\left(U\right)}\right)+\log Z_B\left({\beta }_B\right).$$

(74)

Then,

$$\log Z_B({\beta }_B)=-{\beta }_B{E}_B({\rho }_{B,{\beta }_B})+S({\rho }_{B,{\beta }_B}),$$

(75)

and Equation (74) becomes

$$S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right)+S\left({\rho }_B^{\left(U\right)}|{\rho }_{B,{\beta }_B}\right)={\delta }^{\left(U\left(t\right)\right)}S\left({\rho }_A\right)+{\beta }_B{\delta }^{\left(U\left(t\right)\right)}{E}_B\left({\rho }_B\right).$$

(76)

Using the conservation of energy, Equation (46), one obtains

$${\delta }^{\left(U\left(t\right)\right)}W=-{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)-{\delta }^{\left(U\left(t\right)\right)}{F}_A\left({\beta }_B,{\rho }_A\right)-T_B\left[S\left({\rho }^{\left(U\right)}|{\rho }_A^{\left(U\right)}\otimes {\rho }_B^{\left(U\right)}\right)+S\left({\rho }_B^{\left(U\right)}|{\rho }_{B,{\beta }_B}\right)\right].$$

(77)

Here

$${\delta }^{(U(t))}{F}_A({\beta }_B,{\rho }_A)={\delta }^{(U(t))}{E}_A({\rho }_A)-T_B{\delta }^{(U(t))}S({\rho }_A)$$

(78)

is the variation of the non equilibrium free energy of A calculated at the initial temperature T_B of B and

$${\delta }^{(U(t))}{E}_A({\rho }_A)={\mathrm{Tr}}_A\left(H_A({\lambda }^{(U)}){\rho }_A^{(U)}\right)-{\mathrm{Tr}}_A(H_A({\lambda }_0){\rho }_{A,0}).$$

(79)

In particular

$${\delta }^{(U(t))}W\le -{\delta }^{(U(t))}{E}_V(\rho )-{\delta }^{(U(t))}{F}_A({\beta }_B,{\rho }_A),$$

(80)

which gives a general upper bound for the work production from heat exchanges between an arbitrary system A and a system B initially at equilibrium (not necessarily a heat bath). In this relation, equality is realized if and only if the two relative entropy terms of Equation (77) are zero, which means that

$${\rho }_B^{(U)}={\rho }_{B,{\beta }_B}\text{and}{\rho }^{(U)}={\rho }_A^{(U)}\otimes {\rho }_{B,{\beta }_B}.$$

(81)

Remark 7: By convention, a thermal bath is in a thermal state which is assumed to remain constant during the evolution. Our system B is not a thermal bath in this sense; its state varies during the evolution.

5. A System Coupled Only to an External Work Source

While Carnot and many others primarily considered model machines exchanging heat with several reservoirs, new thermodynamic relations have recently been announced [19] concerning exchanges of a single system with a work source. We now focus on this case.

5.1. Hypotheses

We consider a system coupled only to an external work source, so that the Hamiltonian of the system is H(λ).

At time t = 0, the state of the system is supposed to be a thermal state ${\rho }_{{\beta }_0}({\lambda }_0)$. The external observer imposes an evolution λ(t) of the parameter λ from λ₀ to λ^(U), inducing a unitary or symplectic evolution U of the whole system. The work that the external observer must perform to realize this evolution is obviously the variation of the energy of the system. With the convention of Section 4.1, we denote by δ^(U(t))W the work counted positive if the external source receives it from the system. We are now in a particular case of Section 4.1 when the system is A, there is no system B and no V. Thus from Equation (46)

$${\delta }^{(U(t))}W=-{\delta }^{(U(t))}E(\rho )=\text{Tr}({\rho }_{{\beta }_0}({\lambda }_0)H({\lambda }_0)-{\rho }^{(U)}H({\lambda }^{(U)})).$$

(82)

5.2. Identities for the Work

From Equations (56) and (57) we obtain immediately

$${\delta }^{(U(t))}W=-\mathrm{Tr}\left({\rho }^{(U)}(H({\lambda }^{(U)})-H({\lambda }_0))\right)-\frac{1}{{\beta }_0}S({\rho }^{(U)}|{\rho }_{{\beta }_0}({\lambda }_0))$$

(83)

and

$${\delta }^{(U(t))}W=F({\beta }_0,{\lambda }_0)-F^{(U)},$$

(84)

with F^(U) the non equilibrium free energy at temperature β₀.

$$F^{(U)}=\mathrm{Tr}({\rho }^{(U)}H({\lambda }^{(U)}))-\frac{1}{{\beta }_0}S({\rho }^{(U)})$$

(85)

We now prove the following identity

$${\delta }^{(U(t))}W=F({\beta }_0,{\lambda }_0)-F({\beta }_0,{\lambda }^{(U)})-\frac{1}{{\beta }_0}S({\rho }^{(U)}|{\rho }_{{\beta }_0}({\lambda }^{(U)})).$$

(86)

This is a particular case of the result of [19].

Proof of Equation (86): We start from Equation (84) written as

$${\delta }^{(U(t))}W=F({\beta }_0,{\lambda }_0)-F^{(U)}=F({\beta }_0,{\lambda }_0)-F({\beta }_0,{\lambda }^{(U)})+F({\beta }_0,{\lambda }^{(U)})-F^{(U)}.$$

(87)

Now

$${\beta }_0(F^{(U)}-F({\beta }_0,{\lambda }^{(U)}))=-S({\rho }^{(U)})+{\beta }_0\mathrm{Tr}(H({\lambda }^{(U)}){\rho }^{(U)})-{\beta }_{0}F({\beta }_0,{\lambda }^{(U)}).$$

(88)

But

$$S({\rho }^{(U)}|{\rho }_{{\beta }_0}({\lambda }^{(U)}))=-S({\rho }^{(U)})+{\beta }_0\mathrm{Tr}(H({\lambda }^{(U)}){\rho }^{(U)})+\log Z({\beta }_0,{\lambda }^{(U)}),$$

(89)

so that comparing Equations (88) and (89), one has

$${\beta }_0(F^{(U)}-F({\beta }_0,{\lambda }^{(U)}))=S({\rho }^{(U)}|{\rho }_{{\beta }_0}({\lambda }^{(U)})),$$

(90)

and from Equation (87) we then deduce Equation (86).

Remark 8: Since the transition under discussion is adiabatic, free energy is less suitable for inequalities of the form (86) than is internal energy. See Section 5.6.

5.3. Inequalities for the Work

5.3.1. From Equation (83)

From Equation (83) we deduce

$${\delta }^{(U(t))}W\le -\mathrm{Tr}({\rho }^{(U)}(H({\lambda }^{(U)})-H({\lambda }_0))),$$

(91)

with equality if and only if ${\rho }^{(U)}={\rho }_{{\beta }_0}({\mathrm{\lambda }}_0)$,i.e., the final state is the initial state.

5.3.2. From Equation (86)

From Equation (86) we deduce

$${\delta }^{(U(t))}W\le F({\beta }_0,{\lambda }_0)-F({\beta }_0,{\lambda }^{(U)})$$

(92)

with equality if and only if

$${\rho }^{(U)}={\rho }_{{\beta }_0}({\lambda }^{(U)}).$$

(93)

That is, ρ^(U) is the thermal state at the initial temperature and final value λ^(U) of λ. Note that a necessary condition for this is that the entropy of the final thermal state is the same as the entropy of the initial state.

5.4. Relation to the Identity of Jarzynski

Let z denote a point in the phase space of the system. In this section we assume that the dynamics is classical.

We denote by z(s|z₀) the classical trajectory of the phase space point at time s starting from z₀ at time s = 0, for the classical evolution U. The external observer imposes the variation λ(s) of λ from λ₀ to λ^(U) = λ(t). The identity of Jarzynski is [20]:

(94)

Because the exponential function is strictly convex, Jensen’s inequality implies that

(95)

so that using Equation (94) and taking the logarithm, one obtains

$${\delta }^{(U(t))}W\le F({\beta }_0,{\lambda }_0)-F({\beta }_0,{\lambda }^{(U)}),$$

(96)

which is the inequality (92).

But if the inequality (96) is an equality, we deduce ${\rho }^{(U)}={\rho }_{{\beta }_0}({\lambda }^{(U)})$ as in Equation (93), but we also deduce that the inequality of Jensen (95) is an equality. Because the exponential function is strictly convex, this implies that the differences

$$H(z(t|z_0),{\lambda }^{(U)})-H(z_0,{\lambda }_0)=C,$$

(97)

where C is a constant independent of z₀ (but obviously dependent on λ₀, λ^(U) and t); in other words, the “microscopic work” is independent of the microscopic trajectory. Although this equality would seem impossible, it turns out that identity (97) can be realized for certain systems and evolutions of λ (see appendix A).

5.5. Effective Temperatures

Let H(λ) be a Hamiltonian depending on λ and ρ a state (classical or quantum) with energy E(ρ) = Tr (ρH(λ)). We can define two temperatures for ρ.

(i)

The temperature β_e(ρ, λ) is the temperature such that

$$E(\rho )=E({\beta }_e,\lambda ),$$

(98)

with $E({\beta }_e,\lambda )=\mathrm{Tr}({\rho }_{{\beta }_e}(\lambda )H(\lambda ))$. It is known that ∂E(β, λ)/∂β < 0, so that Equation (98) defines β_e unambiguously. The basic identity (4) shows that

$$S({\rho }_{{\beta }_e}(\lambda ))-S(\rho )=S(\rho |{\rho }_{{\beta }_e}(\lambda )),$$

(99)

so that

$$S({\rho }_{{\beta }_e}(\lambda ))\ge S(\rho ),$$

(100)

which is the well known fact that ${\rho }_{{\beta }_e}(\lambda )$ maximizes the entropy among all states ρ having a fixed energy. The quantity β_e(ρ, λ) can be called the effective temperature.

(ii)

There is a second temperature β_a(ρ, λ) such that

$$S(\rho )=S({\beta }_a,\lambda ).$$

(101)

In this definition, S(β, λ) is the entropy of a thermal state with temperature β and external parameter λ. We call this the adiabatic temperature, and by the same arguments as given above it is well-defined. From Equation (100) and Equation (101), one has

$$S({\beta }_e,\lambda )\ge S({\beta }_a,\lambda ).$$

(102)

Because

$${\frac{\partial E}{\partial S(\beta ,\lambda )}|}_{{}_{\lambda \text{fixed}}}=\frac{1}{\beta }$$

(103)

we deduce from Equation (102) that

$$E({\beta }_a,\lambda )\le E({\beta }_e,\lambda )=E(\rho )$$

(104)

and

$${\beta }_a\ge {\beta }_e.$$

(105)

Because S is a strictly increasing function of E (for λ fixed), one sees that in Equation (102) or (104), one has equality if and only if β_a = β_e. Moreover, one has the identity

$$S\left(\rho |{\rho }_{{\beta }_a}\left(\lambda \right)\right)-S\left(\rho |{\rho }_{{\beta }_e}\left(\lambda \right)\right)=S\left({\rho }_{{\beta }_e}\left(\lambda \right)|{\rho }_{{\beta }_a}\left(\lambda \right)\right),$$

(106)

which can immediately be verified.

5.6. A More Precise Expression for the Work

In thermodynamics, for an adiabatic evolution, the work is related to the internal energy by dE = −dW, rather than to the free energy. Similarly, the work is related to the adiabatic temperature rather than to the effective energy temperature.

Given the state ρ^(U) (corresponding to the evolution U, the parameter varying from λ₀ to λ^(U)) we can define the adiabatic temperature ${\beta }_a^{\left(U\right)}$ such that

$$S\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right)=S\left({\rho }^{\left(U\right)}\right)=S\left({\beta }_0,{\lambda }_0\right).$$

(107)

We prove the following identity

$${\delta }^{\left(U\left(t\right)\right)}W=E\left({\beta }_0,{\lambda }_0\right)-E\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right)-\frac{1}{{\beta }_a^{\left(U\right)}}S\left({\rho }^{\left(U\right)}|{\rho }_{{\beta }_a^{\left(U\right)}}\left({\lambda }^{\left(U\right)}\right)\right).$$

(108)

Proof of Equation (108): One has by definition (82)

$$-{\delta }^{\left(U\left(t\right)\right)}W=E\left({\rho }^{\left(U\right)}\right)-E\left({\beta }_0,{\lambda }_0\right)=E\left({\rho }^{\left(U\right)}\right)-E\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right)+E\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right)-E\left({\beta }_0,{\lambda }_0\right).$$

(109)

Then

(110)

because $S\left({\rho }^{\left(U\right)}\right)=S\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right)$ by the definition (107). From this result and Equation (109) we deduce Equation (108).

As a consequence of Equation (108), we deduce the inequality

$${\delta }^{\left(U\left(t\right)\right)}W\le E\left({\beta }_0,{\lambda }_0\right)-E\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right).$$

(111)

In standard thermodynamics, for system thermally isolated and coupled to a work source, one has dE = −dW, because δ^(U(t)) S = 0 for an adiabatic (thermally isolated) process and we recover equality in Equation (111). In this situation, the inequality (92) comparing the work to the difference of free energies is not relevant, because the temperature does not remain constant.

Note that the work upper bound (111), given in terms of energy and the adiabatic temperature, is sharper than the bound given by (92), which is in terms of free energy. This is proved in the next subsection.

5.7. Upper Bounds on the Work Delivered by a System. Comparison of Equations (92) and (111)

We next show that using internal energy for the work inequality gives a sharper result than using the free energy. Specifically,

$${\delta }^{\left(U\left(t\right)\right)}W\le E\left({\beta }_0,{\lambda }_0\right)-E\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right)\le F\left({\beta }_0,{\lambda }_0\right)-F\left({\beta }_0,{\lambda }^{\left(U\right)}\right).$$

(112)

Proof of Equation (112): We need only prove that

$$\mathrm{\Delta }\equiv F\left({\beta }_0,{\lambda }_0\right)-E\left({\beta }_0,{\lambda }_0\right)-\left(F\left({\beta }_0,{\lambda }^{\left(U\right)}\right)-E\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right)\right)\ge 0.$$

(113)

Using the definition of the equilibrium free energy and Equation (107) we have

$$\mathrm{\Delta }=-\frac{1}{{\beta }_0}\left[S\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right)-S\left({\beta }_0,{\lambda }^{\left(U\right)}\right)\right]+\left[E\left({\beta }_a^{\left(U\right)},{\lambda }^{\left(U\right)}\right)-E\left({\beta }_0,{\lambda }^{\left(U\right)}\right)\right].$$

(114)

Note that in Equation (114) all terms involving λ are evaluated at λ^(U). Therefore

$$\mathrm{\Delta }={\displaystyle {\int }_{{\beta }_0}^{{\beta }_a^{\left(U\right)}}\left[\frac{\partial E\left(\beta ,{\lambda }^{\left(U\right)}\right)}{\partial \beta }-\frac{1}{{\beta }_0}\frac{\partial S\left(\beta ,{\lambda }^{\left(U\right)}\right)}{\partial \beta }\right]}d\beta .$$

(115)

But

$$\frac{\partial S\left(\beta ,\lambda \right)}{\partial \beta }=\frac{\partial S}{\partial E}\frac{\partial E\left(\beta ,\lambda \right)}{\partial \beta }=\beta \frac{\partial E\left(\beta ,\lambda \right)}{\partial \beta }.$$

(116)

Using Equation (116) in Equation (115), we obtain

$$\mathrm{\Delta }={\displaystyle {\int }_{{\beta }_0}^{{\beta }_a^{\left(U\right)}}\frac{\partial E\left(\beta ,{\lambda }^{\left(U\right)}\right)}{\partial \beta }\left[1-\frac{\beta }{{\beta }_0}\right]d\beta }.$$

(117)

But $\frac{\partial E\left(\beta ,{\lambda }^{\left(U\right)}\right)}{\partial \beta }$ < 0, so that ∆ ≥ 0. Note that this does not depend on which of β₀ and ${\beta }_a^{\left(U\right)}$ is larger.

5.8. The Case of Equalities in Equations (111) and (92)

5.8.1. Equality in Equation (111)

In this case, one has $S\left({\rho }^{\left(U\right)}|{\rho }_{{\beta }_a^{\left(U\right)}}\left({\lambda }^{\left(U\right)}\right)\right)=0$ in Equation (108) so

$${\rho }^{\left(U\right)}={\rho }_{{\beta }_a^{\left(U\right)}}\left({\lambda }^{\left(U\right)}\right).$$

(118)

In particular, ρ^(U) is a thermal state so that

$${\beta }_e^{\left(U\right)}={\beta }_a^{\left(U\right)}.$$

(119)

However, if one has equality in Equation (111), this does not improve the upper bound of Equation (92) for the free energy,

$${\delta }^{\left(U\left(t\right)\right)}W\le F\left({\beta }_0,{\lambda }_0\right)-F\left({\beta }_0,{\lambda }^{\left(U\right)}\right).$$

(120)

In other words, the optimal bound for δ^(U(t)) W is given by the internal energy and not the free energy (so that the internal energy in general yields a better bound than that given in [20]).

5.8.2. Equality in Equation (92)

From Equation (93) we deduce that

$${\rho }^{\left(U\right)}={\rho }_{{\beta }_0}\left({\lambda }^{\left(U\right)}\right),$$

(121)

so that ρ^(U) is a thermal state and thus

$${\beta }_e^{\left(U\right)}={\beta }_0={\beta }_a^{\left(U\right)}.$$

(122)

This implies that we also have equality in Equation (111)

$${\delta }^{\left(U\left(t\right)\right)}W=E\left({\beta }_0,{\lambda }_0\right)-E\left({\beta }_0,{\lambda }^{\left(U\right)}\right).$$

(123)

5.9. The Case λ^(U) = λ₀

If one assumes that the final value λ^(U) of λ is equal to its initial value, we see immediately that ${\beta }_a^{\left(U\right)}={\beta }_0$.Indeed

$$S\left({\beta }_a^{\left(U\right)},{\lambda }_0\right)=S\left({\rho }^{\left(U\right)}\right)=S\left({\beta }_0,{\lambda }_0\right),$$

(124)

so that the temperatures are equal ${\beta }_a^{\left(U\right)}={\beta }_0$. In this case, one has from Equation (108)

$${\delta }^{\left(U\left(t\right)\right)}W=-\frac{1}{{\beta }_0}S\left({\rho }^{\left(U\right)}|{\rho }_{{\beta }_0}\left({\lambda }_0\right)\right)\le 0,$$

(125)

with equality if and only if

$${\rho }^{\left(U\right)}={\rho }_{{\beta }_0}\left({\lambda }_0\right),$$

(126)

so that the state has returned to its initial value.

Remark 9: If the external observer imposes a variation λ(t) of the control parameter with λ(0) = λ₀, λ(t₁) = λ₁, λ(t_f) = λ₀, inequality (125) says that at the end of the cycle, the observer has always lost work. In particular, the work that the external observer has put in the system in the time interval [0, t₁] cannot be entirely recovered in the time interval [t₁, t_f] whatever one does, except if the final state ρ^(U) is the initial state.

Remark 10: When λ^(U) = λ₀, one can also recover Equation (125) from the identity (86). This identity reduces to

$${\delta }^{\left(U\left(t\right)\right)}W=-\frac{1}{{\beta }_0}S\left({\rho }^{\left(U\right)}|{\rho }_{{\beta }_0}\left({\lambda }_0\right)\right).$$

(127)

6. Relative Entropy, Energy Dissipation and Fourier’s Law

In this Section we derive dissipation in the quantum context and show it to be intimately related to the relative entropy.

6.1. The Born Approximation

A quantum system has a Hamiltonian

$$H=H_0+V.$$

(128)

Let ${\psi }_k^{\left(0\right)},E_k^{\left(0\right)}$ be the eigenstates and eigenvalues of H₀. In the Born approximation, the state $|{\psi }_n^{\left(0\right)}\rangle$ becomes at time t a state $|{\psi }_n\left(t\right)\rangle$ with

$$|{\psi }_n\left(t\right)\rangle ={\displaystyle \sum _k{a}_k^{\left(n\right)}\left(t\right)e^{-i{E}_k^{\left(0\right)}t/\hslash }|{\psi }_k^{\left(0\right)}\rangle }.$$

(129)

The quantities $a_k^{\left(n\right)}\left(t\right)={\delta }_{k,n}+{\tilde{a}}_k^{\left(n\right)}\left(t\right)$ satisfy

$$i\hslash \frac{\mathrm{d}{\tilde{a}}_k^{\left(n\right)}}{\mathrm{d}t}={\displaystyle \sum _l{V}_{k,l}}\left(t\right)\left({\delta }_{l,n}+{\tilde{a}}_l^{\left(n\right)}\right),$$

(130)

where

$$V_{k,l}\left(t\right)=V_{k,l}\exp \left(\frac{i}{\hslash }\left(E_k^0-E_l^{\left(0\right)}\right)t\right).$$

(131)

We assume here V_n,_n = 0 for all n. One readily deduces that in the Born approximation

$$a_k^{\left(n\right)}\left(t\right)=\frac{V_{k,n}}{E_k^{\left(0\right)}-E_n^{\left(0\right)}}\left(1-e^{i\left(E_k^{\left(0\right)}-E_n^{\left(0\right)}\right)\frac{t}{\hslash }}\right)\left(k\ne n\right)$$

(132)

and by unitarity ${\displaystyle {\sum }_k{\left|a_k^{\left(n\right)}\left(t\right)\right|}^2=1,}$, so to second order in ${\tilde{a}}_k^{\left(n\right)}$

$$2\text{Re}{\tilde{a}}_n^{\left(n\right)}\left(t\right)=-{\displaystyle \sum _{k\ne n}{\left|{\tilde{a}}_k^{\left(n\right)}\left(t\right)\right|}^2.}$$

(133)

Let ρ₀ be an initial state diagonal in the basis ${\psi }_n^{\left(0\right)}$

$${\rho }_0={\displaystyle \sum p_{0,n}|{\psi }_n^{\left(0\right)}\rangle }\langle {\psi }_n^{\left(0\right)}|.$$

(134)

Then, at time t, the state becomes

(135)

If L is a Hermitian operator diagonal in the basis ${\psi }_n^{\left(0\right)}$ with eigenvalues λ_n, using Equation (135) one obtains in the Born approximation

$$\mathrm{Tr}\left(L\left({\rho }^{\left(U\left(t\right)\right)}-{\rho }_0\right)\right)=\frac{1}{2}{\displaystyle \sum _{k\ne n}{\left|{\tilde{a}}_k^{\left(n\right)}\left(t\right)\right|}^2\left({\lambda }_k-{\lambda }_n\right)\left(p_{0,n}-p_{0,k}\right).}$$

(136)

6.2. Two Interacting Systems

We consider two quantum systems A, B with Hamiltonians H_A, H_B respectively, interacting. Denote by V = V_A,_B the interaction energy and

$$H=H_A+H_B+V.$$

(137)

We call $|{\psi }_{A,k}^{\left(0\right)}\rangle ,E_{A,k}^{\left(0\right)}(\text{resp.}|{\psi }_{B,l}^{\left(0\right)}\rangle ,E_{B,l}^{\left(0\right)})$ the eigenstates and eigenvalues of H_A (resp. H_B), and we apply the Born approximation to H, with H₀ = H_A + H_B. The non perturbed Hamiltonian H₀ has eigenstates $|{\psi }_{A,k}^{\left(0\right)}\rangle |{\psi }_{B,l}^{\left(0\right)}\rangle$ with eigenvalues $E_{A,k}^{\left(0\right)}+E_{B,l}^{\left(0\right)}$.

We assume that at time t = 0, the state of the system A + B is ρ₀ = ρ_A ⊗ ρ_B with

(138)

so that they are diagonal in the eigenbasis of H_A and H_B and therefore commute with H_A +H_B. At time t, the initial state ρ₀ = ρ_A ⊗ ρ_B evolves to ρ(t). Then

$$S\left(\rho \left(t\right)|{\rho }_A\otimes {\rho }_B\right)=\mathrm{Tr}\left(\rho \left(t\right)\log \rho \left(t\right)\right)-\mathrm{Tr}\left(\rho \left(t\right)\log \left({\rho }_A\otimes {\rho }_B\right)\right).$$

(139)

But S(ρ(t)) = S(ρ₀) by unitarity of the evolution, so that

$$S\left(\rho \left(t\right)|{\rho }_A\otimes {\rho }_B\right)=-\mathrm{Tr}\left[\left(\rho \left(t\right)-{\rho }_A\otimes {\rho }_B\right)\left(\log {\rho }_A+\log {\rho }_B\right)\right].$$

(140)

This is of the form of Equation (136) with

$$L=-\left(\log {\rho }_A+\log {\rho }_B\right).$$

(141)

L has eigenvectors $|{\psi }_{A,k}^{\left(0\right)}\rangle |{\psi }_{B,l}^{\left(0\right)}\rangle$ with eigenvalues log p_A,_k + log p_B,_l; ρ_A ⊗ ρ_B has the same eigenvectors with eigenvalues p_A,_k + p_B,_l. Applying Equation (136), one obtains in the Born approximation

(142)

Notice that the quantity in the right hand side is automatically non-negative. Here, we have

(143)

with $V_{\left(k,l\right)}^{\left(n,m\right)}=\langle {\psi }_{A,n}^{\left(0\right)}\otimes {\psi }_{B,m}^{\left(0\right)}|V|{\psi }_{A,k}^{\left(0\right)}\otimes {\psi }_{B,l}^{\left(0\right)}\rangle .$.

We also deduce from this result that in this approximation S(ρ(t)|ρ_A ⊗ ρ_B) = 0 if and only if V = 0 (recall that the diagonal elements of V are 0).

6.3. The Case Where Both Initial States are Thermal

Assume that at time $t=0,{\rho }_A={\rho }_{A,{\beta }_A}$ and ${\rho }_B={\rho }_{B,{\beta }_B}$ are the thermal states of A and B respectively. From Equation (37) one has

$${\beta }_A{\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)+{\beta }_B{\delta }^{\left(U\left(t\right)\right)}{E}_B\left({\rho }_B\right)=S\left(\rho \left(t\right)|{\rho }_{A,{\beta }_B}\right).$$

(144)

Moreover, from conservation of energy

$${\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)+{\delta }^{\left(U\left(t\right)\right)}{E}_B\left({\rho }_B\right)+{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)=0,$$

(145)

so that eliminating δ^(U(t)) E_B(ρ_B), one obtains

$$\left({\beta }_A-{\beta }_B\right){\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)={\beta }_B{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)+S\left(\rho \left(t\right)|{\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}\right).$$

(146)

We now estimate both terms on the right hand side of Equation (146).

6.3.1. Estimate of the Relative Entropy

From Equation (142) we deduce

(147)

Moreover, when t → ∞, as in the usual Born approximation, Equation (143) shows that

$${\left|{\tilde{a}}_{\left(k,l\right)}^{\left(n,m\right)}(t)\right|}^2\simeq \frac{2\pi }{\hslash }{\left|V_{\left(k,l\right)}^{\left(n,m\right)}\right|}^2\delta \left(E_{A,k}^{\left(0\right)}+E_{B,l}^{\left(0\right)}-E_{A,n}^{\left(0\right)}-E_{B,m}^{\left(0\right)}\right)t.$$

(148)

Thus if f_A and f_B denote the density of states for A and B, we obtain from Equation (147)

(149)

6.3.2. Estimate of the Interaction Energy

Because δ^(U(t)) V (ρ) = −δ^(U(t)) E_A(ρ) − δ^(U(t)) E_B(ρ), one has

$${\delta }^{\left(U\left(t\right)\right)}{V}_{A,B}\left(\rho \right)=\mathrm{Tr}\left(-\left(H_A+H_B\right)\left(\rho \left(t\right)-{\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_A}\right)\right).$$

(150)

This is of the form of Equation (136) with L = −H_A − H_B, and so

(151)

Up to a sign, this expression is formally identical to the expression Equation (142), except that the difference of energies (E_A,_k + E_B,_l − E_A,_n − E_B,_m) replaces the quantity β_A(E_A,_k − E_A,_n) + β_B(E_B,_l − E_B,_m). As a consequence E_A,_k + E_B,_l − E_A,_n − E_B,_m partially cancels the denominator of ${\left|{\tilde{a}}_{\left(k,l\right)}^{\left(n,m\right)}\left(t\right)\right|}^2$ and one sees that ${\beta }_B{\delta }^{\left(U\left(t\right)\right)}{E}_V\left(\rho \right)$ is negligible when t → ∞.

Then from Equations (146) and (149), one sees that

$${\delta }^{\left(U\left(t\right)\right)}{E}_A\left({\rho }_A\right)\simeq \frac{S\left(\rho \left(t\right)|{\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}\right)}{{\beta }_A-{\beta }_B}\simeq \left({\beta }_A-{\beta }_B\right)Kt.$$

(152)

In Equation (152) K is the positive constant

(153)

with

(154)

It is obvious that φ ≥ 0. Note that K does not vanish for β_A close to β_B.

The expression (152) is a form of Fourier’s law for heat transport from B to A, (β_A − β_B)K being the rate of dissipation. In this case, one sees that the significance of the relative entropy $S\left(\rho \left(t\right)|{\rho }_{A,{\beta }_A}\otimes {\rho }_{B,{\beta }_B}\right)$ is that of a transport coefficient, here the transport of energy from one part of a system to another part.

7. Coarse Grained States

Coarse-graining is omnipresent in in macroscopic and mesoscopic physics, since microscopic variables are often not what is observed. In general coarse-graining represents a loss of information, hence an increase in entropy. In this section we consider a variety of coarse-graining procedures, and consistent with our work in this article, relative entropy plays a significant role both in the definition of coarse-graining and in the measures of entropy increase.

7.1. Definition

Let ρ and ρ′ be two states of the same system (classical or quantum). We say that ρ′ is obtained from ρ by a coarse graining operation if

$$\mathrm{Tr}\left(\left(\rho -\rho \prime \right)\log \rho \prime \right)=0.$$

(155)

The idea is that the information associated with ρ′ (namely log ρ′) is the same whether one averages with ρ′ or with the more detailed distribution ρ. Using the basic identity, Equation (4), we can say that ρ′ is obtained from ρ by a coarse graining operation, if and only if

$$S\left(\rho \prime \right)-S\left(\rho \right)=S\left(\rho |\rho \prime \right).$$

(156)

In particular, S(ρ′) ≥ S(ρ), so that the entropy increases by coarse-graining. (See the comment after Equation (3).)

A coarse-graining mapping is a mapping Γ which associates to any state ρ (or to some states of a given class), a coarse grained state ρ′ = Γ(ρ).

7.2. Examples of Coarse-graining Mappings

Example 1: Maximum entropy.

Let A₁,…, A_n be observables of the system, so they are either functions in the phase space or hermitian operators on the Hilbert space of the system. We consider the class of states ρ such that

$$\mathrm{Tr}\left(A_{i\rho }\right)<\infty ,i=1,\mathrm{..},n.$$

(157)

One can then consider the state ρ′ such that ρ′ has maximal entropy given the relation

$$\mathrm{Tr}\left(A_i{\rho }^{\prime }\right)=\mathrm{Tr}\left(A_i\rho \right).$$

(158)

It is immediately seen that

$${\rho }^{\prime }=C\exp \left({\displaystyle \sum _{i=1}^n{\alpha }_i{A}_i}\right),$$

(159)

where C is a normalization constant and α_i are the “conjugate parameters”, (provided ρ′ is normalizable). The mapping Γ: ρ → ρ′ is indeed a coarse grain mapping in the sense of the previous definition, because by Equation (159)

$$\mathrm{Tr}\left(\left(\rho -{\rho }^{\prime }\right)\log {\rho }^{\prime }\right)={\displaystyle \sum _{i=1}^n\mathrm{Tr}}\left(\left(\rho -{\rho }^{\prime }\right)A_i\right)=0.$$

(160)

In particular, one has Equation (156).

The case of the thermal state is the best known, where one takes A = H, the Hamiltonian of the system.

Example 2: Naive coarse graining; the observables as characteristic functions.

(i)

Classical case: Let Z be the phase space of the system and {Z_i} a finite partition of Z ( $Z={\cup }_{i=1}^n{Z}_i$ and Z_i∩Z_j = Ø for i ≠ j). We choose $A_i={\chi }_{Z_i}$ (i.e. the characteristic function of Z_i). This is a particular case of example 1 and if ρ is a state

$${\rho }^{\prime }=C\exp \left({\displaystyle \sum _{i=1}^n{\alpha }_i{\chi }_{Z_i}}\right).$$

(161)

Using the condition (156), namely,

$${\displaystyle {\int }_{Z_i}{\rho }^{\prime }\mathrm{d}z}={\displaystyle {\int }_{Z_i}\rho \mathrm{d}z},$$

(162)

one can deduce from Equations (161) and (162)

$${\rho }^{\prime }{|}_{Z_i}=\frac{1}{\text{Vol}\left({\mathrm{Z}}_i\right)}{\displaystyle {\int }_{Z_i}\rho \mathrm{d}z}\text{or}{\rho }^{\prime }={\displaystyle \sum _{i=1}^n({\rho }^{\prime }{|}_{Z_i}){\chi }_{Z_i}.}$$

(163)

This equation implies that ρ′ is normalized ∫ ρ′dz = 1. We recover the usual coarse graining.

(ii)

Quantum case: Let $\mathscr{H}$ be the Hilbert space of the system and P_i a resolution of the identity by orthogonal projectors

$$\text{Id}={\displaystyle \sum P_i}\text{and}{P}_i{P}_j=P_i{\delta }_{i,j}.$$

(164)

Then the analogue of Equation (163) is

$${\rho }^{\prime }={\displaystyle \sum _{i=1}^n\frac{\mathrm{Tr}{\left(\rho P\right)}_i}{\dim P_i\left(\mathscr{H}\right)}}{P}_i.$$

(165)

Example 3: Coarse graining by marginals.

(i)

Classical case: We assume that the system consists of several parts, and that its phase space is a Cartesian product, $Z={\displaystyle {\prod }_{i=1}^n{Z}_i}$, corresponding to various subsystems with phase space Z_i. If ρ is a state on Z, we denote by ρ_i its marginal probability distribution on Z_i, so

$${\rho }_i\left(z_i\right)=\int \dots \int \rho \left({\zeta }_1,\dots ,{\zeta }_{i-1},z_i,{\zeta }_{i+1},\dots ,{\zeta }_n\right){\displaystyle \prod _{j\ne i}\mathrm{d}{\zeta }_j.}$$

(166)

Let Γ be the mapping that associates the product of its marginals to ρ(z)

$$\Gamma \left(\rho \right)\left(z_1,\dots ,z_n\right)={\displaystyle \prod _{i=1}^n{\rho }_i\left(z_i\right).}$$

(167)

Then the condition (155) is satisfied. It is easy to see that ${\displaystyle {\prod }_{i=1}^n{\rho }_i\left(z_i\right)}$ is the state ρ′ that maximizes the entropy among all the states ρ″ such that ${{\rho }^{″}}_i={\rho }_i$ for any i.

(i)

Quantum case. The Hilbert space of the system is

$$\mathscr{H}=\underset{i=1}{\overset{n}{\otimes }}{\mathscr{H}}_i,$$ (168)

where the ${\mathscr{H}}_i$ are the Hilbert spaces of the subsystems. If ρ is a state, then its marginal state on ${\mathscr{H}}_i$ is the partial trace on the Hilbert space ${\mathcal{K}}_i$, which is the tensor product of the Hilbert spaces ${\mathscr{H}}_j$ for j different from i

$${\rho }_i=T{r}_{{\mathcal{K}}_i}\rho$$

(169)

and the mapping Γ,

$$\Gamma \left(\rho \right)=\underset{n}{\overset{i=1}{\otimes }}{\rho }_i,$$

(170)

is a coarse grained mapping. Γ(ρ) is again the state ρ′ which maximizes the entropy among all states ρ″ such that ${{\rho }^{″}}_i={\rho }_i$ for all i.

Example 4: Decomposition of Z.

If $Z={\cup }_{i=1}^n{Z}_i$, but the Z_i do not form a partition of Z (they can have intersections of non-zero measure), one can still apply Example 1 to $A_i={\chi }_{Z_i}$ and obtain

$${\rho }^{\prime }=C\exp \left({\displaystyle \sum {\alpha }_i{\chi }_{z_i}}\right).$$

(171)

But now Equation (163) is no longer valid because, for given z, there will be in general several i with z ∈ Z_i.

7.3. Coarse Graining and Relative Entropy

(i)

The case of the naive coarse-graining is distinguished among all types of coarse-graining by the following property. Let $Z={\cup }_{i=1}^n{Z}_i$ a partition of the phase space and p, q two probability distributions on Z. Let $\overline{p}=\Gamma p$ and $\overline{q}=\Gamma q$ be the coarse grained states of p and q associated to this partition. Then one has

$$S\left(\overline{p}|\overline{q}\right)\le S\left(p|q\right).$$

(172)

Proof: call $p_i={\int }_{Z_i}p\mathrm{d}z$ and $q_i={\int }_{Z_i}q\mathrm{d}z$. We have, using the definition of $\overline{p}$ and $\overline{q}$

$$S\left(\overline{p}|\overline{q}\right)={\displaystyle \sum _{i=1}^n{p}_i}\log \frac{p_i}{q_i}.$$

(173)

Now

(174)

But ${\int }_{Z_i}\frac{q\left(z\right)}{{\int }_{Z_i}q\left(z^{\prime }\right)\mathrm{d}{z}^{\prime }}\mathrm{d}z=1$. We use the fact that the function x log x is convex, so that for each i

(175)

Therefore from Equation (175)

$${\displaystyle \sum _i{p}_i}\log \frac{p_i}{q_i}\le {\displaystyle \sum _i{\displaystyle {\int }_{Z_i}p\left(z\right)\log \frac{p\left(z\right)}{q\left(z\right)}\mathrm{d}z=S\left(p|q\right)}}.$$

(176)

(ii)

For the coarse-graining associated to subsystems one has $Z={\displaystyle {\prod }_{i=1}^n{Z}_i}$ and if p, q are states on Z, the coarse grained states are $\tilde{p}={\otimes }_{i=1}^n{p}_i,\tilde{q}={\otimes }_{i=1}^n{q}_i$ and we deduce immediately that

$$S\left(\tilde{p}|\tilde{q}\right)={\displaystyle \sum _{i=1}^{n}S\left(p_i|q_i\right).}$$

(177)

Consider the case i = 1, and call z = (z₁, z′) with z′ = (z₂,…, z_n) and call Z′ = Z₂ × ⋯ × Z_n. Then

(178)

Now ${\int }_{Z^{\prime }}\mathrm{d}{z}^{\prime }\frac{q\left(z_1,z^{\prime }\right)}{{\int }_{Z^{\prime }}q\left(z_1,z^{″}\right)\mathrm{d}{z}^{″}}=1$. As in Equation (175), we use the convexity of x log x and deduce that

(179)

From Equation (177) we deduce that for the coarse graining mapping associated to the division of $Z={\displaystyle {\prod }_{i=1}^n{Z}_i}$ in n subsystems, one has

$$S\left(\tilde{p}|\tilde{q}\right)\le nS\left(p|q\right).$$

(180)

Remark 11: The upper bound of Equation (180) cannot be improved. Indeed consider the case where: p(z₁,…, z_n) = p₁(z₁)δ(z₁ − z₂) … δ(z_n−1 − z_n) q(z₁,…, z_n) = q₁(z₁)δ(z₁ − z₂) … δ(z_n−1 − z_n). Then p_i = p₁ and q_i = q₁, but S(p|q) = S(p₁|q₁) and $S(\overline{p}|\overline{q})=nS(p_1|q_1)$.

(iii)

Thermal coarse graining.

Let Z be a phase space, and p and q two probability distributions on Z, H(z) a function of z ∈ Z.

Let $\tilde{p}$ and $\tilde{q}$ be the thermal coarse grained probability distributions of p and q, respectively, with respect to H. So

$$\tilde{p}\left(z\right)=\frac{1}{Z\left(\beta \left(p\right)\right)}\exp \left(-\beta \left(p\right)H\left(z\right)\right).$$

(181)

where β(p) is the effective temperature of p, i.e., ${\langle H\rangle }_p={\langle H\rangle }_{\tilde{p}}$.

Assuming that p − q is small, an obvious bound, after straightforward calculations (expanding to second order in p − q), is

$$S(\tilde{p}|\tilde{q})\le \frac{{\langle H^2\rangle }_p}{{\langle H^2\rangle }_{\tilde{p}}-{({\langle H\rangle }_p)}^2}S(p|q).$$

(182)

This bound is surely not optimal, because if p and q are already thermal states, $S(\tilde{p}|\tilde{q})=S(p|q)$. Note though that even without the hypotheses on p and q, $S(\tilde{p}|\tilde{q})\le S(p|\tilde{q})$.

8. Conclusions

The results in this article are used to obtain upper bounds for entropy production or energy variation in various situations of thermodynamic interest, with many such results either new or sharper than similar known bounds. Furthermore, the energy dissipated in these processes is expressed in terms of relative entropies, which not only gives a general microscopic interpretation of dissipation, but also, in relevant examples, leads to an explicit, first principles, evaluation of dissipation terms, analogous to the Fourier law.

Although relative entropy has made appearances in many contexts, especially with respect to information theory, our results on a generalized Fourier heat law relates it in a direct way to the notion of dissipation as understood in physics.