A Derivation of a Microscopic Entropy and Time Irreversibility From the Discreteness of Time
Abstract
: The basic microsopic physical laws are time reversible. In contrast, the second law of thermodynamics, which is a macroscopic physical representation of the world, is able to describe irreversible processes in an isolated system through the change of entropy ΔS > 0. It is the attempt of the present manuscript to bridge the microscopic physical world with its macrosocpic one with an alternative approach than the statistical mechanics theory of Gibbs and Boltzmann. It is proposed that time is discrete with constant step size. Its consequence is the presence of time irreversibility at the microscopic level if the present force is of complex nature (F (r) ≠ const). In order to compare this discrete time irreversible mechamics (for simplicity a “classical”, single particle in a one dimensional space is selected) with its classical Newton analog, time reversibility is reintroduced by scaling the time steps for any given time step n by the variable sn leading to the Nosé-Hoover Lagrangian. The corresponding Nosé-Hoover Hamiltonian comprises a term Ndf kB T ln sn (kB the Boltzmann constant, T the temperature, and Ndf the number of degrees of freedom) which is defined as the microscopic entropySn at time point n multiplied by T. Upon ensemble averaging this microscopic entropy Sn in equilibrium for a system which does not have fast changing forces approximates its macroscopic counterpart known from thermodynamics. The presented derivation with the resulting analogy between the ensemble averaged microscopic entropy and its thermodynamic analog suggests that the original description of the entropy by Boltzmann and Gibbs is just an ensemble averaging of the time scaling variable sn which is in equilibrium close to 1, but that the entropy term itself has its root not in statistical mechanics but rather in the discreteness of time.1. Introduction
While the basic (microscopic) physical laws including the fundamental differential equations of mathematical physics Hamilton’s, Lagrange’s, Maxwell’s, Newton’s, Einstein’s, and Schroedinger’s are time reversible, only the second law of thermodynamics describing macroscopic systems brings the arrow of time into play by requesting that the entropy increases in an isolated macroscopic system [1–4]. Following the systematic formulation of statistical mechanics by Gibbs and Boltzmann, entropy S reflects thereby the number of accessible micro-states of the system in study in its thermodynamic equilibrium (for a micro canonical ensemble SG = kB ln Ω with kB the Boltzmann constant, and Ω the number of accessible micro-states [1,5–7] and exerts its presence as being part of the total free energy (for example for an ideal gas the Gibbs free energy is given by G = U + pV − TS with U is the inner Energy, p the pressure, V the volume, and T the temperature; [1,5]). The latter argument brings the term entropy S back to its roots, where Clausius tried to design and understand “heat engines”, which are cyclic machines for the conversion of heat Q into useful work, and found when averaged over many cycles that for an irreversible machine [8]. Although the statistical mechanics argument of entropy increase with time by describing a system tendency towards its most probable state, which is the equilibrium state, is sound, Loschmidt and Zermelo’s reversal and recurrence objections remain as powerful as ever [9–12]. Both objections have been extensively discussed and are just mentioned here in short. The center of Zermelo argument is that if waited long enough any system, which started at a special low entropic state, under a time reversible physics may go back to its special low entropic starting state requesting a decrease of entropy over a long period of action, which is in general not observed. Lohschmidt indicated that any time reversible microscopic process in a closed system can be reversed by reversing all the velocity vectors of the involved particles and if done so yielding a decrease of entropy over a long trajectory, something that is not observed in general as just mentioned.
In addition to these objections of the interpretation of entropy, it is the author’s notion, that the arrow of time is such an important physical measure that it has likely its root deep in physics at the microscopic level and not just at the macroscopic statistical level—a point of view that was also mentioned beforehand by others (for example [2,13]) and is experimentally supported by the observed time symmetry violation of the weak force [14]. The idea of an arrow of time (at the microscopic level) requests the existence of time contrasting the view of many scientists and philosophers, who suggested that time is an illusion [15]. In the following, we will assume time and the arrow of time to be fundamental already at the microscopic level.
But from where could the arrow of time, time irreversibility, and entropy be originated from? As we shall see, it is our attempt to derive the arrow of time and the entropy part of the total free energy from the assumption that time is discrete. Although the introduction of a discrete time is not new and upon energy quantization for quantum mechanics straightforward (for example References [16–18]) it is not a very popular concept, since upon the introduction by Newton, time and space are an infinitely divisible continuum yielding powerful mathematical description in classical physics, quantum mechanics, as well as special and general relativity theories. An experimental argument in favor of the discreteness of time is, that the experimentally measured time is composed of an array of events, which can be exemplified in physics only by an energy-consuming clock measurement, and thus can not be measured continuously because of the uncertainty principle between energy and time (ΔE Δt > h/2 with h being the Planck constant).
There have been a few attempts in the literature that developed theories with time as a discrete parameter (such as [19–27]). To describe the time evolution of Hamiltonian systems with time as a discrete parameter Lee introduced time as a discrete dynamical variable [22]. Lee points out that throughout the development of physics, time always appears as a continuous parameter, while the space coordinates in non-relativistic theories are dynamical operators dependent on time. Lee showed that the introduction of time as a dynamical variable enables the discretization of time without violating the conservation of energy law. Subsequently, by invoking the discrete-time action principle by Cadzow [28] Jaroszkiewicz and coworkers [24,25] succeeded in developing an equation of motion with time as a discrete parameter having time steps of equal size. Valsakumar [27] took a fresh look at the problem under the assumption that the time steps are identical to the Planck time (5.4 × 10−44 s). By adopting the phase space density approach he yields the discrete time-analog of the Liouville equation of the phase space density in classical mechanics. Amongst others, his approach yields an arrow of time that follows from the documentation that the replacement of the time derivative by a backward difference operator only can preserve the non-negativity of the phase space density [28]. In parallel, in attempts to unify the general relativity theory with quantum mechanics including in particular quantum loop theory [15,29] it is assumed at the most fundamental level that time has a granular structure with the Planck time as the smallest time step. Furthermore, it appears that the Dirac equation which describes the free electron is more sound in presence of a discrete time than its continuous analog without loosing Lorentz invariance [15,21].
We follow here the approach by Lee [22] introducing time as a dynamical discrete variable yielding a scaling of time that depends on the potential present. This Ansatz is only applied to classical physics because of simplicity. The consequences of scaling time onto the law of energy conservation requests a reformulation of the Hamiltonian as established by Nosé for isothermal molecular dynamics simulations of macroscopic systems [30–34]. There is a logarithmic term in the Nosé-Hamiltonian which is dependent on the scaling of time. As we shall see, this term is defined as the microscopic entropy and if ensemble-averaged is equivalent to the macroscopic entropy as also exemplified by the simple example of the expansion of an ideal gas. After the introduction of the discrete time (Section 2.1), time irreversibility in a microscopic system is discussed (Section 2.2), followed by the reintroduction of time reversibility through scaling of time (Section 2.3) yielding the microscopic entropy of a single particle (Section 2.5) and a many particles system (Section 2.6). It is then further shown that the averaged microscopic entropy corresponds to the Boltzmann entropy (Section 2.7) as well as the Gibbs entropy (Sections 2.8 and 2.9). In (Section 2.10) the microscopic and macroscopic entropies of the volume expanding gas are calculated, followed by a discussion on time-irreversibility within time reversible descriptions of physical laws (Section 2.11). In Section 2.12 an explicit description of the evolution of a single particle within the established discrete time theory is given, followed by a conclusion.
2. Theory
2.1. Under a Discrete Time
In classical physics, a non-relativistic particle with mass m at the position r(t) at a given time t in a potential V (r) has the following Lagrangian with being the velocity. The use of bold letters indicate thereby the vector character of the physical variables such as r and . In examples having a one dimensional space only they are replaced by normal letters (such as and and r). The classical trajectory of a particle is determined by the minimal extremity of the action Ac, which is usually defined by the time integral over the Lagrangian between the two time points of interest (ti and tf):
denoting c for the continuous or classical case.
In the discrete time formalism, Lee (1983) [22] replaced the continuos function r(t) by a sequence of discrete values:
with (r0, t0) the initial and (rN+1, tN+1) the final position. In this description rn is still continuous, while tn is discrete. In discrete mechanics there are many possible definitions of the concomitant velocity n and acceleration . Since it is the attempt of the present work to introduce a time irreversible microscopic physics, the velocity at time point nn is defined time asymmetric (note, this contrasts to time symmetric definitions such as the leapfrog schemes [5] usually used for example in molecular dynamics simulation to obtain a time-reversible mechanics. Furthermore, we would like to note that although such leapfrog schemes are symmteric in time there is a loss of the “instant in time”). Furthermore, it is defined backward in time in order to determine it from the past permitting a forward progressing description. This approach is in line with our daily experience that the presence is determined by the past and presence (such as experimentally-derived information from the past and presence):
Using this description of the velocity the following action in presence of a discrete time formalism is defined:
(Please note, that the definition of the action is different from the one defined by Lee [22] who uses a mean potential to get a symmetric action along the space coordinate).
According to Lee [22] the discrete analog of Newton’s law can be derived by setting
which yields
with F(rn) is the (vectorial) force of the potential V (rn) at point (rn, tn), which is discrete in time. The acceleration is defined through the Newton’s law of Equation (8) by
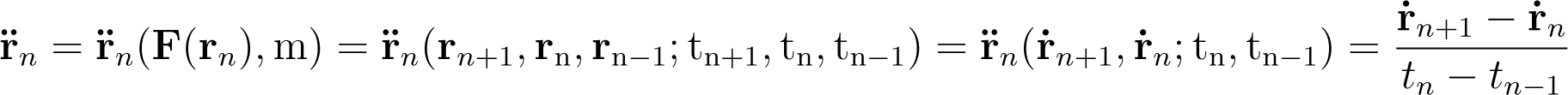
With these definitions n and are bound to the corresponding time tn. n is defined backward in time, while is defined by the force F(rn) through the discrete variant of the Newton’s law of Equation (8). The Newton’s law also defines the velocity forward in time (i.e., n+1) if the time step size is known (such as tn − tn−1 = const). These definitions follow a general correspondence principle between continuous classical mechanics and the presented discrete mechanics introduced in Table 1 and enables the calculation of a time trajectory. Thus, for any time series t1, …..tN+1,the positions r1….., rN+1, velocities 1…….. N+1 and the acceleration can be determined given the starting position (r0, t0) and the potential V (rn) as discussed in details in 3.12 (note, that 0 and are not defined because of the unknown t−1, but they are also not necessary for the determination of the trajectory).
Alternatively, a Lagrangian Ansatz for the derivation of the Newton law given a sequence of time points {tn, n = 0, 1, …, N + 1} in presence of a discrete time can be derived as follows:
We start with the above equation of the Lagrangian (from Equation (4)) being
If the discrete analog of the Lagrangian equation is written following the correspondence principle depicted in Table 1
the same discrete Newton’ law is obtained as above: .
2.2. Time Reversibility/Irreversibility in a One Dimensional Space
Having established the Newton’s law (Equation (8)) in presence of a discrete time, we would like to pursuit the issue of time reversibility or irreversibility. It is immediately evident from the inspection of the discrete Newton’s law (Equation (8)) that under the assumption of having Δtn = tn − tn−1 = const the equation is not time symmetric because of the term F(rn). Only for F(rn) = const or/and at the continuous limit for tn − tn−1 → 0 with time reversibility is obtained. This finding is irrespective of whether the action is symmetric in rn or not. Hence, the discreteness of time with a Δtn = const in presence of a complex force (i.e., F(rn) ≠ const) yields immediately time irreversibility and an arrow of time.
More formally, time reversibility can be described by a two step process having one step forward followed by a step backward. Let us first consider the evolution of the Newton’s law of a single particle with two step forwards in a one dimensional space (i.e.,rn = rn and )
- (i)
- (ii)
If the second step is now backward in time
and if time reversibility is requested
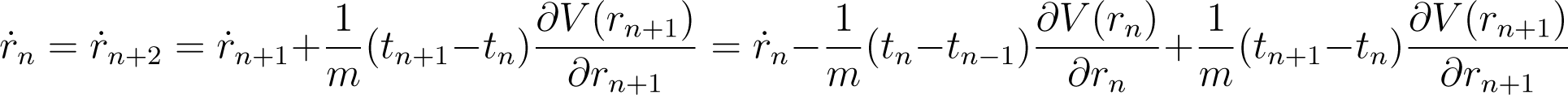
Looking at the last equation with Δtn = const it is evident that only with Equation (15) is fullfilled and thus the process of interest is reversible. Under a more complex force however in presence of Δtn = const the process is irreversible. That complex processes with many particles under a complex force are time irreversible is in line with our daily experiences (such as a cup that falls from a table and breaks into pieces), and thus sound, albeit most of the physical laws are time reversible including the Newton’s mechanics. It is therefore, the view of the author that the presented discrete homogeneous time mechanics (abbreviated diho mechanics) with Δtn = const = Δt (with Δt probably equal to the Planck time 5.4 × 10−44 s) may well describe nature, while the continuous, time reversible Newton mechanics is only an approximation. Usually, this approximation appears to work very well attributed to the small deviation from time reversibility because the time interval Δt is very short. However, in macroscopic processes with many particles the Newton mechanics apparently breaks down since it requires a description of the system by means of thermodynamics including the entropy term and time irreversibility. If the presented discrete time mechanics is a more profound theory than the Newton’s mechanics, on the one hand it should reflect irreversible properties of large complex systems usually described by thermodynamics and statistical mechanics (i.e., time irreversibility and entropy), while on the other hand it should under certain boundary conditions asymptotically approximate the Newton’s mechanics and thus time reversibility.
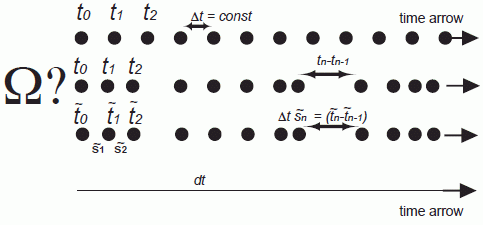
Indeed, by inspection of Equation (15) there is the possibility to obtain also in presence of a discrete time and a complex force (i.e., F (rn) ≠ const) time reversibility by introducing time as a discrete dynamic variable . If time is a discrete dynamic variable it is a function of n and the step sizes are variable as indicated in Figure 2. This so-called discrete scaled representation (abbreviated by the disca representation in Figure 2; note this representation has in addition a scaling variable sn to be introduced below) enables to guarantee the time reversibility of the Newton law (Equation (14)) by requesting
Equation (16) is called in the following the reversibility axiom. (Note, Equation (16) is not defined for F (rn+1) = 0 unless F (rn) is also 0 and thus with F (rn) = const = 0 constant time steps are obtained; correspondingly Equation (15) is fullfilled for ).
In other words, if the potential, respectively its corresponding force, is of complex nature (i.e., F (rn) ≠ const) time is a dynamic variable following Equation (16) to guarantee time reversibility of the system of interest. The request of a dynamic discrete time if the potential is of complex nature has already been mentioned by [22]. One may argue now, that the discrete scaled time description may be superior to the discrete homogeneous one because it enables a time reversible description. However, the following caveats appear: (i) The description of complex physical systems is reversible, which is against our daily experience. Thus, by the introduction of time reversibility consequently the arrow of time got lost; (ii) In a three dimensional space, time has to be expanded to a tensor of second rank as discussed in details in the next section; (iii) A further complexity arises in a many particles system as discussed later yielding time to be a multi-dimensional tensor. These arguments indicate again that Δtn = const (possibly in the order or equal to the Planck time). Under this assumption time reversibility of a system with a complex potential is lost and hence an arrow of time is introduced automatically without the need to introduce a macromolecular ensemble description that follows thermodynamics.
However, by establishing a discrete dynamic time variable combined with Equation (16) a first important connection between the time irreversible discrete, homogeneous mechanics (diho) and its acclaimed approximation the Newton mechanics has been obtained by establishing a discrete but time heterogenous description (disca) of mechanics (compare the characteristics of the three systems in Figure 2). In the next chapters the introduction of the time scaling variable sn will allow to complete the connection between the two mechanics theories, yielding a microscopic entropy description as we shall see. In other words, it is the authors assumption in the following that the time quantum is constant (and therefore independent of the step number n or the potential present) and the dynamic nature of the time is only of use to calculate the progression of the energy as discussed below, respectively, to guarantee energy conservation. Before we go on, we make a short excursion into the description of time reversibility in a three dimensional space.
2.3. Time Reversibility/Irreversibility in a Three Dimensional Space
Let us in the following consider the evolution of the Newton’s law of a single particle in presence of a discrete time in a three dimensional space under the request of time reversibility. By trying to expand our finding about force-dependent scaling of time from the one dimensional case to the corresponding three dimensions the complication arises that the force is now a vector (i.e., ), while so far time was a scalar. In order to enable time reversibility, time is expanded to a diagonal tensor of second rank (e.g. a 2 × 2 matrix with only diagonal elements):
with 1 being the unity matrix and
This extension should be regarded as a mathematical trick as mentioned above in order to enable a formalism for time reversibility under a discrete time.
In accordance to the two step process in one dimension described above, the corresponding two step process in a three dimensional space of one step forward followed by a backward step is described by
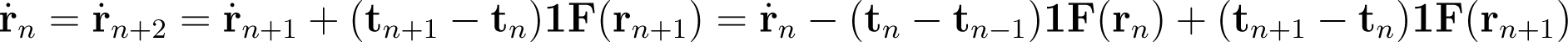
The time reversibility of the Newton’s law requires the time is scaled by
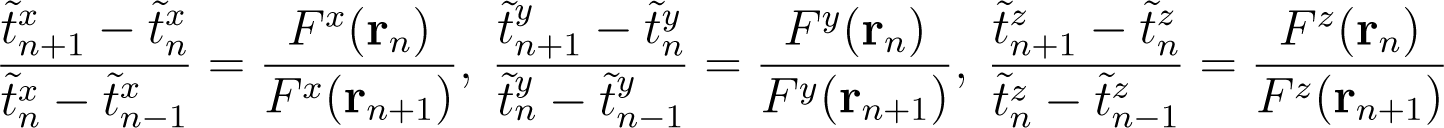
Note, that while in each dimension there appears a separate time scaling and this scaling is dependent on the corresponding spatial component of the forces present, the time evolution of the system is still discrete and the time evolution is defined by the number of steps n and not the step size. While this approach works mathematically it is composed of a bizarre complexity (i.e., multi dimensional time) and hence it is regarded only as a mathematical trick to get insights into entropy as we shall see in the following.
2.4. Scaling of Time in Accordance to Nosé
For simplicity we go back to the single particle in a one dimensional space and its description by the discrete constant time description (diho in Figure 2). We now introduce the scaling variable and scale in parallel the time to yield
with tn − tn−1 = Δt = const. (Please note, that the sn is defined as the corresponding variable s of Nosé with , following the denotation for ~ used in the review by Hünenberger (2005). In this new so called discrete, scaled representation (so called disca representation) described in Figure 2 the time is still a dynamic variable, while the system is extended by the scaling variable . The transformation from the diho to the disca representation is thus obtained by
(and correspondingly ) is thereby defined by defining it forward in time as it has been done for (see Figure 1).
Such an approach of scaling of time has been introduced by Nosé. He established the mathematical formulation of the so called Nosé-Hoover thermostat [32–37] enabling the molecular dynamics simulation of a system to sample configurations of a canonical (constant-temperature) ensemble. It is based on the extension of the real system by an artificial dynamical time scaling variable s. This important relationship serves in the following for the establishment of the microscopic entropy of a single particle (note, that sn is the discrete analog of s). Most importantly thereby is by doing so Nosé introduced a Lagrangian that in presence of the dynamical variable s yields in addition to the Newton law, also a Hamiltonian and guarantees a Boltzmann weighted canonical ensemble desription. Furthermore, its ensemble-averaged Hamiltonian is thereby a constant of motion referring to the energy of the system. Hence, the Nosé-Hoover thermostat introduces a Lagrangian that describes a system on the microscopic level under scaling of time, which yields upon ensemble averaging a macroscopic thermodynamic description of the system bridging the microscopic with the macroscopic world.
Following Nosé and the transformation rules of Table 1, the discrete time analog of the Nosé Lagrangian at time point n for a single particle is then given by
where kB is the Boltzmann constant, a constant Q, which has been described as a “mass”-like term for the motion of with Q > 0 with actual units of energy time squared, and g is equal to the number of degrees of freedom in the real system Ndf. (Note, since sn is according to the reversibility axiom dependent on the force F as we shall see below the system of interest is not an extended system as in the case of Nosé and therefore g = Ndf and not Ndf + 1 as it is the case for the Nosé extended system. In the absence of a requested reversibility the system would be extended though. Furthermore, we would like to mention that although under the given conditions of having a single particle in a one dimensional space g could by defined, the variable is kept here). The first two terms of the Lagrangian represent the kinetic energy minus the potential energy of the system, while the third and fourth terms represent the kinetic energy minus the potential energy associated with the variable. The third term can thus be interpreted as a kinetic energy of a heat bath/the thermostat coupled to the system of interest, and the fourth term describes the heat transfer between the heat bath and the system of interest. The thermostat mimics a bath composed of an infinite collection of harmonic oscillators or one with an infinite number of “particles” in a box and thus shows an infinite heat capacity [36]. The heat or temperature bath is however of another nature than usually defined in thermodynamics because it is a heat bath of the unitless time scaling variable with a mass-like Q with units Js2 (energy · seconds · seconds) and a velocity with unit s−1. Nonetheless, it enables the use of a temperature as highlighted by the explicit presence of the temperature T in the fourth term of the Lagrangian although the system described is of microscopic nature.
By applying the discrete Lagrangian equation (Equation (11)) the Newton’s equation in the new representation is given by
which can be simplified to
This Newton equation is extended by a friction term Hence, after transformation into the discrete, scaled so called disca system (Figure 2) the Newton equation is extended by a friction term which is attributed and dependent on the variables and as well as the corresponding time step. While this equation is in principle reversible, it is interesting to note, that it could be irreversible if the friction term is constrained to values ≧0. The ad hoc introduction of such a friction term is often used in classical mechanics to introduce irreversibility, stochastisity or/and to deal with the interaction of the system of interest with its surrounding as exemplified for example by the Langevin dynamics [5,37]. It is also used to describe and study the quantum mechanical decoherence phenomenon [38].
Equivalent to Equation (24) is the following equation
It is now required that the system in the disca frame must be reversible. Hence, using the Newton equation a step forward yields
the second step backward is then
if time is reversible and and thus
yielding the reversibility axiom in the disca representation to be
In the disca frame the system is thus reversible if Equation (30) is fulfilled.
2.5. The Microscopic Entropy of a Single Particle
Following Nosé [22,37] from the Lagrangian (Equation (22)) in the disca representation the corresponding Hamiltonian can now be writ
This function is a constant of the motion and evaluates to the total energy of the disca system.
Nosé and Hoover figured that the equations of motion can be reformulated to go back to a representation that has a homogenous time sampling yielding the disco representation defined in Figure 2 [32,33,37]. The transformation from the disca system to the disco system variables is thereby achieved through
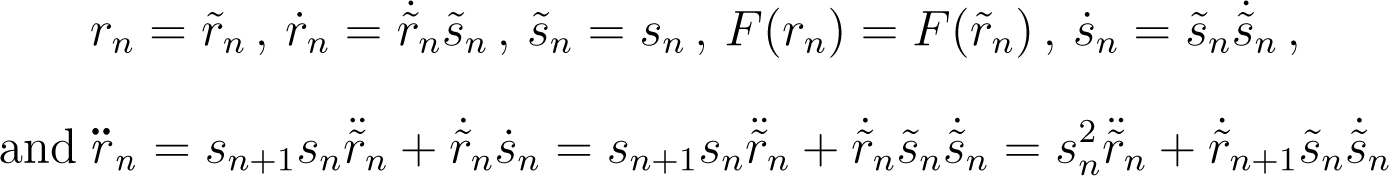
Based on these expressions, the Lagrangian equations of motions can be rewritten
with
An equivalent expression is
The constant of motion evaluating to the total energy of the entire, pseudo extended system is given by
(note, however, that this term is no longer a Hamiltonian; Q is still a “mass”-like term for the motion of sn, and g is equal to the number of degrees of freedom in the real system Ndf [37]).
This constant of motion is composed of the inner energy of the system U described by the first two terms followed by the energy of the bath and the exchange energy (i.e., the latter two terms having the variable sn). The resemblance of this term with the free energy (or Helmholtz Energy) A = U − TS is next put forward (note, the variable A is used instead of the traditionally used letter F for the Helmholtz energy, because F is used here for the force). It is intriguing to define a microscopic entropy of a single particle at time point tn to be
yielding
By using in the definition the word “microscopic”, we follow a suggestion by Prigogine [12] because Sn is a non ensemble-averaged term. Note, since we are in a time reversible description, the microscopic entropy is in general of reversible character and thus not a monotonously increasing quantity (see below and Section 2.11).
2.6. The Microscopic Entropy of a System With Many Particles
To extend the system from one particle to Z particles with Z very large (we are still in a one dimensional space and the particles are not interacting with each other keeping the potential simple Vi(ri,n)) for each particle i there is a separate scaling of time denoted si,n that follows the reversibility axiom which yields
and correspondingly, the microscopic entropy of a Z particles system is defined as
In an attempt to simplify Equation (39) by reducing amongst others the number of scaling factors si,n the following description of the microscopic entropy is introduced by assuming there are J groups of particles and within each group the particles have undistinguishable properties but are still distinct since the system is microscopically described (i.e., within a group each particle has gj degrees of freedom, the same responds to the potential, the same scaling factor, and the same velocity and mass). We define with . For very large systems (i.e., at the thermodynamic limit) pj is also the probability of a particle to be in the j group. Thus, the derived microscopic entropy of the Z particles system at time point tn is given by
with g = Z gi. In the latter part of Equation (40) it is assumed that all particles have the same degree of freedom and thus g = Z gi = Ndf with Ndf being the degree of freedom of the entire system.
In the next step, it is assumed that the scaling of time is very small (i.e., sj,n is very close to 1). This assumption called in the following the “slow changing force limit” is valid if the change of the force from one time step to the next is very small (i.e., F(rn+1) ≈ F (rn) + Δ with Δ small, see also Equation (30)). Support for a sj,n close to 1 is also based on the notion that scaling of time is usually not directly observed in physics. Under this assumption the ln of Equation (40) can be described by a Taylor expansion of first order and the averaging can be put inside the ln, which results in
In accordance, the microscopic entropy difference between two time points n and m for a Z particles system with having all particles the same gi is given by
It is interesting to note that this description can be used to calculate for a Z particles system the microscopic entropy difference between two time points by using averaged time scaling factors.
Furthermore, in contrast to the macroscopic thermodynamic entropy, the microscopic entropy can also be calculated for a system with a single particle or a few particles at any given time point n. In addition, the microscopic entropy difference can be calculated without having the system in both states in equilibrium and the averaging is not over all possible states as in statistical mechanics, but over the observed state. However, the change of the microscopic entropy is in general not a monotonously increasing quantity as requested for the macroscopic entropy, an issue to be discussed below (Section 2.11). Nonetheless, with the above mathematical trickery a close resemblance between the microscopic and macroscopic entropy is obtained.
2.7. Boltzmann Entropy Versus the Microscopic Entropy of a Many Particles System
It is attempted in the following to show a profound relationship between the microscopic entropy and the corresponding macroscopic one. Let us start with the Boltzmann entropy which shall be defined as the macroscopic entropy of a large system of Z independent, identical, indistinguishable particles (such as the ideal gas or diluted gas) for which each micro-state has the same probability. Boltzmann showed that the entropy is then given by
with being the probability of a single particle to be in the state j and the average is a single particle average taken over all the possible states J of the particle. The derivation of this formulation of the Boltzmann entropy is starting with the well known formula
with
describing the number of micro-states that the Z particles system can adopt if there are J distinguishable groups of states that each is composed of Zj particles [7].
Using the Stirling formula (i.e., ) which is true for large Z, Equation (45) can be simplified to
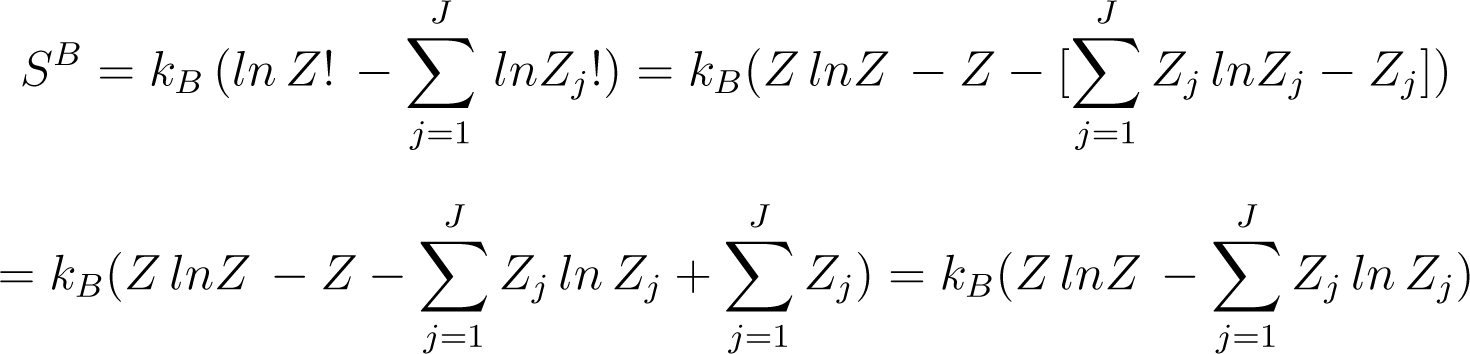
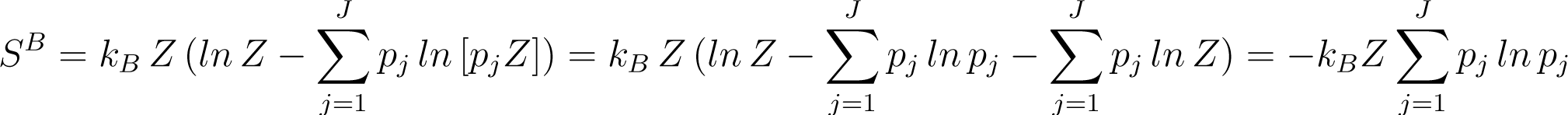
In comparison, the microscopic entropy of this Z particles system is given by with gj = 1, which is for example the case for an ideal monoatomic gas in a one dimensional volume. Because the description is microscopic each particle is distinct and thus requests its own scaling of time (i.e., sj,n). In the “slow exchanging force limit” the averaging can be put inside the ln (Equation (42))
Since the macroscopic entropy is only defined by an averaging, which in the case of interest can be done by a single particle averaging (Equations (44)–(48)), only the single particle average of the microscopic entropy can be compared with its macroscopic counterpart yielding with δlj being the Kronecker’s delta function
A classical thermodynamic system in equilibrium for which the entropy is calculated can be assumed to be in the “slow changing force” limit with sl,n close to 1, yielding
Thus, for a system in the “slow changing force limit” with independent non interacting particles, the average microscopic entropy in equilibrium approximates the Boltzmann entropy of the system. An interpretation of this analogy suggests that the original description of the entropy by Boltzmann is just a statistical averaging of a variable which is close to 1 (i.e., sl,n) but that the entropy term itself has not its root in statistical mechanics but rather in the discreteness of time.
2.8. Gibbs Entropy versus the Microscopic Entropy of a Many Non-Interacting Particles System
Above, we have shown that the average microscopic entropy at equilibrium of a system of Z independent, non-interacting, indistinguishable particles approximates to the Boltzmann entropy. However, in more complex systems the above defined Boltzmann entropy leads to increasingly wrong predictions of entropies and physical behaviors, because it ignores the interactions and correlations between different particles. Instead one must follow Gibbs, and must consider the ensemble of states of the system as a whole, rather than single particle states. If there are totally Ω micro-states k that all together describe the same macro-state the following description corresponds to the Gibbs entropy
with pk being the probability of a macro-state to be in the micro-state k with (note, pk is thus defined differently than above).
In a micro canonically behaving system the probability of each micro-state is equal with yielding the famous entropy formula [7]:
In comparison, the microscopic entropy of a Z non-interacting particles system was described by Sn = − kB Z < ln sn > with < ln sn > the sum of ln sn,i over all particles i multiplied by which is equal to the average over the particles in the thermodynamic limit (Z → ∞ and V → ∞). In addition, in the thermodynamic limit, the ensemble averaging of a function over all the micro-states of the macro-state is identical to the averaging over the particles if they do not interact with each other yielding following the ideas of Equations (41)–(43). Thus,
Since the macroscopic entropy is only defined for an ensemble, only the average over all the micro-states of the microscopic entropy can be compared with its macroscopic counterpart yielding
The delta function δlj thereby guarantees the independency of each micro-state.
Assuming the system to be in the “slow changing force” limit the ensemble-average microscopic entropy in equilibrium is given by
Thus, for a many non interacting particles system in equilibrium in the “slow changing force” limit, the microscopic entropy averaged over all the possible micro-states approximates the Gibbs entropy of the system. The Gibbs and Boltzmann entropies are thus derived from a particle-individual scaling of time. The individual time scalings were thereby requested by the hypothesis of a discreteness of time in combination with the acclaimed time reversibility nature of the established microscopic laws of physics.
It is interesting to note however, that individual time scaling in presence of a continuous time would also yield a microscopic entropy, which would correspond to the Gibbs entropy if ensemble averaged. While the author prefers scaling of time to be a consequence of the simple and sound rational of time being discrete, its continuos analog may have also its merits.
2.9. Gibbs Entropy versus the Microscopic Entropy of a System with Interacting Particles
It remains to be shown that the ensemble average of the microscopic entropy approximates the Gibbs entropy also in a system with many (Z) particles which may interact with each other. In order to describe such systems, a few concepts have been established in statistical mechanics of which we will discuss here the mean field approximation and the “two particles only” or pair approximation [7].
In the presence of an intermolecular potential V (ri,n, rk,n) with a long range in distance such as gravitation with its dependency, it appears that the individual contributions of the interactions in the Hamiltonian/Lagrangian can be approximated by a mean potential described by . This description can be interpreted as the potential that all the particles together induce at the position ri at the given time point n. Obviously, with this approximation the particles are statistically independent of each other relaxing the acclaimed complexity that arises from switching the description from a particle to an ensemble point of view, and thus ensemble averaging and single particle averaging are equivalent. Furthermore, since the mean potential is now of the form of the potential introduced above (for example Equations (10) and (38)) the above derivation of the macroscopic Gibbs entropy from the microscopic one (Equation (56)) can be applied also to interacting particles if their interaction is described adequately with a mean field approximation.
While for long range potentials the mean field approximation appears to be reasonable, it fails for short range potentials such as the interatomic potential in a diluted real gas. In such systems the pair approximation can be put forward, which assumes that the system is composed of two particles only. For diluted systems under short range potentials this approximation is reasonable, because for most of the states not more than two particles will be present within the relevant action distance of the short range potential at any given time yielding a system of statistically independent pairs of particles. The pair of particles is thus the smallest unit for averaging and pairs of particles are independent of each other yielding an equivalence between ensemble averaging over the pair and single pair averaging. If the pair potential acts onto the two particles equivalently with the two particles show also the same scaling factor si,n = sk,n (because of the reversibility axiom) and thus the microscopic entropy of the pair is given by Sn = − kB 2 ln sn yielding for the microscopic entropy of the Z particles system and finally this results in <Sn>≈ SG upon ensemble averaging of the microscopic entropy.
It remains however to be shown that without any assumption of a model the ensemble average of the microscopic entropy is equivalent to its macroscopic analog.
2.10. Example: The Change of the Entropy of a Volume-Expanding Ideal Gas
Although it was demonstrated above theoretically that the ensemble-averaged microscopic entropy approximates the Gibbs entropy, an example is given next for furhter illustration. By doing it, we will however elucidate an important not yet in details considered problem of the theory introduced, which is the problem of time-irreversibility in time reversible descriptions of physical laws (Section 2.11).
In the example the entropy change of the expansion of an ideal gas is calculated following the microscopic entropy expression derived above. The isothermal reversible expansion (i.e., T = const) is along r of an ideal gas located in a box with the area A and the side r from the initial Volume Vi = ri A to the final volume Vf = rf A. From a macroscopic view the expansion of the Z particles system is based on a force F which acts on the area A giving rise to the pressure . Using the conventional thermodynamics the change of the macroscopic entropy is calculated to be .
Using the microscopic entropy definition of the Z particles system (Equation (43)) the change of the microscopic entropy of an expanding gas can be described by
For this derivation, the reversibility axiom of Equation (16) was used (note, it has not been used above for the derivation of the ensemble-averaged microscopic entropy). Furthermore, it was assumed that the averaged force < F (rn) > that acts on the particle is equal to the macroscopic force Fn = pn A (this relationship is based on the principle that in a time reversible isothermal process the split of a force into a sum of smaller forces must follow the summation rule because of the impossibility to make a perpetum mobile).
Furthermore, during the isothermal expansion of the gas the following dependence between the force and the volume is given through the ideal gas equation pV = Z kB T (note, the ideal gas equation is believed to be correct also under a discrete time, because of its time insensitive character and the experimental verification).
For the microscopic entropy change we finally get
This obtained entropy change is equal to the macroscopic entropy change ΔSG multiplied by minus 1 using the classical description of entropy. Obviously, the factor −1 is disturbing. An attempt to resolve this apparent discrepancy is given in the next section.
2.11. The Problem of Time-Irreversibility in Time Reversible Descriptions of Physical Laws
It has been mentioned that there is a fundamental problem to connect the reversible physical description of a microscopic system with its macroscopic analog usually described by statistical mechanics, because it appears to be difficult or impossible to connect a reversible description with an irreversible one [2,12]. In the approach presented, this problem is still puzzling as demonstrated with the example above on the expansion of the idea gas and as discussed in the following.
We did start with a time-irreversible microscopic description of a system under a complex potential by introducing the discreteness of time and by defining the time steps to be of constant size (i.e., Δtn = const). However, since most of the physical laws are time reversible, we (re)introduced time reversibility including the time reversibility axiom (i.e., Equation (16): ) by scaling of time yielding a time reversible description of the energy of the system including the constant of motion evaluating to the entire energy with the microscopic entropy (i.e., and Sn = −g kB ln sn for a single particle, Equations (37)–(40)). Thus, both the microscopic entropy as well as the reversibility axiom are reversible. In other words, for the reversibility axiom and the energy description with the microscopic entropy the arrow of time is lost. The consequence of the loss of the arrow of time for the reversibility axiom is that it is not possible to distinguish between a forward and a backward process. Mathematically, this means that the reversibility axiom is either the one defined in Equation (16): or derived from the corresponding backward process starting with in analogy to Equations (12)–(15) (i.e., followed by the reversion of time of the second step and ). Hence, the loss of the arrow of time due to the introduction of a time reversible discrete physics introduces the following ambiguity for the reversibility axiom:
This finding resolves apparent problems such as the expanding gas discussed above (Section 2.10). Indeed, in the case of the expanding ideal gas, the introduction of the absolute value removes the negative sign in the calculation of the macroscopic entropy change from its microscopic analog yielding an approximate equivalency between the ensemble-averaged microscopic entropy and its macroscopic counterpart.
The remaining caveat is that the constant of motion with Sn = −g kB ln sn is still time reversible. If however, the “mass” Q of the heat bath/the thermostat (or Qi of all the heat baths) goes towards infinity (Q → ∞, Qi → ∞) the oscillatory nature of the Nosé-Hoover “thermostat” is lost and concomitantly time irreversibility is obtained. Note, in molecular dynamics simulations, the value of Q is chosen such, that during a calculation the temperature fluctuates around the temperature of the temperature bath. If Q is set small, there is a fast oscillation, if it is too long the oscillation is too slow and very long simulations are required to obtain a canonical distribution of the system. In the case of Q → ∞, s = 1 and thus a regular molecular dynamics simulation without thermostating is established [30–34]. In the discrete time description of the Hn however sn ≠ 1 (unless F (rn) = const) and thus time irreversibility is obtained.
This ad hoc introduction of requesting Q → ∞ in order to introduce a time irreversible description of the system is strengthened by the following argument. Let us again consider the time reversible evolution of a single particle under a given potential V (rn) at time point n described by the Nosé-Hoover Lagrangian (Equation (31); Hünenberger, 2005 [37]; Nosé 1984a [30])
The time reversible nature of the velocity has been demonstrated above resulting in the reversibility axiom (Section 2.4). However, also the evolution of the scaling factor sn must be time reversible. With the definition of the scaling factor velocity (see Chapter 3.4) the scaling factor evolves in a first step forward to
and accordingly for the second step
If the second step is now backward in time
With the request of time reversibility sn = sn+2 which simplifies the above equation by using tn − tn−1 = const to
which is true for a two step process with a step forward in time followed by a step backward in time. This result is obvious since the change of scaling of time in the step n → n + 1 should be equal to the change of scaling of time of the step backward n + 1 → n multiplied by −1.
In addition, also the scaling factor sn must follow (its) (discrete) Lagrangian equation (i.e., ) yielding
Since the right hand of Equation (71) is not evidently 0, but with the above Equation (68) (i.e., ) the left hand is 0 for Q ≠ ∞, Equation (71) can only be fulfilled with a Q → ∞. Thus, Q → ∞ is a requirement and a consequence of the request of a time reversible scaling factor yielding thereby a time irreversible constant of motion referring to the total energy as expected from a thermodynamic point of view. With setting the “mass” Q of the heat bath/the thermostat (or Qi of all the heat baths in the case of a multi particle system) towards infinity (Q → ∞), the “kinetic” energy of the heat bath of the scaling variable sn (or si,n) is infinite and thus has an infinite capacity to take up the energy that is lost in the discrete time steps of the system. This description may open a discussion about the nature of the heat bath (baths), which is not a regular thermodynamic heat bath because it deals with the unitless scale variable sn (si,n) outside the space-time. While on the one hand it is possible to interpret the scaling of time as an extension of the space-time by additional dimensions (i.e., for each particle three additional dimensions si,x,y or z) as has been done by Nosé in the Nosé-Hoover thermostat (however with a single s only), the author prefers the view, that the introduction of the scaling of time is just a mathematical construct that enables to preserve the first law of thermodynamics, which describes energy conservation.
2.12. Time Progression of a Discrete System Step by Step
For a simulation of a time irreversible system comprising one particle (or many particles) it is potentially interesting to write down the progression of the system step by step. Having constant time steps Δt the evolution of a single particle system in a one dimensional space starting under the (boundary) conditions
V (rn), F (rn), m, 1, t1, r1, and Δt can be calculated step by step as follows:
Using the (discrete) Newton equation
Using the definition of the discrete the velocity of step 2 can be obtained
with the definition of the velocity the coordinate at step 2 can then be obtained
which allows the calculation of the acceleration by
The corresponding microscopic entropy change is then given by
Correspondingly, the step n + 1 can be derived from values from step n by
and
3. Conclusions
It was demonstrated that under the hypothesis that time is discrete with constant time steps the microscopic physical laws in presence of a complex force (F (r) ≠ const) are time irreversible. Upon the introduction of the scaling of the discrete time in order to reintroduce time reversibility a microscopic entropy is obtained, which ensemble average in equilibrium under the “slow changing force” limit appoximates the macroscopic Boltzmann/Gibbs entropy. Thus, an alternative microscopic description of entropy is derived. Since this approach does not rely on the statistical mechanics approach of Gibbs and Boltzmann, the Loschmidt and Zermelo’s reversal and recurrence objections appear to be resolved [9–11], and an arrow of time is obtained already at the microscopic level of physics.
The now arising question is, which entropy derivation is the correct one, the established Gibbs and Boltzmann ensemble-averaged macroscopic entropy or the presented one with the microscopic entropy? In favor of the presented theory are the reversal and recurrence objections and the establishment of a microscopic arrow of time that is connected to the second law of thermodynamics. However, the continuos time descriptions of physics introduced by Newton is highly successful and thus has obviously also its merits. In a first attempt towards answering the question raised, it is required to highlight the differences between the two entropy descriptions (Equations (53) and (56)):
and
Thus, the ensemble averaged microscopic entropy approximates its macroscopic counterpart only at the “slow changing force” limit at which sm,n is close to 1.
In other words, only at the “slow changing force” limit the two entropy descriptions are equivalent. However, if the acting force changes considerably within a time step Δt, which has been hypothesized to be the Planck time (i.e., 5.4 × 10−44 s), the ensemble averaged microscopic entropy is distinct from its Gibbs analog. If experimental data under such conditions would be available insight into the nature of the entropy might be possible. Such conditions may have been present at the beginning of the universe during which the acting potential must have been changed very fast. In this context it is interesting to mention that the observed inflation of the universe might support the presented theory, because the inflation can apparently be explained by a scaling of time [3,15,31,39], and the scaling of time is at the heart of the presented theory being a consequence of a time-reversible description of an irreversible process under a discrete time. In return, if time is discrete in nature, the apparent inflation is an artifact of the established time reversible description of a time irreversible universe. Another area of potential interest, that could eventually help in the elucidation of the origin of the entropy, might be the analysis of the observed time asymmetry of the weak force in particle physics [13]. Alternatively, fast kinetic experiments could elucidate potentially the scaling of time. Currently, the limit for such experiments is in the attosecond range and so far no time anomalies have been reported [40].
In conclusion, an alternative microscopic derivation of entropy is given, which originates from the quantization of time, which is a concept that has only occasionally been investigated in the past. For the author this theory resolves the many objections that have been raised for the Boltzmann/Gibbs entropy and introduces an arrow of time at the microscopic physics level. However, whether time is discrete, whether it is universal or must be classified [41] or/and the presented microscopic entropy is an adequate microscopic representation of the macroscopic entropy state function remains to be demonstrated (experimentally).
Acknowledgments
We would like to thank extensively Dominik Leitz, Gunnar Jeschke, Klaus Hepp, David Neuhaus, Martin Quack, Markus Reiher, Hans-Jakob Wörner, Julien Orts, Daniel Blattmann and Roger Penrose for critical and helpful discussions. This work we dedicate to Martin Quack on the occasion of his status emeritus.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, 3rd ed; Sykes, J.B.; Kearsley, M.J., Translators; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Prize, H. Time’s Arrow and Archimedes’ Point: New Directions for the Physics of Time; Oxford University Press: Oxofrd, UK, 1996. [Google Scholar]
- Penrose, R. Cycles of Time; The Bodley Head: London, UK, 2010. [Google Scholar]
- Penrose, R. The Emperor’s New Mind; Oxford University Press: Oxfort, UK, 1989. [Google Scholar]
- Hoover, W.G. Time Reversibility, Computer Simulation, And Chaos; Advanced Series in Nonlinear Dynamics; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 1999; Volume 13, pp. 1–262. [Google Scholar]
- Boltzmann, L. Über die Mechanische Bedeutung des Zweiten Hauptsatzes der Wärmetheorie. Wien. Ber 1866, 53, 195–220. (In German). [Google Scholar]
- Greiner, W.; Neise, L.; Stöcke, H. Thermodynamik und Statistische Mechanik; Verlag Harri Deutsch: Frankfurt am Main, Germany, 1993. (In German) [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat—With its Applications to the Steam Engine and to Physical Properties of Bodies; John van Voorst: London, UK, 1865. [Google Scholar]
- Steckline, V.S. Zermelo, Boltzmann, and the recurrence paradox. Am. J. Phys 1982, 51, 894–897. [Google Scholar]
- Loschmidt, J. Sitzungsber. Kais. Akad. Wiss. Wien. Math. Naturwiss. Cl 1876, 73, 128–142. (In German). [Google Scholar]
- Poincaré, H. Sur le problème des trois corps et les équations de la dynamique. Acta Math 1890, 13, 1–270. (In French). [Google Scholar]
- Sohrab, H. On a scale invariant model of statistical mechanics, kinetic theory of ideal gas and Riemann hypothesis. In Recent Research in Circuits & Systems, Proceedings of the 16th International Conference on Systems, Kos Island, Greece, 14. July 2012; Balas, E., Koksal, M., Vasek, V., Eds.; WSEAS Press: Singapore, 2012; pp. 505–546. [Google Scholar]
- Prigogine, I. The End of Certainty: Time, Chaos and the New Laws of Nature; The Free Press: New York, NY, USA, 1997. [Google Scholar]
- Christenson, J.H.; Cronin, J.W.; Fitch, V.L.; Turlay, R. Evidence for the 2π Decay of the K20 Meson. Phys. Rev. Lett 1964, 13, 138–140. [Google Scholar]
- Smolin, L. Time Reborn; Houghton Micclin Harcourt: Boston, MA, USA, 2013. [Google Scholar]
- Poincaŕe, H. Derniere Pensees; Ernest Flammarion: Paris, France, 1913. [Google Scholar]
- Farias, R.A.H.; Recami, R.E. Introduction of a Quantum of Time (“chorion”) and its Concequences for Quantum Mechanics 2007, arXiv. quant-ph/9706059.
- Thomson, J.J. The intermittence of electric force. Proc. R. Soc. Edinb 1925, 46, 90–115. [Google Scholar]
- Yang, C.N. On quantized space-time. Phys. Rev 1947, 72, 874–874. [Google Scholar]
- Levi, R. Theorie de l’action universelle et discontunue. J. Phys. Radium 1927, 8, 182–198. [Google Scholar]
- Caldorola, P. A new model of classical electron. Supplmento al Nuovo Cimento 1927, 10, 1747–1804. [Google Scholar]
- Lee, T.D. Can time be a discrete dynamical variable? Phys. Lett 1983, 122, 217–220. [Google Scholar]
- Elze, H.T. Discrete mechanics, “time machines” and hybrid systems 2013, arXiv, 1310.2862.
- Jaroszkiewicz, G.; Norton, K. Principles of discrete time mechanis: I. Particle systems. J. Phys. Math. Gen 1997, 30, 3115–3144. [Google Scholar]
- Jaroszkiewicz, G.; Norton, K. Principles of discrete time mechanis: I. Classical field theory. J. Phys. Math. Gen 1997, 30, 3145–3164. [Google Scholar]
- Jaroszkiewicz, G.; Norton, K. Principles of discrete time mechanis: III. Quantum field theory. J. Phys. Math. Gen 1998, 31, 977–1000. [Google Scholar]
- Valsakumar, M.C. Stochasticity, decoherence and an arrow of time from the discretization of time? Pramana 2005, 64, 593–606. [Google Scholar]
- Cadzow, J.A. Discrete calculus of variations. Inst. J. Control 1970, 11, 393–407. [Google Scholar]
- Rovelli, C. Zakopane lectures on loop gravity 2011, arXiv, 1102.3660.
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys 1984, 81, 511–519. [Google Scholar]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys 1984, 52, 255–268. [Google Scholar]
- Nosé, S. An extension of the canonical ensemble molecular dynamics method. Mol. Phys 1986, 57, 187–191. [Google Scholar]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar]
- Hoover, W.G. Nose-Hoover nonequilibrium dynamics and statistical mechanics. Mol. Simul 2007, 33, 13–19. [Google Scholar]
- Martyna, G.J.; Klein, M.L.; Tuckerman, M. Nose-Hoover chains: The canonical ensemble via continuous dynamics. J. Chem. Phys 1992, 97, 2635–2643. [Google Scholar]
- Campisi, M.; Hänggi, P. Thermostated Hamiltonian Dynamics with Logs Oszillators. J. Phys. Chem. B 2013, 117, 12829–12835. [Google Scholar]
- Hünenberger, P. Thermostat Algorithms for Molecular Dynamics Simulations. Adv. Polym. Sci 2005, 173, 105–149. [Google Scholar]
- Zurek, W.H.; Paz, J.P. Decoherence, Chaos, and the Second Law. Phys. Rev. Lett 1994, 72, 2508–2511. [Google Scholar]
- Masreliez, C.J.; Sclae, Expanding. Cosmos: Theory I—An introduction. Apeiron 2004, 11, 99–133. [Google Scholar]
- Wörner, J.H.; Bertrand, J.B.; Fabre, F.; Higuet, J.; Ruf, H.; Dubrouiil, A.; Oatchkovskii, S.; Spanner, M.; Mairesse, Y.; Blanchet, V.; et al. Conical intersection dynamics in NO2 probed by homodyne high-harmonic spectroscopy. Science 2012, 334, 208–212. [Google Scholar]
- Sohrab, S.H. Quantum theory of fields from Planck to cosmic scales. WSEAS Trans. Math 2010, 9, 734–756. [Google Scholar]


| Continuos mechanics | Discrete mechanics (a) |
|---|---|
| t | tn |
| dt | tn − tn−1 |
| r | rn |
| (b) | |
| (c) |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Riek, R. A Derivation of a Microscopic Entropy and Time Irreversibility From the Discreteness of Time. Entropy 2014, 16, 3149-3172. https://doi.org/10.3390/e16063149
Riek R. A Derivation of a Microscopic Entropy and Time Irreversibility From the Discreteness of Time. Entropy. 2014; 16(6):3149-3172. https://doi.org/10.3390/e16063149
Chicago/Turabian StyleRiek, Roland. 2014. "A Derivation of a Microscopic Entropy and Time Irreversibility From the Discreteness of Time" Entropy 16, no. 6: 3149-3172. https://doi.org/10.3390/e16063149
APA StyleRiek, R. (2014). A Derivation of a Microscopic Entropy and Time Irreversibility From the Discreteness of Time. Entropy, 16(6), 3149-3172. https://doi.org/10.3390/e16063149