1. Introduction
With the high rate of growth of electricity consumption, hydropower plants have been playing a significant role in peak load and frequency regulation of the electric system. Control of hydroturbine speed is economically essential in terms of guaranteeing stability and improving efficiency. Nevertheless, it is challenging because of the complex speed adjusting process characterized by nonlinearity, uncertainty and various disturbances. The principal control target of hydroturbine speed governors, when various disturbances are imposed and/or the set point changes, is to keep the rotor speed within a proper range by tuning the influent flow of the penstock so that the mechanical transmission torque and the generator torque can arrive at a new balance.
Researchers have made a lot of efforts to develop some advanced control strategies for controlling hydroturbine speed governors. In order to be closer to the actual conditions, more and more studies have focused on nonlinear systems [
1]. In the general framework of hydraulic servo systems, Bonchis
et al. [
2] introduced a variable structure methodology into the position control under friction nonlinearity conditions. Sanathanan [
3,
4] proposed the condensability during water hammer situations by using a frequency domain method to determine the optimum proportional-integral-derivative (PID) gains. Lansberry and Wozniak
et al. [
5] proposed that genetic algorithms can be a means of finding the optimal solution over a parameter space in a hydroturbine speed governing system. This method combined a conventional PID controller with an adaptive control strategy to tune parameters online. Zhong [
6] introduced an adaptive inverse control method into hydroturbine speed governing systems with nonlinear, time-variable and non-minimum phase characteristics. This control strategy is based on the function approximation of the wavelet analysis and the self-learning capability of neural network. Considering the disturbance and non-elastic water hammer, Lu
et al. [
7,
8,
9] used a linear optimal approach to obtain a new control method which can be implemented easily. Watanabe [
10] continued Lu’s work by considering the nonlinearity of the state variables. Liu and Cheng
et al. [
11] introduced a new fuzzy control strategy into hydroturbine governing systems. The nonlinear analytical rules were combined with a fuzzy controller to tune fuzzy rules online.
The above advanced strategies have shown their potential use in controller design for hydroturbine speed governing systems. However, when random disturbances are considered, these methods will not achieve ideal control performance. Actually, in the hydroturbine speed governing process, disturbances can cause fluctuations of rotor speed besides variations of load [
12,
13]. Heng [
12] researched
μ robust performance of a hydroturbine speed governing system and proposed the optimization of
μ synthesis robust PI controllers by selecting the appropriate uncertainty weighting function and the performance weighting function. Assuming water, turbine, load power, speed and load angle disturbances to be zero mean, statistically independent and stationary white driving noise sources with finite variance, [
13] proposed a robust single-input multi-output (SIMO) design approach for the governor speed control of a nonlinear hydroturbine model. In this context, disturbances coming from carriers’ position and inlet water flow are considered and a cascade control structure is used to control hydroturbine speed. It can reject carriers’ position disturbances arising in the inner loop and improve the speed and accuracy of system response with parameter variations in the inner loop. Nevertheless, the inlet water flow disturbance is not included in the inner loop and it is usually non-Gaussian, which makes the speed control problem especially difficult to solve.
Fortunately, stochastic distribution control theory has been established to deal with the stochastic systems with non-Gaussian noises [
14,
15,
16,
17,
18,
19,
20]. These results can be mainly divided into two categories: (1) probability density function (PDF) shape control and (2) minimum tracking error entropy control. In [
19], based on the generalized minimum entropy criterion, a novel run-to-run control methodology for semiconductor processes with uncertain metrology delay was developed from both analytical and numerical viewpoints. Considering the control input constraints, [
20] proposed a constrained minimum entropy control algorithm analytically by using the penalty method. However, this constrained stochastic control method was not applied to any real industrial process. Following the presented stochastic distribution control methods presented in [
19,
20], the outer controller in hydroturbine speed cascade control systems is designed in the stochastic distribution control framework using an improved minimum entropy criterion, moreover, further stability analysis is performed in this paper. Simulation results show that the proposed minimum entropy based cascade control strategy can effectively reduce the influence of the non-Gaussian disturbances on the hydroturbine speed.
2. Description of Plant Model
A hydroturbine is a rotary engine that takes energy from moving water. Flowing water is directed onto the blades of a turbine runner, creating a force on the blades. Since the runner is spinning, the force acts through a distance (force acting through a distance is the definition of work). In this way, energy is transferred from the water flow to the turbine. In the energy conversion process, the inlet total head of turbine, fluctuates of flow and water hammer effect would affect the stability of the control system.
The transfer function between the inlet total head
and water flow
can be expressed as [
21]:
where
and
are the friction factor and surge impedance.
is the wave travel time. The hyperbolic function in Equation (1) can be described as [
21]:
The turbine model can be obtained by considering the effects of water hammer, head loss caused by friction and inelastic penstock [
21]:
where
and
are the mechanical power and gate opening, respectively.
and
are the friction factor of the penstock and the normalized hydraulic surge impedance respectively.
The synchronous generator model can be expressed by [
21]:
where
is the speed of the generator;
is the inertia;
is the generator damping.
The servo motor model is described by [
21]:
where
is the output signal of the controller,
and
are the pilot and gate servo motor time constants, respectively.
Carriers’ position and inlet water flow disturbances involved in hydroelectric turbines should be paid high attention, since they can cause fluctuations of rotor speed besides variations of load. These disturbances are usually non-Gaussian, which makes the hydroelectric turbine model be a linear, non-Gaussian stochastic dynamic system. Denoting the target hydro-turbine speed as
, then the tracking error
can be obtained by subtracting the output speed
from
,
, which is also a non-Gaussian stochastic process.
3. Minimum Entropy Based Cascade Controller
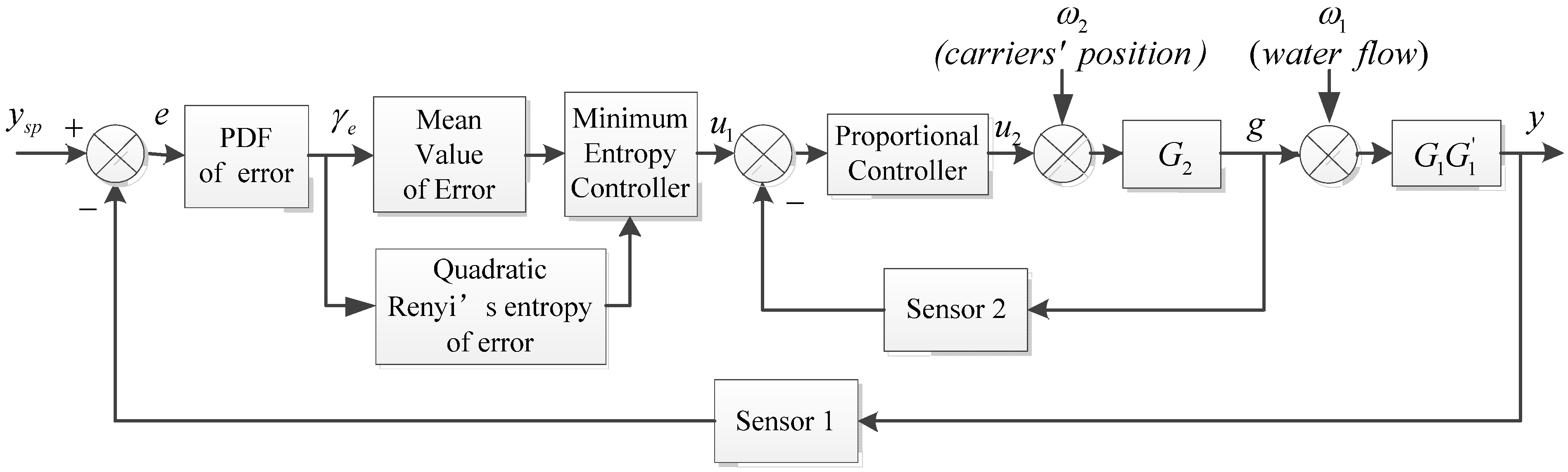
Figure 1 illustrates the general scheme of the proposed minimum entropy based cascade control for the hydroturbine speed governor.
and
are the transfer functions of the hydroturbine and synchronous generator, respectively.
is the transfer function of the penstock hydraulic servo.
stands for the inlet water flow disturbance in the outer loop.
represents the carriers’ position disturbance in the inner loop. To achieve the main task proposed in
Section 2, the outer controller is designed based on the minimum entropy; while the inner controller is a traditional proportional controller, which roughly regulates the inlet water flow.
and
are outputs of the outer controller and inner controller, respectively.
Figure 1.
Minimum entropy based hydro-turbine speed cascade control systems.
Figure 1.
Minimum entropy based hydro-turbine speed cascade control systems.
The main purpose of this paper is to design the outer controller such that the tracking error is minimized both in magnitude and randomness, which means that the PDF of tracking error should be made as sharp and narrow as possible near zero. Since the tracking error
is a non-Gaussian random variable and its PDF may be asymmetric and multimodal, mean and variance cannot characterize the shape of the tracking error PDF. In that case, a more general measure of uncertainty, named Renyi’s entropy, is used in this paper. It is known that small entropy corresponding to a narrow and sharp PDF. Furthermore, the mean value of the tracking error and the control energy also should be minimized simultaneously when designing the controller. In order to simplify the controller design problem, the discrete form of the hydroelectric turbine model is considered. Therefore, the following improved minimum entropy criterion at sample time
is formulated as:
where
and
are the quadratic Renyi’s entropy and mean value of tracking error, respectively;
is the control input to be designed. Then, the outer controller can be obtained by minimizing the performance index (6).
3.2. Optimal Controller Design
The design object of the minimum entropy controller is to make the performance index
minimum,
i.e.,
. In this paper, the following incremental control law is used:
Denote
, the Taylor expansion of
is:
where
,
,
.
According to Equations (13) and (14), the performance index (6) can be rewritten as:
The optimal control input
can be obtained by solving:
Then, the recursive sub-optimal control law can be obtained as follows:
satisfying
.
Remark 1. The above proposed control law is a type of “greedy” control law, which is easy to implement. In the next section, an improved optimal control law will be proposed to guarantee the closed-loop stability of the hydroturbine speed control system.
3.3. Stabilization Controller Design
In order to analyze the stability of the proposed system, the model of the equivalent plant in outer loop should be formulated first.
Denote the transfer functions of inner proportional controller and sensor 2 in
Figure 1 as
and
, respectively. Then, the closed-loop transfer function of the inner loop can be expressed as:
Since the tuned value of
is usually very big,
. Therefore, Equation (18) can be rewritten as:
Therefore, the transfer function of the equivalent plant in outer loop can be formulated by:
where
is the transfer function of sensor 1 in outer loop.
Since cascade control can reject disturbances introduced in the inner loop,
in
Figure 1 is omitted for simplicity when analyzing the stability of the outer close-loop system. Discretize Equation (20) and consider the non-Gaussian disturbance
entered in outer loop, the equivalent plant in the hydro-turbine speed control system can be modeled by a general ARMAX model as follows:
,
and
can be determined from Equation (20) and the calculation processes are omitted here for simplicity.
In order to analyze the closed-loop stability of the hydro-turbine speed control system, the increment form of Equation (21) is formulated as:
where
,
and
.
Motivated by the analytical method in [
24] different from Equation (14), the following approximation for both
and
is presented as:
where
,
,
,
,
and
.
Using the condition (16), we have:
Substituting Equation (24) into Equation (22), we have:
Denote
,
, the following state-space representation of
can then be formulated as:
where
.
Finally, the stability condition of the outer closed-loop system is:
4. Simulation Results
The proposed cascade control method is applied to regulate the hydroturbine rotation speed. In this simulation, the transfer functions of the penstock hydraulic servo system, hydroturbine with elastic water hammer effect and synchronous generator are chosen as,
, and
, respectively [
25].
.
The outer controller is the given optimization controller using minimum entropy criterion and the inner controller is a conventional proportional controller
. The process is also subjected to non-Gaussian carriers’ position disturbance
and inlet water flow disturbance
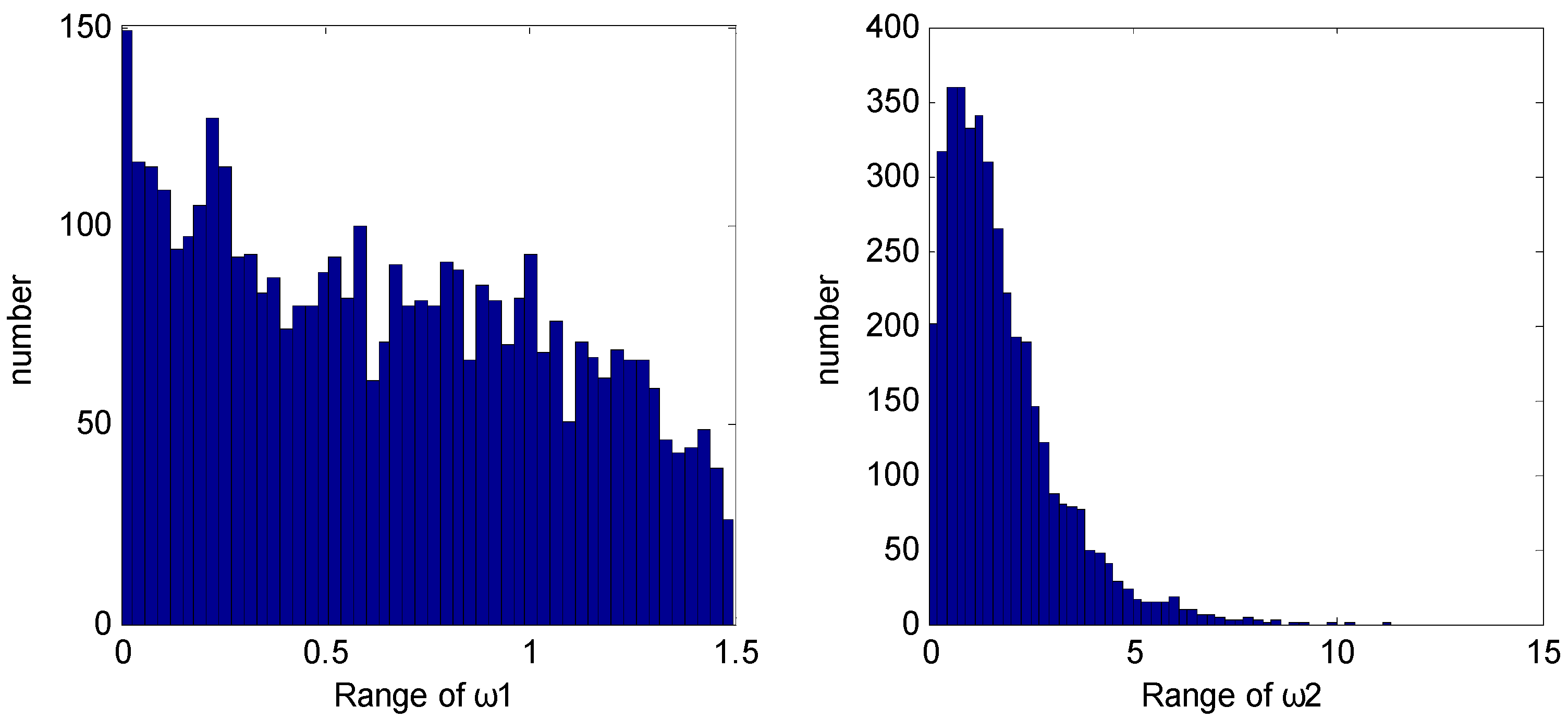
, whose distributions are approximated by
-distribution and
-distribution shown in
Figure 2. The sampling period is
, weights in the performance index (5) are set to
,
and
. In the histogram-based PDF estimation process, the sample and partition numbers are
N = 2500 and
M = 50, respectively. Some comparative results with a conventional PID controller and a model predictive controller (MPC) [
26] for the outer controller are given to illustrate the superiority of the proposed stochastic distribution control (SDC) method. The transfer function of the PID controller is chosen as
. The prediction horizon and control horizon in the MPC algorithm are set to be
and
, respectively.
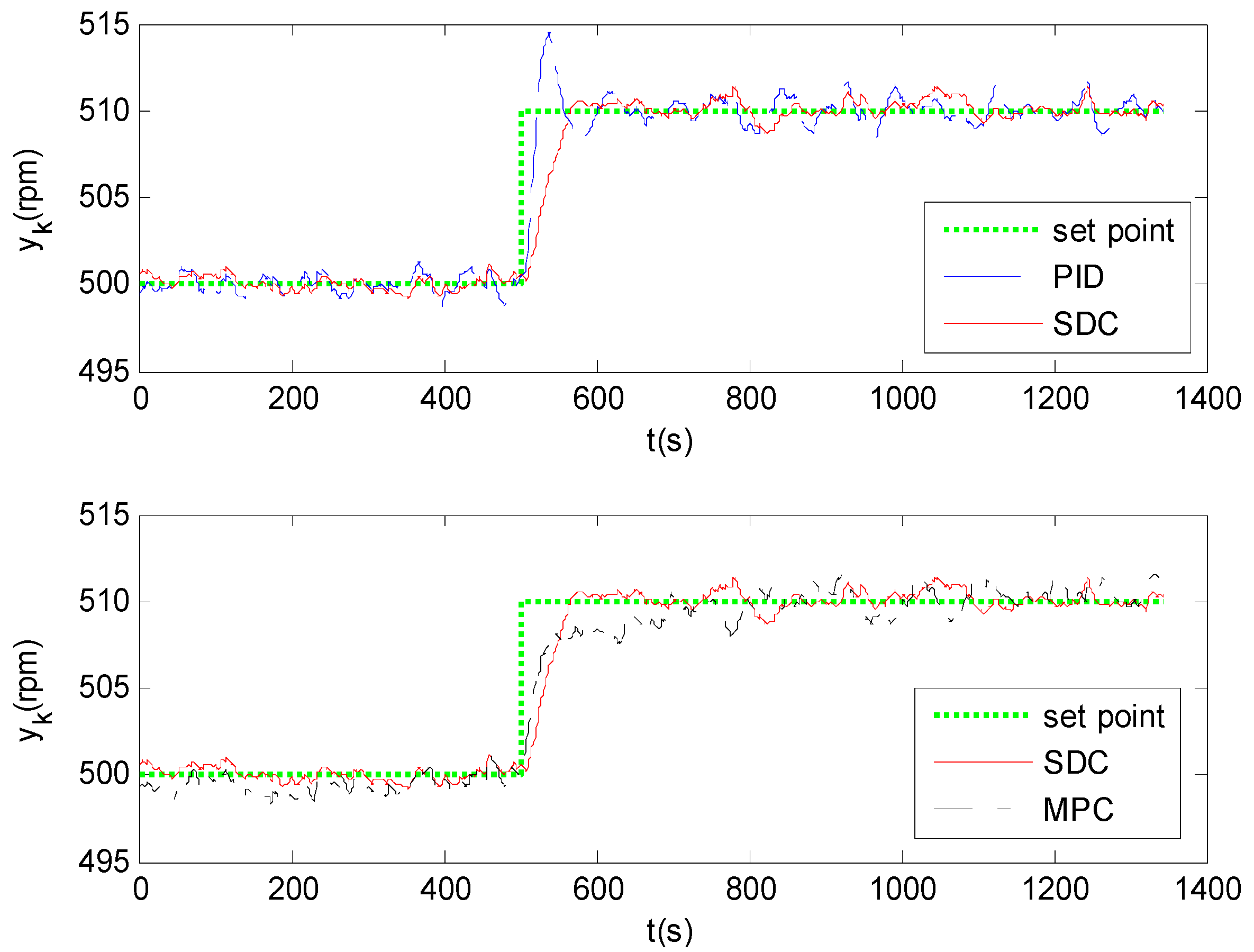
The hydroturbine rotation speed is governed at a steady state before 500 s, the target rotating speed increases from 500 rpm to 510 rpm at 500 s and lasts forever. The responses of the hydroturbine rotation speed with three different controllers are shown in
Figure 3. It can be seen that all three control strategies can stabilize the hydroturbine rotation speed around the set point with small oscillations. Nevertheless, it is obvious that the fluctuation of hydroturbine rotation speed is the smallest using the proposed controller.
Figure 2.
Distributions of disturbances ω1 and ω2.
Figure 2.
Distributions of disturbances ω1 and ω2.
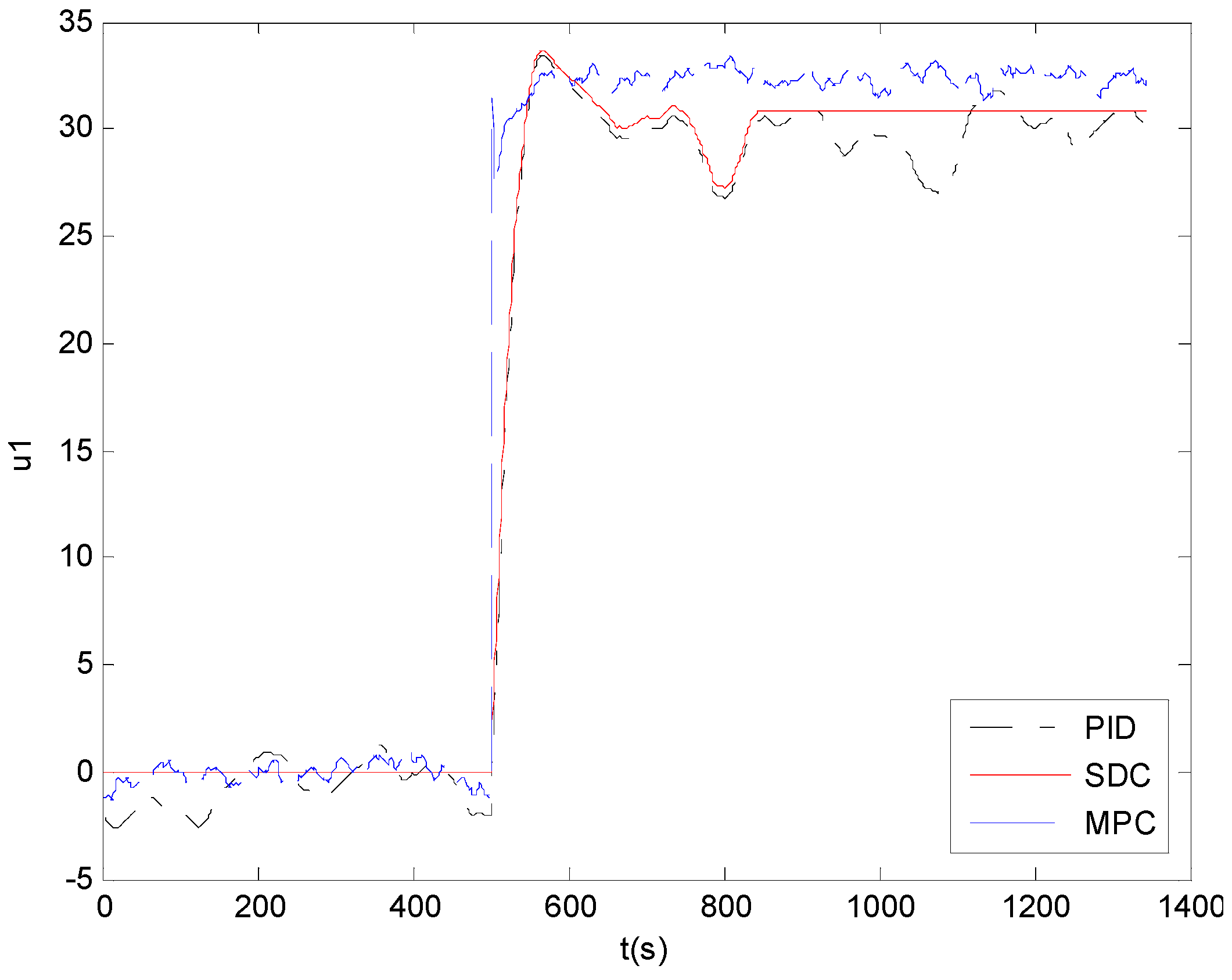
The responses of the outer controllers are shown in
Figure 4. It can be seen that the control input of the proposed controller is more stable than the PID controller and MPC controller.
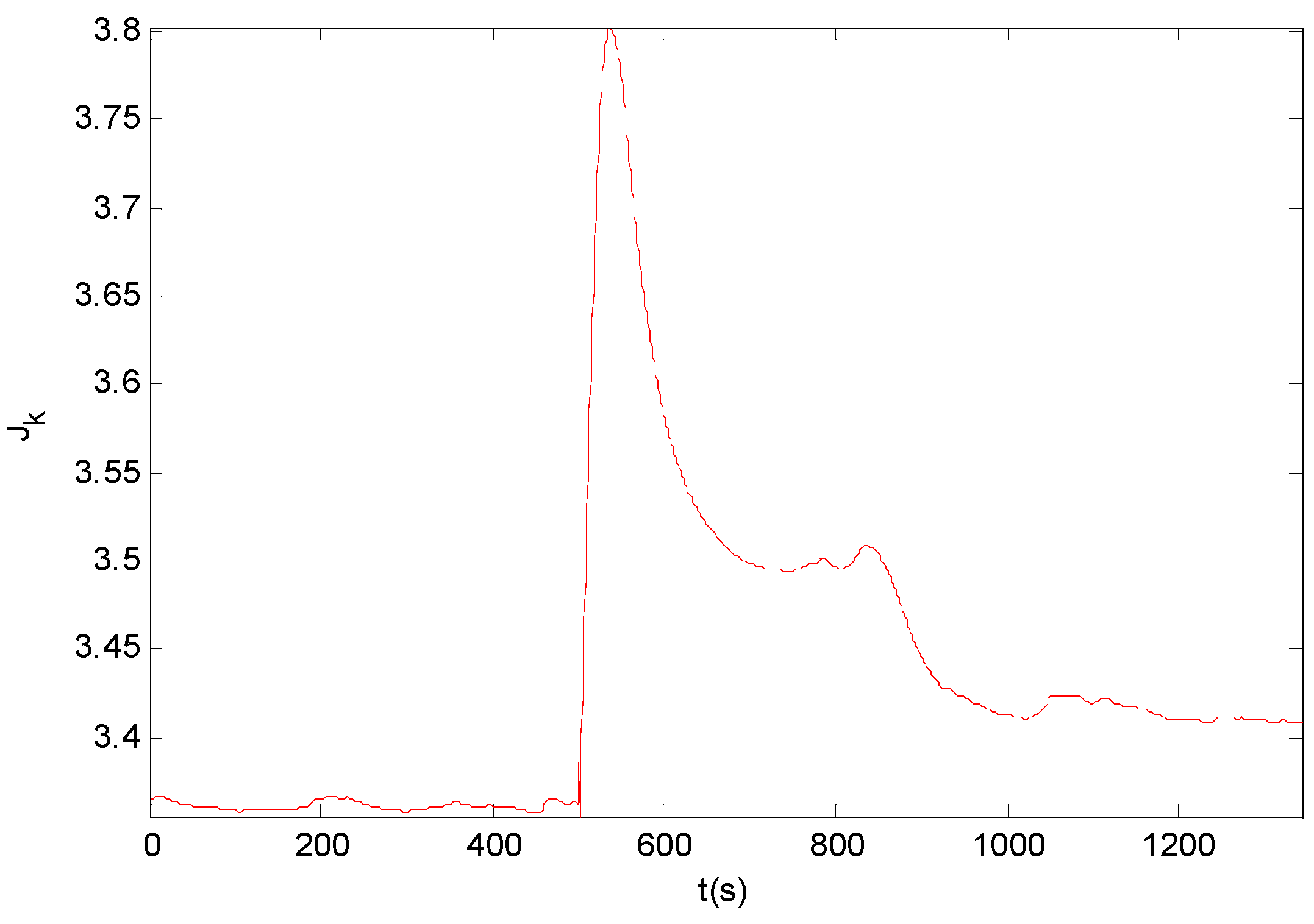
Figure 5 shows the variation trend of the performance index which has a jump at 500 s with the change of set point, then decreases rapidly until it stabilizes at a low level with the minimum entropy controller.
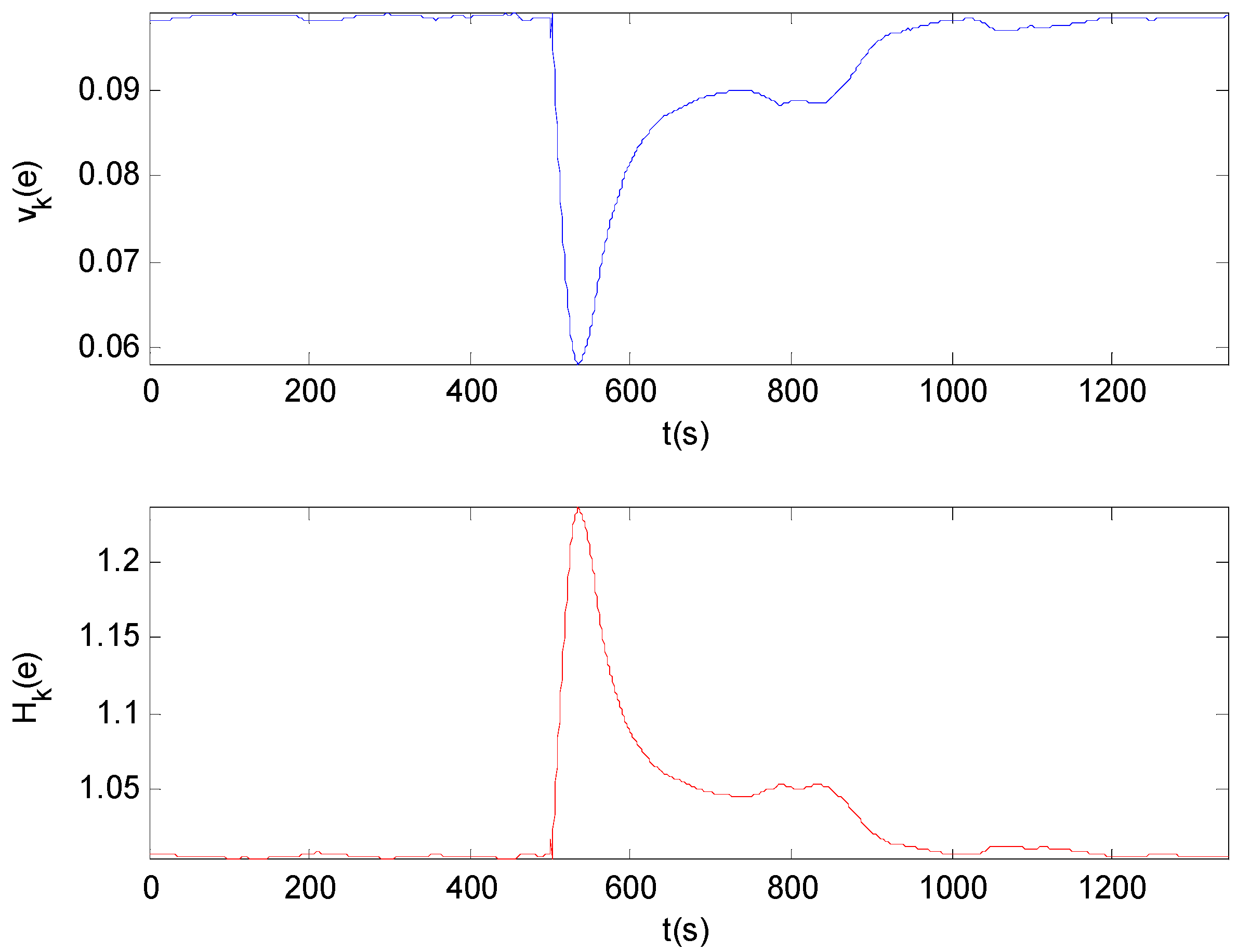
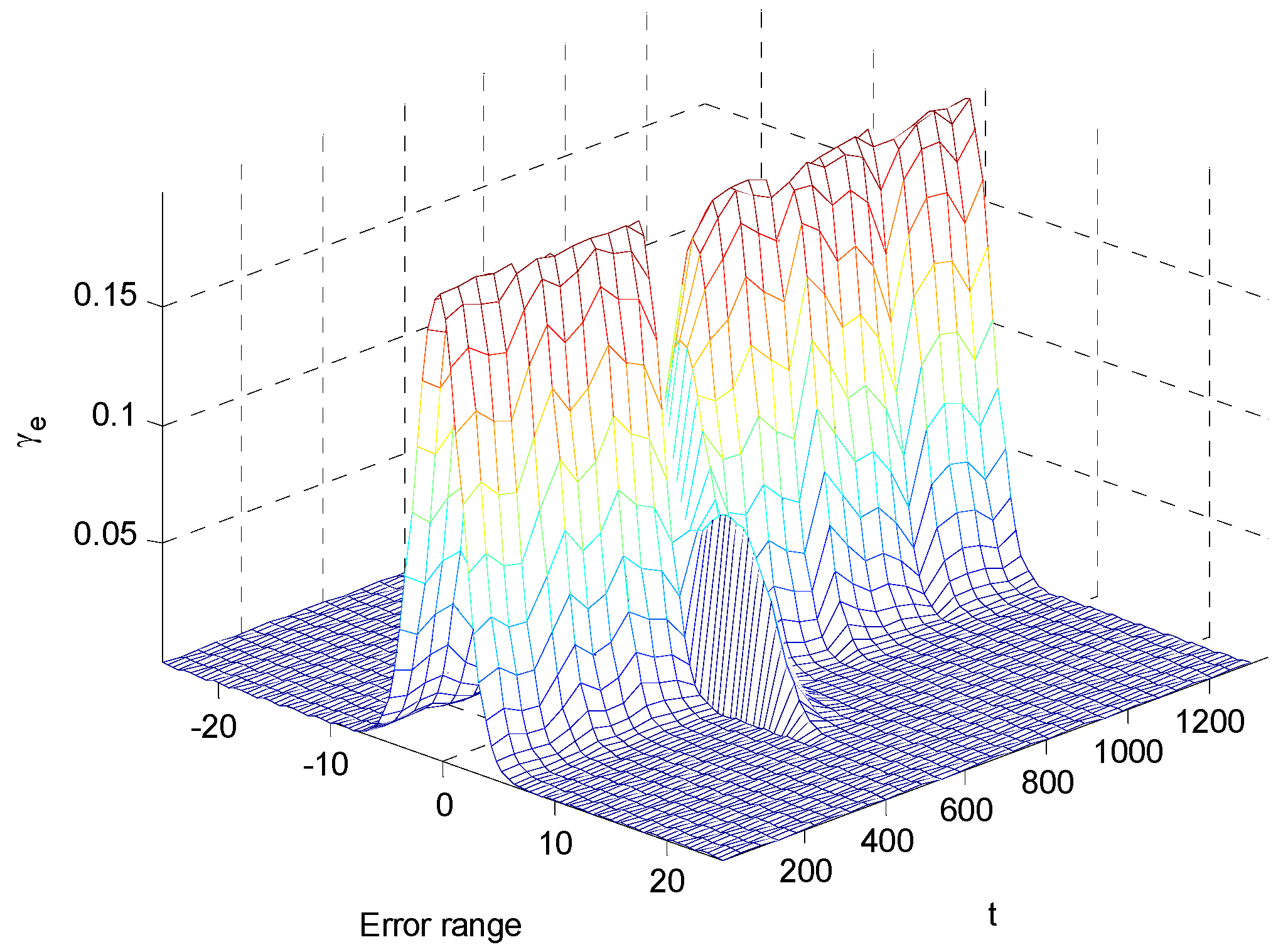
Figure 6 shows that the information potential of the tracking error increases and the entropy decreases corresponding to the performance index. The 3-D mesh plot of the PDF of tracking error is shown in
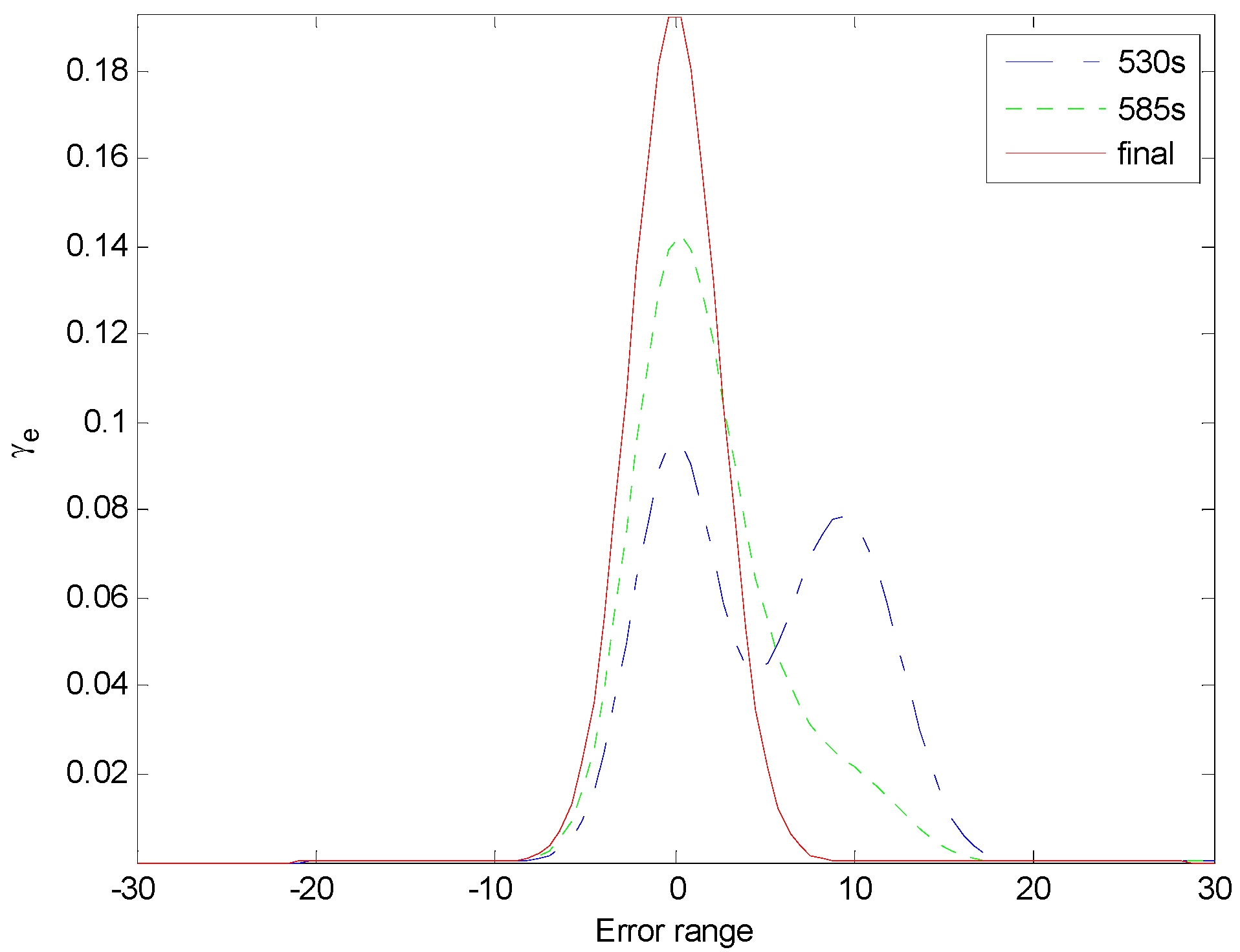
Figure 7. It can be seen that the shape of the PDF becomes more and more sharp and narrow along with the sampling time. It demonstrates that the proposed control strategy has a good effect in dealing with non-Gaussian disturbances. It also can be verified in
Figure 8, where PDFs at some typical instants are given. Therefore, the simulation results are consistent with the theoretical analysis.
Figure 3.
Responses of the hydroturbine rotation speed.
Figure 3.
Responses of the hydroturbine rotation speed.
Figure 4.
Responses of the outer controller.
Figure 4.
Responses of the outer controller.
Figure 5.
Performance index.
Figure 5.
Performance index.
Figure 6.
Information potential and entropy of the tracking error.
Figure 6.
Information potential and entropy of the tracking error.
Figure 7.
PDF of the tracking error.
Figure 7.
PDF of the tracking error.
Figure 8.
PDFs at typical instants.
Figure 8.
PDFs at typical instants.