Fractional Order Generalized Information
Abstract
: This paper formulates a novel expression for entropy inspired in the properties of Fractional Calculus. The characteristics of the generalized fractional entropy are tested both in standard probability distributions and real world data series. The results reveal that tuning the fractional order allow an high sensitivity to the signal evolution, which is useful in describing the dynamics of complex systems. The concepts are also extended to relative distances and tested with several sets of data, confirming the goodness of the generalization.1. Introduction
During the last decades the scientific community paid considerable attention to the generalization of concepts such as information, entropy [1–4] and differentiation [5–8]. Entropy was introduced in thermodynamics by Clausius and Boltzmann and was later adopted by Shannon and Jaynes in information theory [9–11]. Fractional Calculus (FC) was introduced by Leibniz in mathematics and found application in the areas of biology, physics and engineering [12–18]. The progress motivated the formulation of novel entropy indices and fractional operators, often relaxing some properties and allowing their application in complex dynamical systems [19–21].
The generalized concepts motivate further developments and new research avenues emerge. Bearing these ideas in mind, the present study combines both concepts and is organized as follows. Section 2 introduces entropy and fractional calculus in order to formulate the new generalized fractional entropy. Section 3 applies the new index in several types of data, namely two mathematical induced series, the digits of number π [22] and the Weierstrass function, two financial time series, the Dow Jones Industrial Average and the Europe Brent Spot Price [23,24], and one genomic series, the Human chromosome Y [25]. The results are analysed and distinct entropy formulations, for several fractional orders, compared. Section 4 expands the proposed index towards the concepts of distance. The Kullback-Leibler and Jensen-Shannon divergence measures are revisited and rewritten in the light of the fractional perspective. The performance of the index is tested with two sets of data, namely 13 irrational numbers and the whole 24 Human chromosomes, adopting the fractional order that reveals higher sensitivity. Finally, Section 5 outlines the main conclusions.
2. Fractional Generalization of Entropy
Information theory was developed by Claude Shannon in 1948 [26,27] and has been applied in many scientific areas. The fundamental cornerstone is the information content of some event having probability of occurrence pi:
The expected value, called Shannon entropy [28,29], becomes:
where E (·) denotes the expected value operator.
Expression (2) obeys the four Khinchin axioms [30,31] and several generalizations of entropy have been proposed, obeying only a sub-set of them.
Recently Ubriaco brought together information theory and FC and proposed [32] the expression:
where 0 ≤ q ≤ 1 denotes the “order” so that q = 1 yields Expression (2). This formulation obeys the same properties as the Shannon entropy except additivity and is the expected value of information content given by:
It is well known in FC the adoption of a power function for obtaining intermediate values, that is, for “fractionating” classical integer operators. In brief, the Laplace transform of the fractional derivative of order α ∈ ℝ of a signal x (t) with zero initial conditions is given by:
where t represents time, and {·} and s denote the Laplace operator and variable, respectively.
This property motivated the approximation of fractional derivatives by expanding the factor sα both with the Fourier and the

where Γ (·) and ψ (·) represent the gamma and digamma functions.
Expression (7) fails to obey some of the Khinchin axioms with exception of the case α = 0 that leads to the classical Shannon entropy. This behaviour is in line with what occurs in FC, where fractional derivatives fail to obey some of the properties of integer-order operators. By other words, in both cases, by generalizing operators we loose some classical properties.
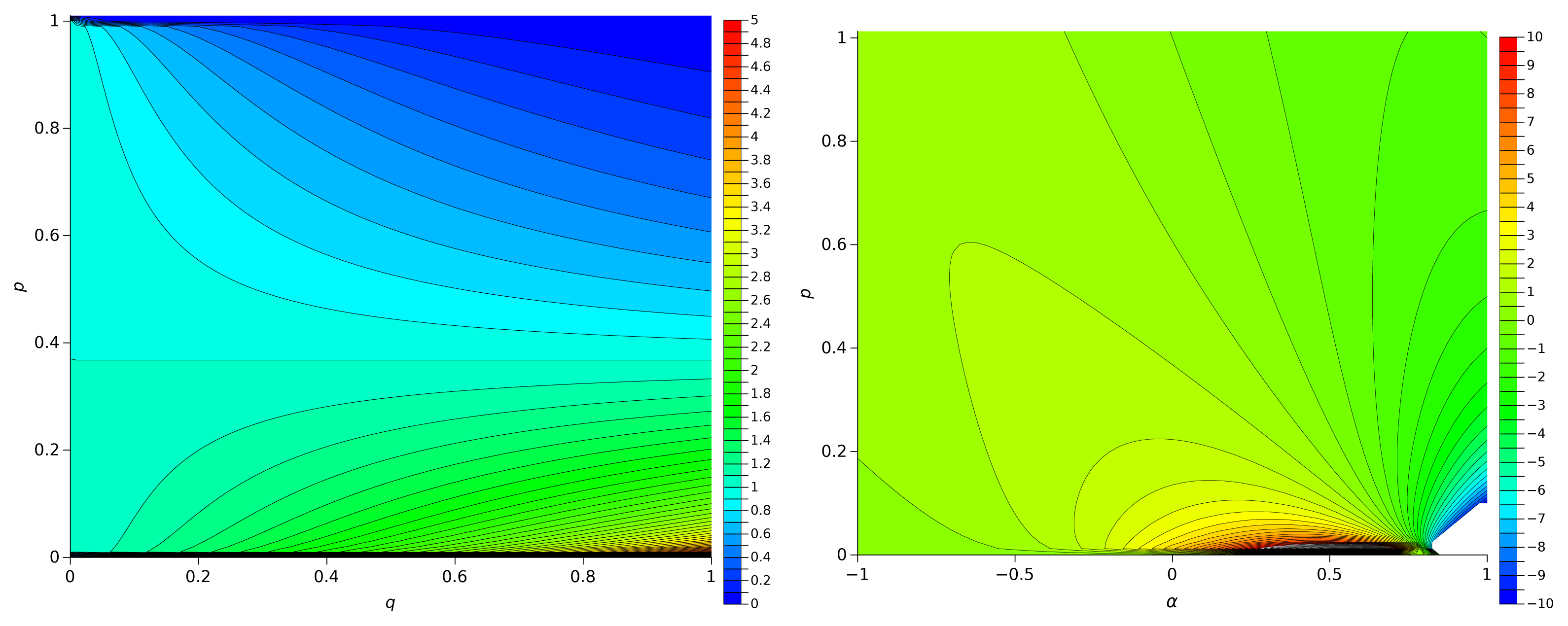
Figure 1 shows the locus of Iq versus (q, p), 0 ≤ q ≤ 1, and Iα versus (α, p), −1 ≤ α ≤ 1. We observe that Iq has a smaller amplitude excursion than Iα. Moreover, we verify that Iα takes not only positive, but also negative values for α > 0. Therefore, Expression (6) assumes also the assumption that we can have negative information, that, for a given value of α > 0, can be interpreted as derived from “misleading events”. While exploring the concept of “deception” is not the objective of the present paper, we should note that related ideas were addressed, in abstract terms, in the scope of negative probabilities [36–41] and, in practical terms, in the scope of robotics [42]. In short, we can say that the parameter α allows us to tune the level of confidence of the information varying from positive (trustworthy) up to negative (deceptive) information.
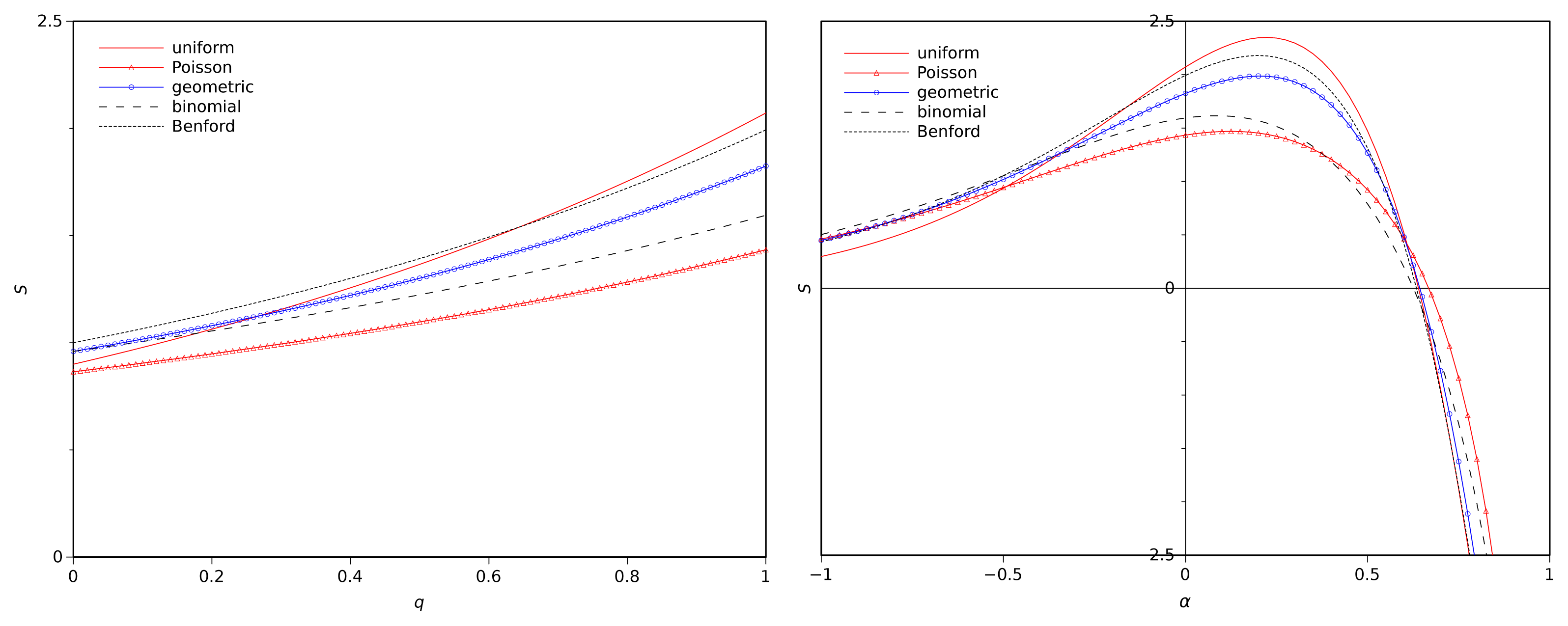
In order to illustrate the behaviour of the new index and to compare the two approaches Figure 2 depicts the entropies Sq and Sα for the uniform, Poisson (α = 2), geometric (p = 0.3), binomial (p = 0.3), and Benford probability distributions. We verify that Sq has a much smaller variation with q than Sα with α. There is a large similarity between the shape of the curves for 0 < q ≤ 1 and −0.5 < α ≤ 0. This is natural since Sq tends to the traditional entropy when q → 1, while Sα tends to the traditional entropy when α → 0. Furthermore, we verify that Sα has maxima for 0.07 < α < 0.23 and reaches null values for 0.62 < α < 0.68. Therefore, in a practical application we can adopt values for α in the first range if information is reliable, or we can consider values of α in the second range if data contains misleading information.
Usually it is of interest to investigate the evolution for a binary distribution, that in our case leads to the expressions:
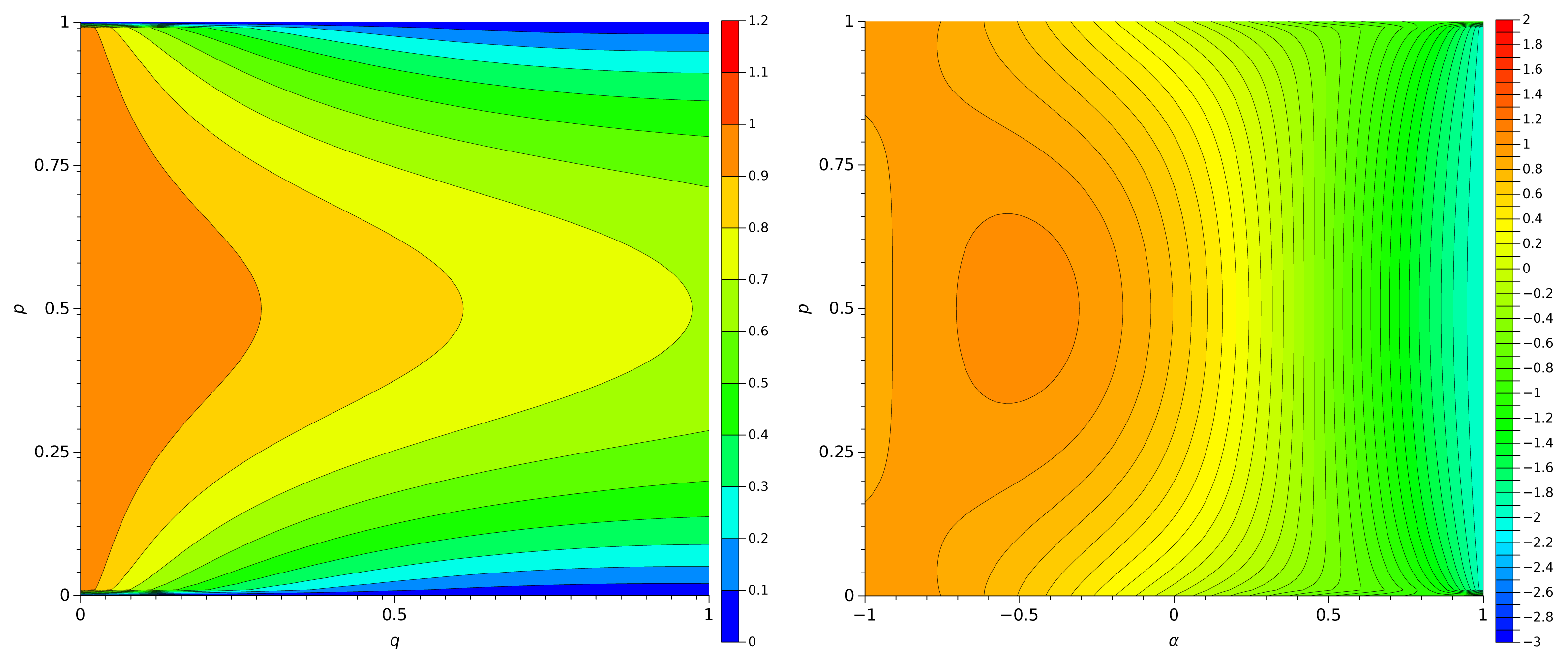
Figure 3 shows the locus of Sq and Sα versus (p, q), 0 ≤ q ≤ 1, and (α, p), −1 ≤ α ≤ 1, respectively. In both cases we have a symmetrical variation relatively to p = 0.5, but Sq is less sensitive than Sα to the variation of the order. In the case of Sα we observe that the chart passes from convex to concave in the region of α = 0.5.
3. Application of the Generalized Entropy
This section applies Sq and Sα to the mathematical constant π, the Weierstrass function, the Dow Jones Industrial Average (closing values) and the Europe Brent Spot Price (USD per barrel) financial time series, and one genomic series, the Human chromosome Y. The mathematical constant π is expanded in base 10, and each digit is considered separately in the series. In the Weierstrass function, are adopted the parameters a = 0.5, b = 3 and the range −2 ≤ ξ ≤ 2. The two financial series correspond to daily values during the period 18 May 1987 up to 14 March 2014. In the four cases we adopt a total of L = 7000 data values. For the calculation of the histograms of relative frequency a non-overlapping sliding time window of W = 100 points is adopted, producing a total of k = 1, · · · , 70 samples. In the case of the genomic series we have four bases denoted {A,C,T,G} that are sampled in groups of 3 producing histograms with 43 bins. A small percentage of triplets involving the symbol N (considered as “not useful” in genomics) are not analysed. Therefore, a sequence of size L = 872 · 104 is adopted and two distinct non-overlapping sliding windows, of W1 = 10, 000 and W2 = 124, 571 points each, are considered producing a total of k = 1, · · · , 872 and k = 1, · · · , 70 samples, respectively.
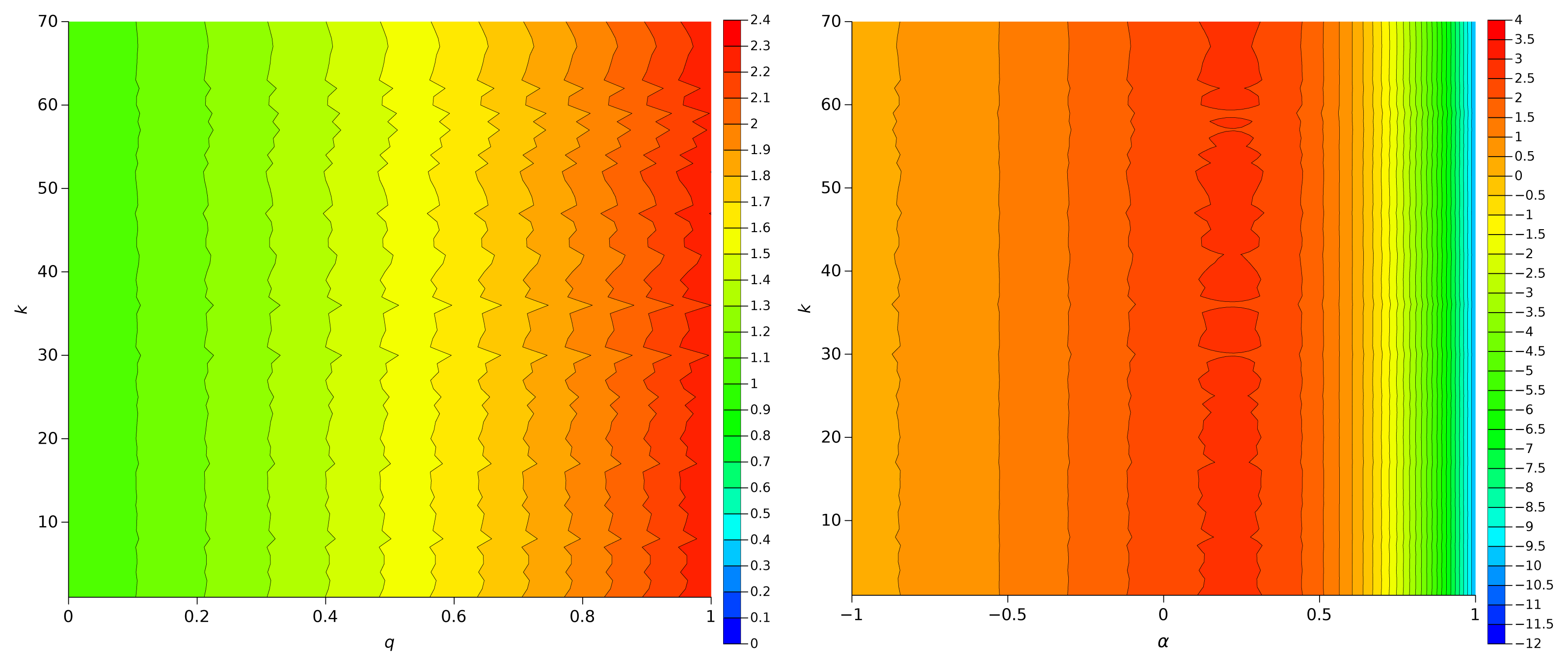
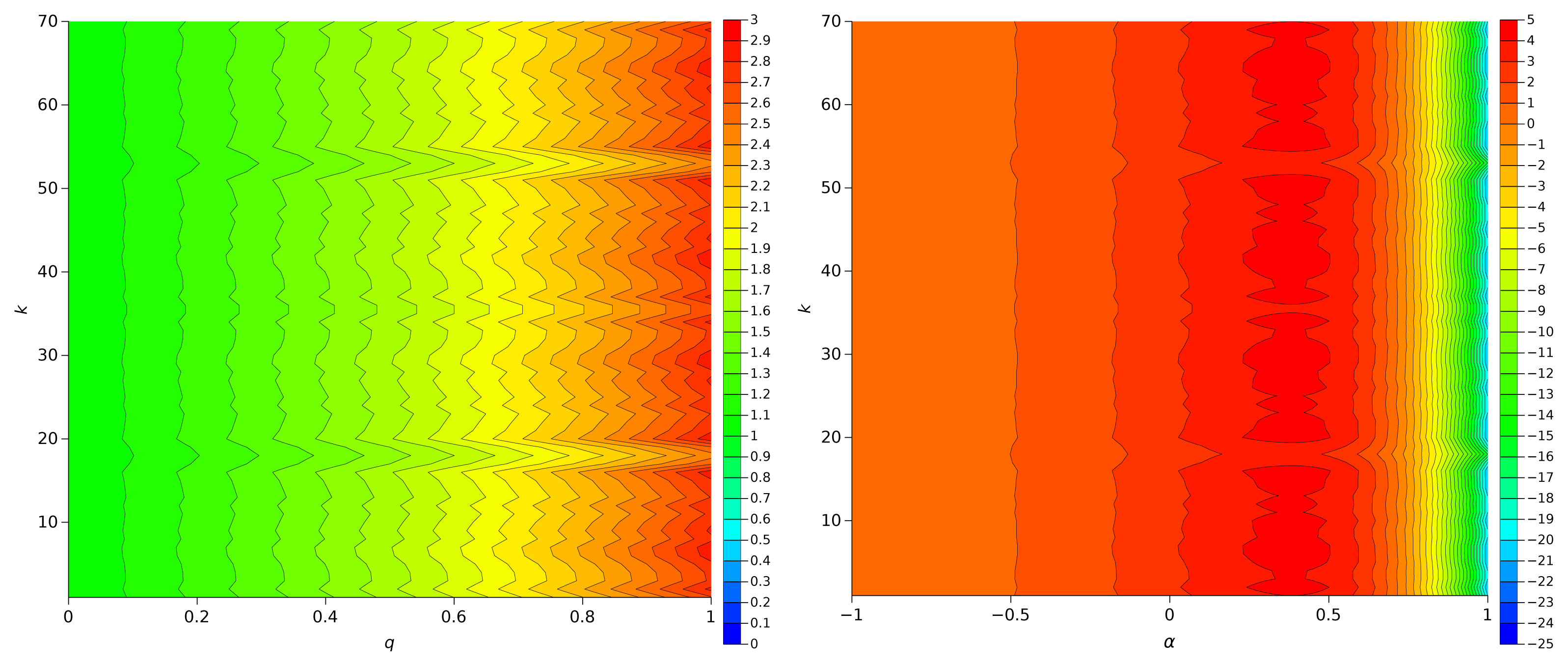
Figures 4 and 5 represent Sq versus (q, p), and Sα versus (α, p), for the π series and the Weierstrass function, respectively. We observe that Sq has a low sensitivity to the dynamics of the series exhibiting significant variations only for q close to one, that is, when it reduces to the Shannon entropy. On the other hand, Sα detects clearly dynamical variations, being particularly sensitive in the region 0 < α < 0.6.
Figures 6 and 7 depict the plots of Sq and Sα for the Dow Jones Industrial Average and Europe Brent Spot Price, respectively. We verify a behaviour similar to the one pointed out previously.
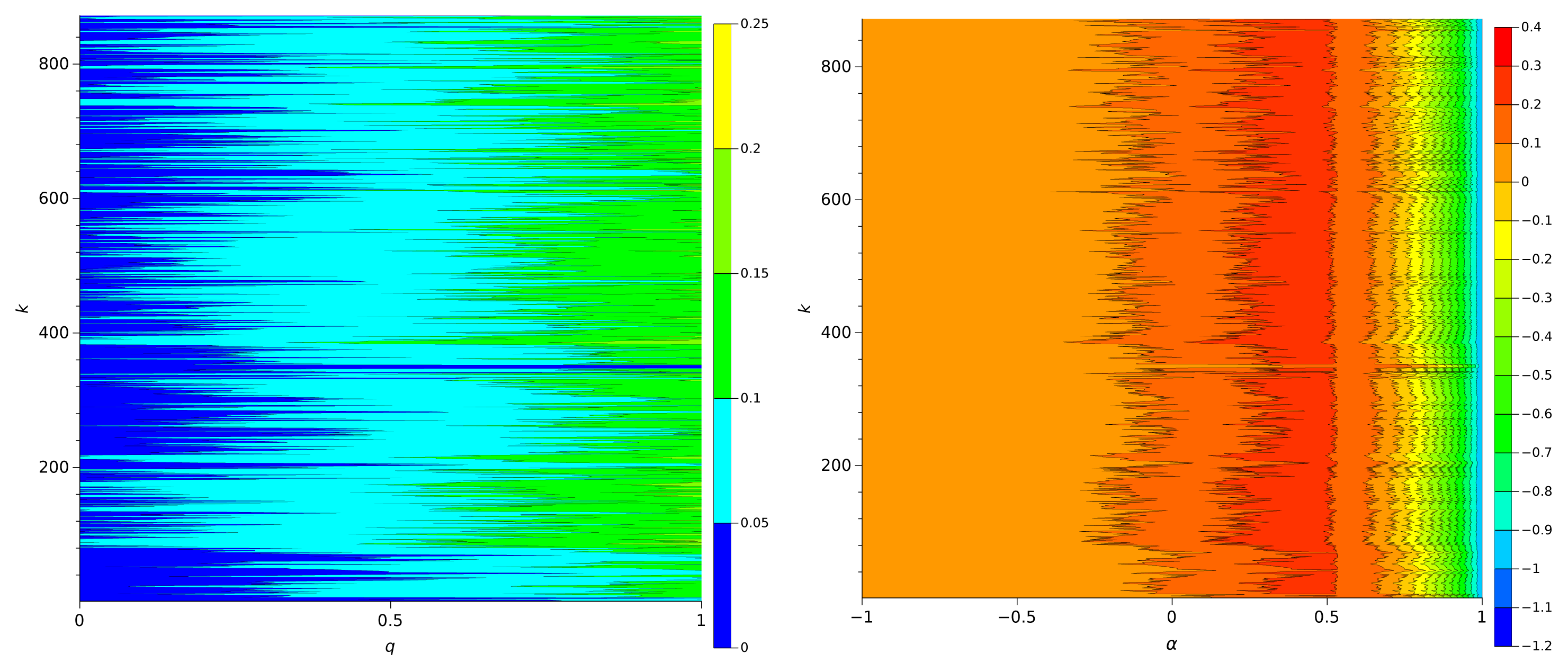
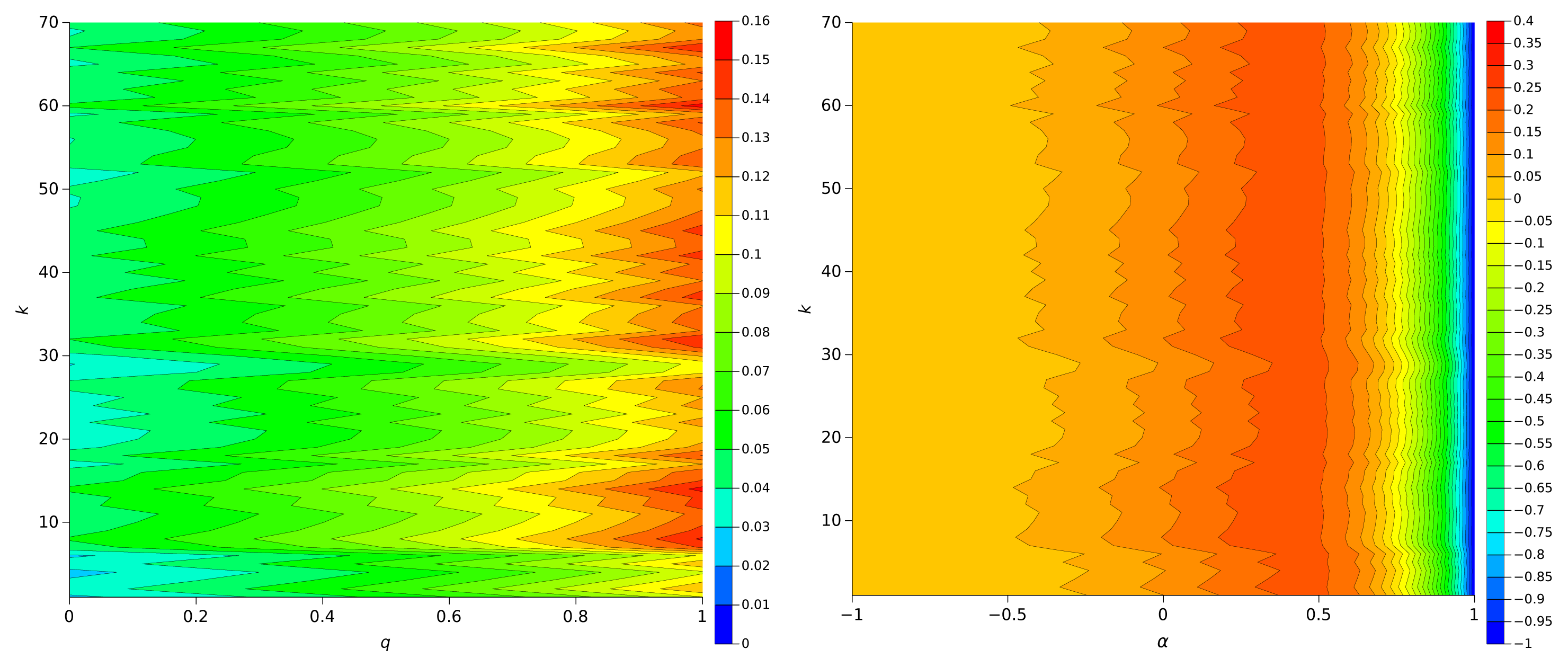
Finally, Figures 8 and 9 show Sq and Sα for the Human chromosome Y, with the only difference being the size and number of sliding windows. As previously the higher sensitivities occur for q = 1 with Sq and for α = 0.5 with Sα. The sliding window W1 is more appropriate for highlighting dynamical evolutions than window W2 that is considerable large and leads to an “averaging” of the information content of the chromosome series.
It is interesting to note that the average entropy over the complete data series characterizes the type of embedded information. In fact, the maxima values are and , for the {π}, {Weierstrass, Dow Jones Industrial Average, Europe Brent Spot Price} and {Human chromosome Y} (both windows) data series, respectively. The results remain identical for other numerical constants and chromosomes to be discussed in the next section.
4. Application of the Generalized Entropy
In this section we explore further the concept of generalized fractional information and entropy. We start by recalling the Kullback-Leibler divergence of Q from P defined as [43–47]:
The Jensen-Shannon divergence JSD(P || Q) is defined as:
where .
Alternatively, we can calculate JSD(P || Q) as:
Having in mind Expressions (4), (6) and (12), the fractional JSD can be written as:
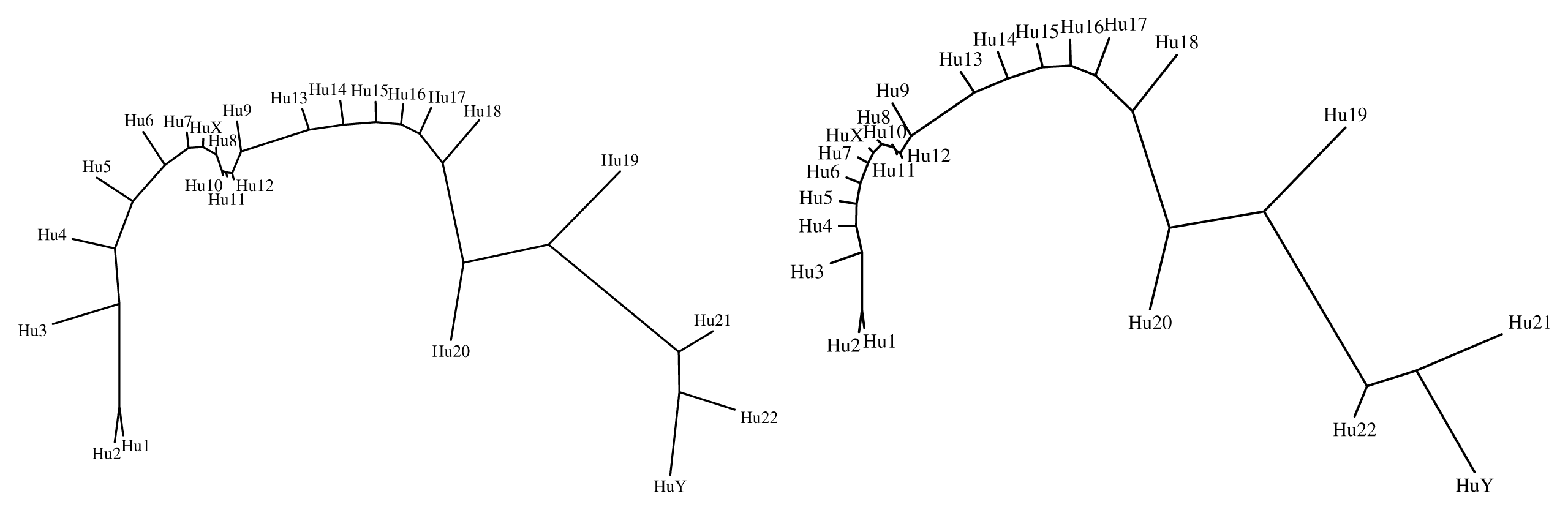
In order to illustrate the fractional-order distance we consider two examples, namely the set


Figures 10 and 11 show the trees for sets

5. Conclusions
This paper presented a generalization of the concept of entropy inspired in the properties of Fractional Calculus. The novel index follows the recent trend in expanding the scope of application of both mathematical tools, by relaxing some properties and allowing their application in new scientific areas. The generalized fractional entropy was first adopted with several typical probability distributions. In a second phase the index was also applied to several types of data, namely of mathematical, financial and biological nature. It was verified that the proposed entropy leads to an higher sensitivity to the signal evolution being useful in describing the dynamics of complex systems. Furthermore, the proposed generalization embeds the concept of positive and negative information, that is, with data either reliable or misleading, allowing the extension of entropy for deceptive cases. The new formulation is then extended for measuring relative distances and tested with two distinct sets of data. The results reveal the goodness of the generalized fractional information concept.
Acknowledgments
The author thanks the anonymous reviewers for their constructive comments.
Conflicts of Interest
The author declares no conflict of interest.
References
- Plastino, A.; Plastino, A.R. Tsallis entropy and Jaynes’ Information Theory formalism. Braz. J. Phys 1999, 29, 50–60. [Google Scholar]
- Li, X.; Essex, C.; Davison, M.; Hoffmann, K.H.; Schulzky, C. Fractional diffusion, irreversibility and entropy. J. Non-Equilib. Thermodyn 2003, 28, 279–291. [Google Scholar]
- Mathai, A.; Haubold, H. Pathway model, superstatistics, Tsallis statistics, and a generalized measure of entropy. Physica A 2007, 375, 110–122. [Google Scholar]
- Anastasiadis, A. Special issue: Tsallis entropy. Entropy 2012, 14, 174–176. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Application of Differentiation and Integration to Arbitrary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Rényi, A. On measures of entropy and information. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Haubold, H.; Mathai, A.; Saxena, R. Boltzmann-Gibbs entropy versus Tsallis entropy: Recent contributions to resolving the argument of Einstein concerning “neither herr Boltzmann nor herr Planck has given a definition of W”? Astrophys. Space Sci 2004, 290, 241–245. [Google Scholar]
- Ben-Naim, A. Statistical Thermodynamics Based on Information: A Farewell to Entropy; World Scientific: Singapore, Singapore, 2008. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, Volume 198: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution, Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Hilfer, R. Application of Fractional Calculus in Physics; World Scientific: Singapore, Singapore, 2000. [Google Scholar]
- Zaslavsky, G. Hamiltonian Chaos and Fractional Dynamics; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Tarasov, V. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: New York, NY, USA, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; Series on Complexity, Nonlinearity and Chaos; World Scientific Publishing Company: Singapore, Singapore, 2012. [Google Scholar]
- Ionescu, C. The Human Respiratory System: An Analysis of the Interplay between Anatomy, Structure, Breathing and Fractal Dynamics; Series in BioEngineering; Springer: London, UK, 2013. [Google Scholar]
- Machado, J.A.T. Entropy analysis of integer and fractional dynamical systems. J. Appl. Nonlinear Dyn 2010, 62, 371–378. [Google Scholar]
- Machado, J.A.T. Fractional dynamics of a system with particles subjected to impacts. Commun. Nonlinear Sci. Numer. Simul 2011, 16, 4596–4601. [Google Scholar]
- Machado, J.A.T. Entropy analysis of fractional derivatives and their approximation. J. Appl. Nonlinear Dyn 2012, 1, 109–112. [Google Scholar]
- Machado, J.T.; Galhano, A.M. Symbolic fractional dynamics. IEEE J. Emerg. Sel. Top. Circuits Syst 2013, 3, 468–474. [Google Scholar]
- Machado, J.T. Complex dynamics of financial indices. Nonlinear Dyn 2013, 74, 287–296. [Google Scholar]
- Machado, J.T. Relativistic time effects in financial dynamics. Nonlinear Dyn 2014, 75, 735–744. [Google Scholar]
- Machado, J.T.; Costa, A.; Quelhas, M. Entropy analysis of DNA code dynamics in human chromosomes. Comput. Math. Appl 2011, 62, 1612–1617. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27, 379–423. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27, 623–656. [Google Scholar]
- Gray, R.M. Entropy and Information Theory; Springer: New York, NY, USA, 1990. [Google Scholar]
- Beck, C. Generalised information and entropy measures in physics. Contemp. Phys 2009, 50, 495–510. [Google Scholar]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Dover: New York, NY, USA, 1957. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev 1957, 106, 620–630. [Google Scholar]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar]
- Machado, J.A.T.; Galhano, A.M.S. Approximating fractional derivatives in the perspective of system control. Nonlinear Dyn 2009, 56, 401–407. [Google Scholar]
- Machado, J.A.T.; Galhano, A.M.; Oliveira, A.M.; Tar, J.K. Approximating fractional derivatives through the generalized mean. Commun. Nonlinear Sci. Numer. Simul 2009, 14, 3723–3730. [Google Scholar]
- Valério, D.; Trujillo, J.J.; Rivero, M.; Machado, J.T.; Baleanu, D. Fractional calculus: A survey of useful formulas. Eur. Phys. J. Spec. Top 2013, 222, 1827–1846. [Google Scholar]
- Dirac, P.A.M. Bakerian Lecture. The physical interpretation of quantum mechanics. Proc. R. Soc. Lond 1942, 180, 1–40. [Google Scholar]
- Feynman, R.P. The concept of probability theory in quantum mechanics. Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability Theory, Berkeley, CA, USA, 31 July–12 August 1950; University of California Press: Berkeley, CA, USA, 1950. [Google Scholar]
- Feynman, R.P. Negative probability. In Quantum Implications: Essays in Honour of David Bohm; Basil, J., Hiley, F.D.P., Eds.; Routledge & Kegan Paul Ltd: London, UK and New York, NY, USA, 1987; pp. 235–248. [Google Scholar]
- Bartlett, M.S. Negative probability. Math. Proc. Camb. Philos. Soc 1945, 41, 71–73. [Google Scholar]
- Székely, G.J. Half of a Coin: Negative Probabilities. Wilmott Magazine 2005, 66–68. [Google Scholar]
- Machado, J.T. Fractional coins and fractional derivatives. Abstr. Appl. Anal 2013, 2013. [Google Scholar] [CrossRef]
- Shim, J.; Arkin, R.C. A taxonomy of robot deception and its benefits in HRI. Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 13–16 October 2013; pp. 2328–2335.
- Sibson, R. Information radius. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1969, 14, 149–160. [Google Scholar]
- Taneja, I.; Pardo, L.; Morales, D.; Ménandez, L. Generalized information measures and their applications: A brief survey. Qüestiió 1989, 13, 47–73. [Google Scholar]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar]
- Cha, S.H. Measures between probability density functions. Int. J. Math. Models Methods Appl. Sci 2007, 1, 300–307. [Google Scholar]
- Deza, M.M.; Deza, E. Encyclopedia of Distances; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- PHYLIP, Available online: http://evolution.genetics.washington.edu/phylip.html accessed on 3 April 2014.
- Tuimala, J. A Primer to Phylogenetic Analysis Using the PHYLIP Package; CSC—Scientific Computing Ltd: Espoo, Finland, 2006. [Google Scholar]
- Costa, A.; Machado, J.T.; Quelhas, M. Histogram-based DNA analysis for the visualization of chromosome, genome and species information. Bioinformatics 2011, 27, 1207–1214. [Google Scholar]
- Machado, J.T.; Costa, A.C.; Quelhas, M.D. Shannon, Rényi and Tsallis entropy analysis of DNA using phase plane. Nonlinear Anal. Ser. B: Real World Appl 2011, 12, 3135–3144. [Google Scholar]
- Machado, J.T.; Costa, A.C.; Quelhas, M.D. Wavelet analysis of human DNA. Genomics 2011, 98, 155–163. [Google Scholar]


 of 13 irrational numbers, compared by means of the indices Iq, q = 1 (left) and Iα, α = 0.5 (right).
of 13 irrational numbers, compared by means of the indices Iq, q = 1 (left) and Iα, α = 0.5 (right).
 of 13 irrational numbers, compared by means of the indices Iq, q = 1 (left) and Iα, α = 0.5 (right).
of 13 irrational numbers, compared by means of the indices Iq, q = 1 (left) and Iα, α = 0.5 (right).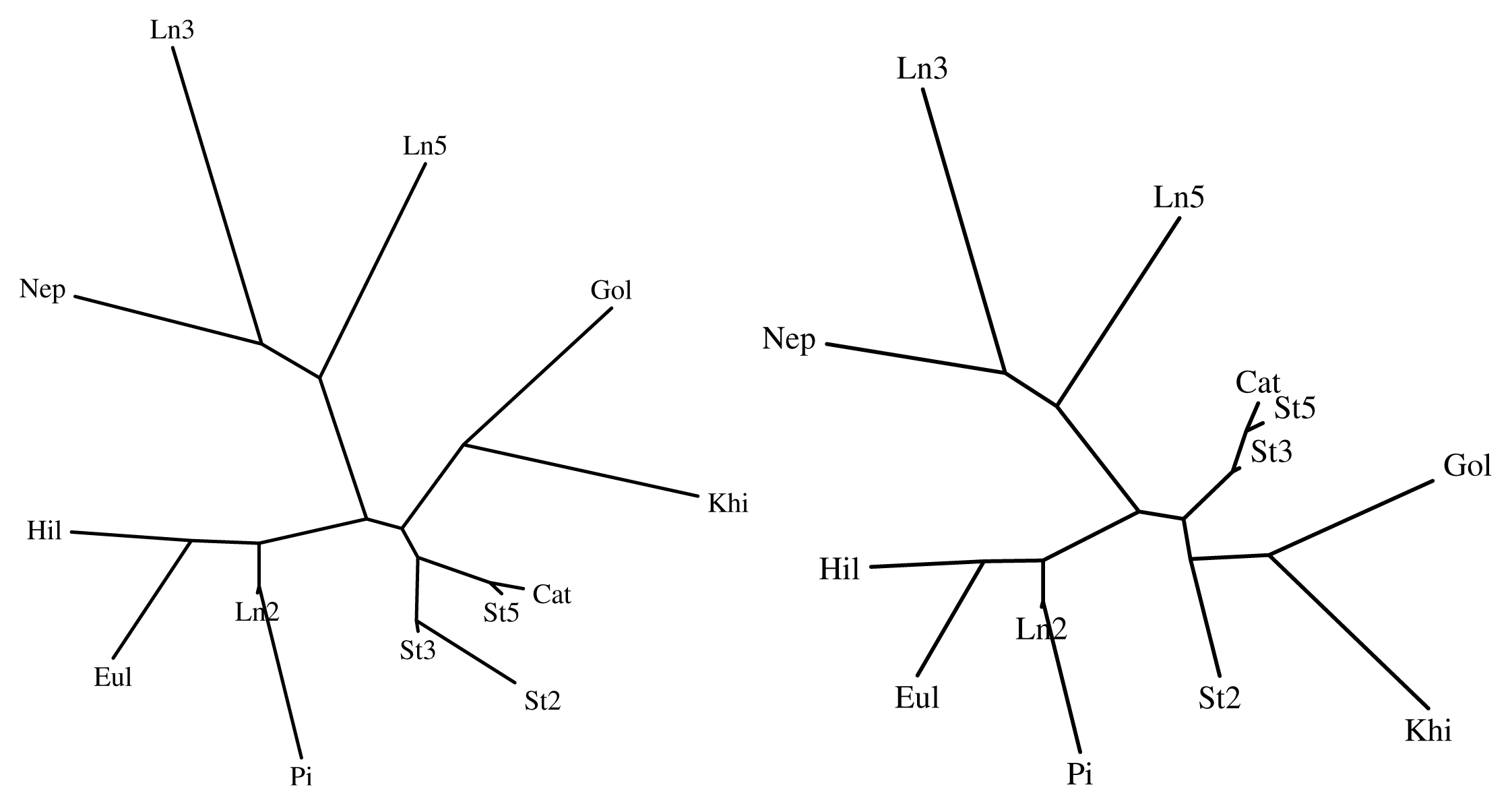
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Machado, J.T. Fractional Order Generalized Information. Entropy 2014, 16, 2350-2361. https://doi.org/10.3390/e16042350
Machado JT. Fractional Order Generalized Information. Entropy. 2014; 16(4):2350-2361. https://doi.org/10.3390/e16042350
Chicago/Turabian StyleMachado, José Tenreiro. 2014. "Fractional Order Generalized Information" Entropy 16, no. 4: 2350-2361. https://doi.org/10.3390/e16042350
APA StyleMachado, J. T. (2014). Fractional Order Generalized Information. Entropy, 16(4), 2350-2361. https://doi.org/10.3390/e16042350




