Contact Geometry of Mesoscopic Thermodynamics and Dynamics
Abstract
: The time evolution during which macroscopic systems reach thermodynamic equilibrium states proceeds as a continuous sequence of contact structure preserving transformations maximizing the entropy. This viewpoint of mesoscopic thermodynamics and dynamics provides a unified setting for the classical equilibrium and nonequilibrium thermodynamics, kinetic theory, and statistical mechanics. One of the illustrations presented in the paper is a new version of extended nonequilibrium thermodynamics with fluxes as extra state variables.PACS Codes: 05.20Dd; 05.20J; 05.70Ln1. Introduction
The classical nonequilibrium thermodynamics (see e.g., Reference [1]) has emerged in the series of extensions that follow the path
Path A
equilibrium thermodynamics → local equilibrium thermodynamics → local conservation laws of classical fluid mechanics supplemented with an equation governing the time evolution of entropy field.
Its modification
Path B
equilibrium thermodynamics → local equilibrium thermodynamics supplemented with extra fields → local conservation laws of classical fluid mechanics supplemented with equations governing the time evolution of the extra fields and the entropy field.
has later led (see References [2–7]) to various versions of extended nonequilibrium thermodynamics. The extra fields can have many different physical interpretations. Their choice, considered as the most appropriate for a given macroscopic system under investigation, determines then a general structure for the equations governing their time evolution. For example, if the extra fields are interpreted as fluxes of the classical hydrodynamic fields and possibly also fluxes of these fluxes etc., the structure is the one emerging in the moment equations generated by the Boltzmann kinetic equation (see more in References [2,4–7] and in Section 4.4). (We recall that the moments are fields—i.e., function of the position vector r—obtained by multiplying the one particle distribution function f(r,v) with tensors constructed from the velocity vector v and then integrating the result over v). In another example, the extra fields characterize microscopic nature of suspended particles (e.g., macromolecules in the case of polymeric fluids) and the structure of equations governing their time evolution comes from mechanics on the microscopic scale (see e.g., References [8,9] and references cited therein).
In this paper we follow another path:
Path C
equilibrium thermodynamics → an abstract geometrical structure extracted from the classical equilibrium thermodynamics → time evolution preserving the structure.
Its main advantage is that it leads to a general mesoscopic nonequilibrium theory that includes as particular realizations the classical nonequilibrium thermodynamics obtained by following Path A, many extended theories obtained by following Path B (see more in Section 3), the Boltzmann kinetic equation (that on Path B serves only as a source of an additional structure for the time evolution equations), other kinetic theories (for example those describing the time evolution in complex fluids and complex solids (see e.g., [9,10]), the Gibbs equilibrium statistical mechanics, and also multiscale dynamical theories combining different levels of description (see an illustration in Section 3). The basic idea behind Path C has been introduced previously in [11,12]. In this paper we are bringing some new physical and mathematical arguments in its favor and explore new illustrations. In particular, we initiate in Section 4.4 a novel viewpoint of extended nonequilibrium thermodynamics with fluxes as extra state variables.
2. Equilibrium Thermodynamics
It has been realized by Gibbs [13] and then more explicitly (and in a more general context and with an alternative physical interpretation) by Jaynes [14] that the essence of equilibrium thermodynamics is maximization of entropy subjected to constraints (the so called MaxEnt principle). This principle is our starting point. The next step toward geometrical formulation of thermodynamics that we use in this paper is a realization that maximization of a convex potential subjected to constraints is, from the mathematical point of view, a Legendre transformation. We conclude therefore that the group of Legendre transformations is the fundamental group of thermodynamics. The following step is to ask the question of what is the geometrical environment in which Legendre transformations are the most natural transformations. The answer to this question is well known: it is the contact geometry since the contact 1-form defining it is preserved under such transformations. Following Hermann [15], we formulate geometrically the classical thermodynamics (in Section 2.1), and then in Section 2.2, following [11,12], a general mesoscopic equilibrium thermodynamics.
2.1. Classical Equilibrium Thermodynamics
The variables characterizing states of a one component macroscopic system at thermodynamic equilibrium are
where e is the energy per unit volume and n the number of moles per unit volume.
The fundamental thermodynamic relation is a function (e,n) ↦ s(e,n) ∈ ℝ, where s denotes entropy per unit volume. The function s(e,n) as well as all other functions introduced below are assumed to be sufficiently regular so that the operations made with them are well defined. We can see the fundamental thermodynamic relation s = s(e,n) geometrically (as Gibbs did, see [13]) as a two dimensional manifold, called a Gibbs manifold, imbedded in the three dimensional space with coordinates (e,n,s) by the mapping: (e,n) ↪ (e,n,s(e,n)).
The macroscopic systems studied in the classical equilibrium thermodynamics interact with their surrounding through thermodynamic walls (passing freely the internal energy, the number of moles and the volume—separately or in combinations). The role of the entropy is to determine the states (called equilibrium states) corresponding to given constraints implied by different arrangements of the thermodynamic walls. According to MaxEnt, they are the states at which the entropy reaches its maximum allowed by constraints. In order to provide an appropriate setting for the maximization process, we shall make, following Hermann [15], an alternative formulation of the fundamental thermodynamic relation. We introduce a five dimensional space with coordinates (e,n,e*,n*,s) and present the fundamental thermodynamic relation as a two dimensional manifold imbedded in this five dimensional space by the mapping
We shall call this manifold a Gibbs-Legendre manifold. The advantage of this formulation is that the five dimensional space with coordinates (e,n,e*,n*,s) is naturally equipped with 1-form: ϑ = ds − e*de − n*dn. This 1-form is preserved in Legendre transformations and equals zero on the Gibbs-Legendre manifold (5). In the standard thermodynamic notation, the coordinates (e*,n*) are denoted respectively 1/T, −μ/T, where T is the temperature and μ the chemical potential. The Legendre transformation carrying the fundamental thermodynamic relation s = s(e,n) into its dual form s* = s*(e*,n*), where s*− = P/T (P denotes the pressure) is made in three steps: (i) we introduce thermodynamic potential φ(e,n;e*,n*) = s(e,n) + e*e + n*n; (ii) we solve equations ∂φ/∂e = 0, ∂φ/∂n = 0; let their solution be eeq(e*,n*), neq(e*,n*); (iii) s*(e*,n*) = φ(eeq(e*,n*), neq(e*,n*);e*,n*). The Legendre image of the Gibbs-Legendre manifold (5) is the image of the mapping
We shall use below the following notation: the space with coordinates (4) will be denoted by the symbol Meq and the space with coordinates (e*,n*) by the symbol . The 1-form in the space is given by ds − ede* − ndn*.
The Gibbs-Legendre manifolds can be naturally provided with an additional geometrical structure, namely with the Riemannian metric generated by the second derivatives of the entropy. The additional insight brought by this viewpoint to the classical equilibrium thermodynamics (see [16,17]) is not exploited in this paper.
2.2. Mesoscopic Equilibrium Thermodynamics
Following [11,12], we translate in this section the setting introduced above into an abstract setting that can be used to formulate a mesoscopic equilibrium thermodynamics on any level of description (including the most microscopic level on which the abstract setting becomes the setting of the Gibbs equilibrium statistical mechanics) and that extends also, as we shall see below in Section 3, to dynamics.
2.2.1. State Space M and Its Structure
We denote the state space by the symbol M and its coordinates with the symbol x (i.e., x ∈ M) For example, M can be the two dimensional space with coordinates (1). In this case the state space M is the same as the space Meq introduced above in the classical equilibrium thermodynamics. On the other hand, x can be 1023—particle distribution functions representing the microscopic characterization of macroscopic systems seen as composed of ~1023 atoms. In this case M becomes a space used in the Gibbs equilibrium statistical mechanics. In other examples, x can denote the classical hydrodynamic fields, or still in other examples the one or more particle distribution functions (for more examples see Section 4).
Next, we equip the spaces M with a structure.
On the space M we introduce three potentials
The potential s, called entropy is required to be a concave function of x, e represents the energy and n number of moles (i.e., e = e(x) and n = n(x) have the same physical meanings as (1)). All three potentials are required to be sufficiently regular so that all operations made with them (for example differentiations) are well defined. The three potentials (3) are called fundamental thermodynamic relations.
It is in these relations where the individual nature of the macroscopic system under consideration is expressed.
In the particular case of the classical equilibrium thermodynamics when M ≡ Meq, the state variable x is given in (1), and the three potentials are:
We thus see that in this case the potentials e and n are universal. There is thus only one fundamental thermodynamic relation s = s(e,n). In Section 2.1 we have indeed called it as such.
In another particular case corresponding to the Gibbs equilibrium statistical mechanics, the state variable x is N-particle distribution function f(N) (N is the number of particles composing the macroscopic system under consideration; we use the shorthand notation: “1” is the element of the phase space of particle “1”, and similarly for the other particles)
and the fundamental thermodynamic relations are
On this microscopic level of description we thus see that the expression for the entropy (and for the number of moles) is universal and the individual nature of the macroscopic system under consideration is expressed only in the energy (in the microscopic Hamiltonian). The situation is thus completely reversed from the one in the classical equilibrium thermodynamics where the individual nature of macroscopic systems is expressed only in the entropy and the expressions for the energy and the number of moles are universal.
On mesoscopic levels (some examples are discussed in Section 4), a universal expression exists usually only for the number of moles n(x), the individual nature of the system under consideration is expressed in both the energy and the entropy.
2.2.2. Gibbs-Legendre Manifold
Now we proceed to the geometrical formulation. From M we construct a new space
with coordinates (x,x*,e*,n*,e,n,φ) ∈
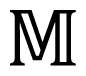
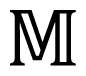
From the potentials (3) we construct a new potential
that we shall call a thermodynamic potential; Φ:
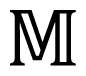
In order to simplify the presentation, we shall use hereafter an abbreviated notation . The appearance of a symbol in the position of lower index will always mean derivative with respect to the quantity represented by the symbol. We cannot however avoid to use the lower index occasionally also for denoting indices of vectors (e.g., r = (r1,r2,r3)) or, for example the subscript “eq”, for denoting equilibrium (as we have already used in Section 2.1). This type of exceptions will always be explained or they will be clear from the context.
Now, we are in position to represent the fundamental thermodynamic relations (3) as well as the maximization of the entropy and the fundamental thermodynamic relation in
implied by (3) geometrically. An appropriate setting for such representation is provided by the spaces
By we denote a manifold imbedded in the space
We note that in various projections of this manifold we see geometrically all the elements of the maximization of entropy subjected to constraints. Namely:
- (i)
The manifold |e*=0,n*=0, displays the fundamental thermodynamic relations (3) in M. Indeed, this manifold is the image of the mapping x ↪ (x,−sx(x),0,e(x),n(x),−s(x)).
- (ii)
Restriction of the manifold to x* = 0, i.e., the manifold |x*=0 displays the states that represent in M the states in Meq (we shall call them equilibrium states and denote them by the symbol xeq(e*,n*)) that (as we shall see in Section 3) are reached as t → ∞, and also the fundamental thermodynamic relation in implied by the fundamental thermodynamic relation s = s(x) in M. Indeed, the manifold
|x*=0 is the image of the mapping
Relations s* = s*(e*,n*), e = e(xeq(e*,n*)), n = n(xeq(e*,n*)) are the fundamental thermodynamic relations in implied by the fundamental thermodynamic relations (3) in M.
Summing up, in the geometrical formulation presented above, mesoscopic thermodynamics in the state space M is represented by the Gibbs-Legendre manifold and the implied by it classical equilibrium thermodynamics in Meq is represented by another Gibbs-Legendre manifold |x*=0.
3. Mesoscopic Thermodynamics and Dynamics
We now assume that both the mesoscopic thermodynamics in M and the classical equilibrium thermodynamics in Meq are well established in the sense that consequences derived from the fundamental thermodynamic relations (3) and (4) agree with results of experimental observations made on both levels. This assumption implies that if we keep the system under the constraints provided by thermodynamic walls, then, given a sufficiently long time, the mesoscopic level on which M serves as the state space reduces to the level of the classical equilibrium thermodynamics on which Meq plays this role. The time evolution involved in this approach is in fact a preparation process for applicability of the classical equilibrium thermodynamics on which (e,n) are used as state variables. We have seen in Section 2.2 that, in the context of equilibrium theories, the passage from M to Meq is made by maximizing the entropy s(x) subjected to constraints e(x) and n(x). We now introduce the time evolution that does such reduction. Such time evolution maximizes the entropy s(x) subjected to constraints e(x), n(x) and proceeds, in the geometrical setting of Section 2.2, as a continuous sequence (parametrized by the time t) of contact structure preserving transformations.
We begin by recalling (see e.g., [18]) the canonical form of the time evolution preserving the 1-form ϑ in the space
The problem is now to identify the potential Ψ:
The contact Hamiltonian Ψ satisfying the above four requirements is
where
and
By Ξ we denote dissipation potential Ξ:
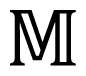
| (Ξ) |
The symbol <,>denotes the pairing in M.
By L(x) we denote a Poisson bivector satisfying the following two properties:
| (L) |
It can easily be verified that with this contact Hamiltonian the time evolution in
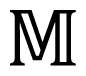
Next, we investigate qualitative properties and physical interpretations of their solutions.
3.1. Properties of Solutions of Equation (14)
We begin by proving that Equations (14) satisfy the four requirements listed in the text following Equation (10).
3.1.1. Proof of Requirement 1
We see indeed that [Ψ] = 0. Note that
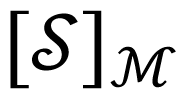
3.1.2. Proof of Requirement 2
We see immediately that on the first three equations (Equation (14)) become:
Since [ẋ*] = Φxxẋ, the second equation in Equation (15) is equivalent to the first (provided Φ satisfies the properties enumerated in the text that follows Equation (8)) and consequently the Gibbs-Legendre manifold is invariant.
3.1.3. Proof of Requirement 3
Due to the properties (Ξ) required from the dissipation potential Ξ, the right hand side of the third equation in Equation (15) is nonnegative. This means that the thermodynamic potential Φ(x,e*,n*) plays the role of the Lyapunov function for the approach x → xeq, and consequently, → []x*=0 as t → ∞. We thus see indeed, that on the time evolution (14) describes the time evolution representing the preparation process for applicability of the classical equilibrium thermodynamics.
3.1.4. Proof of Requirement 4
Another way to introduce an abstract mesoscopic dynamics could be to collect well established (i.e., well tested with experimental observations) examples of mesoscopic dynamics (as e.g., the classical nonequilibrium thermodynamics, Boltzmann’s kinetic theory) and attempt to extract from them a common structure. This has indeed been the way in which equations of the type (15) have originally emerged. First, the Hamiltonian structure of the Euler (i.e., nondissipative part) of the governing equations of the classical hydrodynamics has been discovered by Clebsch in [19]. It has then been realized in [20] that also the nondissipative part of the Boltzmann and other kinetic equations possess the Hamiltonian structure. The dissipative part of the time evolution has been put into the form appearing in Equation (15) in [21–23]. Both Hamiltonian and dissipative dynamics has been combined in [24–32]. In [30,31] the combination of both structures has been cast into the form of the first equation in Equation (15) and called GENERIC (an acronym for General Equation for Non-Equilibrium Reversible-Irreversible Coupling). We can therefore regard the way we have arrived in this paper at GENERIC Equation (15) as its derivation from thermodynamics.
3.1.5. Variational Formulation
We have seen that the time evolution that takes place on ⊂
A direct verification shows that the first two equations in Equation (10) are Euler-Lagrange equations corresponding to the functional:
In other words, the functional given in Equation (21) reaches its extremum on the trajectories (x(t), x*(t)) generated in
As for the physical meaning of , we see that on the Gibbs-Legendre manifold (i.e., []) it becomes the total entropy generated during the time evolution (indeed, we recall (see Section 3.1.1) that [Ψ] = 0 and we clearly see that −<x*,ẋ>] = ⋅). We can thus formulate this observation as follows: The total entropy generated during the mesoscopic time evolution reaches its extremum.
It is interesting to note that this type of variational formulation of nonequilibrium thermodynamics has been introduced previously by using arguments that are completely different from those used in this paper (see e.g., Reference [33]).
3.2. Physical Interpretation of the Contact Hamiltonian Ψ
Does the viewpoint of mesoscopic dynamics that we follow in this paper provide a new insight into the physical meaning of entropy and other concepts arising in thermodynamics? First, we recall the insight provided by the Gibbs equilibrium statistical mechanics which is a particular case of the mesoscopic thermodynamics introduced in Section 3 that corresponds to the choice (5) of state variables in M, to the choice (6) of the entropy, energy and number of moles, and to the time evolution (10) replaced by the ergodic hypothesis. In this particular case the macroscopic entropy becomes (if we restrict ourselves to still a more special case when the volume, the number of moles, and the macroscopic energy are kept fixed—the so called microcanonical ensemble) logarithm of the volume of the microscopic state space with coordinates (1, …, N) corresponding to one macroscopic state with fixed volume and the coordinates (e,n).
The general mesoscopic dynamics (10) offers an additional insight into the physical interpretation of entropy s. Not only we see in s an information about how micro and macro descriptions relate to each other, we also see that s plays the role of a potential generating the time evolution during which a micro description reduces to the macro description. Moreover, both micro and macro entropies determine geometry that is naturally associated with thermodynamics (namely the geometry of the Gibbs-Legendre manifolds). In addition, the starting micro description (that is in the Gibbs theory always chosen to be the most microscopic description with Equation (5) as state variables) can be replaced with any well established (i.e., well tested with experiments) mesoscopic description.
Next, we turn to discussing physical interpretation of the remaining quantities entering the contact Hamiltonian Ψ. We begin with the Poisson bivector L. From the physical point of view, L expresses mathematically the kinematics of state variables. We can see it well in the context of classical mechanics. In this example the state variables x = (q,p), where q stands for position vectors of particles and p for their momenta. The state space M is a cotangent bundle M = T*Q, q ∈ Q, . The Poisson bivector in this case is the matrix which indeed expresses the fact that p is a conjugate to the velocity q̇ ∈ TqQ. The Poisson bracket corresponding to the above Poisson bivector is {A,B} = <(Aq,Ap)TL(Bq,Bp)>=AqBp − BqBp, where A and B are sufficiently regular real valued functions of (q,p). What is the physical interpretation of the degeneracy requirement (L)? We have seen that degeneracy of L is essential for keeping the entropy constant during the Hamiltonian (nondissipative) time evolution. We note that if we begin our investigation with classical mechanics of particles with the state variables x = (q,p) then we are not able to satisfy the degeneracy requirement (L) since the matrix is obviously nondegenerate. If we indeed want to take as our point of departure the classical mechanics we have to therefore choose its another representation in which the Poisson bivector is degenerate. We choose it to be the Liouville reformulation of classical mechanics in which state variables are not x = (q,p) but distribution functions (5). In this setting the Poisson bracket expressing kinematics of fN(1, …, N) takes the form [19] {A,B} = ∫ d 1…∫d N fN [(AfN)q(BfN)p − (AfN)q(BfN)p]. This Poisson bracket is indeed degenerate. It can easily be verified directly (see Appendix) that {A,C} = 0 for all functions A and for C that are pointwise functions of fN (i.e., (1,…,N) ↦ fN ↦ C). Functions C for which that {A,C} = 0 for all functions A are called Casimirs of the bracket {A,B}. We note that the entropy s given in Equation (6) is a Casimir of the bracket {A,B} = ∫ d 1…∫d N fN [(AfN)q(BfN)p − (AfN)q(BfN)p]. We thus conclude that an attempt to find a formulation of classical mechanics that could serve as a starting point for an analysis of the time evolution of the type (10) leads us to statistical mechanics (i.e., to use fN(1, …, N) instead of (1, …, N) as state variables). We have thus identified an alternative route (alternative to the one based on the original Maxwell and Gibbs arguments) to statistical mechanics.
Now we turn to discussing the physics involved in the dissipation potential Ξ. It has been established on Path A that the entropy production σ has the form σ = ∑iJiXi, where Ji are fluxes and Xi are thermodynamic forces. Moreover, the fluxes are related to the forces by the Onsager relation Ji = ∑kΛikXk, where Λ is a symmetric matrix of Onsager coefficients. The nonlinear version of the Onsager relation takes the form Ji = ξXi, where ξ, called a dissipation potential X ↦ ξ(X) ∈ ℝ; X = (X1,X2, …), is required to satisfy the following three properties (compare with(Ξ)):
| (ξ) |
(note that the nonlinear Onsager relation reduces to the linear Onsager relation if , where Λ is a non negative operator independent of X, but possibly dependent on x). With such nonlinear generalization of the linear Onsager relation, the entropy production σ = ∑iJiXi becomes
The question arises of how this viewpoint of the entropy production, that is one of the founding stones on which the classical nonequilibrium thermodynamics stays, relates to the mesoscopic nonequilibrium thermodynamics (10) introduced in this section. To answer it we proceed as follows. From the third equation in Equation (15) we have:
It is easy to see that Equations (17) and (18) become identical if:
where α > 0 is a constant and the function X(x*) satisfies the property:
This property is obviously satisfied for X = x*. In Section 4 we shall see other examples of the thermodynamic forces X satisfying (19) and (20).
As for the physical interpretation of the contact Hamiltonian Ψ itself, the properties of solutions of Equation (10) that we have investigated above indicate that we can regard as the rate of energy and
Finally, we recall that the most fundamental contribution that has arisen on Path A and Path B is that equations governing the time evolution of state variables are supplemented with an equation governing the time evolution of entropy. On Path C this feature is an integral part of the geometrical formulation of dynamics (see the seventh equation in Equation (10), third equation in Equation (14) and the third equation in Equation (15)). In addition, we also see on Path C that it is natural to supplement the equations governing the time evolution of the state variables with equations governing the time evolution of the conjugate state variables (see the second equations in Equations (10), (14) and (15)). Usefulness of this addition has in fact also arisen on Path B in the investigations directed toward the mathematical regularity of the governing equations. We shall give more details about this result obtained on Path B in Section 3.3 and 4.4 below.
3.3. Generalizations and Alternative Formulations of Mesoscopic Dynamics
An important generalization of the formulation developed above consists in replacing the state space Meq of equilibrium thermodynamics with Mslow ⊂ M composed of state variables that evolve in slower pace than the rest of the state variables in M. The time evolution governed by Equation (15) becomes in this more general context the fast time evolution describing approach to Mslow in which then the time evolution continues in a slower pace (slow time evolution). We note that Meq is indeed a particular case of Mslow in which the “slow” becomes “still”. This type of generalization of Equation (15), worked out in [9,12,34], is based on previous observations made in [35,36].
An independent investigation of the separation of the time evolution into fast and slow has been made in [37,38] and in [7,39,40]. A particularly new feature appearing in the formulation based on Equation (15) is the emergence of the fundamental thermodynamic relation in Mslow. This new thermodynamics in Mslow emerges in the same way as the equilibrium thermodynamics (the equilibrium fundamental thermodynamic relation) has emerged in Sections 2 and 3 in Meq.
A different route leading to extensions of MaxEnt principle to dynamics has been followed in [41–43]. Still another route to an abstract setting for mesoscopic dynamics has been explored in [4,44–46]. This latter route has been motivated by an attempt to pursue mathematical rigor in the formulations arising on Path B. We now briefly sketch this approach.
We begin with restricting the choice of state variables. Only real valued functions of the position vector r (called fields) are admissible as state variables, i.e.,
The fields q are moreover required to include one scalar field e(r) having the physical interpretation of energy, i.e.,
where q′(r) denote the remaining fields.
The equations generating the time evolution of q(r) are required to have the form:
where the quantities and ϑ̂ satisfy some properties listed below.
First, we turn to the properties of , i = 1,2, …, n, j = 1,2,3. These fields (functions of q(r)) denote fluxes corresponding to the fields q. The time evolution Equation (23) with ϑ̂ absent are called local conservation laws since they imply , where Q = ∫Ω d rq(r), provided appropriate boundary conditions have been chosen (i.e., boundary conditions guaranteeing ∫∑ · n = 0; ∑ denotes the boundary of Ω ⊂ ℝ3 and n the vector perpendicular to the boundary). In particular, due to the presence of the energy field e(r) in the set of state variables (see Equation (22)), the total energy E = ∫ d re(r) is conserved in the time evolution governed by Equation (23) with ϑ̂(q) ≡ 0. The fluxes are required to satisfy the following two properties:
Property 1
The fields depend on the fields q(r) but not on their derivatives.
Property 2
The time evolution Equation (23) with ϑ̂(q) ≡ 0 imply another local conservation law
where s(q) and , called entropy field and entropy flux respectively, are functions of q(r). As for the functional dependence of s on q, we require that
The first requirement expresses the thermodynamic stability and the second the positivity of the absolute temperature (recall that , where T is the local absolute temperature).
The problem now is to identify for which Equation (23) implies Equation (24) provided ϑ ≡ 0. Godunov has noted in [44] that such identification can best be done if conjugate fields, denoted by the symbol p(r), are brought into the consideration. This Godunov observation is, of course, very much in the spirit of using contact geometry to formulate mesoscopic dynamics. We now present Godunov’s observation. Let s*(p) be the Legendre transformation of the potential s(q) arising in Equation (24) (i.e., s*(p) = [−s(q)]+<p,q>]q=qeq(p), where qeq(p) is a solution of ). Moreover, we can now regard the potential s(q) as a Legendre transformation of s*(p) (i.e., s(q) = [−s*(p)]+<p,q>]p=peq, where peq(p) is a solution of ). Now we note that if the fields p(r) evolve in time according to:
then an additional conservation law
is automatically implied (it is sufficient to multiply each equation in Equation (26) by pk and sum them up). Moreover, Equation (27) implies also:
which means that Equation (26) is a symmetric hyperbolic (or hyperbolic in the sense of Friedrichs [46]) system of partial differential equations. This in turn means that the initial value problem (Cauchy problem) for Equation (26) with sufficiently smooth initial data is well posed. Such connection between thermodynamics and well-posedness of differential equations of continuum mechanics was first recognized by Godunov in [44]. (The notation that we have used in the equations above and that we shall continue to use it in the rest of this paper is the following: is n-vector, is n × n-matrix, and similarly for other potentials; moreover, we use also the summation convention (i.e., summation over repeated indices)).
As for the term ϑ̂(q) appearing in Equation (23), we choose it in such a way that it depends on q but not on its derivatives, that the energy remains conserved and the entropy s(q) (introduced in Equation (24)) does not decrease during the time evolution governed by Equation (23). In its specification, one can follow the same concepts and arguments that we have used in the discussion of the dissipative time evolution in Equation (15).
Now we make a few observations about the relation between the mesoscopic dynamics (10) obtained by following Path C and Equation (29) obtained by following Path B.
- (i)
There is no limitation on the choice of the state variables x in Equation (10) but there is one in Equation (23) (only fields (21) are allowed).
- (ii)
The Hamiltonian structure of the nondissipative time evolution in Equation (10) is replaced in Equation (23) by local conservation laws. We shall see in Sections 4.2 and 4.4 that the Hamiltonian structure and the structure of local conservation laws can coexist but the problem for what appearing in Equation (23) the time evolution governed by Equation (23) with ϑ̂(q) ≡ 0 is Hamiltonian remains open.
- (iii)
We have seen that the Legendre transformations that have arisen naturally in the context of the mesoscopic dynamics and thermodynamics (10) arise also naturally in the Godunov analysis of the compatibility of the dynamics (23) with thermodynamics. We note that in the context of Equation (23) the association with Legendre transformations also implies results about mathematical regularity of the formulation (namely the well-posedness of the initial value problem).
4. Illustrations
Let us now consider a problem of deriving a model describing dynamical and thermodynamical behavior of a specific family of macroscopic systems. The point of departure is an identification of the macroscopic systems and of our interest in them. The interest is determined by experimental observations in our disposition and by intended applications. For example, the macroscopic systems may be polymeric liquids, the experimental observations those developed in experimental rheology, and the intended application an assistance in fabrication of objects made of plastic materials. The next step in the model derivation is a microscopic formulation of the physics involved. In the development that follows we can then choose among three different routes.
On the first route (called direct simulations—see e.g., [47,48]) we begin with a microscopic (particulate) formulation. Next, we calculate trajectories of all the particles composing the macroscopic systems under investigation and then reduce this detailed microscopic information to a less detailed mesoscopic information that is related more directly to our interests. The passage from micro to meso descriptions is thus done with the assistance of computers (in the calculation of the trajectories) and with two additional interventions, one in determination of forces (acting on particles) that originate in macroscopic constraints (e.g., forces due to an imposed temperature gradient) and the other in the way the predictions directly related to our mesoscopic an macroscopic observations are extracted from the calculated microscopic trajectories.
On the second route, the original microscopic formulation is followed by its reduction to a mesoscopic formulation that addresses more directly our interests in the macroscopic systems under investigation. Solutions to the mesoscopic governing equations predict the behavior which we directly observe in our mesoscopic measurements. Again, the main difficulty on this route is in the reduction process. The question that arises on both routes is the following: how shall we make the reductions in order that the essential features of the mechanics put into the original microscopic formulation is kept intact and the compatibility with thermodynamics of both microscopic and mesoscopic formulations is guaranteed.
The third route addresses this question. The reduction with which the second route begins is done in a modular way which guarantees the compatibility with mechanics and thermodynamics. By a modular reduction we understand the following process. The starting assumption is that the mesoscopic dynamics that we want to derive possesses the abstract structure (10). This assumption guarantees that, irrespectively of what we do next, the mesoscopic time evolution that we shall eventually derive will be compatible with mechanics and thermodynamics. The derivation of the model becomes a problem of constructing a particular realization of Equation (10) representing the macroscopic systems under investigation. The abstract dynamical system (10) involves four modules: Module 1, state variables x, Module 2, their kinematics expressed in the Poisson bracket {A,B}, Module 3, thermodynamic forces X and dissipation potential ξ(X), Module 4, thermodynamic potential Φ(x). These four modules are discussed, one after the other, from microscopic or other types of insights into the macroscopic systems under investigation. Below, we shall derive in this way three well known mesoscopic theories (namely the Boltzmann kinetic equation and the equations of classical fluid mechanics, and mesoscopic dynamics involving fluctuations) and a new example of extended mesoscopic fluid mechanics.
4.1. Boltzmann Kinetic Theory
We construct a particular realization of the abstract mesoscopic dynamical system (10) corresponding to the Boltzmann kinetic theory. With this we illustrate the abstract Equation (10), we illustrate the derivation of mesoscopic models described in the previous paragraph, and present a new alternative derivation of the Boltzmann kinetic equation. We begin illustrations with the Boltzmann equation since this equation (rather than the Navier-Stokes-Fourier equations of fluid mechanics that arise naturally on Path A and Path B and are discussed the next section) has been historically the first equation possessing the structure (10). It is also the Boltzmann equation that has served as a prototype equation from which Equation (15) has been extracted. We shall proceed systematically from Module 1 to Module 4. We recall that in the Boltzmann theory the physical systems under investigation are dilute gases and our interest in them is determined by observations providing its experimental basis.
Module 1, state variables x
The objective in this module is to choose state variables x with which we can concentrate our attention on the essence of the physics of our interest and ignore the rest. Since we never know in advance what is important and what can be ignored, the choice of x is always a trial-and-error procedure guided by an experience. In this example we follow Boltzmann and choose:
where f(r, v) is one particle distribution function, r ∈ Ω ⊂ ℝ3 is the position vector and v ∈ ℝ3 is the momentum of one particle. As for the conditions on the boundary ∂Ω, we assume in this paper that f|∂Ω is such that all the integrals over ∂Ω that arise below in by parts integrations equal zero.
Module 2, kinematics of f(r, v)
The Poisson bracket expressing kinematics of f(r, v) is given by:
where we use the summation convention; A and B are real valued sufficiently regular functions of f(r, v); Af(r, v) denotes the functional derivative of A with respect to f(r, v). As for the integration over the position vector r, we shall always assume in this paper (not only in this section) that the volume of the region over which we integrate equals one and the boundary conditions are such that all the integrals over the boundary that arise in by parts integrations equal zero.
How can we derive the bracket (30)? There are several ways to do it. Our first comment about Equation (36) does not amount to its derivation but offers its direct physical understanding. We recall that in classical mechanics the Poisson bracket expressing kinematics of (1,2, …, N) particles (we use the notation introduced in Equation (5); 1 = (r(1),v(1), …) is given by:
where a,b are real valued and sufficiently regular functions of (r, v). Now we note that the Poisson bracket (31) turns into the Poisson bracket (31) if the distribution function f(r, v) is the Klimontovich distribution function f(r, v) = δ(r − r(1))δ(v − v(1))…δ(r − r(N))δ(v − v(N)) and the functions A and B in Equation (30) are linear functions A(f) = ∫ d r ∫ d vf(r, v)a(r, v) and similar for B. By δ(…) we denote the Dirac delta function. We thus see that if in the ensemble of N particles represented by the distribution function f(r, v) we consider only one in which particles have sharply specified coordinates (1, …, N) then, with another restriction to only linear functions, the Poisson bracket (30) is indeed the standard Poisson bracket of classical mechanics.
The actual derivation of Equation (30) provided in [20] is based on the relation between Lie groups and Poisson brackets. We just recall here the arguments. The Lie group describing kinematics of a particle in classical mechanics is the group of canonical transformations (i.e., transformations preserving the relation between r and v, namely that v is an element of the cotangent space attached to the position space with the coordinate r). The one particle distribution function is an element of the dual space to the Lie algebra corresponding to this Lie group. According to a general result derived in symplectic geometry, Lie group structure induces a Poisson bracket in the dual space of its corresponding Lie algebra. The Poisson bracket (30) is such bracket.
Regarding the degeneracy requirement in (L), we easily convince ourselves by a direct verification (see Appendix), that the bracket (30) is degenerate (as we have already noted in Section 3.2) in the sense that {A,C} = 0 for all A and for C that are pointwise functions of f (i.e., (r, v) ↦ f ↦ C where the second mapping is ℝ → ℝ). For example, the Boltzmann entropy introduced below in Module 4 is such a function.
Module 3, thermodynamic forces X and dissipation potential ξ(X)
Following Boltzmann, the source of dissipation in dilute gases are binary collisions. Binary because the dilution, and collisions because during these events large changes in momenta occur in a very short time which makes it then impossible to follow (with the chosen mesoscopic state variables) all the details of particle trajectories. The resulting loss of information brings about dissipation and time irreversibility.
In order to identify the thermodynamic forces and the dissipation potential that correspond to binary collisions, it is useful to regard collisions as chemical reactions. This viewpoint then makes it possible to use results derived in chemical kinetics (that has been put into the form Equation (10) in [49]). If we consider momentum v as a label of chemical species (that we denote V) then indeed the binary collision is a chemical reaction V + V1 ⇋ V′ + V′1 where the incoming two particles have momenta v and v1 and the outgoing particles v′ and v′1. The thermodynamic force X corresponding to this reaction is the chemical activity (see [39]):
Continuing further with the general chemical kinetics [39], the thermodynamic potential is:
where W satisfies the following three properties: (a) W equals zero unless the relations:
hold, (b) W is symmetric with respect to the exchange of v and v1 and exchange of (v, v1) and (v′, v′1), and (c) W > 0 if Equation (34) holds. The classical mechanics of two colliding particles is represented in Equation (33) in the requirements (a) and (b). The requirement (c) is needed to satisfy (Ξ).
Module 4, hermodynamic potential Φ(f)
We choose the distribution function f(r, v) to be normalized in such a way that the number of moles n(f) = ∫ d r ∫ d vf(r, v). Since the macroscopic systems under investigations are dilute gases we choose the energy to be simply the average kinetic energy of the particles (i.e., , m denotes mass of one particle). We could also, following Vlasov [50], include particle-particle interactions in the additional term , where V(|r − r1|) is the interaction potential between two particles with the position coordinates r and r1. Following Boltzmann, we choose the entropy (f) = − kB ∫ d r ∫ d v f(r, v) ln f(r, v), where kB is the Boltzmann constant. We note that indeed {A, η} = 0 for all A as it is required in (L).
The thermodynamic potential Equation (8) thus become:
With these four modules, the abstract Equation (15) becomes indeed the Boltzmann kinetic equation (we leave the routine calculations that are involved to the reader):
where
W is the quantity introduced in Equation (33). We note that in this example the coefficient α introduced in Equation (20) equals one.
We end this illustration by asking a question of what new in kinetic theory itself have we achieved by formulating it as a particular realization of Equation (10)? We suggest a few answers.
First, the new derivation offers a new way to see physics involved in Boltzmann’s kinetic theory. Second, we are also getting a new insight into mathematical aspects of kinetic theory. For example, Boltzmann’s H-theorem is directly imbedded into our formulation. Moreover, the kinetic equation written in its conjugate form (that appears naturally in our formulation) may show more mathematical regularity. This indeed happens for time evolution equations arising in continuum theories (see Equation (26) and it may also be the case for the Boltzmann equation. We recall that the first step in the proof of the existence of global solutions for the Boltzmann equation in [51] is to consider solutions in a renormalized sense. Such solutions are similar to solutions to the conjugate Boltzmann equation. In addition, the other mathematical features of Equation (10), for example the variational formulation discussed in Section 3.1.5, may prove to be useful in the analysis of both the mathematical regularity and numerical solutions.
Finally, the formulation of the Boltzmann equation developed above unifies the Boltzmann theory with other mesoscopic dynamical theories and provides a setting for its various extensions. For instance we can choose other than the Boltzmann entropy and other type of collisions (see Section 3.1.3 in [9]).
4.2. Classical Nonequilibrium Thermodynamics
In this illustration we are turning to the classical nonequilibrium thermodynamics that has originally been introduced on Path A. We shall see below how this classical theory arises on Path C. We recall that the macroscopic systems under investigation in the classical nonequilibrium thermodynamics are simple fluids that are investigated experimentally and theoretically in the classical hydrodynamics. In the presentation we shall again proceed systematically from Module 1 to Module 4.
Module 1, state variables x
The state variables are those used in the classical equilibrium thermodynamics (see (1)) except that they are local (i.e., they depend on the position vector r) and a new field (absent in the equilibrium thermodynamics) is adopted. The new field is the field of local overall momentum u(r) of the fluid. At thermodynamic equilibrium there is no macroscopic motion and consequently u is not needed. We thus have in this illustration
where ρ(r) is the mass density that is related to the number of moles n(r) by ρ(r) = Mmoln(r); Mmol is the molar mass. By e(r) we denote the total energy density that includes the internal energy (i.e., the one introduced in (1) but now dependent on r) and also the kinetic energy dependent on the newly adopted field u (see more in Module 4 below). The position vector r ∈ Ω ⊂ ℝ3. The boundary conditions are assumed to be such that all the integrals over ∂Ω that arise in by parts integrations are equal zero.
In Module 4 we shall introduce the entropy field s(r) as a function of Equation (38): s(r) = s(ρ, u, e; r). Following Path A, we regard the fluids as being in local equilibrium which then means that s is locally the same function of (e, n) as in equilibrium thermodynamics and that s is independent of the newly adopted field u. However, since e(r) is the total energy and we consider s(r) to be a function of the total energy e(r), the entropy s(r) depends now on u(r) (see more in the discussion of Module 4 below).
As we have seen in Section 2.1, in the classical equilibrium thermodynamics , where T is the absolute temperature. We therefore interpret as inverse of the local absolute temperature. If we consider fluids for which the absolute temperature is positive then we can replace e in Equation (38) by s and consider alternatively
as state variables. Using the terminology of Callen [52], we call Equation (38) state variables in the entropy representation and Equation (39) state variables in the energy representation. Both state variables (38) and (39) are related by a one-to-one transformation. We recall that the derivatives of s with respect the state variables (38) are related to derivatives of e with respect the state variables (39) by:
The way we discuss Module 2 and Module 3 in this and also in the subsequent section requires existence of the one-to-one transformation between energy and entropy representations and thus positivity of the absolute temperature. If it were necessary to investigate fluids with both positive and negative absolute temperatures then another technique to discuss Module 2 and Module 3 would have to be used. In this paper we limit ourselves to fluids with positive absolute temperature.
Module 2, kinematics of (ρ(r), u(r), s(r))
Kinematics of Equation (8) is expressed in the Poisson bracket:
where ∂j = ∂/∂rj and A, B are real valued sufficiently regular functions of Equation (45). We directly verify that {A, S} = {A, M} = 0 for all A and for S = ∫ d rs(r) and M = ∫ d rρ(r) and thus the degeneracy required in Equation (15) is demonstrated. It is the easiness of the verification of the degeneracy that makes it convenient to discuss first the kinematics of Equation (39) rather than Equation (38).
Now we turn to the derivation of Equation (41). As in the case of the Poisson bracket (30), there are several ways to achieve it. We shall derive Equation (41) in Section 4.4 below as a particular case of a more general bracket (58). In this section we therefore only briefly recall other two derivations. The first (see e.g., [19]) is again based on the relation between Lie groups and Poisson brackets (see the paragraph following Equation (30)). The Lie group in this case is the group of transformations ℝ3 → ℝ3 which indeed represents kinematics of continua. The momentum field u is an element of the dual space corresponding to its Lie algebra and the remaining two scalar fields ρ and s are included into the analysis through the concept of the so called semi direct product (these two scalar fields are simply advected—Lie dragged—with the motion generated by the momentum field). The second derivation (see [20]) begins with the Lagrangian viewpoint of fluid motion in which the fluid is seen as composed of “fluid particles” whose kinematics is expressed in the standard Poisson bracket of classical mechanics. The passage from the Lagrangian viewpoint to the Eulerian viewpoint that we consider if we use the state variables (38) or (39) is a reduction by the group of relabeling the fluid particles.
Since the state variables (38) and (39) are related by a one-to-one transformation, the Poisson bracket (41) representing kinematics of Equation (39) transforms into another Poisson bracket:
representing kinematics of Equation (38). By S we denote S = ∫ d rs(ρ, u, e;r). The one-to-one relation between Equations (38) and (39) guarantees that both brackets (41) and (42) are Poisson brackets and that they both satisfy the properties (L).
Module 3, thermodynamic forces X and dissipation potential ξ(X)
The need to satisfy the degeneracy requirement appearing in (L) made us to begin the analysis of Module 2 with the state variables (39). The degeneracy requirement appearing in (Ξ) makes us to start this module with the state variables (38). Following again the insights introduced on Path A, there are two sources of dissipations: Fourier and Navier-Stokes. The corresponding to them thermodynamic forces are:
representing the Fourier force and
representing the Navier-Stokes force (for the sake of brevity we are omitting another force proportional to the divergence of velocity). It is important to note that the force X(NS) is a nonlinear function of e*. This is because this force, according to Navier and Stokes, is proportional to the gradient of velocity and the velocity v is expressed in terms of the conjugate state variables as v = eu = − u*/e* (see Equation (40) and Module 4 below).
Next, we specify the dissipation potential. If we limit ourselves to states that are not too far from equilibrium, the thermodynamic forces remain small (recall that the thermodynamic forces disappear at equilibrium) and we can therefore choose the following quadratic potential:
where λ > 0 (called a coefficient of heat conductivity) and ζ > 0 (called a viscosity coefficient) are two parameters expressing in dissipative processes the individual features of the fluid under consideration. We emphasize that while ξ given in Equation (45) is a quadratic function of the dissipation forces (43) and (44), its dependence on e* is more complex (because of the nonlinear dependence of the force X(NS) on e*). We directly verify that all the requirements that appear in (Ξ) are verified for Equation (45).
Module 4, thermodynamic potential Φ(ρ(r), u(r), e(r))
The physical considerations on which we shall base our specification of the thermodynamic potential Φ are those introduced originally on Path A. We regard the fluid as being locally at equilibrium. If we use the state variables (38) we thus have , where eint(r) denotes now the energy appearing in (4) at the point with the spatial coordinate r; ; and s(ρ, u, e) = ∫ d rs(ρ, u, e;r) where s(ρ, u, e;r) depends on and in the same way as s depends on (n, e) in the classical equilibrium thermodynamics (see Section 2). Consequently,
Passage to the alternative state variables (39) is one-to-one since the derivative of s with respect to e, which is from the physical point of view inverse of the temperature, is always positive.
We have now collected all what we need to write explicitly Equation (15). Such equation becomes indeed the standard Navier-Stokes-Fourier equation
where is the local hydrodynamic temperature, u* = −τsu is the fluid velocity,
is the Navier-Stokes extra stress tensor,
is the Fourier heat flow, and
the local hydrodynamic pressure.
The calculations leading to Equation (47) are completely standard. We just emphasize that in order to obtain the third term on the right hand side of the third equation in Equation (47) as a part of Ξe* (see Equation (15)), it is absolutely essential that Ξ depends on e* in the way appearing in Equation (45).
Before leaving the classical fluid mechanics, we make a comment similar to the one made in the previous illustration. How have we contributed to the classical fluid mechanics itself by formulating it as a particular realization of Equation (10)? The answers that we suggested in the previous illustration apply also here. As for the mathematical regularity, we recall that in this context the conjugate formulation does indeed bring it (see Equation (26)). Regarding the unification and new possibilities of extension, we show it in the next illustrations.
4.3. Extension toward a Mesoscopic Theory by Including Fluctuations
The question arises of how can we extend the classical nonequilibrium thermodynamics presented in the previous section to a mesoscopic theory involving a more microscopic physics. There are of course many types of the microscopic physics and consequently many ways to proceed. We present below two examples. We illustrate on them the formalism developed in Section 3.
The new physics entering the first illustration that is discussed in this subsection is the physics of fluctuations. Let x be the state variable used in Section 2.2.1. We now promote it to a random variable x̂. From the physical point of view, this means that our measurements of x became so precise that their outcome is influenced by microscopic processes that are not explicitly taken into account in our description and consequently the measured values are seen to fluctuate. We now replace x̂ by f(x) denoting the distribution of the fluctuations. The following problem arise: given nonequilibrium thermodynamics with the state variable x, formulate corresponding to it nonequilibrium thermodynamics with the state variable f(x). In other words, the problem is to lift nonequilibrium thermodynamics from x to f(x). Such lift has been made in [53,54]. Nonequilibrium thermodynamics extended in this way has important applications for small systems where fluctuations play a very important role (see [54,55]). Fluctuating nonlinear chemical kinetics has been discussed in [39] with the help of the formalism of Section 3.
Our starting point is the nonequilibrium thermodynamics with x serving as state variables. This means that we know all four modules; i.e., state variables x, their kinematics L, dissipation potential Ξ, and the thermodynamic potential Φ. The problem is to lift (x, L, Ξ, Φ) to (f(x), L(fl), Ξ(fl), Φ(fl)) representing the nonequilibrium thermodynamics extended by taking into account fluctuations.
As for Module 2, we put {A, B}(fl) = ∫ d xf(x){Af, Bf}, where A, B are real valued functions of f(x) and {a, b} = <ax, Lbx> is the Poisson bracket appearing in Equation (15) with x as state variables; a and b are sufficiently regular real valued functions of x.
In Module 3, we choose , where Λ > 0 is a material parameter.
Finally, in Module 4, the thermodynamic potential Φ(fl)(f) = ∫ d xf(x)(Φ(x) + kB ln f(x)). The first term is just an average of the free energy appearing in Equation (15). The second term is new, it expresses the contribution to the entropy due to fluctuations; kB is the Boltzmann constant.
With these specifications, Equation (15) with f(x) serving as state variables becomes:
The first term on the right hand side of this equation is the term arising in the Liouville equation corresponding to the original nondissipative time evolution equation ẋ = LΦx(x). The last two terms on the right hand side are dissipative terms. The first one is just the term that appears in the Liouville equation corresponding to the dissipative term −[Ξx*]x*=Φx, where . The second term is a new (Fokker-Planck) term that arises due to fluctuations. The fact that the coefficient Λ is the same in both terms is equivalent to what is called in alternative derivations of Equation (51) a fluctuation-dissipation theorem. We thus see that in our setting this theorem arises simply from requiring that both the equations governing the time evolution of x and f(x) are particular realizations of Equation (15).
We make two comments.
Both Equations (36) and (51) are kinetic equations governing the time evolution of a distribution function. In the context of the Boltzmann Equation (36) we begin with one particle with coordinates (r, v). By passing from (r, v) to f(r, v) we are indirectly (statistically) taking into account the other particles that collectively form the fluid. In the context of Equation (51), the passage from x to f(x) is also a passage to a more microscopic level of description but the passage is somewhat more implicit than in the case of the Boltzmann equation. In the context of Equation (36) we really have in mind the other particles (by specifying the collision dissipation potential Equation (33) or the Vlasov term in the thermodynamic potential). On the other hand, the presence of levels of description that are more microscopic than the one on which x serves as state variable remains very implicit in the derivation of Equation (51). It is nevertheless the microscopic physics taking place on the more microscopic levels that is responsible for the fluctuations and that determines them.
In the next subsection, we shall make another type of extension of the classical nonequilibrium thermodynamics, namely an extension in which the fluxes arising in Equation (47) are adopted as independent state variables. The following question then arises: how to lift this type of extended theory to a theory involving fluctuation? This question has been investigated, with the formalism of Section 3, in the context of the fully nonlinear chemical kinetics in [49]. One of the interesting results that have arisen in this investigation is that the distribution of fluctuations of fluxes is not determined by the entropy (as it is the case for the distribution of fluctuations of hydrodynamic fields) but by the entropy production.
4.4. Extension toward a Mesoscopic Theory by including an Extra Inertia
In this illustration we shall use the formalism developed in Section 3 to introduce a new viewpoint of the dynamical theories that have arisen on Path B in References [2–7]. The physics behind this type of extension is the introduction of an additional inertia into the classical nonequilibrium thermodynamics (see Section 4.2) by promoting the fluxes arising in the local conservation laws (47) to the status of independent state variables. In this paper we shall limit ourselves to discussing only the first two modules.
Module 1, state variables x
Motivated by Grad’s reformulation of the Boltzmann equation into Grad’s hierarchy, the state variables chosen in the classical extended nonequilibrium thermodynamics (References [2–7]) is a sequence of fields:
where N > 0 is an integer, supplemented with the entropy field s(r). The field is interpreted physically as a flux corresponding to the field .
In this illustration we make the same choice but we also adopt the entropy field s(r) and the one particle distribution function f(r, v) itself as additional state variables. Consequently, in this illustration, we have
The energy e = ∫ d re(r), where e(r) is a function of the state variables (52) (i.e., e(r) = e(f, s, F(0), F(1), …, F(N), r)). The field F(0)(r) is interpreted physically as a local number of moles so that the number of total moles n = ∫ d rF(0)(r), e = ∫ d re(r), and s = ∫ d rs(r) are the quantities entering the thermodynamic potential Equation (8). In this paper we do not discuss Module 4 and we shall therefore leave the function e(f, s, F(0), F(1), …, F(N), r) undetermined. As in the previous illustrations, r ∈ Ω ⊂ ℝ3, and the boundary conditions are such that all the integrals over the boundary ∂Ω that arise in by parts integrations equal zero.
Module 2, kinematics of (f(r, v), s(r), F(0)(r), )
Now we turn to the physics that is behind our choice of Equation (52). The reason why Grad has written the Boltzmann equation in the form of N → ∞ Grad’s hierarchy is to make eventually a projection of the Boltzmann equation on a simpler set of equations governing the time evolution of a finite number of fields (i.e., functions of only the position vector r). Thermodynamic considerations have entered (see References [2–7]) in an attempt to project the infinite Grad hierarchy on a finite hierarchy. The requirement of the thermodynamic compatibility is that the entropy growth seen in solutions to the Boltzmann equation and thus also in solutions of the infinite hierarchy is required to hold also for solutions to the finite hierarchy. We follow the same objective but our requirement of the compatibility is stronger, we require that both infinite and finite hierarchies are particular realizations of Equation (10). In this illustration we shall not solve this problem completely. Its partial investigation presented below brings however new results in the domain of Grad’s hierarchies.
We begin with expressing (see e.g., [4]) the fields F(0)(r), in terms of f(r, v):
From this point our approach to Grad’s hierarchy differs substantially from the conventional approach. First, we express also the entropy field s(r) in terms of f:
where η: ℝ → ℝ is a function of f, for example, η(f) = −f ln f. We note that (as it follows from the discussion presented in Module 2 in Section 4.1) ∫ d r ∫ d vη(f(r, v)) is Casimir of the Poisson bracket (30).
The second and the most important difference is that the projection (53) and (54) is not applied on the Boltzmann equation but only on its kinematics, i.e., only on the Poisson bracket (30)).
The third difference is that the higher order than N-th moments in the infinite hierarchy are represented by the distribution function f(r, v) itself. The resulting hierarchy is thus a prolongation of the Boltzmann equation rather than its projection. We recall that the classical example of a prolongation is the prolongation of a partial differential equation made by keeping the original equation and supplementing it with equations obtained by differentiating the original equation (see e.g., Section 5.1 in [56]). We do the same thing but the supplemented equations are obtained by integrating rather than differentiating the original equation.
Now we proceed to derive the Poisson bracket expressing kinematics of Equation (52). We replace Af and Bf in Equation (30) by
that follows from Equations (53) and (54). We shall make the resulting bracket explicit for N = 0,1,2. Some details of the calculations involved can be found in Appendix.
4.4.1. N = 0
In the case of N = 0 we arrive at:
The corresponding to it time evolution equations are:
First, we note that Equation (57) involve two local conservation laws for the fields s(r) and F(0)(r) (the last two equations in Equation (57)) and another one for the field e(r), that is implied, due to the Hamiltonian nature of Equation (57), by the remaining equations. We also note that when the scalar fields s(r) and F(0)(r) are absent then the first equation in Equation (57) is the classical nondissipative Boltzmann equation (i.e., Equation (36) without the Vlasov and the collision terms). If, on the other hand, f(r, v) is absent in Equation (57) then we see that the scalar fields s(r) and F(0)(r) remain unchanged during the time evolution. In the case that both the distribution function and the scalar fields are present then we see a coupling in the time evolution. The distribution function brings fluxes into the time evolution of s and F(0) and these two scalar fields bring new forces into the time evolution of f. In addition, the coupling enters of course the time evolution in the thermodynamic potential Φ that we leave at this point undetermined.
4.4.2. N = 1
Now we proceed to the case N = 1. The Poisson bracket takes the form:
and the corresponding to it time evolution equations are
where
and
Again, this system of equations involves two local conservation laws, namely the second and the third equations governing the time evolution of the fields s(r) and F(0)(r), and another local conservation law for the filed e(r) that is implied by Equation (59) due to its Hamiltonian nature. In addition, we note that the last equation in Equation (59) is also a local conservation law. From the physical point of view, this local conservation law expresses the conservation of momentum.
Next, we note that when f is absent in Equation (58) then Equation (58) becomes the bracket (41) expressing kinematics of the classical hydrodynamic fields. Indeed, if we omit in Equation (58) all the lines that are multiplied by f and replace in the second line of Equation (56)Bf by and similarly Af by then we recover the bracket (41). This observation amounts to a rigorous derivation of the hydrodynamic bracket (41) from the bracket (30).
We now compare the time evolution Equation (59) with f missing with the first two equations of Grad’s hierarchy
(obtained by applying the projection (53) on the Boltzmann kinetic equation (i.e., Equation (36) without the Vlasov term).
First, we see that Equation (62) involve the second moment F(2). Consequently, in order that Equation (62) be a closed system of time evolution equations, F(2) has to be expressed in terms of F(0) and F(1). Second, Equation (59) with f missing involve also an entropy fields and are compatible with mechanics (they are Hamiltonian equations) and with thermodynamics (the total entropy S = ∫ d rs(r) remains unchanged during the time evolution—recall that in this section we do not consider the dissipative part of the time evolution).
If all the state variables (f, s, F(0), F(1)) are present then we see in Equation (59) new coupling terms. The kinetic equation is modified by new forces coming from the entropy and the mass fields. The entropy as well as the mass fluxes appearing in the second and the third equations in Equation (59) have new contributions that originate in the microscopic processes and need the distribution function f to be expressed mathematically. In the equation governing the time evolution of the momentum (the fourth equation in Equation (59) we see the tensorial contribution (61) to the stress tensor. Such contribution means that the fluid is viscoelastic (due to the microscopic influences expressed with the distribution function f).
4.4.3. N = 2
If N = 2, we arrive at
which then implies
where
and
As it is the case in Equations (57) and (59) and also in the equations that arise for any integer N > 0, this system of Equation (64) implies another conservation law for the energy field e(r). If we compare Equation (64) with Equation (59) we see new coupling terms (new forces in the kinetic equation, new contributions to the entropy and the mass fluxes, and new contributions to the scalar as well as tensorial pressure). In addition, we have the last equation governing the time evolution of F(2). We note that this equation is not a local conservation law and that it involves F(3) moments. If we keep in our set of state variables the distribution function f then, of course, we know how F(3) is expressed (namely ) and there is no need for a closure. A closure is needed, of course, if we want to eliminate f (and thus also the first equation in Equations (57), (59) and (64)) and keep only the moments as it is the case in the hierarchies discussed in References [2–7]. We intend to investigate this closure problem in the new setting presented above in a future paper.
5. Concluding Remarks
The objective of this paper is to identify a setting in which dynamics of macroscopic systems on all scales can be formulated. On the most microscopic scale the dynamics is Hamiltonian (classical mechanics of ~1023 particles). On the most macroscopic scale the dynamics is a gradient dynamics (a pure relaxation, governed by equations of the Cahn-Hilliard and Ginzburg-Landau type, to thermodynamic equilibrium states at which the classical equilibrium thermodynamics applies). In both Hamiltonian and gradient dynamics the time evolution is generated by a potential. In the Hamiltonian dynamics the potential has the physical interpretation of energy and in the gradient dynamics of entropy. What mainly distinguishes these two types of dynamics is the structure transforming gradient of the potential into a vector (i.e., into the right hand side of the time evolution equation). In the Hamiltonian dynamics it is a symplectic structure (in the simplest case a skew-symmetric matrix) and in the gradient dynamics a Riemannian structure (in the simplest case a symmetric matrix). In the contact-structure-preserving dynamics that unifies both the Hamiltonian and the gradient dynamics the structure transforming gradient of a potential into a vector is universal (the contact structure), the difference is expressed in the generating potential. The potential, called a contact Hamiltonian, is a sum of two terms, one is mechanical and the other thermodynamical. The mechanical part has the physical interpretation of the rate of energy and the thermodynamic part the rate of entropy. If only the mechanical part is present, the contact-structure-preserving dynamics is just an equivalent reformulation of the Hamiltonian dynamics (it can be the classical mechanics of ~1023 particles. or it Hamiltonian and gradient dynamics the time evolution is generated by a potential. In the Hamiltonian dynamics the potential has the physical interpretation of energy and in the gradient dynamics of entropy. What mainly distinguishes these two types of dynamics is the structure transforming gradient of the potential into a vector (i.e., into the right hand side of the time evolution equation). In the Hamiltonian dynamics it is a symplectic structure (in the simplest case a skew-symmetric matrix) and in the gradient dynamics a Riemannian structure (in the simplest case a symmetric matrix). In the contact-structure-preserving dynamics that unifies both the Hamiltonian and the gradient dynamics the structure transforming gradient of a potential into a vector is universal (the contact structure), the difference is expressed in the generating potential. The potential, called a contact Hamiltonian, is a sum of two terms, one is mechanical and the other thermodynamical. The mechanical part has the physical interpretation of the rate of energy and the thermodynamic part the rate of entropy. If only the mechanical part is present, the contact-structure-preserving dynamics is just an equivalent reformulation of the Hamiltonian dynamics (it can be the classical mechanics of ~1023 particles. or it can also be the Euler continuum dynamics). If, on the other hand, only the thermodynamic part of the contact Hamiltonian is present then the contact-structure-preserving dynamics is just an equivalent reformulation of the gradient dynamics. Looking at the contact structure setting from the thermodynamics side, it appears as a natural extension of the geometrical setting of classical thermodynamics. It is in this way that the contact-structure-preserving dynamics is introduced in this paper.
As illustrations, we have first shown that the classical well established mesoscopic theories, as for instance the Boltzmann kinetic theory and the Navier-Stokes-Fourier hydrodynamics, are indeed particular realizations of the general theory. In the fourth illustration (in Section 4.4) we have initiated a novel viewpoint of extended nonequilibrium thermodynamic theories that are motivated by Grad’s hierarchy. In all four illustrations we have also demonstrated that the general theory provides a well organized modular procedure for constructing thermodynamic and dynamic models. The construction is in fact a search for a particular realization of four modules appearing in the theory. The general theory itself guarantees agreement with certain basic observations made in mechanics and thermodynamics. How well the model predictions reflect results of more specific experimental observations depends on how well is the microscopic physics that is pertinent to the observations expressed in the four modules.
Acknowledgments
The research reported in this article was partially supported by Natural Sciences and Engineering Research Council of Canada.
Appendix: Calculations with the Bracket (30)
The calculations involved in Section 4 are straightforward but not obvious. In order to simplify the reading of this paper, we shall briefly recall some details.
A1. From Brackets to Equations
Having an explicit expression for the bracket {A, B}, how do we arrive at the explicit form of the time evolution equations ẋ = LΦx? The simples way to achieve it is the following: We rewrite ẋ = LΦx as Ȧ = {A, Φ} holds for all A. Since Ȧ = <Ax, ẋ>, we rewrite (by using by parts integrations) {A, Φ} =<Ax, (•••)>. The time evolution equation is then ẋ = (•••).
A2. {A, η} = 0 for all A
The function η(f) is defined by (r, v) ↦ f ↦ η where the second mapping is ℝ → ℝ. We have to prove that
for all A. We rewrite the first term (by using by parts integration) as
and the second term as
We thus obtain
which equals
A3. (Intermediate result 1 )
We prove that
By using by parts integration and the fact that Bs is independent of v, we arrive at
where […] are terms that are independent of v.
A4. (Intermediate result 2a)
We prove that
By using by parts integrations we rearrange the integrand into
The second equality follows from the fact that we can always find F(f) that, for a given η(f), solves the equation Ff = fηfηf f (recall that f ∈ ℝ and η ∈ ℝ).
A5. (Intermediate result 3a)
We prove that
From the first two lines we construct new two lines by switching the second terms in them. The new first line can be written as
The first line in this expression gives no contribution, the second line equals
The first square bracket equals zero, the second equals . We then make the same arrangements with the new second line and conclude the proof.
Conflicts of Interest
The author declares no conflict of interest.
References
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover: New York, NY, USA, 1984. [Google Scholar]
- Müller, I.; Ruggeri, T. Rational Extended Thermodynamics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Jou, D.; Casas-Vàzquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th ed; Springer: Berlin, Gremany, 2010. [Google Scholar]
- Ruggeri, T. The entropy principle: From continuum mechanics to hyperbolic systems of balance laws. Bull. UMI 2005, 8, 1–20. [Google Scholar]
- Struchtrup, H. Macroscopic Transport Equations for Rarefied Gases. In Approximation Methods in the Kinetic Theory; Springer: Heidelberg, Germany, 2005. [Google Scholar]
- Müller, I.; Weiss, W. Thermodynamics of irreversible processes—Past and present. Eur. Phys. J. H 2012, 37, 139–236. [Google Scholar]
- Gorban, A.N.; Karlin, I.V. Invariant Manifolds for Physical and Chemical Kinetics: Lecture Notes in Physics; Springer: Berlin, Gremany, 2005; Volume 660. [Google Scholar]
- Bird, R.B.; Hassager, O.; Armstrong, R.C.; Curtiss, C.F. Dynamics of Polymeric Fluids; John Wiley and Sons: New York, NY, USA, 1977; Volume 1–2. [Google Scholar]
- Grmela, M. Multiscale equilibrium and nonequilibrium thermodynamics in chemical engineering. Adv. Chem. Eng 2010, 39, 76–128. [Google Scholar]
- Grmela, M. Extensions of nondissipative continuum mechanics toward complex fluids and complex solids. Contin. Mech. Thermodyn 2013, 25, 55–75. [Google Scholar]
- Grmela, M. Thermodynamical lift of the nonlinear onsager-casimir vector field. Proceedings of the Workshop on Hamiltonian Systems, Transformation Groups and Spectral Transform Methods, Montreal, Canada, 20–26 October 1989; Centre De Recherches Mathematiques: Multiscal, Canada, 1990; pp. 199–206. [Google Scholar]
- Grmela, M. Role of thermodynamics in multiscale physics. Comput. Math. Appl 2013, 65, 1457–1470. [Google Scholar]
- Gibbs, J.W. Collected Works. In Longmans; Green and Comp: New York, NY, USA, 1984. [Google Scholar]
- Jaynes, E.T., Tribus, M., Levine, R.D., Eds.; The Maximum Entropy Formalism; MIT Univ. Press: Cambridge, USA, 1978.
- Hermann, R. Geometry, Physics and Systems; Marcel Dekker: New York, NY, USA, 1984. [Google Scholar]
- Ruppeiner, G. Riemannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys 1995, 67, 605. [Google Scholar]
- Mrugala, R.; Nulton, J.D.; Schoen, J.C.; Salamon, P. Statistical approach to the geometric structure of thermodynamics. Phys. Rev. A 1990, 41, 3156–3160. [Google Scholar]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer: New York, NY, USA, 1989. [Google Scholar]
- Clebsch, A. Über die Integration der hydrodynamische Gleichungen. J. Reine Angew. Math 1895, 56, 1–10. [Google Scholar]
- Marsden, J.E.; Weinstein, A. Coadjoint orbits, vortices and Clebsch variables for incompressible fluids. Phys. D 1983, 7, 305. [Google Scholar]
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductivity. Zhur. Eksp. Theor. Fiz 1950, 20, 1064–1082. [Google Scholar]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. Interfacial free energy. J. Chem. Phys 1958, 28, 258. [Google Scholar]
- Ziegler, H. An Introduction to Thermomechanics: Field Theory and Variational Principles; North-Holland: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Dzyaloshinskii, I.E.; Volovick, G.E. Poisson brackets in condense matter physics. Ann. Phys 1980, 125, 67–97. [Google Scholar]
- Grmela, M. Particle and bracket formulations of kinetic equations. Contemp. Math 1984, 28, 125–132. [Google Scholar]
- Kaufman, A.N. Dissipative Hamiltonian systems: A unifying principle. Phys. Lett. A 1984, 100, 419. [Google Scholar]
- Morrison, P.J. Bracket formulation for irreversible classical fields. Phys. Lett. A 1984, 100, 423. [Google Scholar]
- Grmela, M. Bracket formulation of diffusion-convection equations. Phys. D 1986, 21, 179–212. [Google Scholar]
- Beris, A.N.; Edwards, B.J. Thermodynamics of Flowing Systems; Oxford Univ. Press: Oxford, UK, 1994. [Google Scholar]
- Grmela, M. Öttinger, H.C. Dynamics and thermodynamics of complex fluids: General formulation. Phys. Rev. E 1997, 56, 6620–6633. [Google Scholar]
- Öttinger, H.C.; Grmela, M. Dynamics and thermodynamics of complex fluids: Illustration of the general formalism. Phys. Rev. E 1997, 56, 6633–6650. [Google Scholar]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lucia, U. Stationary open systems: A brief review on contemporary theories on irreversibility. Phys. A 2013, 392, 1051–1062. [Google Scholar]
- Grmela, M.; Grazzini, G.; Lucia, U.; Yahia, L. Multiscale mesoscopic entropy of driven macroscopic systems. Entropy 2013, 15, 5053–5064. [Google Scholar]
- Grmela, M. Reductions in dynamical theories. J. Chem. Phys 1986, 85, 5689–5697. [Google Scholar]
- Grmela, M. Thermodynamics of driven systems. Phys. Rev 1993, 48, 919–930. [Google Scholar]
- Keck, J.C. Rate-controlled constrained equilibrium method for treating reactions in complex systems. In The Maximum Entropy Principle; Levine, R.D., Tribus, M., Eds.; MIT Press: Camridge, MA, USA, 1979; pp. 219–245. [Google Scholar]
- Beretta, G.P.; Keck, J.C.; Janbozorgi, M.; Metgalchi, H. The rate-controlled constrained-equilibrium approach to far-from-local-equilibrium thermodynamics. Entropy 2012, 14, 92–130. [Google Scholar]
- Gorban, A.N.; Karlin, I.V. Method of invariant manifold for chemical kinetics. Chem. Eng. Sci 2003, 58, 4751–4768. [Google Scholar]
- Gorban, A.N.; Karlin, I.V. Hilbert’s 6th problem: Exact and approximate hydrodynamic manifolds for kinetic equations. Bull. Am. Math. Soc. S 2013. [Google Scholar] [CrossRef]
- Beretta, G.P. Well-behaved nonlinear evolution equation for steepest-entropy ascent dissipative quantum mechanics. Int. J. Quantum Inform 2007, 5, 249–255. [Google Scholar]
- Beretta, G.P. Steepest-Entropy-Ascent and Maximal-Entropy-Production Dynamical Models of Irreversible Relaxation to Stable Equilibrium State. Unified Treatement for Six Non-Equilibrium Frameworks. Proceedings of the 12th Joint European Thermodynamics Conference, Brescia, Italy, 1–5 July 2013; pp. 100–109.
- Beretta, G.P. Modeling non-equilibrium dynamics of a discrete probability distribution: General rate equation for maximal entropy generation in a maximum-entropy landscape with time-dependent constraints. Entropy 2008, 10, 160–182. [Google Scholar]
- Godunov, S.K. An interesting class of quasilinear systems. Sov. Math. Dokl 1961, 2, 947–949. [Google Scholar]
- Godunov, S.K.; Romensky, E. Thermodynamics, conservation laws and symmetric forms of differential equations in mechanics of continuous media. In Computational Fluid Dynamics Review; Wiley: New York, NY, USA, 1995; pp. 19–31. [Google Scholar]
- Friedrichs, K.O.; Lax, P.D. Systems of conservation equations with a convex extension. Proc. Natl Acad. Sci. USA 1971, 68, 1686–1688. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulations of Liquids; Clarendon Press: Oxford, UK, 1989. [Google Scholar]
- Kotelyanskii, M., Theodorou, D.N., Eds.; Simulations Methods for Polymers; Marcel Dekker: New York, NY, USA, 2004.
- Grmela, M. Fluctuations in extended mass-action-law dynamics. Phys. D 2012, 241, 976–986. [Google Scholar]
- Vlasov, A.A. Many Particle Theory and Its Application to Plasma; Gordon and Breach: New York, NY, USA, 1961. [Google Scholar]
- DiPerna, R.J.; Lions, P.L. Global solutions of boltzmann’s equation and the entropy inequality. Arch. Ration. Mech. Anal 1991, 114, 47–55. [Google Scholar]
- Callen, H.B. Thermodynamics; Wiley: New York, NY, USA, 1960. [Google Scholar]
- Rubi, J.M.; Mazur, P. Nonequilibrium thermodynamics of hydrodynamic fluctuations. Phys. A 2000, 276, 477–488. [Google Scholar]
- Reguera, D.; Rubi, J.M.; Vilar, J.M.G. The mesoscopic dynamics of thermodynamic systems. J. Phys. Chem. B 2005, 109, 21502–21515. [Google Scholar]
- Rubi, J.M. Mesoscopic thermodynamics. Phys. Scr 2012, T151, 014027. [Google Scholar]
- Alekseevskij, D.V.; Vinogradov, A.M.; Lychagin, V.V. Basic Ideas and Concepts of Differential Geometry; Springer Verlag: Heidelberg, German, 1991. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Grmela, M. Contact Geometry of Mesoscopic Thermodynamics and Dynamics. Entropy 2014, 16, 1652-1686. https://doi.org/10.3390/e16031652
Grmela M. Contact Geometry of Mesoscopic Thermodynamics and Dynamics. Entropy. 2014; 16(3):1652-1686. https://doi.org/10.3390/e16031652
Chicago/Turabian StyleGrmela, Miroslav. 2014. "Contact Geometry of Mesoscopic Thermodynamics and Dynamics" Entropy 16, no. 3: 1652-1686. https://doi.org/10.3390/e16031652
APA StyleGrmela, M. (2014). Contact Geometry of Mesoscopic Thermodynamics and Dynamics. Entropy, 16(3), 1652-1686. https://doi.org/10.3390/e16031652