Heat and Gravitation: The Action Principle
Abstract
: Some features of hydro- and thermo-dynamics, as applied to atmospheres and to stellar structures, are puzzling: (1) the suggestion, first made by Laplace, that our atmosphere has an adiabatic temperature distribution, is confirmed for the lower layers, but the explanation for this is very controversial; (2) the standard treatment of relativistic thermodynamics does not favor a systematic treatment of mixtures, such as the mixture of a perfect gas with radiation; (3) the concept of mass density in applications of general relativity to stellar structures is less than completely satisfactory; and (4) arguments in which a concept of energy and entropy play a role, in the context of hydro-thermodynamical systems and gravitation, are not always convincing. It is proposed that a formulation of thermodynamics as an action principle may be a suitable approach to adopt for a new investigation of these matters. This paper formulates the thermodynamics of ideal gases in a constant gravitational field in terms of the Gibbsean action principle. This approach, in the simplest cases, does not deviate from standard practice, but it lays the foundations for a more systematic approach to the various extensions, such as the incorporation of radiation, the consideration of mixtures and the integration with general relativity. We study the interaction between an ideal gas and the photon gas and the propagation of sound in a vertical, isothermal column. We determine the entropy that allows for the popular isothermal equilibrium and introduce the study of the associated adiabatic dynamics. This leads to the suggestion that the equilibrium of an ideal gas must be isentropic, in which case, the role of solar radiation would be merely to compensate for the loss of energy by radiation into the cosmos. An experiment with a centrifuge is proposed, to determine the influence of gravitation on the equilibrium distribution with a very high degree of precision.1. Introduction
The premise of this paper is the conviction that the internal consistency of any physical theory is improved, if not assured, by a formulation that is based on a dynamical action principle. The consistency of a set of equations is a delicate matter. When a modification has to be made somewhere, to include additional effects or another degree of freedom, then adjustments may have to be made elsewhere for consistency; whence the importance of the Onsager symmetry conditions. However, a correction made to the Lagrangian automatically produces a new and complete set of variational equations satisfying the symmetry conditions. A fully developed action principle treats all dynamical variables on an equal footing and without constraints. Such a theory is said to be “off shell”, a concept that has been crucial in the development of relativistic field theories. When a change or a generalization is contemplated, it is done by modifying the Lagrangian; changes in all equations of motion are generated automatically and are believed to be mutually consistent. Another advantage is that the equations of motion constitute a complete set of equations that defines the theory; once the Lagrangian is fixed, one need not worry about the possibility that some relation has been overlooked, as may happen in standard applications of thermodynamics.
Action principles have been used for some problems in hydro-thermodynamics, but as far as we know, the injunction to avoid all constraints has not been respected, with a very important exception. The principles of thermodynamics, as laid down by Gibbs, consist of a statement about quantities taking their extreme values, and variations of the temperature are central to the theory. Hydrodynamics takes the temperature to be related to the other variables by what amounts to a constraint, making it a partial projection of a complete dynamical theory on the space of solutions.
This paper is a study of atmospheres consisting of an ideal gas, characterized by the ideal gas law and the expression for the internal energy. A well-known hydrodynamic action principle is expanded to include the temperature among the independent dynamical variables. The specification of the Gibbs surfaces of equilibrium configurations appears among the variational equations of motion. The Hamiltonian is identified with the thermodynamic function F + ST + PT, where F(V, T) is the free energy, S is the entropy and V is the volume. Variation of the Lagrangian with respect to T and V leads to the thermodynamic relations:
In the case of an ideal gas, the first equation is related to the polytropic relation ρ/T n = constant. On shell, that is, by virtue of these relations, the Hamiltonian density reduces to the familiar formula for the internal energy, U = nT. This is standard equilibrium thermodynamics; what is new in this paper is the incorporation of thermodynamics into a dynamical, Eulerian field theory of adiabatic hydro-thermodynamical processes.
It is important to ask to what extent the observed polytropic relations are to be attributed to the intrinsic properties of the gas or to radiation. Although the question is somewhat academic, since it does not directly affect the main applications, it is natural to ask: what are the natural configurations of an isolated atmosphere, one that is not exposed to radiation? Our understanding of atmospheres will not be complete without an answer to this question.
The statement that any two thermodynamic systems, each in a state of equilibrium with a well defined temperature, and in thermal equilibrium with each other, must have the same temperature is a central tenet of thermodynamics. A natural generalization is that the temperature, in an extended, but closed system in a state of equilibrium, that must be uniform, and there is a wide spread opinion that this remains true in the presence of gravitational fields. This is important for the understanding of terrestrial and stellar atmospheres, where the gravitational forces create a non-uniform density distribution.
1.1. Outline
Hydrodynamics is a theory of continuous distributions of matter, described in the simplest case by two fields or distributions: a density field and a velocity field, both defined over IR3 or a portion thereof. The role of temperature is constrained, as it is taken to be determined by the density and the pressure. Classical thermodynamics, on the other hand, is the study of states of equilibrium, with uniform density and temperature, and relations between such states. In this context, extremum principles first formulated by Gibbs (1878) [1] play an important role; see for example Callen (1960) [2], but the extension of thermodynamics to systems in which the dynamical variables are fields on IR3 is not immediate. Investigations that deal with the flow of matter or with temperatures that vary in time and space are found under the heading of heat transfer, fluctuations, thermodynamics of irreversible processes and radiation hydrodynamics. See, for example, Stanyukovich (1960) [3], Castor (2004) [4] and Müller (2007) [5].
In Section 2, we study a simple system from the point of view of hydrodynamics, on the basis of a well-known action principle that incorporates the continuity equation and Bernoulli’s equation. In this theory, the temperature is not an independent variable, but is assumed to be given by the ideal gas law. We stress the role of mass (Section 2.5). The potential is chosen appropriately for an atmosphere that is either isothermal or polytropic.
In applications to the earthly atmospheres, and to stellar structure, as well, the polytropic model is the universally preferred starting point (a book of more than 700 pages, devoted entirely to polytropes, has appeared recently [6]). Section 2.6 is an introduction to polytropic atmospheres. It is remarkable that this theory already predicts the observed temperature lapse rate for our atmosphere. The only parameters are the known values of the adiabatic index and the effective atomic weight of the gas. There is no parameter that can be interpreted as a measure of the influence of radiation and no indication within the theory that the radiative equilibrium becomes isothermal in the limit when the radiation is turned off. We offer a brief review of the history of the polytropic atmosphere (Section 2.7).
In Section 3, we take the action principle off shell, to include the temperature as an independent field variable. Variation of the Lagrangian with respect to the temperature is related to a standard, thermodynamical relation, ∂F/∂T = –S. The potential is adapted to give the correct expression for the internal energy on shell; the off shell Hamiltonian appears to be new.
In Section 3.5, we include interactions with the photon gas by adding the Stefan–Boltzmann energy to the Hamiltonian. The n energy to the Hamiltonian. The radiation pressure appears as an addition to the thermodynamic pressure. The effect is to change the effective polytropic index towards the asymptotic limit of three, from either side, at extreme temperatures. Thermodynamics, when formulated as a dynamic action principle, allows a simple and effective integration into the general theory of gravitation. No approximation of the kind pgas/ptotal = constant, used by Eddington and valid only in the case that n = 3, is needed.
When this approach is compared to modern hydro-thermodynamics, restricted to adiabatic processes, we find that, so long as the radiation pressure is small in comparison with the gas pressure, all the basic equations are identical. However, the incorporation of radiation and other features is much more straightforward within the variational formulation.
Section 3.6 examines the intimate integration of this action principle with the thermodynamics of Gibbs. It is shown that the action principle, restricted to stationary configurations, is in full accord with the extremal conditions formulated by Gibbs, for energy and for entropy. When the (localized) internal energy is interpreted as a Hamiltonian, one recovers all the equations of motion derived from the action principle.
The equilibrium state of any ideal gas with a finite adiabatic index is essentially polytropic. Here, it is important to make precise what we mean by equilibrium. We use the term in the context of a mathematical model; it refers to a solution of the equations of motion with the property that all flows vanish and all the fields are time independent. Polytropic models of earthly and stellar atmospheres are very widely used, and the stationary configurations of such atmospheres are equilibria in this sense, although the physical configurations that they are meant to represent are not states of true thermodynamic equilibrium. An issue that we wish to understand is the precise role that is played by radiation. We should hope to develop an understanding of what would happen if the intensity of radiation were continuously reduced to zero. The possibility that the limit might turn out to be other than isothermal is not easy to accept, for it goes against one of the basic tenets of thermodynamics: Clausius’ statement of the second law (Section 3.7). The question is not entirely academic, but it has no direct bearing on the validity of our approach, for we apply it to the standard, polytropic atmospheres, just as has been done since the pioneering work of Lane (1870) [7].
It is important to incorporate the isothermal atmosphere into a dynamical framework; that is, to develop a system of equations of motion that predict the uniformity of the temperature at equilibrium. We suggest that the standard theory of polytropic atmospheres should incorporate a parameter or variable to represent the intensity of radiation and that would allow the effect of radiation to be reduced parametrically to zero, resulting in an isothermal equilibrium in the limit. In the event that an experiment should validate the isothermal atmosphere, the need to construct such a theory would become urgent.
There seems to be a dearth of experimental data. We study an ideal gas in a centrifuge and invoke the equivalence principle to relate this situation to atmospheres. Experiments are proposed. (Section 3.8).
There is an extensive literature on the propagation of shock waves in a polytropic atmosphere, but, as far as we know, none that deals with the vertical propagation of a disturbance (sound waves or shock waves) in an isolated, isothermal gas in a gravitational field. A brief report on a recent study of this problem is in Section 3.9. The result is unexpected and provokes further examination of the standard theory.
Some further speculations are in the Appendix.
1.2. Applications to Astrophysics
The simplest form of the action principle studied here is the non-relativistic approximation to a fully relativistic theory that, with the addition of the Einstein–Hilbert action for the metric, has been applied to the dynamics of certain stars (Fronsdal, 2007, 2008 [8,9]) and to the problem of dark matter (Fronsdal and Wilcox, 2011 [10]). The results are close to those of the traditional approach, except for certain features that make the present approach more attractive to us, such as the preservation of the non-relativistic equation of continuity. The present study was undertaken as a preparation for an attempt to take into account the radiation field. In this paper, the radiation energy (Stefan–Boltzmann energy) is included in the Lagrangian; this automatically generates a radiative correction to the pressure (Section 3.5).
Units
Units are in cgsthroughout. A density of 0.0012 means a density of 0.0012 g/cm3.
2. The Action Principle
2.1. Hydrodynamics
Basic hydrodynamics deals with a density field, ρ, and a velocity field, v⃗, over IR3, subject to two fundamental equations, the equation of continuity,
and the hydrodynamical equation (Bernoulli, 1738 [11]),
This involves another field, the scalar field, p, interpreted as the local pressure. The theory requires an additional equation relating p to ρ. It is always assumed that this relation is local, giving p(x) in terms of the density (and the temperature) at the same point, x, and instantaneously.
2.2. Irrotational Flow
Since there is enough to do without taking on difficult problems of turbulence, we shall assume, here and throughout, that the velocity field can be represented as the gradient of a scalar field,
In this case, the hydrodynamical condition (2.2) is reduced to:
To complete this system, one still needs a relation between the fields, p and ρ.
Assume that there is a local functional, W [ρ], such that:
In this case:
and Equation (2.4) becomes, if ρ ≠ = 0,
or,
The potential W [ρ] is defined by p modulo a linear term, so that the appearance of an arbitrary constant is natural. It will serve as a Lagrange multiplier.
The introduction of a velocity potential allows us to interpret the energy functional as a fully-fledged Hamiltonian.
It will turn out that W, with the inclusion of a term linear in ρ that remains undetermined at this stage, is related to the entropy.
2.3. Variational Formulation
Having restricted our scope, to account for irrotational flows only, we have reduced the fundamental equations of simple hydrodynamics to the following two equations,
together with the defining equations,
It is well known that these equations are the Euler–Lagrange equations associated with the action (Fetter and Walecka, 1980 [12]),
The value of this last circumstance lies in the fact that the variational principle is a better starting point for generalizations, including the incorporation of symmetries, of special relativity and the inclusion of electromagnetic and gravitational interactions. It also gives us a valid concept of a total energy functional.
2.4. On Shell Relations
The action (2.10) contains only the fields Φ and ρ. The Euler–Lagrange equations define a complete dynamical framework, after specification of the functional, W [ρ]. The pressure was defined by
Equation (2.9), p = ρW′ − W, and one easily verifies that, by virtue of the equations of motion (we shall use the term “on shell”, adopted from quantum theories, to indicate relations that are valid by virtue of the adiabatic equations of motion),
This fact has been noted and has led to the suggestion that the action principle amounts to the minimization of ∫ p with respect to variations of p defined by thermodynamics (Taub, 1954 [13], Bardeen, 1970 [14], Schutz, 1970 [15]). However, an off shell action is needed. The Lagrangian density is not a thermodynamic function, since it depends on the time derivatives of the variables. After adopting the action (2.10), it remains to relate the choice of the potential, W, to the thermodynamical properties of the fluid. We shall find that the properties that define an ideal gas lead to a unique expression for W.
It is useful to reflect on the meaning of Equation (2.6), as well. In a more general situation, in which the potential, W, depends on the temperature, we would have, instead of (1.6), the identity:
Expression (2.5) for the pressure would be valid “on shell” if the action principle includes variations of the temperature as an independent variable, giving the on shell condition ∂V/∂T = 0.
There is a unique thermodynamical function that is a prime candidate for being identified with the potential, W. It is the function,
of three independent variables, where f and s are the free energy density and the entropy density. The integration with thermodynamics is explored in Section 3.
2.5. The Mass
To speak of a definite, isolated physical system, we must fix some attributes, and among such defining properties, we include the mass. We insist on this, as it shall turn out to be crucial to the stability of stellar atmospheres (Fronsdal, 2008 [9]). The density, ρ, will be taken to have the interpretation of mass density, and the total mass is the constant of the motion:
Such integrals, with no limits indicated, are over the domain, ∑, of the definition of ρ, the total extension of our system in IR3.
Since the total mass is a constant of the motion, it is natural to fix it in advance and to vary the action subject to the constraint ∫∑ d3x ρ(x) = M. The parameter, λ, takes on the role of a Lagrange multiplier, and the action takes the form:
The conservation of mass has implications for boundary conditions (Fronsdal, 2011 [16]).
2.6. Equation of State and Equation of Change
An ideal gas at equilibrium, with constant temperature, obeys the gas law:
Pressure and density are in cgs units and:
where μ is the molecular weight. The gas law is assumed to hold, locally at each point of the gas. Approximate values of μ are:
Equation (2.12) is the only equation that will be referred to as an “equation of state”. Other relations, to be discussed next, are “equations of change”, this term taken from Emden’s “Zustandsänderung”, for their meaning is of an entirely different sort. Most important is the polytropic relation:
This relation defines a polytropic path or polytrope in the p, V diagram (V = 1/ρ). A polytropic atmosphere is one in which, as one moves through the gas, the variables, ρ and p, change, so as to remain always on the same polytrope. Equation (2.13) is a statement about the system, not about the gas per se. The validity of Equation (2.13) for an actual atmosphere cannot be inferred from the early laboratory experiments.
The index of the polytrope is the positive number, n′, defined by:
Important special cases are:
Numbers γ, n are defined by:
The number, n, is the adiabatic index of the gas. According to statistical mechanics, 2n is the number of degrees of freedom of each molecule in the gas. That atmospheres tend to be polytropic is an empirical fact.
The case that γ′ = γ is of a special significance. A polytrope with γ′ = γ is a path of constant specific entropy; changes along such polytropes are reversible and adiabatic; these polytropes and no others are adiabats.
Fix the constants, A, γ′, in Equation (2.13) and consider an associated stationary, polytropic atmosphere. If both Equations (2.12) and (2.13) hold, we have (Poisson, 1835 [17]):
In any displacement along a polytrope from a point with pressure p and temperature T, we shall have dρ/ρ = (1/γ′)dp/p, so that an increase in pressure leads to an increase in density that is greater for a smaller value of γ′. If a parcel of gas in this atmosphere is pushed down to a region of higher pressure, by a reversible process, then it will adjust to the ambient pressure. If γ > γ′, then it will acquire a density that is lower than the environment; it will then rise back up. This atmosphere is stable. However, if γ′ > γ, then the parcel will be denser than the environment, and it will sink further; this atmosphere is unstable to convection. Thus, we have: A stable, polytropic atmosphere must have γ′ < γ, n′ > n [18]. Most stable is the isothermal atmosphere, γ′ = 1. In hydrodynamics, the isothermal atmosphere can be given a Lagrangian treatment by taking:
We suppose that the gas is confined to the section z0 < z < z0 + h of a vertical cylinder with base area

We may consider this an isolated system with fixed mass and fixed extension.
At equilibrium Φ̇ = 0, v⃗ = 0, ρ̇ = 0, and the equation of motion is: W′ = T(1 + ln ρ) = λ − gz, hence:
and after elimination of λ:
There is no difficulty in taking the limit h → ∞. The volume becomes infinite, but it can be replaced as a variable by the parameter, z0. This atmosphere is stable.
The isothermal atmosphere is usually abandoned in favor of the polytropic atmosphere. A polytropic gas can be described by the Lagrangian (2.10), with:
Variation with respect to ρ gives:
The temperature does not appear explicitly, but is taken to be determined by the gas law, p = ρT . Among the many applications, the following are perhaps the most important. In the case of sound propagation, the gas is initially awakened from equilibrial torpor and then left in an isolated, frenzied state of oscillating density and pressure, with the temperature keeping pace in obedience to the gas law (Laplace 1825) [19]. All three of the relations (2.14) are believed to hold, with γ′ = γ. The oscillations are usually too rapid for the heat to disseminate and equalize the temperature, so that the neglect of heat transfer is justified.
In applications to atmospheres, one often postulates the polytropic equation of change (2.13) and obtains the temperature from the gas law. The resultant temperature gradient in terms of convection, or as the effect of the heating of the air by solar radiation, or both, is one of the main issues on which we have hoped to gain some understanding.
At mechanical equilibrium v⃗ = 0, ρ̇ = 0 and λ − gz = âγρ1/n, hence:
Since the density must be positive, one does not fix the volume, but assumes that the atmosphere ends at the point z1 = λ/g. Then:
This fixes h and, thus, z1 and λ. If the atmosphere is an ideal gas, then the temperature varies with altitude according to:
Because the Lagrangian does not contain T as a dynamical variable, it is possible to impose this condition by hand.
One would not apply this theory down to absolute zero temperature, but even without going to extremes, it seems risky to predict the temperature of the atmosphere without having made any explicit assumptions about the absorption or generation of heat that is required to sustain it. Yet, this has been the basis for the phenomenology of stellar structure, as well as the Earth’s atmosphere, from the beginning [7,20].
The success of the polytropic model is amazing, but the theory is incomplete, since it does not account for heat flow, nor convection, both of which are needed to complete the picture.
For air, with molecular + weight 29, = 2.87 × 106 ergs/gK and n = 2.5. At sea level, g = 980 cm/s2, the density is ρ = 1.2 × 10−3 g/cm3 and the pressure p = 1.013 × 106 dyn/cm2. Thus:
and the dry lapse rate at low altitudes is –T′ = 294/ z1= 9.75 K/km. The opacity that is implied by this is mainly due to the presence of CO2 in the atmosphere. Humidity increases the opacity and decreases the lapse rate by as much as a factor of two (a temperature difference of 70 degrees over 12,000 m was observed by the author on a recent flight over Europe).
The specific internal energy of this hydrodynamical model is np/ρ = nT, as it should be for an ideal gas.
2.7. Historical Notes on Polytropic Atmosphere
Observations of reversible transformations of near-ideal gases, carried out during the 19th century, can be summarized in what is sometimes called the laws of Poisson,
In the original context, all the variables are constant and uniform. The exponents, as well as the coefficients of proportionality are the same for all states that are related by reversible transformations. Statistical mechanics explained this result and confirmed the experimental value γ′ = γ = CP/CV. As far as can be ascertained, the presence of terrestrial gravitation and ambient radiation had no effect on these experiments. In the first extrapolation, the same relations were taken to hold locally in dynamic situations, as in the case of sound propagation. The gas is not in thermal equilibrium, and the variation of the temperature from point to point, and with time, is obtained from the gas law. This extension of an important thermodynamical relation to the case of a nonuniform system is taken for granted.
For the atmosphere of the Earth, it was at first proposed that the temperature would be uniform. However, the existence of a temperature gradient was soon accepted as an incontrovertible experimental fact. The first recorded recognition of this, together with an attempt at explaining the same, may be that of Sidi Carnot, in the paper in which he created the science of thermodynamics [21]. Carnot quotes Laplace: “N’est-ce pas au refroidissement de l’air par la dilatation qu’il faut attribuer le froid des régions superieures de l’atmosphere? Les raisons données jusqu’ici pour expliquer ce froid sont tout a fait insuffisantes; on dit que l’air des régions elevées, recevant peu de chaleur reflechie par la terre, et rayonnant lui meme vers les espaces celestes, devait perdre de calorique, et que c’etait lá la cause de son refroidissement; ... ” This may be the first time that the influence of radiation is invoked. The temperature gradient is attributed to the greenhouse effect, and Laplace was an early skeptic, for he continues “...mais cette explication ce trouve detruite si l’on remarque qu’a égale hauteur le froid regne aussi bien et meme avec plus d’intensité sur les plaines elevées que sur les sommets des montagnes ou que dans les parties d’atmosphere éloignees du sol.” It is not clear that the two explanations are at odds with each other; Laplace apparently postulates that the atmospheres over lands at different elevations are related to adiabatic transformations, but without explaining why [22].
By rejecting the role of radiation as the cause of the temperature gradient, Laplace seems to suggest that the same would be observed in an atmosphere subject to gravitation, but totally isolated from radiation, neither exposed to the radiation coming from the sun nor radiating outwards. As was strongly emphasized in later phases of this debate, this would contradict the belief that the thermal equilibrium of any isolated system, gravitation and other external forces notwithstanding, is characterized by a uniform temperature.
In 1862, W. Thomson, in the paper “On the convective equilibrium of the temperature in the atmosphere” [23,24], defines convective equilibrium with these words “When all parts of a fluid are freely interchanged and not sensibly influenced by radiation and conduction, the temperature is said to be in a state of convective equilibrium.” He then goes on to say that an atmosphere that is in convective equilibrium is a polytrope, and we think that he means an adiabat, because of the words “freely interchanged”, although the value of the polytropic index is taken from experiment and not from statistical mechanics. At first sight, the clause “and not sensibly influenced by radiation” would seem to imply that his remarks apply to an isolated atmosphere, indicating that a temperature gradient would persist in the absence of radiation, but this conclusion would be premature, as we shall see.
Later, Lord Kelvin had doubts about what he called the Boltzmann–Maxwell doctrine and especially its application to the isolated atmosphere. See his Baltimore lectures, onwards (Kelvin, 1904 [25]) (“The time integral of the kinetic energy of any atom will be equal to the time integral of the kinetic energy of any other atom. This truism is simply and solely all that the Boltzmann–Maxwell doctrine asserts for a vertical column of a homogeneous monatomic gas.”).
In 1870, H.J. Lane made the bold assumption that the laws of Poisson may be satisfied in the Sun [7]. The terrestrial atmosphere (or part of it) had already been found to be well represented by the same relations. Referring to Lane’s paper, Thomson, now Lord Kelvin, explains how convective equilibrium comes about (Thomson, 1907 [26,27]). He argues that the atmosphere is not, cannot be, at rest, and this time, radiation plays an essential role. The upper layers loose heat by radiation, and the lower temperature leads to an increase in density. This produces a downward current that mixes with a compensating upward drift of warmer air. This continuing mixing takes place on a time scale that is too short for adjacent currents to exchange a significant amount of heat by conduction or radiation, especially since the variations of temperature are very small. It is evident that Thomson offers his explanation of the temperature gradient to account for its absence in an isolated atmosphere, for he says that, “an ideal atmosphere, perfectly isolated from absorption, as well as emission of radiation, will, after enough time has passed, reach a state of uniform temperature, irrespective of the presence of the gravitational field”. Thomson accepts the mechanism of Laplace and Carnot, as it is at work in the real atmosphere, but he goes further. He believes that the lower temperature aloft is intimately tied to the existence of radiation, implying that it is driven by net outwards radiation (the effect of solar radiation on the terrestrial atmosphere is not explicitly mentioned). It is difficult to judge whether or not Thomson is in disagreement with Laplace, but the precision of his statements represents a marked improvement over his predecessors and his earlier work.
The principal developers of the field, Ritter (1878–1883) [20] and Emden (1907) [18], seem to accept the idea of convective equilibrium. It may be pointed out, however, that this mechanism is in no way expressed by the equations that these and other authors use to predict the behavior of real atmospheres. The concept of convective equilibrium is introduced for one purpose only: to avoid contradiction with the firmly established belief in the isothermal equilibrium of isolated systems. It receives no quantitative theoretical treatment.
Nor was it accepted by everybody. A famous incidence involves Loschmidt (1876) [28], who believed that an isolated atmosphere, at equilibrium in a gravitational field, would have a temperature gradient. However, arguments presented by Maxwell and Boltzmann (1896) [29] led Loschmidt to withdraw his objections, which is hardly surprising given the authority of these two. Nevertheless, it may be pointed out that no attempt was made, to our knowledge, to settle the question experimentally, until recently (Graeff, 2007 [30]).
An alternative to convective equilibrium was proposed by Schwarzschild (1906) [31] and critically examined by Emden. To understand how it works, we turn to Emden’s book of 1907 [18], beginning on page 320. Here, he invokes a concept that is conspicuously absent from all his calculations on polytropic spheres in the rest of the book: heat flow. He posits that the atmosphere is not completely transparent and that heat flow is an inevitable consequence of the existence of a temperature gradient. The most important observation is that heat flow is possible in stationary configurations (Ṫ = 0), provided that the temperature gradient is constant. We take this to be an implicit reference to the heat equation, the first such reference in the book(!). The heat flux due to conduction and radiation is usually thought to be expressed as:
where the tensor, C, includes the thermal conductivity, as well as the effective coefficient of heat transfer by radiation. The divergence of the flux is the time rate of change of the temperature due to conduction and radiation. In a stationary, terrestrial atmosphere, with no local energy creation, this must vanish. Emden’s atmospheres are polytropes, with temperature gradients that are constant. It appears that he takes C to be uniform. That is surprising, and interesting, for he suggests that the entire edifice implicitly demands that this condition, of a constant heat flow, must be satisfied.
We note that the direction of flow is from hot to cold, outwards. In applications to planetary atmospheres, with no local energy generation, this calls for an explanation, since the ultimate source of energy is above. Here, we have to return to the oldest explanation of the existence of a temperature gradient, dismissed by Laplace (op. cit.): the greenhouse effect. The atmosphere is highly transparent to the (high frequency) radiation from the Sun, but opaque to the thermal radiation to which it is converted by the ground. The atmosphere is thus heated from below!
If the atmosphere is stable in the sense discussed above, when γ′ ≤ CP/CV, then it is not necessary to assume that any convection takes place. In this case, one speaks of (stable) “radiative equilibrium”. Convective equilibrium may step in when the stationary atmosphere is unstable, but it is no longer used to explain the existence of a temperature gradient.
A difficulty is present in all accounts of stellar structure up to 1920. The energy observed to be emitted by the Sun, attributed to the contraction of the mass and the concomitant release of internal energy, was far too small to account for the age of the sun as indicated by the geological record. The situation changed with the discovery of thermonuclear energy generation. Now, there is plenty of energy available. At the same time, there arose the realization that convection sometimes plays a very modest role; the concept of convective equilibrium was put aside and with it, Kelvin’s explanation of the temperature gradient. According to Eddington (1926) [32], who is more concerned with stars than with our atmosphere, “convective equilibrium” must be replaced by “radiative equilibrium”, in the sense of Schwarzschild. He does not claim that this new concept accounts for the temperature gradient as well as Kelvin’s convective equilibrium does, but in fact, the local generation of heat by thermonuclear processes creates an outward flow of heat and is expected to explain the existence of a negative temperature gradient (it does, at least, explain the persistence of high temperatures in a system that is open to the cosmos).
It is an indication of the incompleteness of this picture that it contains no parameter that can be associated with the strength of radiation and, a forteriori, it does not allow us to investigate the result of turning off the radiation.
3. Thermodynamics
3.1. The Ideal Gas in Statistical Mechanics
Here, again, we consider a gas that consists of identical particles (Boltzmann statistics), each with mass m and subject to no forces. It is assumed that the i-th particle has momentum p⃗i and kinetic energy . It is assumed that the number, N, of particles with energy E is given by the Maxwell distribution:
which implies a constant density in configuration space. Now, place this gas in a constant gravitational field, with potential φ(x, y, z) = gz, g constant. Since the potential varies extremely slowly on the atomic scale, it is plausible that, at equilibrium, each horizontal layer (φ constant) is characterized by a constant value of the temperature, density and pressure. Since neighboring layers are in thermal contact with each other, the temperature must (?) be the same throughout,
The energy of a particle at level z is p⃗2/2m + mgz, and Equation (2.1) now implies the following distribution in configuration space,
in agreement with Equation (2.17). This supports the expression for the potential, Equation (2.15), which is strange, since that potential is not appropriate for an ideal gas. Both derivations of the distribution rest on the assumption that the temperature is constant throughout the system.
About the influence of gravitation on the temperature distribution, there has been some debate; see, e.g., Waldram (1985) [33], page 151. It is said that the kinetic energy of each atom in a monatomic gas is 3kT/2 and that, when the temperature is the same everywhere, this is paradoxical, because it does not take into account the potential energy of the atom in the gravitational field. The incident involving Loschmidt, Maxwell and Boltzmann has already been mentioned. All speculation along these lines falls short of being compelling. See the Kelvin quote in Section 2.7.
3.2. The First Law and the Internal Energy
Can we extend the action principle to the case that the temperature varies with time? The action must be modified, for the temperature becomes a dynamical field. Is the temperature one of the variables with respect to which the action must be minimized? The usual approach is to lay down the additional equation by fiat (Section 2.6); is this completely satisfactory? Would it perhaps be preferable to have it appear as the result of minimizing the action with respect to variations of the temperature field? We hope to show that there are important advantages.
To prepare for the generalization, we shall examine some of the main tenets of thermodynamics in the context of the action principle. Assume for the moment that the system is one of uniform density and pressure.
Suppose that the system is in thermal and mechanical isolation, except for a force that is applied to the boundary. The system is in an equilibrium state with temperature T. The applied force is needed to hold the gas within the boundary of the domain, ∑, then decreased by a very small amount, leading to a displacement of the boundary and an increase of the volume by a small amount, dV . Assume that this process is reversible. The work done by the applied force is:
The first law states that, if the system is in thermal isolation, then this quantity is the differential of a function, U(V, S), that is referred to as the internal energy of the system.
Here, it should be recalled that the natural variables of U are V and S. When one says that the internal energy of an ideal gas is nTM, what is meant is that this is the value obtained when S is eliminated in favor of T and V . Locally, as we shall see in Section 3.6,
We regard u as the on shell value of the function W = f + sT .
Consider the system that consists of an ideal gas confined to a volume, V, and experiencing no external forces, not even gravitation. If the gas expands at constant pressure, the work done by the gas is pdV, and the ideal gas law Equation (2.12) tells us that:
The idea of energy conservation suggests a concept of “internal energy”. It is assumed that, under certain circumstances (dS = 0), the work done by the gas is at the expense of an internal energy, U, so that:
or:
It is an experimental fact (Gay-Lussac, 1827 [34], Joule, 1857 [35]) that the internal energy of an ideal gas is independent of the volume (see above), and the more precise statement that the on shell internal energy density u is proportional to Tρ is often included in the definition of the ideal gas. Thus:
Statistical mechanics gives ĉV = n, where n is the adiabatic index, and takes the value of 3/2 for a monatomic gas. Thus, TMdV/V + dU = TMdV/V + nMdT = 0, which implies that:
The conclusion is that the two conditions that define an ideal gas, p = ρT and u = nρT, imply the polytropic relation ρ/T n = constant for adiabatic changes. The calculation from Equation (3.4) onward was done with the understanding that M = ρV is fixed.
At the deepest level, the concept of energy derives its importance from the fact that it is conserved with the passage of time, by virtue of the dynamics. In modern versions of thermodynamics, and especially in the thermodynamics of irreversible processes and in radiation thermodynamics, conservation laws are all important, but they are postulated, one by one, not derived from basic axioms, as is the case in other branches of physics, and they have a formal aspect, serving to define various fluxes. See, e.g., Stanyukovich (1960) [3] and Castor (2004) [4].
3.3. The First Law and the Hamiltonian
Having adopted an action principle approach, we are bound to relate the internal energy with the Hamiltonian.
The Hamiltonian density is determined by the equations of motion only up to the addition of a constant multiple of the density. When we decide to adopt a particular expression to be used as internal energy over a range of temperatures, we are introducing a new assumption. Any expression for the internal energy, together with the implication that applied forces increase it by an amount determined by the work done, is a statement about a family of systems, indexed by the equilibrium temperature or the entropy. This cannot come out of the gas law and implies an independent axiom.
If we adopt the simplest expression for the Hamiltonian, that of the isothermal atmosphere, with the Lagrangian density of Equation (2.16),
interpreting the potential as the “internal energy”, then we shall get, in the static case,
with:
The second term compensates for pdV, and so, dT = 0, the temperature does not change. The temperature of this gas is an adiabatic invariant.
This contradicts experimental results for ideal gases. In fact, the Hamiltonian density h = W = T ρ ln ρ is not the correct expression for the internal energy density of an ideal gas (we shall have more to say about this later).
3.4. The Adiabatic Lagrangian
In the absence of gravity, the equilibrium configurations all have uniform temperature, density and pressure. The equilibrium configurations described by the Lagrangian are related by reversible transformations involving no heat transfer, exactly the configurations examined in the earliest experiments. In the presence of gravity, we shall assume only that the expression for the internal energy density has the same form, namely:
Two kinds of additions can be made to the Lagrangian (2.16) without spoiling the equations of motion that are essential to hydrodynamics.
Adding a term linear in ρ, we consider:
The continuity equation is unchanged, and the hydrodynamical equation remains:
where p = ρ(∂W/∂ρ) – W is unchanged, since the new term in the potential is linear in ρ and since ∂W/∂T vanishes on shell (Section 2.4).
Variation with respect to T gives:
On shell, or, more precisely, by virtue of this equation, the potential reduces to:
This is the on shell “free”, static Hamiltonian density (gravitational potential and kinetic energy omitted) that we expect to identify with the internal energy density (2.6). This requires that:
leaving free only the constant, T0. The on shell Hamiltonian density takes the form:
Finally, the equation of motion (3.8), with ψ [T] as in Equation (3.9), reduces to:
This is just the adiabatic relation ρ/T n = constant. It was derived, once more, from the two conditions that define an ideal gas.
The equation of motion that is obtained by variation with respect to ρ is:
Combined with Equation (3.10), it reduces, in the static case, to:
which has the same form as Equation (3.18) studied in Section 2.6, expressing the fact that the lapse rate is constant.
We have thus found an action principle, with dynamical variables, ρ and T, that reproduces all of the equations that characterize the equilibrium configurations, as well as the standard, hydrodynamical relations of an ideal gas.
The Lagrangian density is:
3.5. The Radiation Term
Since the advent of Schwarzschild’s paper (1909) [31] and especially after the adoption of his ideas by Eddington (1926) [32], the analysis of the effect of radiation has not changed significantly. The conclusion, in the simplest approximation, is that the internal energy is augmented by the Stefan–Boltzmann expression for the energy of black body radiation. Thus:
The term, ρμ [T], in Equation (3.7) has been included in the potential, with: k = ρ/T n.
The constant a = 7.64 × 10−15 ergs/K4 is the Stefan–Boltzmann constant, and the new term is the pressure of the photon gas, or of black body radiation.
The new expression for the on shell internal energy is:
and the pressure, defined either by the modified hydrodynamical equation or by dU + pdV = 0, is:
in agreement with the theory of black body radiation and with the principle that the pressure in a mixture of gases is additive.
Variation with respect to T now gives:
and in the important case when n = 3,
which is equivalent to Poisson’s law k = T3/ρ = constant. This reflects an affinity between the polytropic ideal gas with n = 3 and radiation, strongly emphasized by Eddington (1926) [32]. The value n = 3 has a cosmological significance, as well, it is characteristic of the changes in ρ, p, T induced by uniform expansion (Ritter [20], Emden 1907 [18]; see Chandrasekhar 1938, page 48 [36]). For other values of n, Equation (3.12) is a mild modification of the polytropic equation of change in the presence of radiation. The standard approach maintains the polytropic relation without change in the presence of radiation.
The fact that the inclusion of the radiative term in the Hamiltonian leads to a modification of the polytropic relation illustrates the new perspective that characterizes the action principle formulation of dynamics. It deserves to be emphasized that our approach does not allow us to determine a relation between dynamical variables (such as ρ ∝ Tn or even P = Tρ) until the Lagrangian has been completed. The modification of the polytropic relation that results from including the energy of the radiation field is not a feature of the traditional theory.
We have thus found an action that, varied with respect to ρ,Φ and T reproduces all of the equations that define the ideal, polytropic gas with polytropic index n = 3, radiation included, as well as the standard, hydrodynamical relations. For any value of n, it describes a gas that has its an effective polytropic index increased from the “natural” adiabatic value, approaching the critical value of three at very high temperatures.
We suggest that using the Lagrangian (3.11) is preferable to the usual assumption that β = pgas/ptot is constant, which is true only when n = 3.
3.6. Thermodynamics
The basis for a close integration of the action principle with thermodynamics is the identification of the Hamiltonian with the function:
a function of four independent variables: V, T, S and P.
The states of thermodynamic equilibrium are the points in this four-dimensional manifold at which H is extremal with respect to variations of T and V,
In the case of an ideal gas,
and these relations give:
and:
The on shell internal energy density is:
There is a symmetry between energy and entropy, already emphasized by Gibbs (1878) [1]. One can regard the entropy as a function of V, H and P,
The conditions that this function be stationary with respect to the variables of T and V are exactly the same,
and:
The choice of the function, F(V, T), characterized the system. The variable, S, remains a free parameter that is fixed when the system is isolated.
Local Relations
The local extrapolation of thermodynamics seeks to promote these relations to field equations that describe local, but stationary, configurations. The functions, F, H, S, are given new interpretations as specific densities, the variable, V, as specific volume. The mass density is ρ = 1/V and densities f, h, s are defined by:
The Hamiltonian is:
Variation with respect to T, with ρ, S, T treated as independent variables, leads to:
Variation with respect to ρ, with the mass and the volume fixed, gives:
The local thermodynamic pressure is defined by:
Then, the last relation (3.14) reduces to:
A complimentary variation of the density, with the mass fixed, but the volume not, gives the result that the internal pressure, p, must agree with the “external” pressure, p, on the boundary. This is the only way that the external pressure, p, affects the equations of motion, so the values assigned to p in the interior play no role. However, one may wish to assure that every part of the system is in equilibrium; that amounts to placing imaginary boundaries; then, p represents the pressure on the boundary by the molecules that are on “the outside”, and then, it has to match the thermodynamic pressure, p, everywhere. In this interpretation, p is the pressure, an independent variable, and the condition for equilibrium is that it take the value of the thermodynamic pressure, p, everywhere.
In the case of the ideal gas:
The on shell value of h is the internal energy density,
and the variational equations reduce to:
The first Equation (2.13), gives an expression for the entropy in terms of the density and the temperature. It must be interpreted as a condition to be satisfied by ρ and T once the entropy, S, is given. In Gibbs’ original setting, S was just a parameter; here, it is a distribution, but the interpretation is the same. Variation of the energy gives no information about the entropy distribution. It retains its role as a free parameter, fixed for an isolated system.
The other equation, in the general case of Equation (3.15), must be compared with the Bernoulli equation. There is, however, an obstruction, for Equation (3.15) reads:
with the gravitational potential, φ, now included, while the Bernoulli equation is,
Now,
The first term is grad ρ (p/ρ2) = (1/ρ) grad p – grad (p/ρ), so that the equation of motion is
and the Bernoulli equation is obtained under the condition that the specific entropy density is uniform.
This, it turns out, is a very interesting requirement.
Reversing the roles of h and s, we extremize the total entropy:
Variation with respect to T, with ρ, T, P and H = h/ρ treated as independent variables, gives the same result, ∂f/∂T + s = 0, but variation with respect to ρ gives an additional constraint,
This result brings relief to what is the greatest difficulty of localized thermodynamics, finding the correct way to deal with the entropy. It also relates the two difficulties that arose in connections with the equations of motion; the (inconsequential) one of fixing the role of the external pressure and the serious one of justifying the Bernoulli equation, to each other. In fact, both problems are solved, since we can show that P = p, and in that case, the entropy is uniform.
The result (3.16) is thus remarkable. The alternate form of Gibbs’ axiom actually provides exactly the additional information that is needed to relate the axiom of maximum energy to the laws of hydrodynamics, provided that the interpretation of P is correct.
In the case of the earthly atmosphere, the implication is that, if the total entropy is extremal, then the entropy, and not the temperature, is uniform.
In this section, we have not invoked our action principle, only classical ideas about the energy and the entropy being extremal at equilibrium. Let us point out that the function that we referred to as the Hamiltonian actually deserves the name. We need to introduce a variable that is the canonical conjugate to the variable, ρ. The velocity potential, Φ, fills the role admirably, with v⃗ = –grad Φ by definition. The continuity equation takes the form Φ̇ = δH/δρ.
The variational principle is thus thoroughly integrated with the thermodynamics of Gibbs.
3.7. The Puzzle
We return to our analysis of the isolated, ideal gas, before the introduction of the radiation term in Section 3.5. It was based on only two assumptions: the familiar expression for the internal energy of an ideal gas and the ideal gas law. The adiabatic equation of change, ρ/T n = constant, was not postulated, but derived from those assumptions. In the absence of gravity, the result is standard. In particular, the equations of motion allow for stationary states with uniform density and temperature. The effect of gravity was included by adding the gravitational potential energy to the Hamiltonian; which is standard practice. The result of that modification is that, in the presence of the gravitational field, there are no longer any stationary solutions with uniform temperature. Instead, both density and temperature decrease with elevation. This should be welcome as being in agreement with what is observed in real atmospheres. The fact that a portion of the atmosphere of the Earth exhibits the same temperature profile is a surprise; it suggests that the temperature gradient is not a product of radiation.
The problem is that nothing could justify an application of this theory to phenomena that are significantly influenced by radiation. Nothing that went into building up the theory suggests that the gas is not in isolation. However, there is a very strong conviction among physicists that, in an isolated system, the temperature must be uniform, gravitation notwithstanding. We have built a theory that, surprisingly, seems to apply to the irradiated and gravitating atmosphere, but we have not solved the more basic problem: to provide a dynamical theory that incorporates the isothermal atmosphere.
Why is the prediction of a temperature gradient in an isolated atmosphere so shocking? Imagine a large heat bath located in the region z > 0 in IR3. A vertical tube, filled with an ideal gas, has its upper end in thermal contact with the bath; otherwise, it is isolated. Assume that, at equilibrium, the lower part of the tube has a temperature that is higher than that of the bath. Now, extract a small amount of heat from the bottom of the tube; then, the restoration of equilibrium demands that heat must flow from the bath to the warmer, lower part of the tube, in violation of one of the statements of the second law, namely:
“Heat cannot pass by itself from a colder to a hotter body” (Clausius, 1887 [37]). (According to a recent experiment, it can!A recent preprint (Graeff, 2007 [30]) describes an experiment, carried out over a period of several months, in which a persistent temperature gradient was observed in a column of carefully isolated water.)
Concerning the status of this formulation by Clausius of the second law of thermodynamics, we quote I. Müller (2007) [5]:
“This statement, suggestive though it is, has often been criticized as vague. And indeed, Clausius himself did not feel entirely satisfied with it. Or else he would not have tried to make the sentence more rigorous in a page-long comment, which, however, only succeeds in removing whatever suggestiveness the original statement may have had”. Additionally, Müller continues: “We need not go deeper into this because, after all, in the end there will be an unequivocal mathematical statement of the second law”.
We note that Maxwell (1868) [38], in refuting Loschmidt, did not make use of the statement, but argued that the arrangement could be turned into a second class perpetuum mobile. However, the argument is incomplete.
3.8. The Centrifuge and the Atmosphere
Kelvin justified the polytropic model of the atmosphere in terms of radiation and convection. Eddington discounted the role of convection and relied on a concept of radiative equilibrium. To find out what happens in the case of complete isolation, we study the analogous situation in a centrifuge.
Consider an ideal gas. By a series of experiments in which gravity does not play a role, involving reversible changes in temperature and pressure, it is found that, at equilibrium, the laws p/ρ = T and ρ ∝ Tn are satisfied, constant n being fixed. When supplemented by the laws of hydrodynamics, they are found to hold, or at least they are strongly believed to hold, in configurations involving flow, over a limited time span, in the absence of external forces. In addition, it is believed that, at equilibrium, the temperature must be uniform. Let us refer to this last statement as “the rule”. We have in mind a fixed quantity of gas contained in a vessel, the walls of which present no friction and pass no heat.
Let the walls of the vessel be two vertical, concentric cylinders (this flow is not irrotational; there is no velocity potential, and we cannot use our Lagrangian formulation), and construct a stationary solution of the equations of motion. In terms of cylindrical coordinates, take vz = vr = 0, vθ = ω, constant. The continuity equation is satisfied with ρ for any function of r alone. Then, neither T nor p is constant, for the hydrodynamical equations demand that:
At first sight, this does not seem to violate the rule, for this is not a static configuration. However, when the equivalence principle is brought to bear, then it is argued, and we must concede, that the rule should be generalized to cover this situation, as well.
Instead, if we accept the foregoing calculations, and if we also accept the equivalence principle, then we shall be led to expect that a vertical column of an ideal gas, in mechanical equilibrium under the influence of terrestrial gravity, and perfectly isolated, will have a pressure and temperature gradient exactly of the form predicted by Homer Lane. This contradicts the prevailing opinion of atmospheric scientists, that the temperature gradient owes its existence to the heating associated with solar radiation.
Further measurements in the atmosphere may throw light on this, but isolation is difficult. Experiments with a centrifuge may be more realistic. The temperature lapse rate is rω2 × 10−7 K/cm. If the acceleration is 10,000× g at the outer wall, then the lapse rate will be 1 K per 10 cm, using air. The question of the existence of a temperature gradient is the most urgent. Once this is resolved, one way or another, the approach to equilibrium is worthy of an investigation.
3.9. The Isothermal Atmosphere
We report on a recent study of entropy by Fronsdal and Pathak (2011) [39]. The subject is thermodynamics as approached here, a Eulerian field theory formulated independently of its connections to statistics and kinetic theory. Two simple systems were studied:
- (a)
The slab, an ideal gas contained between two parallel plates maintained at temperatures T1 and T2, in a stationary configuration with no hydrodynamic flow. An attempt to derive the usual equations that are taken to govern systems of this type led to the following result. Starting from the fundamental equations of thermodynamics, assuming an entropy density of the form,
it was found that the second term is required in order to satisfy the boundary conditions. The pressure satisfies,
and this reduces to the usual hydrostatic condition if the the two terms on the right-hand side cancel each other. We have no reason to suggest that S is anything but uniform. We do not know whether the pressure profile has ever been determined experimentally.
- (b)
In the case of an atmosphere, isolated, but in a gravitational field, it is not enough to add the gravitational energy to the Hamiltonian, for that leads to a temperature gradient that is anathema to most physicists. It is necessary to include an unexpected contribution to the entropy, just as in the case of the slab, with,
where ρ0 and T0 refer to the state of equilibrium. This makes it possible to develop adiabatic dynamics around the isothermal atmosphere, something that, as far as we have been able to verify, has never been done. One selects an equilibrium state characterized by a uniform temperature, T0, and density,
and fixes the entropy as above. Then, it is a straightforward matter to calculate, for example, the velocity of the propagation of sound, seen as a first order perturbation of the equilibrium configuration. Without first fixing the entropy, in accordance with the postulated equilibrium configuration, this would not be possible, as there is not enough information.
The conclusion of this study is that the requirement of an isothermal equilibrium is consistent with thermodynamics, but at a price that may be too high. If the implications for the gravitational interaction are unacceptable, then work remains to be done, and the need for an experiment remains urgent.
4. Conclusions
4.1. On Variational Principles
The principal reasons for preferring an action principle formulation of thermodynamics were stressed in the Introduction. Here, we add some comments.
Variational principles have a very high reputation in most branches of physics; they even occupy a central position in the classical thermodynamics of Gibbs (1878) [1] (see, for example, the authoritative treatment by Callen (1960) [2]). An action is available for the study of irrotational flows in hydrodynamics (see, e.g., Fetter and Walecka (1960) [12]), though it does not seem to have been used much. Without the restriction to irrotational flows, it remains possible to formulate an action principle (Taub, 1954 [13], Bardeen, 1970 [14], Schutz, 1970 [15]), but the proliferation of velocity potentials is confusing, and no application is known to us.
In this paper, we rely on an action principle formulation of the laws that are believed to govern the behavior of an ideal gas, in the presence of gravity and radiation. We have restricted our attention to irrotational hydrodynamical flows. With a Hamiltonian formulation, there is a natural way to include the energy and pressure of radiation, to cover the whole range from a dense gas at low temperatures to a very dilute gas at the highest temperatures.
It was shown that there is an action that incorporates all of the essential properties that characterize an ideal gas, expressed as variational equations. The independent dynamical variables are the density, the velocity potential and the temperature. The idea of varying the action with respect to the temperature is unusual, but much in the classical tradition and the integration of the theory with classical thermodynamics is complete (Section 3.6). The Hamiltonian gives the correct expression for the internal energy and the pressure.
It was shown that the action principle is fully integrated and compatible with thermodynamics, in particular, with Gibbs’ extremum axioms of energy and entropy.
4.2. On Isothermal Atmospheres
In this framework, the inclusion of a gravitational field is natural. Inevitably, it leads to pressure gradients and, thus, also temperature gradients. The theory, as it stands, predicts the persistence of a temperature gradient in an isolated system at equilibrium. The existence of a temperature gradient in an isolated thermodynamical system is anathema to tradition, and further work is required to find a way to avoid it or to live with it. In the absence of experimentation, the question may be said to be academic, for it has little or no bearing on the application of the theory to actual atmospheres. However, it touches on the foundations of thermodynamics, and it deserves to be settled, or at least debated. Here, we shall try to summarize what it is that we feel is missing in the official position.
Suppose we start with a vertical column that, for one reason or another, is isentropic. At a certain moment, we turn off the incoming radiation and isolate the gas column from its environment. Assume that the column eventually becomes isothermal and that the dissipation of the temperature gradient is a slow process, during which the gas passes through a sequence of adiabatic equilibrium configurations. The question is this: what are those intermediary configurations, and what is the adiabatic dynamics around the ultimate equilibrium? Recent work by Fronsdal and Pathak (2011) [39] has attempted to answer this question, but this work may raise more questions than it set out to answer.
4.3. Heat Loss
The action principle advocated in this paper does not incorporate the heat equation:
where A is related to heat capacity and the tensor, C, to conductivity.
Let us suppose that conductivity and related phenomena that contribute to C are very small, so that the time scale of diffusion is much longer than that of the adiabatic excitations described by the equations of motion. In normal atmospheres, this is surely an excellent approximation. Then, the heat equation will describe the slow cooling of the atmosphere that will set in when radiation is switched off, and the system will pass through a succession of configurations that we may take to be stationary and even static on the time scale of adiabatic processes. For this to happen, the equations of motion must contain a variable that parameterizes these configurations. Our Lagrangian does, in fact, contain just one free parameter.
The constant, k0, appears in the Hamiltonian in the term:
identified with entropy. As we shall see (Appendix), this is very much like terms that appear when the interaction of the gas with external fields (electromagnetism) is taken into account. The interpretation must be that natural losses cause the decay of k0 and that the effect of the radiation that is incident on stable atmospheres compensates for this loss.
We have not been able erase all doubt about the fundamental rule, that equilibrium implies a uniform temperature in all cases. Tolman (1934, page 314) [40] shows that, according to general relativity, the temperature of an isolated photon gas in a gravitational field is not quite uniform. The predicted magnitude of this effect is very small, but it shows that there are circumstances in which statistical mechanics is not the absolute truth.
The interaction of the ideal gas with electromagnetic fields has been discussed in a provisional manner in the Appendix. The transfer of entropy between the two gases is in accord with the usual treatment of each system separately. We found no suggestion that the interaction is responsible for the temperature gradient.
4.4. Suggestions
- (1)
We propose the use of the Lagrangian (3.19), or its relativistic extension, with T treated as an independent dynamical variable and n′ = n, in astrophysics. Variation with respect to T yields the adiabatic relations between ρ and T, so long as the pressure of radiation is negligible, but for higher temperatures, when radiation becomes important, the effect is to increase the effective value of n′ towards the ultimate limit of three, regardless of the adiabatic index, n, of the gas. See, in this connection, the discussion by Cox and Giuli (1968) [41], page 271.
In the case that n = 3, there is Eddington’s treatment of the mixture of an ideal gas with the photon gas. However, most gas spheres have a polytropic index somewhat less than three, and in this case, the ratio β = pgas/ptot may not be constant throughout the star. The Lagrangian (3.11), with n identified with the adiabatic index of the gas, gives all the equations that are used to describe atmospheres, so long as radiation is insignificant. With greater radiative pressure, the polytropic index of the atmosphere is affected. It is not quite constant, but nearly so, and it approaches the upper limit of three when the radiation pressure becomes dominant. Eddington’s treatment was indicated, because he used Tolman’s approach to relativistic thermodynamics, where there is room for only one density and only one pressure. Many kinds of mixtures have been studied, but the equations that govern them do not supplement Tolman’s gravitational concepts in a natural manner, in our opinion. Be that as it may, it is patent that the approximation β = constant, in the works of Eddington and Chandrasekhar, is a device designed to avoid dealing with two independent gases.
- (2)
In a subsequent paper, we make use of the platform that is provided by the action principle to study the stability of atmospheres. A useful, exact virial theorem is derived from the equations of motion. It is argued that expressions for the total energy are not enough to determine stability; what is needed is an expression for the Hamiltonian, in terms of the dynamical variables of the theory (Fronsdal, 2011 [16]).
- (3)
The theory has a natural extension to mixtures, incorporating the Gibbs–Dalton hypothesis. It is being applied to mixed atmospheres, to chemical reactions and to changes of phase (Fronsdal, 2010) [42].
- (4)
Observation of the diurnal and seasonal variations of the equation of state of the troposphere may lead to a better understanding of the role of radiation in our atmosphere. The lapse rate has been measured from the equator to the poles, summer and winter. The presence of convection in the early hours of the day, known as gliders, reduces the lapse rate, but interpretation is difficult. Observed reduction by as much as a factor of two in the lapse rate is also difficult to interpret, since the variation may be due, in part, to unrecorded changes in the composition of the atmosphere. What is needed is a survey of the normalized lapse rate:
where μ is the mean atomic weight. An observed relative constancy of this parameter would support the expectations of the theory.
The temperature lapse rate has been observed under conditions that would not seem to favor it, between a snow covered surface and an inversion layer. This is difficult to reconcile with the traditional point of view.
- (5)
The centrifuge may be a more practical source of enlightenment. We understand that modern centrifuges are capable of producing accelerations of up to 106 × g. Any positive result for the temperature gradient in an isolated gas would have important theoretical implications.
Note added in proof: Papers that disagree with these conclusions abound. At the suggestion of the referee, the following references have been added: Combes and Laue, 1985 [43], Manabe and Strickler, 1964 [44], Roman, White and Velasco, 1995 [45], and Velaso, Roman and White, 1996 [46].
Acknowledgments
I thank Robert Finkelstein, Robert Huff, Alexander Kusenko, Joseph Rudnik, Philip Venturelli and Gary Williams for discussions.
Appendix
A. Electromagnetic Fields
We write the Maxwell Lagrangian as follows,
and add it to the ideal gas Lagrangian,
Since the susceptibility of an ideal gas is small, the dielectric constant may be expressed by:
Paramagnetic effects will be ignored at present. An interaction between the two systems occurs through the dependence of the susceptibility on ρ. The source, S, has become –(D⃗2/2ρ)(κ/T ). If this quantity has a constant value, then it produces a shift in the value of the parameter, k0.
Two interpretations are possible. The electromagnetic field may represent an external field, produced mainly by the source, J, and affecting the gas by way of the coupling implied by the dependence of the dielectric constant on ρ. Alternatively, the field is produced by microscopic fluctuations, quantum vacuum fluctuations, as well as the effects of the intrinsic dipoles of the molecules of the gas. In this latter case, the main effect of radiation is represented by the radiation term, aT4/3. Our difficulty is that neither interpretation is complete and that we do not have a sufficient grasp of the general case when either interpretation is only half right. The following should therefore be regarded as tentative.
Variation of the total action, with Lagrangian
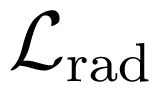
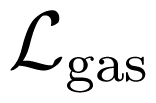
and:
Taking into account the first three equations, we find for the static Hamiltonian:
With the help of Equation (A.7), it becomes:
The last term, from the point of view of the thermodynamical interpretation of electrostatics, is recognized as the entropy (Panofsky and Phillips, 1955 [47]). On a suitable choice of the functional, κ, it merges into the internal energy. For example, if κ = ρT, it takes the form ρTS with S = D⃗2.
B. Using T As a Dynamical Variable
Let us examine the total Lagrangian,
So long as ε, μ and J are independent of ρ, T and v⃗, the variational equations of motion that are obtained by variation of v⃗, ρ, A⃗, H⃗ and D⃗ are all conventional, at least when n = 3 (for all n, if radiation is negligible). It would be possible to be content with that and fix T by fiat, as is usual; in the case of the ideal gas without radiation, the result is the same. However, if ε depends on ρ and on T, which is actually the case, then we get into a situation that provides the strongest justification, yet for preferring an action principle formulation with T as a dynamical variable. The equations of motion include a contribution from the variation of ε with respect to ρ, so that one of the basic hydrodynamical equations is modified. Thus, it is clear that the extension of the theory, to include the effect of radiation, is not just a matter of including additional equations for the new degrees of freedom. The presence of the term, D⃗2/2ε [ρ, T], certainly introduces the density, ρ, into Maxwell’s equations; that it introduces D⃗ into the hydrodynamical equations is clear, as well. The overall consistency of the total system of equations can probably be ensured by heeding Onsager’s principle of balance, but the action principle makes it automatic.
Variation of the action with respect to T offers additional advantages. The usual procedure, that amounts to fixing ρ = kTn, k and n constant, gives the same result when radiation is a relatively unimportant companion to the ideal gas, but in the other limiting case, when the gas is very dilute and the material gas becomes an insignificant addition to the photon gas, it is no longer tenable. We need an interpolation between the two extreme cases, and this is provided naturally by the postulate that the action is stationary with respect to variations of the temperature field.
In the absence of the ideal gas, we have another interesting system, the pure photon gas. The analogy between the photon gas and the ideal gas is often stressed; there is an analogue of the polytropic relation that fixes the temperature in terms of ρ; the pressure of the photon field is (a/3)T4. Our Lagrangian already contains this pressure; we should like to discover a closer connection between it and the electromagnetic field. In the limit when the density of the ideal gas is zero, Equation (A.7) becomes:
In the absence of the gas, it is reasonable to impose Lorentz invariance, so we include magnetic effects by completing the last to:
If we suppose that κ [ρ, T], in the limit ρ = 0, takes the form αT2, then:
The radiation from a gas of Hertzian dipoles can be shown, with the help of the Stefan–Boltzmann law and Wien’s displacement law, to satisfy a relation of precisely this form. Whether the same relation holds in vacuum is uncertain, but it is suggested by an analysis of the effective Born–Infeld Lagrangian calculated on the basis of the scattering of light by light (Euler, 1936 [48], Karplus and Neuman, 1950 [49]). See also McKenna and Platzman (1962) [50] and Fronsdal (2007) [8].
Conflicts of Interest
The authors declare no conflicts of interest.
References and Notes
- Gibbs, J.W. On the equilibrium of heterogeneous substances. Trans. Conn. Acad. Arts Sci 1878, 2, 300–320. [Google Scholar]
- Callen, H.B. Thermodynamics; John Wiley: New York, NY, USA, 1960. [Google Scholar]
- Stanyukovich, K.P. Unsteady Motion of Continuous Media; Pergamon Press: New York, NY, USA, 1960. [Google Scholar]
- Castor, J. Radiation Hydrodynamics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Müller, I. A History of Thermodynamics; Springer: Berlin, Germany, 2007. [Google Scholar]
- Horedt, G.P. Polytropes: Applications in Astrophysics and Related Fields; Springer: Berlin, Germany, 2004. [Google Scholar]
- Lane, H.J. On the theoretical temperature of the sun, under the hypothesis of a gaseous mass maintaining its volume by its internal heat, and depending on the laws of gases as known to terrestrial experiment. Am. J. Sci. Arts 1870, 4, 57–74. [Google Scholar]
- Fronsdal, C. Reissner-Nordstrom and charged polytropes. Lett. Math. Phys 2007, 82, 255–273. [Google Scholar]
- Fronsdal, C. Stability of polytropes. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Fronsdal, C.; Wilcox, T. J. An Equation of State for Dark Matter; UCLA Preprint: Los Angeles, CA, USA, 2011. [Google Scholar]
- Bernoulli, D. Hydrodynamica, sive De viribus et motibus fluidorum commentarii; Johann Reinhold Dulssecker: Strasbourg, Frence, 1738. [Google Scholar]
- Fetter, A.L.; Walecka, J.D. Theoretical Mechanics of Particles and Continua; MacGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Taub, A.H. General relativistic variational principle for perfect fluids. Phys. Rev 1954, 94, 1468–1470. [Google Scholar]
- Bardeen, J.M. A variational principle for rotating stars in General Relativity. Astrophys. J 1970, 7, 71. [Google Scholar]
- Schutz, B.F., Jr. Perfect fluids in General Relativity: Velocity potentials and a variational principle. Phys. Rev. D 1970, 2, 2762–2771. [Google Scholar]
- Fronsdal, C. Heat and gravitation. II. Stability. Gen. Relativ. Gravit 2011, 43, 107–126. [Google Scholar]
- Poisson, S.D. Théorie Mathmatique de la Chaleur; Bachelier: Paris, France, 1838. [Google Scholar]
- Emden, R. Gaskugeln; Teubner: Wiesbaden, Hesse, Germany, 1907. [Google Scholar]
- Laplace, P.S. Traitée de Mechanique Celeste; duPrat: Paris, France, 1825. [Google Scholar]
- Ritter, A. A series of papers in Wiedemann Annalen, now Annalen der Physik, For a list see Chandrasekhar 1938 [36]. The volumes 5–20 in Wiedemann Annalen appear as the volumes 241–256 in Annalen der Physik.
- Carnot, S. quoted by Emden. 1907. [18].
- Fourier, J.B.J. Théorie Analytique de la Chaleur; Didot: Paris, France, 1822. [Google Scholar]
- Kelvin, T.W. Collected Mathematical and Physical Papers; Cambridge University Press: Cambridge, Cambridge, UK, 1911; Volume 3, pp. 255–260. [Google Scholar]
- Kelvin, T.W. On the convective equilibrium of temperature in the atmosphere. Manch. lit. Philos. Soc 1862, 2, 170–176. [Google Scholar]
- Kelvin, T.W. Baltimore Lectures; C.J. Clay and Sons: London, UK, 1904. [Google Scholar]
- Kelvin, T.W. Collected Mathematical and Physical Papers; Cambrige University Press: Cambridge, UK, 1884; Volume 5, pp. 232–235. [Google Scholar]
- Thomson, W.; Lord, K. On Homer Lane’s problem of a spherical gaseous nebula. Nature 1907, 75, 232–235. [Google Scholar]
- Loschmidt, L. über den Zustand des Wärmegleichgewichtes eines Systems von Körpern mit Rcksicht auf die Schwerkraft, I. Sitzungsber. Kais. Akad. Wiss. Wien Math.-Naturwiss 1876, 73, 128–142. (in German). [Google Scholar]
- Boltzmann, L. Wissenschaftlidhe Abhandlungen; Hasenoehrl: Leipzig, Germany, 1909. [Google Scholar]
- Graeff, R.W. Viewing the Controversy Loschmidt-Boltzmann/Maxwell through Macroscopic Measurements of the Temperature Gradients in Vertical Columns of Water, Preprint. Additional Results Are on the Web Page, 2007. Available online: http://www.firstgravitymachine.com accessed on 1 September 2013. [Google Scholar]
- Schwarzschild, K. Ueber das Gleighgewicht der Sonnenatmosphäre; Göttinger Nachrichten: Gottingen, Germany, 1906; pp. 41–53. [Google Scholar]
- Eddington, A.S. The Internal Constitution of Stars; Dover: New York, NY, USA, 1959. [Google Scholar]
- Waldram, J.R. The Theory of Electrodynamics; Cambridge U. Press: Cambridge, UK, 1985. [Google Scholar]
- Gay-Lussac, J.L. The expansion of gases by heat. Ann. Chim 1802, 43, 137. [Google Scholar]
- Joule, J.P. Remarks on the heat and constitution of elastic fluids. Phil. Mag. IV 1857, 14, 211–216. [Google Scholar]
- Chandrasekhar, S. An Introduction to Stellar Structure; U. Chicago Press: Chicago, IL, USA, 1938. [Google Scholar]
- Clausius, R. Der mechanische Wärmetheorie; Vieweg Verlag: Braunschwei, Germany, 1887. [Google Scholar]
- Maxwell, J.C. On the dynamical theory of gages. Phil. Trans. R. Soc. Lond 1868, 157. [Google Scholar] [CrossRef]
- Fronsdal, C.; Pathak, A. On entropy in Eulerian thermodynamics. Proceedings of the AAAS Second Law Symposium, San Diego, CA, USA, 14–15 June 2011.
- Tolman, R.C. Relativity, Thermodynamics and Cosmology; Clarendon: Oxford, UK, 1934. [Google Scholar]
- Cox, J.P.; Giuli, R.T. Principles of Stellar Structure; Gordon and Breach: New York, NY, USA, 1968. [Google Scholar]
- Fronsdal, C. “Local Thermodynamics”, monograph under construction, the webpage is: fronsdal.physics.ucla.edu. last posted December 2013.
- Combes, C.A.; Laue, H. A paradox concerning the temperature distribution of a gas in a gravitational field. Am. J. Phys 1985. [Google Scholar] [CrossRef]
- Manabe, S.; Strickler, R.F. Thermal equilibrium of the atmosphere with a convective adjustment. J. Atmos. Sci 1964, 21, 361–385. [Google Scholar]
- Roman, F.L.; White, J.A.; Velasco, S. Microcanonical single-particle distributions for an ideal gas in a gravitational field. Eur. J. Phys 1995, 16, 83–90. [Google Scholar]
- Velasco, S.; Roman, F.L.; White, J.A. On a paradox concerning the temperature distribution of an ideal gas in a gravitational field. Eur. J. Phys 1996, 17, 43–44. [Google Scholar]
- Panofsky, W.K.H.; Philips, M. Classical Electricity and Magnetism; Addison-Wesley, Reading Mass: Boston, MA, USA, 1962. [Google Scholar]
- Euler, H. Über die Streuung von Licht an Licht nach der Diracschen Theorie. Ann. Phys 1936, 26, 398–420. [Google Scholar]
- Karplus, R.; Neuman, M. Non-linear interactions between electromagnetic fields. Phys. Rev 1950, 80, 380–385. [Google Scholar]
- McKenna, J.; Platzman, P.M. Nonlinear interaction of light in vacuum. Phys. Rev 1962, 129, 2354–236. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Frønsdal, C. Heat and Gravitation: The Action Principle. Entropy 2014, 16, 1515-1546. https://doi.org/10.3390/e16031515
Frønsdal C. Heat and Gravitation: The Action Principle. Entropy. 2014; 16(3):1515-1546. https://doi.org/10.3390/e16031515
Chicago/Turabian StyleFrønsdal, Christian. 2014. "Heat and Gravitation: The Action Principle" Entropy 16, no. 3: 1515-1546. https://doi.org/10.3390/e16031515
APA StyleFrønsdal, C. (2014). Heat and Gravitation: The Action Principle. Entropy, 16(3), 1515-1546. https://doi.org/10.3390/e16031515



