Analysis of Solar Neutrino Data from Super-Kamiokande I and II
Abstract
: We are going back to the roots of the original solar neutrino problem: the analysis of data from solar neutrino experiments. The application of standard deviation analysis (SDA) and diffusion entropy analysis (DEA) to the Super-Kamiokande I and II data reveals that they represent a non-Gaussian signal. The Hurst exponent is different from the scaling exponent of the probability density function, and both the Hurst exponent and scaling exponent of the probability density function of the Super-Kamiokande data deviate considerably from the value of 0.5, which indicates that the statistics of the underlying phenomenon is anomalous. To develop a road to the possible interpretation of this finding, we utilize Mathai’s pathway model and consider fractional reaction and fractional diffusion as possible explanations of the non-Gaussian content of the Super-Kamiokande data.1. Introduction
This paper summarizes briefly a research programme, comprised of five elements: (i) standard deviation analysis and diffusion entropy analysis of solar neutrino data [1,2]; (ii) Mathai’s entropic pathway model [3,4]; (iii) fractional reaction and extended thermonuclear functions [5,6]; (iv) fractional reaction and diffusion [7,8]; and (v) fractional reaction-diffusion [9–12]. Boltzmann translated Clausius’ second law of thermodynamics “The entropy of the Universe tends to a maximum” into a crucial quantity that links equilibrium and non-equilibrium (time dependent) properties of physical systems and related entropy to probability, S = k log W, which, later, Einstein called Boltzmann’s principle [13]. Based on this principle of physics, Planck found the correct formula for black-body radiation that lead him to the discovery of the elementary quantum of action that initiated the development of quantum theory. Extremizing the Boltzmann entropic functional under appropriate constraints produces the exponential functional form of the distribution for the respective physical quantity. Today, a question under intense discussion in statistical mechanics is how to generalize Boltzmann’s entropic functional, if extremized under appropriate constraints, to accommodate power law distribution functions observed so frequently in nature. One of such generalizations is Tsallis statistics [14] that contains Boltzmann statistics as a special case. Tsallis statistics is characterized by q-distributions, which seem to occur in many situations of scientific interest and have significant consequences for the understanding of natural phenomena. One such phenomena concerns the neutrino flux emanating from the gravitationally stabilized solar fusion reactor [15,16]. R. Davis Jr. established the solar neutrino problem, which was resolved by the discovery of neutrino oscillations [17,18]. A remaining question to date is still the quest for more information hidden in solar neutrino records of numerous past and currently operating solar neutrino experiments [19]. Greatly stimulated by the question, raised long time ago, by R.H. Dicke “Is there a chronometer hidden deep in the Sun?” [20,21], Mathai’s research programme on the analysis of the neutrino emission of the gravitationally stabilized solar fusion reactor focused on non-locality (long-range correlations), non-Markovian effects (memory), non-Gaussian processes (Lévy) and non-Fickian diffusion (scaling), possibly evident in the solar neutrino records, taking also into account the results of helio-seismology and helio-neutrino spectroscopy [22]. The original research programme, devised by Mathai, is contained in three research monographs [23–25], and the results of this research programme were summarized recently in [26].
2. Solar Neutrino Data
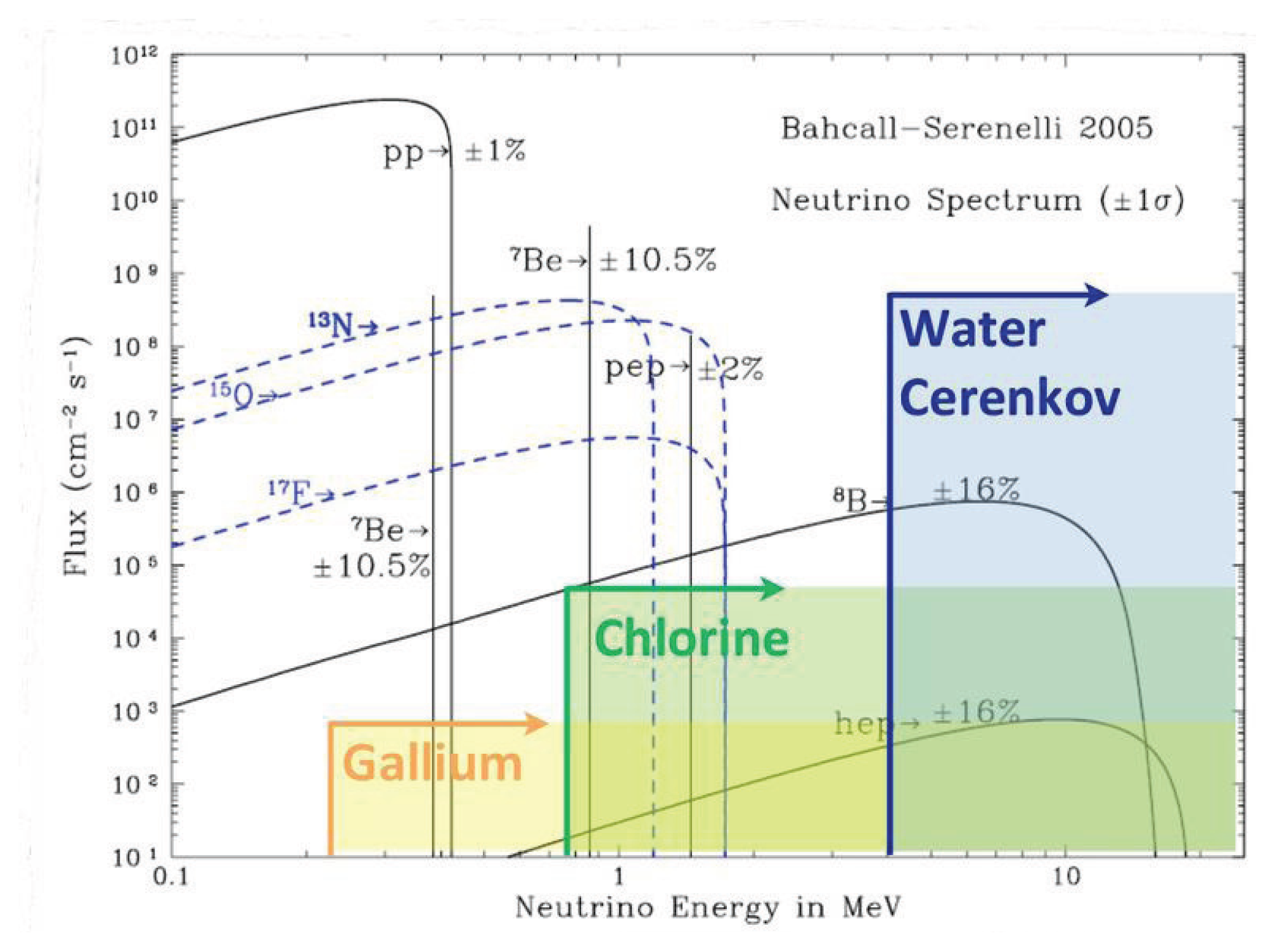
Over the past 40 years, radio-chemical and real-time solar neutrino experiments have proven to be sensitive tools to test both astrophysical and elementary particle physics models and principles. Solar neutrino detectors (radio-chemical: Homestake, GALLEX+ GNO, SAGE, real-time: Super-Kamiokande, SNO, Borexino) (Oser 2012 [19]; Haxton et al. 2012 [27]) have demonstrated that the Sun is powered by thermonuclear fusion reactions. Two distinct processes, the pp-chain and the sub-dominant CNO-cycle, are producing solar neutrinos with different energy spectra and fluxes (see Figure 1). To date, only fluxes from the pp-chain have been measured: 7Be, 8B and, indirectly, pp. Experiments with solar neutrinos and reactor anti-neutrinos (KamLAND; see [27] have confirmed that solar neutrinos undergo flavor oscillations (the Mikheyev-Smirnov-Wolfenstein (MSW) model; see [17]). Results from solar neutrino experiments are consistent with the Mikheyev-Smirnov-Wolfenstein large mixing angle (MSW-LMA) model, which predicts a transition from vacuum-dominated to matter-enhanced oscillations, resulting in an energy-dependent electron neutrino survival probability. Non-standard neutrino interaction models derived such neutrino survival probability curves that deviate significantly from MSW-LMA, particularly in the 1–4 MeV transition region. The mono-energetic 1.44 MeV pepneutrinos, which belong to the pp-chain and whose standard solar model (SSM) predicted flux has one of the smallest uncertainties, due to the solar luminosity constraint, are an ideal probe to test these competing non-standard neutrino interaction models in the future [28].
3. Standard Deviation Analysis and Diffusion Entropy Analysis
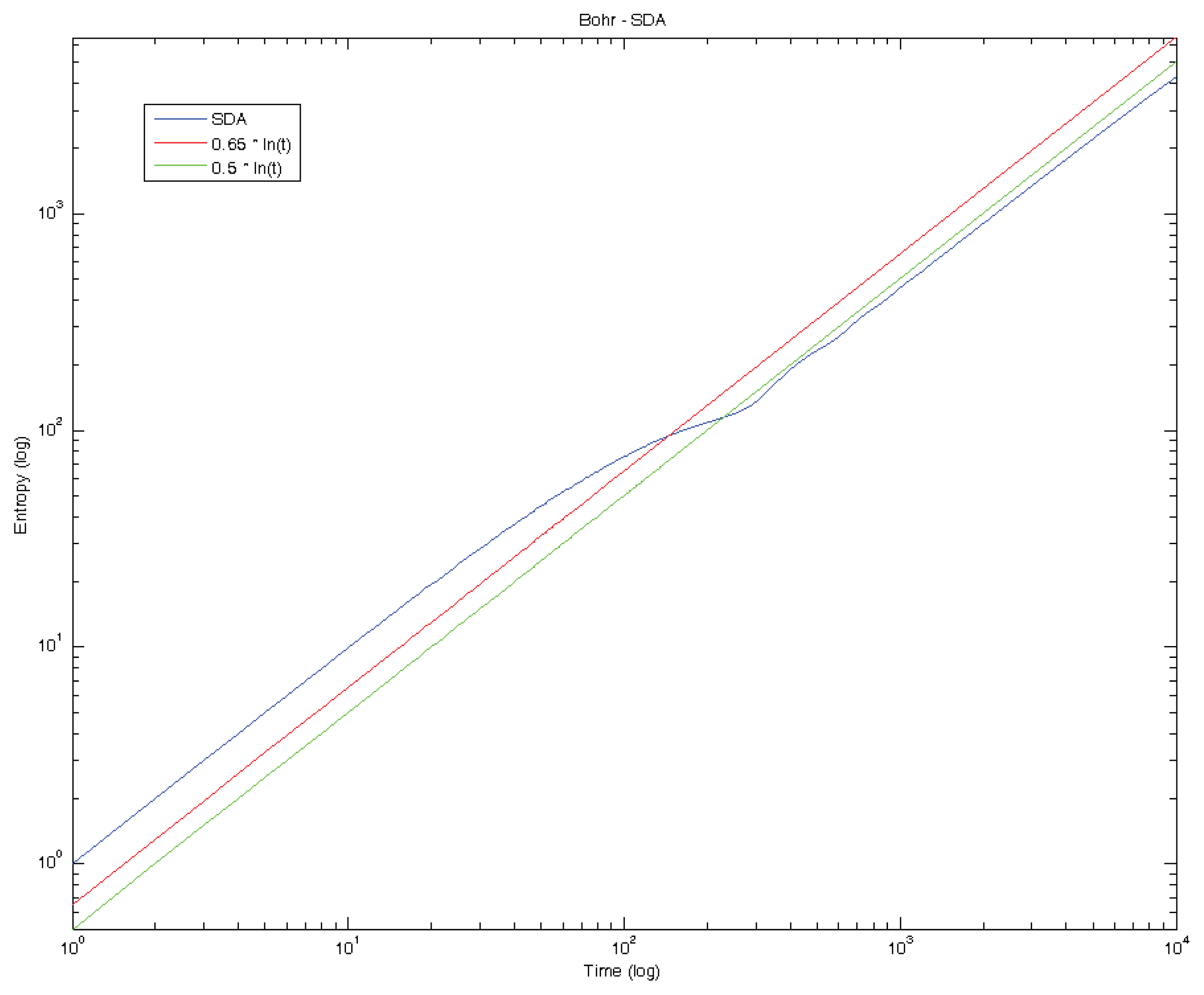
For all radio-chemical and real-time solar neutrino experiments, periodic variation in the detected solar neutrino fluxes have been reported, based mainly on Fourier and wavelet analysis methods (standard deviation analysis) [29–32]. Other attempts to analyze the same datasets, particularly undertaken by the experimental collaborations of real-time solar neutrino experiments themselves, have failed to find evidence for such variations of the solar neutrino flux over time. Periodicities in the solar neutrino fluxes, if confirmed, could provide evidence for new solar, nuclear or neutrino physics beyond the commonly accepted physics of vacuum-dominated and matter-enhanced oscillations of massive neutrinos (MSW model) that is, after 40 years of solar neutrino experiment and theory, considered to be the ultimate solution to the solar neutrino problem. Specifically, subsequent to the analysis made by the Super-Kamiokande collaboration [33–35], the SNO experiment collaboration has painstakingly searched for evidence of time variability at periods ranging from 10 years down to 10 min. SNO has found no indications for any time variability of the 8B flux at any timescale, including in the frequency window in which g-mode oscillations of the solar core might be expected to occur [36]. Despite large efforts to utilize helio-seismology and helio-neutrino spectroscopy, at present time, there is no conclusive evidence in terms of physics for the time variability of the solar neutrino fluxes from any solar neutrino experiment [17,22]. If such a variability over time would be discovered, for example, in the Borexino experiment, a mechanism for a chronometer for solar variability could be proposed based on relations between the properties of thermonuclear fusion and g-modes. All the above findings encouraged the conclusion that Fourier and wavelet analysis, which are based upon the analysis of the variance of the respective time series (standard deviation analysis (SDA)) [37,38], should be complemented by the utilization of diffusion entropy analysis (DEA), which measures the scaling of the probability density function (pdf) of the diffusion process generated by the time series, thought of as the physical source of fluctuations [39,40]. For this analysis, we have used the publicly available data of Super-Kamiokande I and Super-Kamiokande II (see Figure 2). Such an analysis does not reveal periodic variations of the solar neutrino fluxes but shows how the pdf scaling exponent departs in the non-Gaussian case from the Hurst exponent. Figures 3–6 show the Hurst exponents (SDA) and scaling exponents (DEA) for the Super-Kamiokande I and II data. Super-Kamiokande is sensitive mostly to neutrinos from the 8B branch of the pp nuclear fusion chain in solar burning. Above approximately 4 MeV, the detector can pick out the scattering of solar neutrinos off atomic electrons, which produces Cherenkov radiation in the detector. The 8B and rarer hepneutrinos have a spectrum, which ends near 20 MeV (see Figure 1).
Assuming that the solar neutrino signal is governed by a probability density function with scaling given by the asymptotic time evolution of a pdf of x, obeying the property:
where δ denotes the scaling exponent of the pdf. In the variance-based methods, scaling is studied by direct evaluation of the time behavior of the variance of the diffusion process. If the variance scales, one would have:
where H is the Hurst exponent. To evaluate the Shannon entropy of the diffusion process at time t, Scafetta et al. (2002; Scafetta 2010) [39,40] defined S(t) as:
and with the previous p(x, t), one has:
The scaling exponent, δ, is the slope of the entropy against the logarithmic time scale. The slope is visible in Figures 4 and 6 for the Super-Kamiokande data measured for 8B and hep. The Hurst exponents (SDA) are H = 0.66 and H = 0.36 for 8B and hep, respectively, shown in Figures 3 and 5. The pdf scaling exponents (DEA) are δ = 0.88 and δ = 0.80 for 8B and hep, respectively, as shown in Figures 4 and 6. The values for both SDA and DEA indicate a deviation from Gaussian behavior, which would require that H = δ = 0.5. A preliminary analysis, for Super-Kamiokande I data exclusively, was undertaken recently by [1]. A test computation for the application of SDA and DEA to data that are known to exhibit non-Gaussian behavior have been published recently by [2]. In this test, SDA and DEA, applied to the magnetic field strength fluctuations recorded by the Voyager-I spacecraft in the heliosphere, clearly revealed the scaling behavior of such fluctuations, as previously already discovered by non-extensive statistical mechanics considerations that lead to the determination of the non-extensivity q-triplet [14].
4. Mathai’s Entropic Pathway Model
From a general point of view of fitting experimental data to mathematical functions, a model, which moves from the generalized Type-1 beta family to the Type-2 beta family to the generalized gamma family to the generalized Mittag-Leffler family and, eventually, to the Lévy distributions, has been developed by Mathai [3]. All these different parametric families of functions are connected through Mathai’s pathway parameter α > 1. To generalize Shannon’s entropy to an entropic pathway, Mathai introduced the generalized entropy of order α that is also associated with Shannon (Boltzmann-Gibbs), Rényi, Tsallis and Havrda-Charvat entropies [4,26]. Applying the maximum entropy principle with normalization and energy constraints to Mathai’s entropic functional, the corresponding parametric families of distributions of generalized Type-1 beta, Type-2 beta, generalized gamma, generalized Mittag-Leffler and Lévy are obtained in the following form:
with α < 1 for Type-1 beta, α > 1 for Type-2 beta, α → 1 for gamma and δ = 1 for Tsallis statistics. In principle, any entropic functional in Mathai’s pathway can be tested through the above diffusion entropy analysis against experimental data. The deviation of the statistical properties of the Super-Kamiokande data analyzed above from the Gaussian should be captured by Equation (6).
5. Fractional Reaction and Extended Thermonuclear Functions
Solar nuclear reactions, producing neutrinos, occur preferably between nuclei in the high-energy tail of the energy distribution and are sensitive to deviations from the standard equilibrium thermal energy distribution (Maxwell-Boltzmann distribution) [6,15,41]. Reaction and relaxation processes in thermonuclear plasmas are governed by ordinary differential equations of the type:
for exponential behavior. The quantity, c, is a thermonuclear function, which is governed by the average of the Gamow penetration factor over the Maxwell-Boltzmann velocity distribution of reacting species and has been extended to incorporate more general distributions than the normal distribution [26]. The coefficient, c, itself can be considered to be a statistical quantity subject to accommodating a distribution of its own [4]. To address the non-exponential properties of a reaction or relaxation process, the first-order time derivative can be replaced formally by a derivative of fractional order in the following way [26]:
where denotes a Riemann-Liouville fractional integral operator, and the solution can be represented in terms of Mittag-Leffler functions Eν by:
Considering c to be a random variable itself, N(t) is to be taken as N(t | c) and can be written as:
which represents a generalized Mittag-Leffler function and is a random variable having a gamma type density:
with μ/ω being the mean value of c. The integration of N(t | c) over g(c) gives the unconditional density, as:
with γ + 1 = 1/(α − 1), α > 1 → γ = (α − 2)/(α − 1) and ω−ν = b(α − 1), b > 0, which corresponds to Tsallis statistics for μ = 1, ν = 1, b = 1 and α = q > 1, physically meaning that the common exponential behavior is replaced by a power-law behavior, including Lévy statistics. Both the translation of the standard reaction Equation (7) to a fractional reaction Equation (8) and the probabilistic interpretation of such equations lead to deviations from the exponential behavior to the power law behavior expressed in terms of Mittag-Leffler functions (9) or, as can be shown for Equation (12), to power law behavior in terms of H-functions [26]. H-functions are representable in terms of Mellin-Barnes integrals of the product of gamma functions and are therefore suited to represent statistics of products and quotients of independent random variables, thus providing a very useful tool in presenting a new perspective on the statistics of random variables [42].
6. Fractional Diffusion and the Joint Action of Reaction and Diffusion
In recent time, an analytic approach to non-conventional reaction and diffusive transport by taking into account fractional space and time derivatives has been developed [43]. The probability density function for the above Super-Kamiokande data is non-Gaussian and exhibits stretched power-law tails, as can be shown by further exploring Equations (6), (9) and (12). In order to model these analytic findings, a transport model for the pdf, based on fractional diffusion, which includes both non-local and non-Gaussian features, was proposed [26]. Reaction and diffusion in the solar thermonuclear fusion plasma are non-linear phenomena, which may be subject to non-Fickian transport (non-locality), non-Markovian effects (memory) and non-Gaussian scaling (Lévy). Fractional diffusion operators are integro-differential operators that incorporate the former three phenomena in a natural way and may, in this regard, constitute spatio-temporal elements of the fundamental theory of physics. This issue is currently under intense research. Continuous time random walk (CTRW) balance equations (master equations) with temporal memory, generation/destruction terms and spatio-transport/relaxation elements yield non-linear fractional reaction-diffusion equations, whose solutions are the focus of current research, and only very special cases have been dealt with, so far. Equally difficult to reveal is the interplay between fractional reaction and fractional diffusion in such non-linear equations. This difficulty is amplified by the fact that various definitions of fractional operators exist (Riemann-Liouville, Caputo, Weyl, Grünwald-Letnikov, Riesz-Feller, etc.). At this point of time, there is no general understanding under which specific mathematical and physical conditions a probabilistic interpretation can be given to unified fractional reaction-diffusion equations, and this difficulty is even further amplified by the observation that the replacement of integer order with fractional order time derivatives changes the fundamental concept of time and violates the principle that time evolution (change) is time translation and that fractional order space derivatives are bridging the respective differential equation between the case of the diffusion equation and the wave equation.
7. Conclusions
The use of solar neutrino detection records, by analyzing the average neutrino flux of the experiments, have led to the discovery of new elementary particle physics, the MSW effect, and, thus, resolved the solar neutrino problem. This confirmed that the standard solar model is implementing physical principles correctly. The quest for the variation of the solar neutrino flux over time remains an open question. Additionally, the utilization of standard deviation analysis (scaling of the variance) and diffusion entropy analysis (scaling of the pdf) leads to the discovery of an unknown phenomenon related to a non-equilibrium signature in the gravitationally stabilized solar fusion reactor, as explored by looking at Mathai’s pathway model and taking into account fractional reaction, fractional diffusion and, possibly, a combination of both of them.
Acknowledgements
The authors acknowledge the cooperation of Alexander Haubold of the Department of Computer Science, Columbia University, New York, NY, USA. The authors would like to thank the Department of Science and Technology, Government of India, New Delhi, for the financial assistance under project SR/S4/MS:287/05.
Conflicts of Interest
The authors declare no conflict of Interest.
- Author ContributionsAll authors contributed to the manuscript. Hans J. Haubold, Arak M. Mathai and Ram K. Saxena have contributed to the research methods and the results have been discussed among all authors and Alexander Haubold. Alexander Haubold took the lead in the numerical evaluation of the solar neutrino data. All authors read and approved the final manuscript.
References
- Haubold, A.; Haubold, H.J.; Kumar, D. Solar neutrino records: Gauss or non-Gauss is the question 2012. arXiv: 1202.1549v1 [physics.gen-ph].
- Haubold, A.; Haubold, H.J.; Kumar, D. Heliosheath: Diffusion entropy analysis and nonextensivity q-triplet 2012. arXiv: 1202.3417v1 [physics.gen-ph].
- Mathai, A.M. A pathway to matrix-variate gamma and normal densities. Linear Algebra Appl 2005, 396, 317–328. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. Pathway model, superstatistics, Tsallis statistics, and a generalized measure of entropy. Physica A 2007, 375, 110–122. [Google Scholar]
- Haubold, H.J.; Mathai, A.M. The fractional kinetic equation and thermonuclear functions. Astrophys. Space Sci 2000, 273, 53–63. [Google Scholar]
- Kumar, D.; Haubold, H.J. On extended thermonuclear functions through the pathway model. Adv. Space Res 2010, 45, 698–708. [Google Scholar]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Unified fractional kinetic equation and a fractional diffusion equation. Astrophys. Space Sci 2004, 209, 299–310. [Google Scholar]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Solutions of certain fractional kinetic equations and a fractional diffusion equation. J. Math. Phys 2010, 51, 103506. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Further solutions of fractional reaction-diffusion equations in terms of the H-function. J. Comput. Appl. Math 2011, 235, 1311–1316. [Google Scholar]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Fractional reaction-diffusion equations. Astrophys. Space Sci 2006, 305, 289–296. [Google Scholar]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Reaction-diffusion systems and nonlinear waves. Astrophys. Space Sci 2006, 305, 297–303. [Google Scholar]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Solution of generalized fractional reaction-diffusion equations. Astrophys. Space Sci 2006, 305, 305–313. [Google Scholar]
- Brush, S.G. Irreversibility and indeterminism: Fourier to Heisenberg. J. Hist. Ideas 1976, 37, 603–630. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Degl’Innocenti, S.; Fiorentini, G.; Lissia, M.; Quarati, P.; Ricci, B. Helioseismology can test the Maxwell-Boltzmann distribution. Phys. Lett. B 1998, 441, 291–298. [Google Scholar]
- Wolff, C.L. Effects of a deep mixed shell on solar g-modes, p-modes, and neutrino flux. Astrophys. J 2009, 701, 686–697. [Google Scholar]
- Pulido, J.; Das, C.R.; Picariello, M. Remaining inconsistencies with solar neutrinos: Can spin flavor precession provide a clue? J. Phys. Conf 2010, 203, 012086. [Google Scholar]
- Smirnov, A.Y. The MSW effect and solar neutrinos 2003. arXiv: 0305106 [hep-ph].
- Oser, S.M. An experimentalist’s overview of solar neutrinos. J. Phys. Conf 2012, 337, 012056. [Google Scholar]
- Dicke, R.H. Is there a chronometer hidden deep in the Sun? Nature 1978, 276, 676–680. [Google Scholar]
- Perry, C.A. Speculations on a solar chronometer for climate. NASA Conf. Publ 1990, 3086, 357–364. [Google Scholar]
- Goupil, M.J.; Lebreton, Y.; Marques, J.P.; Samadi, R.; Baudin, F. Open issues in probing interiors of solar-like oscillating main sequence stars: 1. From the Sun to nearly suns. J. Phys. Conf 2011, 271, 012031. [Google Scholar]
- Mathai, A.M.; Pederzoli, G. Characterizations of the Normal Probability Law; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Mathai, A.M.; Rathie, P.N. Basic Concepts in Information Theory and Statistics: Axiomatic Foundations and Applications; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Mathai, A.M.; Saxena, R.K. The H-function with Applications in Statistics and Other Disciplines; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Haxton, W.C.; Hamish Robertson, R.G.; Serenelli, A.M. Solar neutrinos: Status and prospects 2012. arXiv: 1208.5723v1 [astro-ph.SR].
- Ludhova, L.; Bellini, G.; Benziger, J.; Bick, D.; Bonfini, G.; Bravo, D.; Buizza Avanzini, M.; Caccianiga, B.; Cadonati, L.; Calaprice, F.; et al. Solar neutrino physics with Borexino I 2012. arXiv: 1205.2989v1 [hep-ex].
- Davis, R., Jr.; Cleveland, B.T.; Rowley, J.K. Variations in the Solar Neutrino Flux. Proceedings of the 20th International Cosmic Ray Conference, Moscow, USSR, 02 August 1987.
- Sakurai, K.; Haubold, H.J.; Shirai, T. The variation of the solar neutrino fluxes over time in the Homestake, GALLEX (GNO) and the Super-Kamiokande Experiments. Space Radiat 2008, 5, 207–216. [Google Scholar]
- Vecchio, A.; Carbone, V. Spatio-temporal analysis of solar activity: Main periodicities and period length variations. Astron. Astrophys 2009, 502, 981–987. [Google Scholar]
- Vecchio, A.; Laurenza, M.; Carbone, V.; Storini, M. Quasi-biennial modulation of solar neutrino flux and solar and galactic cosmic rays by solar cyclic activity. Astrophys. J. Lett 2010, 709, L1–L5. [Google Scholar]
- Abe, K.; Hayato, Y.; Iida, T.; Ikeda, M.; Ishihara, C.; Iyogi, K.; Kameda, J.; Kobayashi, K.; Koshio, Y.; Kozuma, Y.; et al. Solar neutrino results in Super-Kamiokande-III. Phys. Rev. D 2011, 83, 052010. [Google Scholar]
- Cravens, J.P.; Abe, K.; Iida, T.; Ishihara, K.; Kameda, J.; Koshio, Y.; Minamino, A.; Mitsuda, C.; Miura, M.; Moriyama, S.; et al. Solar neutrino measurements in Super-Kamiokande-II. Phys. Rev. D 2008, 78, 032002. [Google Scholar]
- Yoo, J.; Ashie, Y.; Fukuda, S.; Fukuda, Y.; Ishihara, K.; Itow, Y.; Koshio, Y.; Minamino, A.; Miura, M.; Moriyama, S.; et al. Search for periodic modulations of the solar neutrino flux in Super-Kamiokande-I. Phys. Rev. D 2003, 68, 092002. [Google Scholar]
- Aharmim, B.; Ahmed, S.N.; Anthony, A.E.; Barros, N.; Beier, E.W.; Bellerive, A.; Beltran, B.; Bergevin, M.; Biller, S.D.; Boudjemline, K.; et al. Searches for high-frequency variations in the 8B solar neutrino flux at the Sudbury Neutrino Observatory. Astrophys. J 2010, 710, 540–548. [Google Scholar]
- Haubold, H.J.; Gerth, E. On the Fourier spectrum analysis of the solar neutrino capture rate. Sol. Phys 1990, 127, 347–356. [Google Scholar]
- Haubold, H.J.; Mathai, A.M. Wavelet analysis of the new solar neutrino capture rate for the Homestake experiment. Astrophys. Space Sci 1998, 258, 201–218. [Google Scholar]
- Scafetta, N. Fractal and Diffusion Entropy Analysis of Time Series: Theory, concepts, applications and computer codes for studying fractal noises and Lévy walk signals; VDM Verlag: Saarland, Germany, 2010. [Google Scholar]
- Scafetta, N.; Latora, V.; Grigolini, P. Levy statistics in coding and non-coding nucleotide sequences. Phys. Lett. A 2002, 299, 565–570. [Google Scholar]
- Critchfield, C.L. Analytic forms of the thermonuclear function. In Cosmology, Fusion and Other Matters; Colorado Associated University Press: Boulder, CO, USA, 1972; pp. 186–191. [Google Scholar]
- Cottone, G.; Di Paola, M.; Metzler, R. Fractional calculus approach to the statistical characterization of random variables and vectors. Physica A 2010, 389, 909–920. [Google Scholar]
- Del-Castillo-Negrete, D. Fractional diffusion models of anomalous transport. In Anomalous Transport: Foundations and Applications; Klages, R., Radons, G., Sokolov, I. M., Eds.; Wiley: Weinheim, Germany, 2008; pp. 163–212. [Google Scholar]




© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Analysis of Solar Neutrino Data from Super-Kamiokande I and II. Entropy 2014, 16, 1414-1425. https://doi.org/10.3390/e16031414
Haubold HJ, Mathai AM, Saxena RK. Analysis of Solar Neutrino Data from Super-Kamiokande I and II. Entropy. 2014; 16(3):1414-1425. https://doi.org/10.3390/e16031414
Chicago/Turabian StyleHaubold, Hans J., Arak M. Mathai, and Ram K. Saxena. 2014. "Analysis of Solar Neutrino Data from Super-Kamiokande I and II" Entropy 16, no. 3: 1414-1425. https://doi.org/10.3390/e16031414
APA StyleHaubold, H. J., Mathai, A. M., & Saxena, R. K. (2014). Analysis of Solar Neutrino Data from Super-Kamiokande I and II. Entropy, 16(3), 1414-1425. https://doi.org/10.3390/e16031414



