Learning from Complex Systems: On the Roles of Entropy and Fisher Information in Pairwise Isotropic Gaussian Markov Random Fields
Abstract
: Markov random field models are powerful tools for the study of complex systems. However, little is known about how the interactions between the elements of such systems are encoded, especially from an information-theoretic perspective. In this paper, our goal is to enlighten the connection between Fisher information, Shannon entropy, information geometry and the behavior of complex systems modeled by isotropic pairwise Gaussian Markov random fields. We propose analytical expressions to compute local and global versions of these measures using Besag’s pseudo-likelihood function, characterizing the system’s behavior through its Fisher curve, a parametric trajectory across the information space that provides a geometric representation for the study of complex systems in which temperature deviates from infinity. Computational experiments show how the proposed tools can be useful in extracting relevant information from complex patterns. The obtained results quantify and support our main conclusion, which is: in terms of information, moving towards higher entropy states (A –> B) is different from moving towards lower entropy states (B –> A), since the Fisher curves are not the same, given a natural orientation (the direction of time).1. Introduction
With the increasing value of information in modern society and the massive volume of digital data that is available, there is an urgent need for developing novel methodologies for data filtering and analysis in complex systems. In this scenario, the notion of what is informative or not is a top priority. Sometimes, patterns that at first may appear to be locally irrelevant may turn out to be extremely informative in a more global perspective. In complex systems, this is a direct consequence of the intricate non-linear relationship between the pieces of data along different locations and scales.
Within this context, information theoretic measures play a fundamental role in a huge variety of applications once they represent statistical knowledge in a systematic, elegant and formal framework. Since the first works of Shannon [1], and later with many other generalizations [2–4], the concept of entropy has been adapted and successfully applied to almost every field of science, among which we can cite physics [5], mathematics [6–8], economics [9] and, fundamentally, information theory [10–12]. Similarly, the concept of Fisher information [13,14] has been shown to reveal important properties of statistical procedures, from lower bounds on estimation methods [15–17] to information geometry [18,19]. Roughly speaking, Fisher information can be thought of as the likelihood analog of entropy, which is a probability-based measure of uncertainty.
In general, classical statistical inference is focused on capturing information about location and dispersion of unknown parameters of a given family of distribution and studying how this information is related to uncertainty in estimation procedures. In typical situations, an exponential family of distributions and independence hypothesis (independent random variables) are often assumed, giving the likelihood function a series of desirable mathematical properties [15–17].
Although mathematically convenient for many problems, in complex systems modeling, independence assumption is not reasonable, because much of the information is somehow encoded in the relations between the random variables [20,21]. In order to overcome this limitation, Markov random field (MRF) models appear to be a natural generalization of the classical approach by the replacement of the independence assumption by a more realistic conditional independence assumption. Basically, in every MRF, knowledge of a finite-support neighborhood around a given variable isolates it from all the remaining variables. A further simplification consists in considering a pairwise interaction model, constraining the size of the maximum clique to be two (in other words, the model captures only binary relationships). Moreover, if the MRF model is isotropic, which means that the parameter controlling the interactions between neighboring variables is invariant to change in the directions, all the information regarding the spatial dependence structure of the system is conveyed by a single parameter, from now on denoted by β (or simply, the inverse temperature).
In this paper, we assume an isotropic pairwise Gaussian Markov random field (GMRF) model [22,23], also known as an auto-normal model or a conditional auto-regressive model [24,25]. Basically, the question that motivated this work and that we are trying to elucidate here is: What kind of information is encoded by the β parameter in such a model? We want to know how this parameter, and as a consequence, the whole spatial dependence structure of a complex system modeled by a Gaussian Markov random field, is related to both local and global information theoretic measures, more precisely the observed and expected Fisher information, as well as self-information and Shannon entropy.
In searching for answers for our fundamental question, investigations led us to an exact expression for the asymptotic variance of the maximum pseudo-likelihood (MPL) estimator of β in an isotropic pairwise GMRF model, suggesting that asymptotic efficiency is not granted. In the context of statistical data analysis, Fisher information plays a central role in providing tools and insights for modeling the interactions between complex systems and their components. The advantage of MRF models over the traditional statistical ones is that MRFs take into account the dependence between pieces of information as a function of the system’s temperature, which may even be variable along time. Briefly speaking, this investigation aims to explore ways to measure and quantify distances between complex systems operating in different thermodynamical conditions. By analyzing and comparing the behavior of local patterns observed throughout the system (defined over a regular 2D lattice), it is possible to measure how informative those patterns for a given inverse temperature are, or simply β (which encodes the expected global behavior).
In summary, our idea is to describe the behavior of a complex system in terms of information as its temperature deviates from infinity (when the particles are statistically independent) to a lower bound. The obtained results suggest that, in the beginning, when the temperature is infinite and the information equilibrium prevails, the information is somehow spread along the system. However, when temperature is low and this equilibrium condition does not hold anymore, we have a more sparse representation in terms of information, since this information is concentrated in the boundaries of the regions that define a smooth global configuration. In the vast remaining of this “universe”, due to this smooth constraint, the strong alignment between the particles prevails, which is exactly the expected global behavior for temperatures below a critical value (making the majority of the interaction patterns along the system uninformative).
The remainder of the paper is organized as follows: Section 2 discusses a technique for the estimation of the inverse temperature parameter, called the maximum pseudo-likelihood (MPL) approach, and provides derivations for the observed Fisher information in an isotropic pairwise GMRF model. Intuitive interpretations for the two versions of this local measure are discussed. In Section 3, we derive analytical expressions for the computation of the expected Fisher information, which allows us to assign a global information measure for a given system configuration. Similarly, in Section 4, an expression for the global entropy of a system modeled by a GMRF is shown. The results suggest a connection between maximum pseudo-likelihood and minimum entropy criteria in the estimation of the inverse temperature parameter on GMRFs. Section 5 discusses the uncertainty in the estimation of this important parameter by defining an expression for the asymptotic variance of its maximum pseudo-likelihood estimator in terms of both forms of Fisher information. In Section 6, the definition of the Fisher curve of a system as a parametric trajectory in the information space is proposed. Section 7 shows the experimental setup. Computational simulations with both Markov chain Monte Carlo algorithms and some real data were conducted, showing how the proposed tools can be used to extract relevant information from complex systems. Finally, Section 8 presents our conclusions, final remarks and possibilities for future works.
2. Fisher Information in Isotropic Pairwise GMRFs
The remarkable Hammersley–Clifford theorem [26] states the equivalence between Gibbs random fields (GRF) and Markov random fields (MRF), which implies that any MRF can be defined either in terms of a global (joint Gibbs distribution) or a local (set of local conditional density functions) model. For our purposes, we will choose the latter representation.
Definition 1 An isotropic pairwise Gaussian Markov random field regarding a local neighborhood system, ηi, defined on a lattice S = {s1, s2, . . . , sn} is completely characterized by a set of n local conditional density functions p(xi|ηi,θ⃗), given by:
2.1. Maximum Pseudo-Likelihood Estimation
Maximum likelihood estimation is intractable in MRF parameter estimation, due to the existence of the partition function in the joint Gibbs distribution. An alternative, proposed by Besag [24], is maximum pseudo-likelihood estimation, which is based on the conditional independence principle. The pseudo-likelihood function is defined as the product of the LCDFs for all the n variables of the system, modeled as a random field.
Definition 2 Let an isotropic pairwise GMRF be defined on a lattice S = {s1, s2, . . . , sn} with a neighborhood system, ηi. Assuming that denotes the set corresponding to the observations at time t, the pseudo-likelihood function of the model is defined by:
Note that the pseudo-likelihood function is a function of the parameters. For better mathematical tractability, it is usual to take the logarithm of L(θ⃗ ; X(t)). Plugging Equation (1) into Equation (2) and taking the logarithm leads to:
By differentiating Equation (3) with respect to each parameter and properly solving the pseudo-likelihood equations, we obtain the following maximum pseudo-likelihood estimators for the parameters, μ, σ2 and β:
Since the cardinality of the neighborhood system, k = |ηi|, is spatially invariant (we are assuming a regular neighborhood system) and each variable is dependent on a fixed number of neighbors on a lattice, β̂MPL can be rewritten in terms of cross-covariances:
2.2. Fisher Information of Spatial Dependence Parameters
Basically, Fisher information measures the amount of information a sample conveys about an unknown parameter. It can be thought of as the likelihood analog of entropy, which is a probability-based measure of uncertainty. Often, when we are dealing with independent and identically distributed (i.i.d) random variables, the computation of the global Fisher information presented in a random sample is quite straightforward, since each observation, xi, i = 1, 2, . . . , n, brings exactly the same amount of information (when we are dealing with independent samples, the superscript, t, is usually suppressed, since the underlying dependence structure does not change through time). However, this is not true for spatial dependence parameters in MRFs, since different configuration patterns (xi ∪ ηi) provide distinct contributions to the local observed Fisher information, which can be used to derive a reasonable approximation to the global Fisher information [27].
2.3. The Information Equality
It is widely known from statistical inference theory that, under certain regularity conditions, information equality holds in the case of independent observations in the exponential family [15–17]. In other words, we can compute the Fisher information of a random sample regarding a parameter of interest, θ, by:
However, given the intrinsic spatial dependence structure of Gaussian Markov random field models, information equilibrium is not a natural condition. As we will discuss later, in general, information equality fails. Thus, in a GMRF model, we have to consider two kinds of Fisher information, from now on denoted by Type I (due to the first derivative of the pseudo-likelihood function) and Type II (due to the second derivative of the pseudo-likelihood function). Eventually, when certain conditions are satisfied, these two values of information will converge to a unique bound. Essentially, β is the parameter responsible to control whether both forms of information converge or diverge. Knowing the role of β (inverse temperature) in a GMRF model, it is expected that for β = 0 (or T → ∞), information equilibrium prevails. In fact, we will see in the following sections that as β deviates from zero (and long-term correlations start to emerge), the divergence between the two kinds of information increases.
In terms of information geometry, it has been shown that the geometric structure of the exponential family of distributions is basically given by the Fisher information matrix, which is the natural Riemmanian metric (metric tensor) [18,19]. So, when the inverse temperature parameter is zero, the geometric structure of the model is a surface since the parametric space is 2D (μ and σ2). However, as the inverse temperature parameter starts to increase, the original surface is gradually transformed to a 3D Riemmanian manifold, equipped with a novel metric tensor (the 3 × 3 Fisher information matrix for μ, σ2 and β). In this context, by measuring the Fisher information regarding the inverse temperature parameter along an interval ranging from βMIN = A = 0 to βMAX = B, we are essentially trying to capture part of the deformation in the geometric structure of the model. In this paper, we focus on the computation of this measure. In future works we expect to derive the complete Fisher information matrix in order to completely characterize the transformations in the metric tensor.
2.4. Observed Fisher Information
In order to quantify the amount of information conveyed by a local configuration pattern in a complex system, the concept of observed Fisher information must be defined.
Definition 3 Consider an MRF defined on a lattice S = {s1, s2, . . . , sn} with a neighborhood system, ηi. The Type I local observed Fisher information for the observation, xi, regarding the spatial dependence parameter, β, is defined in terms of its local conditional density function as:
Hence, for an isotropic pairwise GMRF model, the Type I local observed Fisher information regarding β for the observation, xi, is given by:
Definition 4 Consider an MRF defined on a lattice S = {s1, s2, . . . , sn} with a neighborhood system, ηi. The Type II local observed Fisher information for the observation, xi, regarding the spatial dependence parameter, β, is defined in terms of its local conditional density function as:
In case of an isotropic pairwise GMRF model, the Type II local observed Fisher information regarding β for the observation, xi, is given by:
Therefore, we have two local measures, ϕβ (xi) and ψβ (xi), that can be assigned to every element of a system modeled by an isotropic pairwise GMRF. In the following, we will discuss some interpretations for what is being measured with the proposed tools and how to define global versions for these measures by means of the expected Fisher information.
2.5. The Role of Fisher Information in GMRF Models
At this point, a relevant issue is the interpretation of these Fisher information measures in a complex system modeled by an isotropic pairwise GMRF. Roughly speaking, ϕβ(xi) is the quadratic rate of change of the logarithm of the local likelihood function at xi, given a global value of β. As this global value of β determines what would be the expected global behavior (if β is large, a high degree of correlation among the observations is expected and if β is close to zero, the observations are independent), it is reasonable to admit that configuration patterns showing values of ϕβ(xi) close to zero are more likely to be observed throughout the field, once their likelihood values are high (close to the maximum local likelihood condition). In other words, these patterns are more “aligned” to what is considered to be the expected global behavior, and therefore, they convey little information about the spatial dependence structure (these samples are not informative once they are expected to exist in a system operating at that particular value of inverse temperature).
Now, let us move on to configuration patterns showing high values of ϕβ(xi). Those samples can be considered landmarks, because they convey a large amount of information about the global spatial dependence structure. Roughly speaking, those points are very informative once they are not expected to exist for that particular value of β (which guides the expected global behavior of the system). Therefore, Type I local observed Fisher information minimization in GMRFs can be a useful tool in producing novel configuration patterns that are more likely to exist given the chosen value of inverse temperature. Basically, ϕβ(xi) tells us how informative a given pattern is for that specific global behavior (represented by a single parameter in an isotropic pairwise GMRF model). In summary, this measure quantifies the degree of agreement between an observation, xi, and the configuration defined by its neighborhood system for a given β.
As we will see later in the experiments section, typical informative patterns (those showing high values of ϕβ(xi)) in an organized system are located at the boundaries of the regions defining homogeneous areas (since these boundary samples show an unexpected behavior for large β, which is: there is no strong agreement between xi and its neighbors).
Let us analyze the Type II local observed Fisher information, ψβ(xi). Informally speaking, this measure can be interpreted as a curvature measure, that is, how curved is the local likelihood function at xi. Thus, patterns showing low values of ψβ(xi) tend to have a nearly flat local likelihood function. This means that we are dealing with a pattern that could have been observed for a variety of β values (a large set of β values have approximately the same likelihood). An implication of this fact is that in a system dominated by this kind of patterns (patterns for which ψβ(xi) is close to zero), small perturbations may cause a sharp change in β (and, therefore, in the expected global behavior). In other words, these patterns are more susceptible to changes once they do not have a “stable” configuration (it raises our uncertainty about the true value of β).
On the other hand, if the global configuration is mostly composed of patterns exhibiting large values of ψβ(xi), changes on the global structure are unlikely to happen (uncertainty on β is sufficiently small). Basically, ψβ(xi) measures the degree of agreement or dependence among the observations belonging to the same neighborhood system. If at a given xi, the observations belonging to ηi are totally symmetric around the mean value, ψβ (xi) would be zero. It is reasonable to expect that in this situation, as there is no information about the induced spatial dependence structure (this means that there is no contextual information available at this point). Notice that the role of ψβ (xi) is not the same as ϕβ(xi). Actually, these two measures are almost inversely related, since if at xi the value of ϕβ(xi) is high (it is a landmark or boundary pattern), then it is expected that ψβ (xi) will be low (in decision boundaries or edges, the uncertainty about β is higher, causing ψβ (xi) to be small). In fact, we will observe this behavior in some computational experiments conducted in future sections of the paper.
It is important to mention that these rather informal arguments define the basis for understanding the meaning of the asymptotic variance of maximum pseudo-likelihood estimators, as we will discuss ahead. In summary, ψβ(xi) is a measure of how sure or confident we are about the local spatial dependence structure (at a given point, xi), since a high average curvature is desired for predicting the system’s global behavior in a reasonable manner (reducing the uncertainty of β estimation).
3. Expected Fisher Information
In order to avoid the use of approximations in the computation of the global Fisher information in an isotropic pairwise GMRF, in this section, we provide an exact expression for ϕ̂β and ψ̂β as Type I and Type II expected Fisher information. One advantage of using the expected Fisher information instead of its global observed counterpart is the faster computing time. As we will see, instead of computing a single local measure for each observation, xi ∈ X, and then taking the average, both Φ β and Ψβ expressions depend only on the covariance matrix of the configuration patterns observed along the random field.
3.1. The Type I Expected Fisher Information
Recall that the Type I expected Fisher information, from now on denoted by Φβ, is given by:
The Type II expected Fisher information, from now on denoted by Ψβ, is given by:
We first proceed to the definition of Φβ. Plugging Equation (3) in Equation (13), and after some algebra, we obtain the following expression, which is composed by four main terms:
Hence, the expression for Φβ is composed by four main terms, each one of them involving a summation of higher-order cross-moments. According to Isserlis’ theorem [28], for normally distributed random variables, we can compute higher order moments in terms of the covariance matrix through the following identity:
Then, the first term of Equation (15) is reduced to:
The third term of Equation (15) can be rewritten as:
Before proceeding, we would like to clarify some points regarding the estimation of the β parameter and the computation of the expected Fisher information in the isotropic pairwise GMRF model. Basically, there are two main possibilities: (1) the parameter is spatially-invariant, which means that we have a unique value, β̂(t), for a global configuration of the system, X(t) (this is our assumption); or (2) the parameter is spatially-variant, which means that we have a set of β̂s values, for s = 1, 2, . . . , n, each one of them estimated from (we are observing the outcomes of a random pattern along time in a fixed position of the lattice). When we are dealing with the first model (β is spatially-invariant), all possible observation patterns (samples) are extracted from the global configuration by a sliding window (with the shape of the neighborhood system) that moves through the lattice at a fixed time instant, t. In this case, we are interested in studying the spatial correlations, not the temporal ones. In other words, we would like to investigate how the the spatial structure of a GMRF model is related to Fisher information (this is exactly the scenario described above, for which n = 1). Our motivation here is to characterize, via information-theoretic measures, the behavior of the system as it evolves from states of minimum entropy to states of maximum entropy (and vice versa) by providing a geometrical tool based on the definition of the Fisher curve, which will be introduced in the following sections.
Therefore, in our case (n = 1), Equation (21) is further simplified for practical usage. By unifying s and r to a unique index, i, we have a final expression for Φβ in terms of the local covariances between the random variables in a given neighborhood system (i.e., for the eight nearest neighbors):
3.2. The Type II Expected Fisher Information
Following the same methodology of replacing the likelihood function by the pseudo-likelihood function of the GMRF model, a closed form expression for Ψβ is developed. Plugging Equation (3) into Equation (14) leads us to:
In order to simplify the notations and also to make computations easier, the expressions for Φβ,and Ψβ, can be rewritten in a matrix-vector form. Let Σp be the covariance matrix of the random vectors p⃗i, i = 1, 2, . . . , n, obtained by lexicographic ordering of the local configuration patterns xi ∪ η i. Thus, considering a neighborhood system, ηi, of size K, we have Σp given by a (K + 1) × (K + 1) symmetric matrix (for K + 1 odd, i.e., K = 4, 8, 12, . . .):
Definition 5 Let an isotropic pairwise GMRF be defined on a lattice S = {s1, s2, . . . , sn} with a neighborhood system, ηi, of size K (usual choices for K are even values: four, eight, 12, 20 or 24). Assuming that denotes the global configuration of the system at time t and ρ⃗ and are defined as Equations (25) and (24), the Type I expected Fisher information, Φβ, for this state, X(t), is:
Definition 6 Let an isotropic pairwise GMRF be defined on a lattice S = {s1, s2, . . . , sn} with a neighborhood system, ηi, of size K (usual choices for K are four, eight, 12, 20 or 24). Assuming that denotes the global configuration of the system at time t and is defined as Equation (24), the Type II expected Fisher information, Ψβ, for this state, X(t), is given by:
3.3. Information Equilibrium in GMRF Models
From the definition of both Φβ and Ψβ, a natural question that raises would be: under what conditions do we have Φβ = Ψβ in an isotropic pairwise GMRF model? As we can see from Equations (26) and (27), the difference between Φβ and Ψβ, from now on denoted by Δβ (ρ⃗, ), is simply:
4. Entropy in Isotropic Pairwise GMRFs
Our definition of entropy is done by repeating the same process employed to derive Φβ and Ψβ. Knowing that the entropy of random variable x is defined by the expected value of self-information, given by −log p(x), it can be thought of as a probability-based counterpart to the Fisher information.
Definition 7 Let an isotropic pairwise GMRF be defined on a lattice S = {s1, s2, . . . , sn} with a neighborhood system, ηi. Assuming that denotes the global configuration of the system at time t, then the entropy, Hβ, for this state X(t) is given by:
After some algebra, the expression for Hβ becomes:
Definition 8 Let an isotropic pairwise GMRF be defined on a lattice S = {s1, s2, . . . , sn} with a neighborhood system, ηi. Assuming that denotes the global configuration of the system at time t and ρ⃗ and are defined as Equations (25) and (24), the entropy, Hβ, for this state, X(t), is given by:
Note that Shannon entropy is a quadratic function of the spatial dependence parameter, β. Since the coefficient of the quadratic term is strictly non-negative (Ψβ is the Type II expected Fisher information), entropy is a convex function of β. Furthermore, as expected, when β = 0 and there is no induced spatial dependence in the system, the resulting expression for Hβ is the usual entropy of a Gaussian random variable, HG. Thus, there is a value, , for the inverse temperature parameter, which minimizes the entropy of the system. In fact, β̂MH is given by:
5. Asymptotic Variance of MPL Estimators
It is known from the statistical inference literature that unbiasedness is a property that is not granted by maximum likelihood estimation, nor by maximum pseudo-likelihood (MPL) estimation. Actually, there is no universal method that guarantees the existence of unbiased estimators for a fixed n-sized sample. Often, in the exponential family of distributions, maximum likelihood estimators (MLEs) coincide with the UMVU (uniform minimum variance unbiased) estimators, because MLEs are functions of complete sufficient statistics. There is an important result in statistical inference that shows that if the MLE is unique, then it is a function of sufficient statistics. We could enumerate and make a huge list of several properties that make maximum likelihood estimation a reference method [15–17]. One of the most important properties concerns the asymptotic behavior of MLEs: when we make the sample size grow infinitely (n → ∞), MLEs become asymptotically unbiased and efficient. Unfortunately, there is no result showing that the same occurs in maximum pseudo-likelihood estimation. The objective of this section is to propose a closed expression for the asymptotic variance of the maximum pseudo-likelihood of β in an isotropic pairwise GMRF model. Unsurprisingly, this variance is completely defined as a function of both forms of expected Fisher information, Ψβ and Φβ; as for general values of the inverse temperature parameter, the information equality condition fails.
5.1. The Asymptotic Variance of the Inverse Temperature Parameter
In mathematical statistics, asymptotic evaluations uncover several fundamental properties of inference methods, providing a powerful and general tool for studying and characterizing the behavior of estimators. In this section, our objective is to derive an expression for the asymptotic variance of the maximum pseudo-likelihood estimator of the inverse temperature parameter (β) in isotropic pairwise GMRF models. It is known from the statistical inference literature that both maximum likelihood and maximum pseudo-likelihood estimators share two important properties: consistency and asymptotic normality [29,30]. It is possible, therefore, to completely characterize their behaviors in the limiting case. In other words, the asymptotic distribution of β̂MPL is normal, centered around the real parameter value (since consistency means that the estimator is asymptotically unbiased), with the asymptotic variance representing the uncertainty about how far we are from the mean (real value). From a statistical perspective, β̂MPL ≈ N (β, υβ), where υβ denotes the asymptotic variance of the maximum pseudo-likelihood estimator. It is known that the asymptotic covariance matrix of maximum pseudo-likelihood estimators is given by [31]:
Definition 9 Let an isotropic pairwise GMRF be defined on a lattice S = {s1, s2, . . . , sn} with a neighborhood system, ηi. Assuming that denotes the global configuration of the system at time t, and ρ⃗ and are defined as Equations (25) and (24), the asymptotic variance of the maximum pseudo-likelihood estimator of the inverse temperature parameter, β, is given by (using the same matrix-vector notation from the previous sections):
Note that when information equilibrium prevails, that is Φ β = Ψβ, the asymptotic variance is given by the inverse of the expected Fisher information. However, the interpretation of this equation indicates that the uncertainty in the estimation of the inverse temperature parameter is minimized when Ψβ is maximized. Essentially, this means that on average, the local pseudo-likelihood functions are not flat, that is small changes on the local configuration patterns along the system cannot cause abrupt changes in the expected global behavior (the global spatial dependence structure is not susceptible to sharp changes). To reach this condition, there must be a reasonable degree of agreement between the neighboring elements throughout the system, a behavior that is usually associated to low temperature states (β is above a critical value and there is a visible induced spatial dependence structure).
6. The Fisher Curve of a System
With the definition of Φ β, Ψβ and Hβ, we have the necessary tools to compute three important information-theoretic measures of a global configuration of the system. Our idea is that we can study the behavior of a complex system by constructing a parametric curve in this information-theoretic space as a function of the inverse temperature parameter, β. Our expectation is that the resulting trajectory provides a geometrical interpretation of how the system moves from an initial configuration, A (with a low entropy value for instance), to a desired final configuration, B (with a greater value of entropy, for instance), since the Fisher information plays an important role in providing a natural metric to the Riemannian manifolds of statistical models [18,19]. We will call the path from global State A to global State B as the Fisher curve (from A to B) of the system, denoted by . Instead of using time as the parameter to build the curve, F⃗, we parametrize F⃗ by the inverse temperature parameter, β.
Definition 10 Let an isotropic pairwise GMRF be defined on a lattice S = {s1, s2, . . . , sn} with a neighborhood system, ηi, and X(β1), X(β2),…, X(βn) be a sequence of outcomes (global configurations) produced by different values of βi (inverse temperature parameters) for which A = βMIN = β1 <β2 < … <βn = βMAX = B. The system’s Fisher curve from A to B is defined as the function F⃗:ℜ → ℜ3 that maps each configuration, X(βi), to a point (Φ βi = ψβi,Hβi) from the information space, that is:
In the next sections, we show some computational experiments that illustrate the effectiveness of the proposed tools in measuring the information encoded in complex systems. We want to investigate what happens to the Fisher curve as the inverse temperature parameter is modified in order to control the system’s global behavior. Our main conclusion, which is supported by experimental analysis, is that . In other words, in terms of information, moving towards higher entropy states is not the same as moving towards lower entropy states, since the Fisher curves that represent the trajectory between the initial State A and the final State B are significantly different.
7. Computational Simulations
This section discusses some numerical experiments proposed to illustrate some applications of the derived tools in both simulations and real data. Our computational investigations were divided into two main sets of experiments:
- (1)
Local analysis: analysis of the local and global versions of the measures (ϕβ, ψβ, Φ β, Ψβ and Hβ), considering a fixed inverse temperature parameter;
- (2)
Global analysis: analysis of the global versions of the measures (Φ β, Ψβ and Hβ) along Markov chain Monte Carlo (MCMC) simulations in which the inverse temperature parameter is modified to control the expected global behavior.
7.1. Learning from Spatial Data with Local Information-Theoretic Measures
First, in order to illustrate a simple application of both forms of local observed Fisher information, ϕβ and ψβ, we performed an experiment using some synthetic images generated by the Metropolis– Hastings algorithm. The basic idea of this simulation process is to start at an initial configuration in which temperature is infinite (or β = 0). This basic initial condition is randomly chosen, and after a fixed number of steps, the algorithm produces a configuration that is considered to be a valid outcome of an isotropic pairwise GMRF model. Figure 1 shows an example of the initial condition and the resulting system configuration after 1,000 iterations considering a second order neighborhood system (eight nearest neighbors). The model parameters were chosen as: μ = 0, σ2 = 5 and β = 0.8.
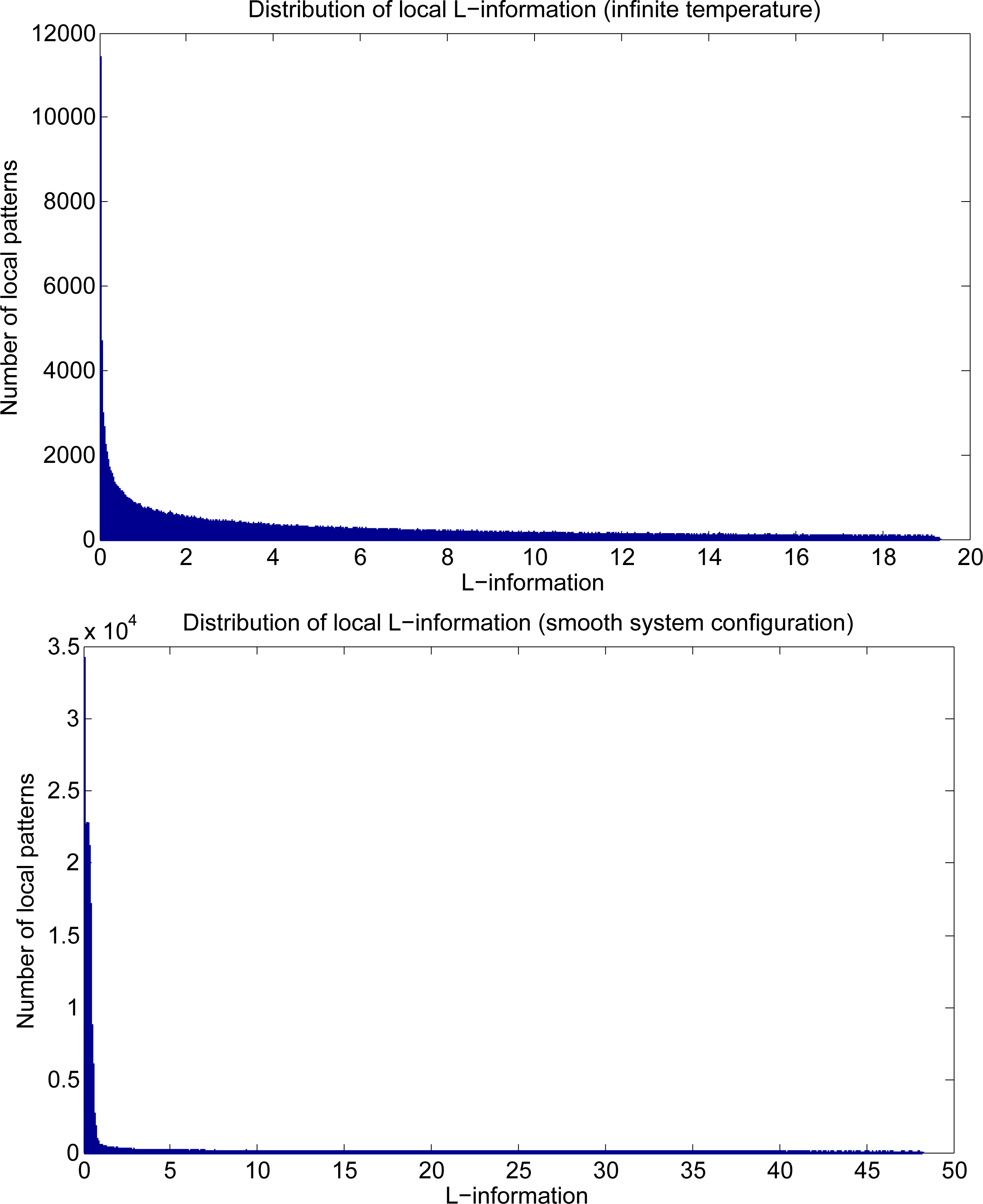
Three Fisher information maps were generated from both initial and resulting configurations. The first map was obtained by calculating the value, ϕβ(xi), for every point of the system, that is for i = 1, 2, . . . , n. Similarly, the second one was obtained by using ψβ(xi). The last information map was built by using the ratio between ϕβ(xi) and ψβ(xi), motivated by the fact that boundaries are often composed of patterns that are not expected to be “aligned” to the global behavior (and, therefore, show high values of ϕ (xi)) and also are somehow unstable (show low values of β (xi)). We will recall this measure, Lβ (xi) = ϕβ(xi)/ψβ(xi), the local L-information, once it is defined in terms of the first two derivatives of the logarithm of the local pseudo-likelihood function. Figure 2 shows the obtained information maps as images. Note that while ϕβ has a strong response for boundaries (the edges are light), ψβ has a weak one (so the edges are dark), evidence in favor of considering L-information in boundary detection procedures. Note also that in the initial condition, when the temperature is infinite, the informative patterns are almost uniformly spread all over the system, while the final configuration shows a more sparse representation in terms of information. Figure 3 shows the distribution of local L-information for both systems’ configurations depicted in Figure 1.
7.2. Analyzing Dynamical Systems with Global Information-Theoretic Measures
In order to study the behavior of a complex system that evolves from an initial State A to another State B, we use the Metropolis–Hastings algorithm, an MCMC simulation method, to generate a sequence of valid isotropic pairwise GMRF model outcomes for different values of the inverse temperature parameter, β. This process is an attempt to perform a random walk on the state space of the system, that is, in the space of all possible global configurations in order to analyze the behavior of the proposed global measures: entropy and both forms of Fisher information. The main purpose of this experiment is to observe what happens to Φβ, Ψβ and Hβ when the system evolves from a random initial state to other global configurations. In other words, we want to investigate the Fisher curve of the system in order to characterize its behavior in terms of information. Basically, the idea is to use the Fisher curve as a kind of signature for the expected behavior of any system modeled by an isotropic pairwise GMRF, making it possible to gain insights into the understanding of large complex systems.
To simulate a system in which we can control the inverse temperature parameter, we define an updating rule for β based on fixed increments. In summary, we start with a minimum value βMIN (when βMIN = 0, the temperature of the system is infinite). Then, the value of β in the iteration, t, is defined as the value of β in t − 1 plus a small increment (Δβ), until it reaches a pre-defined upper bound, βMAX. The process in then repeated with negative increments −Δβ, until the inverse temperature reaches its minimum value, βM I N, again. This process continues for a fixed number of iterations, NM A X, during an MCMC simulation. As a result of this approach, a sequence of GMRF samples is produced. We use this sequence to calculateΦβ, Ψβ and Hβ and define the Fisher curve F⃗, for β = βM I N , . . . ,βM A X. Figure 4 shows some of the system’s configurations along an MCMC simulation. In this experiment, the parameters were defined as: βM I N = 0, Δβ= 0.001, βM A X = 0.15 and NM A X = 1, 000, μ = 0, σ2 = 5 and ηi = {(i−1, j −1), (i−1, j), (i−1, j +1), (i, j −1), (i, j +1), (i+1, j −1), (i+1, j), (i+1, j +1)}.
A plot of both forms of the expected Fisher information, Φ β and Ψβ, for each iteration of the MCMC simulation is shown in Figure 5. The graph produced by this experiment shows some interesting results. First of all, regarding upper and lower bounds on these measures, it is possible to note that when there is no induced spatial dependence structure (β ≈ 0), we have an information equilibrium condition (Φ β = Ψβ and the information equality holds). In this condition, the observations are practically independent in the sense that all local configuration patterns convey approximately the same amount of information. Thus, it is hard to find and separate the two categories of patterns we know: the informative and the non-informative ones. Once they all behave in a similar manner, there is no informative pattern to highlight. Moreover, in this information equilibrium situation, Ψβ reaches its lower bound (in this simulation, we observed that in the equilibrium Φ β ≈ Ψβ ≈ 8), indicating that this condition emerges when the system is most susceptible to a change in the expected global behavior, since the uncertainty about β is maximum at this moment. In other words, modification in the behavior of a small subset of local patterns may guide the system to a totally different stable configuration in the future.
The results also show that the difference between Φ β and ψβ is maximum when the system operates with large values of β, that is, when organization emerges and there is a strong dependence structure among the random variables (the global configuration shows clear visible clusters and boundaries between them). In such states, it is expected that the majority of patterns be aligned to the global behavior, which causes the appearance of few, but highly informative patterns: those connecting elements from different regions (boundaries). Besides that, the results suggest that it takes more time for the system to go from the information equilibrium state to organization than the opposite. We will see how this fact becomes clear by analyzing the Fisher curve along Markov chain Monte Carlo (MCMC) simulations. Finally, the results also suggest that both Φ β and Ψβ are bounded by a superior value, possibly related to the size of the neighborhood system.
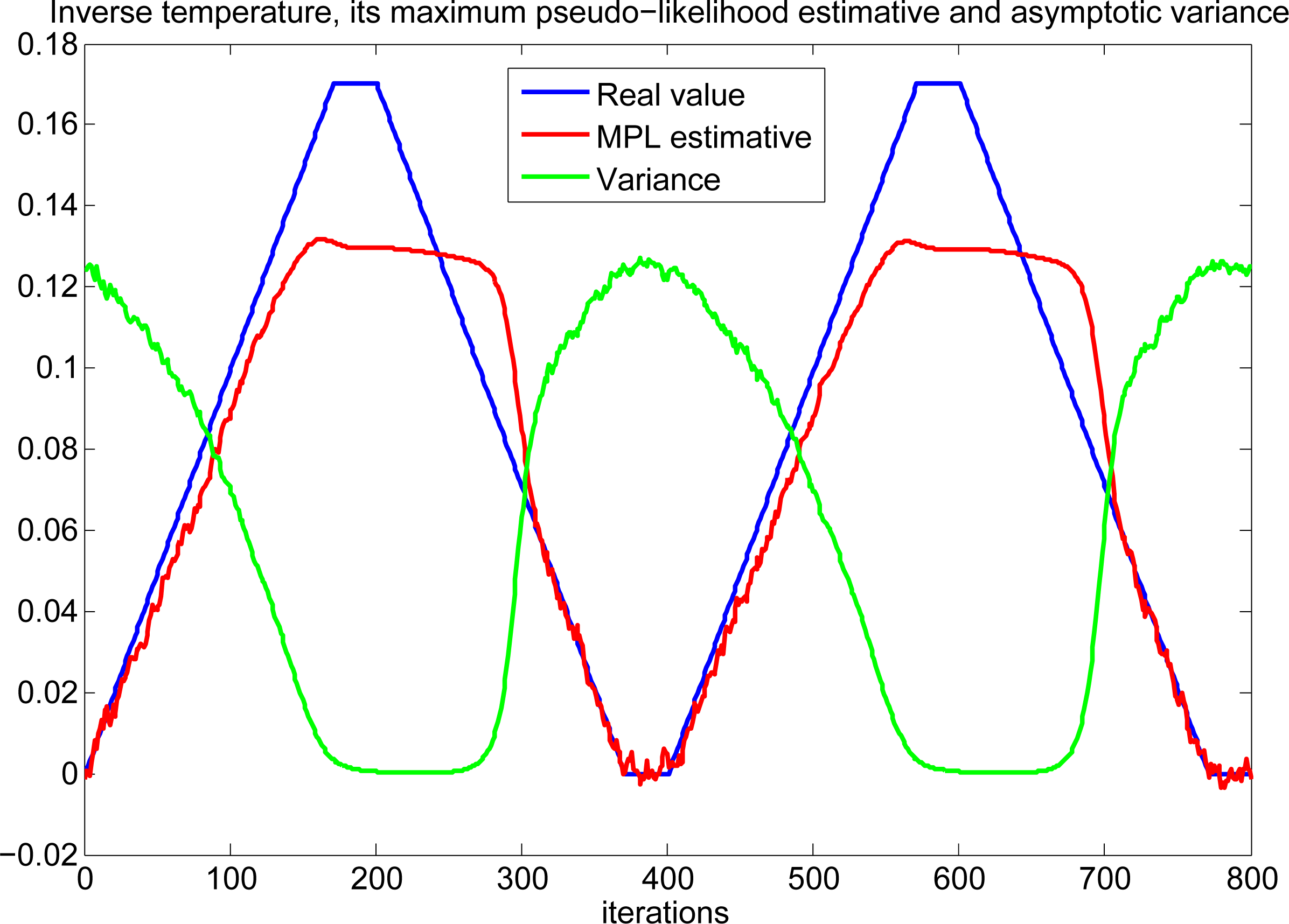
Figure 6 shows the real parameter values used to generate the GMRF outputs (blue line), the maximum pseudo-likelihood estimative used to calculate Φ β and Ψβ (red line) and also a plot of the asymptotic variances (uncertainty about the inverse temperature) along the entire MCMC simulation.
We now proceed to the analysis of the Shannon entropy of the system along the simulation. Despite showing a behavior similar to Ψβ, the range of values for entropy is significantly smaller. In this simulation, we observed that 0 ≤ Hβ ≤ 4.5, 0 ≤ Φ β ≤ 18 and 8 ≤ Ψβ ≤ 61. An interesting point is that knowledge of Φ β and Ψβ allows us to infer the entropy of the system. For example, looking at Figures 5 and 7, we can see that Φ β and Ψβ start to diverge a little bit earlier (t ≈80), then the entropy in a GMRF model begins to grow (t ≈ 120). Therefore, in an isotropic pairwise GMRF model, if the system is close to the information equilibrium condition, then Hβ is low, since there is little variability in the observed configuration patterns. When the difference between Φ β and Ψβ is large, Hβ increases.
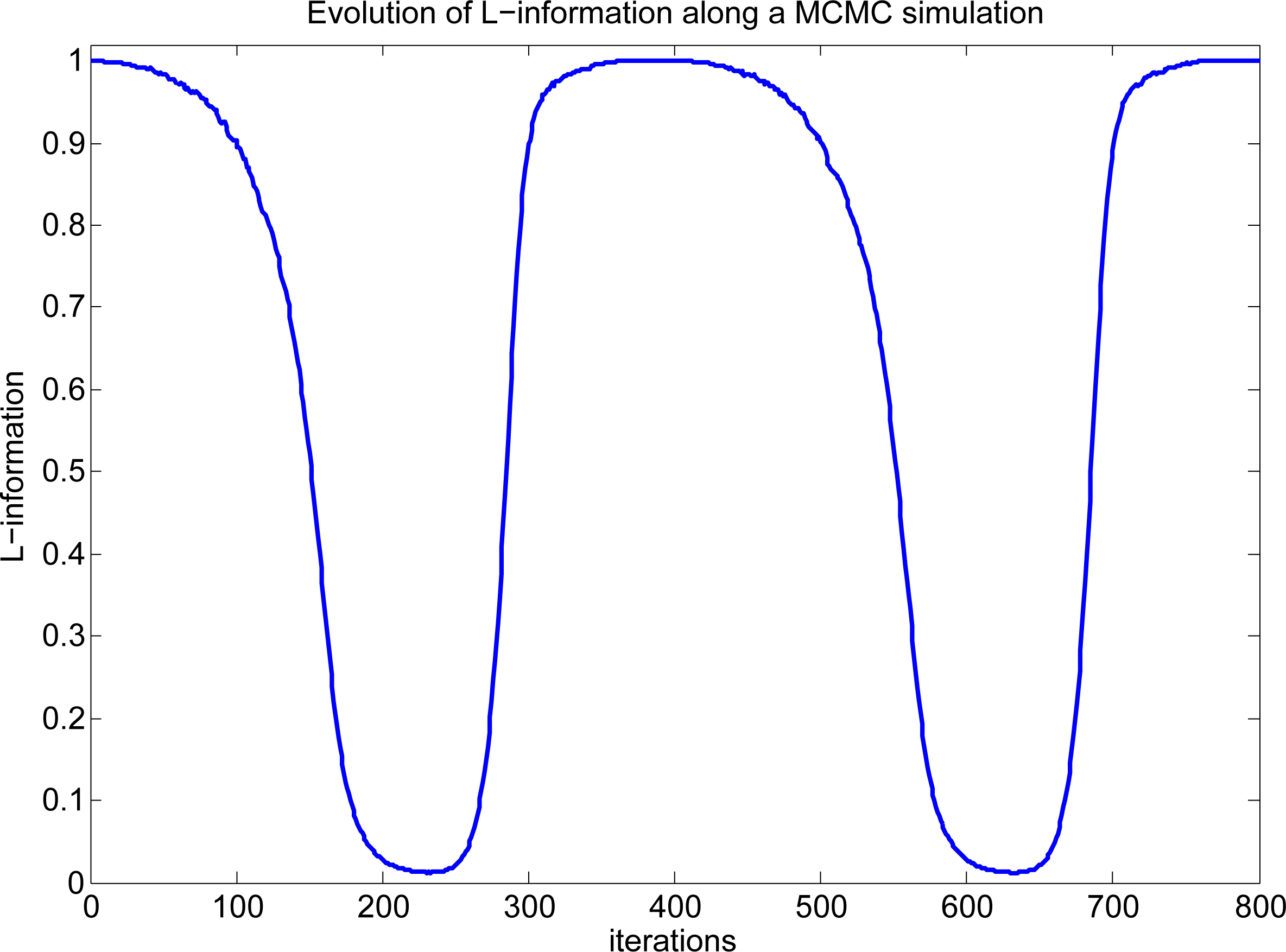
Another interesting global information-theoretic measure is L-information, from now on denoted by Lβ , since it conveys all the information about the likelihood function (in a GMRF model, only the first two derivatives of L(θ⃗; X(t)) are not null). Lβ is defined as the ratio between the two forms of expected Fisher information, Φ β and Ψβ. A nice property about this measure is that 0 ≤ Lβ ≤ 1. With this single measurement, it is possible to gain insights about the global system behavior. Figure 8 shows that a value close to one indicates a system approximating the information equilibrium condition, while a value close to zero indicates a system close to the maximum entropy condition (a stable configuration with boundaries and informative patterns).
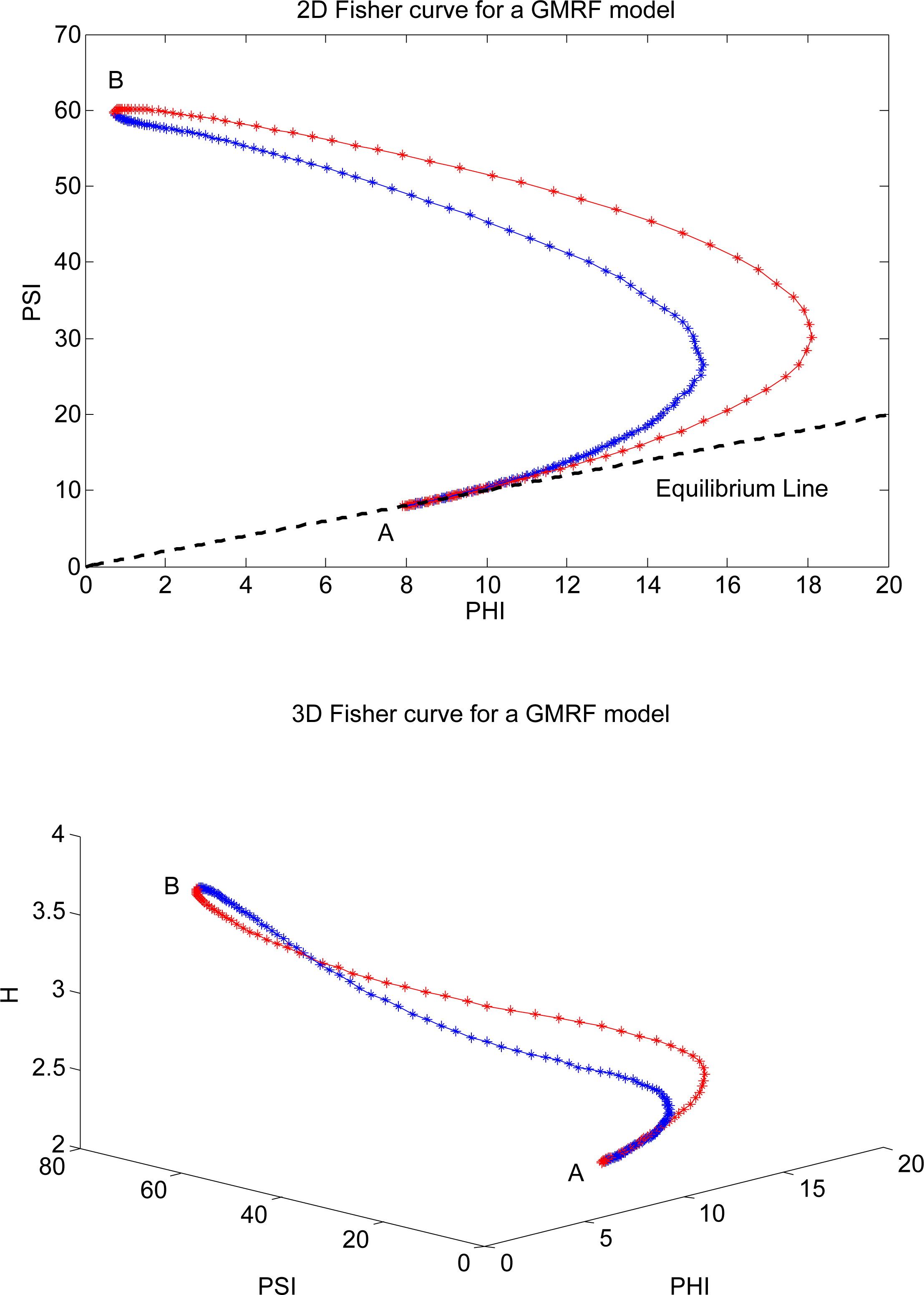
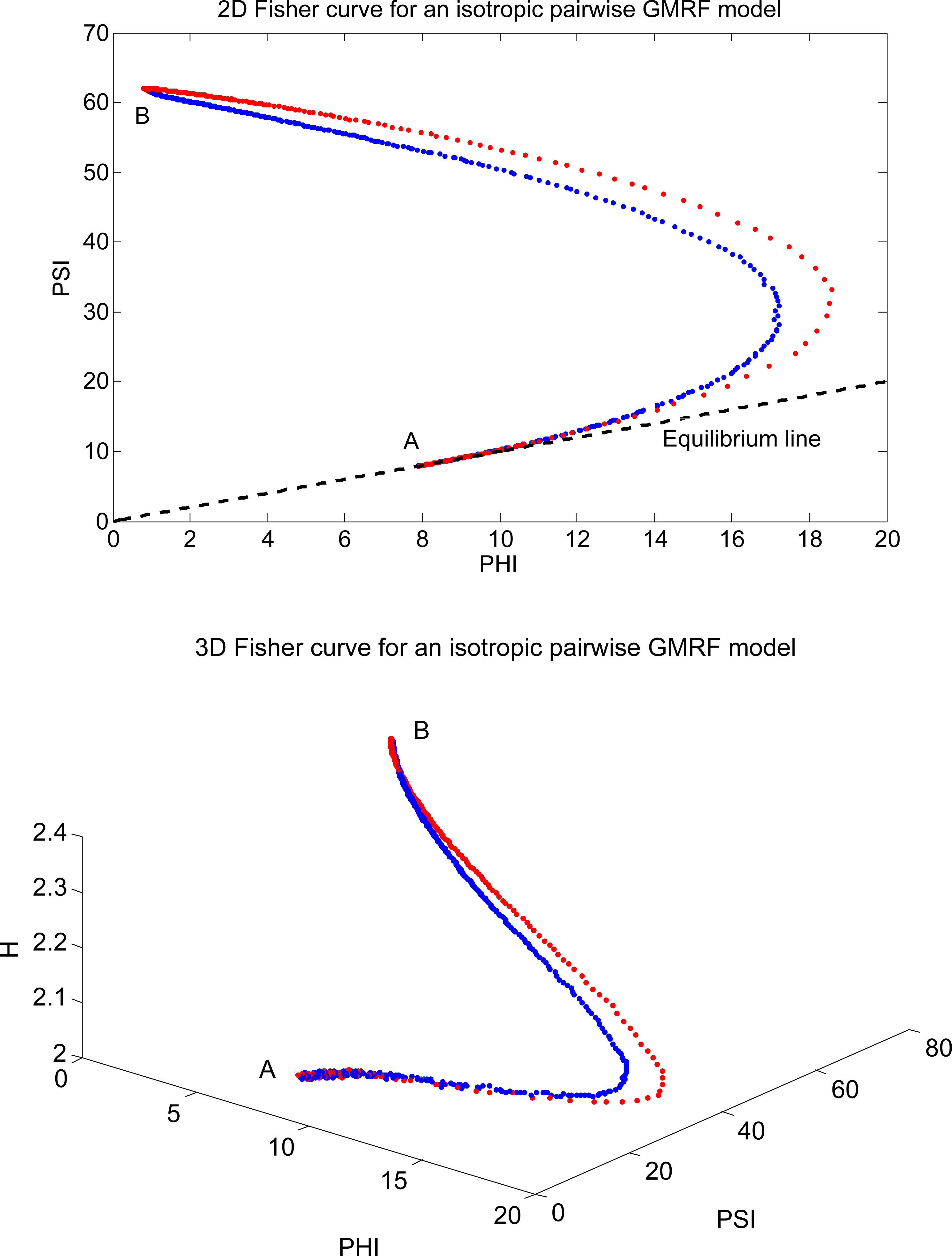
To investigate the intrinsic non-linear connection between Φ β, Ψβ and Hβ in a complex system modeled by an isotropic pairwise GMRF model, we now analyze its Fisher curves. The first curve, which is a planar one, is defined as F⃗ (β) = (Φ β, Ψβ), for A = βmin to B = βmax and shows how Fisher information changes when the inverse temperature of the system is modified to control the global behavior. Figure 9 shows the results. In the first image, the blue piece of the curve is the path from A to B, that is, , and the red piece is the inverse path (from B to A), that is, . We must emphasize that is the trajectory from a lower entropy global configuration to a higher entropy global configuration. On the other hand, when the system moves from B to A, we are moving towards entropy minimization. To make this clear, the second image of Figure 9 illustrates the same Fisher curve as before, but now in three dimensions, that is, F⃗ (β) = (Φ β, Ψβ, Hβ). For comparison purposes, Figure 10 shows the Fisher curves for another MCMC simulation with different parameter settings. Note that the shape of the curves are quite similar to those in Figure 9.
We can see that the majority of points along the Fisher curve is concentrated around two regions of high curvature: (A) around the information equilibrium condition (an absence of short-term and long-term correlations, since β = 0); and (B) around the maximum entropy value, where the divergence between the information values are maximum (self-organization emerges, since β is greater than a critical value, βc). The points that lie in the middle of the path connecting these two regions represent the system undergoing a phase transition. Its properties change rapidly and in an asymmetric way, since for a given natural orientation.
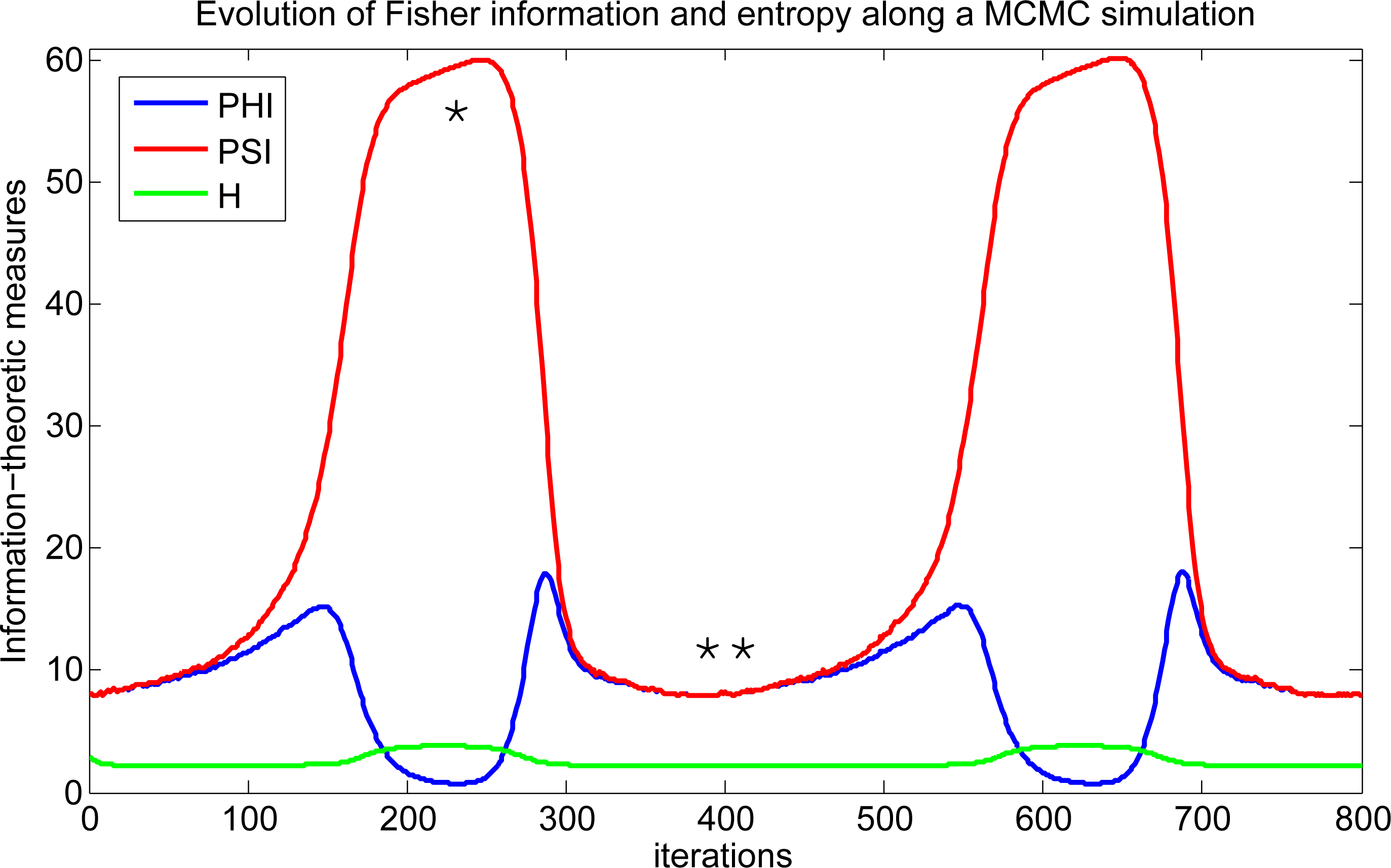
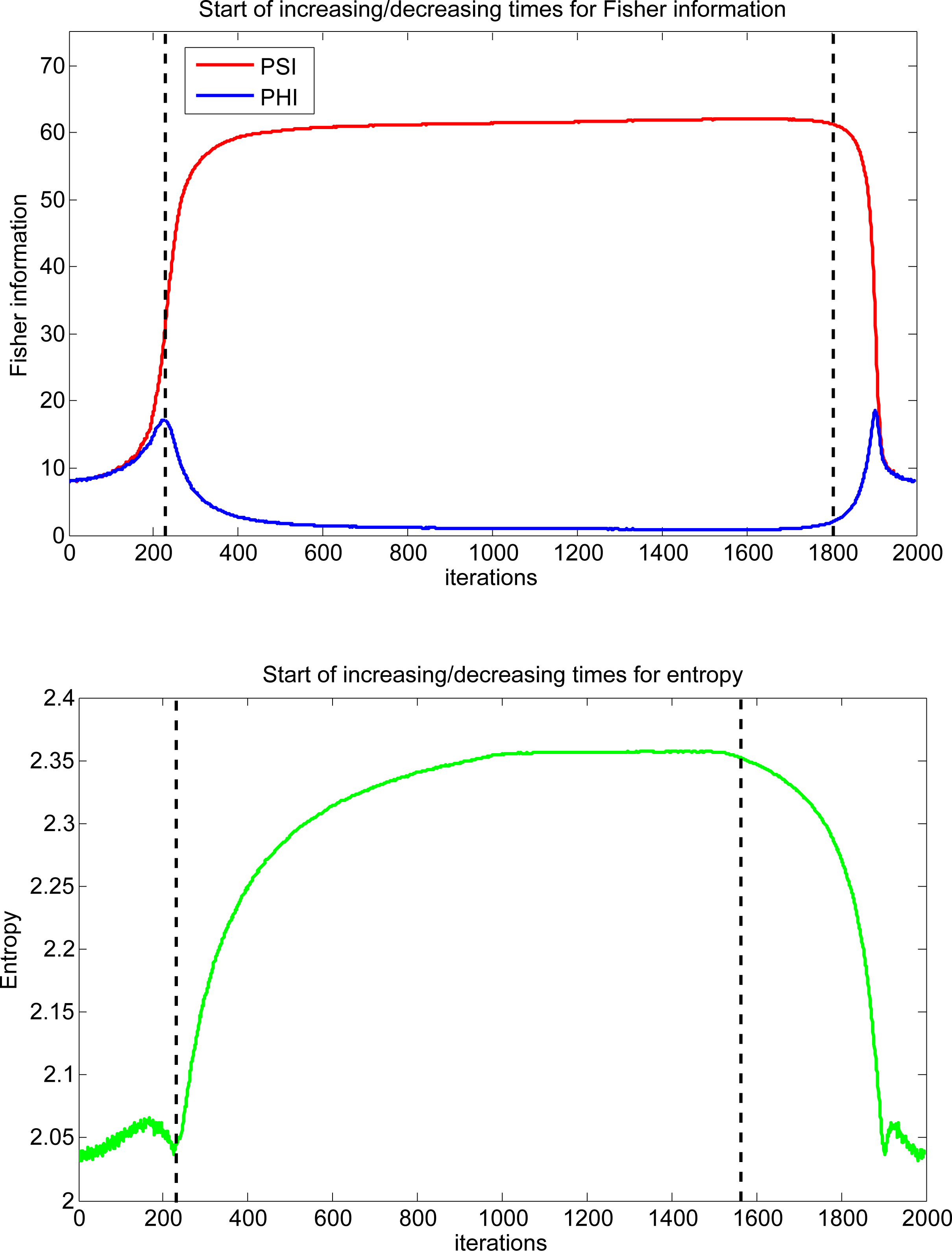
By now, some observations can be highlighted. First, the natural orientation of the Fisher curve defines the direction of time. The natural A–B path (increase in entropy) is given by the blue curve and the natural B–A path (decrease in entropy) is given by the red curve. In other words, the only possible way to walk from A to B (increase Hβ) by the red path or to walk from B to A (decrease Hβ) by the blue path would be moving back in time (by running the recorded simulation backwards). Eventually, we believe that a possible explanation for this fact could be that the deformation process that takes the original geometric structure (with constant curvature) of the usual Gaussian model (A) to the novel geometric structure of the isotropic pairwise GMRF model (B) is not reversible. In other words, the way the model is “curved” is not simply the reversal of the “flattering” process (when it is restored to its constant curvature form). Thus, even the basic notion of time seems to be deeply connected with the relationship between entropy and Fisher information in a complex system: in the natural orientation (forward in time), it seems that the divergence between Φ β and Ψβ is the cause of an increase in the entropy, and the decrease of entropy is the cause of the convergence of Φβ and Ψβ. During the experimental analysis, we repeated the MCMC simulations with different parameter settings, and the observed behavior for Fisher information and entropy was the same. Figure 11 shows the graphs of Φβ, Ψβ and Hβ for another recorded MCMC simulation. The results indicate that in the natural orientation (in the direction of time), an increase in Ψβ seems to be a trigger for an increase in the entropy and a decrease in the entropy seems to be a trigger for a decrease in Ψβ. Roughly speaking, Ψβ “pushes Hβ up” and Hβ “pushes Ψβ down”.
In summary, the central idea discussed here is that while entropy provides a measure of order/disorder of the system at a given configuration, X(t), Fisher information links these thermodynamical states through a path (Fisher curve). Thus, Fisher information is a powerful mathematical tool in the study of complex and dynamical systems, since it establishes how these different thermodynamical states are related along the evolution of the inverse temperature. Instead of knowing whether the entropy, Hβ, is increasing or decreasing, with Fisher information, it is possible to know how and why this change is happening.
7.2.1. The Effect of Induced Perturbations in the System
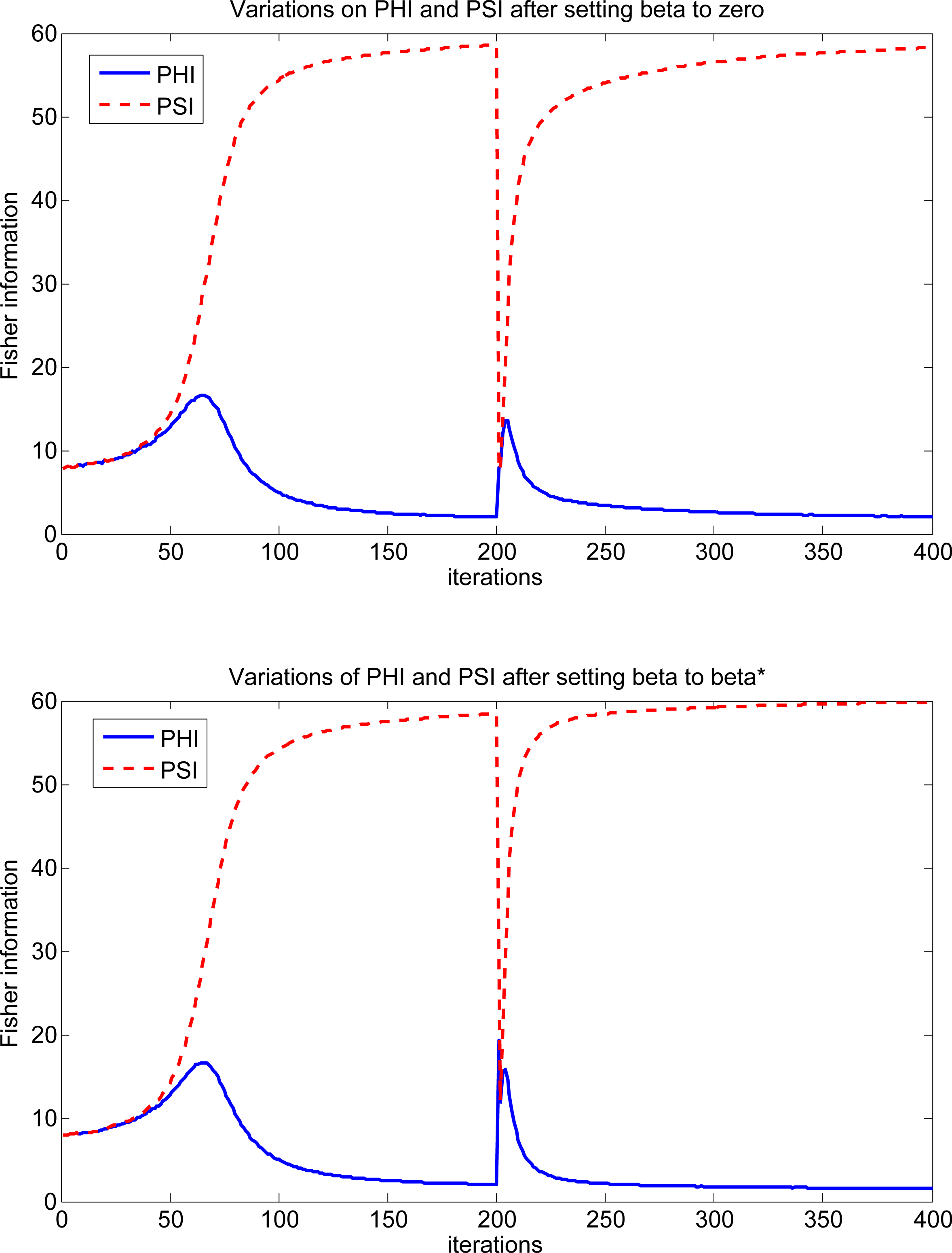
To test whether a system can recover part of its original configuration after a perturbation is induced, we conducted another computational experiment. During a stable simulation, two kinds of perturbations were induced in the system: (1) the value of the inverse temperature parameter was set to zero for the next consecutive two iterations; (2) the value of the inverse temperature parameter was set to the equilibrium value, β* (the solution of Equation 28), for the next consecutive two iterations. We should mention that in both cases, the original value of β is recovered after these two iterations are completed.
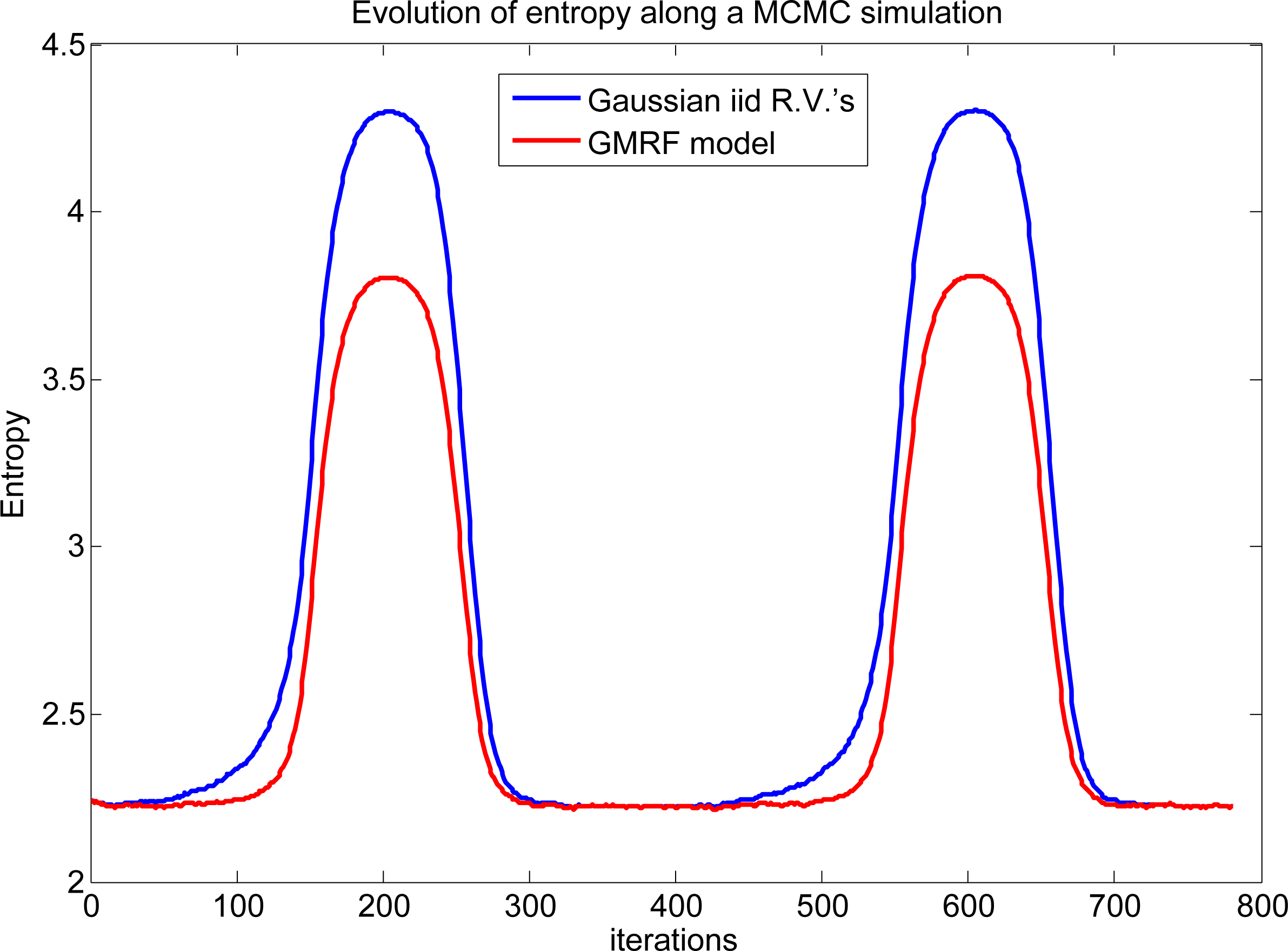
When the system is disturbed by setting β to zero, the simulations indicate that the system is not successful in recovering components from its previous stable configuration (note that Φβ and Ψβ clearly touch one another in the graph). When the same perturbation is induced, but using the smallest of the two β* values (minimum solution of Equation 28), after a short period of turbulence, the system can recover parts (components, clusters) of its previous stable state. This behavior suggests that this softer perturbation is not enough to remove all the information encoded within the spatial dependence structure of system, preserving some of the long-term correlations in data (stronger bonds), slightly remodeling the large clusters presented in the system. Figures 12 and 13 illustrate the results.
7.3. Considerations and Final Remarks
The goal of this section is to summarize the main results obtained in this paper, focusing on the interpretation of the Fisher curve of a system modeled by a GMRF. First, our system is initialized with a random configuration, simulating that in the moment of its creation, the temperature is infinite (β = 0). We observe two important things at this moment: (1) there is a perfect symmetry in information, since the equilibrium condition prevails, that is, Φ β = Ψβ; (2) the entropy of the system is minimal. By a mere convention, we name this initial state of minimal entropy, A.
By reducing the global temperature (β increases), this “universe” is deviating from this initial condition. As the system is drifted apart from the initial condition, we clearly see a break in the symmetry of information (Φ β diverges from Ψβ), which apparently is the cause for an increase in the system’s entropy, since this symmetry break seems to precede an increase in the entropy, H. This is a fundamental symmetry break, since other forms of ruptures that will happen in the future and will give rise to several properties of the system, including the basic notion of time as an irreversible process, follow from this first one. During this first stage of evolution, the system evolves to the condition of maximum entropy, named B.
Hence, after the break in the information equilibrium condition, there is a significant increase in the entropy as the system continues to evolve. This stage lasts while the temperature of the system is further reduced or kept established. When the temperature starts to increase (β decreases), another form of symmetry break takes place. By moving towards the initial condition (A) from B, changes in the entropy seem to precede changes in Fisher information (when moving from A to B, we observe exactly the opposite). Moreover, the variations in entropy and Fisher information towards A are not symmetric with the variations observed when we move towards B, a direct consequence of that first fundamental break of the information equilibrium condition. By continuing this process of increasing the temperature of the system until infinity (β is approaching zero), we take our system to a configuration that is equivalent to the initial condition, that is, where information equilibrium prevails.
This fundamental symmetry break becomes evident when we look at the Fisher curve of the system. We clearly see that the path from the state of minimum entropy, A, and the state of maximum entropy, B, defined by the curve, (the blue trajectory in Figure 9), is not the same as the path from B to A, defined by the curve, (the red trajectory in Figure 9). An implication of this behavior is that if the system is moving along the arrow of time, then we are moving through the Fisher curve in the clockwise orientation. Thus, the only way to go from A to B along (the red path) is going back in time.
Therefore, if that first fundamental symmetry break did not exist, or even if it had happened, but all the posterior evolution of Φ β, Ψβ, and Hβ were absolutely symmetric (i.e., the variations in these measures were exactly the same when moving from A to B and when moving from B to A), what we would actually see is that . As a consequence, to decrease/increase the system’s temperature would be like moving towards the future/past. In fact, the basic notion of time in that system would be compromised, since time would be a perfectly reversible process (just similar to a spatial dimension, in which we can move in both directions). In other words, we would not distinguish whether the system is moving forward or moving backwards in time.
8. Conclusions
The definition of what is information in a complex system is a fundamental concept in the study of many problems. In this paper, we discussed the roles of two important statistical measures in isotropic pairwise Markov random fields composed of Gaussian variables: Shannon entropy and Fisher information. By using the pseudo-likelihood function of the GMRF model, we derived analytical expressions for these measures. The definition of a Fisher curve as a geometric representation for the study and analysis of complex systems allowed us to reveal the intrinsic non-linear relation between these information-theoretic measures and gain insights about the behavior of such systems. Computational experiments demonstrate the effectiveness of the proposed tools in decoding information from the underlying spatial dependence structure of a Gaussian-Markov random field. Typical informative patterns in a complex systems are located in the boundaries of the clusters. One of the main conclusions of this scientific investigation concerns the notion of time in a complex system. The obtained results suggest that the relationship between Fisher information and entropy determines whether the system is moving forward or backward in time. Apparently, in the natural orientation (when the system is evolving forward in time), when β is growing, that is, the temperature of the system is reducing, an increase in Fisher information leads to an increase in the system’s entropy, and when β is reducing, that is the temperature of the system is growing, a decrease in the system’s entropy leads to a decrease in the Fisher information. In future works we expect to completely characterize the metric tensor that represents the geometric structure of the isotropic pairwise GMRF model by specifying all the elements of the Fisher information matrix. Future investigations should also include the definition and analysis of the proposed tools in other Markov random field models, such as the Ising and Potts pairwise interaction models. Besides, a topic of interest concerns the investigation of minimum and maximum information paths in graphs to explore intrinsic similarity measures between objects belonging to a common surface or manifold in ℜn. We believe this study could bring benefits to some pattern recognition and data analysis computational applications.
Acknowledgments
The author would like to thank CNPQ(Brazilian Council for Research and Development) for the financial support through research grant number 475054/2011-3.
Conflict of Interest
The authors declare no conflict of interest.
References
- Shannon, C.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, Chicago, IL & London, USA, 1949. [Google Scholar]
- Rényi, A. On measures of information and entropy. Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys 1988, 52, 479–487. [Google Scholar]
- Bashkirov, A. Rényi entropy as a statistical entropy for complex systems. Theor. Math. Phys 2006, 149, 1559–1573. [Google Scholar]
- Jaynes, E. Information theory and statistical mechanics. Phys. Rev 1957, 106, 620–630. [Google Scholar]
- Grad, H. The many faces of entropy. Comm. Pure. Appl. Math 1961, 14, 323–254. [Google Scholar]
- Adler, R.; Konheim, A.; McAndrew, A. Topological entropy. Trans. Am. Math. Soc 1965, 114, 309–319. [Google Scholar]
- Goodwyn, L. Comparing topological entropy with measure-theoretic entropy. Am. J. Math 1972, 94, 366–388. [Google Scholar]
- Samuelson, P.A. Maximum principles in analytical economics. Am. Econ. Rev 1972, 62, 249–262. [Google Scholar]
- Costa, M. Writing on dirty paper. IEEE T. Inform. Theory 1983, 29, 439–441. [Google Scholar]
- Dembo, A.; Cover, T.; Thomas, J. Information theoretic inequalities. IEEE T. Inform. Theory 1991, 37, 1501–1518. [Google Scholar]
- Cover, T.; Zhang, Z. On the maximum entropy of the sum of two dependent random variables. IEEE T. Inform. Theory 1994, 40, 1244–1246. [Google Scholar]
- Frieden, B.R. Science from Fisher Information: A Unification; Cambridge University Press: Cambridge, London, 2004. [Google Scholar]
- Frieden, B.R.; Gatenby, R.A. Exploratory Data Analysis Using Fisher Information; Springer: London, UK, 2006. [Google Scholar]
- Lehmann, E.L. Theory of Point Estimation; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Bickel, P.J. Mathematical Statistics; Holden Day: New York, NY, USA, 1991. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed; Duxbury: New York, NY, USA, 2002. [Google Scholar]
- Amari, S; Nagaoka, H. Methods of information geometry (Translations of mathematical monographs vol. 191; AMS Bookstore: Tokyo, Japan, 2000. [Google Scholar]
- Kass, R.E. The geometry of asymptotic inference. Stat. Sci 1989, 4, 188–234. [Google Scholar]
- Anandkumar, A.; Tong, L.; Swami, A. Detection of Gauss-Markov random fields with nearest-neighbor dependency. IEEE T. Inform. Theory 2009, 55, 816–827. [Google Scholar]
- Gómez-Villegas, M.A.; Main, P.; Susi, R. The effect of block parameter perturbations in Gaussian Bayesian networks: Sensitivity and robustness. Inform. Sci 2013, 222, 439–458. [Google Scholar]
- Moura, J.; Balram, N. Recursive structure of noncausal Gauss-Markov random fields. IEEE T. Inform. Theory 1992, 38, 334–354. [Google Scholar]
- Moura, J.; Goswami, S. Gauss-Markov random fields (GMrf) with continuous indices. IEEE Trans. Inform. Theory 1997, 43, 1560–1573. [Google Scholar]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. Roy. Stat. Soc. B Stat. Meth 1974, 36, 192–236. [Google Scholar]
- Besag, J. Statistical analysis of non-lattice data. The Statistician 1975, 24, 179–195. [Google Scholar]
- Hammersley, J.; Clifford, P. (University of California, Berkeley, Oxford and Bristol). Markov Field on Finite Graphs and Lattices. Unpublished work, 1971.
- Efron, B.F.; Hinkley, D.V. Assessing the accuracy of the ml estimator: Observed versus expected fisher information. Biometrika 1978, 65, 457–487. [Google Scholar]
- Isserlis, L. On a formula for the product-moment coefficient of any order of a normal frequency distribution in any number of variables. Biometrika 1918, 12, 134–139. [Google Scholar]
- Jensen, J.; Künsh, H. On asymptotic normality of pseudo likelihood estimates for pairwise interaction processes. Ann. Inst. Stat. Math 1994, 46, 475–486. [Google Scholar]
- Winkler, G. Image Analysis, Random Fields and Markov Chain Monte Carlo Methods: A Mathematical Introduction; Springer-Verlag New York, Inc: Secaucus, NJ, USA, 2006. [Google Scholar]
- Liang, G.; Yu, B. Maximum pseudo likelihood estimation in network tomography. IEEE T. Signal Proces 2003, 51, 2043–2053. [Google Scholar]




© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Levada, A. Learning from Complex Systems: On the Roles of Entropy and Fisher Information in Pairwise Isotropic Gaussian Markov Random Fields. Entropy 2014, 16, 1002-1036. https://doi.org/10.3390/e16021002
Levada A. Learning from Complex Systems: On the Roles of Entropy and Fisher Information in Pairwise Isotropic Gaussian Markov Random Fields. Entropy. 2014; 16(2):1002-1036. https://doi.org/10.3390/e16021002
Chicago/Turabian StyleLevada, Alexandre. 2014. "Learning from Complex Systems: On the Roles of Entropy and Fisher Information in Pairwise Isotropic Gaussian Markov Random Fields" Entropy 16, no. 2: 1002-1036. https://doi.org/10.3390/e16021002
APA StyleLevada, A. (2014). Learning from Complex Systems: On the Roles of Entropy and Fisher Information in Pairwise Isotropic Gaussian Markov Random Fields. Entropy, 16(2), 1002-1036. https://doi.org/10.3390/e16021002



