1. Introduction
The study of multiagent system (MAS) has attracted the interests of researchers from various fields for its potential application prospects in distributed computing, sensor networks and multi-robots system [
1–
4]. From the viewpoint of automatic control, consensus-oriented flocking and formation control of MAS are widely discussed in previous articles [
5–
9]. For all kinds of difficulties appearing in the multiagent system, complex networks involved in synchronization of MAS is among the most significant ones since it is relatively inconvenient to model the exact structure. As a consequence, several entropy measurements have been introduced into the area of multiagent control to describe the property of networks recently [
10–
12]. In addition, coordination methods are also proposed from entropy view with measurements depicting characteristics of the MAS [
13,
14]. Apart from the problems resulting from network, cooperative control of MAS depending on delayed information is also an extensively studied topic due to the inevitabilities of unreliable communication link, bandwidth limitation, packets loss and computing constraint [
15–
18]. In this case, in order to guarantee the consensus of the multiagent system, assumptions are usually made about the delays and conditions concerning the control parameters are derived at the same time. Furthermore, for multiagent system with discrete feedbacks, the designed controllers can only rely on sampled states data of agents and the input values are zero-order-hold during sampling instants. As a result, the dynamics of multiagent systems can be presented as discrete ones and the corresponding consensus analyses are also brought out in previous researches [
19–
22]. Most of the above mentioned consequences are acquired depending on Lyapunov theory and stochastic matrix theory. For example, in [
23], consensus of the system with communication delays is obtained based on the property of SIA (Stochastic, Indecomposable and Aperiodic) matrix. In [
24], the leader following consensus problem is solved taking use of Lyapunov-Krasovskii functional. Without any doubt, as two classic methods used in the field of MAS, both Lyapunov theory and stochastic matrix theory have their own advantages. Nevertheless, in order to apply the Lyapunov theory, it is always required that the adjacent matrix of communication graph is symmetric and the results obtained can hardly directly extended to the asymmetric situations. On the other hand, to implement results from stochastic matrix, system matrix needs to be nonnegative with row sum value of one. Efforts have been made to overcome these obstacles. In [
25], based on stochastic approximation, ergodicity approach is applied to prove mean square consensus for systems that the existing Lyapunov approaches cannot handle. Through establishing relations between consensus and ergodic backward products, an effective tool to solve consensus problems is proposed. In [
26], an auxiliary system is introduced and sophisticated transformations are made to make the consensus analysis more convenient. The requirement that rows of transition matrix are identical plays an important role in the proofs. Actually, it can be viewed as a modification of the unit row sum condition when states of the system, other than error states of the system, are discussed.
The aim of this paper is to provide a new method to study about the consensus problem of discrete multiagent system with consideration of practical constraints. First of all, sampling period of the multiagent system is assumed to be time varying. This is often the case for MAS with centralized feedback system such as the vision-based position feedback system for multiple small UAVs (Unmanned Aerial Vehicles) and ground vehicles teams guided by UAVs or satellites. In addition, information delay between two connected agents is formulated as combination of sending delay and receiving delay. With this kind of formulation, different causes of time delay are analyzed more clearly. Additionally, conditions about time delays are also discussed as two separated ones regarding sending delay and receiving delay respectively. Considering about the delayed system constructed as above, we propose a new idea to prove the consensus of multiagent systems consist of first-order discrete agent based on the Halanay inequality discussed in [
27]. In fact, researchers of multiagent system have begun to implement various inequality results from mathematics recently. For example, Gronwall-Bellman-Halanay type differential inequality has been applied in [
28] to handle the stochastic consensus seeking problem. In [
29], an improved Halanay inequality has been utilized for impulsive differential systems. In this paper, due to the similarity between the discrete multiagent system constructed and the Halanay inequality studied in [
27], results in [
27] are applied here to analyze the consensus of the multiagent system.
In addition, this paper further discusses situations where environmental disturbances exist in the feedback system. Here, environmental disturbances mainly indicate the influences of environment on sensors in measuring the states of agents. For example, ocean waves usually add disturbances on velocity and depth measurements of marine vehicles and light reflections will also impact the accuracy of vision-based localization for small UAVs mentioned above. As a consequence, the feedback states of agents in the system are corrupted. To better illustrate this problem, the definition of consensus error is proposed in this paper to describe the consensus state of the system. With the unstructured disturbances, the results in [
27] are not applicable anymore. To take care of this problem, the discrete Halanay inequality is first time extended into a more general one with asymptotical boundedness, as shown in Lemma 2 in Section 3. With the implementation of Lemma 2, it is proved that the consensus error of the multiagent system with environmental disturbances and time delays is still bounded.
The main contributions of this paper are as follows.
The introduction of Halanay inequality into the area of discrete multiagent system control with various delays. Comparing with Lyapunov dependent methods, the advantage of Halanay inequality lies in the easy extension of results from undirected graphs to directed graphs. At the same time, unlike the stochastic matrix theory, no row sum condition is necessary to guarantee the consensus by Halanay inequality. Even though the method proposed in this paper is preliminary and not capable of solving all kinds of consensus problems in multiagent systems, it can still be viewed as a supplement of traditional tools for situations where they can hardly be applied.
Extension of the discrete Halanay inequality into a more general one. With the extension, the obtained result is more suitable for complex problems with disturbances. It should also be noticed that the extension we have made is a fundamental one and the potential applications are not limited in multiagent systems.
The reminder of the paper is organized as follows. In Section 2, problem concerned in this paper is formulated. Then main results of this paper are presented in Section 3. At last, simulations are proposed to demonstrate the feasibility of the obtained results.
2. Problem Formulation
Consider a multiagent system consists of
n agents with discrete dynamics as below
where
xi(
k) ∈ ℝ indicates the state of agent
i,
k is the
kth update instant,
T(
k) is the sampling period between instant
k and
k + 1 with assumption that
denotes the control input of agent
i. In this paper, it is assumed that all agents are identical, that is, ∀
i ∈ {1, 2,⋯,
n},
pi =
p and
qi =
q. In addition, the states of all agents are scalars to avoid possible complexity in expression and all results obtained in this paper can be easily extended into multiple states agents with kronecker product.
Remark 1. From Equation (1), it is assumed that the sampling period of the whole system is time varying. Under this assumption, the obtained results can be applied to more general situations. Usually, for feedback systems based on sensors, the sampling period is determined by configurations and always fixed. However, for the situation where centralized feedback system is deployed, such as the vision-based position feedback of indoor multi-UAVs system, the sampling period maybe time-varying from time to time due to the computing time of the central server. For the multiagent system, the interactions among agents are modeled as a communication graph G(υ, ε) with vertex set υ = {1, 2,⋯, n} and edge set ε = {(j, i) : i, j ∈ ε} ⊂ υ × υ. If agent i can receive message from agent j, we have (i, j) ∈ ε and aij = 1. Adjacency matrix of the graph can be denoted as A = (aij)n×n and the neighbor set of agent i is Ni = {j ∈ υ : (i, j) ∈ ε}. A path in a graph is denoted as a sequence of ordered edges (i, i1), (i1, i2),⋯, (im, j) and if there is a path to i from any vertex in the graph, i is called a globally reachable vertex. Besides, diagonal matrix is defined as D = diag{d1, d2, ⋯, dn} with
. In the rest of this paper, it is assumed that the graph is connected and undirected.
Definition 1. The consensus of multiagent system consists of Equation (1) is reached if for any initial states of agents, there exists Denote a globally reachable agent in the system as agent
n, according to Definition 1, the consensus error of the MAS at instant
k is presented as ζ(
k) with definition
Based on the definition of consensus error, the bounded consensus of multiagent system is proposed in this paper to describe the situation where consensus cannot be reached.
Definition 2. The bounded consensus of multiagent system consists of Equation (1) is called achieved if there exist a constant C > 0,
that With the above Definitions, it can be concluded that the consensus of multiagent system can be viewed as a special case of bounded consensus with
C = 0. It should be noticed that in [
30], the definition of practical consensus is proposed to depict a similar consensus state for multiagent systems resulting from quantization effect. Even though there exist similarities, the bounded consensus defined in this paper is aiming at describing the situation where consensus of MAS is influenced by disturbances. For bounded consensus, it needs to prove that the consensus error of the system is bounded and the convergent set is influenced by bound of disturbance.
The purpose of this paper is to design the structure of control input
ui(
k) depending only on local information to reach consensus or bounded consensus for the multiagent system with consideration of various delays and disturbances. To solve the consensus problems proposed as above, the following control protocol is constructed at first
where,
αi and
βi are positive control parameters to be designed,
τ(
k) is bounded sending delay satisfying 1 ≤
τ(
k) ≤
r. In addition, with receiving delays
μ(
k) concerned in this paper, it should be noticed that shared information from neighbored agents will not be effective until agent
i receives it. As a result, the control input of agent
i should be revised as
where
and delay
μ(
k) satisfies 0 ≤
μ(
k) ≤
T (
k) − ∆
T. ∆
T > 0 is a constant value.
Remark 2. From the formulation process of the controller (6), the time delays between agents are formulated as combination of sending delay and receiving delay in this paper. Through dividing delays into two different parts, a more clear description about sources of delays is obtained. It is assumed that τ(
k) ≥ 1,
indicating that agents cannot instantly send the feedback data out to neighbors due to the limitation from system resources or structures. In addition, since the discrete systems are sampled-data dependent, τ(
k)
is an integer number. On the other hand, the receiving delay depicts the information delay between agents within one sampling period. From practical point of view, the kind of delay always results from instruments or transmissions. Combining two kinds of delays, the total information delay between two connected agents can be calculated as.
In previous researches, conditions about the total delay are usually discussed. With this kind of construction, we can analyze the influence of delays on the system with better clearness through considering the sending delay and receiving delay separately. In the next section, with the introduction of the Halanay inequality, main results of this paper are presented regarding the consensus and bounded consensus problem designed.
3. Main Results
Based on the control protocol
Equation (6), the dynamics of agent
i can be described as
Define
X(
k) = [
x1(
k),
x2(
k),⋯,
xn(
k)]
T,
P =
pIn and
Q =
qIn, the dynamics of multiagent system can be expressed in compact form as
where
Tα(
k) is a diagonal matrix with
ith diagonal item as
αi(
T(
k)−
μ(
k)), and
Tβ(
k) is a weighted adjacency matrix as
Since all the agents in the system have identical discrete dynamics, we can adopt the same controller gain for all agents as
αi =
α and
βi =
β. Considering about the consensus error defined as
(3), the state error vector of multiagent system can be presented as
with
ei(
k) =
xi(
k) −
xn(
k). According to the
Equation (8), the dynamics of error vector can be derived. Since the following relation exists
By calculating, we have
and
Further
where
C is related with the communication graph of whole system as
where
Dn−1 is the first
n − 1 rows and the first
n − 1 columns of matrix
D and A
n−1 has similar definitions.
is formed by the first
n − 1 items of
nth rows of matrix A.
MC ∈ R
1×(n−1) can also be calculated, the detailed structure of
MC is omitted here. Now, the discrete dynamics of state error vector
E(
k) can be obtained as follows
Based on Definition 1, the consensus problem of multiagent system is transformed into the stability problem of the multi-state system depicted as
Equation (14). Before introducing Theorem 1, the following lemma from [
27] is presented.
Lemma 1. Let 0 <
a(
n) ≤
Ma < 1, 0 <
b(
n) ≤ 1,
and let {
yn}
n≥−r be a sequence of real numbers satisfying the Halanay-type inequalitywhere, ∆
yn =
yn+1 −
yn If there exist positive constants Γ ∈
Z+,
and λ
l ∈ (0, 1)
such thatthen With Lemma 1, Theorem 1 can be presented as one of the main results of this paper.
Theorem 1. For multiagent system consist of agent with dynamics as Equation (1), with the control protocol designed as Equation (6) and assumptions made about the sending and receiving delays, the consensus of the system is guaranteed if following conditions are satisfied by proper choice of control parameters α and β. where, 0 < d0 < 1, λα(k) = |p − qα(T(k) − μ(k))|, λβ(k) = |p − qβ(T(k) − μ(k))| and λC = ║C║ is constant value for fixed communication graph.
Proof. According to
Equation (14), the error dynamics of multiagent system can be expressed as follows.
where, ║ · ║ indicates the 2-norm. With the definition of λ
α, λ
β and λ
C Define γ(
k) = ║E(
k)║, we have the Halanay-type inequality presented in Lemma 1 as below
From condition (
iii), we have
In addition, it is obvious that γ(
k −
τ) ≤ max{γ(
k), γ(
k − 1),⋯, γ(
k −
τ)} and with conditions (
i) and (
ii), Lemma 1 can be applied to prove that
Based on above inequality, it can be found that as n → ∞, γ(k) = 0. Considering about the definition of consensus error, that is ζ(k) = γ2(k), the consensus of the multiagent system is reached. Theorem 1 is proved.
Remark 3. During the discussion of Theorem 1, it can be concluded that one advantage of implementing the Halanay inequality in proving stability of the multiagent system is the avoidance of dependence on symmetry of communication graph. As a matter of fact, even though the communication graph is assumed to be connected and undirected, conditions (i–iii) in Theorem 1 are not dependent on this assumption.
Remark 4.
The existence of α and β satisfying conditions (i) and (ii) is actually decided by the dynamics of agents, receiving delay and communication graph together. Since the situations can vary from case to case, it is difficult to obtain general expressions for conditions of α and β. However, with particular dynamics of agents and communication graph, the values of α and β can be easily chosen according to definitions of λ
α and λ
β. Here, a typical situation where p > 0
and q > 0
is presented for a better illustration. According to conditions (i) and (ii), we haveandwith and.
Besides, Equations (20) and (21) also imply requirements for ∆
T as As for condition (iii), the value of r indicates the maximum sending delay tolerant by the system. During the implementation of Theorem 1, condition (iii) can be verified with chosen control parameters and r. For other situations, similar process can be carried out to decide values of α and β. □
In Theorem 1, we have proved that for the discrete system as
Equation (1) with control protocol
(5), the consensus of multiagent system can be obtained even though different kinds of delays are involved. However, in practical environment, not only delays critically influences the performance of system, but also the environmental disturbances that bring inaccuracy to feedback data will severely impair the consensus of the system. In the following part of this paper, we will further discuss about the situation where disturbances exist. In this case, the control protocol
(6) should be further revised as
where
δi(
k) and
δj(
k −
τ(
k)) denote bounded state disturbances of agent
i and
j respectively. Due to the uncertainty of disturbance,
δj(
k −
τ(
k)) can also be presented as
δj(
k). Based on the protocol, the dynamics of the multiagent system can be presented as
where
Tδ =
Tα(
k) −
Tβ(
k) and Ξ(
k) = [
δ1(
k),
δ2(
k),⋯,
δn (
k)]
T. The error dynamics of the system should be revised as
where Λ(
k) = [
δ1(
k) −
δn(
k),⋯,
δn−1(
k) −
δn (
k)]
T.
Due to the existence of state disturbances, the discrete error dynamics of the MAS is presented as
Equation (25). It can be found that Lemma 1 can no longer be directly used to prove the consensus of the system. In fact, the consensus of multiagent system defined in Definition 1 can no longer be obtained. In this case, the concept of bounded consensus proposed in Definition 2 is used to describe the performance of the control protocol under environmental disturbances. In order to prove the bounded consensus of the system, the Halanay inequality in Lemma 1 should be extended into a more general case with consideration of disturbances. As a result, Lemma 2 is proposed as follows. Comparing with Lemma 1, a positive value c is added in the Halanay inequality to make the obtained result capable of handling the bounded consensus problem.
Lemma 2. Let 0 <
a(
n) ≤
Ma < 1, 0 <
b(
n) ≤ 1,
c ≥ 0
and let {
zn}
n≥−r be a sequence of real numbers satisfying the inequality If there exist two constant Γ ϵ Z
+ and 0 < λ
l < 1
such thatwhere,
thenwherewhere ϵ = 1 −
a +
κb with a = min{
a(
i)},
b = max{
b(
i)},
i ϵ {1, 2,⋯,
n},
and ρ > 1.
Proof. Define an auxiliary system as below
We can assume that there is a
n1 ≥ 0 such that
zs =
ys,
s ∊ {
n1,
n1 − 1, …,
n1 −
r}, then
Define another auxiliary system
By iterative computation, we have
where
Using
(27) and noting 1 − a(
i) + κb(
i) ≤ 1 + κ, we obtain that
Define variables
ψ0 and
ω as
where
ε is a positive integer satisfying
Then
ψ can be presented as
ψ0 and
ω have the following relations
This together with
(33), we have
Since
zn ≤
yn for
n >
n1,
Based on Lemma 2, Theorem 2 can be proposed as follows.
Theorem 2. For multiagent system consist of agents with dynamics as Equation (1), with the control protocol presented as Equation (23) and conditions assumed in Theorem 1, the bounded consensus of the system is guaranteed. Proof. According to
Equation (25), similar as the proof in Theorem 1, we have
where λ
δ = λ
α+λ
β. It is obviously that above equation can satisfy the condition of Lemma2 with Γ = 1. Since the environmental disturbances concerned are bounded, the value of
ω = sup
k→∞{λ
δλ
C║Λ(
k)║} is also bounded. As a consequence, the boundedness of the multiagent system is guaranteed. And the bound of consensus error can be calculated as
Theorem 2 is proved. □
4. Simulations
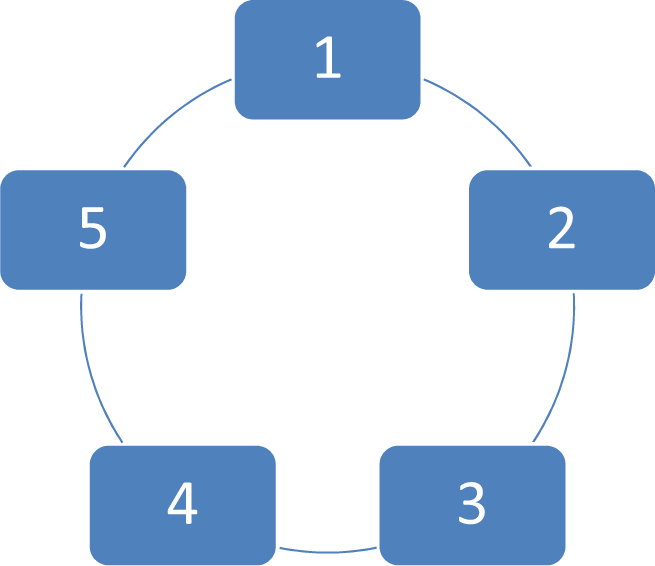
In this section, examples are given to illustrate the effectiveness of results obtained in this paper. A multiagent system consists of five identical agents is concerned with
a = 1.1,
b = 2. The communication graph among agents can be depicted as
Figure 1. In both examples, we assume that
T(
k) = 0.5 for simplicity. The receiving delay is supposed to be 0.2 ≤
μ(
k) ≤ 0.3 and the sending delay
τ(
k) is randomly chosen from {1, 2}, that is,
r = 2. With the choice of control parameters
α = 0.5 and
β = 0.1, it can be verified that all conditions in Theorem 1 can be satisfied.
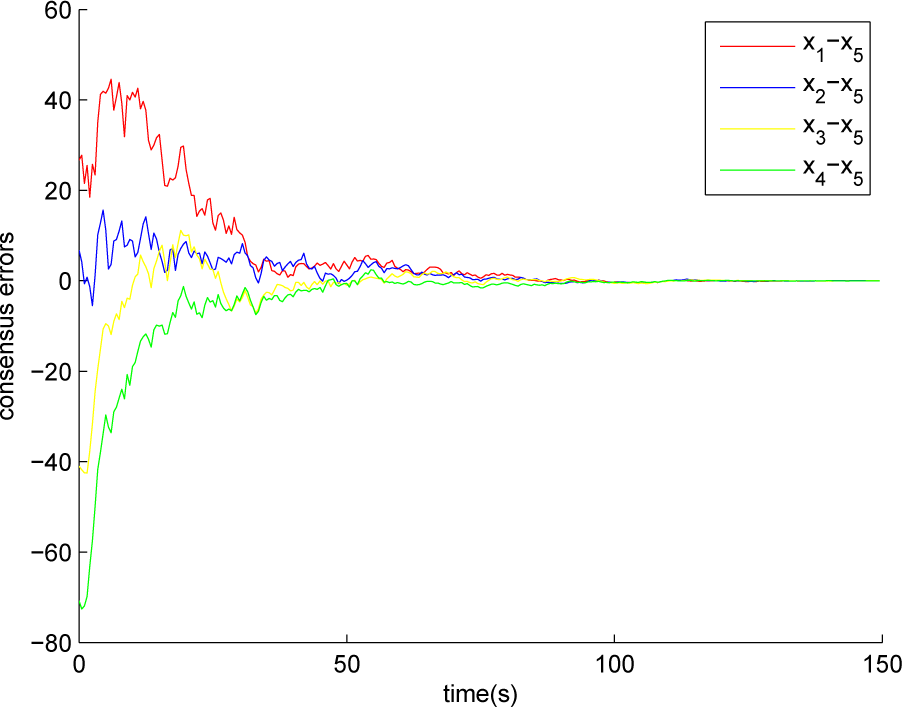
The simulation result is shown in
Figure 2 without consideration of disturbances, it is obvious that as time goes to infinity, the consensus error of the system converges to zero. In
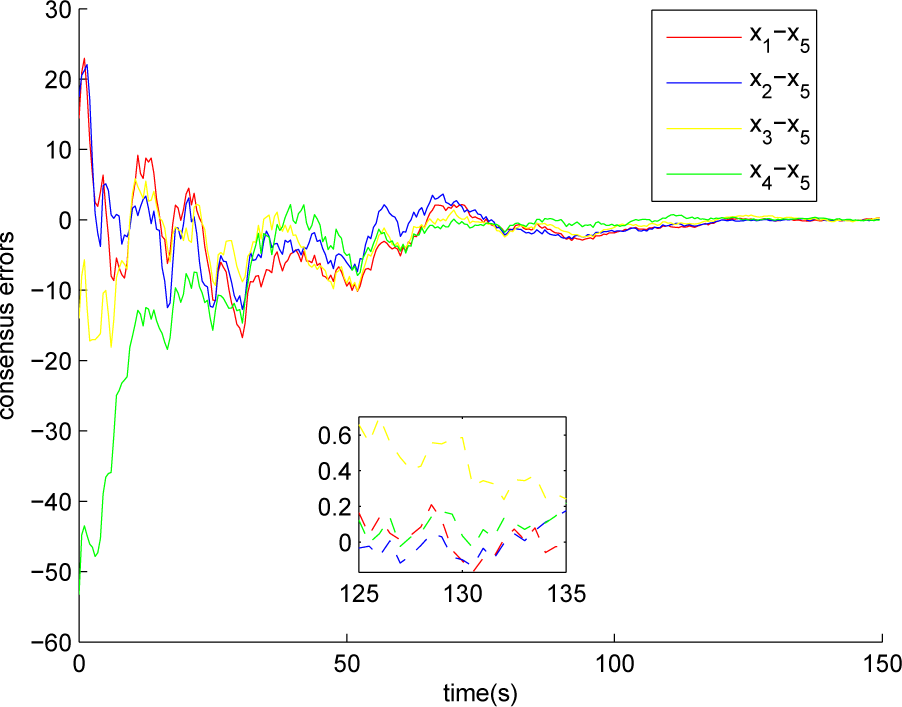
Figure 3, it is assumed that there are environmental disturbances
δ(
k) in all feedback links and the disturbances are chosen from [−0.5 0.5]. From the simulation results, it can be concluded that the consensus error of the multiagent system is still bounded.
In the simulations, we assume the communication graph is connected and undirected. In fact, from the derivation of the theorems, it is known that as long as the strong connectivity of graph is guaranteed, similar results can also be reached with directed communication links according to the same process of proof in this paper. In addition, from Lemma 1 and Lemma 2, it is known that conditions proposed in Theorem 1 are relative conservative. In the future studies, more strict conditions will be derived with consideration of more complex agent dynamics and switching communication graphs.