Abstract
Certain fluctuations in particle number, n, at fixed total energy, E, lead exactly to a cut-power law distribution in the one-particle energy, ω, via the induced fluctuations in the phase-space volume ratio, Ωn(E − ω)/Ωn(E) = (1 − ω/E)n. The only parameters are 1/T = ⟨β⟩ = ⟨n⟩/E and q = 1−1/⟨n⟩ +Δn2/⟨n⟩2. For the binomial distribution of n one obtains q = 1−1/k, for the negative binomial q = 1+1/(k+1). These results also represent an approximation for general particle number distributions in the reservoir up to second order in the canonical expansion ω ≪ E. For general systems the average phase-space volume ratio ⟨eS(E−ω)/eS(E)⟩ to second order delivers q = 1−1/C +Δβ2/⟨β⟩2 with β = S′(E) and C = dE/dT heat capacity. However, q ≠ 1 leads to non-additivity of the Boltzmann–Gibbs entropy, S. We demonstrate that a deformed entropy, K(S), can be constructed and used for demanding additivity, i.e., qK = 1. This requirement leads to a second order differential equation for K(S). Finally, the generalized q-entropy formula, K(S) = ∑piK(− ln pi), contains the Tsallis, Rényi and Boltzmann–Gibbs–Shannon expressions as particular cases. For diverging variance, Δβ2 we obtain a novel entropy formula.
1. Introduction
We have been studying generalizations of the Boltzmann–Gibbs–Shannon (BGS) entropy formula [1–6] since decades. Our studies included the investigation of the role of multiplicative noise [7,8], kinetic theory [9–11], non-extensive equilibration [12–14] and thermodynamical compatibility [15–18], also with respect to infinite repetitions of abstract composition rules [19]. Recently, in the quest for mechanisms explaining the occurence of a statistical power law distribution in canonical ensembles, we emphasized the role of finite reservoir effects in the mathematical derivation [20–23]. The majority attitude to nonextensive physics is in general to start with the presentation of a formula for the entropy and then deriving mathematical relations from it, in order to demonstrate that the traditional requirements, like concavity, unique equilibrium state or the Lagrange multiplier handling of secondary constraints, are fulfilled as well as in the original approach [24–28]. Comparisons to experimental data then usually supplement the results of such investigations [29–31].
Our present approach reveals a different path: We start with the traditional postulates and formulas, and then try to show why and how a “deformation” of the original classical BGS entropy formula becomes unavoidable. As a by-product of such a procedure we obtain the physical background interpretation for the parameters T and q, characterizing the ubiquitous cut power law probability distribution. In the limit q = 1 the BGS framework is reconstructed [17,28,32,33].
As we shall demonstrate below, the common physical cause of q ≠ 1 is the finiteness of the physical environment, a finite heat bath [22,32,34–36]. Whether the finite size corrections may become negligible is a case by case problem, entangled with the physical properties of the system under study. Some systems, called “non-extensive”, may behave as finite ones in this respect even in large volumes—since some effects behind q ≠ 1 depend on ratios of large quantities [6]. To gain a feeling about the magnitude of such effects we remind that besides the Avogadro number O (1024), considered in classical thermodynamics of atomic matter, complex networks, like, e.g., the human brain include about the square root of this number of elements O (1012). The internet contains approximately 107 hubs and 1010 connections. On the other hand a relativistic heavy ion collision produces a fireball of several O (103) new hadrons (strongly interacting particles), while in a more elementary pp collision about O (10) particles are detected[37–39]. Since one expects that the relative (scaled) fluctuations grow with the decreasing number of participants, it is evident that the high energy physics experiments are able to reveal finite reservoir effects quantitatively [21,22,26,27,33,40–45].
In this paper we seek answer to the following two questions: (i) What is the physics behind q ≠ 1 and (ii) what K(S) deformation of the entropy S is necessary to achieve qK = 1? We note that q = 1 signalizes an additive composition rule, so the second question is equivalent for seeking an additive (“K-additive”) description in case of non-negligible finite size corrections on the classical thermodynamics [16,18,22].
However, before going into the details, we would like to present our particular view on (non-)extensivity and (non-)additivity. The cut power-law formula as a form approaching the exponential in a given limit has already been established by Euler,
Therefore, any time when seeking to establish a physical model of almost thermally behaving (complex) systems finite size effects already induce a deviation from the exponential law. It is known that the ideal gas, with a fixed finite number of particles and therefore with a fixed heat capacity, leads to a cut power-law distribution in the single particle energy in a microcanonical treatment [20]. Also, a nice example of superstatistics, given by Beck, refers to a distribution of the sum of the squares of random Gaussian variables (e.g., the classical kinetic energy sum for a finite number of particles) as being Euler Gamma distributed for a finite number of variables [17,46,47]. While the product formula of the cut power-law requires a non-additivity of its arguments,
it does not mean non-extensivity. The latter can be established only then if in the large system size limit, in this example in the n → ∞ limit, the non-additivity of the arguments still holds. The distinction between non-additivity and non-extensivity is important, as it has been emphasized in [5,6]. In the physical models, we shall be discussing in this paper, we leave the question of this limit open and seek for general solutions and approximations valid both for finite non-additive and for infinite non-extensive systems. This classification scheme approach then should be specialized case by case, and the large system limits has to be considered in particular applications.
2. Finite Heat Bath and Fluctuation Effects
In this section we review the traditional, Boltzmann–Gibbs–Planck–Einstein thermodynamical approach to the thermodynamical statistical weight assuming a uniform phase-space distribution of microstates [48]. At the beginning we present a very simple model of particle production, where the total energy, E, is fixed (in experiments ΔE/E ≲ 10−3), but the number of produced particles, n, fluctuates appreciably. Its distribution will be considered first in terms of the simplest possible assumptions about combining occupied and unoccupied phase-space cells in a finite observed section of the available total phase-space. Following this analysis more general n distributions and finally a general heat bath, described by its equation of state, S(E), is considered. During this chain of models we seek answer for the question: What is the physics behind the parameter q ?
Our starting point is an ideal gas in a finite phase-space [20,30,36,48]. We describe the microcanonical statistical weight for having a one-particle energy, ω, out of total energy, E. In a one-dimensional relativistic jet it is distributed according to the ratio of corresponding phase-space volumes as
Here Ωn+1(E) is the total phase-space, while Ωn(E−ω) is the phase-space for the reservoir, missing one particle with energy ω. The number of particles, n, itself can have a distribution (based on the physical model of the reservoir and on the event by event detection of the spectra).
However, already by fixed n and E the statistical weight formula for such an ideal gas (the factor besides ρ(ω) in the above formula),
represents a finite size (microcanonical) approach to the Euler exponential. Only in the large number, large energy limit, n → ∞, and E → ∞, while the ratio is kept constant according to an equipartition law, E = nT, does it approach the traditional canonical exponential
Non-extensive systems must undermine (or circumvent) this basic correspondence. Either the scaling in the equipartition law is different, or the cut power law is deformed, or the large n limit is effectively never achieved; e.g., because of some irregular fluctuation properties of the quantity n or E.
We consider now the fluctuation of n by fixed E in statistically ideal reservoirs. In the case of hadronization in high energy physics experiments n is distributed according to a negative binomial n-distribution, obtained from the following, statistically simplest argumentation. We distribute n particles among k cells: bosons in
ways, fermions in
ways. By observation we detect a subspace (n, k) out of a bigger (N, K) reservoir. The limit K → ∞, N → ∞ with a fixed average occupancy f = N/K, constitutes the traditional canonical limit. However, we keep here several finite size factors. We obtain
for bosons and
for fermions.
Since most hadrons produced in high-energy experiments are pions, which are bosons, we consider first the bosonic reservoir described by Bn,k(f). The average statistical weight factor, wE(ω), with fixed E and the negative binomial distribution (NBD) of n becomes
Note that ⟨n⟩= (k + 1)f for NBD. Then with the notation T = E/⟨n⟩ and
we get
This is exactly a q > 1 Tsallis–Pareto distribution. The opposite correspondence, namely that an assumed Tsallis–Pareto distribution leads to an NBD multiplicity distribution, has been pointed out by Wilk and Wlodarczyk [27,28,49]. Experimental NBD distributions of total charged hadron multiplicites stemming from Au + Au collisons at
and 200 GeV can be inspected, e.g., in reference [37]. Characteristically k ≈ 10 – 20, therefore q ≈ 1.05 – 1.10, which roughly agrees with fits to pT spectra in the same experiments [37–39].
For a fermionic reservoir n is distributed according to the Bernoulli distribution (BD). The average phase-space volume ratio becomes
Note that ⟨n⟩ = kf for BD. Then with T = E/⟨n⟩ and
we obtain exactly a q < 1 Tsallis–Pareto distribution,
It is enlightening to consider the Boltzmann–Gibbs limit of the above. In case of low occupancy in the phase-space, k ≫ n and both the BD and NBD distributions approach a Poissonian:
The resulting statistical factor is exactly the Boltzmann–Gibbs exponential with T = E/⟨n⟩,
In all of the three above cases the parameter T is defined by the (one-dimensional, extreme relativistic) equipartition, and q is related to the scaled variance of the produced particle number:
For general n-fluctuations, Pn, not necessarily BD or NBD or Poissonian ones, the above result also applies, albeit only as an approximation. In the above detailed philosophy of the microcanonical approaching the canonical for large systems, we expand our formulas for ω ≪ E. The Tsallis–Pareto distribution as an approximation reads as
The ideal reservoir phase-space ratio up to second order in this limit results in
Comparing the corresponding coefficients one concludes that Equation (13) as an approximation holds also for a general n-distribution, and the “non-extensivity parameter” q is related to the second order subleading term.
Finally, we deal with a general environment, given by its equation of state, S(E). In the expansion for E ≫ ω the phase-space volume ratio becomes
Comparing it with the expansion of the Tsallis–Pareto distribution, Equation (14), one concludes
This is the final interpretation of the parameters T and q for a general reservoir in the framework of the Einstein postulate averaged over reservoir fluctuations. Later, in the next chapter, we shall aim to construct an additive deformed entropy, K(S), which renders not only the form (15), but also the more general form (16) to be multiplicative. Note that due to ⟨S″(E)⟩ = −1/CT2, our result is expressed via the heat capacity of the reservoir, defined as 1/C = dT/dE. In general we have opposite sign contributions from ⟨S′2⟩ − ⟨S′⟩2 and from ⟨S″⟩. In the light of this result one realizes that
- q > 1 and q < 1 are both possible,
- for any relative variance it is exactly q = 1,
- and for fixed E ∝ n/β we have Δβ/⟨β⟩ = Δn/⟨n⟩.
At the end of this section we sketch the relation of our approach to superstatistics[46,47,50–52]. In its original formulation superstatistics dealt with fluctuations of the Lagrange multiplier β. Demanding that we describe the same non-exponential statistics, only in two different ways, one arrives at the relation
Note that
. Using now the Taylor series of the first exponential one obtains
The converting factor is a Poissonian with the parameter
. Inverting the above procedure one seeks for a superstatistics from the n-distribution. Applying the correspondence Equation (18) for ω = E:
Inverse Laplace transformation then, in principle, delivers the superstatistical factor
Expanding for E ≫ ω, however, one gets ⟨β⟩ = ⟨n⟩/E and ⟨β2⟩ = ⟨n(n − 1)⟩/E2, leading to
One immediately realizes that for some n-distributions, alike the BD, Δβ2 would have to be negative. It is impossible. This problem is also reflected in the fact that there is no guarantee that an inverse Laplace transformation results in an overall positive function. In this way the superstatistics due to n-fluctuations, Pn(E), seems to be more general, than the approach with solely a β-distribution, γ(β). In particular a superstatistical β-distribution cannot ever match a q < 1 result.
3. Deformation of the Entropy
Once we understood how and why finite reservoir effects lead to q ≠ 1, and emerging from this to a non-exponential statistical weight, the need for mending this salient feature arises. Generalizing the Boltzmann–Gibbs exponential to another formula, containing finite reservoir corrections, also abandons the remarkable basic property of the exponential: the additivity of the arguments by the product. Since this property connected the dynamical independence (energy additivity) with the statistical independence (probability factorization or equivalently entropy additivity), its missing is a severe conundrum.
In this section we show that if the original logarithmic definition due to Boltzmann or equivalently its exponential inverse due to Einstein, postulating the phase-space volume to be proportional to the exponential of the entropy, fails to some degree, then one may search for another expression of the entropy, K(S), in order to restore “K-additivity”. We comprise our quest into the simple question: If S leads to q ≠ 1, what K(S) achieves qK = 1?
3.1. The Additive Entropy K(S)
We call “deformed entropy” the quantity K(S), being additive while S was non-additive. In the basic postulate we use K(S) instead of S in the exponential in order to gain more flexibility for handling the subleading terms in the E ≫ ω expansion discussed above and shown to interpret the parameter q. It has been already realized that in the non-extensive statistical physics the product formula inherent in the Einstein postulate can only be viewed as a deformed exponential of a q-summed expression of the entropy [53]. We have shown [16] that such deformed addition rules and deformed functions satisfy the zeroth law of thermodynamics only then if one uses a K(S) function of the original entropy variable, add these, and considers the inverse K-function of the result. In this manner we consider
Note that
and
. Now we compare this expression with the Tsallis–Pareto power-law. Using previous average notations and assuming that K(S) is independent of the reservoir fluctuations (a certain universality) one obtains:
By choosing a particular K(S) we shall manipulate qK. In order to simplify the differential equation posed on K(S) by requiring a given value for qK we introduce the notations F = 1/K′ = TK/T and Δβ2/⟨β⟩2 = λ/C. Then the qK parameter for the K(S) entropy is expressed as
Re-arranged this represents a very simple differential equation with q = 1 + (λ − 1)/C:
From this form it is easy to realize that two special choices are worth to be considered: qK = q and qK = 1. Since we seek for entropy deformations with the property K(0) = 0 and K′ (0) = 1, one fixes the condition F(0) = 1. In this case the only solution for qK= q is F = 1, K(S) = S. It is obvious that the other choice, qK = 1, is the only purposeful deformation for reaching K-additivity [16,18]. Equation (26) becomes then easily solvable. We call this form of the qK = 1 requirement the “Additivity Restoration Condition” (ARC):
3.2. Classification by Fluctuation Models
qK = 1 also means a re-exponentialization of the ω-expansion of the statistical weight based on the deformed entropy phase-space,
. In this way the effective equilibrium condition, the common temperature, least depends on the one-particle subsystem energy, ω. In earlier publications we called this the “Universal Thermostat Independence” (UTI) principle [22].
Now we explore the solutions of the ARC Equation (27) under different assumptions about the heat capacity and the reservoir fluctuations. In the simplest case we do not consider reservoir fluctuations at all, we put Δβ2 = 0 and therefore λ = 0. Applying our previous general result for this value we have to solve
Replacing back the definition F = 1/K′, one arrives at the original UTI equation [22]:
For ideal gas C = 1/(1 − q) is constant, and the solution of Equation (29) with K(0) = 0, K′(0) = 1 delivers [20,32,35]
From this result one arrives upon using K(S) = ∑ipiK(−ln pi) at the statistical entropy formulas of Tsallis and Rényi: [1–4,6]
Next we obtain the deformed entropy formula with C and λ constant. Using Equation (27) one obtains the general differential equation
with CΔ = C + λ. Its first integral,
and second integral,
represent the optimal deformation of the entropy formula in this case. With the above result (34) the K(S)-additive composition rule, K(S12) = K(S1) + K(S2), is equivalent to
with
This is a combination of the ideal gas entropy-deformation, h(S) and an original Tsallis composition law [6,54] with q −1 = λ/CΔ. Using the auxiliary function, hC(S) = C(eS/C −1), we have h∞(S) = S and the entropy deformation function can also be written as
- For λ = 1 it is obviously K1(S) = S. This is the Gaussian fluctuation model, considered in several textbooks, and also believed to lead to the smallest physically possible variance due to a “thermodynamical uncertainty” principle [55–58]. Since β = S′(E), the variances are related as Δβ = |S″(E)|ΔE = ΔE/CT2. Then from Δβ · ΔE ≥ 1 it follow and . A straightforward consequence of this is λ/C = Δβ2/⟨β⟩2 ≥ 1/C and therefore λ ≥ 1. We note, that if this “uncertainty” principle were correct, then only q > 1 canonical distributions of ω would exist in Nature.
- For no fluctuations λ = 0 and we get K0(S) = hC(S). We regain the Tsallis and Rényi formulas presented above in Equation (31).
- It is also very intriguing to inspect the following particular limit: C → ∞, λ → ∞ but finite. In this non-extensive limit the fluctuations are much larger than the normal Gaussian ones, and we obtain a nontrivial entropy deformation:The K-additivity, K(S12) = K(S1) + K(S2), in this case leads to the non-additivity formula , – investigated formerly in depth by Tsallis and Abe [6,54,59–64].
In the finite heat capacity, finite temperature variance case we arrive at a Generalized Tsallis Formula based on K(S) = ∑i pi K(− ln pi):
- For normal fluctuations K1(S) = −∑i pi ln pi is exactly the Boltzmann entropy.
- Without fluctuations is the Tsallis entropy with q = 1 − 1/C and S the corresponding Rényi entropy.
- Finally considering extreme large fluctuations and a finite heat capacity, C(S) which however may be an arbitrary function of the total entropy, S, we obtain the non-extensive result Equation (38) with :The canonical pi distribution maximizing this parameterless deformed entropy is also expressed in terms of Lambert-W function, it shows tails like the Gompertz distribution [65–67], known from extreme value statistics and nonequlibrium growth models for demography and tumors.
The extreme large fluctuation case, modeled by λ = ∞ and presented in Equation (40), leads to an allover concave entropy for the two state system: K∞(S[p, 1 − p]) is shown on the Figure 1 by the full line, while the back–deformed “Rényi-type” entropy formula is plotted by the dashed line. These curves are close to each other for the very low (and very high) probability, and maximally differ at the equiprobability point p = 0.5. However, in the latter point S[p, 1−p] has the same value as the traditional Boltzmann–Gibbs curve, for which S and K(S) coincide due to λ = 1.
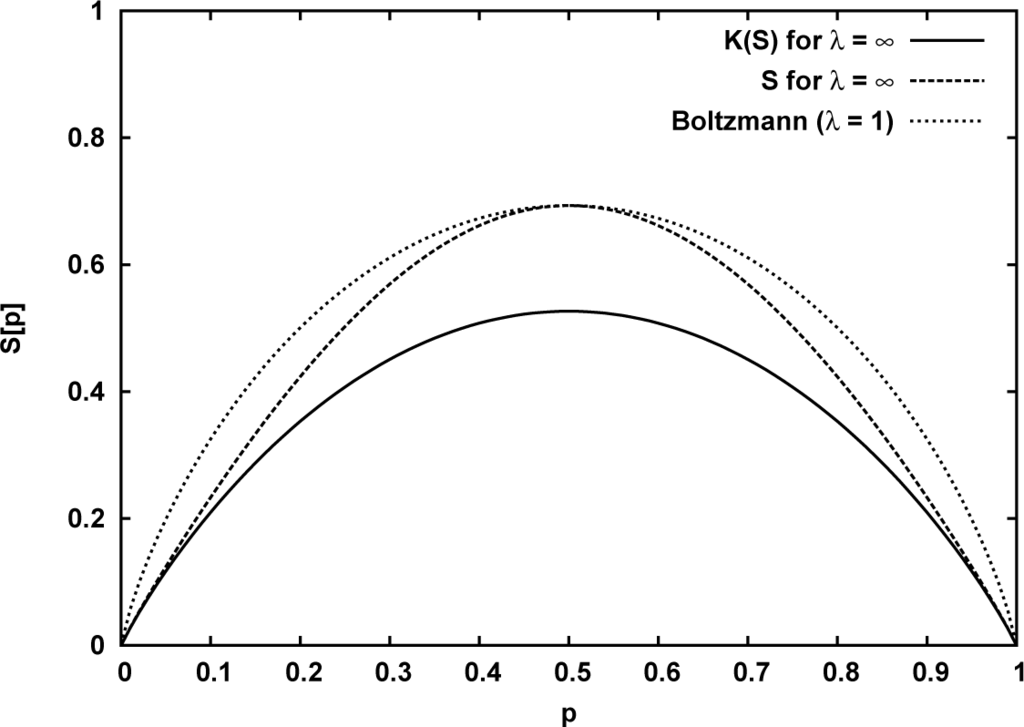
Figure 1.
The general entropy K(S) (full line) and S (dashed line) are plotted for λ = ∞, meaning divergently large fluctuations with respect to the Gaussian model. For comparison the λ = 1 case, the traditional Boltzmann–Gibbs formula is indicated by the dotted line.
For investigating the concavity of the Equation (40) the second derivatives of the respective expressions, K∞(S∞), S∞ and the Boltzmann–Gibbs formula K1(S1) = S1 for the two-state system have to be inspected. This quantity is plotted on Figure 2 demonstrating that its value is negative in the whole range.
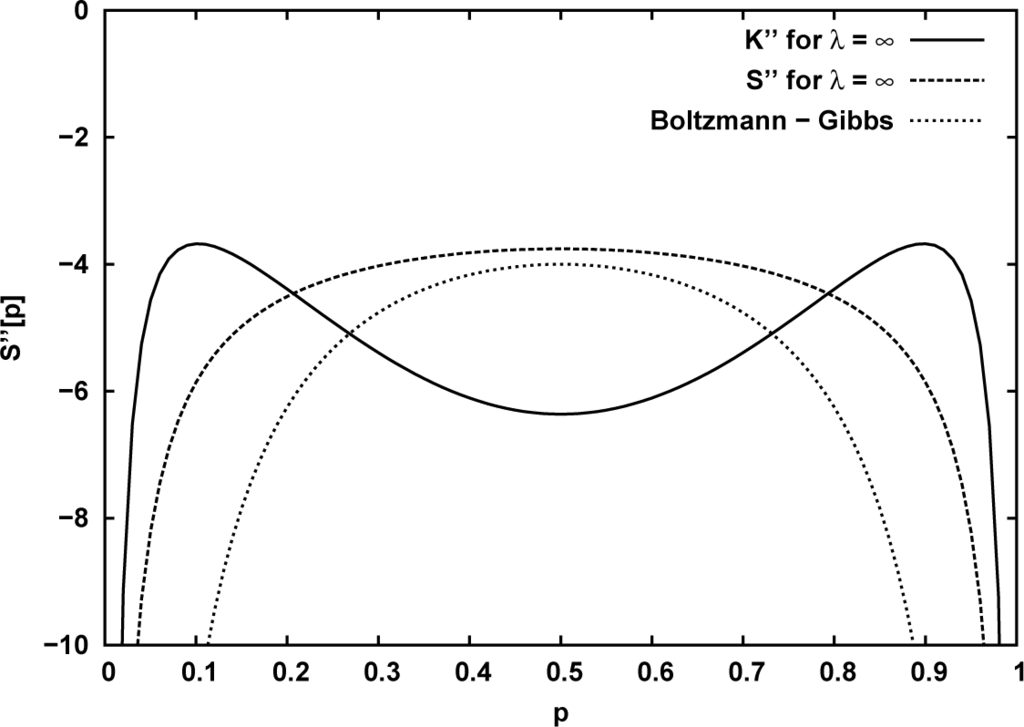
Figure 2.
The second derivatives of the general entropy K(S) (full line) and S (dashed line) are plotted for λ = ∞. For comparison the same derivative for the λ = 1 (Boltzmann) case is indicated by the dotted line.
Let us briefly discuss the canonical distribution following from and the concavity of the general entropy formula given in Equation (39). The deformed entropy is of a form K(S) = ∑i g(pi), its properties are determined by those of the function g(p). First we note that g(0) = 0 and g(1) = 0 rendering the totally ordered state, {pi} = {1, 0, 0, …}, to zero entropy. The canonical solution is obtained by its derivative:
with
The quantity w defined this way to simplify the algebraic manipulations is always between zero and one for probabilities with the same property. From the above canonical condition it follows
As a check, for λ = 1 one obtains w = p1/CΔ and ln p = −(1 + α + βω) as usual. In the non-extensive limit, λ ≫ C, it reduces to
having a solution in terms of the Lambert-W function, L(z):
In the general case the solution of Equation (43) for w can also be expressed by the Lambert-W function. It is straightforward to derive, as follows: The Lambert-W function of a variable, say z, is defined by the L(z) satisfying L eL = z. Replacing z = e−x and taking the logarithm of both sides leads to
Seeking for a solution of ln w + aw = −x, one considers L = aw, and achieves the canonical solution of Equation (43) as
with
The corresponding probability is then reconstructed by inverting Equation (42) as
The stability of the entropy formula can be tested by the sign of the second derivative g″(p). Using the above notations
One has to investigate the sign of the expression between the square brackets only. For λ > 1 it is obviously positive (and hence the general entropy formula concave). For λ < 1 (but positive, since it scales the variance) the content of the square bracket is positive if CΔ ≥ (1 − λ)w. But since w ≤ 1 and CΔ ≥ C ≥ 1 for any reservoir containing at least one unit of heat capacity (at least one relativistic particle in at least one dimension or at least one massive particle in at least two dimensions) this requirement is fulfilled for all parameter values.
Before summarizing the main points let us make some remarks on the equipartition properties of our general ansatz. In the microcanonical maximal entropy state all states have equal probability, due to the normalization this value is the reciprocial of the number of all microstates: pi = 1/W for all i = 1, … W. Due to construction then we have
from which Seqp = ln W follows, whatever the K(S) function was. In this way the Rényi-entropy type expression S(pi) at equiprobability is additive for multiplicative numbers of states; it is by construction extensive. The same cannot be told about K(S), this deformed entropy may become non-extensive. On the other hand, assuming K(S)-additivity, as we did by prescribing the additivity restoration condition (ARC, Equation (27)), the product rule for the equipartioned probabilities is deformed—signalling statistical entanglement.
4. Conclusions and Outlook
In conclusion we have shown that in terms of traditional phase-space models the statistical cut power-law behavior can be interpreted as being primarily a particle number fluctuation effect during hadronization in high energy collisions. The q > 1 and q < 1 Tsallis–Pareto distributions are exact for NBD and BD distributions of the particle number, respectively, in a one-dimensional phase-space characteristic for high energy jets. The Boltzmann–Gibbs exponential weight factor is restored for the common limiting case of these distributions, for the Poissonian, leading to q = 1.
For general particle number distributions with fixed energy the Tsallis–Pareto cut power-law is only an approximation to subleading order in the expansion for large system energy, E ≫ ω. We have obtained and interpreted the parameters T and q by comparing coefficients of the respective expansions and concluded that T = E/⟨n⟩ is an equipartition temperature, while q = 1 + Δn2/⟨n⟩2 −1/⟨n⟩ reflects both the particle number variance and due to its expectation value the size of the reservoir. This formula also explains why both q > 1 and q < 1 cases can be observed in natural phenomena.
Further generalization towards the thermodynamical treatment considers the reservoir environment described by a simplified equation of state, S(E). Repeating the above described approximations one concludes that 1/T = ⟨β⟩ = ⟨S′(E)⟩, i.e., the parameter T also plays the role of a thermodynamical temperature. The parameter q is again related both to the size (total heat capacity, C) of the reservoir and to the variance of the fluctuating quantity β = S′ (E). The general formula follows the structure obtained in the high energy model, q = 1 + Δβ2/⟨β⟩2 − 1/C, with 1/C = dT/dE = −T2 ⟨S″(E)⟩.
It is, however, known for long that the cut power-law does not follow the product rule, as the Boltzmann–Gibbs exponential does, for additive energy. The root of this behavior is the non-additivity of the Boltzmannian entropy, S, for finite and fluctuating reservoirs. S(E1 + E2) ≠ S(E1) + S(E2) for q ≠ 1 is a weakness of the classical thermodynamics which has to be cured. Our approach here was to look for a function, K(S), which restores additivity by leading to qK = 1. This requirement for such a function concludes in the additivity restoring condition, ARC, in a differential equation satisfied by K(S). Finally the usual canonical treatment must then be based on the additivity of K(S), applied to an ensemble of configurations, which in turn provides the general formula K(S) =∑pi K(−ln pi) (cf. Equation (40) and [20]).
The Boltzmann–Gibbs–Shannon formula is restored for q = 1 (when also K(S) = S is the only solution), in particular for the traditional Gaussian approach to fluctuations when
is taken for granted. When the fluctuations are negligible, the Tsallis entropy formula arises for K(S) and the corresponding Rényi formula for S with q = 1 − 1/C. In the extreme large variance limit a new, up to now not considered entropy – probability formula arises.
The canonical distribution belonging to this extreme case is given in terms of the Lambert-W function of single particle energy, defined as the L(z) function, which satisfies LeL = z. Recently, the Lambert-W function was met in relation to a study of scaling properties of a general two-parameter ansatz for non-additive entropy formulas by Hanel and Thurner [68] and in a non-extensive diffusion model by Andrade et al. [69]. Although these and ours are quite different contexts, a far analogy on the level of similar behavior at extreme low probabilities cannot be ab initio excluded.
As to the general scaling property, the λ ≫ C → ∞ case might be related to the c = 1, d = 0 point in Thurner’s and Hanel’s scheme [68]. However we have to emphasize that our present approach aimed and achieved the construction of a deformed entropy, which compensates finite reservoir size non-additivity as well as fluctuation effects even before taking the large system limit.
These initial results are encouraging for further pursuit of such a theoretical approach. The research of large systems, where λ = CΔβ2/⟨β⟩ 2 ≫ C ≫ 1 with a finite limit for λ/C, shall deal with genuine non-extensivity of the K(S) entropy. The physical modelling of the reservoir environment, in particular with emphasis on the variable number of particles relevant for high energy physics, leads to more complex descriptions than presented here: a dependence like C(S) and λ(S) can be quite common. In such cases the ARC differential equation leads to further entropy formulas. Our approach provides a procedure to find the optimal entropy – probability relation from the viewpoint of the non-additive composition of two (or gradually more) subsystems. In addition, the superstatistics, originally conceptualized as a β-distribution behind non-Gibbsean factors in the statistics, may be extended to studies considering physical systems which cannot be described simply by an overall positive weight factor γ(β) under an integral.
Acknowledgments
This work was supported by the Hungarian National Research Fund OTKA (Grants K 104260, NK 106119) and by a bilateral Chinese-Hungarian grant NIH TET_12_CN-1-2012-0016. Gergely Gábor Barnaföldi thanks the support in form of the János Bolyai Research Scholarship of the Hungarian Academy of Sciences.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rényi, A. On measures of entropy and information. Proceedings of 4th Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; Newman, J., Ed.; University of California Press: Berkeley, CA, USA, 1961. [Google Scholar]
- Rényi, A. Probability Theory; North Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys 1988, 52, 479–487. [Google Scholar]
- Tsallis, C. Nonextensive statistics: Theoretical, experimental and computational evidences and connections. Braz. J. Phys 1999, 29, 1–35. [Google Scholar]
- Touchette, H. When is a quantity additive and when is it extensive? Physica A 2002, 305, 84–88. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Biró, T.S.; Jakovác, A. Power-law tails from multiplicative noise. Phys. Rev. Lett 2005, 94, 132302. [Google Scholar]
- Biró, T.S.; Rosenfeld, R. Microscopic origin of non-Gaussian distributions of finacial returns. Physica A 2008, 387, 1603–1612. [Google Scholar]
- Biró, T.S.; Purcsel, G. Non-extensive Boltzmann equation and hadronization. Phys. Rev. Lett 2005, 95, 162302. [Google Scholar]
- Biró, T.S.; Kaniadakis, G. Two generalizations of the Boltzmann equation. Eur. Phys. J. B 2006, 50, 3–6. [Google Scholar]
- Biró, T.S.; Purcsel, G. Equilibration of two non-extensive subsystems in a parton cascade model. Phys. Lett. A 2008, 372, 1174–1179. [Google Scholar]
- Biró, T.S.; Purcsel, G.; Györgyi, G.; Jakovác, A.; Schram, Z. Power-law tailed spectra from equilibrium. Nucl. Phys. A 2006, 774, 845–848. [Google Scholar]
- Biró, T.S.; Purcsel, G. Non-extensive equilibration in relativistic matter. Cent. Eur. J. Phys 2009, 7, 395–400. [Google Scholar]
- Biró, T.S.; Purcsel, G.; Ürmössy, K. Non-extensive approach to quark matter. Eur. Phys. J. A 2009, 40, 325–340. [Google Scholar]
- Biró, T.S.; Peshier, A. Limiting temperature from a parton gas with power-law tailed distribution. Phys. Lett. B 2006, 632, 247–251. [Google Scholar]
- Biró, T.S.; Ván, P. Zeroth law compatibility of non-additive thermodynamics. Phys. Rev. E 2011, 83, 061147. [Google Scholar]
- Biró, T.S. Is There a Temperature? Conceptual Challenges at High Energy, Acceleration and Complexity; Springer: New York, NY, USA, 2011. [Google Scholar]
- Ván, P.; Barnaföldi, G.G.; Biró, T.S.; Ürmössy, K. Nonadditive thermostatistics and thermodynamics. J. Phys. Conf. Ser. 2012, 394, 012002. [Google Scholar]
- Biró, T.S. Abstract composition rule for relativistic kinetic theory in the thermodynamical limit. Europhys. Lett. 2008, 84, 56003. [Google Scholar]
- Biró, T.S. Ideal gas provides q-entropy. Physica A 2013, 392, 3132–3139. [Google Scholar]
- Biró, T.S.; Barnaföldi, G.G.; Ván, P.; Ürmössy, K. Statistical power-law spectra due to reservoir fluctuations; 2014; Volume arxiv, p. 1404.1256. [Google Scholar]
- Biró, T.S.; Ván, P.; Barnaföldi, G.G. Quark-gluon plasma connected to finite heat bath. Eur. Phys. J. A 2013, 49. [Google Scholar] [CrossRef]
- Biró, T.S.; Barnaföldi, G.G.; Ván, P. New entropy formula with fluctuating reservoir. Physica A 2015, 417, 215–220. [Google Scholar]
- Wong, C.Y.; Wilk, G. Tsallis fits to pT spectra for pp collisions at the LHC. Acta Phys. Pol. B 2012, 43, 2047–2054. [Google Scholar]
- Wong, C.Y.; Wilk, G. Tsallis fits to pT spectra and multiple hard scattering in pp collisions at LHC. Phys. Rev. D 2013, 87, 114007. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Power laws in elementary and heavy ion collisions: A story of fluctuations and non-extensivity? Eur. Phys. J. A 2009, 40, 299–312. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Consequences of temperature fluctuations in observables measured in high-energy collisions. Eur. Phys. J. A 2012, 48. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Interpretation of the nonextensivity parameter q in some applications of Tsallis statistics and Levy distribution. Phys. Rev. Lett 2000, 84. http://dx.doi.org/10.1103/PhysRevLett.84.2770. [Google Scholar]
- Ürmössy, K.; Biró, T.S. Cooper–Frye Formula and non-extensive coalescence at RHIC energy. Phys. Lett. B 2010, 689, 14–17. [Google Scholar]
- Ürmössy, K.; Barnaföldi, G.G.; Biró, T.S. Microcanonical jet-fragmentation in proton-proton collisions at LHC energy. Phys. Lett. B 2012, 718, 125–129. [Google Scholar]
- Ürmössy, K.; Barnaföldi, G.G.; Biró, T.S. Generalised Tsallis statistics in electron-positron collisions. Phys. Lett. B 2011, 701, 111–116. [Google Scholar]
- Almeida, M.P. Generalized entropies from first principles. Physica A 2001, 300, 424–432. [Google Scholar]
- Begun, V.V.; Gazdzicki, M.; Gorenstein, M.I. Power-law in microcanonical ensemble with scaling volume fluctuations. Phys. Rev. C 2008, 78, 024904. [Google Scholar]
- Campisi, M.; Zahn, F.; Hänggi, P. On the origin of power laws in equilibrium. Europhys. Lett. 2012, 99, 60004. [Google Scholar]
- Bagci, G.B.; Oikonomou, T. Tsallis power-laws and finite baths with negative heat capacity. Phys. Rev. E 2013, 88, 042126. [Google Scholar]
- Parvan, A.S. Microcanonical ensemble extensive thermodynamics of Tsallis statistics. Phys. Lett. A 2006, 350, 331–338. [Google Scholar]
- Adare, A.; PHENIX Collaboration. Charged hadron multiplicity fluctuations in Au + Au and Cu + Cu collisions from to 200 GeV. Phys. Rev. C 2008, 78, 044902. [Google Scholar]
- Abelev, B.; ALICE Collaboration. Centrality dependence of π, K and p production in Pb-Pb collisions at TeV. Phys. Rev. C 2013, 88, 044910. [Google Scholar]
- Abelev, B.; ALICE Collaboration. Centrality dependence of charged particle production at large transverse momentum in Pb-Pb collisions at TeV. Phys. Lett. B 2013, 720, 52–62. [Google Scholar]
- Begun, V.V.; Gazdzicki, M.; Gorenstein, M.I. Semi-inclusive observables in statistical models. Phys. Rev. C 2009, 80, 064903. [Google Scholar]
- Jeon, S.; Koch, V.; Redlich, K.; Wang, X.N. Fluctuations of rare particles as a measure of chemical equilibrium. Nucl. Phys. A 2002, 697, 546–562. [Google Scholar]
- Begun, V.V.; Gazdzicki, M.; Gorenstein, M.I.; Zozulya, O.S. Particle number fluctuations in a canonical ensemble. Phys. Rev. C 2004, 70, 034901. [Google Scholar]
- Gorenstein, M.I. Identity method for particle number fluctuations and correlation. Phys. Rev. C 2011, 84, 024902. [Google Scholar]
- Gorenstein, M.I.; Grebieszkow, K. Strongly intensive measures for the momentum and particle number fluctuations. Phys. Rev. C 2014, 89, 034903. [Google Scholar]
- Begun, V.V.; Gorenstein, M.I. Particle number fluctuations in relativistic Bose and Fermi gases. Phys. Rev. C 2006, 73, 054904. [Google Scholar]
- Beck, C.; Cohen, E.G.D. Superstatistics. Physica A 2003, 322, 267–275. [Google Scholar]
- Abe, S.; Beck, C.; Cohen, E.G.D. Superstatistics, thermodynamics and fluctuations. Phys. Rev. E 2007, 76, 031102. [Google Scholar]
- Ma, S.K. Statistical Mechanics; World Scientific: Singapore, Singapore, 1985. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Stohastic network view on hadron production. Acta Phys. Pol. B 2004, 35, 2141–2147. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. The imprints of superstatistics in multiparticle production processes. Cent. Eur. J. Phys 2012, 10, 568–575. [Google Scholar]
- Beck, C. Dynamical foundations of nonextensive statistical mechanics. Phys. Rev. Lett 2001, 87, 180601. [Google Scholar]
- Kodama, T.; Elze, H.T.; Aguiar, C.E.; Koide, T. Dynamical correlations as origin of nonextensive entropy. Europhys. Lett 2005, 70, 439–445. [Google Scholar]
- Tsallis, C.; Haubold, H.J. Boltzmann-Gibbs entropy is sufficient but not necessary for the likelihood factorization required by Einstein. 2014, arXiv, 1407.6052. [Google Scholar]
- Abe, S. General pseudoadditivity of composable entropy by the existence of equilibrium. Phys. Rev. E 2001, 63, 061105. [Google Scholar]
- Uffink, J.; van Lith, J. Thermodynamic uncertainty relations. Found. Phys 1999, 29, 655–692. [Google Scholar]
- Lavenda, B.H. Comments on “Thermodynamic Uncertainty Relations” by J. Uffink and J. van Lith. Found. Phys. Lett 2000, 13, 487–492. [Google Scholar]
- Uffink, J.; van Lith, J. Thermodynamic uncertainty relations again: A reply to Lavenda. Found. Phys. Lett 2001, 14, 187–193. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Generalized thermodynamic uncertainty relations. Physica A 2011, 390, 3566–3572. [Google Scholar]
- Abe, S. Axioms and uniqueness theorem for Tsallis entropy. Phys. Lett. A 2000, 271, 74–79. [Google Scholar]
- Abe, S. A note on the q-deformation theoretic aspect of the generalized entropies in nonextensive physics. Phys. Lett. A 1997, 224, 326–330. [Google Scholar]
- Abe, S.; Rajagopal, A.K. Non-uniqueness of canonical ensemble theory entropy from microcanonical basis. Phys. Lett. A 2000, 272, 341–345. [Google Scholar]
- Abe, S.; Rajagopal, A.K. Justification of power law canonical distributions based on generalized central limit theorem. Europhys. Lett 2000, 52, 610–614. [Google Scholar]
- Abe, S.; Rajagopal, A.K. Macroscopic thermodynamics of equilibrium characterized by power law canonical distributions. Europhys. Lett 2001, 55, 6–11. [Google Scholar]
- Abe, S.; Bagci, G.B. Necessity of q-expectation value in nonextensive statistical mechanics. Phys. Rev. E 2005, 71, 016139. [Google Scholar]
- Gompertz, B. On the nature of the function expressing of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc 1825, 115, 513–583. [Google Scholar]
- Casey, A.E. The experimental alteration of malignacy with an homologous mammalian tumour material. Am. J. Cancer 1934, 21, 760–775. [Google Scholar]
- Apostol, B.E. Euler’s transform and a generalized Omori’s law. Phys. Lett. A 2005, 351, 175–176. [Google Scholar]
- Hanel, R.; Thurner, S. A comprehensive classification of complex statsitical systems and an axiomatic derivation of their entropy and distribution functions. Europhys. Lett 2011, 93. [Google Scholar] [CrossRef]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett 2010, 105, 260601. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).