Abstract
The aim of this paper is to develop a comprehensive study of the geometry involved in combining Bregman divergences with pooling operators over closed convex sets in a discrete probabilistic space. A particular connection we develop leads to an iterative procedure, which is similar to the alternating projection procedure by Csiszár and Tusnády. Although such iterative procedures are well studied over much more general spaces than the one we consider, only a few authors have investigated combining projections with pooling operators. We aspire to achieve here a comprehensive study of such a combination. Besides, pooling operators combining the opinions of several rational experts allows us to discuss possible applications in multi-expert reasoning.
1. Background
1.1. Introduction
Information geometry has been studied as a powerful tool for tackling various problems. It has been applied in neuroscience [1], expert systems [2], logistic regression [3], clustering [4] and probabilistic merging [5]. In this paper, we aim to present a comprehensive study of information geometry over a discrete probabilistic space in order to provide some specialized tools for researchers working in the area of multi-expert reasoning.
In the context of this paper, the domain of information geometry is the Euclidean space ℝJ, for some fixed natural number J ≥ 2, where we measure a divergence from one point to another one. A divergence is, in general asymmetric, a notion of distance, and we will represent it here by an arrow. A divergence can represent a cost function having various constraints, so many engineering problems correspond to the minimization of a divergence.
For example, in the areas of neuroscience and expert systems, given evidence v and a training set of known instances W, we may search for an instance w ∈ W, which is “closest” to the evidence v, so as to represent it in the given training set W. An illustration is depicted in Figure 1.

Figure 1.
An illustration of a divergence.
A similar pattern of minimization appears also in the areas of clustering and regression. The aim of the former is to categorize several points into a given number of nodes in such a way that the sum of divergences from each point to its associated node is minimal. The aim of regression is to predict an unknown distribution of events based on the previously obtained statistical data by defining a function whose values minimize a sum of divergences to the data.
While several domains for divergences are considered in the literature, in the current presentation of information geometry, however, we will confine ourselves to the domain of positive discrete probability functions ⅅJ, where ⅅJ is the set of all w ∈ ℝJ restricted by
and w1 > 0, …, wJ > 0. In our presentation, J ≥ 2 will be always fixed, but otherwise arbitrary.
Although in information geometry, it does not make sense to talk about beliefs, applications in multi-expert reasoning are often developed from that perspective. It is then argued that rational beliefs should obey the laws of probability, for example the Dutch book argument by Ramsey and de Finetti [6] is perhaps the most compelling argument. It is therefore of a particular interest to develop information geometry over a probabilistic space if we wish to eventually apply it to multi-expert reasoning.
In addition to our restriction to discrete probability functions, we will confine ourselves to a special type of divergence, called a Bregman divergence [7], which has recently attracted attention in machine learning and plays a major role in optimization; cf. [3]. A Bregman divergence over a discrete probabilistic space is defined by a given strictly convex function f: (0, 1)J → ℝ, which is differentiable over ⅅJ. For any v, w ∈ ⅅJ, the Bregman divergence generated by the function f is given by:
where
is the gradient of f and · denotes the inner (dot) product of two vectors, i.e.,
We say that Df(w‖v) is a Bregman divergence from v ∈ ⅅJ to w ∈ ⅅJ. Figure 2 depicts a geometrical interpretation of a Bregman divergence.
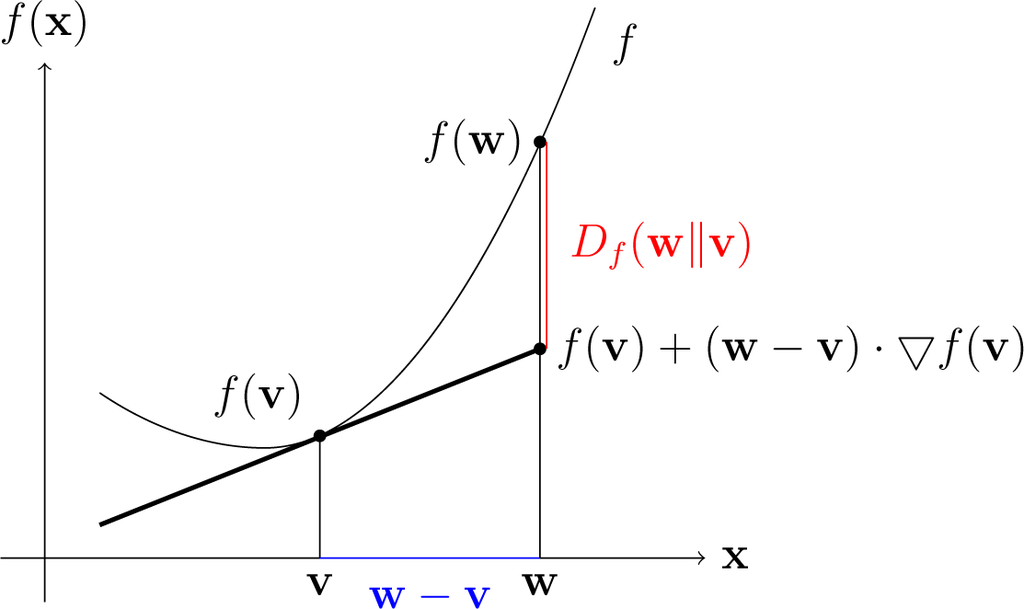
Figure 2.
A Bregman divergence.
By the first convexity condition applied to the (convex and differentiable) function f (see, e.g., [8]), Df(w‖v) ≥ 0 with equality holding only if w = v. This is the condition that makes Df(·‖·) a divergence as defined in information geometry. Note that, since a differentiable convex function is necessarily continuously differentiable (see [9]), Df(w‖v) is a continuous function. However, note that this is not sufficient to establish the differentiability of Df.
It is worth mentioning that the restriction w1 > 0,…, wJ > 0 for a probability function w that we have adopted here is important for the definition of a Bregman divergence. Some Bregman divergences do not have their generating function f differentiable over the whole space of probability functions. However, it is possible to define the notion of a Bregman divergence even if this condition is left out, but at the cost of some restrictions on f. We kindly refer the interested reader to [10] for further details. Nonetheless, the setting developed in [10] uses a rather complicated notation, which could prove to be impenetrable at first glance if it were adopted in the current paper.
In this paper, we study mainly Bregman divergences Df(·‖·), which are convex, i.e., for all λ ∈ [0, 1] and all w(1), w(2), v(1), v(2) ∈ ⅅJ:
Note that if D(·‖·) is a convex function, then D(·‖·) is a convex function also in each argument separately.
The following are examples of a convex Bregman divergence.
Example 1 (Squared Euclidean Distance). For any. Then, the divergence:
will be denoted by E2, and exceptionally, this divergence is symmetric.
Example 2 (Kullback–Leibler Divergence). For any, where log denotes the natural logarithm. (Note that in the information theory literature, this logarithm is often taken with base two. However, this does not affect the results of this paper in any way.) The well-known divergence:
will be denoted by KL.
The convexity of the KL-divergence is easy to observe and is well known; see, e.g., [10].
1.2. Projections
For given v ∈ ⅅJ, a Bregman divergence Df(w‖v) is a strictly convex function in the first argument. This can be easily seen by considering
where v is constant. f(v) is therefore constant, as well, and the claim follows, since strict convexity of f is not affected by adding the linear term
.
Owing to the observation above, if v ∈ ⅅJ is given and W ⊆ ⅅJ is a closed convex nonempty set, we can define the Df-projection of v into W. It is that unique point w ∈ W that minimizes Df(w‖v) subject only to w ∈ W. This property is crucial for the applicability of Bregman divergences. Note, however, that Df(·‖·) is not necessarily convex in its second argument; for a counterexample, consider the case
.
Perhaps the most useful property that a Df-projection has is the extended Pythagorean property:
Theorem 1 (Extended Pythagorean Property). Let Df be a Bregman divergence. Let w be the Df-projection of v ∈ ⅅJ into a closed convex nonempty set W ⊆ ⅅJ. Let a ∈ W. Then:
This property, in the case of the Kullback–Leibler divergence, was proven first by Csiszár in [11]. The proof of the generalized theorem above is given in [1,12], where the interested reader can find a comprehensive study of Bregman divergences within the context of differential geometry. We illustrate the theorem in Figure 3.
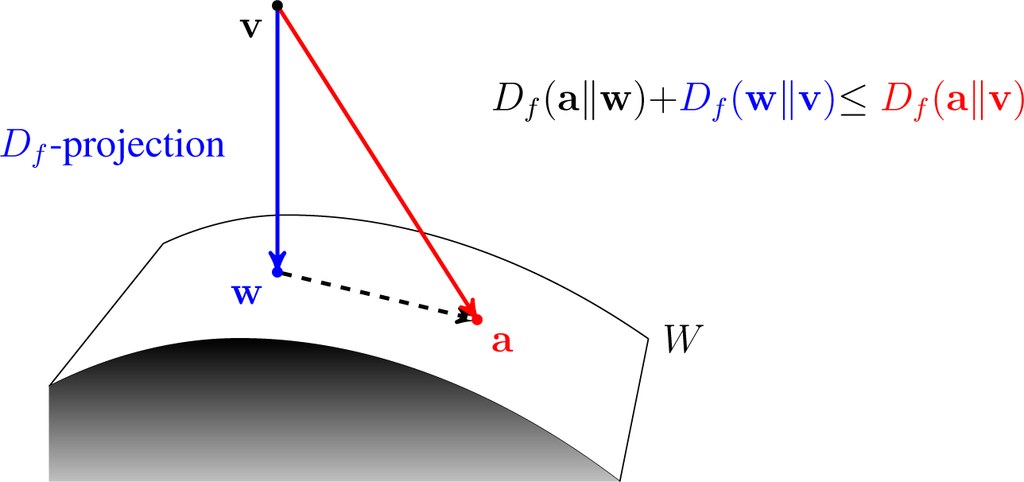
Figure 3.
The extended Pythagorean property.
Notice that the squared Euclidean distance has a special role among all other Bregman divergences. It is symmetric, and it interprets the extended Pythagorean property “classically” as the relation of the sizes of the squares constructed on the sides of a triangle.
It is well-known that the Kullback–Leibler divergence is closely connected to the Shannon entropy defined for any w ∈ ⅅJ by:
where log denotes the natural logarithm. The importance of the Shannon entropy is that it could be described as a measure of the level of disorder, which in the context of information theory, can be interpreted as a measure of informational content. The higher the entropy of w is, the less information is carried by w. In some contexts, one can then argue that given several seemingly equally probable choices of a probability function, one should choose the one that carries the least additional information [13]. Given a closed convex nonempty set W, the most entropic point in W will be denoted by ME(W).
Now, trying to find the most entropic point in a closed convex nonempty set W ⊆ ⅅJ is, in fact, equivalent to finding a special KL-projection (the KL-projection of the uniform probability function
) since:
where arg minx∈X f(x) denotes that unique argument x ∈ X, where f has its global minimum, whenever such a unique point exists. The expression arg max is defined accordingly.
Given the extensive justification of the Shannon entropy in various frameworks (see, e.g., [14,15]), it is perhaps not surprising that a common method of projecting in probabilistic expert systems is by means of the KL-projection; see [2,16]. In connection to the Shannon entropy, the KL-divergence is often referred to as the cross-entropy, and the projecting is called updating.
The above may perhaps be also an appealing reason to use projections in general to “represent” a given closed convex set of probability functions by a single point, in particular in expert reasoning. Moreover, recent use of projections by a Bregman divergence has become popular in other contexts; see, e.g., [4]. Remarkably, projections by a Bregman divergence also provide a unifying framework for a variety of techniques used in expert systems, such as logistic regression; see [3]. It is therefore of particular interest to investigate the geometry of Bregman divergences.
1.3. Pooling
In this subsection, we introduce probabilistic pooling, which is a method of aggregating several probability functions. Formally, a pooling operator Pool is defined for each n ≥ 1 as a mapping:
Recall that J is a fixed natural number greater than or equal to two, which is otherwise arbitrary.
One possibility for choosing a pooling operator is to define one by means of a Bregman divergence. In particular, given a Bregman divergence
and a ∈ ⅅn, we can ask which point v ∈ ⅅJ has the least sum of Bregman divergences Df from w(1),…, w(n) weighted by a1,…, an, respectively. It turns out that the resulting probability function is unique, and in each coordinate, it is simply the weighted arithmetic mean of the corresponding coordinates of w(1),…, w(n) ∈ ⅅJ. In other words:
For a given family
of weighting vectors, we define the pooling operator
by Equation (1) for every a ∈
. Instead of the right-hand side of Equation (1), we will simply write LinOpa(w(1),…, w(n)) if a ∈
. A special choice for
is the family
, and the pooling operator
is well known in the literature as the LinOp-pooling operator.
The fact that Equation (1) actually holds can be observed by employing the following theorem, which is folklore in information theory.
Theorem 2 (Parallelogram Theorem). Let Df be a Bregman divergence, w(1),…, w(n), v ∈ ⅅJ and a ∈ ⅅn. Then:
Proof. Let w = LinOpa(w(1),…, w(n)). The equality is easy to observe by:
Since
. □
Since Df(w‖v) = 0, only if w = v, and otherwise, it is positive, the unique minimum of the left-hand side of Equation (1) is at the point v = LinOpa(w(1),…, w(n)).
The situation above can be naturally interpreted in terms of random variables. Assume that X is a random variable taking values in {w(1),…, w(n)} ⊆ ⅅJ with the probability distribution a ∈ ⅅn, and we are given the problem of finding a random variable Y, such that the expected value:
is minimal. The unique answer to this question is then
. This underlines the reason why the
-pooling operator is so popular in the decision theory literature, where several experts, each with his own probability function w(i) representing his beliefs, seek to find a single probability function to represent their joint beliefs. The
-pooling operator simply yields the expected value as if expert’s beliefs were statistically obtained.
It is certainly interesting that the result above holds for any Bregman divergence, but as is shown in [17], Theorem 4, it is even more remarkable that Bregman divergences are the only divergences with such a property. However, we note that in order to establish this claim, a slightly more general setting was considered and that we have restricted the formulation of the original theorem to the only domain considered here (0, 1)J:
Theorem 3 (Banerjee, Guo, Wang). Let F: (0, 1)J × (0, 1)J → ℝ be a divergence. Assume that are all continuous. Let (Ω, P,
) be an arbitrary probability space, and let be a sub-σ-algebra of. For all random variables X taking values in (0, 1)J, if:
then F (x‖y) = Df(x‖y) for some strictly convex and differentiable function f : (0, 1)J → ℝ.
While in the statistical sense, the
-pooling operator, where
is a family of weighting vectors, seems to be well placed, in the fields of multi-expert reasoning and probabilistic merging, the so-called
-pooling operator often appeals more. For every n ≥ 1 and every a ∈
, it is defined by:
If w(1),…, w(n) are considered to be beliefs of n-experts, respectively, then the
-pooling operator appears to favor agreement over the expected value. For instance, consider the following example from utility theory. Say that Eleanor and George are looking for a film to watch and they have three options, A, B and C. Eleanor hates Movie A and under no circumstances would agree to watch it, while George absolutely loves it. Now, consider that the situation with respect to Film C is swapped: George hates it, while Eleanor would prefer to see it. They both consider Movie B uninteresting, but are willing to see it. The following probability functions could represent the preferences of Eleanor and George towards Movies A, B and C: (0, 0.1, 0.9) and (0.9, 0.1, 0), respectively. Moreover, we value the opinions of both of them equally, i.e.,
. Now, while the
-pooling operator gives inconclusive (0.45, 0.1, 0.45) by the
-pooling operator (in the literature, this operator is simply known as the LogOp-pooling operator), we obtain (0, 1, 0). If we take the advice, then Eleanor and George should see the only film that is acceptable for both of them.
The example above illustrates why taking products rather than the arithmetic mean is popular when considering utilities. However, recently, the
-pooling operator attracted attention also in multi-expert probabilistic reasoning; a prominent example here is the social entropy process by Wilmers [18]. An intriguing idea that originates in the social entropy process is to swap the direction of the Kullback–Leibler projections and establish the corresponding conjugated KL-projection of w ∈ ⅅJ into V ⊆ ⅅJ as arg minv∈V KL(w‖v) (it is easy to check that KL(·‖·) is strictly convex in its second argument) and the conjugated parallelogram theorem [10]:
Theorem 4. Let w(1),…, w(n), v ∈ ⅅJ and a ∈ ⅅn. Then:
Proof. Let w = LogOpa(w(1),…, w(n)). First note that:
Now:
where we have used the fact that
. □
As a consequence, for given w(1),…, w(n) ∈ ⅅJ, we get:
Therefore, the
-pooling operator can be naturally interpreted in information geometry. The question now arises as to whether this can be done with some other Bregman divergences. We will investigate this later.
The reader perhaps wonders which are the main practical differences in using different pooling operators. The
-pooling operator, for example, satisfies the marginalization property, that is the values on the coordinates of the resulting probability function depend only on the corresponding coordinates of the probability functions that are pooled. The
-pooling operator does not have this property. On the other hand, the
-pooling operator, unlike the
-pooling operator, is externally Bayesian. That is the order in which we combine pooling and Bayesian updating is irrelevant. See [19] for more details.
We, however, do not seek any conclusive answer as to which pooling operator to use in any particular context. In this paper, we only aim to provide geometric tools that can be used in multi-expert reasoning. For elaborate work on pooling operators, we refer to the literature, e.g., [19] for a survey, [20] for a classical problem of the relationship between pooling and probabilistic independence or [18] for a modern account on
and
-pooling operators in probabilistic knowledge merging.
2. Projections and Pooling Combined
2.1. Averaging Projective Procedures
While the geometry of projections and the theory of pooling operators have been extensively studied in the literature (see the previous section), much less attention, however, was been devoted to the combination of them. A detailed study of this problem and a comprehensive analysis of the geometry involved is the main aim of this paper.
The central geometrical notion connecting projections and pooling in this paper is an averaging projective procedure F, which consists of a family of mappings
, where sets W1,…, Wn ⊆ ⅅJ are closed convex and nonempty. A particular F is given by a family of strictly convex functions dv, v ∈ ⅅJ and a pooling operator Pool and is defined by the following two-stage process.
- For an argument v ∈ ⅅJ, .
- Set .
For instance, the function dv(·) can be Df(·‖v) for some Bregman divergence Df and in such a particular case
first Df-projects the argument v into each of W1,…, Wn, and then, it “averages” the resulting probability functions by a pooling operator Pool. Hence, the name: an averaging projective procedure. An illustration of F is depicted in Figure 4.
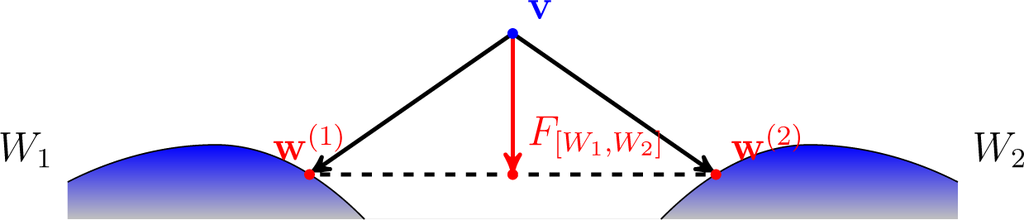
Figure 4.
An illustration of an averaging projective procedure F.
Note that W1,…, Wn play dual roles in the definition above, which may perhaps appear clumsy. When they are fixed,
is a mapping ⅅJ → ⅅJ. However, the option to consider them also as variables will be the key to our following investigation and to the applicability of an averaging projective procedure in multi-expert reasoning, where W1,…, Wn will represent the respective knowledge of n experts. A straightforward interpretation is that the first stage simplifies sets to single probability functions, which then are being merged to a final social belief function of the college of experts.
With regard to previous research, the cases of dv(·) being KL(·‖v) and KL(v‖·) with Pool be taken to the
-pooling operator and the
-pooling operator, respectively, were introduced and investigated by Matúš in [21]. The idea of combining the projections by means of the squared Euclidean distance E2 with the
-pooling operator was first introduced by Predd et al. in [22].
Example 3. In the definition of an averaging projective procedure, take dv to be KL(·‖v) and Pool to be the -pooling operator. Now, F is the mapping ⅅJ → ⅅJ for every n ≥ 1 and all closed convex nonempty sets W1,…, Wn ⊆ ⅅJ given by above.
In particular, takeand. Then, the KL-projecion of v into W1 is actually v itself, since v ∈ W1 and the KL-projection of v intoW2 is. Therefore:
2.2. Obdurate Operators
In this section, we approach averaging projective procedures using the framework of probabilistic knowledge merging as defined in [5]. A probabilistic merging operator:
is a mapping that maps a finite collection of closed convex nonempty subsets of ⅅJ, say W1,…, Wn, to a single closed convex nonempty subset of ⅅJ. In the area of multi-expert reasoning, we can perhaps interpret ∆(W1,…, Wn) as a representation of W1,…, Wn, which themselves individually represent knowledge bases of n experts.
A merging operator O is obdurate if, for every n ≥ 1 and any W1,…, Wn ⊆ ⅅJ, we have that
, where v is some fixed argument and F is an averaging projective procedure. Note that this operator always produces a singleton. Obdurate processes thus first represent sets as single probability functions, and then, they pool them by a pooling operator.
Although this may sound like a fairly restrictive setting, many existing natural probabilistic merging operators are of this form. The prominent example is the merging operator of Kern-Isberner and Rödder (KIRP) [23]. In this particular case, v is the uniform probability function, dv(·) is KL(·‖v) and Pool is given by:
Recall that H(w(i)) is the Shannon entropy of w(i), which is, in fact, the most entropic point in Wi.
In [23], Kern-Isberner and Rödder argue that W1,…, Wn ⊆ ⅅJ can by considered as marginal probabilities in a subset U ⊆ ⅅJ+n, such that every probability function v ∈ U marginalizes to a ⅅJ -probability function belonging to one and only one set Wi. Since then, the point which KIRP produces is, in fact, the ⅅJ-marginal of the most entropic point in U, following the justification of the Shannon entropy, they conclude that such a point is a natural interpretation of W1,…, Wn by a single probability function. KIRP thus maps the uniform probability function to the ⅅJ-marginal of the most entropic point in U. To date, KIRP has received much attention in the area of probabilistic knowledge merging.
However, any obdurate merging operator seems to be challenged by its violation of the following principle.
(CP) Consistency Principle. Let ∆ be a probabilistic merging operator. Then, we say that ∆ satisfies the consistency principle if, for every n ≥ 1 and all W1,…, Wn ⊆ ⅅJ:
(CP) can be interpreted as saying that if the knowledge bases of a set of experts are collectively consistent, then the merged knowledge base should not consist of anything else than what the experts agree on.
This principle often falls under the following philosophical criticism. One might imagine a situation where several experts consider a large set of probability functions as admissible, while one believes in a single probability function. Although this one is consistent with the beliefs of the rest of the group, one might argue that it is not justified to merge the knowledge of the whole group into that single probability function.
More rigorously, Williamson [24] introduces a particular interpretation of the epistemological status of an expert’s knowledge base, which he calls “granting”. He rejects (CP), as several experts may grant the same piece of knowledge for inconsistent reasons.
On the other hand, Adamčík and Wilmers in [5] assume that the way in which the knowledge was obtained is considered irrelevant, and each expert has incorporated all of his relevant knowledge into what he is declaring, contrary to Williamson’s granting. This is sometimes referred to as the principle of total evidence [25] or the Watts assumption [26]. They argue that, although overall knowledge of any human expert can never be fully formalized, as a formalization is always an abstraction from reality, the principle of total evidence needs to be imposed in order to avoid confusion in any discussion related to methods of representing the collective knowledge of experts. Otherwise, there would be an inexhaustible supply of invalid arguments produced by a philosophical opponent challenging one’s reasoning using implicit background information, which is not included in the formal representation of a knowledge base.
However, in this paper, we do not wish to probe further into this philosophical argument, and instead, we present the following rather surprising theorem, which appeared for the first time in [10].
Theorem 5. There is no obdurate merging operator O that satisfies the consistency principle (CP).
Proof. Suppose that J ≥ 3. Let d be the function to minimize from the definition of O, where, for simplicity, we suppress the constant superscript. Let v ∈ ⅅJ be the unique minimizer of d over some sufficiently large closed convex subset W of ⅅJ. Let w, u ∈ W be such that d(v) < d(w) < d(u) and w = λv + (1 − λ)u for some 0 < λ < 1 (in particular, w is a linear combination of v and u).
Let s ∈ W be such that d(v) < d(s) < d(w) and s is not a linear combination of v and u. Then, there is s′, such that s′ = λs + (1 − λ)w for some 0 < λ ≤ 1, and d is strictly increasing along the line from s′ to w. This is because d is strictly convex and d(s) < d(w). Note that if J = 2, then s would be always a linear combination of v and u. Moreover, for sufficiently large W ⊆ ⅅ3, we can always choose w, u, s and s′ in W as above.
Now, we show that d is also strictly increasing along the line from s′ to u. Assume this is not the case. Then, by the same argument as before, there is s″, such that d(s″) < d(s′). Due to the construction, the line from v to s″ intersects the line from s′ to w; let us denote the point of intersection as r. Since d is strictly increasing along the line from s′ to w, we have that d(r) > d(s′) > d(s″) > d(v). This, however, contradicts the convexity of d. The situation is depicted in Figure 5.
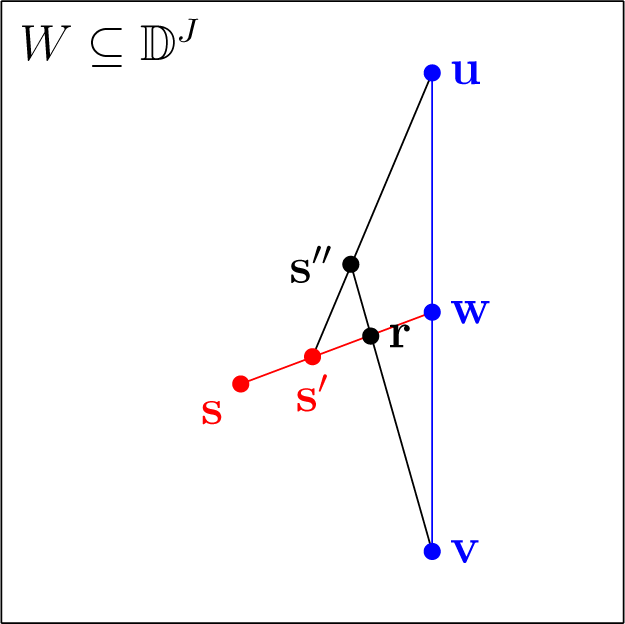
Figure 5.
The situation in the proof of Theorem 5.
Now, assume that W1 = {λv + (1 − λ)w : λ ∈ [0, 1]}, W2 = {λs′ + (1 − λ)w : λ ∈ [0, 1]}, V1 = {λv + (1 − λ)u : λ ∈ [0, 1]} and V2 = {λs′ + (1 − λ)u : λ ∈ [0, 1]}. Since v minimizes d and along the lines from s′ to w and from s′ to u, the function d is strictly increasing, we have that:
where Pool is a pooling operator used in the second stage of O. Suppose that O satisfies (CP). Then, O(W1, W2) = {w} and O(V1, V2) = {u}, which contradicts Equation (2).
The theorem above in some philosophical contexts can be used as an argument against the consistency principle, while from another perspective, it casts a shadow on the notion of an obdurate merging operator. This unfortunately includes the natural merging operator OSEP, or obdurate social entropy process, defined as follows. For every n ≥ 1 and all W1,…, Wn ⊆ ⅅJ:
Recall that ME(Wi) denotes the most entropic point in Wi or equivalently the KL-projection of the uniform probability function into Wi, and
is the family of weighting vectors
, one for every n ≥ 1. It is easy to observe that OSEP is really an obdurate merging operator.
In [10], it is proven that OSEP is (thus far, the only known) probabilistic merging operator satisfying a particular version of the independence principle, a principle that is an attempt to resurrect the notion of the independence preservation of pooling operators [20] in the context of probabilistic merging operators.
One may say that the reason behind an obdurate merging operator not satisfying (CP) is its “forgetting” nature. In the first stage, it transforms sets W1,…, Wn into w(1),…, w(n) individually without taking into account other sets, thus “forgetting” any existing connections, such as the consistency. However, instead of changing the definition of an averaging projective procedure so as to make it not “forgetting”, we will take a different viewpoint on the procedure itself in the following subsection.
2.3. Fixed Points
Our second approach to an averaging projective procedure F consists of considering the set of the fixed points of F. That is, for given n ≥ 1 and given closed convex nonempty sets W1,…, Wn ⊆ ⅅJ, we are interested in whether there are any points v ∈ ⅅJ, such that:
Following the convincing justification for combining Bregman projections with the
-pooling operator (see Section 1.3), for every convex Bregman divergence Df and a family of weighting vectors
, we consider here the averaging projective procedure
defined for every n ≥ 1 and all closed convex nonempty sets W1,…, Wn ⊆ ⅅJ by the following.
- For an argument v ∈ ⅅJ, take w(i) the Df-projection of v into Wi for all 1 ≤ i ≤ n.
- Set , where a ∈ .
The restriction to convex Bregman divergences is needed for some later theorems and is adopted ad hoc. Therefore, unfortunately, we cannot provide any elaborate justification for it.
Given closed convex nonempty sets W1,…, Wn ⊆ ⅅJ, we will denote the set of all fixed points of
defined above by
, where a ∈
.
On the other hand, the conjugated parallelogram theorem (Theorem 4), suggesting the combination of the conjugated KL-projection with the LogOp-pooling operator, leads us to the consideration of those convex Bregman divergences, which are strictly convex also in the second argument. The squared Euclidean distance and the Kullback–Leibler divergence are instances of such divergences. A fairly general example is a Bregman divergence Df, such that
, where g is a strictly convex function (0, 1) → ℝ, which is three times differentiable, and g″(vj) − (wj − vj)g‴(vj) > 0 for all 1 ≤ j ≤ J and all w, v ∈ ⅅJ (this is easy to check by the Hessian matrix). Apart from the two divergences mentioned above, this condition is satisfied in particular if g(v) = vr, 2 ≥ r > 1. Note that the Bregman divergence generated by such a function g is also convex in both arguments.
Assuming strict convexity in the second argument of Df, we can define the conjugated Df-projection of v ∈ ⅅJ into a closed convex nonempty set W ⊆ ⅅJ as that unique w ∈ W that minimizes ⅅf(v‖w) subject only to w ∈ W. Moreover, since a sum of strictly convex functions is a strictly convex function, for any w(1),…, w(n) ∈ ⅅJ, there exists a unique minimizer of:
which we denote
. Thus, for a family of weighting vectors
, we can define the
-pooling operator. Note that
and that we do not need strict convexity in the second argument in these cases.
Theorem 6 (Conjugated Parallelogram Theorem). Let Df be Bregman divergence,
ⅅJ and a ∈ ⅅn. Then:
Proof. Let
. We need to prove that:
or equivalently:
Since
, differentiation using the Lagrange multiplier method (since a differentiable convex function f is necessarily continuously differentiable (see [9]), the partial derivatives used above are all continuous and the Lagrange multiplier method is permissible) applied to the condition
produces
, where λ is a constant independent of j. Therefore, Equation (3) is equal to
, and the theorem follows.
The idea of defining a spectrum of pooling operators where the pooling operators LinOp and LogOp are special cases was developed previously in a similar manner, but in a slightly different framework of alpha-divergences; cf. [27].
Here, following [1,12], we will point out a geometrical relationship between pooling operators LinOp and PoolDf, which will be helpful in illustrating some results of this paper.
Recall that the generator of a Bregman divergence Df is a strictly convex function f : (0, 1)J → ℝ, which is differentiable over ⅅJ. Let w ∈ ⅅJ. We define w∗ = ∇f(w). Since f is a strictly convex function, the mapping w → ∇ f (w) is injective; thus, the coordinates of w∗ form a coordinate system. There are two kinds of affine structures in ⅅJ. Df(w‖v) is convex in w with respect to the first structure and is convex in v∗ with respect to the second structure.
Therefore, the proof above, in fact, gives
, where
is a normalizing vector induced by
.
The only other type of averaging projective procedure
that we consider here will be generated by a convex differentiable Bregman divergence Df, which is strictly convex in its second argument, and a family of weight A and is defined for every n ≥ 1 and all closed convex nonempty sets W1,…, Wn ⊆ ⅅJ by the following.
- For an argument v ∈ ⅅJ, take w(i) the conjugated Df-projection of v into Wi for all 1 ≤ i ≤ n.
- Set , where a ∈ .
Given closed convex nonempty sets W1,…, Wn ⊆ ⅅJ, we will denote the set of all fixed points of F^Df, A defined above by
, where a ∈
.
Note that we always require an additional assumption of Df being differentiable for this type of averaging projective procedure. This assumption is essential to the proofs of some results concerning this procedure. We note that both divergences KL and E2 are differentiable.
Given a family of weighting vectors
, our aim is to investigate
and
as operators acting on
. In particular, we ask the following questions. Given any closed convex nonempty sets W1,…, Wn ⊆ ⅅJ and a ∈
:
- Are and always nonempty?
- Are these sets always closed and convex?
If both answers are positive, then we can consider
and
as probabilistic merging operators. In such a case, the following question makes sense.
- As probabilistic merging operators, do they satisfy the consistency principle (CP)?
The fact that the answer to all three questions is “yes” is perhaps surprising, given that the much simpler obdurate merging operators do not satisfy (CP). We prove the above results in the following sequence of theorems, which conclude Section 2.
The following well-known lemma is a simple, but useful observation.
Lemma 1. Let Df be a Bregman divergence and a, v, w ∈ ⅅJ. Then:
Theorem 7. Let Df be a convex Bregman divergence, W1,…, Wn ⊆ ⅅJ be closed convex nonempty sets and a ∈ ⅅn. Let v, w ∈ ⅅJ, u(1) ∈ W1,…, u(n) ∈ Wn and w(1) ∈ W1,…, w(n) ∈ Wn be such that v = LinOpa (u(1),…, u(n)), w = LinOpa(w(1),…, w(n)) and u(i) are the Df-projection of v into Wi, 1 ≤ i ≤ n. Then:
Proof. First of all, by the extended Pythagorean property, we have that:
By the parallelogram theorem:
Hence:
Since we assume that Df(·‖·) is a convex function in both arguments by the Jensen inequality:
The Inequalities (4) and (5) give:
as required. □
Figure 6 depicts the situation in the proof above for n = 2. Arrows indicate corresponding divergences.
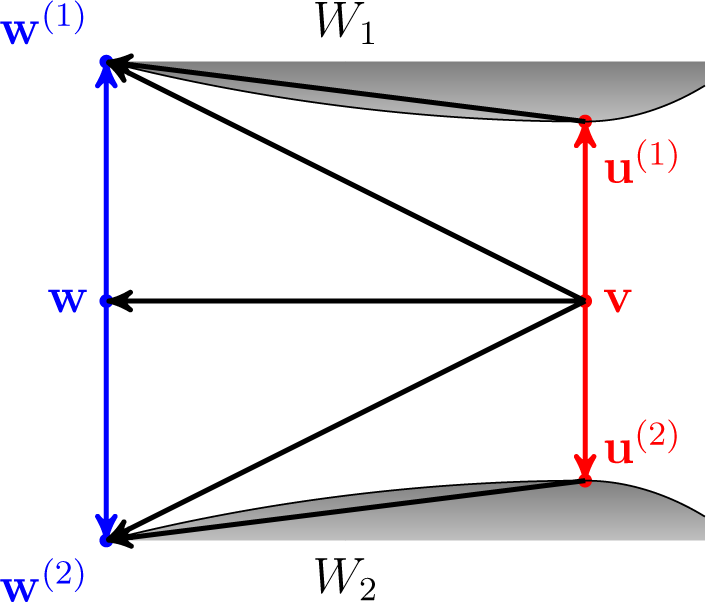
Figure 6.
The situation in the proof of Theorem 7 for n = 2.
An interesting question related to conjugated Bregman projections arises as to whether a similar property to the Pythagorean property holds. It turns out that the corresponding property is the so-called four-point property, from to Csiszár and Tusnády. The following theorem in the case of the KL-divergence is a specific instance of a result in [28], Lemma 3, but the formulation using the term “conjugated KL-projection” first appeared in [21]. An illustration is depicted in Figure 7.
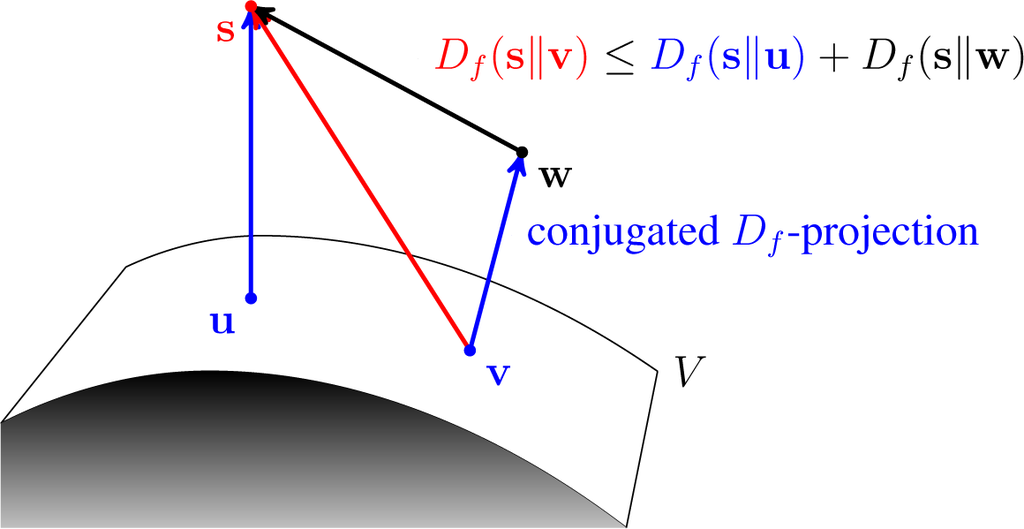
Figure 7.
The illustration of the four-point property.
Theorem 8 (Four-Point Property). Let Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument. Let V be a convex closed nonempty subset of ⅅJ, and let v, u, w, s ∈ ⅅJ be such that v is the conjugated Df-projection of w into V and u ∈ V is arbitrary. Then:
Proof. By Lemma 1, we have that:
We can rewrite the above as:
Since Df(·‖·) is a convex differentiable function, by applying the first convexity condition twice, we have that:
Expressions (6) and (7) give that:
However, since v is the conjugated Df-projection of w into V, the gradient of Df(w‖·) at (w, v) in the direction to (w, u) must be greater than or equal to zero:
and the theorem follows. □
The following result appeared for the first time in [10], but without considering the weighting.
Theorem 9 (Characterization Theorem for
). Let Df be a convex Bregman divergence, a ∈ ⅅn and W1,…, Wn ⊆ ⅅJ be closed convex nonempty sets. Then:
where the right hand-side denotes the set of all possible minimizers. That is the set of all probability functions v ∈ ⅅJ, which globally minimize, subject only to w(1) ∈ W1,…,w(n) ∈ Wn.
Proof. It is easy to see that, given closed convex nonempty sets W1,…, Wn ⊆ ⅅJ, we have that those w(1) ∈ W1,…, w(n) ∈ Wn, which together with v ∈ ⅅJ, globally minimize:
are also the Df-projections of v into W1,…, Wn respectively. This, together with Equation (1) (the equation preceding Theorem 2), gives:
Now, assume that
and
Let us denote the Df-projections of v into W1,…, Wn by w(1) …, w(n), respectively. Accordingly, let us denote the Df-projections of u into W1,…, Wn by r(1) …, r(n), respectively. Suppose that
, i.e.,
This contradicts Theorem 7, and therefore:
□
Let us now deviate for a while from the goals of this subsection and stress the importance of the restriction to the positive discrete probability functions, which was detailed in Section 1.1. The problem with the KL-divergence is that the function
is not differentiable if some xj = 0. Without the adopted restriction, the KL-divergence is therefore usually defined by:
If vj = 0 implies wj = 0 for all 1 ≤ j ≤ J, we say that v dominates w and write
.
The first problem we would face with this definition is whether the notion of the KL-projection makes sense. For given v ∈ ⅅJ and closed convex nonempty set W ⊆ ⅅJ, the KL-projection of v into W makes sense only if there is at least one w ∈ W, such that
.
However, even if adding this condition to all of the discussion concerning the KL-projection above (this is perfectly possible, as seen in [10]), Theorem 9 still could not hold, as the following example demonstrates.
Example 4. Let and. Assume that It is easy to check that and are both fixed points, but the former does not belong to the set of global minimizers v of subject to w(1) ∈ W1 and w(2) ∈ W2. An illustration is depicted in Figure 8.
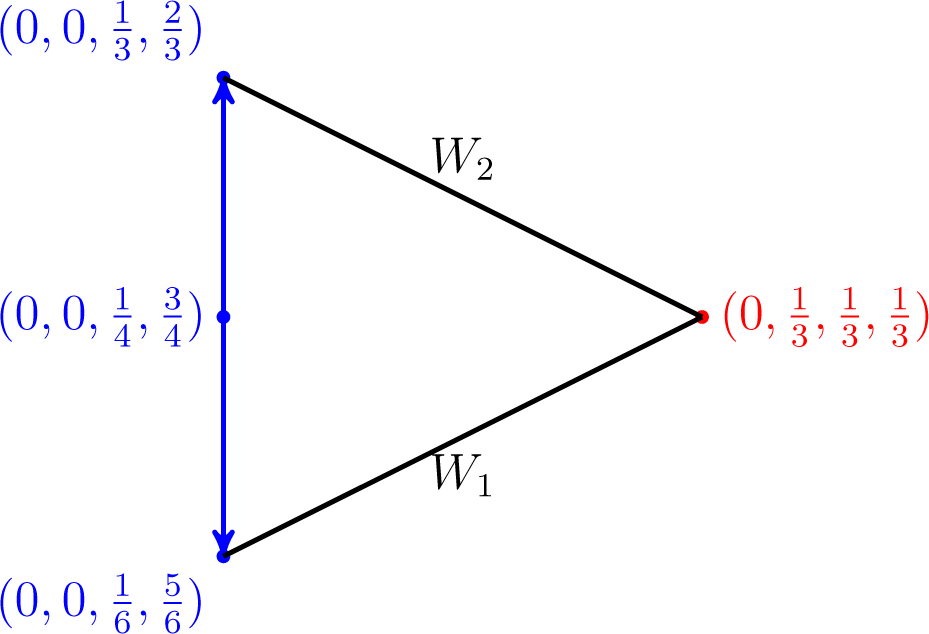
Figure 8.
The illustration of Example 4.
Moreover, some variant of the above example would show that the set
is not convex, which would wreck our aims; more details are given in [10].
On the other hand, neither of those Bregman divergences, which generate functions, are differentiable over the whole space of discrete probability functions (e.g., the squared Euclidean distance) and would encounter the difficulties of the KL-divergence. In particular, Theorem 9 formulated over the whole space of discrete probability functions (as opposed to only the positive ones) would still hold for such Bregman divergences.
Now, we shall go back and prove a theorem similar to Theorem 9 for the
-operator. In order to do that, we will need the following analogue of Theorem 7.
Theorem 10. Let Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument, and let W1,…, Wn ⊆ ⅅJ be closed convex nonempty sets and a ∈ ⅅn. Let v, w ∈ ⅅJ and u(1) ∈ W1,…, u(n) ∈ Wn and w(1) ∈ W1,…, w n) ∈ Wn be such that,
and u(i) are the conjugated Df-projection of v into Wi, 1 ≤ i ≤ n. Then:
Proof. By Theorem 6, we have that:
which by the four-point property (notice that we need the differentiability of Df to employ the four-point property) (Theorem 8) becomes:
and hence:
as required, see Figure 9. □
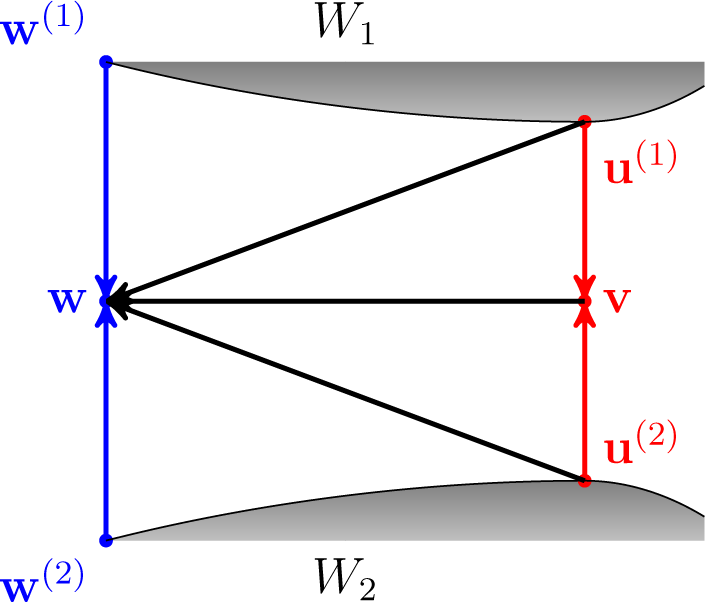
Figure 9.
The situation in the proof of Theorem 10 for n = 2.
The theorem above is fairly similar to Theorem 7. Let us use the dual affine structure in ⅅJ defined after the proof of Theorem 6 to analyze this more closely. For W ⊂ ⅅJ, define W ∗ = {w∗; w ∈ W} and define the dual divergence
to the divergence Df by
. Since, by Theorem 6, we have that
, where
is a normalizing vector induced by
, the theorem above can be rewritten as follows.
Let Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument, and let W1,…, Wn⊆ ⅅJ be closed convex nonempty sets and a ∈ ⅅn. Let v, w ∈ ⅅJ, u(1)∈ W1,…, un) ∈ Wn and w(1) ∈ W1.,…, w(n)∈ Wn be such that v∗ = LinOp ([u(1)]∗,…, [u(n)]*) + cv, w∗ = LinOpa([w(1)]∗ …, [w(n)]∗) + cw and [u(i)]∗ are the
-projection of v∗ into
, 1 ≤ i ≤ n. Then:
This illustrates that if Df is a convex differentiable Bregman divergence that is strictly convex in its second argument, then Theorems 7 and 10 are dual with respect to ∗.
Theorem 11 (Characterization Theorem for
. Let Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument, and let W1,…, Wn ⊆ ⅅJ be closed convex nonempty sets and a ∈ ⅅn. Then:
where the right hand-side denotes the set of all possible minimizers.
Proof. The proof is similar to the proof of Theorem 9. First, given closed convex nonempty sets W1,…, W ⊆ ⅅJ, we have that those w(1) ∈ W1,…, w(n) ∈ Wn, which together with v ∈ ⅅJ, globally minimize:
that are also the conjugated Df-projections of v into W1,…, Wn, respectively. This together with the definition of
gives:
Second, assume that
and:
Let us denote the conjugated Df-projections of v into W1,…, Wn by w(1), …, w(n), respectively. Accordingly, let us denote the conjugated Df-projections of u into W1,…, Wn by r(1),…, r(n), respectively. Suppose that:
i.e.,
. This contradicts Theorem 10, and therefore:
□
The following simple observation originally from [10] based on Equation (1) (alternatively on the parallelogram theorem) will be used in the proof of the forthcoming theorem.
Lemma 2. Let Df be a convex Bregman divergence and a ∈ ⅅn. Then, the following are equivalent:
- The probability functions v, w(1),…, w(n) ∈ ⅅJ minimize the quantity:subject to w(1) ∈ W1,…, w(n) ∈ Wn.
- The probability functions w(1),…, w(n) ∈ ⅅJ minimize the quantity:subject to w(1) ∈ W1,…, w(n) ∈ Wn and v = LinOpa(w(1),…, w(n)).
Theorem 12. Let Df be a convex Bregman divergence. Then, for all nonempty closed convex sets W1,…, Wn ⊆ ⅅJ and a ∈ ⅅn, the set is a nonempty closed convex region of ⅅJ.
Proof. This proof is from [10]. Let v, s ∈
, as the set is clearly nonempty. For convexity, we need to show that λv + (1 − λ)s ∈
for any λ ∈ [0, 1].
Assume that w(1) ∈ W1,…, w(n) ∈ Wn are such that v = LinOpa(w(1),…, w(n)) and u(1) ∈ W1,…, u(n) ∈ Wn are such that s = LinOpa(u(1),…, u(n)). It is easy to observe that the convexity of Df(·k·) implies convexity of: Df( ‖ ) implies convexity of:
over the convex region specified by constraints x(i) ∈ Wi, 1 ≤ i ≤ n. Moreover, the function g attains its minimum over this convex region at points (w(1),…, w(n)) and (u(1),…, u(n)). We need to show that g also attains its minimum at the point:
for any λ ∈ [0, 1]. Since g is convex by the Jensen inequality, we have that:
Since g(w(1),…, w(n)) = g(u(1),…, u(n)), the inequality above can only hold with equality, and therefore, by Lemma 2,
for any λ ∈ [0, 1].
Moreover, since convexity implies continuity, the minimization of a convex function over a closed convex region produces a closed convex set. Therefore, the fact that W1,…, Wn are all closed and convex implies that the set of n-tuples (w(1),…, w(n)), which are global minimizers of g over the region specified by w(i) ∈ Wi, 1 ≤ i ≤ n, is closed. Additionally, since closed regions are preserved by projections in the Euclidean space, the set given by LinOpa(w(1),…, w(n)) is closed, as well.
The following observation immediately follows by the definition of
.
Lemma 3. Let Df be a convex Bregman divergence and a ∈ ⅅn. Then, the following are equivalent:
- The probability functions v, w(1),…, w(n) ∈ ⅅJ minimize the quantity:subject to w(1) ∈ W1,…, w(n) ∈ Wn.
- The probability functions w(1),…, w(n) ∈ ⅅJ minimize the quantity:subject to w(1) ∈ W1,…, w(n) ∈ Wn.and
Theorem 13. Let Df be a convex Bregman divergence. Then, for all nonempty closed convex sets W1,…, Wn ⊆ ⅅJ and a ∈ ⅅn, the set a nonempty closed convex region of ⅅJ.
Proof. Let v, s ∈
, as the set is clearly nonempty. For convexity, we need to show that λv + (1 − λ)s ∈
for any λ ∈ [0, 1].
Assume that w(1) ∈ W1,…, w(n) ∈ Wn are such that
and u(1) ∈ W1,…, u(n) ∈ Wn are such that
. Now, for any λ ∈ [0, 1],
where the first inequality follows by convexity of Df(·‖·) and the second by the definition of
as the unique minimizer. However, the inequality above can only hold with equality and, by Lemma 3,
for any λ ∈ [0, 1].
Moreover, since convexity implies continuity, the minimization of a convex function over a closed convex region produces a closed convex set. Therefore, the fact that W1,…, Wn are all closed and convex implies that the set of n-tuples (w(1),…, w(n)), which are global minimizers of
over the region specified by w(i ∈ Wi, 1 ≤ i ≤ n, is closed. Additionally, since closed regions are preserved by projections in the Euclidean space, the set given by
is closed, as well. □
Finally, we can establish our initial claims:
Theorem 14. Let be a family of weighting vectors. The operator, where Df is a convex Bregman divergence, and the operator, where Df is a convex differentiable Bregman divergence, which is strictly convex in its second argument, are well defined probabilistic merging operators that satisfy (CP).
Proof. First, the fact that
is well defined as a probabilistic merging operator follows Theorems 9 and 12. Accordingly,
is a well-defined probabilistic merging operator by Theorems 11 and 13.
Second, let a ∈
(in particular a ∈ ⅅn) and W1,…, Wn ⊆ ⅅJ be closed, convex, nonempty and have a nonempty intersection. Clearly, every point in that intersection minimizes
and
subject to w(1) ∈ W1,…, w(n) ∈ Wn with both expressionsPattaining the zero value. Since Df(w‖v) = 0 only if w = v, those points in the intersection are the only points minimizing the above quantities. □
It turns out that, given closed convex nonempty sets W1,…, Wn ⊆ ⅅJ and weighting a, the sets of fixed points
and
posses attractive properties, which make the operators
and
suitable for probabilistic merging. The following example taken from [10] illustrates a possible philosophical justification for considering the set of all fixed points of a mapping consisting of a convex Bregman projection and a pooling operator.
Example 5. Assume that there are n experts, each with his own knowledge represented by closed convex nonempty sets W1,…, Wn ⊆ ⅅJ, respectively. Say that an independent chairman of the college has announced a probability function v to represent the agreement of the college of experts. Each expert then naturally updates his own knowledge by what seems to be the right probability function. In other words, the expert “i” projects v to Wi, obtaining the probability function w(i). Each expert subsequently accepts w(i) as his working hypothesis, but he does not discard his knowledge base Wi; he only takes into account other people’s opinions. Then, it is easy for the chairman to identify the average of the actual beliefs w(1),…, w(n) of the experts. If he found that this average v′ did not coincide with the originally announced probability function v, then he would naturally feel unhappy about such a choice, so he would be tempted to iterate the process in the hope that, eventually, he will find a fixed point.
It seems that, in a broad philosophical setting, such as in the example above, we ought to study any possible combination of Bregman projections with pooling operators. The question as to which other combination produces a well-defined probabilistic merging operator satisfying the consistency principle (CP) is open to investigation.
3. Convergence
3.1. Iterative Processes
In this section, we continue the investigation of the averaging projective procedures
and
. Recall that, given a convex Bregman divergence Df and a family of weighting vectors
,
, was defined in the previous section for every n ≥ 1 and all closed convex nonempty sets W1,…, Wn ⊆ ⅅJ by the following.
- For an argument v ∈ ⅅJ, take w(i) as the Df-projection of v into Wi for all 1 i ≤ n.
- Set , where a ∈ .
For Df, which is moreover differentiable and strictly convex in the second argument,
was defined analogously by conjugated projections and the
-pooling operator.
Our current aim is to find out what will happen if we iterate the application of averaging projective procedures
and
. In particular:
- Will the resulting sequences converge?
We shall find the answer in this subsection.
It is intriguing that we can abstractly define a “conjugated projection” with respect to a summation of a convex differentiable Bregman divergence Df. Let w(1),…, w(n) ⅅJ and a ∈ ⅅn. Then, the “conjugated projection” of (w(1),…, w(n))into ⅅJ is defined by the global minimizer of
, which, by Equation (1), is v = LinOpa(w(1),…, w(n)).
The claim that this behaves as a “conjugated projection” is supported by the following analogue of the four-point property illustrated in Figure 10.
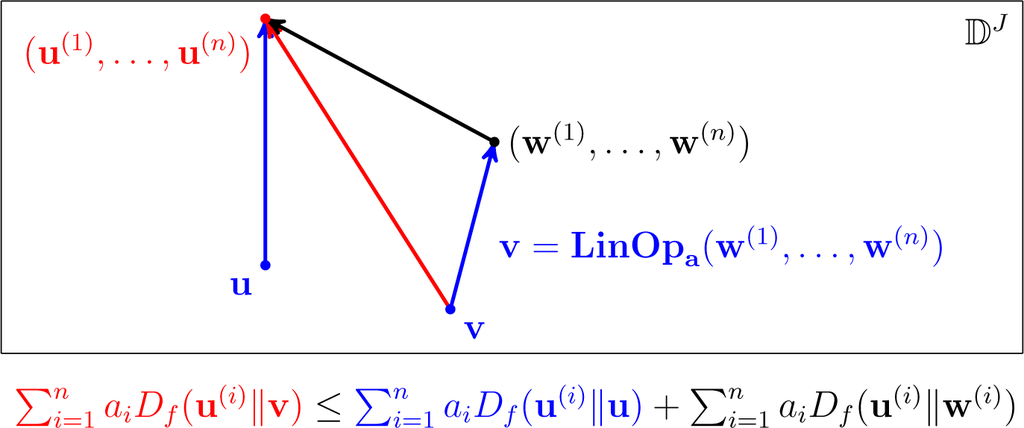
Figure 10.
The illustration of Theorem 15.
Theorem 15. Let Df be a convex differentiable Bregman divergence. Let a ∈ ⅅn, w(1),…, w(n) ∈ ⅅJ and v = LinOp (w(1),…, w(n)). Let u(1),…, u(n) ∈ ⅅJ and u ∈ ⅅJ. Then:
Proof. The proof is similar to the one of the actual four-point property (Theorem 8) only with a slightly different argument at the end: after obtaining:
we proceed with:
since
for all 1 ≤ k ≤ J, and the theorem follows. □
Similarly, given w(1),…, w(n) ∈ ⅅJ, a ∈ ⅅn and a convex differentiable Bregman divergence Df, which is strictly convex in its second argument, we can consider
the “projection” of (w(1),…, w(n)) into ⅅJ, since Theorem 6 resembles (a special case of) the extended Pythagorean property: for any u ∈ ⅅJ:
The two observations above and the following lemma will be essential to the proofs of the two main theorems of this subsection.
Lemma 4. Let Df be a convex Bregman divergence. Assume that we are given a closed convex nonempty set W, v[i] ∈ ⅅL, i = 1, 2,… and w[i] ∈ ⅅJ, i = 1, 2,…, such that w[i] is the D -projection of v[i] into W for all i = 1, 2,…. Assume that converges to v ∈ ⅅJ and converges to w ∈ ⅅJ. Then, w is the Df-projection of v into W.
Proof. For a contradiction, assume that the Df-projection of v into W denoted by
is distinct from w. Then, by the extended Pythagorean property,
. Since Df(·‖·) is continuous (see Section 1.1), we have that:
Therefore:
, which contradicts the assumption that
is the Df-projection of v into W. □
Finally, we are going to answer the question about whether the iteration of the averaging projective procedures
and
converges; however, the result for
will be limited only to the case when Df is differentiable. Both results below should be attributed to a number of people. First, the results are applications of well-known alternative projections due to Csiszár and Tusnády; see [28], Theorem 3. In a particular case of the Kullback–Leibler divergence, the theorems were observed and proven by Matúš in [21]. Last, but not least, Eggermont and LaRiccia reformulated original alternative projections in terms of Bregman divergences in [29].
Theorem 16. Let Df be a convex differentiable Bregman divergence, A be a family of weighting vectors and a ∈
be such that a ∈ ⅅn and W1,…, Wn ⊆ ⅅJ are closed, convex and nonempty. Then, for any v ∈ ⅅJ, the sequence:
where v[0] = v and converge to some probability function in. (Recall that is the set of the fixed points of, i.e., all points v, such that.)
Proof. This proof is inspired by [21].
Denote the Df-projections of v[i] into W1,…, W by π1 v[i],…, πnv[i], respectively. Then, it is easy to observe that:
for all i = 1, 2,…. Due to the monotonicity of this sequence, the limit
exists. Thanks to the compactness of W1,…, Wn, the sequence
has a convergent subsequence. Let us denote the limit of this subsequence (π1v,…, πnv, v). Due to Lemma 4, πkv is really the Df-projection of v into Wk for all 1 ≤ k ≤ n. Moreover
By Theorem 15:
This is because
. Moreover, by the extended Pythagorean property:
An illustration of the situation is depicted in Figure 11.
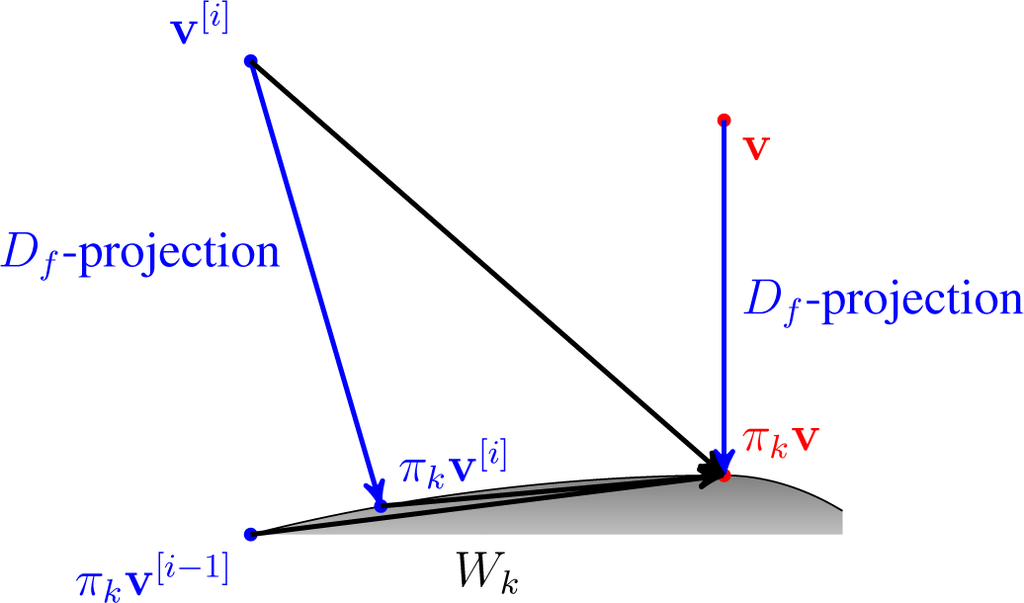
Figure 11.
The situation in the proof of Theorem 16.
Now, since:
and
for all i = 1, 2,…, Equations (8) and (9) give that:
for all i = 1, 2,…. We conclude that this is possible only if:
exists.
However, we already know that a subsequence of
converges to (π1v,…, πnv); hence, a subsequence of the sequence
decreases to zero, which by Equation (10), forces the whole sequence to converge to zero. Due to the fact that Df(x‖y) = 0, only if x = y and, by the continuity, we get:
It follows that
exists and is equal to v. Moreover,
, and therefore, v is a fixed point of the mapping
; hence,
.
The following analogue of Lemma 4 will be needed in the forthcoming theorem.
Lemma 5. Let Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument. Assume that we are given a closed convex nonempty set W , v[i] ∈ ⅅL, i = 1, 2,… and w[i] ∈ ⅅJ, i = 1, 2,…, such that w[i] is the conjugated D -projection of v[i] into W for all i = 1, 2,…. Assume that converges to v ∈ ⅅJ and converges to w ∈ ⅅJ. Then, w is the conjugated Df-projection of v into W.
Proof. For a contradiction, assume that the conjugated Df-projection of v into W denoted by
is distinct from w. Then, by the four-point property,
. Since Df(·‖·) is continuous, we have that:
Therefore:
, which contradicts the assumption that
is the conjugated Df-projection of v into W. □
Theorem 17. Let Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument,
be a family of weighting vectors and a ∈
be such that a ∈ ⅅn and W1,…, Wn ⊆ ⅅJ are closed, convex and nonempty. Then, for any v ∈ ⅅJ, the sequence:
where, converges to some probability function in. (Recall that is the set of the fixed points of, i.e., all points v, such that).
Proof. Denote the conjugated Df-projections of v[i] into W1,…, W by
, respectively. Then, it is easy to observe that:
for all i = 1, 2,…. Due to the monotonicity of this sequence, the limit
exists. Thanks to the compactness of W1,…, Wn sequence
has a convergent subsequence. Let us denote the limit of this subsequence (π1v,…, πnv, v). Due to Lemma 5, πkv is really the conjugated Df-projection of v into Wk for all 1 ≤ k ≤ n. Moreover:
By the four-point property:
Moreover, by Theorem 6:
That is because
. An illustration of the situation is depicted in Figure 12.
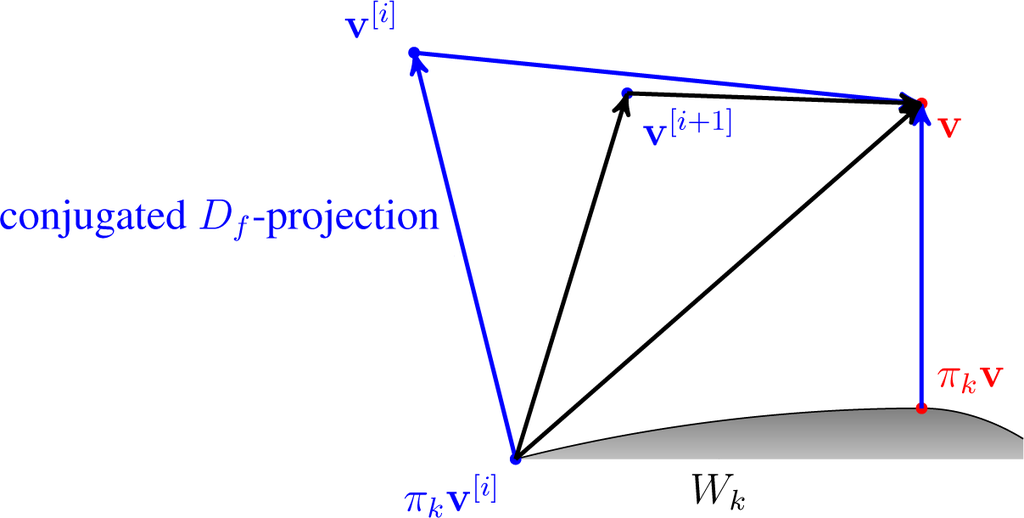
Figure 12.
The situation in the proof of Theorem 16.
Now, since:
and
for all i = 1, 2,…, the expressions (11) and (12) give that:
for all i = 1, 2,…. We conclude that this is possible only if:
exists.
However, we already know that a subsequence of
converges to v; hence, a subsequence of the sequence
decreases to zero, which by Equation (13), forces the whole sequence to converge to zero. Due to the fact that Df(x‖y) = 0 only if x = y and by the continuity, we get:.
and, subsequently,
(the subsequence of
has πkv as a limit, and
is monotonic).
Moreover,
since
is continuous
is continuous and strictly convex in the first argument). Therefore, v is a fixed point of the mapping
, and hence,
. □
The problem of characterizing the limits of Theorems 16 and 17 more precisely remains open. On the other hand, the theorems suggest a way to compute at least some points in
and
, although we have not investigated how fast the sequences converge. Moreover, also the question of how effective it is to compute Df-projections and conjugated Df-projections was left unanswered. This latter problem was nevertheless addressed in the literature, at least in the case of the KL-divergence and sets W1,…, Wn generated by finite collections of marginal probability functions. In such a case, the well-known iterative projective fitting procedure IPFP can be effectively employed [16].
3.2. Chairmen Theorems
In this section, for a convex differentiable Bregman divergence Df, which is strictly convex in its second argument, and a family of weighting vectors
, we investigate the susceptibility of
and
-merging operators to a small bias by an arbitrary probability function in ⅅJ. The study of this problem first occurred in [18], where Wilmers argued that an independent adjudicator, whose only knowledge consists of what is related to him by the given college of experts, can rationally bias the agreement procedure by including himself as an additional expert, whose personal probability function is the uniform one (not arbitrary), in order to calculate a single social probability function and then find what would happen to this social probability function if his contribution happened to be infinitesimally small relative to that of the other experts. He showed that in the case of the
-merging operator, this point of agreement is characterized by the most entropic point in the region defined by
. A similar theorem for the
-merging operator was proven in [10]. In what follows, we adapt these results to our general situation.
The following theorem will tell us that, in some particular case of W1,…, Wn ⊆ ⅅJ, we can always tell that the set
is a singleton.
Theorem 18. Let W1,…, Wn ⊆ ⅅJ be closed, convex, nonempty and such that, for at least one i Wi is a singleton. Let Df be a convex Bregman divergence, which is strictly convex in its second argument and a ⊆ ⅅn. Then,
is a singleton.
Proof. Without loss of generality, assume that W1 = {v}. For a contradiction, suppose that w, r ∈
and w ≠ r. Denote w(2),…, w(n) the Df-projections of w into W2,…, Wn, respectively, and r(2),…, r(n) the Df-projections of r into W2,…, Wn, respectively. By definition, w = LinOpa(v, w(2),…, w(n)) and r = LinOpa(v, r(2),…, r(n)).
Now, consider x = λw + (1 − λ)r for some λ ∈ (0, 1). By Theorems 9 and 12, we have that
. Since Df(·‖·) is a convex function, by the Jensen inequality, we have that:
However, since
and λw(i)+ (1 − λ)r(i) ∈ Wi, 1 ≤ i ≤ n, the above is possible only with the equality.
On the other hand, since Df is strictly convex in its second argument, the following Jensen inequality is strict:
Note that the border points λ = 0, 1 are excluded. Therefore, Equation (14) yields:
However, this contradicts the Jensen inequality.
Theorem 19 (Chairman Theorem for
). Let I ⊆ ⅅJ be a singleton consisting of an arbitrary probability function t ⊆ ⅅJ. Let W1,…, Wn ⊆ ⅅJ be closed, convex and nonempty, a ∈
be such that a ∈ ⅅn and Df be a convex Bregman divergence, which is strictly convex in its second argument. For 1 > λ > 0, define (by the previous theorem, the following set is a singleton):
Then,
exists and equals
i.e., it equals the conjugated Df-projection of the probability functiont into.
Proof. This proof is inspired by [30], where a slightly stronger result is proven for the special case of
. We note that Theorem 9 from Section 2.3 is implicitly used in what follows.
First, denote
as the minimal value of:
subject to w(i) ∈ Wi, 1 ≤ i ≤ n and v ∈ ⅅJ. Furthermore, we denote Eλ as the minimal value of:
subject to w(i) ∈ Wi, 1 ≤ i ≤ n and v ∈ ⅅJ. By the definition of
, we have that 0 ≤ Eλ for all 1 > λ > 0.
Note that for a fixed λ, if v ∈ ⅅJ globally minimizes Equation (15) subject to w(i) ∈ Wi, 1 ≤ i ≤ n, then
(by Theorem 18, such a v is unique), and conversely,
, then v minimizes Equation (15), subject to the above constraints.
Now,
. Since
, it follows that for all 1 > λ > 0, we have that:
Since ⅅJ ⊆ ℝJ is a compact space, there exists a sequence
, such that
converges. Let w(i)[λm] be the Df-projection of v λm] into Wi for all 1 ≤ i ≤ n and m = 1, 2,…. By Equation (16), the sequence:
converges to
.
Note that we already know that
exists, and we denote it by v. However, we do not know whether the same is true for
, 1 ≤ i ≤ n. On the other hand, since W1,…, Wn are compact, the considered sequences have convergent subsequences. Let us denote the corresponding limits w(1),…, w(n). Since Df(·‖·) is a continuous function in both variables, the value of
must be equal to
. However, this means that we have found a global minimizer (w(1),…, w(n), v) of
subject to w(i) ∈ Wi, 1 ≤ i ≤ n, and v ∈ ⅅJ.
It follows that
. By Equation (16):
Hence,
for all m = 1, 2,…. However, by definition of r, this is possible only if r = v.
In fact, we have proven that for every sequence
, such that limm→∞ λm = 0 and
is convergent,
must converge to r. Therefore, assume that there is a sequence
, such that limm→∞ λm = 0, but {v λm]}∞m=1 is not convergent. Then, there is an open neighborhood of the point r outside of which there are an infinite number of the members of the sequence
Since ⅅJ is compact, this sequence must have a convergent subsequence with a limit distinct from r. That, however, contradicts our previous claim.
The theorem above is illustrated in Figure 13. Indeed, if
is a singleton, then the limit in the theorem above is obvious. By Theorem 18, this happens in particular when at least one of W1,…, Wn is a singleton. However, it is not hard to observe an interesting case; consider that W1,…, Wn have a nonempty intersection, which is not a singleton. In this case, the limit above is, in fact, the conjugated Df-projection of the probability function t into that intersection. Such a conjugated projection depends on t. In particular, we can recover any point in the intersection by setting it to be the point t.
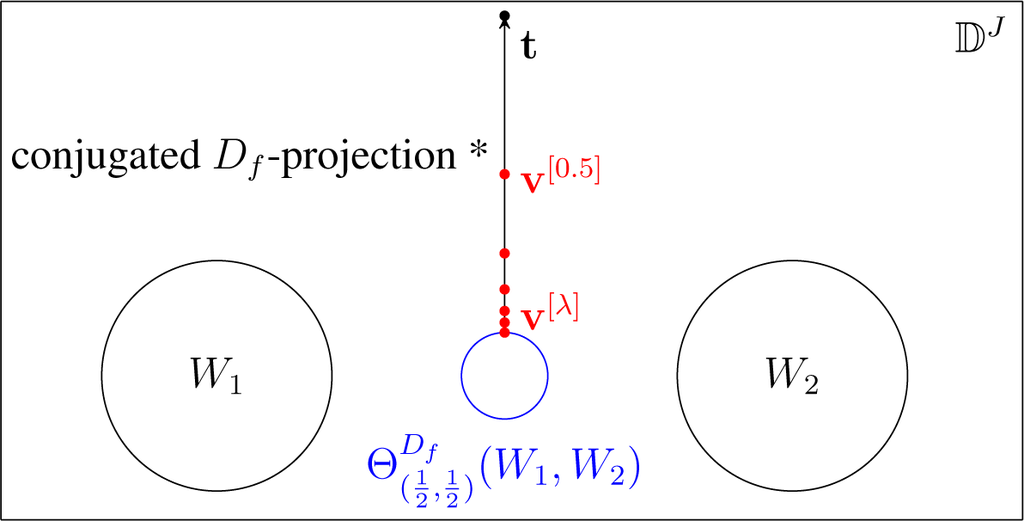
Figure 13.
The illustration of the chairman theorem for
.* Note that the fact that v[λ]-s lie on the arrow does not have any meaning.
The following analogue of Theorem 18 has a fairly similar proof.
Theorem 20. Let W1,…, Wn ⊆ ⅅJ be closed, convex, nonempty and such that, for at least one i Wi is a singleton. Let Df be a convex Bregman divergence, which is strictly convex in its second argument and a ∈ ⅅn. Then,
is a singleton.
Theorem 21 (Chairman Theorem for
. Let I ⊆ ⅅJ be a singleton consisting of an arbitrary probability function t ∈ ⅅJ. Let W1,…, Wn ⊆ ⅅJ be closed, convex and nonempty, a ∈
be such that a ∈ ⅅn and Df be a convex differentiable Bregman divergence, which is strictly convex in its second argument. For 1 > λ > 0, define:
Then,
exists and equals:
i.e., it equals the Df-projection of the probability function t into.
The proof is analogous to the one of Theorem 19, so we omit it.
4. Applications
4.1. Relationship to Inference Processes
In this subsection, we will discuss some striking relationships between the chairmen theorems and the framework of inference processes [26]. Inference processes are methods of reasoning by which an expert may select a single probability function from a nonempty closed convex set of possible options. In our framework, it is simply a problem of choosing a single probability function in a closed convex nonempty set W ⊆ ⅅJ. This selection is, however, not arbitrary, and it is expected to satisfy some rational principles based on symmetry and consistency, as discussed in [15]. The maximum entropy (ME) inference process, which chooses the most entropic point in a given closed convex nonempty set, is uniquely justified by a list of such principles, as Paris and Vencovská showed [15].
As discussed in Section 1.2, the most entropic point in a closed convex nonempty set W ⊆ ⅅJ coincides with the KL-projection of the uniform probability function into W. This can be immediately applied to the chairman theorem for
, where
is a family of weighting vectors:
Let I ⊆ ⅅJ be a singleton consisting of the uniform probability function t ∈ ⅅJ. Let W1,…, Wn ⊆ ⅅJ be closed, convex and nonempty and a ∈
be such that a ∈ ⅅn. For 1 > λ > 0, define:
Then:
For the family of weighting vectors:
the operator that results by applying the ME-inference process to the operator
is, in fact, a probabilistic merging operator, which was introduced and studied by Wilmers in [18] under the name “social entropy process” or SEP, for short. In that paper, Wilmers argues that this merging operator is, to date, the most appealing with respect to symmetry and consistency; somehow, in the spirit of the original justification for the ME-inference process, although the problem of finding a complete justification is still open.
Whether SEP will turn out to be the most appealing probabilistic merging operator or not, by the same manner as above, we can define several probabilistic merging operators related to several other classical inference processes.
For example, the conjugated KL-projection of the uniform probability function into a closed convex nonempty set W ⊆ ⅅJ in fact generates the so-called CM∞-inference process (a limit version of the central mass process [26]). We write simply CM∞(W ) to denote the point of the projection, which is explicitly given by:
The chairman theorem for
then suggests considering the probabilistic merging operator defined for every n ≥ 1 and all closed convex nonempty sets W1,…, Wn ⊆ ⅅJ by:
where a ∈ ⅅn and a ∈
. We will call this operator the conjugated social entropy process coSEP.
What is really appealing about the operators SEP and coSEP is that there are singletons; we simply say that they satisfy the singleton principle (SP). Furthermore, the consistency principle (CP) is obviously satisfied by all of them. However, there is an interesting principle that can never be satisfied by a probabilistic merging operator that satisfies (CP) and is always a singleton: the disagreement principle introduced in [5].
(DP) Disagreement Principle. Let Δ be a probabilistic merging operator. Then, we say that Δ satisfies the disagreement principle if, for every n, m ≥ 1 and all W1,…, Wn ⊆ ⅅJ and V1,…, Vm ⊆ ⅅJ:
implies:
We cite [5] on the desirability of this principle: the principle (informally) says “… that a consistent group who disagrees with another group and then merges with them can be sure that they have influenced the opinions of the combined group.”
Theorem 22. There is no probabilistic merging operator that satisfies all (SP), (CP) and (DP).
Proof. Let Δ be a probabilistic merging operator. Assume that V ⊊ W ⊆ ⅅJ and that V is a singleton. Suppose that Δ(W) ≠ V = Δ(V). Then, by (CP), Δ(W, V) = V, which contradicts (DP).
Theorem 23. The probabilistic merging operators and, where Df is a convex Bregman divergence for the prior and is additionally differentiable and strictly convex in its second argument for the latter, satisfy (DP).
Proof. We prove the theorem only for
. The proof for
is similar.
Let W1,…, Wn, V1,…, Vm ⊆ ⅅJ be closed convex and nonempty. For a contradiction, assume that
,
and, at the same time,
.
Denote v(i) the conjugated Df-projection of v into Vi, 1 ≤ i ≤ m. Then, there is u ∈ ⅅJ, such that
, i.e.,
. Since every Bregman divergence is strictly convex in its first argument, we have that:
Now, denote w(i) the conjugated Df-projection of v into Wi, 1 ≤ i ≤ n. Since
and
the strict convexity of divergences in their first argument gives also: Bregman
and:
However, this contradicts Equation (17). □
We can conclude that, before deciding which probabilistic merging operator to use, we need to establish which two of the three properties we want the operator to satisfy. In this paper, we have seen instances of all three options, as listed in Table 1.

Table 1.
Examples for three saturated possibilities with respect to the consistency principle (CP), disagreement principle (DP) and singleton principle (SP). KIRP, Kern-Isberner and Rödder; OSEP, obdurate social entropy process; SEP, social entropy process; coSEP, conjugated social entropy process.
Recall that KIRP is the operator due to Kern-Isberner and Röder and OSEP is the obdurate social entropy process; see Section 2.2 for more details. A proof that KIRP and OSEP satisfy (DP) can be easily obtained as a modification of the proof of Theorem 23, so we omit it.
4.2. Computability
In this subsection, we would like to propose a method corresponding to the classical method of projection, but in the multi-expert context. The possible use could be similar; if the knowledge of a college of experts could be characterized by a closed convex nonempty set of probability functions, then we would like to find such a probability function in that set that is “closest” to a given piece of information represented by another probability function. We only need to specify a way to represent the knowledge of the college by such a single set and pair it with an appropriate method of projection.
Throughout this subsection, assume that we are given closed convex nonempty sets of probability functions W1,…, Wn ⊆ ⅅJ with weighting a ∈
, where ai is the weight of Wi and a probability function v ∈ ⅅJ to represent.
If the measure of “being closed” is quantified by a projection by means of a convex differentiable Bregman divergence Df, which is strictly convex in its second argument, our proposed method consists of the following. First, represent W1,…, Wn by a single, closed and convex set
, and then, take the Df-projection of v into
.
On the other hand, if the measure of “being closed” is quantified by a conjugated projections by means of a convex differentiable Bregman divergence Df, which is strictly convex in its second argument, we first represent W1,…, Wn by a single, closed convex set
and then take the conjugated Df-projection of v into
.
The methods have two distinguishing features:
- If all of the sets W1,…, Wn are singletons, the methods reduce to and -pooling operators respectively.
- If W1,…, Wn have a nonempty intersection V, they reduce to Df and conjugated Df-projections into V, respectively.
In this subsection, we shall investigate how effective it is to compute the results of those two methods. Notice that SEP and coSEP, defined in Section 4.1, are specific instances of those procedures, respectively, in which case, we are interested in KL-projections and conjugated KL-projections of the uniform probability function.
There are indeed some serious computational issues. The most essential is the following. A closed convex nonempty set W ⊆ ⅅJ is often given by a set of constraints on ⅅJ. How can we effectively verify that the resulting set W is nonempty? Unfortunately, it is not even possible to find a random Turing machine running in polynomial time that upon input given by a set of constraints on probability functions verifies the consistency of this set of constraints (given that the problems solvable in a randomized polynomial time cannot be solved in a polynomial time); see Theorem 10.7 of [26].
However, some computational problems closely related to projections have been extensively studied in the literature. As we have noted in Section 3.1, this includes procedures for finding a KL-projection to a closed convex set of probability functions. These show that in many particular practical implementations, the problem of intractability does not arise, e.g., as in the case when given closed convex nonempty sets are generated by marginal probability functions and where the IPFP-procedure can be applied to effectively find a KL-projection; see [16]. Therefore, we will assume that some effective procedures for Df-projections and conjugated Df-projections are given.
Under such an assumption, the iterative processes from Section 3.1 and the Chairmen theorems offer a way how to compute (although possibly ineffectively) the results of the two methods above. We shall start with the latter.
By Theorem 16, we know that the sequence:
where v[0] = t is arbitrary in ⅅJ and
, converges to some probability function in
. Notice that Df is required to be differentiable in order to establish this conclusion.
Recall that by Theorem 18,
is a singleton when at least one of W1,…, Wn is a singleton. Let I ∈ ⅅJ be such that I = {v}. For every 1 > λ > 0, we define the sequence
by
(t can be arbitrary) and:
By Theorem 16:
By the chairman theorem for
:
i.e., equals the conjugated Df-projection of the probability function v into
.
Now, notice that if the limits in Equation (18) were interchangeable, then this would offer an answer to the question from Section 3.1 to closely characterize the limit limi→∞v[i] but with no claims to any theoretical results on the complexity of the computation). Unfortunately, the following simple example introduced in [10] shows that these limits are not interchangeable.
Example 6. Let and. Assume that the weighting is, Df = KL and the probability function v ∈ ⅅ4 to interpret is the uniform probability function. In other words, we are looking for coSEP(W1, W2).
Then, the members of the sequence can be computed by two minimization problems: find and that minimize:
and another couple and that minimize:
Then,
and After setting it turns out that in each iteration,
and.
After performing the numerical computation for the first one hundred iterations, we obtain:
The rate of convergence for the first coordinate of probability functions is depicted in Figure 14 by the bottom red line.
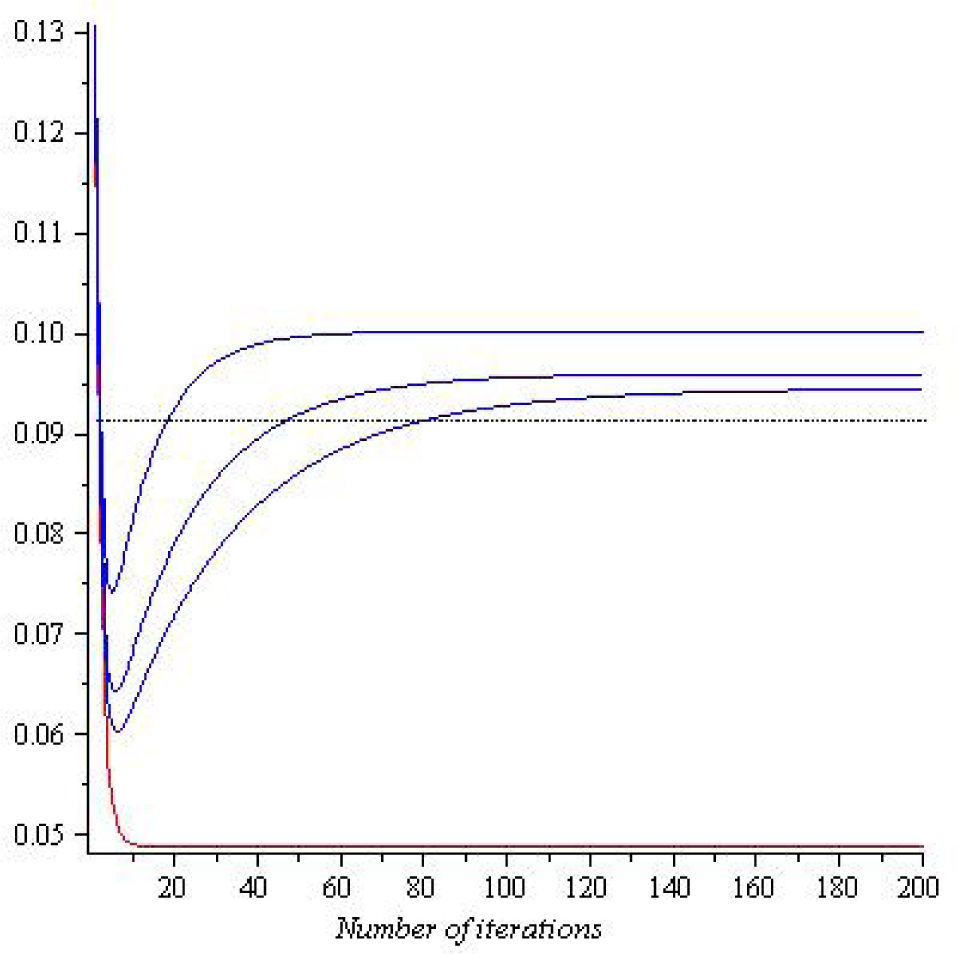
Figure 14.
The numerical computation for Example 7. Blue lines from the top are for
and
. This graph is taken from [10].
However, since W1 and W2 are jointly consistent, we have that:
We compute that CM∞(W1 ∩ W2) (the conjugated KL-projection of the uniform probability function) is approximately:
which is obviously not equal to the limit of the sequence.
It seems that the only viable way to use Equation (18) to estimate a result of the conjugated Df-projection into
is to choose a sufficiently small λ, and for this λ, iterate the sequence
. However, the rate of convergence heavily depends on λ, and in fact, this often materializes in a negative way for a practical computation [10]:
Example 7. Consider the situation from Example 6. We compute numerically the first coordinate of initial members of the sequence for several values of λ, and we compare them with the first coordinate of the sequence. The algorithm we use is as follows. Note that due to the design of the sets, only one minimization problem is sufficient to solve in each iteration, as we have pointed out in the previous example.
for i from 1 by 1 to 200 do
Minimize end do;
The numerical result for is plotted in Figure 14. We can see that as λ decreases, the limit points of sequences are converging to the first coordinate of CM∞(W1 ∩ W2), which is denoted by the black dotted line. The red line denotes the first coordinate of the sequence.
The numerical result for is plotted in Figure 15. We can conclude that, although the eventual precision rises as λ decreases, the rate of convergence is affected severely. Therefore, there is a significant trade-off between the precision and the number of iterations.
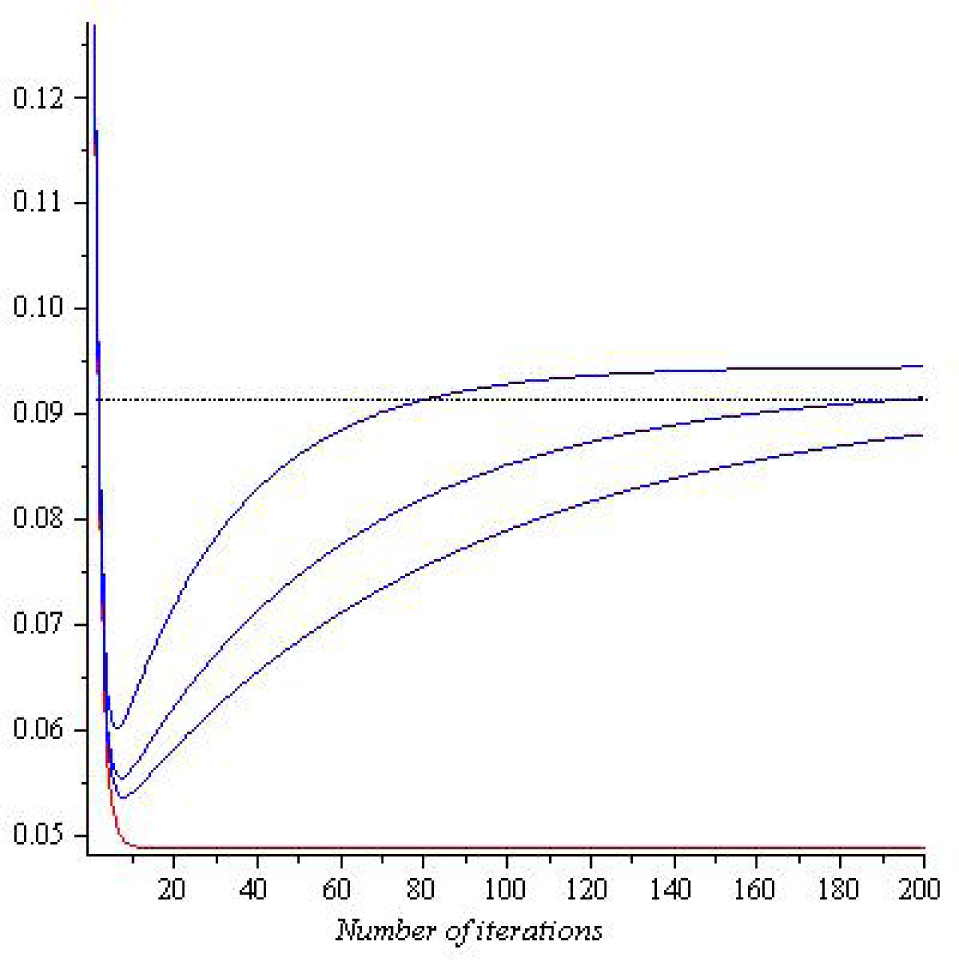
Figure 15.
The numerical computation for Example 7. Blue lines from the top are for
and
. This graph is taken from [10].
Notice that, as λ decreases, the blue lines point-wise converge to the red line. This convergence is, however, obviously not uniform.
Now, consider the prior method, which follows a fairly similar computation idea. By Theorem 17, we know that the sequence:
where u[0] = t is arbitrary in ⅅJ and
, converges to some probability function in
. This procedure can be, for instance, immediately used to compute SEP(W1,…, Wn) in a case when
is a singleton. By Theorem 20, this happens when at least one of W1,…, Wn is a singleton.
One may perhaps expect that if u[0] is the uniform probability function, then {limi→∞u[i]} = SEP(W1,…, Wn). In the following example from [10], we will, however, see that this is not true in general. Note that we cannot use Example 6, since in that case, actually, {limi→∞u[i]} = SEP(W1,…, Wn).
Example 8. Let J = 8,
and:
W1 and W2 have a nonempty intersection;, and we can compute that SEP(W1, W2) is the most entropic probability function from the set above with x equal to approximately 0.013888.
However, the sequence is already constant after one iteration and equals CM∞(W1) = CM∞(W2) = CM∞(W1 ∩ W2), in which case, x ≈ 0.029231.
By the aid of the chairman theorem for
, we also suggest a way to approximate the Df-projection of v into
, but we have no claims to any theoretical results on the complexity of computation. Let I = {v}. For every 1 > λ > 0, we define the sequence
by
, which is arbitrary, and:
By Theorem 17:
By the chairman theorem for
:
i.e., equals the Df-projection of the probability function v into
.
In particular, to approximate SEP(W1,…, Wn) using Equation (19), one needs to choose a sufficiently small λ and then iterate the sequence
, where
is the uniform probability function,
and Df = KL. However, the question of how to determine such an λ and i in order to achieve a specific level of accuracy merits further investigation.
The special case of the problem above when W1,…, Wn have a nonempty intersection was extensively studied in the literature, and many scientific and engineering problems can be expressed as a problem of finding a point in such an intersection. Bregman in [7] showed the convergence of (what is now called) cyclic Bregman projections to a point in the intersection (the notion of a Bregman divergence is used only for the Euclidean space, but in [7], a more general topological vector space was considered). Many cyclic algorithms with appealing applications have been developed since then; see, e.g., [31,32].
Although the approach we propose offers the option of an empty intersection, it always leads to a meaningful point, and in particular, if the intersection is nonempty, it chooses a point inside the intersection; our study cannot be considered as an extension of the classical method of cyclic projections, which was developed over (possibly infinite) Banach spaces [33] in contrast to a limited discrete probabilistic space, which we are considering.
It is also worth mentioning that the method of cyclic projections, even in the case of an empty intersection, often provides more useful results than our method. An example is the noise reduction algorithm from [34].
One can perhaps conclude that the approach offered in this paper is at its best only another contribution to the problem of finding a point in a convex set by means of geometry, which, however, offers some interesting insights into the combination of Bregman projections with pooling operators.
Acknowledgments
The author is indebted to George Wilmers, whose support and wisdom allowed the creation of this paper. Thanks goes also to Alena Vencovská and František Matúš for sharing their ideas with me and to an anonymous reviewer for pointing out the connections to the dual affine structure in the probabilistic simplex.
The paper is an extension of some results that the author obtained as a Ph.D. student at the University of Manchester while supported by the (European Community’s) Seventh Framework Programme (FP7/2007-2013) under Grant Agreement No. 238381.
Last, but not least, the author is grateful for the support received from the Assumption University in Thailand, without which the paper could not be finished.
Conflicts of Interest
The author declares no conflict of interest other than disclosed above in acknowledgments.
References
- Amari, S. Divergence, Optimization and Geometry. In Neural Information Processing: 16th International Conference; Leung, C., Lee, M., Chan, J.H., Eds.; Iconip: Bangkok, Thailand, 2009; pp. 185–193. [Google Scholar]
- Hájek, P.; Havránek, T.; Jiroušek, J. Uncertain Information Processing in Expert Systems; Raton, B., Arbor, A., Eds.; CRC Press: London, UK, 1992. [Google Scholar]
- Collins, M.; Schapire, R.E. Logistic Regression, AdaBoost and Bregman Distances. Mach. Learn. 2002, 48, 253–285. [Google Scholar]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman Divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Adamčík, M.; Wilmers, G.M. 2015, in press.
- De Finetti, B. Sul Significato Soggettivo della Probabilitá. Fund. Math. 1931, 17, 298–329. [Google Scholar]
- Bregman, L.M. The relaxation method of finding the common points of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; pp. 1–716. [Google Scholar]
- Rockafeller, R.T. Convex Analysis. Princeton Landmarks in Mathematics; Princeton University Press: Princeton, NJ, USA, 1997; pp. 1–469. [Google Scholar]
- Adamčík, M. Collective Reasoning under Uncertainty and Inconsistency. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2014; pp. 1–150. [Google Scholar]
- Csiszár, I. I-Divergence Geometry of Probability Distribution and Minimization Problems. Ann. Probab. 1975, 3, 146–158. [Google Scholar]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; AMS and Oxford University Press: New York, NY, USA, 2000; pp. 1–206. [Google Scholar]
- Jaynes, E.T. Where do we Stand on Maximum Entropy? In The Maximum Entropy Formalism; Levine, R.D., Tribus, M., Eds.; M.I.T. Press: Cambridge, MA, USA, 1979; pp. 15–118. [Google Scholar]
- Paris, J.B.; Vencovská, A. On the Applicability of Maximum Entropy to Inexact Reasoning. Int. J. Approx. Reason. 1989, 3, 1–34. [Google Scholar]
- Paris, J.B.; Vencovská, A. A Note on the Inevitability of Maximum Entropy. Int. J. Approx. Reason. 1990, 4, 183–224. [Google Scholar]
- Vomlel, J. Methods of Probabilistic Knowledge Integration. Ph.D. Thesis, Czech Technical University, Prague, Czech, 1999; pp. 1–123. [Google Scholar]
- Banerjee, A.; Guo, X.; Wang, H. On the optimality of conditional expectation as a Bregman predictor. IEEE Trans. Inf. Theory 2005, 51, 2664–2669. [Google Scholar]
- Wilmers, G.M. The Social Entropy Process: Axiomatising the Aggregation of Probabilistic Beliefs. In Probability, Uncertainty and Rationality; Hosni, H., Montagna, F., Eds.; CRM Series; Pisa, Italy, 2010; pp. 87–104. [Google Scholar]
- Genest, C.; Zidek, J.V. Combining probability distributions: A critique and an annotated bibliography. Stat. Sci. 1986, 1, 114–135. [Google Scholar]
- Genest, C.; Wagner, C.G. Further Evidence Against Independence Preservation in Expert Judgement Synthesis. Aequ. Math. 1986, 32, 74–86. [Google Scholar]
- Matúš, F. On iterated averages of I-projections. In Statistiek und Informatik; Universität Bielefeld: Bielefeld, Germany, 2007; pp. 1–12. [Google Scholar]
- Predd, J.B.; Osherson, D.N.; Kulkarni, S.R.; Poor, H.V. Aggregating Probabilistic Forecasts from Incoherent and Abstaining Experts. Decis. Anal. 2008, 5, 177–189. [Google Scholar]
- Kern-Isberner, G.; Rödder, W. Belief Revision and Information Fusion on Optimum Entropy. Int. J. Intel. Syst. 2004, 19, 837–857. [Google Scholar]
- Williamson, J. Deliberation, Judgement and the Nature of Evidence. Econ. Philos. 2014, in press. [Google Scholar]
- Carnap, R. On the application of inductive logic. Philos. Phenomenol. Res. 1947, 8, 133–148. [Google Scholar]
- Paris, J.B. The Uncertain Reasoner Companion; Cambridge University Press: Cambridge, UK, 1994; pp. 1–224. [Google Scholar]
- Amari, S. Integration of stochastic models by minimizing alpha-divergence. Neural Comput 2007, 19, 2780–2796. [Google Scholar]
- Csiszár, I.; Tusnády, G. Informational Geometry and Alternating Minimization Procedures. Stat. Decis. 1984, 1, 205–237. [Google Scholar]
- Eggermont, P.P.B.; LaRiccia, V.N. On EM-like algorithms for minimum distance estimation; Preprint 1998; University of Delaware: Delaware, NC, USA; pp. 1–29.
- Wilmers, G.M. Generalising the Maximum Entropy Inference Process to the Aggregation of Probabilistic Beliefs; Preprint 2011, Version 6; The University of Manchester: Manchester, UK; pp. 1–40.
- Bauschke, H.H. Projection Algorithms and Monotone Operators. Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, 1996; pp. 1–223. [Google Scholar]
- Censor, Y.; Zenios, S.A. Parallel Optimization: Theory, Algorithms, and Applications; Oxford University Press: New York, NY, USA, 1997; pp. 1–541. [Google Scholar]
- Bauschke, H.H.; Borwein, J.M.; Combettes, P.L. Bregman monotone optimization algorithms. SIAM J. Control Optim. 2003, 42, 596–636. [Google Scholar]
- Tofighi, M.; Kose, K.; Cetin, A.E. Denoising Using Projections Onto Convex Sets (POCS) Based Framework 2013, arXiv, 1309.0700.
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).