Complex Modified Hybrid Projective Synchronization of Different Dimensional Fractional-Order Complex Chaos and Real Hyper-Chaos
Abstract
:1. Introduction
2. Preliminaries
2.1. The Definition of Fractional Derivative
2.2. The Stability of Fractional-Order Systems
- Asymptotically stable if and only if:where arg(λℓ(A)) denotes the argument of the eigenvalue λℓ of A. In this case, each component of the states decays toward zero like t−α.
- Stable if and only if:and those critical eigenvalues λi that satisfy |arg(λℓ(A))| = απ/2 (ℓ = 1, 2,⋯, n), have geometric multiplicity one.
3. CMHPS Scheme of a Different Dimensional Fractional-Order Real Hyper-Chaotic (Chaotic) Drive System and Complex Chaotic Response System
3.1. Mathematical Model and Problem Descriptions
3.2. General Method of CMHPS
4. CMHPS Scheme of Different Dimensional Fractional-Order Complex Chaotic Drive Systems and Real Hyper-Chaotic (Chaotic) Response Systems
4.1. Mathematical Model and Problem Descriptions
4.2. General Method of CMHPS
5. CMHPS Scheme of Different Dimensional Fractional-Order Complex Chaotic Systems
6. Numerical Examples
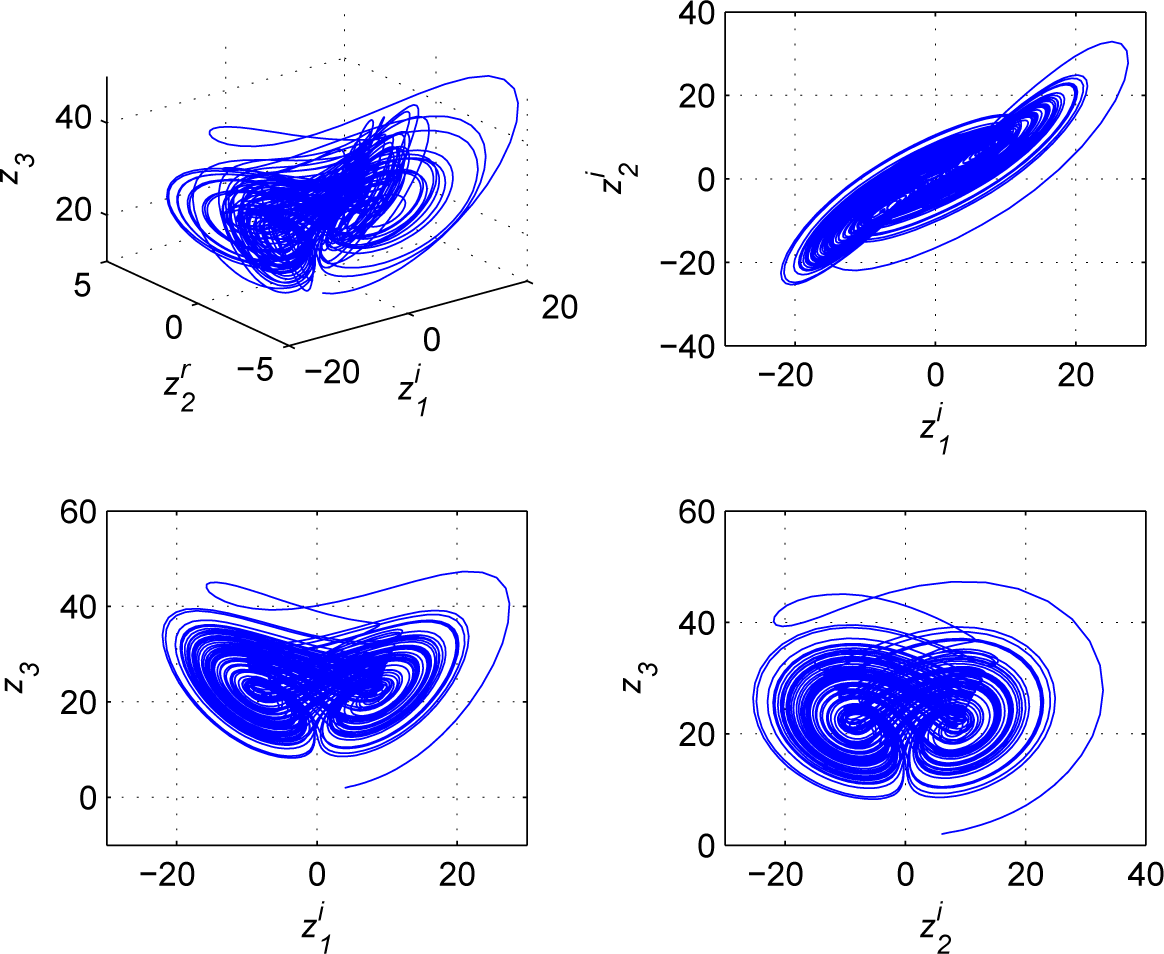
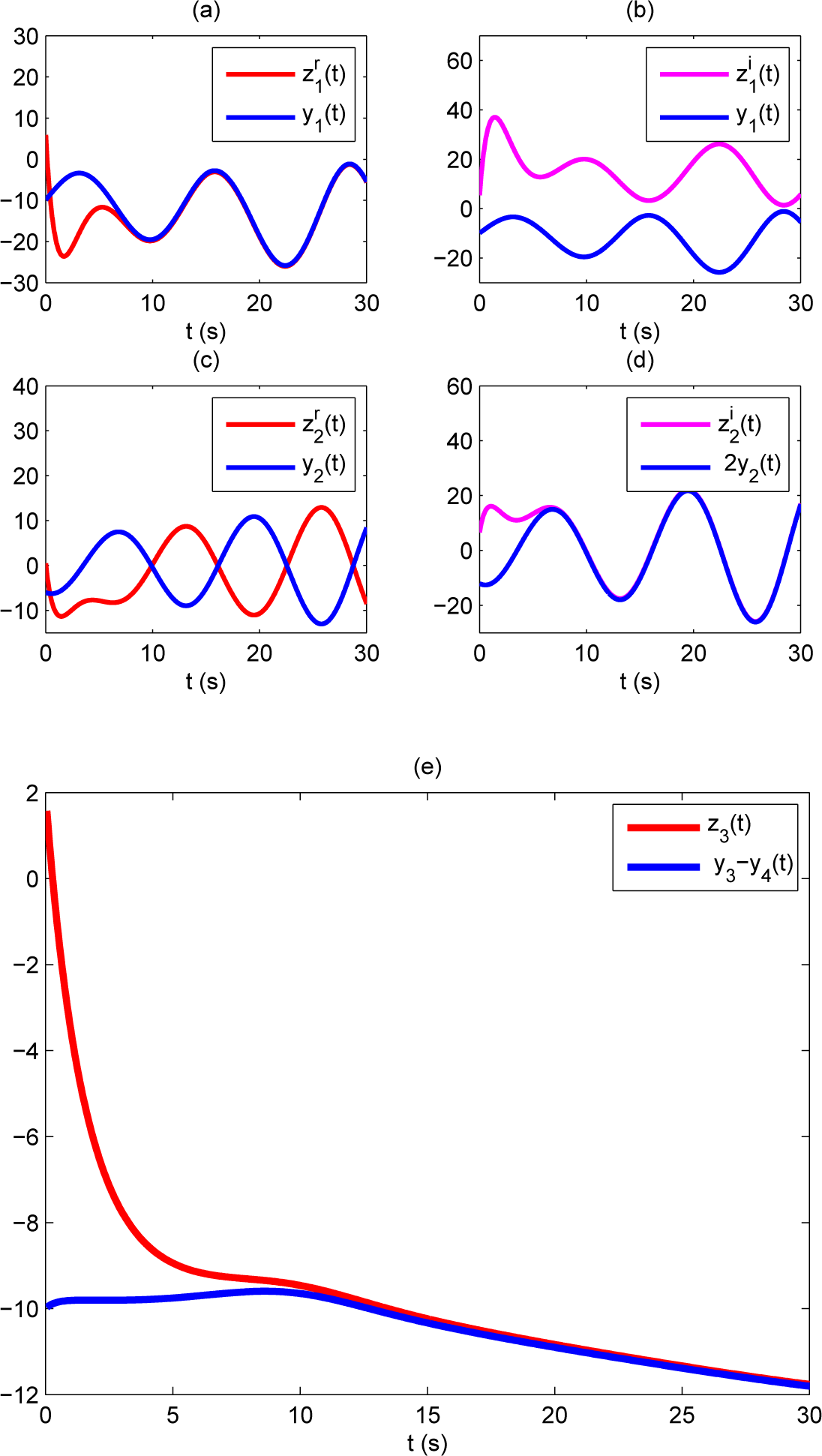
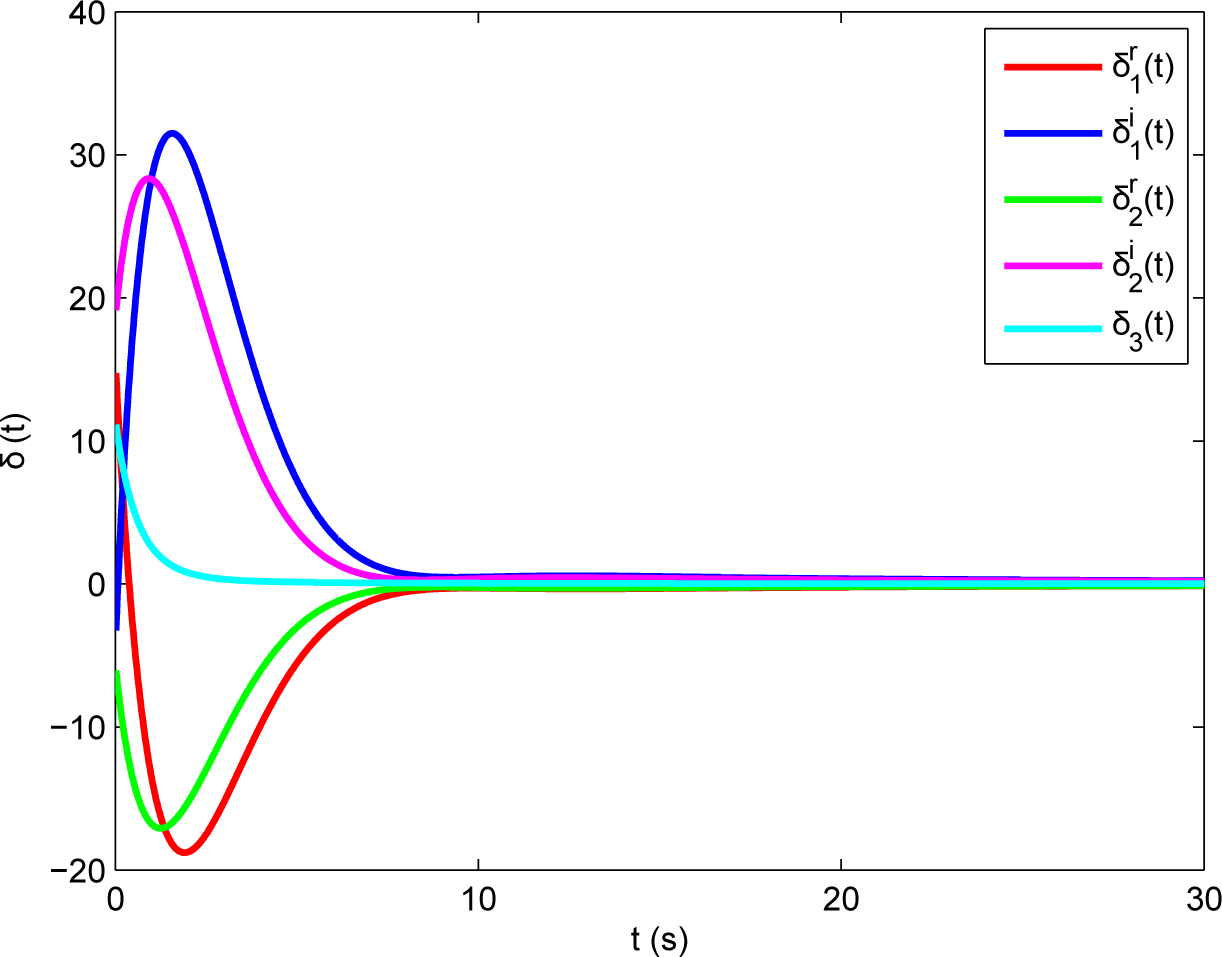
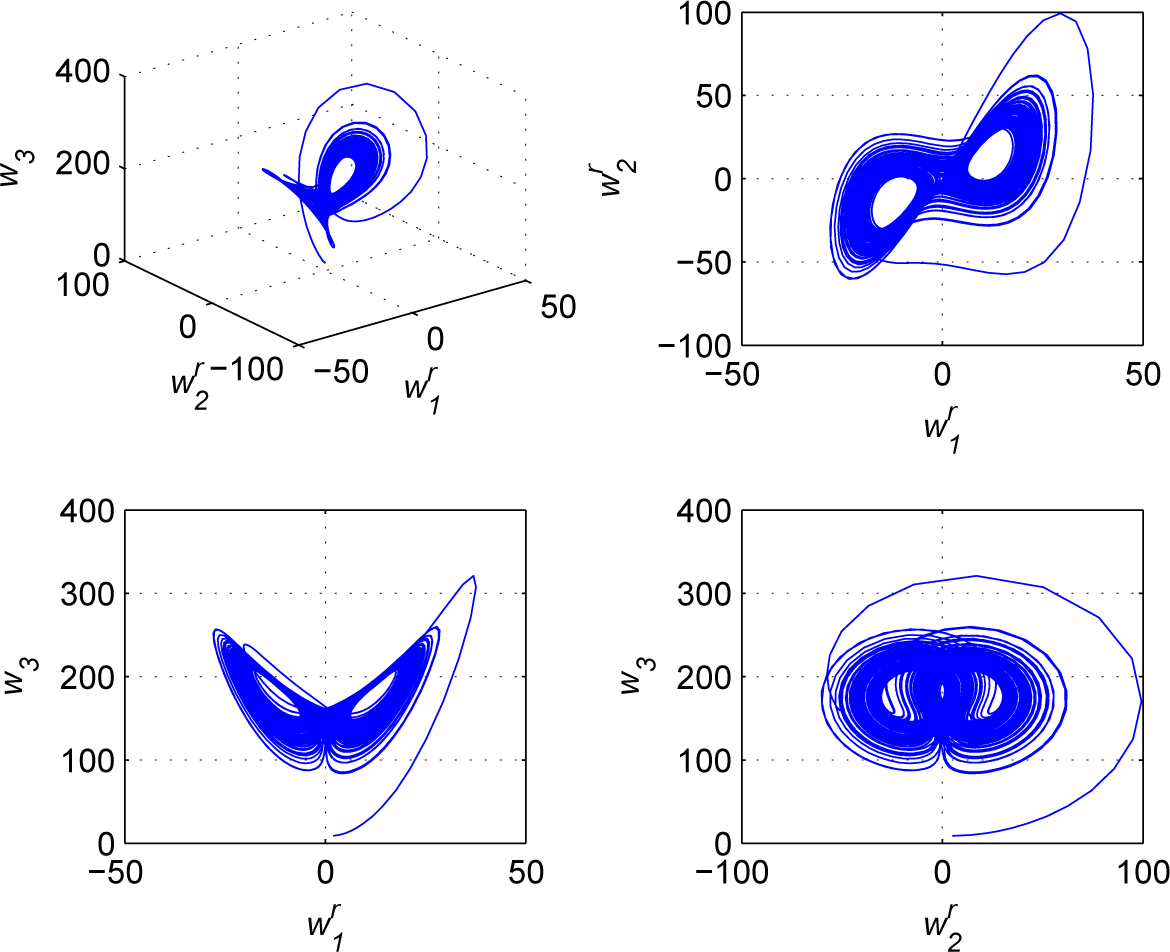
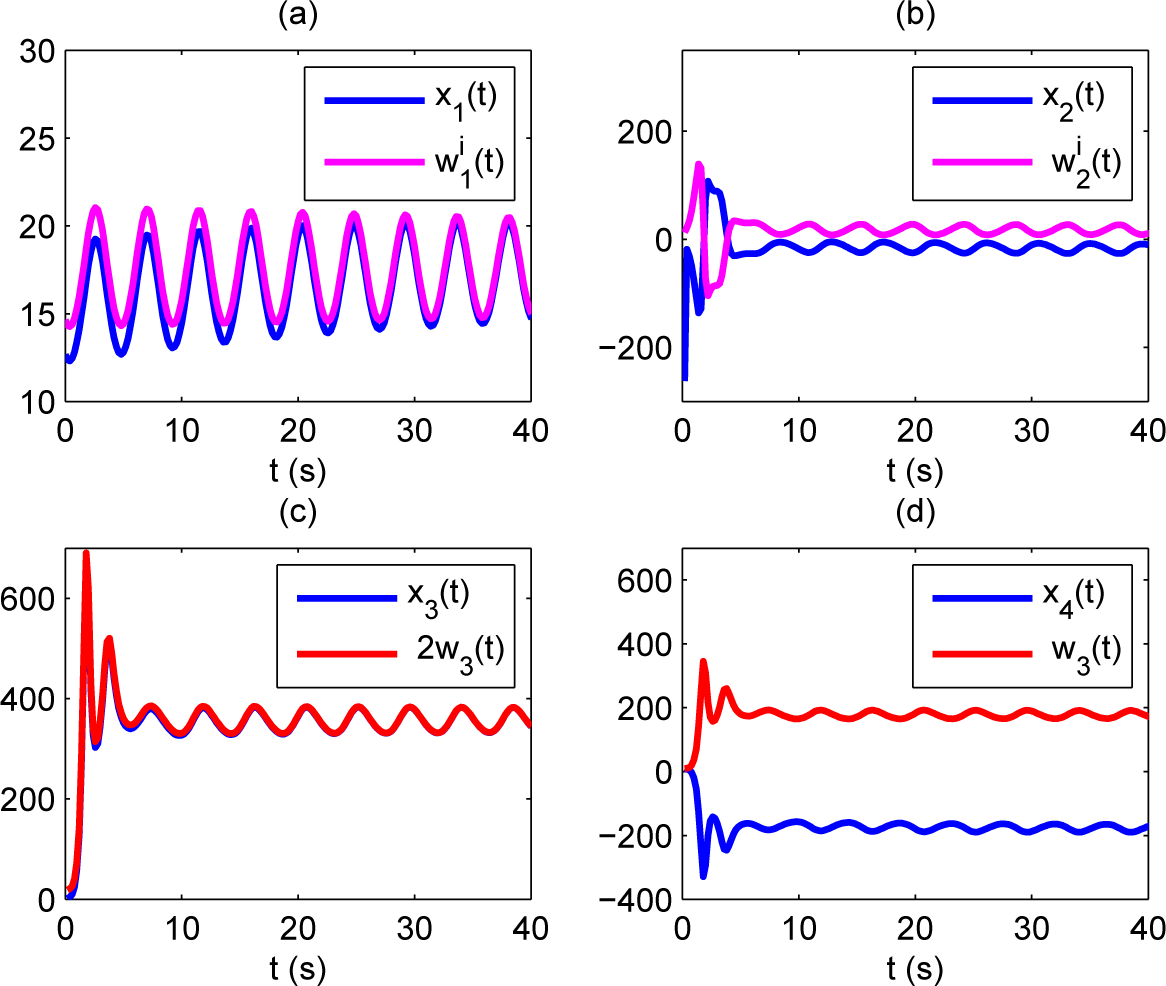
6.1. Reduced Order CMHPS
6.2. Increased Order CMHPS
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bagley, R.L.; Calico, R.A. Fractional-order state equations for the control of viscoelastically damped structures. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar]
- Sun, H.H.; Abdelwahad, A.A.; Onaral, B. Linear approximation of transfer function with a pole of fractional-order. IEEE Trans. Autom. Control 1984, 29, 441–444. [Google Scholar]
- Laskin, N. Fractional market dynamics. Physica A 2000, 287, 482–492. [Google Scholar]
- Kunsezov, D.; Bulagc, A; Dang, G.D. Quantum Levy processes and fractional kinetics. Phys. Rev. Lett. 1999. [Google Scholar]
- Gyorgyi, G.; Szepfalusy, P. Calculation of the entropy in chaotic systems. Phys. Rev. A 1985. [Google Scholar]
- Steeb, W.H.; Solms, F.; Stoop, R. Chaotic systems and maximum entropy formalism. J. Phys. Math. Gen. 1994, 27, 399–402. [Google Scholar]
- Hartley, T.T.; Lorenzo, C.F.; Qammer, H.K. Chaos in a fractional-order Chua’s system. IEEE Trans Circuits Syst. I 1995, 42, 485–490. [Google Scholar]
- Li, C.; Chen, G. Chaos and hyperchaos in the fractional-order Rössler equations. Physica A 2004, 341, 55–61. [Google Scholar]
- Daftardar-Gejji, V.; Bhalekar, S. Chaos in fractional ordered Liu system. Comput. Math. Appl. 2010, 59, 1117–1127. [Google Scholar]
- Srivastava, M.; Ansari, S.P.; Agrawal, S.K.; Das, S.; Leung, A.Y.T. Anti-synchronization between identical and non-identical fractional-order chaotic systems using active control method. Nonlinear Dyn. 2014, 76, 905–914. [Google Scholar]
- Zhao, M.; Wang, J. Outer synchronization between fractional-order complex networks: A non-fragile observer-based control scheme. Entropy 2013, 15, 1357–1374. [Google Scholar]
- Sun, J.; Yin, Q.; Shen, Y. Compound synchronization for four chaotic systems of integer order and fractional order. Europhys. Lett. 2014, 106. [Google Scholar] [CrossRef]
- Wu, X.; Lu, Y. Generalized projective synchronization of the fractional-order Chen hyperchaotic system. Nonlinear Dyn. 2009, 57, 25–35. [Google Scholar]
- Liu, J.; Liu, S.; Yuan, C. Modified generalized projective synchronization of fractional-order chaotic Lü systems. Adv. Differ. Equ. 2013, 374, 1–13. [Google Scholar]
- Luo, C.; Wang, X. Chaos in the fractional-order complex Lorenz system and its synchronization. Nonlinear Dyn. 2013, 71, 241–257. [Google Scholar]
- Luo, C.; Wang, X. Chaos generated from the fractional-order complex Chen system and its application to digital secuer communication. Int. J. Mod. Phys. C 2013, 24. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Complex modified projective synchronization of two chaotic complex nonlinear systems. Nonlinear Dyn. 2013, 73, 2231–2240. [Google Scholar]
- Zhang, F.; Liu, S. Full state hybrid projective synchronization and parameters identification for uncertain chaotic (hyperchaotic) complex systems. J. Comput. Nonlinear Dyn. 2013, 9. [Google Scholar] [CrossRef]
- Liu, P. Adaptive hybrid function projective synchronization of general chaotic complex systems with different orders. J. Comput. Nonlinear Dyn. 2014, in press. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.; Zhang, F. A novel four-wing hyperchaotic complex system and its complex modified hybrid projective synchronization with different dimensions. Abstr. Appl. Anal. 2014, 2014. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999; pp. 41–136. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar]
- Matignon, D. Stability results for fractional differential equations with applications to control processing, In Proceedings of IMACS/IEEE-SMC Multiconference CESA 96, Lille, France, 9–12 July 1996; pp. 963–968.


| Settings the Matrix Θ | Synchronization Type |
|---|---|
| Θ=Θr+jΘi∈ℂm×n,m≠n | CMHPS |
| Θ=diag{θ1,θ2,⋯,θn}∈ℂn×n,m=n | CGPS |
| Θ=diag{θ,θ,⋯,θ}∈ℂn×n,m=n | CPS |
| Θ∈ℝm×n,m≠n | MHPS |
| Θ∈ℝm×n,m=n | MGPS |
| Θ=diag{θ1,θ2,⋯,θ }∈ℝn×n,m=n | GPS |
| Θ=diag{θ,θ,⋯,θ}∈ℝn×n,m=n | PS |
| Θ=diag{−1, −1,⋯, −1},m=n | CS |
| Θ=diag{−1,−1,⋯,−1},m=n | AS |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J. Complex Modified Hybrid Projective Synchronization of Different Dimensional Fractional-Order Complex Chaos and Real Hyper-Chaos. Entropy 2014, 16, 6195-6211. https://doi.org/10.3390/e16126195
Liu J. Complex Modified Hybrid Projective Synchronization of Different Dimensional Fractional-Order Complex Chaos and Real Hyper-Chaos. Entropy. 2014; 16(12):6195-6211. https://doi.org/10.3390/e16126195
Chicago/Turabian StyleLiu, Jian. 2014. "Complex Modified Hybrid Projective Synchronization of Different Dimensional Fractional-Order Complex Chaos and Real Hyper-Chaos" Entropy 16, no. 12: 6195-6211. https://doi.org/10.3390/e16126195
APA StyleLiu, J. (2014). Complex Modified Hybrid Projective Synchronization of Different Dimensional Fractional-Order Complex Chaos and Real Hyper-Chaos. Entropy, 16(12), 6195-6211. https://doi.org/10.3390/e16126195




