Contributions to the Transformation Entropy Change and Influencing Factors in Metamagnetic Ni-Co-Mn-Ga Shape Memory Alloys
Abstract
:1. Introduction
2. Experimental Procedures
3. Results and Discussion
3.1. Composition and Atomic Order Effects on the Magnetic and Structural Transformations
3.2. Contributions to the Entropy Change at the Magnetostructural Transformation
3.3. Composition Dependence of the Transformation Entropy
3.4. Atomic Order Dependence of the Transformation Entropy
3.5. Quantitative Evaluation of the Magnetic Entropy
4. Conclusions
- (1)
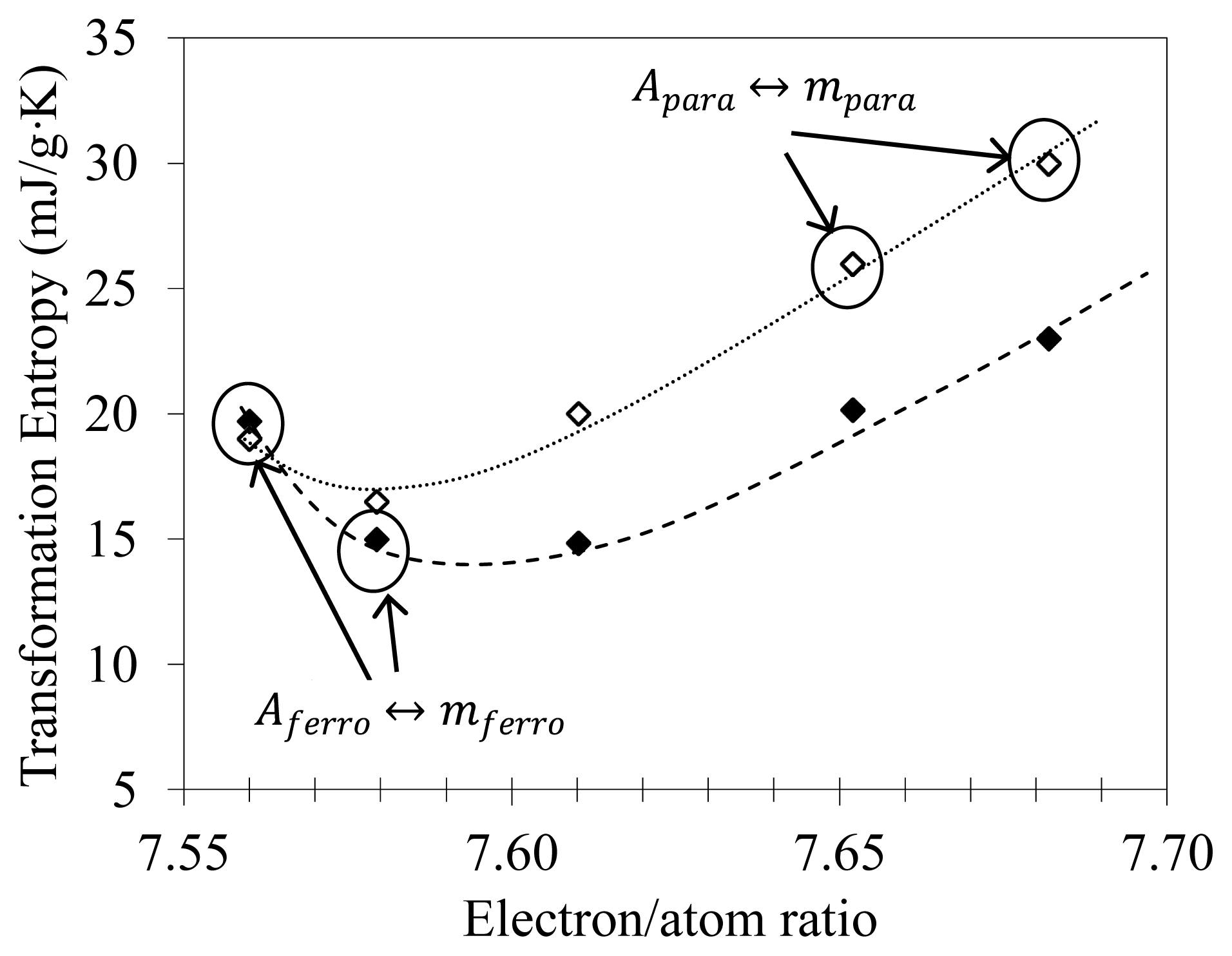
- if neither austenite nor martensite exhibit magnetic order, as in a Apara↔mpara transformation; instead, (and ) in a metamagnetic Aferro↔mpara MT. For a Aferro↔mferro MT, can be either positive or negative depending on the relative value of magnetization of austenite and martensite. For metamagnetic MTs, |ΔSmag| increases with increasing ( ), hence the overall ΔS diminishes. However, owing to the thermal hysteresis of the MT, , so in general and |ΔSA→m|<|ΔSm→A|.
- (2)
- The transformation entropy increases towards higher e/a values, for which ( ) decreases; for low e/a, the MT changes from Aferro↔mpara to Aferro↔mferro for which ΔM is smaller, the corresponding ΔSmag decreases and thus the (absolute value) overall transformation entropy increases. In any case, ΔSmag is the highest for the e/a values for which the MT switches from Aferro↔mpara to Aferro↔mferro, where decrease triggered by the increasingly ferromagnetic martensite starts.
- (3)
- ΔS reflects the changes of atomic order degree produced by thermal treatments, again recalling the relationship between ΔS and ( ). The evolution of ΔS as a function of post-quench ageing time shows different stages related to the occurrence of the Apara↔mpara, Aferro↔mpara and Aferro↔mferro transitions.
- (4)
- The magnetic contribution to the transformation entropy can be quantitatively evaluated by means a phenomenological model which has been recently developed, based on a Bragg–Williams approximation. The model provides an expression for ΔSmag as a function of the reduced temperature differences and , and has been applied to the data obtained for Ni50−xCoxMn25+yGa25−y (x = 3–8, y = 5–7) alloys subjected to different thermal treatments. Excellent fitting between the calculated and the experimental values of ΔSmag is obtained, including the switching from one transformation sequence to another. In this way, the magnetic origin of the stages observed in the ΔS vs ageing time evolution is also validated by the model, strengthening its validity regardless of the alloy composition and atomic order condition.
- (5)
- For the studied Ni-Co-Mn-Ga alloys, the maximum value of the magnetic entropy change amounts to 10–12 J·kg−1·K−1 (about 40% of the structural contribution) and corresponds to the switch from Aferro↔mpara to Aferro↔mferro.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sutou, Y.; Imano, Y.; Koeda, N.; Omori, T.; Kainuma, R.; Ishida, K.; Oikawa, K. Magnetic and martensitic transformations of NiMnX (X=In, Sn, Sb) ferromagnetic shape memory alloy. Appl. Phys. Lett 2004, 85, 4358–4360. [Google Scholar]
- Kainuma, R.; Imano, Y.; Ito, W.; Morito, H.; Sutou, Y.; Oikawa, K.; Fujita, A.; Ishida, K.; Okamoto, S.; Kitakami, O.; Kanomata, T. Metamagnetic shape memory effect in a Heusler-type Ni43Co7Mn39Sn11 polycrystalline alloy. Appl. Phys. Lett 88, 13.
- Yu, S.Y.; Cao, Z.X.; Ma, L.; Liu, G.D.; Chen, J.L.; Wu, G.H.; Zhang, B.; Zhang, X.X. Realization of magnetic field induced reversible martensitic transformation in NiCoMnGa alloys. Appl. Phys. Lett 2007, 91, 102507. [Google Scholar]
- Oikawa, K.; Ito, W.; Imano, Y.; Sutou, Y.; Kainuma, R.; Ishida, K.; Okamoto, S.; Kitakami, O.; Kanomata, T. Effect of magnetic field on martensitic transition of Ni46Mn41In13 Heusler alloy. Appl. Phys. Lett 2006, 88, 122507. [Google Scholar]
- Koyama, K.; Watanabe, K.; Kanomata, T.; Kainuma, R.; Oikawa, K.; Ishida, K. Observation of field-induced reverse transformation in ferromagnetic shape memory alloy Ni50Mn36Sn14. Appl. Phys. Lett 2006, 88, 132505. [Google Scholar]
- Krenke, T.; Duman, E.; Acet, M.; Wassermann, E.F.; Moya, X.; Mañosa, L.; Planes, A. Inverse magnetocaloric effect in ferromagnetic Ni-Mn-Sn alloys. Nat. Mater 2005, 4, 450–454. [Google Scholar]
- Sharma, V.K.; Chattopadhyay, M.K.; Shaeb, K.H.B.; Chouhan, A.; Roy, S.B. Large magnetoresistance in Ni50Mn34In16 alloy. Appl. Phys. Lett 2006, 89, 222509. [Google Scholar]
- Kainuma, R.; Imano, Y.; Ito, W.; Sutou, Y.; Morito, H.; Okamato, H.; Kitakami, S.; Oikawa, O.; Fujita, A.; Kanomata, T. Magnetic-field-induced shape recovery by reverse phase transformation. Nature 2006, 439, 957–960. [Google Scholar]
- Yu, S.Y.; Ma, L.; Liu, G.D.; Liu, Z.H.; Chen, J.L.; Cao, Z.X.; Wu, G.H.; Zhang, B.; Zhang, X.X. Magnetic field-induced martensitic transformation and large magnetoresistance in NiCoMnSb. Appl. Phys. Lett 2007, 90, 242501. [Google Scholar]
- Khovailo, V.V.; Novosad, V.; Takagi, T.; Filippov, D.A.; Levitin, R.Z.; Vasil’ev, A.N. Magnetic properties and magnetostructural phase transitions in Ni2+x Mn1−x Ga shape memory alloys. Phys. Rev. B 2004, 70, 174413. [Google Scholar]
- Sánchez-Alarcos, V.; Pérez-Landazábal, J.I.; Recarte, V.; Gómez-Polo, C.; Rodríguez-Velamazán, J.A. Correlation between composition and phase transformation temperatures in Ni-Mn-Ga-Co ferromagnetic shape memory alloys. Acta Mater 2008, 56, 5370–5376. [Google Scholar]
- Fabbrici, S.; Albertini, F.; Paoluzi, A.; Bolzoni, F.; Cabassi, R.; Solzi, M.; Righi, L.; Calestani, G. Reverse magnetostructural transformation in Co-doped NiMnGa multifunctional alloys. Appl. Phys. Lett 2009, 95, 022508. [Google Scholar]
- Fabbrici, S.; Kamarad, J.; Arnold, Z.; Casoli, F.; Paoluzi, A.; Bolzoni, F.; Cabassi, R.; Solzi, M.; Porcari, G.; Pernechele, C.; et al. From direct to inverse giant magnetocaloric effect in Co-doped NiMnGa multifunctional alloys. Acta Mater 2011, 59, 412–419. [Google Scholar]
- Seguí, C.; Cesari, E. Effect of ageing on the structural and magnetic transformations and the related entropy change in a Ni-Co-Mn-Ga ferromagnetic shape memory alloy. Intermetallics 2011, 19, 721–725. [Google Scholar]
- Seguí, C.; Cesari, E. Composition and atomic order effects on the structural and magnetic transformations in ferromagnetic Ni-Co-Mn-Ga shape memory alloys. J. Appl. Phys 2012, 111, 043914. [Google Scholar]
- Sakon, T.; Sasaki, K.; Numakura, D.; Abe, M.; Nojiri, H.; Adachi, Y.; Kanomata, T. Magnetic field-induced transition in Co-doped Ni41Co9Mn31.5Ga18.5 Heusler alloy. Mater. Trans 2013, 54, 9–13. [Google Scholar]
- Xu, X.; Ito, W.; Umetsu, R.Y.; Koyama, K.; Kainuma, R.; Ishida, K. Kinetic arrest of martensitic transformation in Ni33.0Co13.4Mn39.7Ga13.9 metamagnetic shape memory alloy. Mater. Trans 2010, 51, 469–471. [Google Scholar]
- Sánchez-Alarcos, V.; Pérez-Landazábal, J.I.; Recarte, V.; Cuello, G.J. Correlation between atomic order and the characteristics of the structural and magnetic transformations in Ni-Mn-Ga shape memory alloys. Acta Mater 2007, 55, 3883–3889. [Google Scholar]
- Chernenko, V.A.; Cesari, E.; Pons, J.; Seguí, C. Phase Transformations in Rapidly Quenched Ni-Mn-Ga Alloys. J. Mater. Res 2000, 15, 1496–1504. [Google Scholar]
- Seguí, C.; Pons, J.; Cesari, E. Effect of atomic ordering on the phase transformations in Ni-Mn-Ga shape memory alloys. Acta Mater 2007, 55, 1649–1655. [Google Scholar]
- Sanchez-Alarcos, V.; Recarte, V.; Pérez-Landazabal, J.I.; Gómez-Polo, C.; Rodríguez-Velamazán, J.A. Role of magnetism on the martensitic transformation in Ni-Mn-based magnetic shape memory alloys. Acta Mater 2012, 60, 459–468. [Google Scholar]
- Recarte, V.; Pérez-Landazábal, J.I.; Sánchez-Alarcos, V.; Rodríguez-Velamazán, J.A. Dependence of the martensitic transformation and magnetic transition on the atomic order in Ni-Mn-In Metamagnetic Shape Memory Alloys. Acta Mater 2012, 60, 1937–1945. [Google Scholar]
- Seguí, C. Effects of the interplay between atomic and magnetic order on the properties of metamagnetic Ni-Co-Mn-Ga shape memory alloys. J. Appl. Phys 2014, 115, 113903. [Google Scholar]
- Khovaylo, V.V.; Oikawa, K.; Abe, T.; Tagaki, T. Entropy change at the martensitic transformation in ferromagnetic shape memory alloys Ni2+xMn1−xGa. J. Appl. Phys 2003, 93, 8483–8485. [Google Scholar]
- Ito, W.; Imano, Y.; Kainuma, R.; Sutou, Y.; Oikawa, K.; Ishida, K. Martensitic and magnetic transformation behaviors in Heusler-type NiMnIn and NiCoMnIn metamagnetic shape memory alloys. Metall. Mater. Trans 2007, 38, 759–766. [Google Scholar]
- Kustov, S.; Corró, M.L.; Pons, J.; Cesari, E. Entropy change and effect of magnetic field on martensitic transformation in a metamagnetic Ni-Co-Mn-In shape memory alloy. Appl. Phys. Lett 94, 01.
- Recarte, V.; Pérez-Landazábal, J.I.; Sánchez-Alarcos, V.; Zablotskii, V.; Cesari, E.; Kustov, S. Entropy change linked to the martensitic transformation in metamagnetic shape memory alloys. Acta. Mater 2012, 60, 3168–3175. [Google Scholar]
- Wang, B.M.; Ren, P.; Liu, Y.; Wang, L. Enhanced magnetoresistance through magnetic-field-induced phase transition in Ni2MnGa co-doped with Co and Mn. J. Mag. Mat 2010, 322, 715–717. [Google Scholar]
- Ito, V.; Nagasako, R.; Umetsu, R.Y.; Kainuma, R.; Kanomata, T.; Ishida, K. Atomic ordering and magnetic properties in the Ni45Co5Mn36.7In13.3 metamagnetic shape memory alloy. Appl. Phys. Lett 2008, 93, 232503. [Google Scholar]
- Barandiarán, J.M.; Chernenko, V.A.; Cesari, E.; Salas, D.; Gutiérrez, J.; Lazpita, P. Magnetic field and atomic order effect on the martensitic transformation of a metamagnetic alloy. J. Phys. Condens. Matter 2013, 25, 484005. [Google Scholar]
- Kuz’min, M.D. Shape of temperature dependence of spontaneous magnetization of ferromagnets: Quantitative analysis. Phys. Rev. Lett 2005, 94, 107204. [Google Scholar]
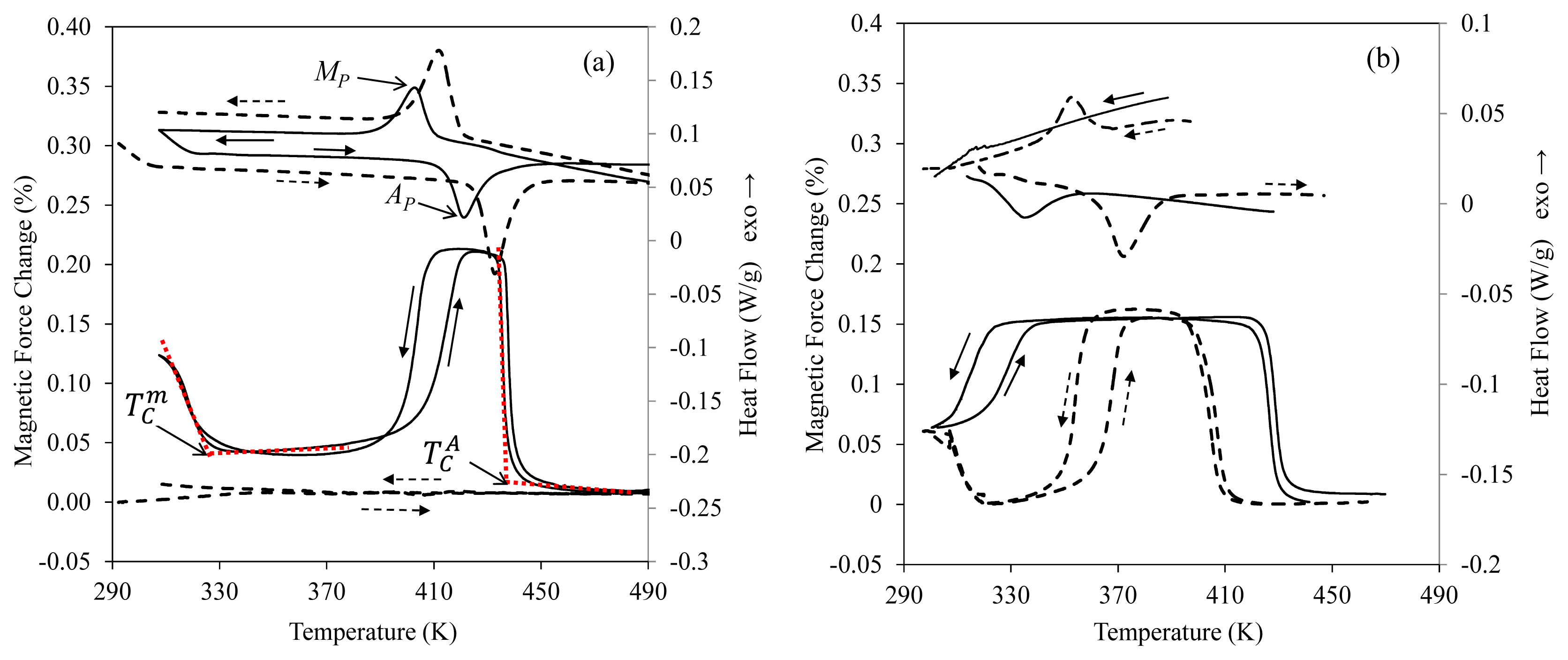

 Ap,
Ap,
 Mp and ●
) with ageing time at 470 K (after water quench from 970 K) for alloys C2 (a) and C4 (b). For
(alloy C2) and
(alloy C4) Curie temperatures are extrapolated and indicated as ×(adapted from [15]).
Mp and ●
) with ageing time at 470 K (after water quench from 970 K) for alloys C2 (a) and C4 (b). For
(alloy C2) and
(alloy C4) Curie temperatures are extrapolated and indicated as ×(adapted from [15]).
 Ap,
Ap,
 Mp and ●
) with ageing time at 470 K (after water quench from 970 K) for alloys C2 (a) and C4 (b). For
(alloy C2) and
(alloy C4) Curie temperatures are extrapolated and indicated as ×(adapted from [15]).
Mp and ●
) with ageing time at 470 K (after water quench from 970 K) for alloys C2 (a) and C4 (b). For
(alloy C2) and
(alloy C4) Curie temperatures are extrapolated and indicated as ×(adapted from [15]).
 | ΔSA→m|) and reverse (
| ΔSA→m|) and reverse (
 | ΔSm→A|) MTs, and temperature gap (
) (●, right axis; open circles are used for extrapolated Curie temperatures), of alloy C1 as a function of ageing time at 570 K after WQ from 1070 K.
| ΔSm→A|) MTs, and temperature gap (
) (●, right axis; open circles are used for extrapolated Curie temperatures), of alloy C1 as a function of ageing time at 570 K after WQ from 1070 K.
 | ΔSA→m|) and reverse (
| ΔSA→m|) and reverse (
 | ΔSm→A|) MTs, and temperature gap (
) (●, right axis; open circles are used for extrapolated Curie temperatures), of alloy C1 as a function of ageing time at 570 K after WQ from 1070 K.
| ΔSm→A|) MTs, and temperature gap (
) (●, right axis; open circles are used for extrapolated Curie temperatures), of alloy C1 as a function of ageing time at 570 K after WQ from 1070 K.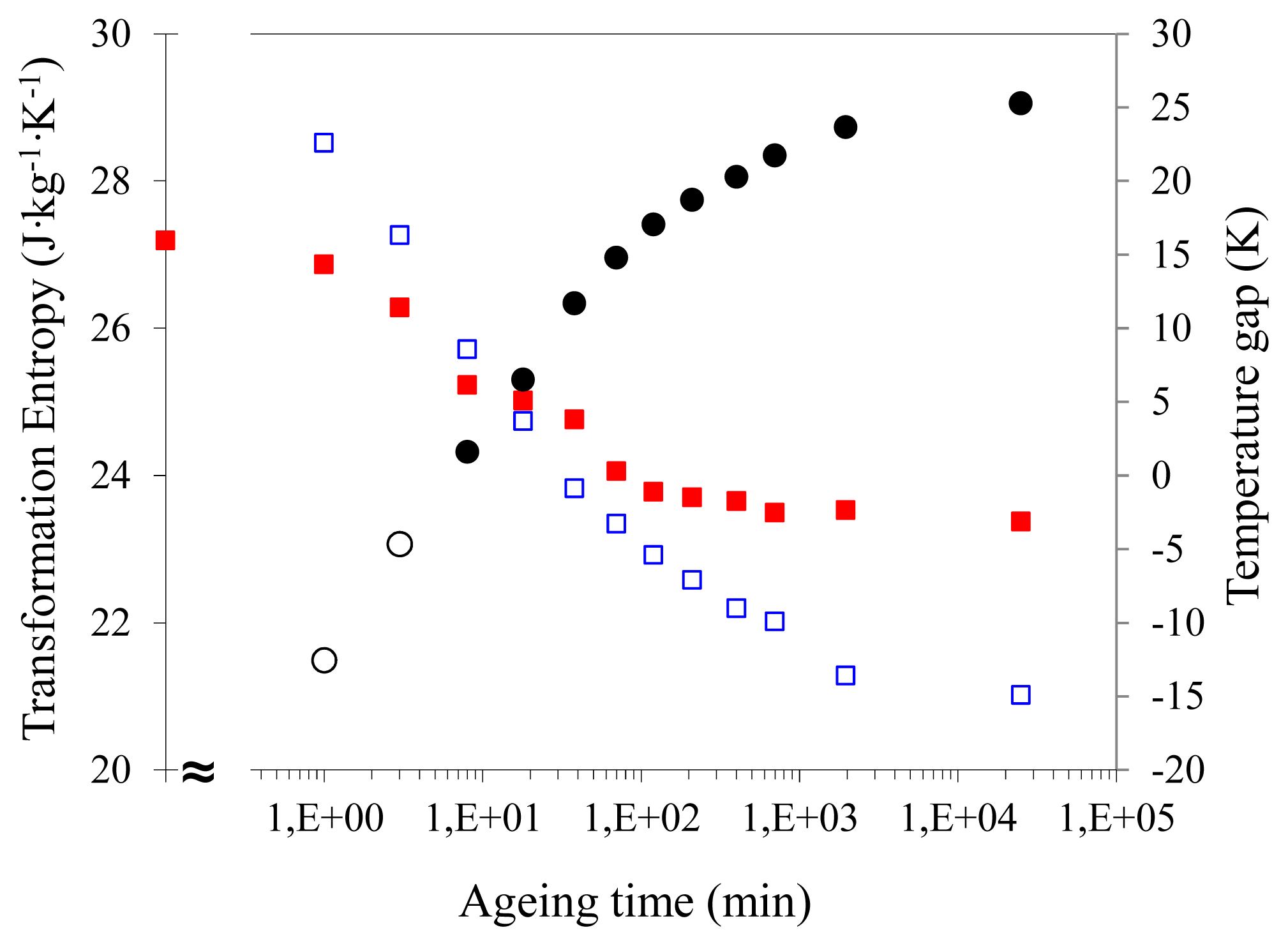
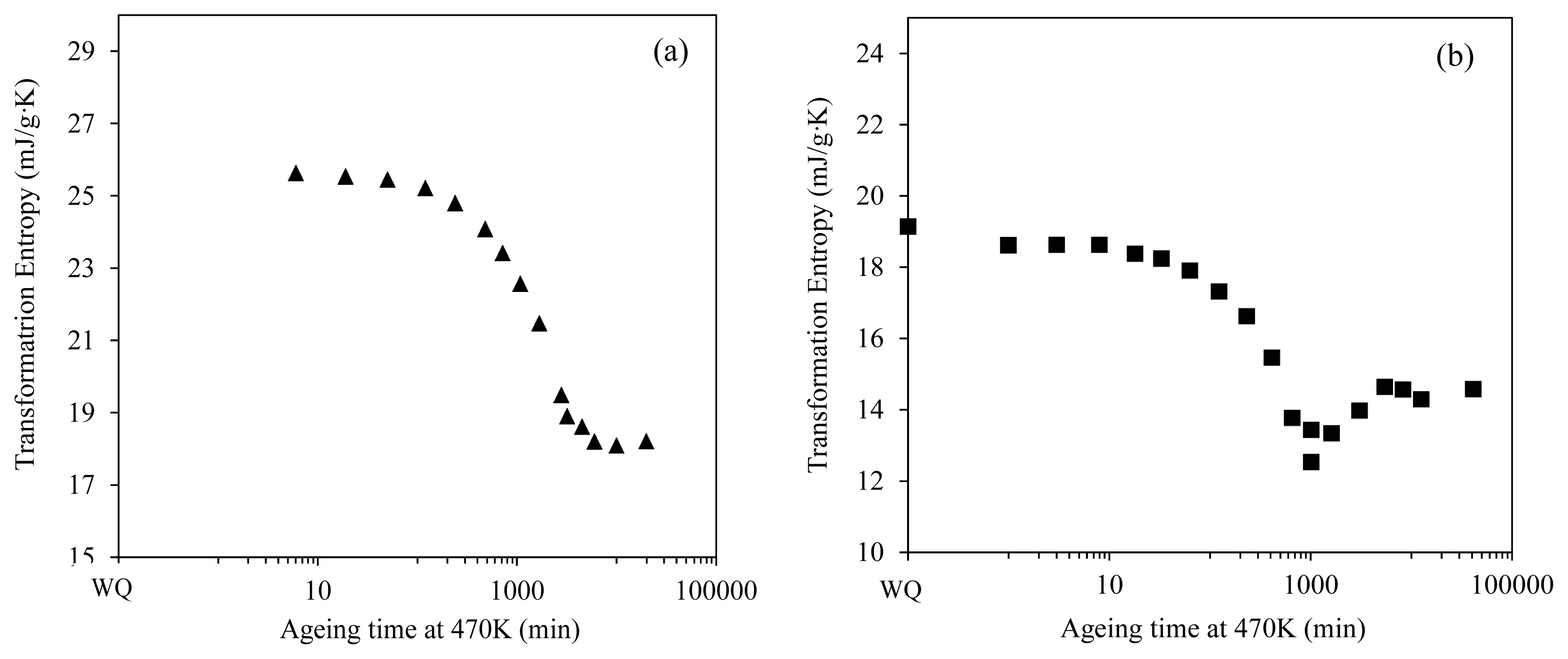
 alloy C4) and calculated magnetic entropy (dashed lines and ✱,
alloy C4) and calculated magnetic entropy (dashed lines and ✱,
 for Aferro↔mpara,
for Aferro↔mpara,
 for Aferro↔mferro MTs) as a function of the reduced temperature difference at the transformation temperature δA(TO). The structural contribution has been chosen as ΔSstrc = 26 J·kg−1·K−1.
for Aferro↔mferro MTs) as a function of the reduced temperature difference at the transformation temperature δA(TO). The structural contribution has been chosen as ΔSstrc = 26 J·kg−1·K−1.
 alloy C4) and calculated magnetic entropy (dashed lines and ✱,
alloy C4) and calculated magnetic entropy (dashed lines and ✱,
 for Aferro↔mpara,
for Aferro↔mpara,
 for Aferro↔mferro MTs) as a function of the reduced temperature difference at the transformation temperature δA(TO). The structural contribution has been chosen as ΔSstrc = 26 J·kg−1·K−1.
for Aferro↔mferro MTs) as a function of the reduced temperature difference at the transformation temperature δA(TO). The structural contribution has been chosen as ΔSstrc = 26 J·kg−1·K−1.
| Al.# | Nominal Composition | Ni | Co | Mn | Ga | e/a |
|---|---|---|---|---|---|---|
| C1 | Ni42Co8Mn32Ga18 | 41.6 | 7.9 | 32.4 | 18.1 | 7.68 |
| C2 | Ni43Co7Mn30Ga20 | 43.2 | 7.4 | 29.6 | 19.8 | 7.65 |
| C3 | Ni43.5Co6.5Mn31Ga19 | 42.7 | 6.1 | 31.5 | 19.8 | 7.61 |
| C4 | Ni43.5Co6.5Mn30Ga20 | 42.7 | 6.5 | 30.1 | 20.8 | 7.58 |
| C5 | Ni45Co5Mn31Ga19 | 44.8 | 2.8 | 31.4 | 21.0 | 7.56 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Seguí, C.; Cesari, E. Contributions to the Transformation Entropy Change and Influencing Factors in Metamagnetic Ni-Co-Mn-Ga Shape Memory Alloys. Entropy 2014, 16, 5560-5574. https://doi.org/10.3390/e16105560
Seguí C, Cesari E. Contributions to the Transformation Entropy Change and Influencing Factors in Metamagnetic Ni-Co-Mn-Ga Shape Memory Alloys. Entropy. 2014; 16(10):5560-5574. https://doi.org/10.3390/e16105560
Chicago/Turabian StyleSeguí, Concepció, and Eduard Cesari. 2014. "Contributions to the Transformation Entropy Change and Influencing Factors in Metamagnetic Ni-Co-Mn-Ga Shape Memory Alloys" Entropy 16, no. 10: 5560-5574. https://doi.org/10.3390/e16105560
APA StyleSeguí, C., & Cesari, E. (2014). Contributions to the Transformation Entropy Change and Influencing Factors in Metamagnetic Ni-Co-Mn-Ga Shape Memory Alloys. Entropy, 16(10), 5560-5574. https://doi.org/10.3390/e16105560






