Cross-Scale Interactions and Information Transfer

Abstract

An information-theoretic approach for detecting interactions and information transfer between two systems is extended to interactions between dynamical phenomena evolving on different time scales of a complex, multiscale process. The approach is demonstrated in the detection of an information transfer from larger to smaller time scales in a model multifractal process and applied in a study of cross-scale interactions in atmospheric dynamics. Applying a form of the conditional mutual information and a statistical test based on the Fourier transform and multifractal surrogate data to about a century long records of daily mean surface air temperature from various European locations, an information transfer from larger to smaller time scales has been observed as the influence of the phase of slow oscillatory phenomena with the periods around 6–11 years on the amplitudes of the variability characterized by the smaller temporal scales from a few months to 4–5 years. These directed cross-scale interactions have a non-negligible effect on interannual air temperature variability in a large area of Europe.

1. Introduction

Emergent phenomena in complex systems consisting of many parts usually cannot be explained by a simple linear sum or a combination of properties of system components. The complex behavior is usually the result of mutual interactions of the intertwined subsystems. Knowledge about the interactions among the system constituents can be the key to understanding complex phenomena. Among various types of interactions and dependence, synchronization [1] plays a specific role in the cooperative behavior of coupled complex systems or their components. Synchronization and related phenomena have been observed in diverse physical, biological and social systems. Examples include cardio-respiratory interactions [2,3], synchronization of neural signals on various levels of organization of brain tissues [4–7], or coherent variability in the Earth atmosphere and climate [8–13]. In such systems it is not only important to detect interactions and possible synchronized states, but also to distinguish mutual interactions from a directional coupling, i.e., to identify drive-response relationships between the systems studied. This problem is a special case of the general question of causality or causal relations between systems, processes or phenomena. For more comprehensive introduction to this topic, see [14].

The first definition of causality that could be quantified and measured computationally, yet very general, was given in 1956 by N. Wiener [15]: “For two simultaneously measured signals, if we can predict the first signal better by using the past information from the second one than by using the information without it, then we call the second signal causal to the first one.”

The introduction of the concept of causality into the experimental practice, namely into analyses of data observed in consecutive time instants, time series, is due to Clive W. J. Granger, the 2003 Nobel prize winner in economy. In his Nobel lecture [16] he recalled the inspiration by Wiener’s work and identified two components of the statement about causality:

(1)

The cause occurs before the effect; and

(2)

The cause contains information about the effect that is unique, and is in no other variable.

As Granger puts it, a consequence of these statements is that the causal variable can help to forecast the effect variable after other data has been first used [16]. This restricted sense of causality, referred to as Granger causality, GC hereafter, characterizes the extent to which a process X_t is leading another process Y_t, and builds upon the notion of incremental predictability. It is said that the process X_t Granger causes another process Y_t if future values of Y_t can be better predicted using the past values of X_t and Y_t rather than only the past values of Y_t. The standard test of GC developed by Granger [17] is based on a linear regression model. A number of approaches have been developed with the aim to extend the GC concept to nonlinear systems. We will briefly review the one based on information theory [18]. We will demonstrate that an information theoretic functional, known as mutual information (MI), is a useful measure of dependence that can be used in the detection of interactions of two systems (or subsystems of a complex system) using time series that record their dynamical evolution. Then the conditional mutual information (CMI) will be used in order to detect directional interactions. Paluš et al. [5] have proposed the conditional mutual information as a tool for the generalization of the GC concept for nonlinear systems. An equivalent information-theoretic quantity called “transfer entropy” has been proposed by Schreiber [19]. Barnett et al. analytically proved the equivalence of the transfer entropy and the conditional mutual information with the GC concept in the case of Gaussian processes [20]. Therefore the causal influence of a process X_t on another process, Y_t, understood in the framework of the GC concept, is also frequently interpreted as an information transfer from X_t to Y_t.

Several authors [21–23] extended the concept of the transfer entropy and conditional mutual information from the bivariate case of two processes into a multivariate case of many processes. In this paper, however, we will restrict the consideration to the bivariate case and we will even focus on one process evolving on many time scales and will develop an approach for detecting interactions and information transfer between dynamics evolving on different time scales.

Considering the detection of the direction of coupling between two systems, it is worthy to note the development tailored specifically for low-dimensional dynamical systems. Arnhold et al. [24] and Quiroga et al. [25] proposed a directional statistic based on distances of points in systems’ state spaces. Paluš and Vejmelka [26] critically assessed this method and compared it to the information-theoretic approach. More recent development of the methods based on the state-space geometry is due to Chicharro and Andrzejak [27] and Sugihara et al. [28]. Evaluation of these new methodological advancements in the context of cross-scale coupling can be an inspiration for further research. Here we will focus on applications of the ideas and tools from information theory [18].

2. Overview of Methods

2.1. Measuring Dependence with Mutual Information

Consider a discrete random variable X with a set of values Ξ. The probability distribution function (PDF) for X is p(x) = Pr{X = x}, x ∈ Ξ. We denote the PDF by p(x), rather than p_X(x), for convenience. Analogously, in the case of two discrete random variables X and Y with the sets of values Ξ and ϒ, respectively, their probability distribution functions will be denoted as p(x), p(y) and their joint PDF as p(x, y). The entropy H(X) of a single variable, say X, is defined as

$$H(X)=-\sum _{x\in \mathrm{\Xi }}p(x)\hspace{0.17em}\text{log\hspace{0.17em}}p(x),$$

(1)

and the joint entropy H(X, Y ) of X and Y is

$$H(X,Y)=-\sum _{x\in \mathrm{\Xi }}\sum _{y\in \mathrm{\Upsilon }}p(x,y)\hspace{0.17em}\text{log\hspace{0.17em}}p(x,y).$$

(2)

The conditional entropy H(Y |X) of Y given X is

$$H(Y\mid X)=-\sum _{x\in \mathrm{\Xi }}\sum _{y\in \mathrm{\Upsilon }}p(x,y)\hspace{0.17em}\text{log\hspace{0.17em}}p(y\mid x).$$

(3)

The average amount of common information, contained in the variables X and Y, is quantified by the mutual information I(X; Y ), defined as

$$I(X;Y)=H(X)+H(Y)-H(X,Y).$$

(4)

Considering Equations (1) and (2) we have

$$I(X;Y)=\sum _{x\in \mathrm{\Xi }}\sum _{y\in \mathrm{\Upsilon }}p(x,y)\hspace{0.17em}\text{log\hspace{0.17em}}\frac{p(x,y)}{p(x)p(y)}.$$

(5)

Note that two variables X and Y are independent if and only if p(x, y) = p(x)p(y), i.e.,

$$\text{log}\frac{p(x,y)}{p(x)p(y)}=0.$$

The mutual information (5) is in fact an averaged value of $\text{log}\frac{p(x,y)}{p(x)p(y)}$, i.e., it quantifies the average digression from independence of the variables X and Y and constitutes a useful measure of general statistical dependence with the following properties:

• I(X; Y ) ≥ 0,
• I(X; Y ) = 0 iff X and Y are independent.

The conditional mutual information I(X; Y |Z) of the variables X, Y given the variable Z is

$$I(X;Y\mid Z)=H(X\mid Z)+H(Y\mid Z)-H(X,Y\mid Z).$$

(6)

For Z independent of X and Y we have

$$I(X;Y\mid Z)=I(X;Y).$$

(7)

By a simple manipulation we obtain

$$I(X;Y\mid Z)=I(X;Y;Z)-I(X;Z)-I(Y;Z),$$

(8)

where I(X; Y ; Z) = H(X) + H(Y ) + H(Z) − H(X, Y, Z). Thus the conditional mutual information I(X; Y |Z) characterizes the “net” dependence between X and Y without a possible influence of another variable, Z.

Consider now n discrete random variables X₁, . . ., X_n with values (x₁, . . . , x_n) ∈ Ξ₁× … ×Ξ_n, with PDF’s p(x_i) for individual variables X_i and the joint distribution p(x₁, . . . , x_n). The mutual information I(X₁;X₂; . . . ;X_n), quantifying the common information in the n variables X₁, . . ., X_n can be defined as

$$I(X_1;X_2;\dots ;X_n)=H(X_1)+H(X_2)+\cdots +H(X_n)-H(X_1,X_2,\dots ,X_n).$$

(9)

It is possible, however, to define mutual information functionals quantifying common information of groups of variables and also various multivariate generalizations of the conditional mutual information, see [29].

All the information theoretic functionals can be defined for continuous random variables. The sums are substituted by integrals and the PDF’s by the probability distribution densities [18,30]. Among the continuous probability distributions a special role is played by the Gaussian distribution. Let X₁, . . ., X_n be an n-dimensional normally distributed random variable with a zero mean and a covariance matrix C. Then (see [29,30] and references therein)

$$I_G(X_1;\dots ;X_n)=\frac{1}{2}\sum _{i=1}^n\text{log}(c_{ii})-\frac{1}{2}\sum _{i=1}^n\text{log}({\sigma }_i),$$

(10)

where c_ii are the diagonal elements (variances) and σ_i are the eigenvalues of the n × n covariance matrix C.

The entropy and information are usually measured in bits if the base of the logarithms in their definitions is 2, here we use the natural logarithm and therefore the units are called nats.

2.2. Inference of Causality with the Conditional Mutual Information

Let {x(t)} and {y(t)} be time series considered as realizations of stationary and ergodic stochastic processes {X(t)} and {Y(t)}, respectively, t = 1, 2, 3, . . . . In the following we will mark x(t) as x and x(t + τ ) as x_τ, and the same notation holds for the series {y(t)}.

The mutual information I(y; x_τ ) measures the average amount of information contained in the process {Y } about the process {X} in its future τ time units ahead (τ -future hereafter). This measure, however, could also contain information about the τ -future of the process {X} contained in this process itself, if the processes {X} and {Y } are not independent, i.e., if I(x; y) > 0. In order to obtain the “net” information about the τ -future of the process {X} contained in the process {Y } we use the conditional mutual information I(y; x_τ |x). The latter was used by Paluš et al. [5] to define the coarse-grained transinformation rate, able to detect direction of coupling of unidirectionally coupled dynamical systems.

We used the standard statistical language in which we considered the time series {x(t)} and {y(t)} as realizations of stochastic processes {X(t)} and {Y(t)}, respectively. If the processes {X(t)} and {Y(t)} are substituted by dynamical systems evolving in measurable spaces of dimensions m and n, respectively, the variables x and y in I(y; x_τ |x) and I(x; y_τ |y) should be considered as n-dimensional and m-dimensional vectors. In experimental practice, however, usually only one observable is recorded for each system. Therefore, instead of the original components of the vectors X⃗(t) and Y⃗(t), the time delay embedding vectors according to Takens [31] are used. Then, back in the time-series representation, we have

$$I(\overrightarrow{Y}(t);\overrightarrow{X}(t+\tau )\mid \overrightarrow{X}(t))=I\left((y(t),y(t-\rho ),\dots ,y(t-(m-1)\rho ));x(t+\tau )\mid (x(t),x(t-\eta ),\dots ,x(t-(n-1)\eta ))\right),$$

(11)

where η and ρ are time lags used for the embedding of the trajectories X⃗(t) and Y⃗(t), respectively. Formally, also X⃗(t + τ ) should be expanded as x(t + τ ), x(t − η + τ ), . . . , x(t − (n − 1)η + τ ), however, only information about one component x(t + τ ) in the τ -future of the system {X} is used for simplicity. The CMI characterizing the influence in the opposite direction I(X⃗(t); Y⃗(t + τ)| Y⃗(t)) is defined in full analogy. Exactly the same formulation can be used for Markov processes of finite orders m and n. Based on the idea of finite-order Markov processes, Schreiber [19] has proposed a “transfer entropy”, which is an equivalent expression for the conditional mutual information (11)—see [14,26].

Extensive numerical experiences [26] suggest that the conditional mutual information in the form

$$I(y(t);x(t+\tau )\mid x(t),x(t-\eta ),\dots ,x(t-(n-1)\eta ))$$

(12)

is sufficient to infer coupling direction between the systems Y⃗(t) and X⃗(t). The dimensionality of the condition must contain full information about the state of the system X⃗(t) (see Section 2.3), while single components y(t) and x(t + τ ) are able to provide information about the directional coupling between the systems Y⃗(t) and X⃗(t).

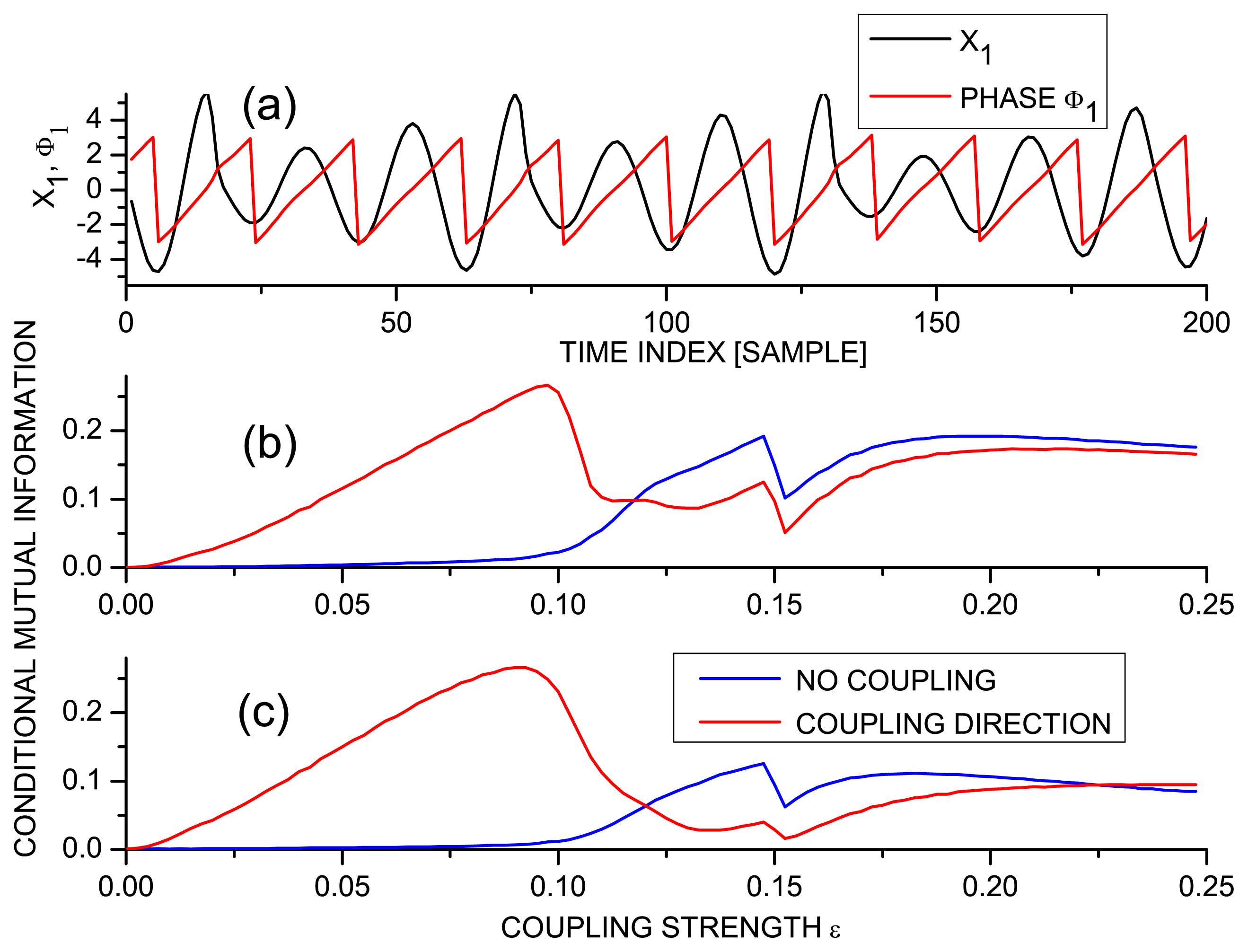
2.3. Example: Unidirectionally Coupled Rössler Systems

As an example of the detection of unidirectional coupling using the conditional mutual information, we consider the unidirectionally coupled Rössler systems, studied in detail by Paluš and Vejmelka [26], given by the equations

$$\begin{array}{l}{\dot{x}}_1=-{\omega }_1{x}_2-x_3\\ {\dot{x}}_2={\omega }_1{x}_1+a_1\hspace{0.17em}{x}_2\\ {\dot{x}}_3=b_1+x_3(x_1-c_1)\end{array}$$

(13)

for the autonomous system {X}, and

$$\begin{array}{l}{\dot{y}}_1=-{\omega }_2{y}_2-y_3+\varepsilon (x_1-y_1)\\ {\dot{y}}_2={\omega }_2{y}_1+a_2\hspace{0.17em}{y}_2\\ {\dot{y}}_3=b_2+y_3(y_1-c_2)\end{array}$$

(14)

for the response system {Y }. We will use the parameters a₁ = a₂ = 0.15, b₁ = b₂ = 0.2, c₁ = c₂ = 10.0, and frequencies ω₁ = 1.015 and ω₂ = 0.985, i.e., the two systems are similar, but not identical. The system {X} is autonomous, and it is the “master” that drives the system {Y } through the diffusive coupling term ε(x₁ – y₁) in the right hand side of the first component of the driven (“slave”) system {Y }. The parameter ε is referred to as the “coupling strength”. We generate time series as solutions of the system (13) and (14) for different coupling strengths ε and estimate the conditional mutual information in order to assess the existence of directional coupling or information transfer from the system {X} to the system {Y } and vice versa.

Figure 1a presents four Lyapunov exponents (LE) of the coupled systems (the two negative LE’s are not shown) as functions of the coupling strength ε. One positive and one zero LE of the driving system {X} are constant, while the LE’s of the driven system {Y }, which are positive and zero without a coupling or with a weak coupling, decrease with increasing ε. The two systems can enter a synchronized regime when the originally positive LE of the response system becomes negative [32].

Comparing LE and CMI as functions of the coupling strength ε brings a very important observation: the direction of coupling can be reliably detected when the two systems are coupled but not yet synchronized (for more details see [26]). Therefore, before inferring the directionality of coupling one should also assess a possibility of synchronization. In the following we will focus on the results for ε between 0 and approximately 0.12.

With the 1-dimensional condition, both CMI I(x(t); y(t + τ)|y(t)) and I(y(t); x(t + τ)|x(t)) (Figure 1b) are increasing with increasing ε. Some authors would interpret the inequality

$$I(x(t);y(t+\tau )\mid y(t))>I(y(t);x(t+\tau )\mid x(t))$$

as an evidence for a causal influence and existence of a positive information flow

$$I(x(t);y(t+\tau )\mid y(t))-I(y(t);x(t+\tau )\mid x(t))>0$$

from {X} to {Y }. Although the direction of the causal influence inferred in such a way is correct in this case, such an inference is not valid in general. Paluš and Vejmelka [26] demonstrate that estimates of CMI are biased, and if the two studied systems are not identical, the bias in the direction X → Y is different from the bias in the direction Y → X. Typically, the bias is larger in the direction from a slower to a faster system (considering main frequencies, ω₁ and ω₂ in our example), or from a system with simpler dynamics to a system with more complex dynamics (e.g., a periodic system seemingly drives a chaotic system). Also different noise levels can differently bias the CMI estimates. Therefore, for the correct inference of a causal influence in the sense of the unidirectional coupling, the causality measure must (asymptotically) vanish in the uncoupled direction. Using CMI (12), this requirement is met with the conditioning dimension, which allows a full description of a state of the driven system in its uncoupled state. For the Rössler system the necessary conditioning dimension is three. It is demonstrated in Figure 1c where I(y(t); x(t+τ )|x(t), x(t−η), x(t − 2η)) in the uncoupled direction stays at a zero level and begins to increase only when ε approaches the synchronization threshold and the possibility to infer the direction of coupling is lost. In the direction of coupling, I(x(t); y(t + τ )|y(t), y(t − η), y(t − 2η)) is distinctly positive from small values of ε up to the synchronization threshold. The behavior of CMI with the 3-dimensional condition (Figure 1c) is the same [26] irrespective of the way how the 3-dimensional condition is constructed—either we use the original components x₁(t), x₂(t), x₃(t) of the system (13), or a time-delay trajectory reconstruction x₁(t), x₁(t − η), x₁(t − 2η) according to Takens embedding theorem [31]. The time delay η is chosen as the first minimum of the auto-mutual information I(x₁(t); x₁(t + η)) following the Fraser–Swinney recipe [33].

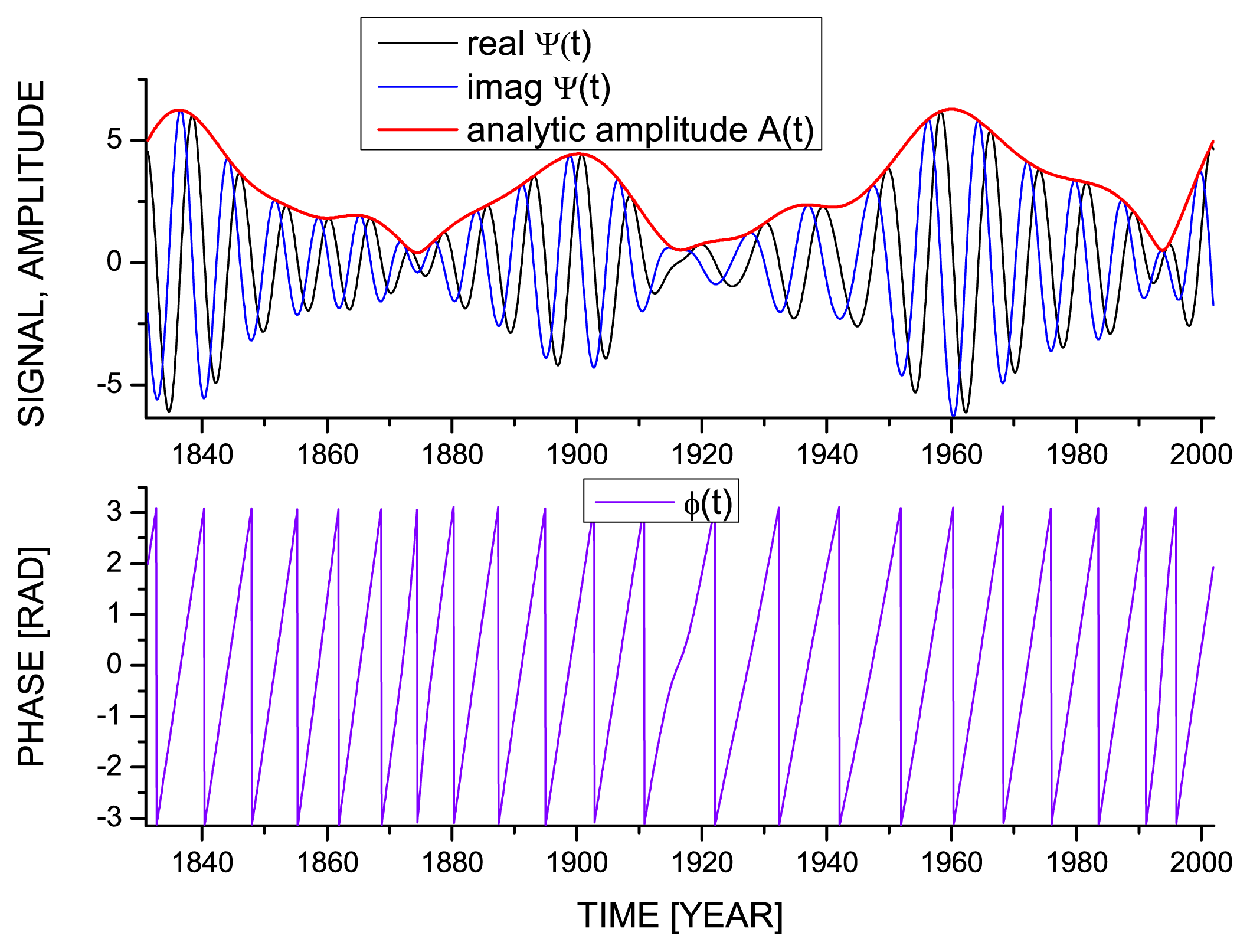
2.4. Interactions over Time Scales

In previous sections we have considered inference of interactions and directed coupling in the case of two different systems (or signals/time series representing two different systems). Let us consider now just one system {X}, characterized by a time series {x(t)}. The system {X} evolves simultaneously on many time scales. How can we find whether dynamics on different time scales evolve in a mutually independent way, or there are some interactions between dynamics on different time scales?

The first step is a scale-wise decomposition of the studied dynamics/time series. Since we focus on interactions over time scales, a relevant scale-wise decomposition is a decomposition of a signal into a number of components with limited frequency bandwidths. A number of authors, e.g., Gans et al. [34] use a set of digital filters. A wavelet transform, decomposing a signal into a set of components with predefined central frequencies and spectral bandwidths [35], is also a frequently used approach. Oscillatory components whose parameters are not pre-defined but emerge from particular analyzed data can be obtained using empirical mode decomposition [36] or singular-system analysis (see [9,37] and references therein).

A (quasi)oscillatory component {s_f(t)} can conveniently be decomposed into its instantaneous phase and amplitude (Figure 2) using the analytic signal approach [1].

For an arbitrary time series s(t) the analytic signal ψ(t) is a complex function of time defined as

$$\psi (t)=s(t)+i\widehat{s}(t)=A(t)e^{i\phi (t)}.$$

(15)

The instantaneous phase φ(t) of the signal s(t) is then

$$\phi (t)=\text{arctan}\frac{\widehat{s}(t)}{s(t)},$$

(16)

and its instantaneous amplitude is

$$A(t)=\sqrt{s{(t)}^2+\widehat{s}{(t)}^2}.$$

(17)

The imaginary part ŝ(t) of the analytic signal ψ(t) is usually obtained by using the Hilbert transform of s(t) [1,34]. Since the Hilbert transform is a unit gain filter at each frequency, broad-band signals from multiscale processes are usually pre-filtered to the frequency band of interest, as in the abovementioned approach of Gans et al. [34]. Also in the case when the empirical mode decomposition (EMD) approach is used for the scale-wise decomposition, the Hilbert transform is applied to each oscillatory mode obtained by the EMD procedure. On the other hand, singular-system analysis (SSA) provides oscillatory modes in twins shifted by π/2, which can be directly used in Equations (16) and (17) for the estimation of the phase φ(t) and the amplitude A(t), respectively [9,38]. Also a continuous complex wavelet transform (CCWT hereafter) [39] can be directly applied to an experimental time series x(t) reflecting the dynamics of a multiscale system. CCWT converts the time series x(t) into a set of complex wavelet coefficients W(t, f):

$$W(t,f)={\int }_{-\infty }^{\infty }\psi (t^{\prime })x(t-t^{\prime })d{t}^{\prime }.$$

(18)

In the following we use the complex Morlet wavelet [39]:

$$\psi (t)=\frac{1}{\sqrt{2\pi {\sigma }_t^2}}\text{exp}(-\frac{t^2}{2{\sigma }_t^2})\hspace{0.17em}\text{exp}(2\pi i{f}_0),$$

(19)

where σ_t is the bandwidth parameter, and f₀ is the central frequency of the wavelet. σ_t determines the rate of the decay of the Gauss function, and its reciprocal value σ_f = 1/πσ_t determines the spectral bandwidth. At each time scale given by the central wavelet frequency, the complex wavelet coefficients can be directly used in Equations (16) and (17) for the estimation of the phase φ(t) and the amplitude A(t), respectively. The CCWT provides both the band-pass filtering of the original multiscale signal and the estimation of the instantaneous phase and the instantaneous amplitude.

Having a multiscale signal (a time series x(t) reflecting the dynamics of a multiscale system) decomposed into a number of scale-specific (or frequency-specific) modes described using their instantaneous phases and amplitudes, it is possible to study cross-scale interactions of the following types:

• phase–phase
• amplitude–amplitude
• phase–amplitude

Some authors also compute the instantaneous frequency as a time derivative of the instantaneous phase [34,40] and assess the cross-frequency coupling between different instantaneous frequencies or combinations of the instantaneous frequency with the instantaneous phase or amplitude [40]. The instantaneous amplitude is also called an envelope (of fast oscillations) and its square is related to power, which is also evaluated in cross-frequency analysis of brain signals [40]. We can also study the cross-scale relations using directly the (filtered) signals s(t) obtained for individual scales, e.g., in the case of the CCWT decomposition defined as s(t) = Real{W(t, f)}. The following example shows, however, that the instantaneous phases φ(t) might have some advantages especially for the inference of directed interactions.

The chaotic solutions of the Rössler systems (13) and (14) oscillate in a relatively narrow frequency band (Figure 3a, black line), therefore it is possible to apply the Hilbert transform directly to the components x₁ and y₁ in order to obtain the instantaneous phases φ₁ and φ₂ of the driving system (13) and the driven system (14), respectively. Then the direction of coupling can be inferred using the conditional mutual information I(φ₁(t); φ₂(t + τ )|φ₂(t)) and I(φ₂(t); φ₁(t + τ )|φ₁(t)) already with the one-dimensional condition (Figure 3b) since the phase represents a simplified one-dimensional description of the Rössler system’s oscillations. Applying a higher-dimensional condition does not change the result (Figure 3c). Note that the one-dimensional condition is sufficient only for the “true” phase of self-sustained oscillators. A formally obtained phase φ(t) for a quasi-oscillatory component s(t) extracted from a multiscale system might require a condition of a higher dimensionality than one. Even in such a case, however, the conditioning dimension necessary for the phase φ(t) is typically lower than that required for the oscillatory component s(t).

2.5. Statistical Evaluation with Surrogate Data

Estimates of mutual information from finite number of samples are always nonzero. In the case of inferring directional coupling with the conditional mutual information (12), even with a sufficient dimension of the condition, the CMI estimates from finite number of samples are not only always nonzero but also always different in the two directions between the studied two systems. Considering possibly different biases, the absolute values of CMI estimates are not informative, but it is necessary to relate the CMI values computed from studied data to ranges of CMI values obtained from uncoupled processes that share important properties of analyzed data. This is the base of the surrogate data testing procedure in which we manipulate the original data in a randomization procedure that preserves original frequency spectra or variance on all relevant time scales; and the autocorrelation function in the cases of the Fourier transform (FT) surrogate data [41], or both the autocorrelation function and auto-mutual information function in the case of the multifractal (MF) surrogate data [42]. The surrogate data with the same sample spectrum as the tested time series can be constructed using the fast Fourier transform (FFT). The FFT of the series is computed, the magnitudes of the (complex) Fourier coefficients are kept unchanged, but their phases are randomized. The surrogate series is then obtained by computing the inverse transform into the time domain. Different realizations of the process are obtained using different sets of the random Fourier phases [41]. The discrete wavelet transform [43] is used for the generation of the multifractal surrogate data. The inspiration for this randomization procedure is the construction of a multifractal process using the wavelet dyadic trees proposed by Benzi et al. [44] and Arneodo et al. [45]. In particular, 2n wavelet coefficients on the scale /2 are obtained by multiplying n coefficients on the scale by a set of multiplicators, randomly drawn from a given distribution. After the construction of such a dyadic tree (always two different random multipliers are chosen in order to obtain two wavelet coefficients on a shorter scale from one wavelet coefficient on the closest larger scale), the inverse discrete wavelet transform produces a realization of a multifractal process mimicking information transfer from larger to smaller scales observed in turbulence. For construction of the multifractal surrogate data, a time series is transformed into a set of discrete wavelet coefficients and multipliers are computed by dividing each pair of coefficients on the scale /2 by the related coefficient on the scale . Then, fixing one or two largest scales, the surrogate wavelet coefficients are recursively computed from larger to smaller scales using randomly permutated original multipliers. See [42] for details.

By construction, in the surrogate data the interactions between different time scales do not exist (FT surrogates), or only those explained by random cascades on wavelet dyadic trees are allowed (MF surrogates).

A pair of descriptors (phase–phase, amplitude–amplitude, phase–amplitude) reflecting the dynamics on two different time scales is chosen and their interactions are assessed by using the mutual information (5); or the conditional mutual information (12) is used for assessing the presence of directional, causal cross-scale coupling. The value I_d of MI or CMI from the studied data is compared with the range of values I_si obtained from a set of surrogate data realizations. Having computed the mean $\overline{I_s}$ of the surrogate values I_si and their variance ${\sigma }_s^2$, we can define the z-score

$$z=\frac{I_d-\overline{I_s}}{{\sigma }_s},$$

(20)

which is a measure how much the MI/CMI from the analyzed data differs from the range of MI/CMI for the surrogate data. The z-score usually gives a stable estimate from several tens of realizations (30–60) and its value can be related to the statistical significance, provided the I_si values have a normal distribution. Unfortunately, the latter is not always the case. Therefore we prefer to compute I_si from a larger number of realizations (1000 in this study) and construct an empirical surrogate data distribution as a histogram of I_si values. Using the cumulative histogram we estimate percentiles of the surrogate distribution and in each particular test we record the largest percentile of I_si distribution that is exceeded by I_d from the analyzed data. We call this percentile “a significance level” since it is directly related to the significance of the statistical test based on the used surrogate data, irrespective of the surrogate I_si value distribution. For instance, the significance level 0.95 means that the I_d value is significantly different from zero with the statistical significance p < 0.05.

The specificity of coupling or causality inference methods can be secured by an appropriate choice of surrogate data that reproduce the bias of an MI/CMI estimator applied to the studied data. The sensitivity of the method can be guaranteed by a certain bound on the estimator variance [26]. Typically, a lower variance requires a larger amount of data or, more precisely, a time series representing a longer epoch of evolution of the studied process [26,46].

3. Results and Discussion

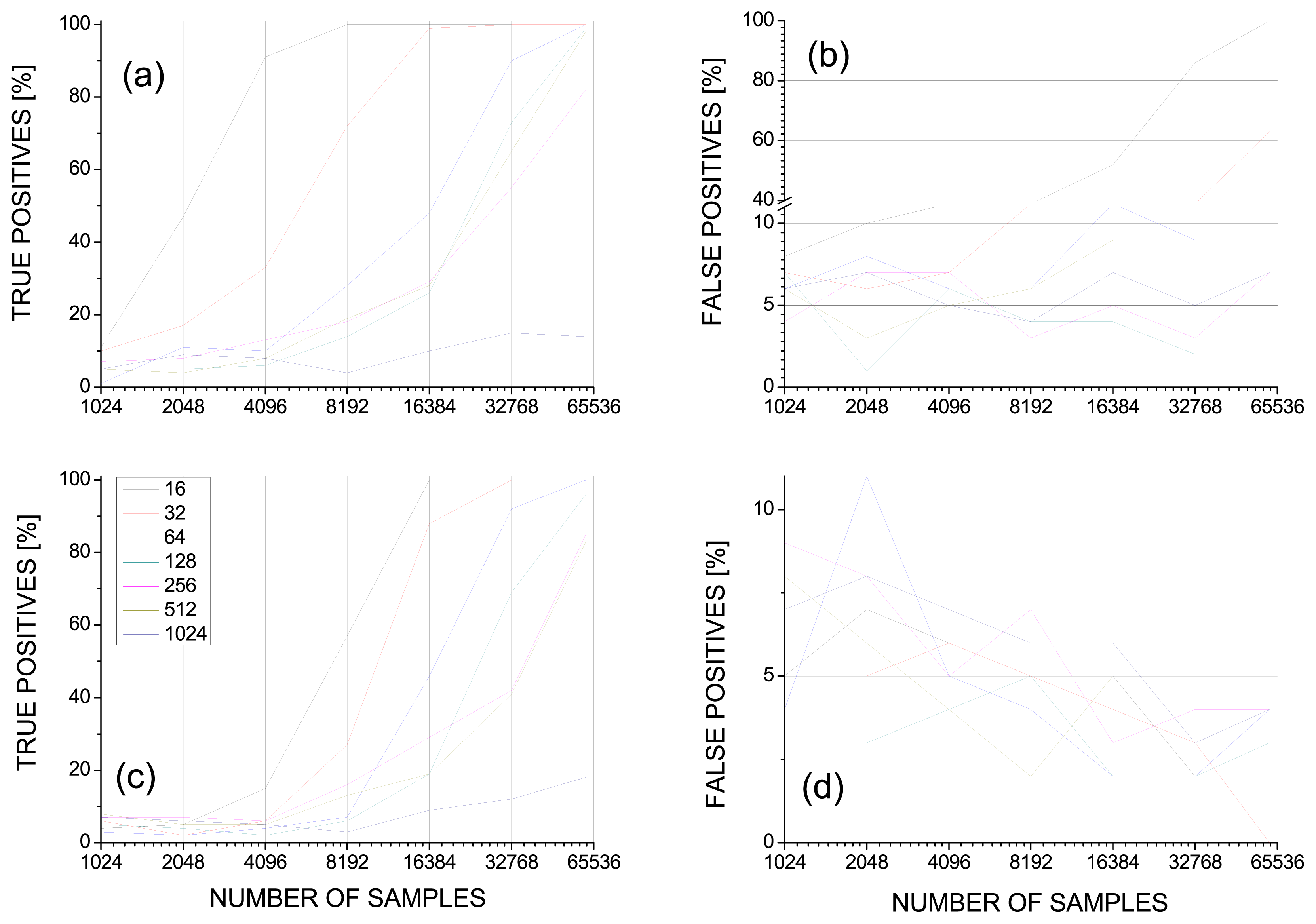
3.1. Coping with Method Errors

Before applying the introduced methods to experimental data, we apply them to artificially generated data representing our null hypotheses. We demonstrate the systematic errors that the used wavelet decomposition can introduce and the way how the surrogate data test copes with these systematic errors.

For the first experiment, 65,536 samples of Gaussian white noise (GWN) were generated. CCWT with the Morlet wavelet was used to decompose the time series into components related to time scales (in samples) from $181\hspace{0.17em}(\approx 128\sqrt{2})$ to $23170\hspace{0.17em}(\approx 32768/\sqrt{2})$. Cross-scale phase–phase interactions were assessed using the mutual information I(φ₁; φ₂) where the phases φ₁ were taken for the larger scales from 2436 to 23170 and the phases φ₂ for the smaller scales from 181 to 1722 samples. The realization of GWN does not support any cross-scale interaction. Even though we compute I(φ₁; φ₂) with φ₁ and φ₂ for disjunct ranges of scales, in Figure 4a we can see areas of elevated values of I(φ₁; φ₂) in the upper left corner of the plot where the large and small scales are the closest (e.g., 2436 and 1722 samples). Clearly, this is a “leakage” of the wavelet transform producing dependent oscillatory modes for relatively close scales. Since this is an artifact of the CCWT, it is present also in I_s(φ₁; φ₂) from the FT surrogate data (Figure 4b), which prevents to recognize the elevated values of I(φ₁; φ₂) in Figure 4a as statistically significant. Both the z-score (Figure 4c) and the significance levels (Figure 4d) show no significantly nonzero I(φ₁; φ₂). However, we need to recognize the multiplicity of the statistical tests—in Figure 4d we code in color each significant level greater than 0.95. It means that we display each pair of scales for which I(φ₁; φ₂) is statistically significant with p < 0.05 in a single test. In a large number of tests (combination of scales) we can encounter up to 5% of false positive results, appearing as randomly located spots in the significance plots.

For the second experiment, a dyadic tree of wavelet coefficients is constructed using random multipliers with a log-normal distribution (see [42] for details). A 65,536-sample realization of a multifractal process is obtained by applying the inverse discrete wavelet transform. Then the generated multifractal time series is decomposed using the complex continuous wavelet transform. For the time scales from 8 to 1024 samples we will consider directly the wavelet components s_i(t) = Real{W(t, f_i)} and again the phases φ_i(t), obtained according to Equation (16) with ŝ_i(t) = Im{W(t, f_i)} as in the previous case. Figure 5a presents cross-scale interactions measured using the mutual information I(s₁; s₂). In this case we use the same range of scales (8–1024 samples) for both s₁ and s₂. Therefore the maximum I(s₁; s₂) is located in the diagonal where the two scales are identical. The MI I(s₁; s₂) decreases with increasing difference between the two scales; however, this decrease is slower for larger scales. From I(s₁; s₂) itself we cannot distinguish the cross-scale interactions in the multifractal data from the artifacts due to the CCWT. In order to detect cross-scale interactions in the studied multifractal process, we compare I_d(s₁; s₂) from the multifractal data with its FT surrogate data. (Applying the MF surrogate data we would obtain similar patterns as in Figure 5a and no significant coupling as in Figure 4d.) The significance levels for I_d(s₁; s₂) in Figure 5b show that the FT surrogates rule out the trivial dependence in the equal scales 8, 16, 32, ... samples, yet confirm the cross-scale interactions with the scale ratio 1:2 (i.e., the scales 8 and 16, or 16 and 32, etc., are coupled). In order to answer whether this coupling is symmetrical or directed, we study directed phase–phase interactions and apply the CMI I(φ₁(t); φ₂(t + τ )|φ₂(t), φ₂(t − η), φ₂(t − 2η)) with the scale for φ₁ on abscissa, and the scale for φ₂ on ordinate. Again, the CMI itself (Figure 5c) shows an interesting pattern but it is not clear what are the true cross-scale interactions in the studied multifractal process. The true cross-scale interactions are uncovered by the significance levels for the CMI obtained using 1000 realizations of the FT surrogate data—in Figure 5d we can see that the scales close to 16 influence the scales close to 8 samples, and the scales close to 32 influence the scales close to 16 samples, etc. 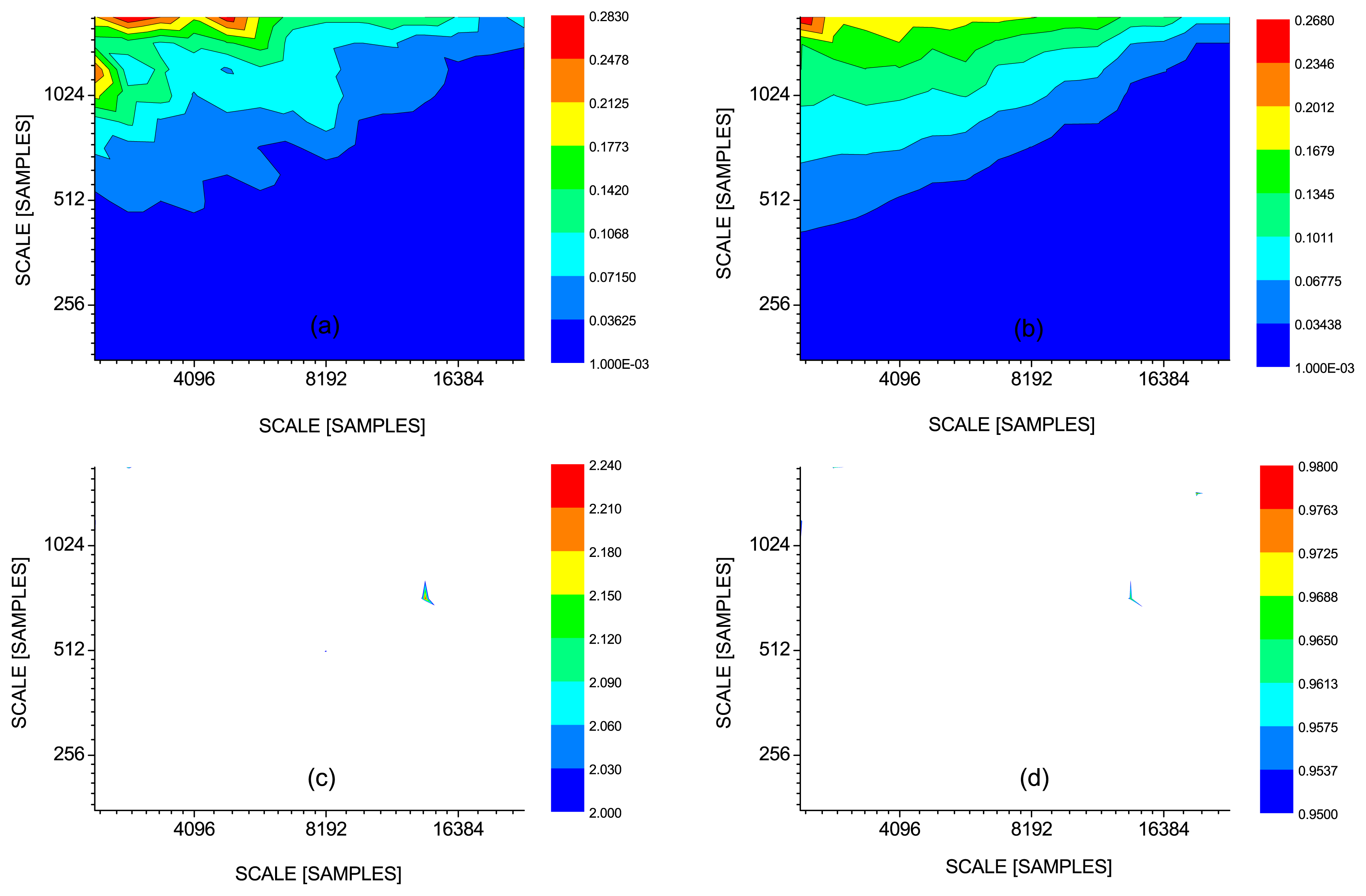The CMI with the FT surrogate data confirmed the information transfer from a scale to a scale /2, or from a time scale characterized by a frequency f to a time scale characterized by a frequency 2f. This information transfer does not reach over the closest smaller scale, i.e., it is restricted to the transfer of information from a certain scale to the next smaller scale approximately equal to one half of the preceding scale, exactly in the way how this realization of a multifractal process was constructed. This numerical construction based on the discrete wavelet transform (described above and in detail in [42]) uses scales given by the consecutive powers of two (2, 4, 8, 16, ... samples), while in the analysis we use the continuous (complex) wavelet transform that gives the possibility to study scales given by real numbers (limited by the available data). A closer look at Figure 5d reveals that there is no significant CMI at scales in the exact ratio 2:1. Apparently, the phases in the exact ratio 2:1 appear as phase-synchronized and the direction of coupling is not identifiable. However, there is always a range of close scales in which the significant CMI confirms the information transfer from scales close to to scales close to /2, e.g., there is no significant CMI for the scales 16:8, but for the scales in ratios such as 15.488:8.712 the CMI is statistically significant (Figure 5d).

We have estimated the CMI with increasing dimension of the condition from one (using I(φ₁(t); φ₂(t + τ )|φ₂(t))) to three (using I(φ₁(t); φ₂(t + τ )|φ₂(t), φ₂(t − η), φ₂(t − 2η)), with η equal to 1/4 of the scale of φ₂). The CMI with the one- and two-dimensional condition brought a large rate of “false positives”, i.e., the cases of the significant CMI indicating the information transfer from smaller to larger scales. The conditioning dimension three appears as sufficient for the correct distinction of the direction of information transfer in the studied multifractal data.

The CMI in this example was estimated using the equiquantal binning algorithm [14,26,46,47]. In order to assess the data requirements for a sensitive and specific inference of the information transfer, we have chosen 7 pairs of scales in the approximate ratio 2:1 and computed the CMI with different conditioning dimensions using different numbers of data samples (time series lengths) for 100 different realizations of the same multifractal process as that studied in Figure 5. The number of correctly detected information transfers from larger to smaller scales (“true positives”, i.e., the significant CMI in the direction of the existing information transfer from a larger to a smaller scale) gives the sensitivity of the test. The number of the significant CMI cases in the opposite direction (“false positives”, the significant CMI cases in the direction from smaller to larger scales) characterizes the specificity of the test. The results for I(φ₁(t); φ₂(t + τ )|φ₂(t))with the one-dimensional condition (CMI-1D in the following) and I(φ₁(t); φ₂(t + τ )|φ₂(t), φ₂(t − η), φ₂(t − 2η)) with the three-dimensional condition (CMI-3D) are presented in Figure 6. Considering the above observation that the information transfer direction cannot be inferred for the exact scale ratio 2:1, we have chosen the scale ratios 15.488:8.712; 31:17; 64:34; 124:68; 265:164; 432:296; 1039.64:534.64. Similar results, however, were obtained for a number of close scales representing the areas of the significant CMI in Figure 5d.

Figure 6 demonstrates that we need less data for the estimation of CMI-1D than for CMI-3D in order to obtain the 100% sensitivity in detecting the information transfer from larger to smaller scales in the studied multifractal process. Considering, e.g., the approximate scale ratio 16:8 (the black line in Figure 6), CMI-1D gives the 100% sensitivity using 8192 samples (or 90% sensitivity using 4096 samples). However, the rate of false positives is over 40%. In order to obtain the 100% sensitivity using the CMI-3D we need 16,384 samples, however, the rate of false positives is under 5%, which is the nominal significance level of the used test. The CMI-1D gives the test that is sensitive but not specific, since it suffers from a large rate of false positives. The results for CMI-2D are similar. Only CMI-3D provides the test that is specific and is sensitive enough using at least 16,384 samples for the scale ratio 16:8 (the black line), 32,768 samples for the scale ratio 32:16 (the red line in Figure 6), etc. Apparently, using the equiquantal binning estimator, the CMI-3D I(φ₁(t); φ₂(t + τ )|φ₂(t), φ₂(t − η), φ₂(t − 2η)) gives a sensitive and specific indicator of the cross-scale information transfer if the analyzed time series contains, at least, approximately 1000 cycles of a slower oscillatory component. Unfortunately, such a requirement cannot be satisfied in many experimental studies and other approaches are necessary.

3.2. Cross-Scale Information Transfer in Atmospheric Dynamics

Uncovering interactions in the many scales of the dynamics of the Earth atmosphere and climate is one of the principal challenges of contemporary science with a potentially high impact for the society. In a search for a low-dimensional explanation of some scales of atmospheric dynamics, in the 1980s several researchers claimed detections of a weather or climate attractor of a low dimension [48–51]. Leading personalities of chaos theory, however, pointed to a limited reliability of chaos-identification algorithms and warned that the observed low-dimensional weather/climate attractors can be spurious [52,53]. Paluš & Novotná [54] even questioned the necessary condition for chaos—the presence of nonlinearity in the air temperature data when the dependence between a temperature time series {x(t)} and its lagged twin {x(t + τ )} was considered. Hlinka et al. [55] questioned nonlinearity in the dependence between the monthly time series of the gridded whole-Earth air temperature reanalysis data. It seems that linear correlation is a good descriptor for interactions in long-term air temperature recordings. Such data, however, reflect a very coarse view to a mixture of dynamics on many spatial and temporal scales. Considering specific spatial scales, a description of climate or weather variability using a low-dimensional nonlinear dynamical system can be plausible, as proposed by Tsonis and Elsner [56]. Recently, Tsonis [57] has uncovered that climate subsystems can act as pacemakers of decadal climate variability. The spatial scales for climate subsystems can be inferred from climate data using classical approaches of rotated principal component analysis combined with more recent surrogate data testing approach [58], or the very modern approach of complex networks [59]. Evolving climate networks can track important short-term climate influencing events such as El Niño episodes or large volcanic eruptions [60] and discern regional from global effects [61]. Besides considering specific spatial scales, a more detailed look on repetitive patterns on specific temporal scales in the air temperature and other meteorological data has led to an identification of oscillatory phenomena possibly possessing a nonlinear origin and exhibiting phase synchronization between oscillatory modes extracted either from different types of climate-related data or data recorded at different locations on the Earth [9–13,37]. Long-term air temperature recordings reflect complex atmospheric dynamics on multiple temporal scales. Oscillatory phenomena with the periods between 6 and 11 years, however, most frequently with the period around 7–8 years, have been observed in the air temperature and other meteorological data from European and Mediterranean areas by many authors (see [10,12] and references therein). Typically these oscillations are hidden in a red-noise background and their estimated amplitudes are small, therefore their relevance for the recent climate change has not been adequately assessed yet. We decided to study possible cross-scale interactions between oscillatory modes with periods between 6 and 12 years and variability with typical time scales from a few months to 4 years. The CCWT with the Morlet wavelet was used in order to obtain the instantaneous amplitudes and phases. We have not found any phase–phase interactions. Then we concentrated on the phase–amplitude coupling. In particular, we study a possible influence of the phase φ₁ of slow oscillations on the amplitude A₂ of higher-frequency variability, using the CMI functional

$$I({\phi }_1(t);A_2(t+\tau )\mid A_2(t),A_2(t-\eta ),\dots ,A_2(t-m\eta )),$$

(21)

where τ is the forward time lag, η is the backward time lag in the m + 1-dimensional condition.

We use daily mean surface air temperature (SAT) time series recorded in various European locations. The data from Bamberg, Basel, De Bilt, Potsdam, Vienna and Zurich from the period 1901–1999 are a part of the data compiled for the European Climate Assessment [62]; the record from Prague-Klementinum is extended till 2008, and the SAT data from a number of German stations extended till 2011 are available due to the German Climate Data Center [63]. The inclusion criterion for this study is the availability of at least 90 years of uninterrupted daily mean SAT recording, since the computations of the CMI (21) have been performed using the time series length 32,768 daily samples. The relatively large amount of data was required in order to obtain reliable estimates and sensitive statistical tests, even though we used an estimator of the mutual information derived for Gaussian processes according to Equation (10). The functional (21) is evaluated and averaged for the forward lags τ from 1 to 750 days. (The CMI time-lag dependence is studied and discussed in the Supplemental Material of [64].) The backward lag η is set to 1/4 of the period of the slower oscillations characterized by the phase φ₁, following the embedding construction recipe based on the first minimum of the mutual information [33].

The temporal evolution of the raw daily mean SAT data from mid-latitude locations is dominated by the annual cycle. In many climate-related studies deseasonalized SAT “anomalies” are used. In this study, however, we are interested in discovering interactions of all relevant temporal scales, therefore the raw SAT data are used for the computation of the CMI (21). The used surrogate data algorithms, however, might not accurately reproduce such a strong cyclic component. The latter is not consistent with the used multifractal model [42] and even the FT surrogate data procedure fails to reproduce a strong cyclicity and/or long coherence times [47]. Therefore, before the randomization, the seasonality in both mean and variance is removed from each SAT time series. This is done by computing the means and the variances for each calendar day. These seasonal means are subtracted from the raw SAT data of the corresponding days and the resultant SAT anomalies (SATA hereafter) are divided by the corresponding seasonal variances. Such deseasonalized data enter either the FT or MF randomization procedure. Then, the original seasonality in variance and mean is added back to each surrogate data realization. Each “seasonalized” surrogate realization undergoes the same processing procedure as the original SAT data—the CCWT is used to obtain the phase φ₁ of slow oscillations and the amplitude A₂ of higher-frequency variability, both used in the CMI (21) estimation. For each pair of the studied temporal scales, one thousand surrogate realizations are used for an empirical estimation of the percentiles of the CMI (21) surrogate distribution. As a result, we record the “significance level,” i.e., the highest percentile exceeded by the value of the CMI (21) computed from the original SAT data.

The significance levels for the CMI I(φ₁(t);A₂(t+τ )|A₂(t), A₂(t − η), . . ., A₂(t − mη)) obtained from the Prague-Klementinum daily SAT data are presented in Figure 7. The results for the CMI with 2, 3 and 4 conditioning variables are depicted in Figure 7a–c, respectively. Since the increase of the conditioning dimension over three does not substantially change the patterns of φ₁ → A₂ interactions, the results for other European locations were obtained by evaluating I(φ₁(t);A₂(t + τ )|A₂(t), A₂(t − η), A₂(t − 2η)) with the 3-dimensional condition. The tests with the two types of the surrogate data bring consistent results (cf. Figure 7b,d).

The choice of the three-dimensional condition does not mean that we consider the dimensionality of the amplitude dynamics equal to three, as in the case of the Rössler system, but that this dimension is sufficient for distinguishing a bidirectional from a unidirectional coupling in this case. Let us compare the results for I(φ₁(t);A₂(t + τ )|A₂(t), A₂(t − η), . . ., A₂(t − mη)) measuring the directional coupling, or the information transfer in the direction φ₁ → A₂ with the CMI I(A₂(t); φ₁(t + τ )|φ₁(t), φ₁(t − η), . . . , φ₁(t − mη)) in the opposite direction A₂ → φ₁ in Figure 8. Considering the significance level p < 0.05 for a single test, we obtain more than 10% of significant tests in the direction φ₁ → A₂ for all conditioning dimensions (Figure 8a–c), while in the direction A₂ → φ₁ there are more than 5% of significant results only in the case of the one-dimensional condition. From the conditioning dimension two, there is always less than 5% of significant results, which is the possible rate of false positives. Moreover, there is no consistent pattern of the (false) positives in the direction A₂ → φ₁ considering SAT data from different locations, while the pattern of the φ₁ → A₂ directional interactions is consistent in SAT recording from many locations in (mainly Central) Europe: The pattern of the φ₁ → A₂ directional interactions in SAT from Prague-Klementinum (longitude 14°25′E, latitude 50°05′N, Figure 7b) is almost the same as that from Potsdam (13°04′E, 52°23′N, Figure 9a) and very similar to the pattern from Hamburg (10°0′E, 53°33′N, Figure 9b).

Some changes can be seen in the pattern from Bamberg (10°53′E, 49°53′N, Figure 9c), while even more changes can be seen when approaching the Netherlands coast—De Bilt (05°11′E, 52°06′N, Figure 9d).

This observation supports the conclusion that in the dynamics (time evolution) of the air temperature there are unidirectional cross-scale interactions, or an information transfer from larger to smaller scales in the sense that the phase of slower oscillations causally influences the variability on shorter scales. These results provide a quantitative evidence for existence of previously unknown phenomenon in atmospheric physics. Understanding of its physical mechanisms is a challenge for further research.

The outputs of the statistical tests, however, are hard to understand in the sense of the effect of this phenomenon and its significance for weather and climate variability. We have already noted the existence of climate oscillations with the period around 7–8 years. References [10,12] give a brief review of observations of this cycle in instrumental as well as model meteorological data. Recently, the 7–8 years cycle has also been observed in soil and ground temperatures from a Prague area [65]. Figures 7 and 9 show that the phase of this cycle influences the air temperature variability in the scale between 2 and 3 years (quasicyclic variability also known as quasibiennial oscillations), at and around the annual cycle, and in short seasonal scales. The structure of the variability on these scales is an interesting topic for further research; here we will take a simplified look at the total temperature variability.

Let us consider the surface air temperature anomalies (SATA) from Prague-Klementinum and the instantaneous phase extracted from this SATA series using the CCWT with the central frequency giving the period 8 years. We can see a tendency of the temperature to have local maxima around the middle and minima near the beginning and the end of each 8-year cycle (Figure 10).

In order to assess a statistical association of the SATA variability and the 8-year cycle, we divide the phase in each 8-year cycle into 8 equidistant bins and compute the mean and variance of the SATA values for each of the eight bins. We obtain in this way the conditional SATA means and variances, conditioned by the phase of the 8-year cycle. If there is no statistical association between the SATA variability and the 8-year cycle, the conditional means and variances should be asymptotically the same. In the finite sample estimate, the conditional means and variances would fluctuate independently of the phase. However, this is not the case. In Figure 11 we can see that the years in the middle of the 8-year cycle are warmer and less variable, while the cycle edges are colder and the temperature is more variable. The MF surrogate data preserve the variance for particular scales, i.e., the presence of the cycle, but not the cross-scale interactions. From the surrogate results we can see that the cycle itself can explain the difference in yearly temperature means about 0.6 °C; however, in the data, the change of the mean temperature within the cycle reaches about 1.7 °C. In this way we can quantify the effect of the observed cross-scale interactions on the interannual temperature variability. This quantification, however, is not robust. It is nonstationary, changing in space and time, however, in the studied European locations, reaching values between 1 and 2 °C, which is a non-negligible variability.

4. Conclusions

Information theory provides useful tools for the detection of interactions in complex systems using experimental time series. A coupling (dependence) can be detected by using the mutual information (MI), while the conditional mutual information (CMI) can be used in the detection of directional coupling or causal interactions in the sense of Granger causality, generalized for nonlinear systems. CMI, also known as the transfer entropy, effectively measures a transfer of information from a system that influences the future of another system. Therefore the causal influence (in the Granger sense) is also interpreted as the information transfer. We have extended the methodology, originally developed to detect interactions and information transfer in the bivariate case of two systems, into the study of interactions between dynamical phenomena evolving on different time scales, however, forming together one complex, multiscale system. MI and CMI are applied to oscillatory components, extracted from a multiscale time series by using the complex continuous wavelet transform (CCWT). The oscillatory components are described using their instantaneous phases and amplitudes, so that various types of cross-scale interactions can be studied. Estimators of MI/CMI can be biased and CCWT can bring some systematic errors into the study of cross-scale interactions. Statistical testing based on surrogate data, however, can cope with these methodological errors. The specificity of surrogate data inference methods can be secured by an appropriate choice of surrogate data that reproduce the bias of a MI/CMI estimator applied to the studied data. The sensitivity of the method can be guaranteed by a certain bound on the estimator variance [26]. Typically, a lower variance requires a larger amount of data or, more precisely, a time series representing a longer epoch of evolution of the studied process [26,46]. The required time series length depends on the used MI/CMI estimator. A review of various estimators is given in [14], and the properties of several estimators in statistical tests are studied in [26,46].

The introduced method is demonstrated using simulated data. We identify cross-scale interactions in a model of a multifractal process that mimics information transfer from larger to smaller scales observed in turbulence. Then we apply the method to time series of long-term records of near-surface air temperature from a number of European locations. We report no cross-scale phase–phase interactions; however, we have reliably detected cross-scale phase–amplitude directed interactions. Here we need to make a remark about estimation algorithms and related data requirements for the sensitive tests for directed interactions. Considering cross-scale phase–phase interactions, we try to identify interactions of oscillations with different frequencies that are linearly independent. Therefore it is necessary to use a nonlinear MI/CMI estimator, which requires large amounts of data for multi-dimensional estimators used. Thus the phase–phase interactions in the studied atmospheric data either do not exist, or the available amount of data is not sufficient for a successful detection.

In the case of cross-scale phase–amplitude interactions, the situation is different. Even though the considered amplitude characterizes faster oscillations, the amplitude itself varies slowly, possibly within the same frequency range as the considered slow oscillations, characterized by the used phase. Therefore it is possible to use the MI/CMI estimator for Gaussian processes and to successfully detect, from the available data, the information transfer from larger to smaller time scales as the influence of the phase of slow oscillations on the amplitude of faster variability.

It is important that by increasing the conditioning dimension in the CMI we were able to prove the existence of an information transfer from larger to smaller scales but not vice versa. We have obtained quantitative support for the first condition of the Granger causality that the (phases of the) slow climate oscillations influence the future character of the fast temperature variability. We did not study, however, the second condition that the cause contains information about the effect that is unique, and is in no other variable. The mechanism of emergence of the 7–8 years oscillations in the air temperature dynamics in a large part of Europe is unknown yet and it is possible that its roots have a more global character. Then the observed directional coupling can be secondary, i.e., induced by another process. The answer to this question is a challenge for further research.