Exploration and Development of High Entropy Alloys for Structural Applications
Abstract
: We develop a strategy to design and evaluate high-entropy alloys (HEAs) for structural use in the transportation and energy industries. We give HEA goal properties for low (≤150 °C), medium (≤450 °C) and high (≥1,100 °C) use temperatures. A systematic design approach uses palettes of elements chosen to meet target properties of each HEA family and gives methods to build HEAs from these palettes. We show that intermetallic phases are consistent with HEA definitions, and the strategy developed here includes both single-phase, solid solution HEAs and HEAs with intentional addition of a 2nd phase for particulate hardening. A thermodynamic estimate of the effectiveness of configurational entropy to suppress or delay compound formation is given. A 3-stage approach is given to systematically screen and evaluate a vast number of HEAs by integrating high-throughput computations and experiments. CALPHAD methods are used to predict phase equilibria, and high-throughput experiments on materials libraries with controlled composition and microstructure gradients are suggested. Much of this evaluation can be done now, but key components (materials libraries with microstructure gradients and high-throughput tensile testing) are currently missing. Suggestions for future HEA efforts are given.1. Introduction
High entropy alloys (HEAs) are a new effort in materials science and engineering. The first publications appeared not quite 10 years ago [1,2], and HEAs are being considered for a wide range of functional and structural applications [3]. This paper discusses the design, evaluation and development of HEAs for structural applications in the transportation (including aerospace) and energy sectors. These applications require high strength, high operating temperatures and low density. Three alloy families are commonly used to meet these requirements. Aluminum alloys have low density but also have relatively low operating temperatures; titanium alloys have moderate densities and operate at higher temperatures; and nickel-based “superalloys” have high densities and even higher operating temperatures. Superalloys have been the material of choice for over 70 years in load-bearing applications at the highest temperatures, especially in fracture-critical components. Key characteristics include excellent strength above 600 °C and useful strength at up to 85% of the insipient melting temperature (use temperatures as high as 1,100 °C); good room temperature ductility and fracture toughness; good resistance to environmental degradation, especially oxidation; good long-term microstructural stability; and good time-dependent behavior (creep and fatigue). Opportunities for improvement include developing higher strength, higher operating temperature or lower density. Numerous concepts have been pursued in the past 50 years to surpass the balance of properties offered by these exceptional materials, but none have been successful in displacing superalloys.
HEA studies presently favor single-phase, disordered solid solution alloys (the terms disordered and solid solution are used interchangeably throughout this manuscript). If the desired properties can be obtained with such an alloy, then this approach is preferred as it avoids complications (and cost) of microstructural control associated with second phases. This may suffice where structural loads are relatively low, where the application temperature is below about half the absolute melting temperature (Tm/2), or where selection criteria favor low cost, ease of forming or environmental resistance. A limited number of single phase, solid solution strengthened conventional metal alloys fit this profile. Bronze and brass are commonly used, especially where their environmental resistance is valued. The 3xxx and 5xxx series of aluminum alloys are strengthened by both solid solution hardening and cold work and find use in architectural applications, boat hulls, pots and pans, and heat exchangers. Alpha and near-alpha titanium alloys are used at cryogenic and elevated temperatures in the aerospace sector. Austenitic stainless steels are primarily Fe-Cr-Ni alloys prized for their environmental resistance, and include such well-known alloys as 304 and 316 stainless steels. Solid solution strengthened Ni-based and Fe-Ni based superalloys are used where formability is important or where solution treatment, quench and aging needed for precipitation strengthening is impractical, such as complex-shaped castings. Common alloys include Incoloy 800H, Incoloy 801, Inconel 600 and Hastelloy B, N and W.
Supporting the single-phase HEA approach, it is believed that solid solution strengthening is more effective in HEAs than in conventional alloys [3]. The problem is complex, and present analysis shows that solid solution hardening in HEAs can be as much as an order of magnitude higher than in binary alloys [4]. However, the potency of HEA solid solution strengthening has not been sufficiently studied, especially for extended loading times or at temperatures above Tm/2. There have been no studies to establish effectiveness of solid solution hardening in creep loading of HEAs.
The highest strength conventional metals and alloys used at high temperatures almost always rely on the controlled distribution of a second phase. The second phase can be a disordered solid solution (as in α/β titanium alloys), but most often is an intermetallic phase. For example, aluminum alloys rely on Al-Cu, Al-Mg-Cu or Al-Mg-Zn compounds; steels depend upon pearlite (a micro-constituent consisting of α-ferrite and Fe3C); and superalloys make extensive use of a Ni3Al-based compound. The potency of particle strengthening derives from the inverse relationship between the strength increase and particle spacing, so that strength increases in a nearly unbounded form as particle spacing approaches nanometer dimensions. Particle sizes and spacings in aluminum alloys are generally controlled over a range of 10–100 nm; the internal dimensions of pearlite typically range from 50–500 nm; and Ni3Al precipitates in superalloys have sizes and spacings that range from 10–1,000 nm. Particle strengthening retains effectiveness at very high temperatures, making this an extremely useful alloy strategy. Other classical strengthening mechanisms (grain boundary strengthening, work-hardening, solid solution strengthening and transformation strengthening) have reduced effectiveness at elevated temperatures, especially over long service lifetimes.
Given the effectiveness of particle strengthening, we propose expanded HEA efforts to include the intentional addition of second phases. This raises the question whether alloys with intermetallic phases can be considered as HEAs—this is discussed in Section 2.1. HEAs give a new approach for controlling the stability of intermetallic precipitates used for strengthening, as will be discussed in Section 2.2 and Section 3.3.2.
Perhaps the most significant benefit of HEAs has little to do with the magnitude of configurational entropy. A major benefit of HEAs is that they stimulate the study of compositionally complex alloys not previously considered. This suggests an astronomical number of compositions, giving great potential for discoveries of scientific and practical benefit. Supporting this view, a wide array of HEA microstructures has been produced, including single phase, multiple phase, nanocrystalline and even amorphous alloys. A relatively small number of HEA systems currently receive a major portion of attention, and we propose the exploration of an expanded range of HEAs. To most effectively explore this vast alloy space, we define a palette of elements from which HEAs can be designed to meet a particular set of target properties (Section 3.2). This is coupled with aggressive use of high-throughput computational and experimental techniques (Section 3.5).
A brief outline of the manuscript is given here. As with any new effort, the excitement of new ideas and results generates a dynamic exchange—and a little debate. Both standard and operational definitions are discussed in Section 2.1 to address some of this controversy, including whether or not alloys with intermetallic compounds can be considered HEAs. A simple calculation is made in Section 2.2 to estimate how effective configurational entropy might be in avoiding compound formation. HEA systems tailored for structural applications at low, medium and high temperatures are proposed (Section 3.1), and an approach for selecting a palette of elements from which HEAs can be devised for each of these temperature ranges is developed in Section 3.2. The design of structural HEAs from the palette of elements is discussed in Section 3.3 for single-phase and two-phase microstructures. Compositional complexity imposes important requirements in the characterization of HEAs, and these are discussed in Section 3.4. Especially, equilibrium studies are rarely conducted in any HEA. This is an essential area for study, especially for applications where the alloy can be at 85% of Tm for thousands of hours (Section 3.4.2). While HEAs offer new promise, they also bring unique challenges. The vast number of compositional possibilities makes rational and efficient exploration difficult. A hierarchical approach that combines computational and experimental high-throughput techniques is described in Section 3.5. Each of these discussions draws on historical expertise in the exploration, characterization and development of structural metals for high temperature applications.
2. Key Concepts in HEAs
2.1. Standard and Operational HEA Definitions
The standard definition of an HEA is an alloy that contains at least five major metallic elements (N ≥ 5), each with concentration between 5–35 atom percent [3,5]. The idea behind this definition is that compositional complexity may not necessarily lead to microstructural complexity (i.e., compound formation) due to the influence of entropy. Specifically, it is suggested that disordered solid solutions might remain stable relative to ordered intermetallic compounds (for simplicity, the terms ordered, intermetallic and compound are used interchangeably in this paper) in alloys with high total entropies of mixing (ΔSmix). Whether or not an alloy satisfies the standard definition is clear based on alloy composition alone, regardless of the magnitude of ΔSmix. However, since the motivation for studying HEAs often includes the magnitude of an alloy’s entropy and its ability to remain a single-phase solid solution at room temperature, some discussion of these two features is necessary. How high is high? Is an alloy an HEA if more than a single disordered phase occurs in the microstructure?
Configurational entropy (ΔSconf) forms a major part of ΔSmix and for ideal and regular solutions is:
Another debate within the HEA community is whether or not an alloy with more than one phase is an HEA. Consider two 5-component equimolar HEAs that are both solid solutions near their melting points. The first, HEA-1, remains a single-phase solution at 300 K while the second, HEA-2, forms a binary compound at a temperature (Trxn) that removes two elements entirely from the solid solution (Figure 1). Both alloys have ΔSconf = 1.61R at high temperature, but ΔSconf of the disordered phase is reduced to 1.10R in HEA-2 below Trxn. Since HEA-2 has two ΔSconf values, we must consider which is used in defining whether or not it is an HEA. It has been suggested that ΔSconf of the low temperature state be used [8]. We suggest the alternate approach, since judging the entropy available to a system by its final (low temperature) state is like judging the strength of an athlete at the end of a race, after all energy has been spent. We discard useful information concerning the athlete’s overall strength and competitiveness and judge the athlete only on whether the current race was won or lost. Phase stability is a competition between entropy, enthalpy and other terms such as strain energy that are summed in the Gibbs free energy equation. The entropic energy (−TΔSconf) becomes less negative with decreasing temperature, and so phases with enthalpies of formation (ΔHf) sufficiently large and negative to overcome −TΔSconf at lower temperature may form in HEAs. These could be called high entro-thalpy alloys since both ΔSconf and |ΔHf| are large, but in the present work these are still considered HEAs as discussed below.
Here we are concerned more broadly with the competitiveness of a single-phase solid solution (which depends primarily on the magnitude of ΔSconf), and less so with whether compounds form in a given alloy (which also depends on ΔHf of all competing phases). Thus, both CoCrFeMnNi and TiCrFeMnNi equimolar alloys are considered HEAs in the present work, although the former is a disordered single-phase and the latter forms intermetallic compounds [8]. Both have the same ΔSconf at high temperature and differ primarily in the magnitude of ΔHf of the competing phases. The magnitude of ΔSconf in an HEA does not guarantee suppression of intermetallic compounds, but it does increase the probability that this will occur (see Section 2.2). Even when ΔSconf is insufficient to suppress compounds, it may nevertheless influence the temperature at which the intermetallic phase dissolves upon heating. The ability to influence the dissolution temperature of a second phase has profound importance via the particle strengthening mechanism. This will be developed in more detail in Section 2.2 and can be applied to the development of new HEAs (Section 3.3.2).
We thus define HEAs by the magnitude of ΔSconf in the high temperature state, since ΔSconf in the high temperature (ideal or regular solution) state is the entropy that is inherent in a system and which must be overcome if competing phases are to form. This approach is convenient, since we only need to know the magnitude of ΔSconf (given by the alloy constitution)—we do not need to know whether or not other phases form (which also depends on ΔHf of the competing phases). This approach is consistent, since alloys with equal ΔSconf (but with different ΔHf) are all considered HEAs. This approach retains information regarding the competitiveness (i.e., relative stability) of the disordered phase by indicating the probability that an alloy retains a single-phase disordered solid solution at room temperature. This approach also gives information regarding the probability that an intermetallic phase, if formed, can be dissolved at some intermediate temperature. There is no single correct approach for classifying HEAs, and both approaches (low temperature or high temperature) are correct within the stated boundary conditions. However, we believe the present approach is more convenient, more consistent and carries richer information.
2.2. Competition Between Entropy and Enthalpy
How likely are entropy values in HEAs to overcome compound formation? We offer a simple, first-order analysis by comparing the Gibbs free energies of HEAs (ΔGHEA) with the Gibbs free energies of competing binary intermetallic compounds (ΔGAxBy). ΔGAxBy is dominated by the enthalpy of formation ( ), since the entropy change for compound formation ( ) is generally small. By comparing values for these terms for a number of binary, metal-metal systems [9], we approximate as /104. Using values from [9], the Gibbs free energy for compound formation is thus estimated as:
The Gibbs free energies for competing solid solution HEAs (ΔGHEA) is given as:
The product σdε is a strain energy term that is usually neglected. We show this term explicitly since lattice strain energies in HEAs may be non-trivial. At present there is no approach to quantify this contribution and so we do not include strain energy in this analysis. Values for the enthalpy of mixing, ΔHmix, are given for binary alloys at the equimolar composition [10]. We estimate as a function of atom fraction B (XB) by fitting a parabola that passes through ΔHmix at XB = 0.5 and through = 0 at XB = 0 and XB = 1. The values used here are for the appropriate composition of each specific AxBy compound. Each of the systems in this comparison (Al-Cr, Al-Y and Ni-Y) have < 0, and are treated as regular solutions, where ΔSconf is the same as for an ideal solution. We use the average ΔSconf for N = 5 and N = 13 from Equation (1). We calculate ΔGHEA at 300 K and 1,300 K using Equation (3). All energies are given in kJ·mol−1 of atoms. The results are shown in Figure 2.
We compare ΔGAxBy and ΔGHEA for compounds with low (Al-Cr), medium (Ni-Y) and high (Al-Y) stability. The Al-Y system is the most stable, and ΔGAxBy is more negative than ΔGHEA at both 300 K and 1,300 K for most compounds, so that their stabilities will be practically unaffected in HEAs. However, ΔGAxBy is between ΔGHEA at 300 K and 1,300 K for Al2Y3 and AlY2. This suggests that these compounds are thermodynamically stable at 300 K but that they become unstable below 1,300 K due to the multiplying effect of temperature on ΔSconf. Most Al-Cr and Ni-Y compounds also fall between ΔGHEA bounds at 300 K and 1,300 K. Consider Ni5Y as an example, which is stable up to its melting point of 1,703 K in the binary system [11]. This makes microstructural control of Ni5Y precipitates difficult, since they form directly on solidification and cannot be re-dissolved. However, it may be possible to dissolve and subsequently nucleate and grow Ni5Y by heat treatment in HEAs containing Ni and Y at ratios where Ni5Y might form. The configurational entropy of HEAs thus opens a new opportunity for microstructural control of the Ni5Y phase that is not possible in conventional alloys. This idea is discussed further in Section 3.3.2.
ΔGAxBy for the AlCr2 compound and three Ni-Y compounds lie above ΔGHEA at both 300 K and 1,300 K, suggesting that these compounds might be totally destabilized in HEAs. Thus, some compounds in this limited comparison are completely destabilized by ΔSconf, some are unaffected by ΔSconf below 1,300 K, and most compounds are stable at 300 K but unstable at 1,300 K.
To estimate the destabilizing potential of HEAs more broadly, we compare ΔGHEA with ΔGAxBy for over 1000 binary compounds. ΔGAxBy from Equation (2) uses values from [9,12–18] and assessed for accuracy as described elsewhere [19]. A histogram of ΔGAxBy values at 300 K is shown in Figure 3a. Since is a minor part of ΔGAxBy, the results are basically the same at 1,300 K. The distribution is skewed toward less negative values—the average ΔGAxBy is −41 kJ·mol−1, the median is −36 kJ·mol−1 and the most common value is between −10 kJ·mol−1 and −15 kJ·mol−1. We also plot the cumulative fraction of compounds with ΔGAxBy less negative than a given value.
ΔGHEA values are calculated for HEAs with N = 5 and N = 13 from Equation (3). is given by ΔHmix calculated from the Miedema model for the element pair in each compound considered [10]. The concentration ratios of pairs of atoms in an HEA (XA:XB, XA:XC, XA:XD…) will generally be close to 1:1, so that adjustment of ΔHmix to match XB for a particular AxBy compound (as was done for the specific binary systems above) is not needed. As before, ΔSconf is given by Equation (1).
The fraction of compounds destabilized in an HEA is given by the value of the cumulative curve in Figure 3a at ΔGAxBy= ΔGHEA and is shown in Figure 3b as a function of temperature for HEAs with N = 5 and N = 13. A curve for binary, solid solution alloys (N = 2) is shown for comparison. The small, non-zero value for the N = 2 curve at T = 300 K comes from errors in the Miedema method used to estimate ΔHmix [10] and from measurement errors in [9,12–19]. This analysis suggests that about 10%–15% of intermetallic phases that are stable in binary alloys may be destabilized in HEAs at 300 K (compare the N = 5, 13 curves to N = 2 at 300 K). These destabilized compounds have ΔGAxBy values less negative than about −15 kJ·mol−1 (see Figure 3a). Alloys become kinetically frozen during solidification, so that the fraction of compounds suppressed at a higher temperature may be more relevant. For example, about 20%–32% of intermetallic compounds are suppressed at 600 K relative to binary systems. The destabilizing effect of entropy increases with temperature, and about 40%–60% of the compounds that are stable in binary alloys may be suppressed at 1,500 K in HEAs.
In terms of absolute probabilities (not relative to binary systems), roughly 1 in 3 HEAs may be single phase at 600 K and roughly two in three may be single phase at 1,500 K. The difference between these two temperatures—HEAs that are single phase at 1,500 K but multi-phase at 600 K—account for roughly one out of three intermetallic phases. These phases offer new opportunities for microstructural design and control (see Section 3.3.2). Roughly one in three compounds remain stable above 1,500 K and are practically unaffected by the higher configurational entropy in HEAs.
This is a first-order approximation. Although ΔGAxBy estimates are probably reasonable there is uncertainty in ΔGHEA due to the Miedema method used to give ΔHmix and in the use of a regular solution model. The error is difficult to quantify, but a minimum value of ±5% is indicated in Figure 3b. Nevertheless, this analysis gives a general expectation for the probability that compounds may be suppressed in HEAs. These results are consistent with a study of the stability of CoCrFeMnNi with various substitutional elements, where it was concluded that ΔHmix in non-ideal solutions and of competing compounds must be considered in the phase stability of HEAs [8].
3. Design and Evaluation of HEA Structural Metals
In this section, new HEA systems are described to meet a range of use temperatures for transportation and energy structural metals. We build a master list of candidate metallic elements and extract more focused palettes of elements for specific application temperature ranges. Guidance is given on selecting specific elements for HEAs from each palette of elements. Both solid solution, single-phase alloys and HEAs strengthened by intentional addition of a second phase are described. Challenges in the characterization of HEAs are discussed, and suggested approaches are given for the rapid computational and experimental exploration of HEAs.
3.1. HEA Families for Low (LOW-T), Medium (MED-T) and High (HI-T) Use Temperatures
The main focus of this paper is to discuss the development of HEAs as structural materials for the transportation and energy sectors. These require high strength, and since structural components or the entire system (or both) are dynamic, low density is also essential. A range of use temperatures exists in transportation and energy systems, and an alloy is usually used at its highest operating temperature. Three alloy families are used to meet these needs: aluminum alloys, titanium alloys and nickel-based superalloys. Characteristic properties for these alloy families are given in Table 1.
Structural materials must also have good damage tolerance. This is well-known, but the challenge associated with achieving both excellent strength and good fracture properties is often underestimated. It seems to be relatively simple to produce strong alloys, but very difficult to do this in an alloy that also has good damage tolerance. By damage tolerance, we mean ≥5% room temperature tensile ductility and Mode I fracture toughness ≥30 MPa-m1/2. Conventional structural metal alloys meet these criteria (Table 1). Throughout this manuscript, discussion of structural properties is understood to include damage tolerance.
A brief survey of the literature suggests an emphasis on HEAs containing Co, Cr, Cu, Fe, Mn and Ni [1–3,5,8,20–42]. These HEAs could be considered an extension of austenitic stainless steels, which have Fe, Cr and Ni as major constituents but may also contain significant concentrations of Mn. This early focus is surprising in a field that offers such a vast number of compositional possibilities. We suggest pursuing a broader range of systems that includes HEAs for structural applications at low temperature (called LOW-T in this paper), intermediate temperature (MED-T) and high temperature (HI-T). Goal properties for these three HEA families should exceed the characteristic properties in Table 1 by a margin sufficient to warrant the extra risk and cost of development, scale-up, certification and insertion. Improvements in the range of 10%–30% in some key property are typically adequate to motivate insertion of a new alloy. An approach to identify groups of elements from which LOW-T, MED-T and HI-T HEAs can be produced is given below.
3.2. “Master List” and “Palette of Elements” for Targeted HEAs
The first step is to develop a master list of elements for structural metal HEAs. Starting with the periodic table of elements, we exclude all non-metals (H, C, N, O, P, S, Se), halogens (F, Cl, Br, I, At), and noble gases (He, Ne, Ar, Kr, Xe, Rn). We eliminate most of the semi-metals (B, Ge, As, Sb, Te, Po), but we retain Si as a compound-forming element for HEAs with an intentional addition of second phases (Section 3.3.2). We remove toxic (Ba, Be, Cd, Pb, Os, Tl) and radioactive elements (Ra, Ac, Th, Pa, U, and all elements with atomic number >92). Finally, we delete elements with Tm less than 700 K (Hg, Fr, Cs, Ga, Rb, K, Na, In, Li, Sn, Bi, Zn). The remaining 45 elements are given in Table 2. This master list contains all elements that we choose to use for structural metal HEAs. The process of exclusion is subjective, and other lists can be devised. For example, more (or all) of the semi-metals could be retained, a Tm other than 700 K could be used to exclude elements, or no melting point cut-off could be used at all. This approach is based on practical considerations and on the compound-forming potential of elements. This master list gives all elements that are consistent with the broad alloy development goal of structural metals, but it is too large to be practical. For example, this list gives over 106 5-element HEAs and 1011 HEAs with 13 elements. A smaller set of elements is needed for more targeted HEA development.
In the second step, we identify a “palette of elements” that will be used to build a particular family of HEAs. These elements are selected from the master list using criteria of importance for the alloys being developed. This step requires some care, as it implicitly assumes that elemental properties can be related to the desired HEA properties. The well-known rule-of-mixtures [43] (called the “cocktail effect” in the HEA literature) gives a good approximation for physical properties such as density and modulus, but is likely to have significant errors for other properties. The primary alloy characteristics for energy and transportation applications are density (ρ), strength and use temperature (Tuse), and some discussion of the last two selection criteria is required.
Alloy strength depends sensitively on microstructural features that cannot easily be drawn from elemental properties. Similarly, Tm of an alloy is sensitive to subtle details of chemical interactions between constituents, relative atom sizes, and concentration. Both positive (congruent melting) and negative (eutectic reactions) deviations of 50% or more from a linear average of elemental melting temperatures are common in binary systems. However, a linear relation is found between the bond strength between atoms in the condensed state (the condensed bond enthalpy, εAA) and Tm for metallic elements [19]. A linear relation is also found between εAA and Young’s modulus (E), although the scatter is rather large. Nevertheless, Tm and E both scale with εAA.
We thus use elemental ρ, Tm and E to select palette elements. Density is important in its own right and E is an indicator of strength. The rule-of-mixtures is expected to give a reasonable approximation of ρ and E in HEAs. Tm is a proxy for the bond energy between atoms, εAA, which is an indicator of strength and also has some relation to Tm and Tuse of the alloy. Given its coarse nature, this last criterion helps select candidate elements but is not intended as a predictive tool. As a qualitative ranking of palette elements, we calculate the value of Tm/ρ for each element—higher values are better.
To select elements from the master list for LOW-T, MED-T and HI-T HEAs, we use cut-off values for ρ, E and Tm. The cut-off values are guided by experience. Cut-off values are larger than characteristic values for Al, Ti and Ni alloys in Table 1, since an upper limit is used for the cut-off and the HEA value will be between the maximum and minimum values. The limits chosen here are ρ ≤ 8, 10, 12 g·cm−3 and E ≥ 40, 60, 80 GPa for LOW-T, MED-T and HI-T HEAs, respectively. To set Tm limits, we start with target Tuse = 200 °C, 600 °C and 1,000 °C (approximately 500 K, 900 K and 1,300 K) for LOW-T, MED-T and HI-T HEAs. Tuse is a fraction of the absolute alloy melting temperature that is usually between 0.5 and 0.85. We use 2/3 here, so that Tm is 50% larger than Tuse. The final elemental Tm cut-off values are thus 750 K, 1,350 K and 1,950 K for LOW-T, MED-T and HI-T alloys. The palettes of elements that meet these criteria are shown in Table 2. Other elemental properties that may be used in designing HEAs such as atom radius (r) and Pauling electronegativity are given in Table 2.
There are 16 LOW-T elements (giving about 63,000 equimolar HEAs) and 17 MED-T elements (producing over 127,000 equimolar HEAs). The five elements that satisfy the constraints for HI-T HEAs give only one equimolar HEA, emphasizing the difficulty in developing new high temperature structural alloys. To expand the list, we include elements with lower Tm (Ti), lower E (Zr) or higher ρ (Ru, Hf, Ta, W, Rh) so that the HI-T alloy family has 12 palette elements, giving 3,302 equimolar HEAs. The HI-T list is slightly expanded from the palette of elements used to construct refractory HEAs [4,27–29], as shown in Table 2. Refractory HEAs show a range of attractive properties, giving an early validation to this approach for designing HEAs. As a general guide, a palette of elements with roughly 10 to 20 elements provides a sufficiently large, yet workable, list of HEAs.
The average values of Tm, ρ and E are given for LOW-T, MED-T and HI-T palettes (Table 2). The average Tm values are well above the criterion for each family, giving a margin to offset the significant errors associated with estimating alloy melting temperature from elemental Tm. The average E values are greater than (LOW-T, MED-T) or equal to (HI-T) target values. Although the average ρ values appear high relative to characteristic values in Table 1, the average ρ for the six lowest values of LOW-T and MED-T families are only about 20% higher than typical values, and the six lowest densities in the HI-T palette give an average ρ that is about 20% lower than typical for conventional high temperature structural metals. If low density is essential, selection criteria for palette elements can be relaxed to include low-density elements. For example, the Tm cut-off can be relaxed for the MED-T palette so that the elements Ca, Mg, Sr and Al are included. Use of the palette of elements to build specific HEAs is discussed in the following section.
3.3. Single-Phase and Two-Phase HEAs
The literature currently shows a strong emphasis on single-phase HEAs. As mentioned in the Introduction, there is an important niche for solid solution strengthened alloys, and continued pursuit of this goal is warranted. However, a wider range of systems intentionally targeted for low, intermediate and high application temperatures is suggested. HEAs also offer possibilities in developing two-phase systems. Each approach is discussed below. Selection of HEA elements from the palette of elements is discussed here, and more detailed exploration that includes varying composition within a given set of elements is covered in Section 3.5.
3.3.1. Single Phase HEAs for Structural Applications in Transportation and Energy
Phenomenological guides can be used to select elements that favor single-phase formation. From the Hume-Rothery rules [46], elements with small differences in atom size or electronegativity can be chosen, or pairs of atoms with extended solubility in binary phase diagrams can be used. If intermetallics form in the constituent binary phase diagrams, then the analysis in Section 2.2 suggests that compounds with between zero and about −15 kJ·mol−1 will often be destabilized by ΔSconf. Consistent with these ideas, it has recently shown that a single phase solid solution can be produced in the as-cast condition when the atom size difference, , is less than about 8% and when ΔHmix is between 5 kJ·mol−1 and −20 kJ·mol−1 [47]. However, intermetallic phases can also form in HEAs over much of this range. To make single-phase disordered HEAs more likely, δr must be below about 4% or ΔHmix must be between 5 kJ·mol−1 and −5 kJ·mol−1. The thermodynamic parameter Ω = (Tm, ΩΔSmix)/|ΔHmix|, where and Tm,i is the melting temperature of element i, has been used together with δr to predict phase stability in HEAs [48]. That work shows that solid solutions form when δr ≤ 6.6% and when Ω ≥ 1.1. As in the previous work, intermetallics can also form in HEAs over some of this range, and to make single-phase disordered HEAs more likely, δr must be below 3.8% or Ω must be above about 10.
Although each palette of elements is built around a narrow set of selection criteria, there is still significant flexibility in HEA characteristics drawn from each palette. Consider refractory HEAs as an example. Both ρ and Tuse are important in dynamic parts, and a CrNbTiVZr HEA has a low density of 6.57 g·cm−3 with usable strength up to 1,000 °C and a melting range of 1,500–1,600 °C [27,49]. However, Tm is more important than ρ in static, land-based components as in a tokamak, and a MoNbTaVW HEA drawn from the same palette of elements has a density of 12.2 g·cm−3 g/cm3 and usable strength up to 1,600 °C [29,50]. In fact, the selection criteria can be changed to reflect this second design option, so that higher density elements such as Pt, Ir and Re may be added to the palette of elements. Other properties not included in the criteria for palette elements can also be considered in the selection of elements for a particular HEA, such as environmental resistance or cost.
3.3.2. Intentional Addition of Second Phases in HEAs
As mentioned in the Introduction, the highest strengths and highest application temperatures are met by alloys with a controlled distribution of a 2nd phase. Particulate strengthening works together with solid solution hardening to produce a potent balance of strength and damage tolerance. HEAs are defined here to include microstructures with intermetallic phases (Section 2.1), and HEAs offer a new approach to control the dissolution of intermetallic phases above room temperature (Section 2.2). Here we outline the idea of a controlled 2nd phase addition in HEAs for high temperature structural use.
In precipitation-strengthened microstructures, the strengthening phase is dissolved above the maximum Tuse. This is the eutectoid temperature in pearlitic steels, the γ′ (Ni3Al) solvus in Ni-based superalloys, and the Al2Cu solvus in many age-hardenable aluminum alloys. Strengthening precipitates are formed by quenching or controlled cooling, followed by annealing. Coherent precipitates give the best strengthening, so that the precipitate and the solid solution phase should share the same basic crystal structure. This is not essential, and bcc α-Fe and orthorhombic Fe3C in pearlite is a common example where the two phases do not share a common base crystal structure.
HEAs that favor compound formation can be made by intentionally breaking the phenomenological rules in Section 3.3.1. Intermetallics are commonly found in HEAs when the atom size difference is in the range of 4%–12% and when ΔHmix is in the range of −5 to −35 kJ·mol−1 [47,48]. Hume-Rothery rules suggest that intermetallics may form in alloys with large electronegativity differences between constituent elements, and atom pairs may be used that form compounds with high Tm or with values more negative than about −15 kJ·mol−1 (from Figure 3a). The average valence electron concentration, VEC, has also been used to rationalize formation of intermetallic phases [51]. Si, Al and Ti form very stable compounds with many metallic elements, and these can be added to the palette of elements (Table 2) to offer more compound-forming options. While these elements do not meet the general selection criteria for MED-T and HI-T HEAs, they usually form compounds that have low ρ, high Tm and high E. Other strong compound-forming elements such as B, C, N, O and P can also be added to the master and palette element lists. The HEA community is already adopting this approach—Al and Ti are often added to HEAs, and all but two of the intermetallic-containing HEAs in recent compilations have Al or Ti or both [42,48].
In theory, HEAs give a new approach for altering the dissolution temperature of strengthening phases. Phenomenological rules are emerging for the occurrence of intermetallic phases [8,42,47,48,52]. These, along with the present work, show that the competition between disordered solid solutions and ordered intermetallic phases depend on the relative magnitudes of ΔSconf, ΔHmix, and atom sizes. It may be possible to control dissolution temperature by selecting systems with intermetallic compounds that have a Gibb’s free energy of formation, ΔGAxBy, within a target range and then varying ΔGHEA through ΔHmix, ΔSconf and strain energy terms based on atom size misfit and perhaps modulus. The estimates in Section 2.2 suggest that as many as 33% of intermetallic compounds might be dissolved between 600 K and 1,500 K, and more might be dissolved at higher temperature. Two recent examples of such systems include a Laves phase that dissolves above 1,500 K in CrNbTiVZr [27] and a B2 phase that dissolves at 1,400 K in Al0.5CoCrCuFeNi [53].
Controlling the dissolution temperature of strengthening phases in HEAs is possible in theory, but it is an extremely challenging task and is not presently possible. Significant work is needed to move from phenomenological relations to a quantitative, mechanistic understanding of the competition between terms that contribute to phase stability in compositionally complex alloys. This may give some degree of control over phase formation and microstructural control of some intermetallic phases in HEAs. Once again, this is a major challenge—entropy is not the only important term [8], and other significant terms ( , ΔHmix, ΔSconf, δr and VEC) are all inter-related through alloy constitution.
3.4. Characterization of HEAs: Special Requirements and Approaches
As-cast metals have defects that may include: elemental segregation, suppression of equilibrium phases and the presence of metastable phases; microscopic and macroscopic residual stresses that can lead to cracking; and porosity. Care is taken to reduce or eliminate these defects in conventional metal alloys. Thermal treatment reduces segregation and residual stresses and hot isostatic pressing (HIP) is used to heal cracks and pores. The best balance of properties is achieved in wrought materials, where additional thermo-mechanical deformation is used to refine the microstructure, giving an improved balance of strength and damage tolerance.
The compositional complexity of HEAs may increase the severity of casting defects. HEAs containing elements with significantly different melting temperatures may give a wide freezing range that can increase elemental segregation. Mass transport in HEAs requires the coordinated motion of many different types of atoms, giving an additional barrier to the formation of equilibrium phases during casting [54]. Atomic-scale stresses resulting from a highly strained lattice may add to microscopic and macroscopic residual casting stresses. In spite of these issues, HEAs are primarily characterized in the as-cast condition. This introduces important uncertainty in the phase constituency and mechanical properties of HEAs. Since suppression of intermetallic phases is sometimes a research objective for HEAs, the uncertainty produced by studying as-cast material is particularly limiting since the as-cast structure does not give a reliable indication of stable phases. Composition gradients, large and non-uniform grain sizes, residual stresses, cracks and pores all decrease mechanical performance and should be reduced or eliminated before investing time for characterization. In limited studies where HEAs have been characterized in the annealed condition or where the material has been deformed to control the microstructure, important changes in phase constitution and properties are found [36,53,55–59]. It is therefore essential to make experimental observations on material where effort is made to reduce or eliminate casting defects in HEAs. The major approaches of homogenization, equilibration and microstructural control are briefly outlined below.
3.4.1. Homogenization
Homogenization heat treatment reduces or eliminates casting segregation. It can also produce microstructures closer to equilibrium by dissolving metastable phases that may have been quenched in from the casting process, or by giving sufficient time at elevated temperature for equilibrium phases that were suppressed upon quenching from the liquid to nucleate and grow. Finally, homogenization heat treatment can reduce microscopic or macroscopic residual stresses.
Homogenization heat treat conditions depend on the alloy. As a general guide, the homogenization temperature should be at least 0.5Tm, however 0.8Tm is more common. Tm can be measured using differential thermal analysis or it can be estimated using calculated phase diagram approaches. Homogenization times typically range from 2 h to 24 h but can be as long as 100 h. Using a diffusion coefficient for HEAs at 0.8Tm to be ∼ 10−14 m2·s−1 [54], diffusion distances given by range from about 8 μm for 2 h to about 60 μm for 100 h. Upset forging accelerates homogenization of as-cast alloys. A 50% or more reduction in height followed by a 2 h homogenization heat treatment redistributes material much more quickly and effectively than diffusion alone.
3.4.2. Equilibration
Service lifetimes up to 10,000 h are not uncommon in the energy and transportation industries, and so knowledge of phase equilibria is essential to guide alloy exploration and development. Phase equilibria studies also give valuable experimental data to validate computational tools and databases. However, measuring phase equilibria is time-consuming, especially at lower temperatures where diffusion coefficients are very small.
Temperatures for equilibration studies can be drawn from the intended use temperature. Differential thermal analysis and phase equilibria calculations can also aid in choosing temperatures for study by identifying possible first-order phase transformations of interest. As a practical guide, equilibrium is reached when the compositions and volume fractions of the phases stop changing with annealing time. In the single HEA equilibrium study to date [53], equilibrium is reached at 1100 °C since the compositions are relatively unchanged between 120 h (5 d) and 480 h (20 d). However, significant composition differences are seen between 120 h and 480 h at 900 °C and 700 °C, showing that longer equilibration times are needed at lower temperatures. Equilibration times of 1,000 h to 2,000 h are not uncommon for high temperature systems [60]. Equilibration time is also influenced by the time needed to sufficiently coarsen the microstructure for accurate composition measurement via conventional electron probe micro-analysis (EPMA) or energy dispersive spectroscopy (EDS), which require phase dimensions as large as 5 μm. However, more advanced analytical techniques offer good compositional accuracy in much smaller volumes, relieving some of the exposure time requirements when these techniques are used.
3.4.3. Microstructural Control
Mechanical properties depend sensitively on microstructure, and the best balance of strength and damage tolerance is achieved in wrought product. Deformation processing breaks up dendritic microstructure, heals casting defects, and gives a more refined and uniform grain size. As-cast material generally has relatively poor strength and ductility, since these properties are often limited by casting defects. Characterization of as-cast material is perhaps acceptable for an initial screening of new alloys, but the growing maturity of the HEA effort—especially in HEAs containing Co, Cr, Cu, Fe, Mn and Ni for which significant results are now available—calls for more careful control of microstructure prior to mechanical properties measurement. Upset forging can be performed with equipment available in most laboratories and effectively removes casting defects and refines microstructure. Rolling is also a common process to refine as-cast microstructures. The limited work currently available in the literature shows an important improvement in mechanical properties after deformation processing [53,57–59].
3.5. Strategies and Approaches for Evaluating Large Numbers of Alloys
Palettes of elements are given in Table 2 from which LOW-T, MED-T and HI-T structural HEAs can be devised. These palettes give nearly 200,000 equimolar HEAs, and give over 500,000 equimolar HEAs when the compound-forming elements Al and Si are added to the MED-T and HI-T palettes. This is the number of systems—the number of alloys is many orders of magnitude larger when non-equimolar compositions are added. This vast composition space offers great potential for useful discoveries. However, this vastness is also the biggest barrier to alloy discovery and development. New approaches are needed to effectively and systematically explore this immense new territory.
We propose a sequential process to quickly screen and evaluate large numbers of alloys against a set of criteria for an intended use. Here we consider structural uses for energy and transportation, but different criteria could be devised for other applications. Selection criteria consist of essential material characteristics and properties—a successful alloy must satisfy all the constraints. Evaluations are conducted in a staged order, and down-selections occur at the end of each stage. The resources (time and effort) used to characterize an alloy at each stage are inversely proportional to the number of candidates. The accuracy is also likely to be inversely proportional to the number of candidates. The initial stage of the process considers the full range of candidates and uses a rapid assessment that may have a rather low accuracy. As the list of candidates becomes smaller at the end of each successive stage, the assessment time and the expected accuracy both increase in following stages. This approach integrates high-throughput computations and experiments with a feedback loop for validation.
The goal of this approach is not to ensure that all systems with development potential are found, but to rapidly identify and characterize a small, workable subset with development potential. We are less concerned with false negative results (alloys with development potential that are rejected) than we are with false positive results (alloys with no development potential that are not rejected), since extra resources are spent on the latter. A major theme of this strategy is to quickly reject systems with some critical deficiency so as to focus resources on characterizing systems with potential, and to not waste time characterizing systems with little development potential.
The first step in this process, Stage 0, applies high-throughput computations of phase equilibria via the CALculated PHAse Diagram (CALPHAD) methodology. High-throughput experiments are performed on materials libraries with controlled composition gradients in Stage 1, and Stage 2 employs high-throughput experiments performed on materials libraries with controlled microstructure gradients. Stage 0 screening can be done with existing tools, most Stage 1 measurements are possible with current techniques, but important Stage 2 high-throughput test techniques are presently unavailable. The selection criteria are taken from elsewhere in this manuscript and from experience in the development of structural metals for energy and transportation uses. The criteria and tests in each stage are given in Table 3 and are discussed below. The current status of the technologies needed to pursue this strategy is given in Section 3.5.4.
3.5.1. High-Throughput CALPHAD Calculations of Phase Equilibria (Stage 0)
Stage 0 screening uses phase diagrams calculated by CALPHAD methods for all candidate HEAs. These are quick assessments with uncertain error, but the potential to remove many candidate alloys. Recent work show that CALPHAD methods correctly predict the presence of BCC and sigma phases in refractory metal HEAs and the eutectic reaction in CrMo0.5NbTa0.5TiZr [27,61]. However, there is disagreement between predictions and observations regarding the number of phases, their volume fractions and compositions. Improved thermodynamic databases are needed to more accurately predict phase diagrams in HEAs. Nevertheless, CALPHAD calculations are proposed here to give only the phases present and phase transformation temperatures, so that progress may be possible with existing databases. Other approaches for calculating phase equilibria are more accurate but require significant computer time and are not practical for screening hundreds of thousands or millions of systems.
The following data are documented from CALPHAD calculations for each system: solidus temperature (Tsol); the ratio Tuse/Tsol; freezing range (Tliq – Tsol, where Tliq is the liquidus temperature); the lowest temperature that gives a single phase solid solution; the number of phases at room temperature and their crystal structures; and all first-order phase transformations. In addition to this data, linear averages are calculated from elemental values for alloy density (ρ) and Young’s modulus (E). Alloys that pass all Stage 0 criteria in Table 3 move to experimental evaluation in Stage 1.
It is clear that Tuse must be below Tsol, but there is no accepted fraction of Tsol. As a guideline, Ni-based superalloys operate at Tuse/Tsol ≈ 0.85, and other structural metals operate at lower fractions. Given the uncertainty in Tsol from CALPHAD, especially in systems without an extensive database, it is probably appropriate in Stage 0 to simply require that Tuse < Tsol. Alloy melting is also characterized by the freezing range, Tliq–Tsol. A small freezing range is desirable, since it reduces casting segregation. The Tuse/Tsol and freezing ranges are not used as selection criteria in Stage 0, but they can be used to prioritize systems that pass Stage 0. In both cases, smaller values are better.
To ensure no fundamental property changes within the service temperature range, structural metals have no first-order phase transformations below Tuse. Thus, the phases at Tuse must remain at room temperature, TRT. From Section 3.3, we accept systems that are either single-phase solid solutions or have 2-phase microstructures at Tuse. If the alloy is 2-phase at Tuse, then one phase must be dissolved at some temperature above Tuse to enable particle strengthening as described in Section 3.3.2. Two-phase systems can have two solid solutions or a solid solution plus an intermetallic phase. From practical experience, the strengthening particle is always the ordered phase in microstructures with a solid solution and an ordered phase, so that the HEA must be a single-phase solid solution at some temperature above Tuse. Systems consisting of 1 or 2 ordered phases or having more than 2 phases of any kind are excluded from further evaluation in this approach. Most structural metals are based on fcc, bcc or hcp phases and their ordered derivatives. Thus, for this evaluation we accept only HEAs that contain these crystal structures. Finally, we estimate Young’s modulus (E) and density (ρ) as a weighted average of elemental values and compare with goals set for these two properties.
Stage 0 gives a restrictive set of requirements and so a large number of HEAs are likely to be rejected. Although the accuracy of CALPHAD predictions in such a broad range of HEAs may be rather low, experimental data will be collected on systems that pass Stage 0, giving essential validation and building databases for improved robustness of future evaluations.
3.5.2. High-Throughput Experiments on Materials Libraries with Composition Gradients (Stage 1)
High-throughput, combinatorial experiments are a mainstay in several fields for rapid materials discovery, screening, evaluation and development [63–67]. These approaches rely on the production of materials libraries—a sample with controlled gradients that cover the material space of interest. Materials libraries commonly use continuous or discrete composition gradients [64,66,67]. Libraries are usually made as thin films (typically < 1 μm) using vapor techniques, but bulk methods such as diffusion multiples [67], additive manufacturing and 3D printing are becoming available. Up to millions of measurements can be made on a single library, giving dramatic increases in throughput. To enable a large number of discrete measurements from a single material library, miniaturized measurement techniques are usually used. As a result, combinatorial measurements currently emphasize physical or functional properties that do not depend sensitively on microstructure. Producing HEA materials libraries with controlled composition gradients of 5 or more elements is challenging. Approaches are now available for controlled composition gradients in 4-component systems using physical vapor deposition (PVD) [68]. Diffusion multiples are commonly used for ternary systems [67], and more complex alloys can be produced with 5 or more elemental wedges meeting at a point (Figure 4a). Such samples give only one HEA and do not cover the full composition space associated with the specified HEA (including all binary, ternary, quaternary and other lower-order elemental combinations), but do give information on the phases that form in the compositions between the particular HEA and each of the constituent elements. More extensive wedge arrays can give many different HEAs in the same diffusion multiple. For example, Figure 4b contains all seven 6-element HEAs from the ABCDEFG system. Additive manufacturing techniques [69,70] may reduce the manual labor currently used in producing such diffusion multiples. The interdiffusion temperature should be at least half the absolute melting temperature and must be less than the lowest Tsol in the system. A diffusion temperature of Tuse allows validation of Stage 0 predictions. The exposure time is chosen to give diffusion distances of the order of ∼100 μm for good composition resolution while avoiding overlap of adjacent diffusion fields [67].
Materials libraries are used to measure the phases present in HEAs that pass Stage 0. EPMA gives accurate compositions, but needs ≥60 seconds for each data point. Energy dispersive spectroscopy (EDS) has acquisition rates of the order of 10–100 ms and is integrated with mapping routines available for most commercial scanning electron microscopes (SEMs). Mapping routines are also available for electron back-scatter detectors (EBSD) that enable crystal structure determination with an acquisition rate of ∼10–100 ms. Thus, both composition and crystal structure can be measured quickly on materials libraries. Phase transformations can be measured with differential thermal analysis (DTA), and high-throughput nano-calorimetry techniques have recently been developed [62]. By combining the phases present at Tuse with the absence of 1st order phase transformations below Tuse from nano-calorimetry, high-throughput experimental validation of Stage 0 calculations is provided.
Environmental coatings extend the life of a part, but the base material requires some intrinsic environmental resistance. For example, alloys based on Nb or Mo have attractive high temperature structural properties but cannot be used due to their catastrophic oxidation. A simple screening test consists of exposing a material library to the maximum Tuse in air. Formation of a dense, adherent, protective oxide is preferred, but an alloy may pass if it does not exhibit catastrophic oxidation.
The final assessment in Stage 1 consists of mechanical properties screening. Elastic modulus is a fundamental property for strength and plasticity and can be measured on materials libraries by a number of established techniques, including instrumented nano-indentation [67]. Modulus is generally considered to be relatively insensitive to microstructure, but elastic anisotropy of some phases and micro-texture may introduce experimental scatter. Nevertheless, this gives a first-order validation of the composition-weighted average modulus estimated in Stage 0. Hardness can also be mapped using nano-indentation. Hardness is not a fundamental material property and it depends on microstructure. Nevertheless, hardness mapping of materials libraries indicates trends and gives a first indication of the capacity for strengthening. Micro-pillar compression gives a more fundamental measure of strength, although size scale effects and microstructure must be considered. Bulk materials libraries are required for micro-compression, and both sample machining and testing can be done in an automated fashion [71]. Alternate micro-machining technologies, such as plasma focused ion beam (FIB) microscopes and femto-second laser machining systems offer the possibility to significantly decrease sample machining time.
Perhaps more important than the capacity for strengthening is the capacity for room temperature tensile plasticity. Tensile plasticity is required for structural applications (Section 3.1) and guarantees availability of 5 active independent modes of deformation without any intervening failure modes. Micro-pillar compression tests give some indication, but the driving force for crack growth in compression is greatly reduced, so that a material can show compressive plasticity but only very limited (or no) tensile plasticity. The pillar volume relative to grain size may also confuse the result. Nevertheless, compressive and tensile plasticity are not completely unrelated. A material that fails in a brittle fashion in compression will almost certainly have no tensile plasticity and can be rejected. A material with extensive compressive plasticity (50% or more) is almost certain to have some amount of tensile plasticity and can be considered to pass Stage 1 screening. The tensile plasticity associated with intermediate levels of compressive plasticity is less certain, and a suitable cut-off in compressive plasticity can be applied to reflect a level of risk that is deemed acceptable. Other test methods may also be used to screen for room temperature tensile plasticity, including cantilevers, two- and four-point bending and double-shear. These approaches do not eliminate the driving force for crack growth and so may give more useful information concerning the occurrence of intervening failure modes. The most direct method for assessing tensile plasticity is tension testing. While micro-tension is more challenging than micro-compression, some progress has been made on the path to high-throughput experiments [72]. Perhaps the most daunting task has been parallel micro-sample preparation. Recently Shade and co-workers have demonstrated a stencil mask method for the parallel production of micro-samples using polycrystalline nickel [73]. Samples were successfully tested using an in-situ tensile stage within a scanning electron microscope. Advances in instrumentation may make this a viable approach for rapid testing employing digital image correlation.
Producing defect-free materials libraries for high-throughput screening of mechanical properties is a challenge. Care is needed to reduce or eliminate microstructural inhomogeneities and processing defects, including those that may be unique to materials production techniques used to make materials libraries. Thermal treatment or thermo-mechanical processing of materials libraries may be required to produce material that will give mechanical properties that are reliable, representative and reproducible.
The data collected in Stage 1 is used to validate Stage 0 computations of phase equilibria and to expand phase stability databases for compositionally complex alloys. This data also reduces the number of alloys in cases where CALPHAD predictions pass an alloy but experimental measurements do not. A further reduction in the number of candidates comes from screening for oxidation resistance and mechanical properties. The results from Stage 1 define two distinct paths for subsequent testing and alloy development. Specifically, single-phase and two-phase alloys have different microstructural requirements. Microstructure is addressed directly in Stage 2, and single-phase and two-phase alloys will undergo different thermo-mechanical treatments prior to testing.
3.5.3. High-Throughput Experiments on Materials Libraries with Microstructure Gradients (Stage 2)
Stage 2 measures strength and ductility on materials libraries of a single composition with controlled microstructure gradients. Grain size is of fundamental importance for strength and fracture properties of single-phase and two-phase alloys, and is a primary microstructural parameter to control in Stage 2. In two-phase alloys, the size, volume fraction and inter-particle spacing (only two of these three features are independent) influence strength and plasticity and are also controlled in Stage 2. The distribution of strengthening particles is also important, but in general a uniform distribution is sought. Other important microstructural parameters include grain shape, crystallographic texture and orientation relationships. These features have a more specialized influence on properties and are more difficult to control in new materials, and so are not emphasized in this screening.
Several approaches have been developed to produce controlled microstructure gradients. The Jominy bar is a standardized test that varies microstructure by varying quench rate [74]. Upset forging of a double-cone test sample (Figure 5a) produces a radial strain gradient that can produce a graded grain size [75]. A wedge plate (Figure 5b) can be forged or rolled to give a strain gradient that has also been used to produce grain size gradients [75]. Annealing material in a thermal gradient can give a controlled grain size gradient. Other approaches may also be possible. In two-phase alloys, a solution treatment and aging (STA) process is used to control the size, volume fraction and spacing of the strengthening particles. An STA is defined by the solution temperature, quench rate, aging temperature and aging time. It is usually sufficient to ensure that the material is just above the solution temperature and that the quench rate is just sufficient to suppress nucleation. Solution temperature and quench rate can be varied in a single sample by placing a rectangular plate in a thermal gradient, then quenching a plate edge that is parallel to the thermal gradient. Once these two parameters are established for an alloy, the aging temperature and time can be varied by placing several identically processed rectangular strips in a thermal gradient furnace and removing strips at specific time intervals. These approaches can produce bulk materials libraries with controlled gradients in grain size and in size, volume fraction and spacing of a strengthening phase in two-phase alloys.
Stage 2 uses high-throughput experiments to measure properties (strength and ductility as a function of temperature) that depend sensitively on microstructure, which is the main variable in the libraries. High-throughput tests usually require miniaturization, and microstructure introduces an intrinsic length scale that must be considered directly in sample design and data analysis. As a generalization, tension or compression sample cross-sections should contain about 100 grains to give data that is representative of the bulk. In the limit of very small samples and large microstructural length scales, samples are single crystals and relationships between single crystal and polycrystalline properties are reasonably well established. Quantitative relationships between measured and bulk properties are less certain between these two extremes. Micro-sample testing has motivated a great deal of work on this topic, and relationships are being sought for both strength and plasticity [76–78] Additional progress is still needed, especially in defining the size of representative volume elements for particular properties of interest. In the meantime, testing samples in the millimeter-to-sub-millimeter length scale regimes may give acceptable results for properties that are driven by mean value microstructural statistics.
Tensile properties are desired at this stage of evaluation. However, there are at present no established high-throughput techniques for measuring tensile strength and ductility. While a qualitative relationship between compressive plasticity and the capacity for tensile ductility may exist, this is inadequate for the level of accuracy desired in this later stage of material selection. This is a major barrier and an opportunity for an important advancement. In addition, performing elevated temperature tests for micro-scale or milli-scale characterization is an unsolved challenge. While some progress has been made, well-controlled and characterized high-temperature sub-scale testing remains a key goal.
3.5.4. Current Status for Exploring Large Numbers of Alloys
The motivation to study compositionally complex alloys is quite new, and systematic studies of phase equilibria and transformation temperatures in complex alloy space have not yet been reported. The calculations in Stage 0 can be done with commercially available software packages and thermodynamic databases. The accuracy of predictions using current databases is a concern [61], especially the phase transformation temperatures. Further, current models use the Bragg-Williams (regular solution) approximation, and this may be inadequate in many systems. An improved approach such as cluster-site expansion should improve the thermodynamic representation of these alloys [79]. With the currently available thermodynamic databases, published results often give poor agreement between predicted and observed phases, especially for compositions and volume fractions [61,80]. Development of advanced thermodynamic databases covering the entire composition ranges for prospective HEAs is required. This is a comprehensive task that is integrated in the current strategy.
Some of the Stage 1 testing can be done on thin film libraries (thickness <1 μm), and some require bulk libraries. PVD is well-established for producing thin-film libraries with controlled composition gradients, but this is not yet validated in alloys with ≥5 elements. PVD gives unique microstructures and defects (including residual stresses) that may need to be controlled or eliminated to measure mechanical properties. Additive manufacturing techniques (laser deposition, 3D printing, directed vapor deposition (DVD) [81], and others) are still evolving and have not been demonstrated in materials libraries needed here. As already mentioned, some post-processing of Stage 1 materials libraries will probably be required to reduce or eliminate defects unique to each processing approach and to give microstructures that are representative of what might be used in an actual application. EDS and EBSD mapping, instrumented nano-indentation and micro-pillar compression testing are all well-established techniques. However, sub-scale testing of mechanical properties has only been demonstrated in laboratory settings, and there are presently no off-the-shelf high-throughput methods that give accurate mechanical properties. Measuring the ability to avoid catastrophic oxidation appears to be straightforward but has not yet been demonstrated. Nano-calorimetry techniques are just now being established and can operate to temperatures of the order of 1,000 °C. While this may be sufficient to ensure that no 1st order phase transformations occur below Tuse, additional temperature capability is needed to measure melting and dissolution temperatures above Tuse.
Although techniques to produce controlled microstructure gradients are well-established (Jominy bar, double cone test, wedged forge/rolling preform), to the authors’ knowledge these have not been used in high-throughput experiments of HEAs. These represent an opportunity for more rapid development of HEAs. Although not developed for high-throughput libraries, a few techniques are available to produce grain size gradients. The high-throughput thermal treatments described here to measure solution temperature and quench rates are notionally possible but have not yet been demonstrated for this purpose. Models to quantify relationships between sample dimensions and microstructural length scales are moving forward quickly but are not fully developed. High-throughput tensile testing is a key component of Stage 2 but is currently not available. While this represents a major barrier, significant progress in the rapid screening and evaluation of compositionally complex alloys can be made.
Progress is being made on other fronts to aid in high-throughput materials evaluation. An entire community is advancing the three-dimensional (3D) characterization of materials. Stages 2,3 use essentially two-dimensional (2D) libraries, and extending these to 3D may offer additional benefits in efficiency. For example, additive manufacturing offers the possibility of producing 3D chemical gradients, but there are presently no approaches for producing controlled 3D microstructural gradients. More importantly, the 3D materials characterization community is establishing automated, multi-modal characterization capabilities that should be of direct benefit to the high-throughput evaluation of materials libraries. These approaches often use a hub-and-spoke design to integrate and automate a number of characterization techniques into a single process [82]. A large and diverse effort on data-driven modeling offers the ability the extract useful, and sometimes unexpected, results from sparse datasets. Although commercial software packages are not widely available for data-driven modeling, this is a growing capability that has significant potential to reduce the number of alloys required to satisfy a given design envelope. Neural network models and models that provide a functional form (such as the Eureka code by Nutonian) are commercially available. In fact, a version of the Eureka code is free. ABAQUS/ANSYS or COMSOL are also commercially available, but this software can only handle relatively small structures in 3D (relative to the complexity that structure can be represented), and the ability to mesh structure explicitly is still evolving. There are small commercial packages like Simpleware that show examples of how to do this [83].
While many of the necessary capabilities are available, they have generally not been sufficiently integrated and reduced to common practice to demonstrate a combinatorial, high-throughput capability for the rapid evaluation of structural materials. Nevertheless, a recent report describes rapid alloy proto-typing of 45 different materials (5 different alloys in 9 microstructural conditions). These materials were produced and evaluated via tensile testing within a timeframe of only 35 h [84].
After Stage 2, characterization follows standard approaches on a single alloy in a single microstructural condition produced by conventional processing techniques. Testing is more conventional and results are more accurate. Measurements include tensile data as a function of temperature, damage tolerance (including fracture toughness), creep and fatigue testing and environmental resistance. A large number of replicate tests are performed to establish statistics and to identify and evaluate extreme events. Processing scale-up efforts are pursued for materials that satisfy requirements, and design datasets with statistical allowables are generated for the final material. The goal of the three-stage process described above is to systematically sort through a very large number of candidate alloys and microstructures to give a small number of materials that warrant the significant investment required for this more extensive characterization.
HEAs offer an exceptional testing ground to develop and implement high-throughput test and evaluation methods described here. As stated in the Introduction, perhaps the most important contribution of the HEA concept is to motivate the systematic exploration of a vast and unexplored composition space, regardless of the magnitude of configurational entropy or its influence on the stability of competing phases. While HEAs represent a truly astronomical number of compositions, they are still only a subset of the full space of compositionally complex alloys that may or may not meet the definitions used to bound HEAs. The strategy outlined here applies to any large number of structural materials, and is by no means limited to HEAs.
4. Summary and Conclusions
In this paper, we give a strategy to explore, evaluate and develop high-entropy alloys (HEAs) for structural applications in the transportation and energy fields. The main ideas are summarized below.
We use an operational definition of HEAs as any alloy with an ideal or regular configurational entropy, ΔSconf ≥ 1.5R (R = 8.314 J·mol−1·K−1). This definition uses ΔSconf in the high-temperature state, which is the entropy that is inherent in the alloy and which must be overcome if competing phases are to form. This definition has more information and is more consistent than definitions based on alloy constitution or on the value of ΔSconf at low temperatures, which may bear little resemblance to the entropy inherent in the system at higher temperatures. This operational definition includes HEAs with two or more phases at low temperatures.
A rough, order-of-magnitude thermodynamic analysis suggests that ΔSconf of HEAs may be sufficient to destabilize 5%–10% of intermetallic compounds (those with the lowest enthalpies of formation, ) at room temperature. An additional 30%–55% of ordered compounds may be suppressed in HEAs at 1,500 K. Roughly 50% of the intermetallic compounds may be stable at 300 K but unstable at 1,500 K, offering a new approach for controlling microstructure (via particle dissolution and subsequent controlled precipitation) and properties in particulate-strengthened HEAs. In addition to ΔSconf of a regular solid solution, the enthalpies of mixing (ΔHmix) and compound formation ( ) are significant and must be considered in the stability of HEAs. We introduce a strain energy term, σdε, which is usually neglected in Gibbs free energies but may be important in HEAs. A quantitative understanding of this term is currently missing.
HEA compositional complexity may increase the severity of defects formed during alloy production that can include casting segregation, the presence of non-equilibrium phases, residual stresses and porosity. Care is taken to reduce or eliminate these defects prior to characterization or use in conventional metal alloys. Homogenization and deformation processing are therefore recommended prior to HEA characterization to improve the quality of measured data. Components in transportation and energy structural applications are often exposed to high temperatures for very long times, and so establishing phase equilibria is of particular importance. Almost no data currently exists for phase equilibria in HEAs, and this is recommended as a future area of effort.
We propose an expanded scope of HEA systems for structural applications in the transportation and energy fields. This includes HEAs designed for low (use temperature, Tuse ≤ 150 °C), medium (Tuse ≤ 450 °C) and high (Tuse up to 1,000 °C and above) temperature applications. A set of physical (density, modulus) and mechanical (strength, ductility, toughness) characteristics is suggested for these three structural HEA families. The highest-performing conventional alloys always have a controlled distribution of a second phase to take advantage of the most potent strengthening mechanisms available—particulate hardening. The strategy developed here thus explicitly includes both single-phase solid solution microstructures and HEAs with an intentional additional of a second phase.
We discuss the design of these three HEA families. Guided by practical considerations, we give a master list of elements from which structural metal HEAs can be built. We use characteristic properties from conventional alloys to define selection criteria for HEA elements to be used at low, medium and high temperatures. These criteria are carefully chosen to represent essential application characteristics and to give some connection between element properties and HEA properties. These criteria reduce the master list to a smaller list—a palette of elements—that is large enough for robust exploration but small enough to focus effort toward specific design properties. Palettes of elements are given for HEA structural metals intended for low, medium and high application temperatures. Use of the palette of elements to build specific HEAs is described. As an early validation, a class of refractory HEAs is based on the palette of elements for high temperature use.
We describe a three-stage approach to systematically screen and evaluate the vast composition space offered by these three HEA families. This approach integrates high-throughput computations and experiments with a feedback loop for validation. The effort used to characterize an alloy at each stage is inversely proportional to the number of candidates at that stage. The accuracy will also generally be inversely proportional to the number of candidates. The idea is to quickly reject systems with some critical deficiency and to focus resources on characterizing the remaining systems. High-throughput computations of phase equilibria via CALculated PHAse Diagram (CALPHAD) techniques are performed in Stage 0. Alloys are rejected that melt below Tuse; that have any 1st order phase transformation below Tuse; that have 2 or more intermetallic phases; or that have more than 2 phases of any type. Single-phase intermetallic alloys are also rejected. Candidate alloys must consist of fcc, bcc or hcp phases or their ordered derivatives. CALPHAD calculations are currently possible, but improved accuracy is sought and is offered here through a feedback loop with data collected in Stage 1. Alloys that pass Stage 0 are evaluated in Stage 1 using high-throughput experiments on materials libraries with controlled composition gradients. The phases present are measured to validate Stage 0 calculations, and the capacity for strengthening and plasticity are evaluated qualitatively using techniques such as instrumented nano-indentation. A high-throughput test for catastrophic oxidation is also suggested. Stage 1 measurements are generally possible with current techniques. In the final screening step, Stage 2 requires high-throughput tensile testing on materials libraries consisting of a single composition with controlled microstructure gradients. This includes single-phase HEAs with gradients in grain size, and 2-phase HEAs with gradients in grain size and in the size, volume fraction and inter-particle spacing of a second phase. Major barriers exist in performing Stage 2 evaluations. The important influence of microstructure on tensile properties makes miniaturization—a hallmark of high-throughput testing—difficult to apply quantitatively. While progress is being made on this topic, high-throughput techniques for measuring tensile properties currently do not exist.
The largest barriers in this staged strategy occur in the later stages, and so significant progress can be made in the rapid screening and evaluation of compositionally complex alloys by integrating currently-available methods. This gives time for progress on the remaining deficiencies. Other advancements also are likely to contribute to the rapid evaluation of large numbers of alloys, including integration and automation of multi-modal characterization methodologies pursued in the three-dimensional materials science community, and the growth of data-driven modeling to extract new knowledge from sparse datasets.
Acknowledgments
The authors would like to thank a number of colleagues for stimulating discussions, including Jien-Wei Yeh, Yunzhi Wang, Easo George, Uwe Glatzel and Lee Semiatin. Work by ONS was supported through the Air Force on-site contract no. FA8650-10-D-5226 conducted by UES, Inc., Dayton, Ohio.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yeh, J.-W.; Chen, S.-K.; Lin, S.-J.; Gan, J.-Y.; Chin, T.-S.; Shun, T.-T.; Tsau, C.-H.; Chang, S.-Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater 2004, 6, 299–303. [Google Scholar]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar]
- Yeh, J.-W. Recent Progress in High Entropy Alloys. Ann. Chim. Sci. Mater 2006, 31, 633–648. [Google Scholar]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Miracle, D.B.; Woodward, C.F. Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy. J. Alloys Compd 2011, 509, 6043–6048. [Google Scholar]
- Yeh, J.-W. Alloy design strategies on high-entropy alloys. JOM 2013, 65, 1759–1771. [Google Scholar]
- Gaskell, D.R. Introduction to the Thermodynamics of Materials, 3rd ed.; Taylor & Francis: Washington, DC, WA, USA, 1995. [Google Scholar]
- Tipler, P.A. Modern Physics; Worth Publishers: New York, NY, USA, 1969. [Google Scholar]
- Otto, F.; Yang, Y.; Bei, H.; George, E.P. Relative effects of enthalpy and entropy on the phase stability of equiatomic high-entropy alloys. Acta Mater 2013, 61, 2628–2638. [Google Scholar]
- Franke, P.; Neuschutz, D. Thermodynamic Properties of Inorganic Materials compiled by SGTE; Springer-Verlag: Berlin, Germany, 2002. [Google Scholar]
- Takeuchi, A.; Inoue, A. Classification of bulk metallic glasses by atomic size difference, heat of mixing and period of constituent elements and its application to characterization of the main alloying element. Mater. Trans 2005, 46, 2817–2829. [Google Scholar]
- Okamoto, H.; Subramanian, P.R.; Kacprzak, L. Binary Alloy Phase Diagrams, 2nd ed.; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
- Hultgren, R.; Orr, R.L.; Anderson, P.D.; Kelley, K.K. Selected Values of Thermodynamic Properties of Metals and Alloys; John Wiley & Sons, Inc: New York, NY, USA, 1963. [Google Scholar]
- de Boer, F.R.; Boom, B.; Mattens, W.C.M.; Miedema, A.R.; Niessen, A.K. Cohesion in Metals: Transition Metal Alloys; Elsevier Science Publishers: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Kubaschewski, O.; Alcock, C.B.; Spencer, P.J. Materials Thermochemistry, 6th ed.; Pergamon Press: Oxford, UK, 1993. [Google Scholar]
- Colinet, C. The thermodynamic properties of rare earth metallic systems. J. Alloys Compd 1995, 225, 409–422. [Google Scholar]
- Fries, S.; Jantzen, T. Compilation of “CALPHAD” formation enthalpy data Binary intermetallic compounds in teh COST 507 Gibbsian database. Thermochim. Acta 1998, 314, 23–33. [Google Scholar]
- Guo, Q.; Kleppa, O.J. Standard enthalpies of formation of some alloys formed between group IV elements and group VIII elements, determined by high-temperature direct synthesis calorimetry: II. Alloys of (Ti, Zr, Hf) with (Co, Ni). J. Alloys Compd 1998, 269, 181–186. [Google Scholar]
- Guo, Q.; Kleppa, O.J. The standard enthalpies of formation of the compounds of early transition metals with late transition metals and with noble metals as determined by Kleppa and co-workers at the University of Chicago—A review. J. Alloys Compd 2001, 321, 169–182. [Google Scholar]
- Miracle, D.B.; Wilks, G.B.; Dahlman, A.G.; Dahlman, J.E. The strength of chemical bonds in solids and liquids. Acta Mater 2011, 59, 7840–7854. [Google Scholar]
- Chen, Y.-L.; Hu, Y.-H.; Tsai, C.-W.; Hsieh, C.-A.; Kao, S.-W.; Yeh, J.-W.; Chin, T.-S.; Chen, S.-K. Alloying behavior of binary to octonary alloys based on Cu–Ni–Al–Co–Cr–Fe–Ti–Mo during mechanical alloying. J. Alloys Compd 2009, 477, 696–705. [Google Scholar]
- Chou, H.-P.; Chang, Y.-S.; Chen, S.-K.; Yeh, J.-W. Microstructure, thermophysical and electrical properties in AlxCoCrFeNi (0 ≤ x ≤ 2) high-entropy alloys. Mater. Sci. Eng. B 2009, 163, 184–189. [Google Scholar]
- Hsu, Y.-J.; Chiang, W.-C.; Wu, J.-K. Corrosion behavior of FeCoNiCrCux high-entropy alloys in 3.5% sodium chloride solution. Mater. Chem. Phys 2005, 92, 112–117. [Google Scholar]
- Li, B.S.; Ren, M.X.; Yang, C.; Fu, H.Z. Effects of Mn, Ti and V on the microstructure and properties of AlCrFeCoNiCu high entropy alloy. Mater. Sci. Eng. A 2008, 498, 482–486. [Google Scholar]
- Li, C.; Li, J.C.; Zhao, M.; Jiang, Q. Effect of alloying elements on microstructure and properties of multiprincipal elements high-entropy alloys. J. Alloys Compd 2009, 475, 752–757. [Google Scholar]
- Ranganathan, S. Alloyed pleasures: Multimetallic cocktails. Curr. Sci 2003, 85, 1404–1406. [Google Scholar]
- Ren, B.; Liu, Z.X.; Li, D.M.; Shi, L.; Cai, B.; Wang, M.X. Effect of elemental interaction on microstructure of CuCrFeNiMn high entropy alloy system. J. Alloys Compd 2010, 493, 148–153. [Google Scholar]
- Senkov, O.N.; Senkova, S.V.; Woodward, C.; Miracle, D.B. Low-density, refractory multi-principal element alloys of the Cr–Nb–Ti–V–Zr system: Microstructure and phase analysis. Acta Mater 2013, 61, 1545–1557. [Google Scholar]
- Senkov, O.N.; Wilks, G.B.; Miracle, D.B.; Chuang, C.P.; Liaw, P.K. Refractory high-entropy alloys. Intermetallics 2010, 18, 1758–1765. [Google Scholar]
- Senkov, O.N.; Wilks, G.B.; Scott, J.M.; Miracle, D.B. Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 2011, 19, 698–706. [Google Scholar]
- Varalakshmi, S.; Rao, G.A.; Kamaraj, M.; Murty, B.S. Hot consolidation and mechanical properties of nanocrystalline equiatomic AlFeTiCrZnCu high entropy alloy after mechanical alloying. J. Mater. Sci 2010, 45, 5158–5163. [Google Scholar]
- Wang, F.J.; Zhang, Y. Effect of Co addition on crystal structure and mechanical properties of Ti0.5CrFeNiAlCo high entropy alloy. Mater. Sci. Eng. A 2008, 496, 214–216. [Google Scholar]
- Wang, F.J.; Zhang, Y.; Chen, G.L. Atomic packing efficiency and phase transition in a high entropy alloy. J. Alloys Compd 2009, 478, 321–324. [Google Scholar]
- Wang, F.J.; Zhang, Y.; Chen, G.L.; Davies, H.A. Cooling rate and size effect on the microstructure and mechanical properties of AlCoCrFeNi high entropy alloy. J. Eng. Mater. Tech 2009, 131, 034501. [Google Scholar]
- Wang, X.F.; Zhang, Y.; Qiao, Y.; Chen, G.L. Novel microstructure and properties of multicomponent CoCrCuFeNiTix alloys. Intermetallics 2007, 15, 357–362. [Google Scholar]
- Wang, Y.P.; Li, B.S.; Ren, M.X.; Yang, C.; Fu, H.Z. Microstructure and compressive properties of AlCrFeCoNi high entropy alloy. Mater. Sci. Eng. A 2008, 491, 154–158. [Google Scholar]
- Zhang, K.B.; Fu, Z.Y.; Zhang, J.Y.; Shi, J.; Wang, W.M.; Wang, H.; Wang, Y.C.; Zhang, Q.J. Annealing on the structure and properties evolution of the CoCrFeNiCuAl high-entropy alloy. J. Alloys Compd 2010, 502, 295–299. [Google Scholar]
- Zhang, K.B.; Fu, Z.Y.; Zhang, J.Y.; Wang, W.M.; Wang, H.; Wang, Y.C.; Zhang, Q.J.; Shi, J. Microstructure and mechanical properties of CoCrFeNiTiAlx high-entropy alloys. Mater. Sci. Eng. A 2009, 508, 214–219. [Google Scholar]
- Zhou, Y.J.; Zhang, Y.; Wang, F.J.; Wang, Y.L.; Chen, G.L. Effect of Cu addition on the microstructure and mechanical properties of AlCoCrFeNiTi0.5 solid-solution alloy. J. Alloys Compd 2008, 466, 201–204. [Google Scholar]
- Zhou, Y.J.; Zhang, Y.; Wang, Y.L.; Chen, G.L. Microstructure and compressive properties of multicomponent Alx(TiVCrMnFeCoNiCu)100−x high-entropy alloys. Mater. Sci. Eng. A 2007, 454, 260–265. [Google Scholar]
- Zhu, J.M.; Fu, H.M.; Zhang, H.F.; Wang, A.M.; Li, H.; Hu, Z.Q. Microstructures and compressive properties of multicomponent AlCoCrFeNiMox alloys. Mater. Sci. Eng. A 2010, 527, 6975–6979. [Google Scholar]
- Zhu, J.M.; Fu, H.M.; Zhang, H.F.; Wang, A.M.; Li, H.; Hu, Z.Q. Synthesis and properties of multiprincipal component AlCoCrFeNiSix alloys. Mater. Sci. Eng. A 2010, 527, 7210–7214. [Google Scholar]
- Guo, S.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Progr. Nat. Sci 2011, 21, 433–446. [Google Scholar]
- Wikipedia: Rule of mixtures. Available online: http://en.wikipedia.org/wiki/Rule_of_mixtures (accessed on 19 August 2013).
- WebElements: the periodic table on the web. Available online: http://www.webelements.com/ (accessed on 16 July 2013).
- Miracle, D.B.; Louzguine-Luzgin, D.; Louzguina-Luzgina, L.; Inoue, A. An assessment of binary metallic glasses: Correlations between structure, glass forming ability and stability. Int. Mater. Rev 2010, 55, 218–256. [Google Scholar]
- Cahn, R.W.; Hassen, P. Physical Metallurgy Vol. 1., 4th ed.; North Holland: Amsterdam, The Netherland, 1996. [Google Scholar]
- Guo, S.; Liu, C.T. Phase selection rules for complex multi-component alloys with equiatomic or close-to-equiatomic compositions. Chin. J. Nat 2013, 35, 85–96. [Google Scholar]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys 2012, 132, 233–238. [Google Scholar]
- Senkov, O.N.; Senkova, S.V.; Miracle, D.B.; Woodward, C. Mechanical properties of low-density, refractory multi-principal element alloys of the Cr–Nb–Ti–V–Zr system. Mater. Sci. Eng. A 2013, 565, 51–62. [Google Scholar]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Meisenkothen, F.; Miracle, D.B.; Woodward, C.F. Microstructure and elevated temperature properties of a refractory TaNbHfZrTi alloy. J. Mater. Sci 2012, 47, 4062–4074. [Google Scholar]
- Tsai, M.-H.; Tsai, K.-Y.; Tsai, C.-W.; Lee, C.; Juan, C.-C.; Yeh, J.-W. Criterion for Sigma Phase Formation in Cr- and V-Containing High-Entropy Alloys. Mater. Res. Lett 2013, 1, 207–212. [Google Scholar]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-solution phase formation rules for Multi-component alloys. Adv. Eng. Mater 2008, 10, 534–538. [Google Scholar]
- Ng, C.; Guo, S.; Luan, J.; Shi, S.; Liu, C.T. Entropy-driven phase stability and slow diffusion kinetics in an Al0.5CoCrCuFeNi high entropy alloy. Intermetallics 2012, 31, 165–172. [Google Scholar]
- Tsai, K.-Y.; Tsai, M.-H.; Yeh, J.-W. Sluggish diffusion in Co-Cr-Fe-Mn-Ni high-entropy alloys. Acta Mater 2013, 61, 4887–4897. [Google Scholar]
- Lin, C.-M.; Tsai, H.-L.; Bor, H.-Y. Effect of aging treatment on microstructure and properties of high-entropy Cu0.5CoCrFeNi alloy. Intermetallics 2010, 18, 1244–1250. [Google Scholar]
- Wen, L.H.; Kou, H.C.; Li, J.S.; Chang, H.; Xue, X.Y.; Zhou, L. Effect of aging temperature on microstructure and properties of AlCoCrCuFeNi high-entropy alloy. Intermetallics 2009, 17, 266–269. [Google Scholar]
- Kao, Y.-F.; Chen, T.-J.; Chen, S.-K.; Yeh, J.-W. Microstructure and mechanical property of as-cast, -homogenized, and -deformed AlxCoCrFeNi (0 ≤ x ≤ 2) high-entropy alloys. J. Alloys Compd 2009, 488, 57–64. [Google Scholar]
- Tsai, C.-W.; Chen, Y.-L.; Tsai, M.-H.; Yeh, J.-W.; Shun, T.-T.; Chen, S.-K. Deformation and annealing behaviors of high-entropy alloy Al0.5CoCrCuFeNi. J. Alloys Compd 2009, 486, 427–435. [Google Scholar]
- Otto, F.; Dlouhy, A.; Somsen, C.; Bei, H.; Eggler, G.; George, E.P. The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy. Acta Mater 2013, 61, 5743–5755. [Google Scholar]
- Miracle, D.B.; Lark, K.A.; Srinivasan, V.; Lipsitt, H.A. Nickel-aluminum-molybdenum phase equilibria. Metall. Trans. A 1984, 15, 481–486. [Google Scholar]
- Senkov, O.N.; Zhang, F.; Miller, J.D. Phase composition of a CrMo0.5NbTa0.5TiZr high entropy alloy: Comparison of experimental and simulated data. Entropy 2013, 15, 3769–3809. [Google Scholar]
- McCluskey, P.; Vlassak, J. Cominatorial nanocalorimetry. J. Mater. Res 2010, 25, 2086–2100. [Google Scholar]
- Green, M.; Takeuchi, I.; Hattrick-Simpers, J.R. Applications of high throughput (combinatorial) methodologies to electronic, magnetic, optical, and energy-related materials. J. Appl. Phys 2013, 113, 231101. [Google Scholar]
- Potyrailo, R.; Rajan, K.; Stoewe, K.; Takeuchi, I.; Chisholm, B.; Lam, H. Cominatorial and high-throughput screening of materials libraries: Review of state of the art. ACS Comb. Sci 2011, 13, 579–633. [Google Scholar]
- Potyrailo, R.; Takeuchi, I. Role of high-throughput characterization tools in combinatorial materials science. Meas. Sci. Technol 2005, 16, 1–4. [Google Scholar]
- Rajan, K. Combinatorial Materials Sciences: Experimental Strategies for Accelerated Knowledge Discovery. Annu. Rev. Mater. Res 2008, 38, 299–322. [Google Scholar]
- Zhao, J.-C. Combinatorial approaches as effective tools in the study of phase diagrams and composition–structure–property relationships. Prog. Mater. Sci 2006, 51, 557–631. [Google Scholar]
- Ludwig, A.; Zarnetta, R.; Hamann, S.; Savan, A.; Thienhaus, S. Development of multimunctional thin films using high-throughput experimentation methods. Int. J. Mater. Res 2008, 99, 1144–1149. [Google Scholar]
- Herderick, E.D. Additive manufacturing of metals: A review. In Materials Science & Technology 2011; TMS: Warrendale, PA, USA, Columbus, OH, USA, 2011; pp. 1413–1425. [Google Scholar]
- Wong, K.V.; Hernandez, A. A review of additive manufacturing. ISRN Mech. Eng 2012, 2012, 208760. [Google Scholar]
- Uchic, M.D.; Dimiduk, D.M. A methodology to investigate size scale effects in crystalline plasticity using uniaxial compression testing. Mater. Sci. Eng. A 2005, 400, 268–278. [Google Scholar]
- Hemker, K.J.; Sharpe, W.N., Jr. Microscale characterization of mechanical properties. Annu. Rev. Mater. Res 2007, 37, 93–126. [Google Scholar]
- Shade, P.A.; Kim, S.-L.; Wheeler, R.; Uchic, M.D. Stencil mask methodology for the parallelized production of microscale mechanical test samples. Rev. Sci. Instrum 2012, 83, 053903. [Google Scholar]
- Standard Test Methods for Determining Hardenability of Steel, ASTM A255-10. Available online: http://www.astm.org/Standards/A255.htm (accessed on 13 September 2013).
- Semiatin, S.L. Workability in forging. In Handbook of Workability and Process Design; Dieter, G.E., Kuhn, H.A., Semiatin, S.L., Eds.; ASM, International: Materials Park, OH, USA, 2004. [Google Scholar]
- Dimiduk, D.M.; Uchic, M.D.; Parthasarathy, T.A. Size-affected single-slip behavior of pure nickel microcrystals. Acta Mater 2005, 53, 4065–4077. [Google Scholar]
- Norfleet, D.M.; Dimiduk, D.M.; Polasik, S.J.; Uchic, M.D.; Mills, M.J. Dislocation structures and their relationship to strength in deformed nickel microcrystals. Acta Mater 2008, 56, 2988–3001. [Google Scholar]
- Shade, P.A.; Uchic, M.D.; Dimiduk, D.M.; Viswanathan, G.B.; Wheeler, R.; Fraser, H.L. Size-affected single-slip behavior of René N5 microcrystals. Mater. Sci. Eng. A 2012, 535, 53–61. [Google Scholar]
- Cao, W.; Chang, Y.A.; Zhu, J.; Chen, S.; Oates, W.A. Application of the cluster/site approximation to the calculation of multicomponent alloy phase diagrams. Acta Mater 2005, 53, 331–335. [Google Scholar]
- Zhang, C.; Zhang, F.; Chen, S.; Cao, W. Computational thermodynamics aided high-entropy alloy design. JOM 2012, 64, 839–845. [Google Scholar]
- Groves, J.F. Directed Vapor Deposition. Ph.D Thesis, University of VA, Charlottesville, VA, USA. 1998. [Google Scholar]
- Uchic, M.; Groeber, M.; Shah, M.; Callahan, P.; Shiveley, A.; Scott, M.; Chapman, M.; Spowart, J. An Automated Multi-Modal Serial Sectioning System for Characterization of Grain-Scale Microstructures in Engineering Materials. In 1st International Conference on 3D Materials Science; Graef, M.D., Poulsen, H.F., Lewis, A., Simmons, J., Spanos, G., Eds.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2012. [Google Scholar]
- Simpleware: Converting 3D Images into Models. Available online: http://www.simpleware.com/industries/materials/ (accessed on 11 October 2013).
- Springer, H.; Raabe, D. Rapid alloy prototyping: Compositional and thermo-mechanical high throughput bulk combinatorial design of structural materials based on the example of 30Mn-1.2C-xAl triplex steels. Acta Mater 2012, 60, 4950–4959. [Google Scholar]
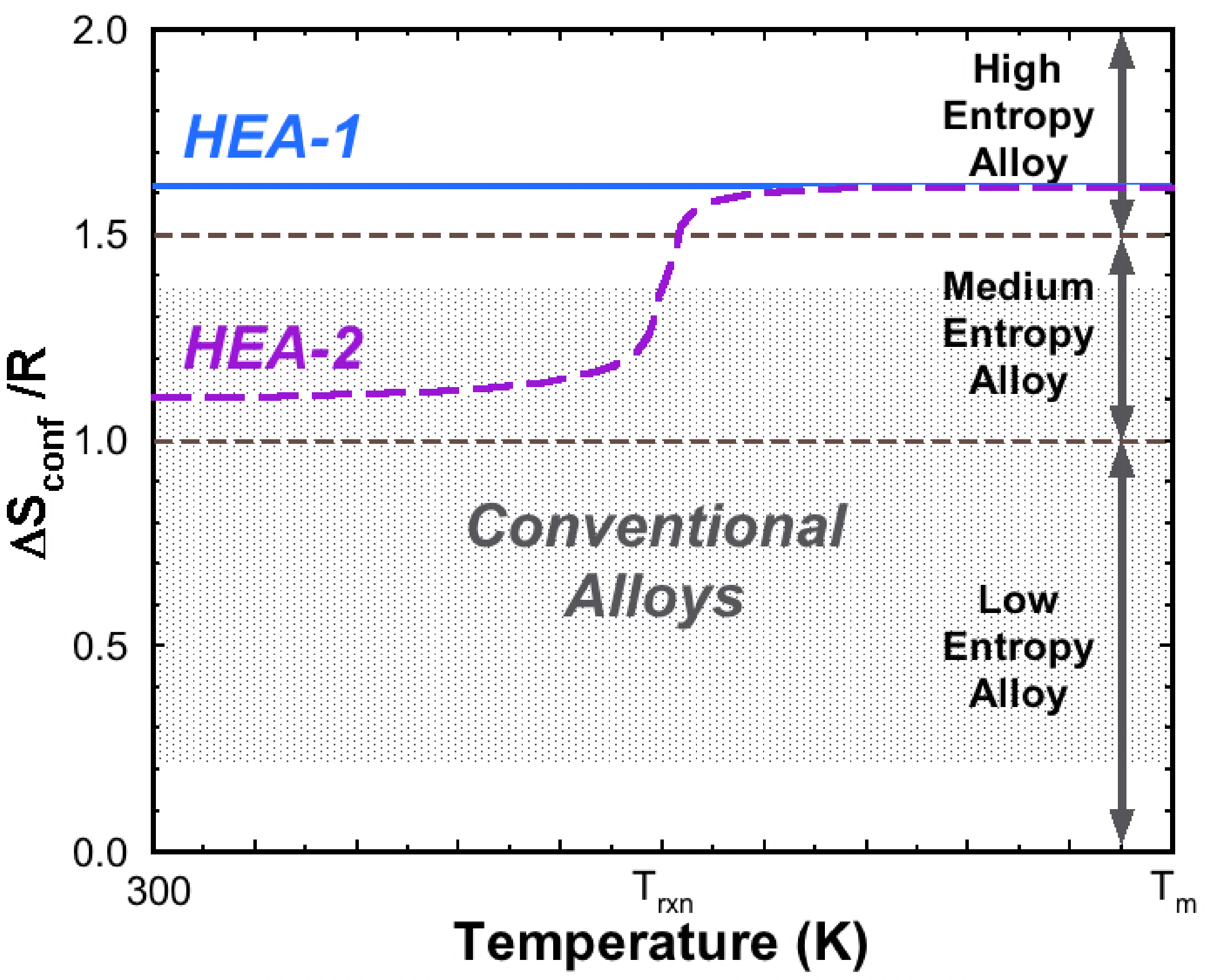
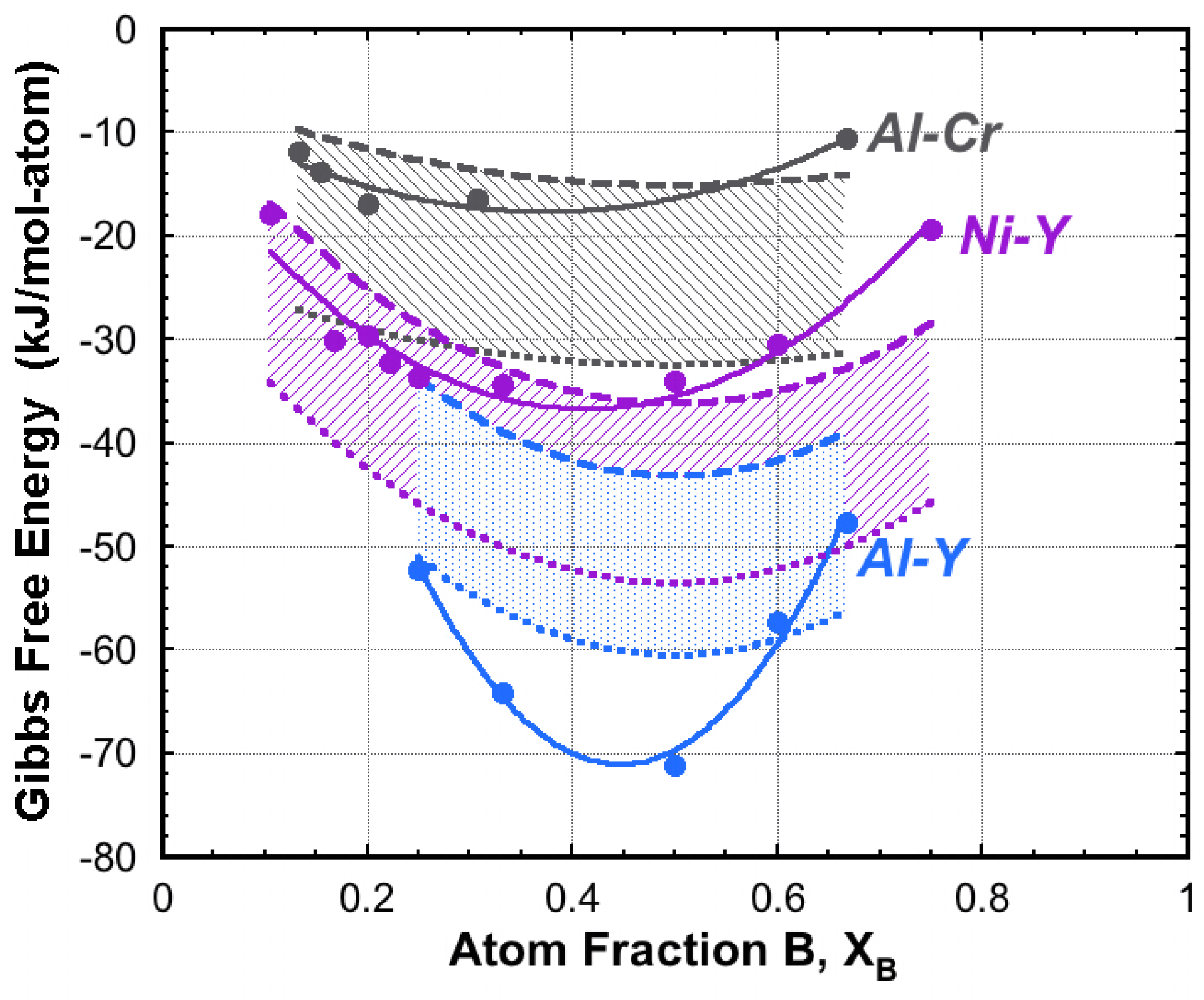
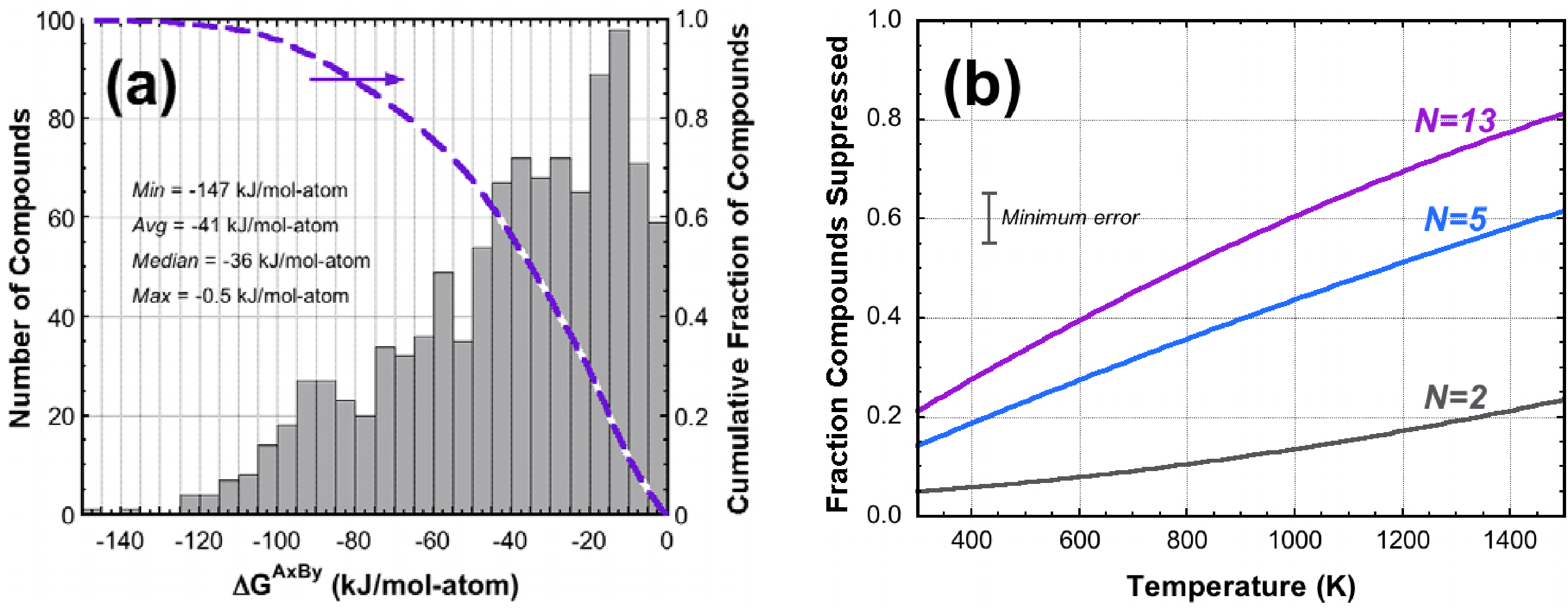
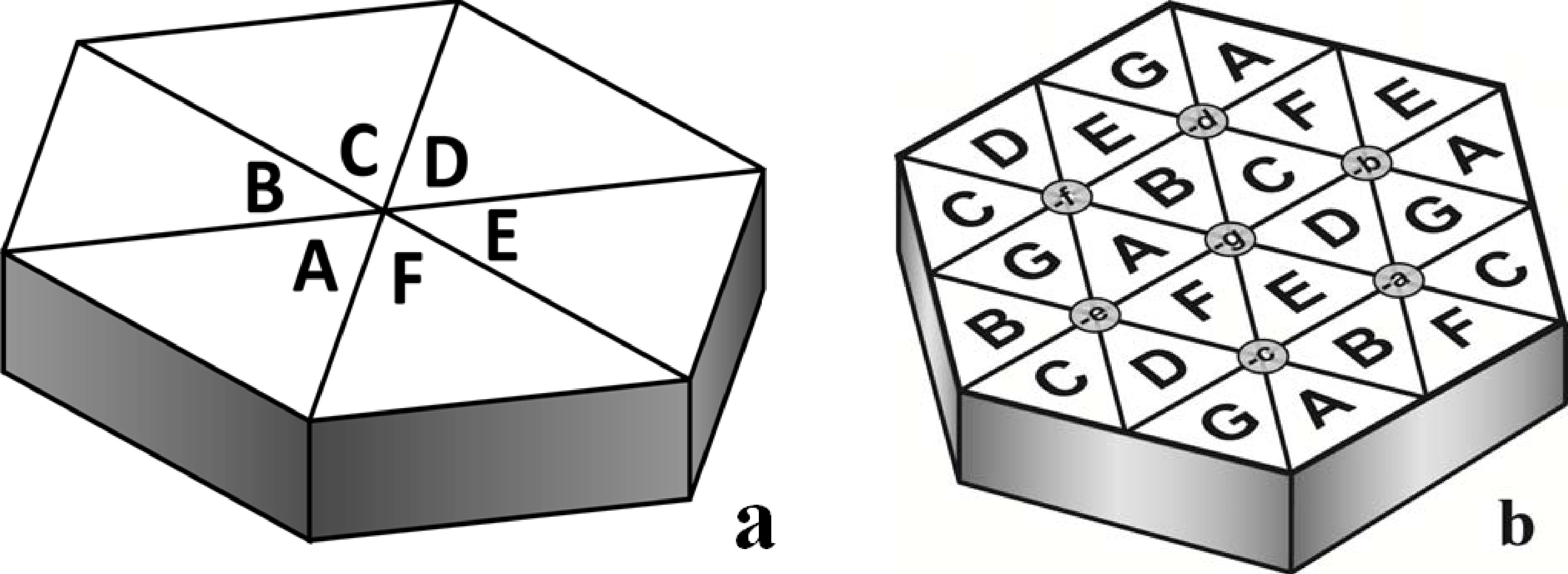
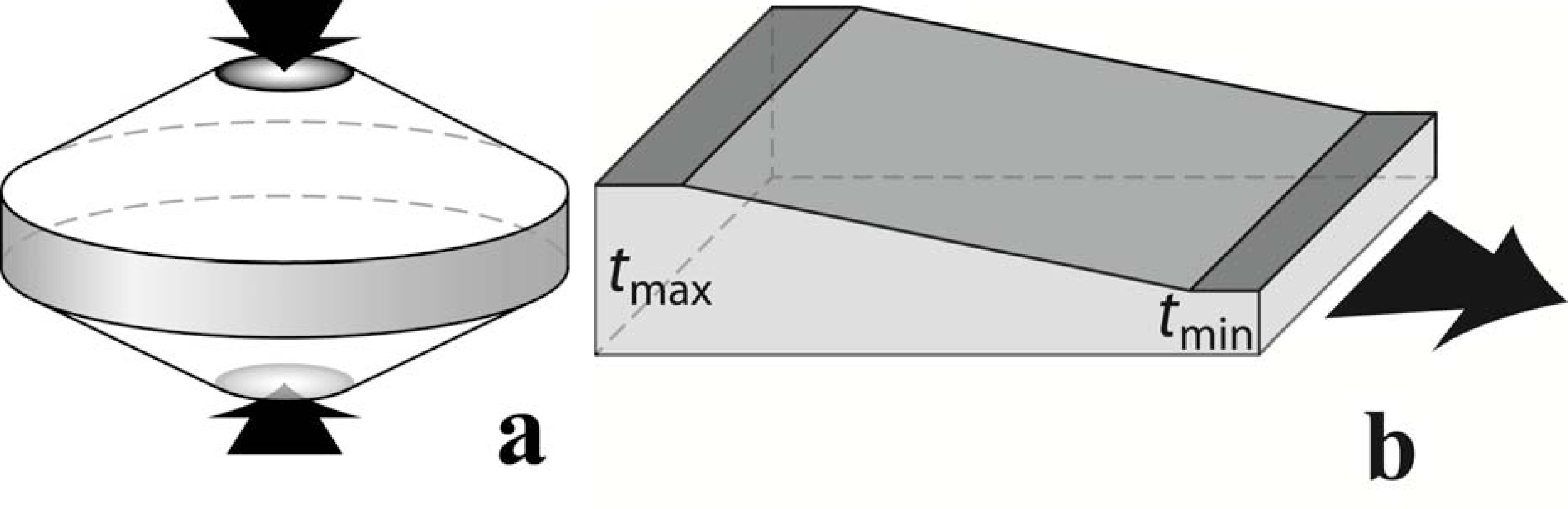
| System | ρ (g·cm−3) | Tuse (°C) | E (GPa) | σy (MPa) | σuts (MPa) | Elongation (%) | KIc (MPa-m−1/2) |
|---|---|---|---|---|---|---|---|
| Al alloys | 2.6–2.9 | ≤150 | ∼70 | 250–550 | 300–600 | ≥10 | ≥30 |
| Ti alloys | 4.4–4.6 | ≤450 | 100–120 | 800–1400 | 900–1600 | 3–15 | 20–110 |
| Ni alloys | 8–9 | ≤1100 | 210–220 | 400–1300 | 1000–1600 | 15–50 | 80–120 |
| Element | Tm(K) [44] | ρ (g·cm−3) [44] | E(GPa) [44] | Atom Radius (pm)[45] | Pauling EN[44] | Tm/ρ | LOW-T | MED-T | HI-T |
|---|---|---|---|---|---|---|---|---|---|
| HEA | HEA | HEA | |||||||
| Tm > 750 K | Tm > 1350 K | Tm > 1950 K | |||||||
| ρ< 8 g·cm−3 | ρ< 10 g·cm−3 | ρ< 12 g·cm−3 | |||||||
| E > 40 GPa | E > 60 GPa | E > 80 GPa | |||||||
| Si | 1,687 | 2.33 | 47 | 112 | 1.9 | 724 | ✓ | C | C |
| Ca | 1,115 | 1.53 | 20 | 192 | 1 | 729 | |||
| Sc | 1,814 | 3.00 | 74 | 162 | 1.36 | 605 | ✓ | ✓ | |
| Mg | 9,23 | 1.74 | 45 | 160 | 1.31 | 532 | ✓ | ||
| Ti | 1,941 | 4.50 | 116 | 142 | 1.54 | 431 | ✓ | ✓ | □ |
| Sr | 1,050 | 2.58 | 212 | 0.95 | 407 | ✓ | |||
| Y | 1,795 | 4.47 | 64 | 173 | 1.22 | 401 | ✓ | ✓ | |
| V | 2,183 | 6.12 | 128 | 134 | 1.63 | 357 | ✓ | ✓ | ☑ |
| Al | 933 | 2.70 | 70 | 141 | 1.61 | 346 | ✓ | C | C |
| Zr | 2,128 | 6.51 | 68 | 158 | 1.33 | 327 | ✓ | ✓ | □ |
| Nb | 2,750 | 8.58 | 105 | 150 | 1.6 | 321 | ✓ | ☑ | |
| Cr | 2,180 | 7.19 | 279 | 130 | 1.66 | 303 | ✓ | ✓ | ☑ |
| Mo | 2,896 | 10.23 | 329 | 139 | 2.16 | 283 | ✓ | ☑ | |
| Fe | 1,811 | 7.88 | 211 | 126 | 1.83 | 230 | ✓ | ✓ | |
| Tc | 2,430 | 11.36 | 136 | 1.9 | 214 | ✓ | |||
| Ru | 2,607 | 12.37 | 447 | 134 | 2.2 | 211 | □ | ||
| Eu | 1,095 | 5.25 | 18 | 196 | 1.01 | 209 | |||
| Tm | 1,818 | 8.84 | 74 | 175 | 1.25 | 206 | ✓ | ||
| Mn | 1,519 | 7.47 | 198 | 132 | 1.55 | 203 | ✓ | ✓ | |
| Gd | 1,586 | 7.90 | 55 | 176 | 1.2 | 201 | ✓ | ||
| Co | 1,768 | 8.84 | 209 | 124 | 1.88 | 200 | ✓ | ||
| Er | 1,802 | 9.06 | 70 | 175 | 1.24 | 199 | ✓ | ||
| Ho | 1,745 | 8.80 | 65 | 177 | 1.23 | 198 | ✓ | ||
| Tb | 1,632 | 8.23 | 56 | 176 | 1.1 | 198 | |||
| Ta | 3,290 | 16.68 | 186 | 154 | 1.5 | 197 | □ | ||
| Dy | 1,685 | 8.55 | 61 | 175 | 1.22 | 197 | ✓ | ||
| Lu | 1,936 | 9.84 | 69 | 175 | 1.27 | 197 | ✓ | ||
| Ni | 1,728 | 8.91 | 200 | 126 | 1.91 | 194 | ✓ | ||
| La | 1,193 | 6.20 | 37 | 187 | 1.1 | 192 | |||
| Pm | 1,373 | 7.17 | 46 | 185 | 1.17 | 192 | ✓ | ||
| W | 3,695 | 19.41 | 411 | 135 | 2.36 | 190 | □ | ||
| Hf | 2,506 | 13.28 | 78 | 158 | 1.3 | 189 | □ | ||
| Nd | 1,289 | 7.01 | 41 | 182 | 1.14 | 184 | ✓ | ||
| Rh | 2,237 | 12.43 | 275 | 132 | 2.28 | 180 | □ | ||
| Sm | 1,345 | 7.53 | 50 | 185 | 1.17 | 179 | ✓ | ||
| Pr | 1,204 | 6.77 | 37 | 183 | 1.07 | 178 | |||
| Re | 3,458 | 21.02 | 463 | 137 | 1.9 | 165 | |||
| Ce | 1,072 | 6.77 | 34 | 182 | 1.12 | 158 | |||
| Yb | 1,097 | 6.97 | 24 | 190 | 1.06 | 157 | |||
| Cu | 1,358 | 8.94 | 130 | 126 | 1.9 | 152 | ✓ | ||
| Pd | 1,828 | 12.43 | 121 | 142 | 2.2 | 147 | |||
| Ir | 2,719 | 22.56 | 528 | 136 | 2.2 | 121 | |||
| Ag | 1,235 | 10.50 | 83 | 144 | 1.93 | 118 | |||
| Pt | 2,041 | 21.46 | 168 | 141 | 2.28 | 95 | |||
| Au | 1,337 | 19.29 | 78 | 143 | 2.54 | 69 | |||
| Number of palette elements | 16 | 17 | 12* | ||||||
| Average Tm (K) | 1,597 | 1,880 | 2,570* | ||||||
| Average ρ (g·cm−3) | 5.38 | 7.50 | 10.7* | ||||||
| Average E (GPa) | 99 | 125 | 220* | ||||||
□ Used as a refractory HEA palette element [4,27–29];*Includes both ✓ and □ elements; C Compound-forming element (see Section 3.3.2).
| STAGE 0 | High-Throughput CALPHAD Calculations of Phase Equilibria |
| Use temperature (Tuse) is less than the solidus temperature (Tsol) Must have no 1st order phase transformation below Tuse Must have 1 or 2 solid solutions or 1 solid solution plus 1 intermetallic phase at T ≤ Tuse Must be single phase solid solution at some temperature above Tuse Phases are fcc, bcc, hcp or ordered derivatives Estimated ρ must be at or below the critical ρ Estimated E must be at or above the critical E | |
| STAGE 1 | High-Throughput Experiments Using Composition Gradients |
| Measure phases present via EDS and EBSD mapping in SEM Measure phase transformations (including melting) via nano-calorimetry [62] Measure E via instrumented nano-indentation Measure strength capacity via instrumented nano-indentation or micro-pillar compression Measure capacity for plasticity via micro-pillar compression Measure capacity for oxidation resistance Refine the thermodynamic database using measured data | |
| STAGE 2 | High-Throughput Experiments Using Microstructure Gradients |
| Measure tensile strength & ductility as function of temperature (techniques not yet established) | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Miracle, D.B.; Miller, J.D.; Senkov, O.N.; Woodward, C.; Uchic, M.D.; Tiley, J. Exploration and Development of High Entropy Alloys for Structural Applications. Entropy 2014, 16, 494-525. https://doi.org/10.3390/e16010494
Miracle DB, Miller JD, Senkov ON, Woodward C, Uchic MD, Tiley J. Exploration and Development of High Entropy Alloys for Structural Applications. Entropy. 2014; 16(1):494-525. https://doi.org/10.3390/e16010494
Chicago/Turabian StyleMiracle, Daniel B., Jonathan D. Miller, Oleg N. Senkov, Christopher Woodward, Michael D. Uchic, and Jaimie Tiley. 2014. "Exploration and Development of High Entropy Alloys for Structural Applications" Entropy 16, no. 1: 494-525. https://doi.org/10.3390/e16010494
APA StyleMiracle, D. B., Miller, J. D., Senkov, O. N., Woodward, C., Uchic, M. D., & Tiley, J. (2014). Exploration and Development of High Entropy Alloys for Structural Applications. Entropy, 16(1), 494-525. https://doi.org/10.3390/e16010494






