Adaptive Switched Generalized Function Projective Synchronization between Two Hyperchaotic Systems with Unknown Parameters
Abstract
: In this paper, we investigate adaptive switched generalized function projective synchronization between two new different hyperchaotic systems with unknown parameters, which is an extension of the switched modified function projective synchronization scheme. Based on the Lyapunov stability theory, corresponding adaptive controllers with appropriate parameter update laws are constructed to achieve adaptive switched generalized function projective synchronization between two different hyperchaotic systems. A numerical simulation is conducted to illustrate the validity and feasibility of the proposed synchronization scheme.1. Introduction
Hyperchaos, which was first introduced by Rössler [1], is usually characterized as a chaotic attractor with more than one positive Lyapunov exponent. The degree of chaos of a system can be measured by a generalization of the concept of entropy for state space dynamics [2,3]. It is a highly desired property to ensure security in a chaos encryption scheme that the larger the entropy, the larger the unpredictability of the system [4]. After the hyperchaotic Rössler system, many other hyperchaotic systems have been reported, including the hyperchaotic Lorenz system [5], hyperchaotic Chen system [6], hyperchaotic Lü system [7]. In [8], the positive topological entropy was calculated, which indicated that the system from two coupled Wien-bridge oscillators was hyperchaotic.
Since the concept of synchronizing two identical chaotic systems from different initial conditions was introduced by Pecora and Carroll in 1990 [9], synchronization in chaotic systems has been extensively investigated over the last two decades. Many synchronization schemes have been proposed, which include complete synchronization [10,11], lag synchronization [12], generalized synchronization [13], phase synchronization [14], anti-synchronization [15,16], partial synchronization [17,18], Q-S synchronization [19,20], projective synchronization [21–32], anticipating synchronization [33], inverse lag synchronization [34] and inverse π-lag synchronization [35,36].
Among the above-mentioned synchronization phenomena, projective synchronization has been investigated with increasing interest in recent years due to the fact that it can obtain faster communication with its proportional feature [23–26]. The concept of projective synchronization was first introduced by Mainieri and Rehacek in 1999 [27], in which the drive and response systems could be synchronized up to a constant scaling factor. Later on, Li [28] proposed a new synchronization scheme called modified projective synchronization (MPS), where the drive and response dynamical states synchronize up to a constant scaling matrix. Afterwards, Chen et al. [29] extended the modified projective synchronization and proposed function projective synchronization (FPS), where the drive and response dynamical states synchronize up to a scaling function matrix, but not a constant one. Recently, Du et al. [30] discussed a new type of synchronization phenomenon, modified function projective synchronization (MFPS), in which the drive and response systems could be synchronized up to a desired scaling function matrix. Many of these synchronization schemes have been applied to investigate chaotic or fractional chaotic systems [37–44]. More recently, Yu and Li [31] have proposed a new synchronization scheme by choosing a more generalized scaling function matrix, called generalized function projective synchronization (GFPS), which is an extension of all the aforementioned projective synchronization schemes. Lately, Sudheer and Sabir [32] reported switched modified function projective synchronization (SMFPS) in hyperchaotic Qi system using adaptive control method, in which a state variable of the drive system synchronize with a different state variable of the response system up to a desired scaling function matrix.
Inspired by the previous works, in this paper, we propose the switched generalized function projective synchronization (SGFPS) between two different hyperchaotic systems using adaptive control method by extending the GFPS and SMFPS schemes, in which a state variable of the drive system synchronizes with a different state variable of the response system up to a more generalized scaling function matrix. Due to the unpredictability of the switched states and scaling function matrix, this synchronization scheme can provide additional security in secure communication.
The rest of this paper is organized as follows. Section 2 gives a brief description of the SGFPS scheme and two new hyperchaotic systems. In Section 3, we propose appropriate adaptive controllers and parameter update laws for the adaptive switched generalized function projective synchronization of two different hyperchaotic systems. Section 4 presents a numerical example to illustrate the effectiveness of the proposed method. Finally, conclusions are given in Section 5.
2. Description of the Switched Generalized Function Projective Synchronization and Two New Hyperchaotic Systems
Consider the following drive and response systems:
The error states between the drive and response systems are defined as
Definition 1. For the two systems described in Equation (1), we say that they are switched generalized function projective synchronous with respect to the scaling function matrix ϕ(x) if there exists a controller vector u(t, x, y) such that
Remark 1. For the SGFPS, we define i ≠ j in the above Equation (3). If i = j, the SGFPS degenerates to the GFPS [25].
Recently, Li et al. [45] proposed a new hyperchaotic Lorenz-type system described by
Lately, Dadras et al. [46] reported the following four-wing hyperchaotic system, which has only one unstable equilibrium
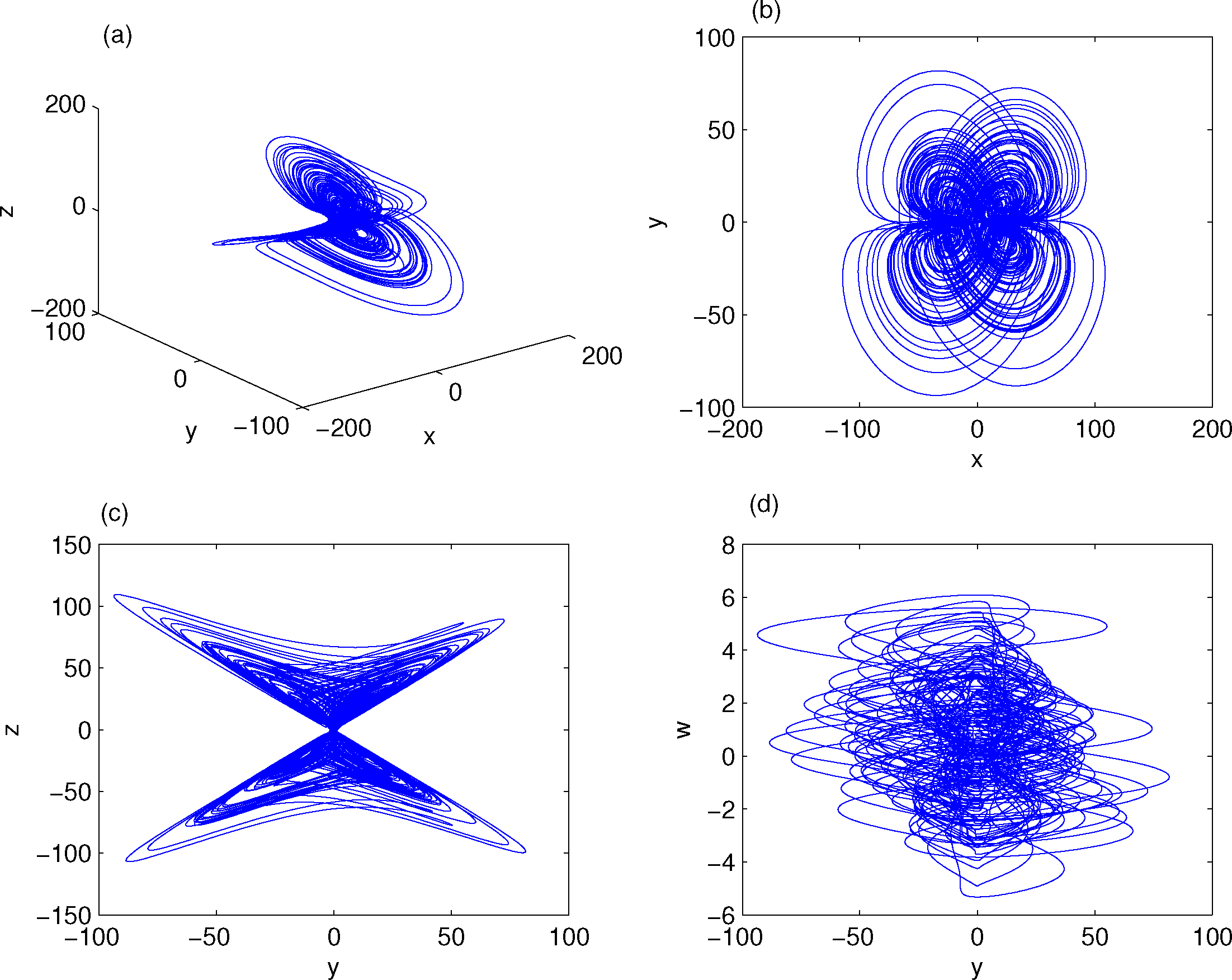
For more information on the dynamical behaviors of these two systems, please refer to [45,46].
3. Switched Generalized Function Projective Synchronization between Two Hyperchaotic Systems
In this section, we investigate the adaptive SGFPS between systems (4) and (5) with fully unknown parameters.
Suppose that system (4) is the drive system whose four variables are denoted by subscript 1 and system (5) is the response system whose variables are denoted by subscript 2. Then the drive and response systems are described by the following equations, respectively,
So the SGFPS error dynamical system is determined as follows
Without loss of generality, the scaling functions can be chosen as ϕ1(x) = m11x1 + m12, ϕ2(x) = m21y1 + m22, ϕ3(x) = m31z1 + m32 and ϕ4(x) = m41w1 + m42, where mij(i = 1, 2, 3, 4; j = 1, 2) are constant numbers. And substituting systems (6) and (7) into system (9), yields the following form:
Our goal is to find the appropriate controllers ui(i = 1, 2, 3, 4) to stabilize the error variables of system (10) at the origin. For this purpose, we propose the following controllers for system (10)
The update laws for the unknown parameters a1, b1, c1, d1, k1, r1, a2, b2 and c2 are given as follows
Theorem 1. For a given continuous differential scaling function matrix ϕ(x) = diag{ϕ1(x), ϕ2(x), ϕ3(x), ϕ4(x)}, and any initial values, the SGFPS between systems (6) and (7) can be achieved by the adaptive controllers (11) and the parameter update laws (12).
Proof. Choose the following Lyapunov function,
Substituting Equation (11) into Equation (14) yields
Since the Lyapunov function V is positive definite and its derivative V̇ is negative definite in the neighborhood of the zero solution for system (10). According to the Lyapunov stability theory, the error dynamical system (10) can converge to the origin asymptotically. Therefore, the SGFPS between the two hyperchaotic systems (6) and (7) is achieved with the adaptive controllers (11) and the parameter update laws (12).
This completes the proof.
4. Numerical Simulation
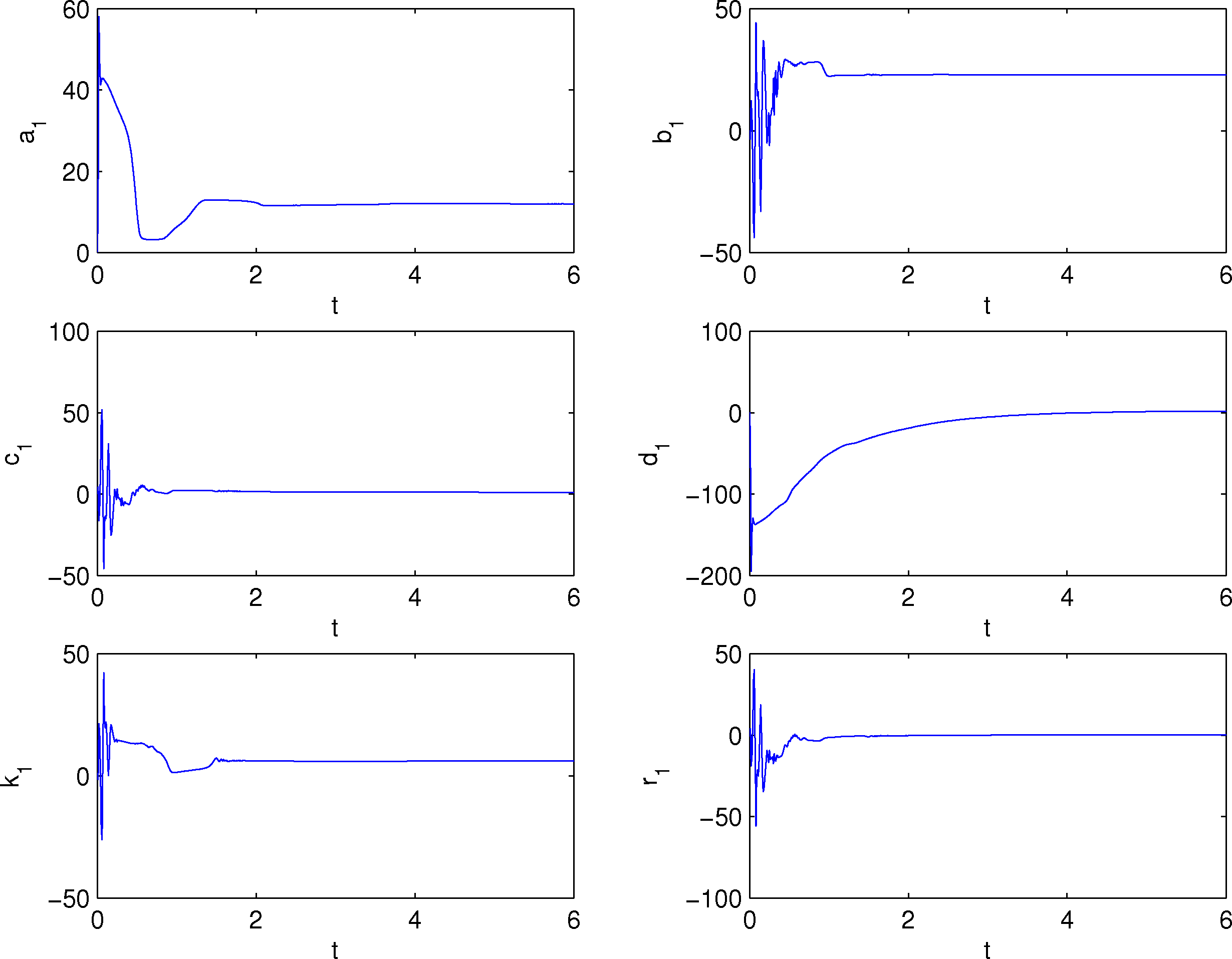
In this section, to verify and demonstrate the effectiveness of the proposed method we consider a numerical example. In the numerical simulations, the fourth-order Runge-Kutta method is used to solve the systems with time step size 0.001. The true values of the “unknown” parameters of systems (6) and (7) are chosen as a1 = 12, b1 = 23, c1 = 1, d1 = 2.1, k1 = 6, r1 = 0.2, a2 = 8, b2 = 40, c2 = 14.9, so that the two systems exhibit hyperchaotic behavior, respectively. The initial values for the drive and response systems are x1(0) = 8.3, y1(0) = 10.8, z1(0) = 17.4, w1(0) = −11.1, x2(0) = −0.2, y2(0) = −0.1, z2(0) = 16.9 and w2(0) = −0.7, and the estimated parameters have initial conditions 0.1. Given that the function factors are ϕ1(x) = 2x1 − 0.3, ϕ2(x) = 2y1 +0.5, ϕ3(x) = 0.5z1 +0.03, ϕ4(x) = −0.5w1 + 0.03, and the gain matrix L is given as diag{10, 10, 10, 10}. The simulation results are shown in Figures 3 and 5. Figure 3 demonstrates the SGFPS errors of the drive system (6) and response system (7). From this figure, it can be seen that the SGFPS errors converge to zero, i.e., these two systems achieved SGFPS. And Figures 4 and 5 show that the unknown system parameters approach the true values.
5. Conclusions
In this paper, we have investigated switched generalized function projective synchronization between two new different hyperchaotic systems with fully unknown parameters, which extended the switched modified function projective synchronization scheme. In this synchronization scheme, a state variable of the drive system synchronizes with a different state variable of the response system up to a generalized scaling function matrix. Due to the unpredictability of the switched states and scaling function matrix, this synchronization scheme can provide additional security in secure communication. By applying the adaptive control theory and Lyapunov stability theory, the appropriate adaptive controllers with parameter update laws are proposed to achieve SGFPS between two different hyperchaotic systems. A numerical simulation was conducted to illustrate the validity and feasibility of the proposed synchronization scheme.
Acknowledgments
This work was supported by the Youth Foundation of Yunnan University of Nationalities under grant No.11QN07, the Natural Science Foundation of Yunnan Province under grants No.2009CD019 and No.2011FZ172, the Natural Science Foundation of China under grant No.61263042.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rössler, O.E. An equation for hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar]
- Cenys, A.; Tamasevicius, A.; Mykolaitis, G.; Namajunas, A. Hyperchaos with high metric entropy. Nonlinear Phenom. Complex Syst 1999, 2, 36–40. [Google Scholar]
- Gao, J.; Liu, F.; Zhang, J.; Hu, J.; Cao, Y. Information entropy as a basic building block of complexity theory. Entropy 2013, 15, 3396–3418. [Google Scholar]
- Vicente, R.; Dauden, J.; Colet, P.; Toral, R. Analysis and characterization of the hyperchaos generated by a semiconductor laser subject to a delayed feedback loop. IEEE J. Quantum Electr 2005, 41, 541–548. [Google Scholar]
- Wang, X.; Wang, M. A hyperchaos generated from Lorenz system. Physica A 2008, 387, 3751–3758. [Google Scholar]
- Li, Y.; Tang, W. K.; Chen, G. Generating hyperchaos via state feedback control. Int. J. Bifur. Chaos 2005, 15, 3367–3375. [Google Scholar]
- Chen, A.; Lu, J.; Lü, J.; Yu, S. Generating hyperchaotic Lü attractor via state feedback control. Physica A 2006, 364, 103–110. [Google Scholar]
- Li, Q.; Yang, X.S. Hyperchaos from two coupled Wien-bridge oscillators. Int. J. Circ. Theor. Appl 2008, 36, 19–29. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett 1990, 64, 821–824. [Google Scholar]
- Fujisaka, H.; Yamada, T. Stability theory of synchronized motion in coupled-oscillator systems. Prog. Theor. Phys 1983, 69, 32–47. [Google Scholar]
- Pikovsky, A.S. On the interaction of strange attractors. Z. Phys. B Conden. Matter 1984, 55, 149–154. [Google Scholar]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. From phase to lag synchronization in coupled chaotic oscillators. Phys. Rev. Lett 1997, 78, 4193–4196. [Google Scholar]
- Rulkov, N.F.; Sushchik, M.M.; Tsimring, L.S.; Abarbanel, H.D.I. Generalized synchronization of chaos in directionally coupled chaotic systems. Phys. Rev. E 1995, 51, 980–994. [Google Scholar]
- Dykman, G.I.; Landa, P.S.; Neymark, Y.I. Synchronizing the chaotic oscillations by external force. Chaos Solitons Fractals 1991, 1, 339–353. [Google Scholar]
- Dou, F.Q.; Sun, J.A.; Duan, W.S.; Lü, K.P. Anti-synchronization of a new hyperchaotic system. Phys. Scr 2008, 78, 015007. [Google Scholar]
- Zhang, R.F.; Chen, D.Y.; Yang, J.G. Anti-synchronization for a class of multi-dimensional autonomous and non-autonomous chaotic systems on the basis of the sliding mode with noise. Phys. Scr 2012, 85, 065006. [Google Scholar]
- Wang, J.W.; Chen, A.M. Partial synchronization in coupled chemical chaotic oscillators. J. Comput. Appl. Math 2010, 233, 1897–1904. [Google Scholar]
- Wagg, D.J. Partial synchronization of nonidentical chaotic systems via adaptive control, with applications to modeling coupled nonlinear systems. Int. J. Bifur. Chaos 2002, 12, 561–570. [Google Scholar]
- Zhao, J.K. Adaptive Q-S synchronization between coupled chaotic systems with stochastic perturbation and delay. Appl. Math. Modell 2012, 36, 3306–3313. [Google Scholar]
- Yan, Z.Y. Chaos Q-S synchronization between Rossler system and the new unified chaotic system. Phys. Lett. A 2005, 334, 406–412. [Google Scholar]
- Mainieri, R.; Rehacek, J. Projective synchronization in three-dimensional chaotic systems. Phys. Rev. Lett 1999, 82, 3042–3045. [Google Scholar]
- Niu, Y.J.; Wang, X.Y. Projective synchronization of different chaotic systems with nonliearity inputs. Int. J. Mod. Phys. B 2012, 26, 1250059. [Google Scholar]
- Feng, C.F.; Zhang, Y.; Sun, J.T.; Qi, W.; Wang, Y.H. Generalized projective synchronization in time-delayed chaotic systems. Chaos Solitons Fractals 2008, 38, 743–747. [Google Scholar]
- Zhou, P.; Zhu, W. Function projective synchronization for fractional-order chaotic systems. Nonlinear Anal.-Real 2011, 12, 811–816. [Google Scholar]
- Wu, X.J.; Wang, H.; Lu, H.T. Modified generalized projective synchronization of a new fractional-order hyperchaotic system and its application to secure communication. Nonlinear Anal.: Real World Appl 2012, 13, 1441–1450. [Google Scholar]
- Elabbasy, E.M.; El-Dessoky, M.M. Adaptive feedback control for the projective synchronization of the Lü dynamical system and its application to secure communication. Chin. J. Phys 2010, 48, 863–872. [Google Scholar]
- Mainieri, R.; Rehacek, J. Projective synchronization in three-dimensioned chaotic systems. Phys. Rev. Lett 1999, 82, 3042–3045. [Google Scholar]
- Li, G.H. Modified projective synchronization of chaotic system. Chaos Solitons Fractals 2007, 32, 1786–1790. [Google Scholar]
- Chen, Y.; Li, X. Function projective synchronization between two identical chaotic systems. Int. J. Mod. Phys. C 2007, 18, 883–888. [Google Scholar]
- Du, H.Y.; Zeng, Q.S.; Wang, C.H. Modified function projective synchronization of chaotic system. Chaos Solitons Fractals 2009, 42, 2399–2404. [Google Scholar]
- Yu, Y.G.; Li, H.X. Adaptive generalized function projective synchronization of uncertain chaotic systems. Nonlinear Anal.-Real 2010, 11, 2456–2464. [Google Scholar]
- Sudheer, K.S.; Sabir, M. Switched modified function projective synchronization of hyperchaotic Qi system with uncertain parameters. Commun. Nonlinear Sci. Numer. Simulat 2010, 15, 4058–4064. [Google Scholar]
- Voss, H.U. Anticipating chaotic synchronization. Phys. Rev. E 2000, 61, 5115–5119. [Google Scholar]
- Li, G.H. Inverse lag synchronization in chaotic systems. Chaos Solitons Fractals 2009, 40, 1076–1080. [Google Scholar]
- Volos, Ch.K.; Kyprianidis, I.M.; Stouboulos, I.N. Various synchronization phenomena in bidirectionally coupled double scroll circuits. Commun. Nonlinear Sci. Numer. Simulat 2011, 16, 3356–3366. [Google Scholar]
- Volos, Ch.K.; Kyprianidis, I.M.; Stouboulos, I.N. Anti-phase and inverse π-lag synchronization in coupled Duffing-type circuits. Int. J. Bifurc. Chaos 2011, 21, 2357–2368. [Google Scholar]
- Wang, S.; Yu, Y.; Wen, G. Hybrid projective synchronization of time-delayed fractional order chaotic systems. Nonlinear Anal.: Hybr. Syst 2014, 11, 129–138. [Google Scholar]
- Wang, X.; Zhang, X.; Ma, C. Modified projective synchronization of fractional-order chaotic systems via active sliding mode control. Nonlinear Dyn 2012, 69, 511–517. [Google Scholar]
- Liu, H.J.; Zhu, Z.L.; Yu, H.; Zhu, Q. Modified Function Projective Synchronization of Fractional Order Chaotic Systems with Different Dimensions. Discrete Dyn. Nat. Soc 2013, 2013, 763564. [Google Scholar]
- Cafagna, D.; Grassi, G. Observer-based projective synchronization of fractional systems via a scalar signal: application to hyperchaotic Rössler systems. Nonlinear Dyn 2012, 68, 117–128. [Google Scholar]
- Xin, B.; Chen, T.; Liu, Y. Projective synchronization of chaotic fractional-order energy resources demand-supply systems via linear control. Commun. Nonlinear Sci. Numer. Simulat 2011, 16, 4479–4486. [Google Scholar]
- Lee, T.H.; Park, J.H. Adaptive functional projective lag synchronization of a hyperchaotic Rössler system. Chin. Phys. Lett 2009, 26, 090507. [Google Scholar]
- Park, J.H. Further results on functional projective synchronization of Genesio-Tesi chaotic system. Modern Phys. Lett. B 2009, 23, 1889–1895. [Google Scholar]
- Park, J.H. Adaptive control for modified projective synchronization of a four-dimensional chaotic system with uncertain parameters. J. Comput. Appl. Math 2008, 213, 288–293. [Google Scholar]
- Li, Y.X.; Liu, X.Z.; Chen, G.R.; Liu, X.X. A new hyperchaotic Lorenz-type system: Generation, analysis, and implementation. Int. J. Circ. Theor. Appl 2012, 39, 865–879. [Google Scholar]
- Dadras, S.; Momeni, H.R.; Qi, G.Y.; Wang, Z.L. Four-wing hyperchaotic attractor generated from a new 4D system with one equilibrium and its fractional-order form. Nonlinear Dyn 2012, 67, 1161–1173. [Google Scholar]

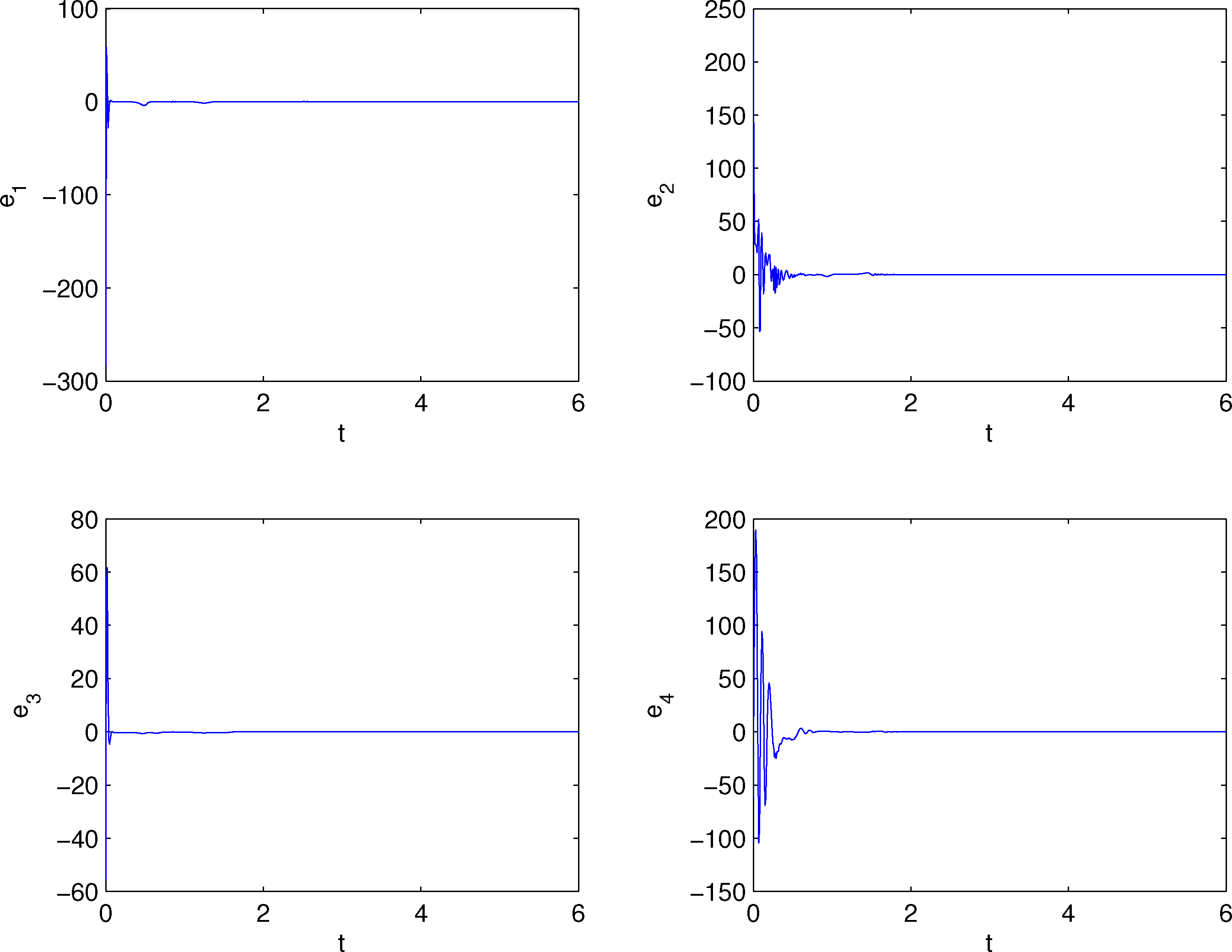

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhou, X.; Xiong, L.; Cai, X. Adaptive Switched Generalized Function Projective Synchronization between Two Hyperchaotic Systems with Unknown Parameters. Entropy 2014, 16, 377-388. https://doi.org/10.3390/e16010377
Zhou X, Xiong L, Cai X. Adaptive Switched Generalized Function Projective Synchronization between Two Hyperchaotic Systems with Unknown Parameters. Entropy. 2014; 16(1):377-388. https://doi.org/10.3390/e16010377
Chicago/Turabian StyleZhou, Xiaobing, Lianglin Xiong, and Xiaomei Cai. 2014. "Adaptive Switched Generalized Function Projective Synchronization between Two Hyperchaotic Systems with Unknown Parameters" Entropy 16, no. 1: 377-388. https://doi.org/10.3390/e16010377
APA StyleZhou, X., Xiong, L., & Cai, X. (2014). Adaptive Switched Generalized Function Projective Synchronization between Two Hyperchaotic Systems with Unknown Parameters. Entropy, 16(1), 377-388. https://doi.org/10.3390/e16010377



