2.1. Bias in Maximum Entropy Models
Our starting point is a fairly standard one in statistical modeling: having drawn K samples of some variable, here denoted, , from an unknown distribution, we would like to construct an estimate of the distribution that is somehow consistent with those samples. To do that, we use the so-called maximum entropy approach: we compute, based on the samples, empirical averages over a set of functions and construct a distribution that exactly matches those averages, but otherwise has maximum entropy.
Let us use
to denote the set of functions and
to denote their empirical averages. Assuming we draw
K samples, these averages are given by:
where
is the
sample. Given the
, we would like to construct a distribution that is constrained to have the same averages as in Equation (
1) and also has maximum entropy. Using
to denote this distribution (with
), the former condition implies that:
The entropy of this distribution, denoted
, is given by the usual expression:
where log denotes the natural logarithm. Maximizing the entropy with respect to
subject to the constraints given in Equation (
2) yields (see, e.g., [
4]):
The
(the Lagrange multipliers of the optimization problem) are chosen, such that the constraints in Equation (
2) are satisfied, and
, the partition function, ensures that the probabilities normalize to one:
Given the
, the expression for the entropy of
is found by inserting Equation (
4) into Equation (
3). The resulting expression:
depends only on
, either directly or via the functions,
.
Because of sampling error, the
are not equal to their true values, and
is not equal to the true maximum entropy. Consequently, different sets of
lead to different entropies and, because the entropy is concave, to bias (see
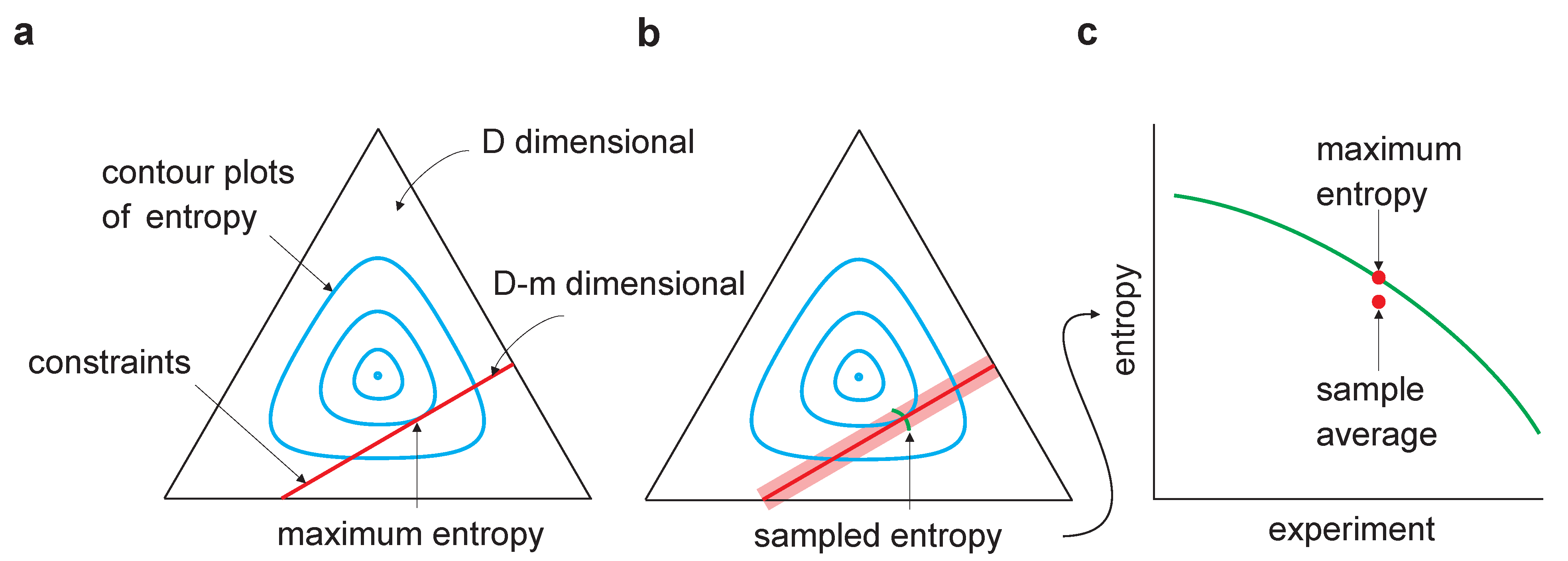
Figure 1). Our focus here is on the bias. To determine it, we need to compute the true parameters. Those parameters, which we denote
, are given by the
limit of Equation (
1); alternatively, we can think of them as coming from the true distribution, denoted
:
Associated with the true parameters is the true maximum entropy,
. The bias is the difference between the average value of
and
; that is, the bias is equal to
, where the angle brackets indicate an ensemble average—an average over an infinite number of data sets (with, of course, each data set containing
K samples). Assuming that
is close to
μ, we can Taylor expand the bias around the true parameters, leading to:
where:
Because
is zero on average [see Equation (
7) and Equation (
9)], the first term on the right-hand side of Equation (
8) is zero. The second term is, therefore, the lowest order contribution to the bias, and it is what we work with here. For convenience, we multiply the second term by
, which gives us the normalized bias:
In the Methods, we explicitly compute
b, and we find that:
where:
and:
Here,
denotes the
entry of
. Because
and
are both covariance matrices, it follows that
b is positive.
Figure 1.
Sampling bias in maximum entropy models. The equilateral triangle represents a D-dimensional probability space (for the binary model considered here, , where n is the dimensionality of ). The cyan lines are contour plots of entropy; the red lines represent the m linear constraints and, thus, lie in a dimensional linear manifold. (a) Maximum entropy occurs at the tangential intersection of the constraints with the entropy contours. (b) The light red region indicates the range of constraints arising from multiple experiments in which a finite number of samples is drawn in each. Maximum entropy estimates from multiple experiments would lie along the green line. (c) As the entropy is concave, averaging the maximum entropy over experiments leads to an estimate that is lower than the true maximum entropy—estimating maximum entropy is subject to downward bias.
Figure 1.
Sampling bias in maximum entropy models. The equilateral triangle represents a D-dimensional probability space (for the binary model considered here, , where n is the dimensionality of ). The cyan lines are contour plots of entropy; the red lines represent the m linear constraints and, thus, lie in a dimensional linear manifold. (a) Maximum entropy occurs at the tangential intersection of the constraints with the entropy contours. (b) The light red region indicates the range of constraints arising from multiple experiments in which a finite number of samples is drawn in each. Maximum entropy estimates from multiple experiments would lie along the green line. (c) As the entropy is concave, averaging the maximum entropy over experiments leads to an estimate that is lower than the true maximum entropy—estimating maximum entropy is subject to downward bias.
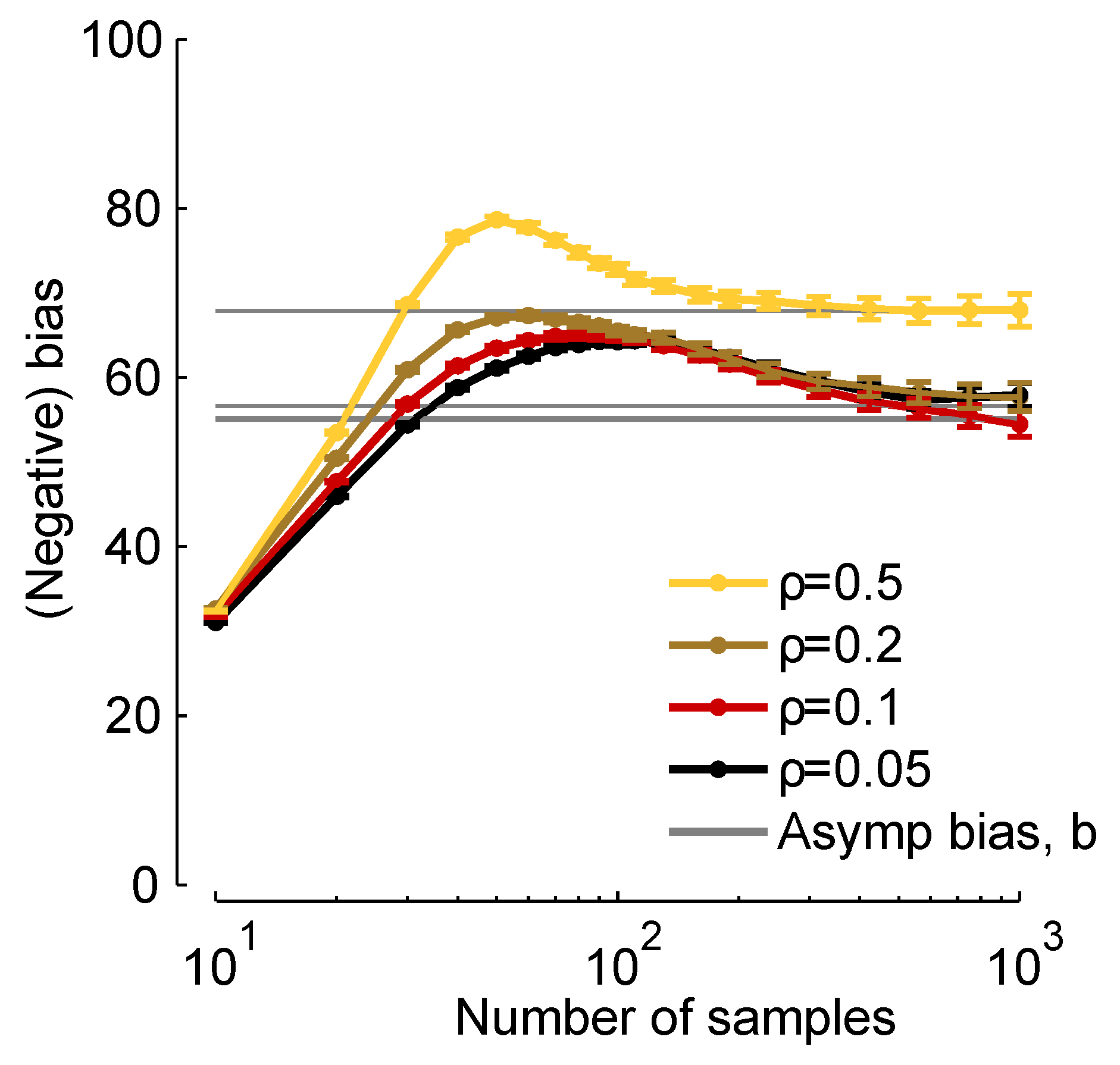
In
Figure 2, we plot
times the true bias (
times the left-hand side of Equation (
8), which we compute from finite samples), and
b [via Equation (
11)]
versus the number of samples,
K. When
K is about 30, the two are close, and when
, they are virtually indistinguishable. Thus, although Equation (
11) represents an approximation to the bias, it is a very good approximation for realistic data sets.
Figure 2.
Normalized bias,
b,
versus number of samples,
. Grey lines:
, computed from Equation (
11). Colored curves:
times the bias, computed numerically using the expression on the left-hand side of Equation (
8). We used a homogeneous Dichotomized Gaussian distribution with
and a mean of 0.1. Different curves correspond to different correlation coefficients [see Equation (
19) below], as indicated in the legend.
Figure 2.
Normalized bias,
b,
versus number of samples,
. Grey lines:
, computed from Equation (
11). Colored curves:
times the bias, computed numerically using the expression on the left-hand side of Equation (
8). We used a homogeneous Dichotomized Gaussian distribution with
and a mean of 0.1. Different curves correspond to different correlation coefficients [see Equation (
19) below], as indicated in the legend.
Evaluating the bias is, typically, hard. However, when the true distribution lies in the model class, so that
, we can write down an explicit expression for it. That is because, in this case,
, so the normalized bias [Equation (
11)] is just the trace of the identity matrix, and we have
(recall that
m is the number of constraints); alternatively, the actual bias is
. An important within model-class case arises when the parametrized model is a histogram of the data. If
can take on
M values, then there are
parameters (the “
” comes from the fact that
must sum to one) and the bias is
. We thus recover a general version of the Miller-Madow [
6] or Panzeri-Treves bias correction [
7], which were derived for a multinomial distribution.
2.2. Is Bias Correction Important?
The fact that the bias falls off as
means that we can correct for it simply by drawing a large number of samples. However, how large is “large”? For definitiveness, suppose we want to draw enough samples that the absolute value of the bias is less than
ϵ times the true entropy, denoted
. Quantitatively, this means we want to choose
K, so that
. Using Equation (
10) to relate the true bias to
b, assuming that
K is large enough that
provides a good approximation to the true bias, and making use of the fact that
b is positive, the condition
implies that
K must be greater than
, where
is given by:
Let us take
to be a vector with
n components:
). The average entropy of the components, denoted
, is given by
, where
is the true entropy of
. Since
, the “independent” entropy of
, is greater than or equal to the true entropy,
, it follows that
obeys the inequality:
Not surprisingly, the minimum number of samples scales with the number of constraints,
m (assuming
does not have a strong
m-dependence; something we show below). Often,
m is at least quadratic in
n; in that case, the minimum number of samples increases with the dimensionality of
.
To obtain an explicit expression for
m in terms of
n, we consider a common class of maximum entropy models: second order models on binary variables. For these models, the functions
constrain the mean and covariance of the
, so there are
parameters:
n parameters for the mean and
for the covariance (because the
are binary, the variances are functions of the means, which is why there are
parameters for the covariances rather than
). Consequently,
and, dropping the “
” (which makes the inequality stronger), we have:
How big is
in practice? To answer that, we need estimates of
and
. Let us focus first on
. For definiteness, here (and throughout the paper), we consider maximum entropy models that describe neural spike trains [
15,
16]. In that case,
is one if there are one or more spikes in a time bin of size
and zero, otherwise. Assuming a population average firing rate of
, and using the fact that entropy is concave, we have
, where
is the entropy of a Bernoulli variable with probability
p:
. Using also the fact that
, we see that
, and so:
Exactly how to interpret
depends on whether we are interested in the total entropy or the conditional entropy. For the total entropy, every data point is a sample, so the number of samples in an experiment that runs for time
T is
. The minimum time to run an experiment, denoted
, is, then, given by:
Ignoring for the moment the factor
and the logarithmic term, the minimum experimental time scales as
. If one is willing to tolerate a bias of 10% of the true maximum entropy (
) and the mean firing rate is not so low (say 10 Hz), then
s. Unless
n is in the hundreds of thousands, running experiments long enough to ensure an acceptably small bias is relatively easy. However, if the tolerance and firing rates drop, say to
and
Hz, respectively, then
s, and experimental times are reasonable until
n gets into the thousands. Such population sizes are not feasible with current technology, but they are likely to be in the not so distant future.
The situation is less favorable if one is interested in the mutual information. That is because to compute the mutual information, it is necessary to repeat the stimulus multiple times. Consequently,
[Equation (
17)] is the number of repeats, with the repeats typically lasting 1–10 s. Again, ignoring the factor
and the logarithmic term, assuming, as above, that
and the mean firing rate is 10 Hz and taking the bin size to be (a rather typical) 10 ms, then
. For
,
, a number that is within experimental reach. When
; however,
. For a one second stimulus, this is about 40 min, still easily within experimental reach. However, for a ten second stimulus, recording times approach seven hours, and experiments become much more demanding. Moreover, if the firing rate is 1 Hz and a tighter tolerance, say
, is required, then
. Here, even if the stimulus lasts only one second, one must record for about 40 min per neuron—or almost seven hours for a population of 10 neurons. This would place severe constraints on experiments.
So far, we have ignored the factor
that appears in Equation (
17) and Equation (
18). Is this reasonable in practice, when the data is not necessarily well described by a maximum entropy model? We address this question in two ways: we compute it for a particular distribution, and we compute its maximum and minimum. The distribution we use is the Dichotomized Gaussian model [
26,
36], chosen because it is a good model of the higher-order correlations found in cortical recordings [
27,
29].
To access the large
n regime, we consider a homogeneous model—one in which all neurons have the same firing rate, denoted
ν, and all pairs have the same correlation coefficient, denoted
ρ. In general, the correlation coefficient between neuron
i and
j is given by:
In the homogeneous model, all the
are the same and equal to
ρ.
Assuming, as above, a bin size of
, the two relevant parameters are the probability of firing in a bin,
, and the correlation coefficient,
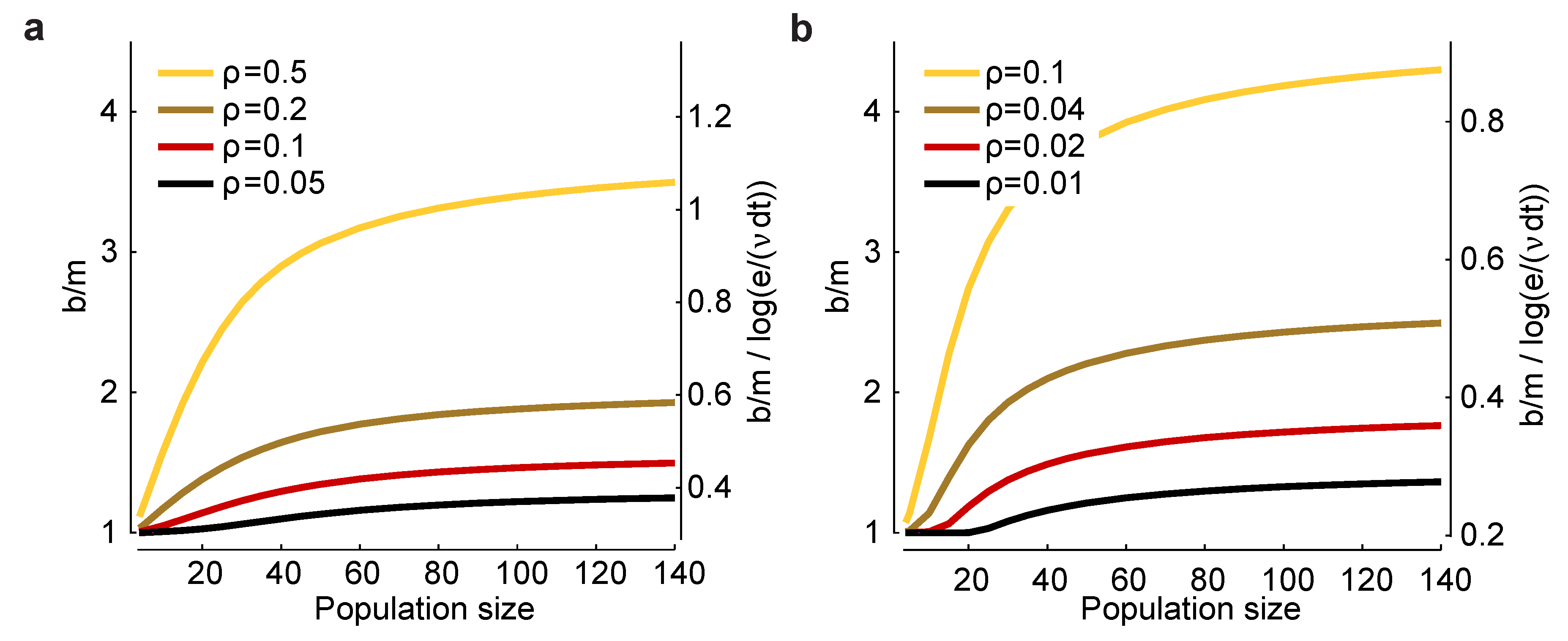
ρ. In
Figure 3a,b, we plot
(left axis) and
(right axis)
versus n for a range of values for
and
ρ. There are two salient features to these plots. First,
increases as
decreases and as
ρ increases, suggesting that bias correction is more difficult at low firing rates and high correlations. Second, the factor
that affects the minimum experimental time,
, has, for large
n, a small range: a low of about 0.3 and a high of about one. Consequently, this factor has only a modest effect on the minimum number of trials one needs to avoid bias.
Figure 3 gives us
for the homogeneous Dichotomized Gaussian model. Does the general picture—that
is largest at low firing rates and high correlations, but never more than about four—hold for an inhomogeneous population, one in which different neurons have different firing rates and different pairs of neurons have different correlation coefficients? To address this question, in
Figure 4, we compare a heterogeneous Dichotomized Gaussian model with
neurons to a homogeneous model: in
Figure 4a, we plot
for a range of median firing rates and correlations coefficients in an inhomogeneous model, and in
Figure 4b, we do the same for a homogeneous model. At very low firing rates, the homogeneous model is slightly more biased than the heterogeneous one, while at very low correlations, it is the other way around. Overall, though, the two models have very similar biases. Although not proof that the lack of difference will remain at large
n, the results are at least not discouraging.
Figure 3.
Scaling of the bias with population size for a homogeneous Dichotomized Gaussian model. (
a) Bias,
b, for
and a range of correlation coefficients,
ρ. The bias is biggest for strong correlations and large population sizes; (
b)
and a range of (smaller) correlation coefficients. In both panels, the left axis is
, and the right axis is
. The latter quantity is important for determining the minimum number of trials [Equation (
17)] or the minimum runtime [Equation (
18)] needed to reduce bias to an acceptable level.
Figure 3.
Scaling of the bias with population size for a homogeneous Dichotomized Gaussian model. (
a) Bias,
b, for
and a range of correlation coefficients,
ρ. The bias is biggest for strong correlations and large population sizes; (
b)
and a range of (smaller) correlation coefficients. In both panels, the left axis is
, and the right axis is
. The latter quantity is important for determining the minimum number of trials [Equation (
17)] or the minimum runtime [Equation (
18)] needed to reduce bias to an acceptable level.
Figure 4.
Effect of heterogeneity on the normalized bias in a small population. (a) Normalized bias relative to the within model class case, , of a heterogeneous Dichotomized Gaussian model with as a function of the median mean, , and correlation coefficient, ρ. As with the homogeneous model, bias is largest for small means and strong correlations. (b) The same plot, but for a homogeneous Dichotomized Gaussian. The difference in bias between the heterogeneous and homogeneous models is largest for small means and small correlations, but overall, the two plots are very similar.
Figure 4.
Effect of heterogeneity on the normalized bias in a small population. (a) Normalized bias relative to the within model class case, , of a heterogeneous Dichotomized Gaussian model with as a function of the median mean, , and correlation coefficient, ρ. As with the homogeneous model, bias is largest for small means and strong correlations. (b) The same plot, but for a homogeneous Dichotomized Gaussian. The difference in bias between the heterogeneous and homogeneous models is largest for small means and small correlations, but overall, the two plots are very similar.
2.3. Maximum and Minimum Bias When the True Model is Not in the Model Class
Above, we saw that the factor
was about one for the Dichotomized Gaussian model. That is encouraging, but not definitive. In particular, we are left with the question: Is it possible for the bias to be much smaller or much larger than what we saw in
Figure 3 and
Figure 4? To answer that, we write the true distribution,
, in the form:
and ask how the bias depends on
; that is, how the bias changes as
moves out of model class. To ensure that
represents only a move out of model class, and not a shift in the constraints (the
), we choose it, so that
satisfies the same constraints as
:
We cannot say anything definitive about the normalized bias in general, but what we can do is compute its maximum and minimum as a function of the distance between
and
. For “distance”, we use the Kullback–Leibler divergence, denoted
, which is given by:
where
is the entropy of
. The second equality follows from the definition of
, Equation (
4) and the fact that
, which comes from Equation (
21).
Rather than maximizing the normalized bias at fixed
, we take a complementary approach and minimize
at fixed bias. Since
is independent of
, minimizing
is equivalent to maximizing
(see Equation (
22)). Thus, again, we have a maximum entropy problem. Now, though, we have an additional constraint on the normalized bias. To determine exactly what that constraint is, we use Equation (
11) and (12) to write:
where:
and, importantly,
depends on
, but not on
[see Equation (
12a)]. Fixed normalized bias,
b, thus corresponds to fixed
. This additional constraint introduces an additional Lagrange multiplier besides the
, which we denote
β. Taking into account the additional constraint, and using the same analysis that led to Equation (
4), we find that the distribution with the smallest difference in entropy,
, at fixed
b, which we denote
, is given by:
where
is the partition function, the
are chosen to satisfy Equation (
7), but with
replaced by
, and
β is chosen to satisfy Equation (
23), but with, again,
replaced by
. Note that we have slightly abused notation; whereas, in the previous sections,
and
Z depended only on
μ, now they depend on both
μ and
β. However, the previous variables are closely related to the new ones: when
, the constraint associated with
b disappears, and we recover
; that is,
. Consequently,
, and
.
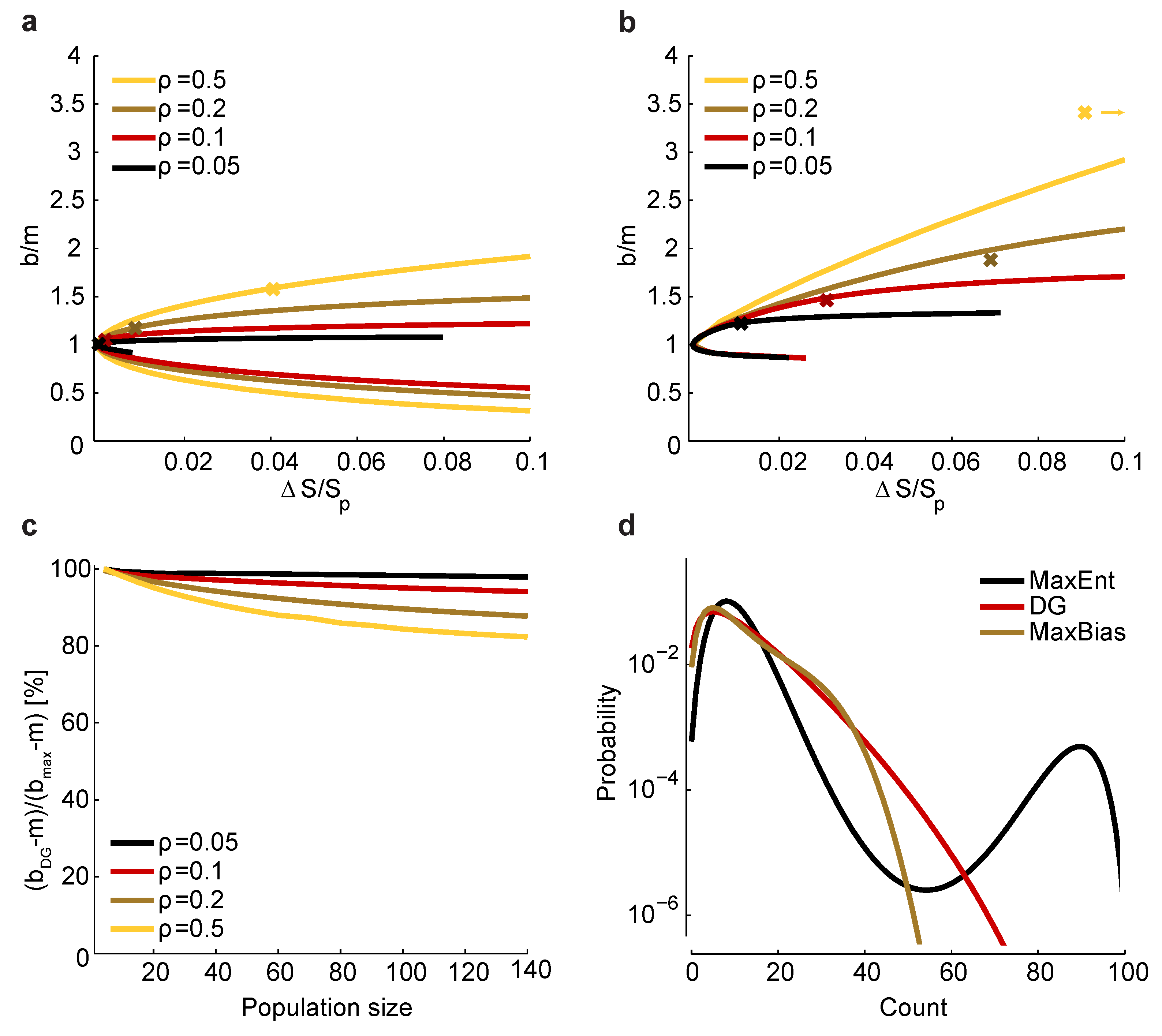
Figure 5.
Relationship between and bias. (a) Maximum and minimum normalized bias relative to m versus (recall that is the entropy of ) in a homogeneous population with size , , and correlation coefficients indicated by color. The crosses correspond to a set of homogeneous Dichotomized Gaussian models with . (b) Same as a, but for . For , the bias of the Dichotomized Gaussian model is off the right-hand side of the plot, at ; for comparison, the maximum bias at and is 3.8. (c) Comparison between the normalized bias of the Dichotomized Gaussian model and the maximum normalized bias. As in panels a and b, we used . Because the ratio of the biases is trivially near one when b is near m, we plot , where and are the normalized bias of the Dichotomized Gaussian and the maximum bias, respectively; this is the ratio of the “additional” bias. (d) Distribution of total spike count () for the Dichotomized Gaussian, maximum entropy (MaxEnt) and maximally biased (MaxBias) models with , and . The similarity between the distributions of the Dichotomized Gaussian and maximally biased models is consistent with the similarity in normalized biases shown in panel c.
Figure 5.
Relationship between and bias. (a) Maximum and minimum normalized bias relative to m versus (recall that is the entropy of ) in a homogeneous population with size , , and correlation coefficients indicated by color. The crosses correspond to a set of homogeneous Dichotomized Gaussian models with . (b) Same as a, but for . For , the bias of the Dichotomized Gaussian model is off the right-hand side of the plot, at ; for comparison, the maximum bias at and is 3.8. (c) Comparison between the normalized bias of the Dichotomized Gaussian model and the maximum normalized bias. As in panels a and b, we used . Because the ratio of the biases is trivially near one when b is near m, we plot , where and are the normalized bias of the Dichotomized Gaussian and the maximum bias, respectively; this is the ratio of the “additional” bias. (d) Distribution of total spike count () for the Dichotomized Gaussian, maximum entropy (MaxEnt) and maximally biased (MaxBias) models with , and . The similarity between the distributions of the Dichotomized Gaussian and maximally biased models is consistent with the similarity in normalized biases shown in panel c.
![]()
The procedure for determining the relationship between
and the normalized bias,
b, involves two steps: first, for a particular bias,
b, choose the
and
β in Equation (
25) to satisfy the constraints given in Equation (
2) and the condition
; second, compute
from Equation (
22). Repeating those steps for a large number of biases will produce curves like the ones shown in
Figure 5a,b.
Since the true entropy,
, is maximized (subject to constraints) when
, it follows that
is zero when
and nonzero, otherwise. In fact, in the Methods, we show that
has a single global minimum at
; we also show that the normalized bias,
b, is a monotonic increasing function of
β. Consequently, there are two normalized biases that have the same
, one larger than
m and the other smaller. This is shown in
Figure 5a,b, where we plot
versus for the homogeneous Dichotomized Gaussian model. It turns out that this model has near maximum normalized bias, as shown in
Figure 5c. Consistent with that, the Dichotomized Gaussian model has about the same distribution of spike counts as the maximally biased models, but a very different distribution from the maximum entropy model (
Figure 5d).
The fact that the Dichotomized Gaussian model has near maximum normalized bias is important, because it tells us that the bias we found in
Figure 3 and
Figure 4 is about as large as one could expect. In those figures, we found that
had a relatively small range—from about one to four. Although too large to be used for bias correction, this range is small enough that one could use it to get a conservative estimate of the minimum number of trials [Equation (
17)] or minimum run time [Equation (
18)] it would take to reduce bias to an acceptable level.
2.4. Using a Plug-in Estimator to Reduce Bias
Given that we have an expression for the asymptotic normalized bias,
b [Equation (
11)], it is, in principle, possible to correct for it (assuming that
K is large enough for the asymptotic bias to be valid). If the effect of model-misspecification is negligible (which is typically the case if the neurons are sufficiently weakly correlated), then the normalized bias is just
m, the number of constraints, and bias correction is easy: simply subtract
from our estimate of the entropy. If, however, there is substantial model-misspecification, we need to estimate covariance matrices under the true and maximum entropy models. Of course, these estimates are subject to their own bias, but we can ignore that and use a “plug-in” estimator; an estimator computed from the covariance matrices in Equation (
11),
and
, which, in turn, are computed from data. Specifically, we estimate
and
using:
Such an estimator is plotted in
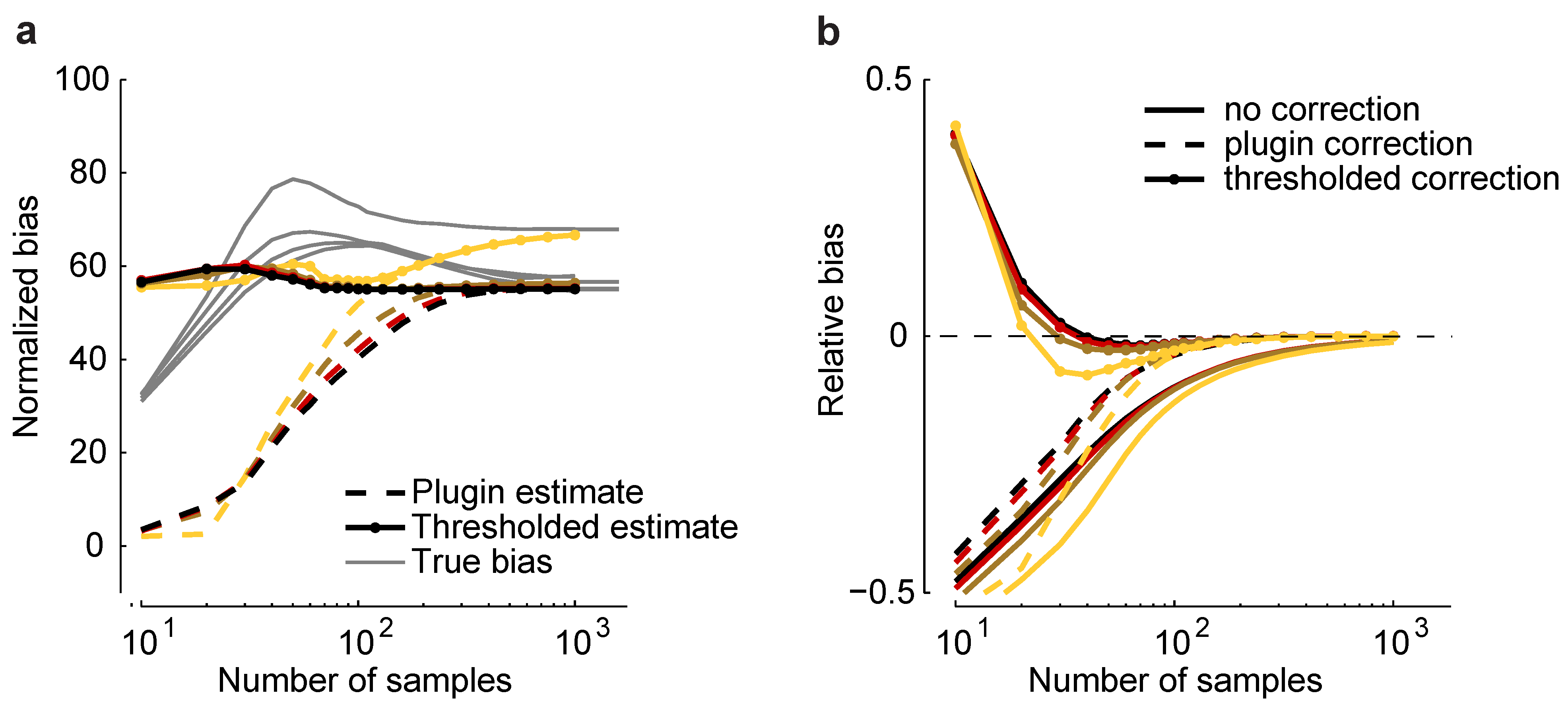
Figure 6a for a homogeneous Dichotomized Gaussian with
and
. Although the plug-in estimator converges to the correct value for sample sizes above about 500, it underestimates
b by a large amount, even when
. To reduce this effect, we considered a thresholded estimator, denoted
, which is given by:
where
comes from Equation (
11). This estimator is motivated by the fact that we found, empirically, that the additional bias due to model misspecification was almost always greater than
m.
Figure 6.
Bias correction. (
a) Plug-in,
, and thresholded,
, estimators
versus sample size for a homogeneous Dichotomized Gaussian model with
and
. Correlations are color coded as in
Figure 5. Gray lines indicate the true normalized bias as a function of sample size, computed numerically as for
Figure 2. (
b) Relative error without bias correction,
, with the plug-in correction,
, and with the thresholded estimator,
.
Figure 6.
Bias correction. (
a) Plug-in,
, and thresholded,
, estimators
versus sample size for a homogeneous Dichotomized Gaussian model with
and
. Correlations are color coded as in
Figure 5. Gray lines indicate the true normalized bias as a function of sample size, computed numerically as for
Figure 2. (
b) Relative error without bias correction,
, with the plug-in correction,
, and with the thresholded estimator,
.
As shown in
Figure 6a,
is closer to the true normalized bias than
. In
Figure 6b, we plot the relative error of the uncorrected estimate of the maximum entropy,
, and the same quantity, but with two corrections: the plug-in correction,
, and the thresholded correction,
. Using the plug-in estimator, accurate estimates of the maximum entropy can be achieved with about 100 samples; using the threshold estimators, as few as 30 samples are needed. This suggests that our formalism can be used to perform bias correction for maximum entropy models, even in the presence of model-misspecification.