1. Introduction
Relative entropies, like Kullback-Leibler [
1,
2] or the Tsallis relative entropy [
3,
4,
5,
6], provide a means to discuss (directed) distances between different probability distributions. These measures are usually not symmetric, so they do not provide a metric on the distributions. Nonetheless, relative entropies allow the comparison of distributions occurring in a variety of different contexts [
7,
8,
9,
10,
11,
12,
13,
14]. Here, we will use these measures to analyze certain features of distributions describing the dynamics of physical systems.
In particular, our motivation is to study anomalous diffusion processes and the corresponding distribution functions of the dispersing particles. Anomalous diffusion processes differ from classical diffusion in that the dispersion of particles proceeds faster (superdiffusion) or slower (subdiffusion) than for the regular case. These anomalous diffusion processes do, for instance, occur in biological tissues [
15,
16] or in chemical systems [
17]. They can also be observed in porous media [
18,
19] or turbulent diffusion [
20,
21]. Such processes are also important in other areas, like target search [
22,
23,
24] or the design of optical materials in which light waves perform a Lévy flight [
25].
The theoretical treatment of such processes has lead to the study of evolution equations using non-linear dependencies on the probability density functions (PDF) [
26,
27] or employing fractional derivatives [
28,
29,
30,
31,
32,
33,
34,
35,
36].
Here, we focus on the space-fractional diffusion equation
not as a modeling tool for an interesting class of superdiffusion processes with remarkable features [
37,
38,
39], but as a bridge to link the usually unrelated classical diffusion equation (iconic irreversibility) to the wave equation (iconic reversibility). For that the parameter
α must vary between one (the (half) wave case) and the (the diffusion case). This bridging regime has been analyzed under different perspectives [
40,
41,
42] and has shown unexpected features. The space-fractional diffusion equation represents a family of processes in the bridge regime that can be ordered by the parameter
α, which will be called the bridge ordering.
In [
43], the relative entropies (e.g., Kullback-Leibler), in contrast to the regular entropies, order the PDF’s from Equation (
1), because of a monotonic relationship in
α, placing the wave and diffusion limits “farthest” from each other, even if not in a metrical sense. This establishes relative entropies as a natural measure for the bridging regime. However, [
43] considered circumstances at one particular time. This paper extends the previous work by asking whether this ordering is preserved over all time. This question is addressed by examining direct computation and deducing asymptotic expressions valid for long times, based on a saddle point approach.
After briefly setting up the formalism of the known probability densities that solve Equation (
1) and the asymptotic methods that are employed, the time dependence of the Kullback-Leibler entropy is discussed, and the cross entropy is introduced. Direct computational analysis of the relative entropy is shown that confirms that the desired monotonic behavior of the relative entropy is persistent at a number of widely ranging times. Then, the asymptotic form is computed for large time, using the saddle point method applied to the cross entropy. This yields an asymptotic form valid for the entire relative entropy. By examining the asymptotic form of the derivative with respect to
α, the sign is shown to be preserved, confirming monotonicity for large times. Comparisons are made between direct computational analysis and the resulting asymptotic forms, showing good agreement.
Completing the picture, a similar treatment is performed for Tsallis relative entropies (), resulting in similar outcomes. Monotonicity is preserved at finite values and asymptotically. An interesting feature is noted, namely that for the Tsallis relative entropies, the values are bounded, which is not so for the Kullback-Leibler case.
2. Stable Distributions
The solution of the space-fractional diffusion equation can be expressed in terms of a stable distribution,
[
37,
43,
44], given as
where
and the parameters are chosen appropriately with
An important feature of stable distributions is their so-called fat tails, i.e., the probability density in the tails falls off with a power law rather than exponentially, thus leading to the non-existence of higher moments. Fat tails are responsible for the non-existence of the Kullback-Leibler entropy for certain combinations of stable distributions.
The following presents properties of stable distributions needed for the calculations below. The stable distribution rescales as
For the parameters discussed here, the support of the stable distributions is the full real line. Apart from special cases, there are no general closed representations of the stable distribution in terms of elementary functions. However, the density at a certain point
x can be expressed as an integral
where
. For
, the integral can be evaluated in closed form, leading to
where
and
is the Gamma function. Similarly, there are expressions for the derivatives of the density based on Equation (
8). The
-th and the
-th derivatives with respect to
x are
We will need the first two derivatives at
, which can again be expressed in closed form as
For
and angles in
The abbreviations
will be used in the following. Ψ is the digamma function. Thus, Equations (
12) and (
13) become
For
, Equation (
1) reduces to the classical diffusion equation. That is reflected in its solution
, which is the well-known Gaussian. That solution can also be expressed in terms of a stable distribution for
as
where
is the normal distribution with mean
and variance
[
44].
In the limit , the scale parameter, , of the stable distribution goes to zero and the mode (i.e., maximum of the distribution) . This constitutes a time-moving δ-distribution centered at , representing the one-sided solution of the wave equation with an initial δ-distribution.
Writing Equation (
1) in the
limit
When the operator
is applied to Equation (
20), the standard wave equation is recovered, ensuring that solutions of Equation (
20) are also solutions of the full wave equation. Equation (
20) thus reflects one of two operator factors for the wave equation, and it is known, accordingly, as the half wave equation. The classical advection equation also reduces to the half wave equation in the one-dimensional solenoidal case.
5. Kullback-Leibler Entropy Time Dependence by Direct Computational Analysis
In [
43], on which this paper builds, it was shown that the Kullback and Tsallis relative entropy might serve to order solutions of the space-fractional diffusion Equation (
1) at a particular time. Here, we show that this property extends over time. One complication dealt with previously is that
does not exist, due to the fat tails of
. Thus, the focus was on
, which does exist.
The Kullback is given by
where
is known as the cross entropy.
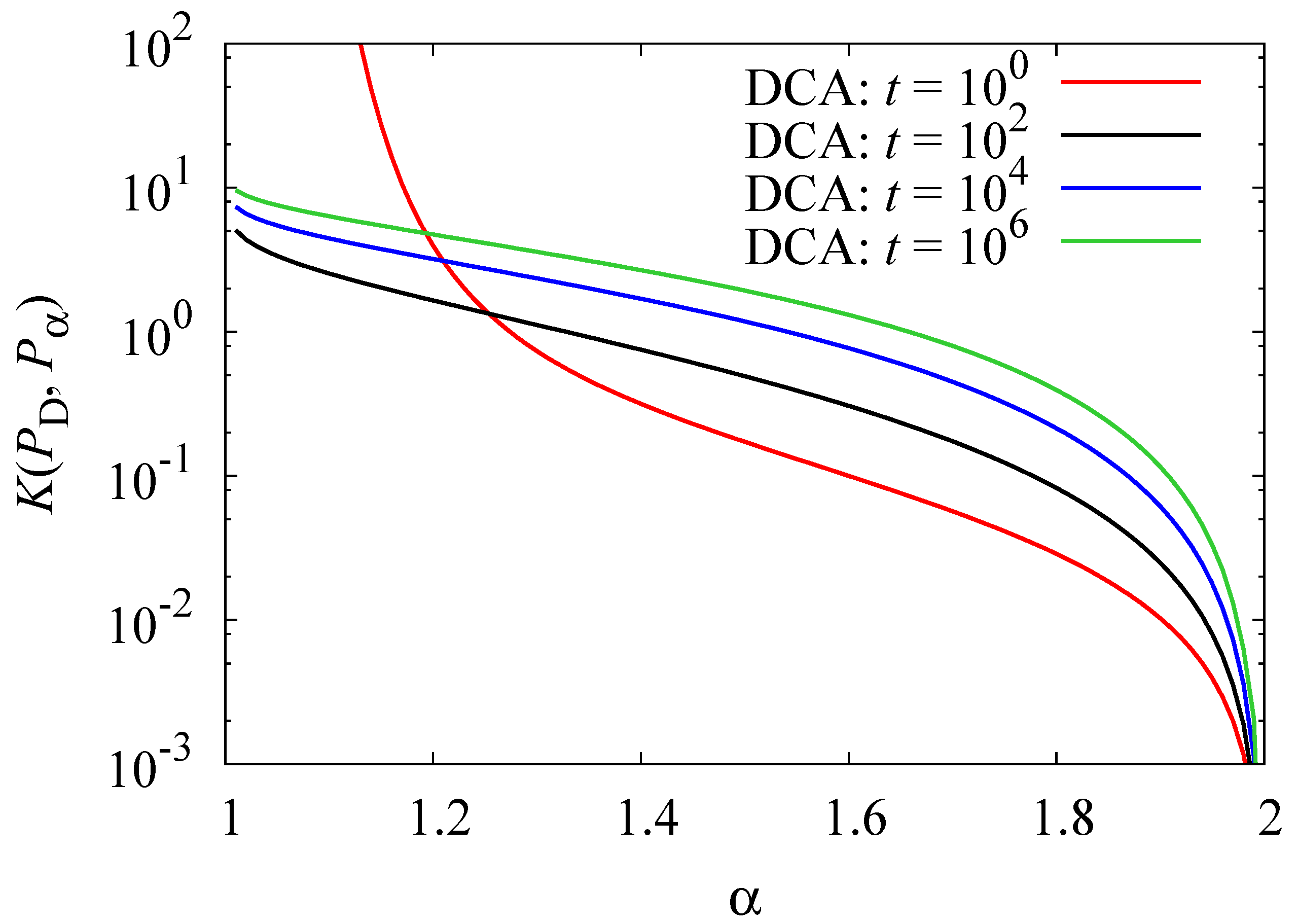
Figure 1.
The Kullback-Leibler entropy, , is plotted over α for different times t. One can see that for all times, exhibits a monotonic decreasing behavior, thus confirming the bridge ordering property of .
Figure 1.
The Kullback-Leibler entropy, , is plotted over α for different times t. One can see that for all times, exhibits a monotonic decreasing behavior, thus confirming the bridge ordering property of .
The previous analysis of
at
showed that the Kullback was compatible with the bridge ordering. However, here in
Figure 1, we show
as a function of
α for a wide range of different times (
). The label DCA stands for “Direct Computational Analysis.” For the analysis,
is obtained by a numerical scheme that makes use of the fact that the tail behavior of the stable distributions is known analytically. Here and in all other figures, we set
. As for
,
approaches a
δ-distribution. Thus, our direct computations were restricted in practice to
.
In
Figure 1, for all cases,
falls off quickly for
α close to one, but more slowly near
. The monotonic relation between
and
α confirms that the bridge ordering at
is maintained across a wide interval of times. Note here that the graph of
for
crosses those at later times. Thus, while the graph shows curves monotonic in
α for fixed
t, they are not generally monotonic in
t for fixed
α.
6. Kullback-Leibler Entropy for Long Times
Though ordering is preserved for a wide range of times, that does not mean that the ordering is preserved for long times. Thus the long-time behavior of is deduced in the following.
The cross entropy from Equation (
27) becomes
where we have made use of Equation (
7) and the normalization property of the Gaussian. Using the substitution
we then get
Note that due to
,
is an
α-dependent quantity, where the exponent of
t is always negative for
. It follows that for
, the inverse ratio
will diverge. For large
t, it will be large too, and thus, we can now make use of the saddle point method.
Using the results of
Section 4 together with the following definitions
and noting that the maximum of
is at
, we obtain an asymptotic expansion for the cross entropy
Combining Equations (
27) and (
35), we conclude
where
is a constant in time, and for
, the factor multiplying
is positive.
decays with time, and thus, for large times,
will diverge.
The constant
and the time-dependent
can be evaluated further making use of the properties of the stable distribution. We note that
simplifies considerably as
for
. Using
we find
and
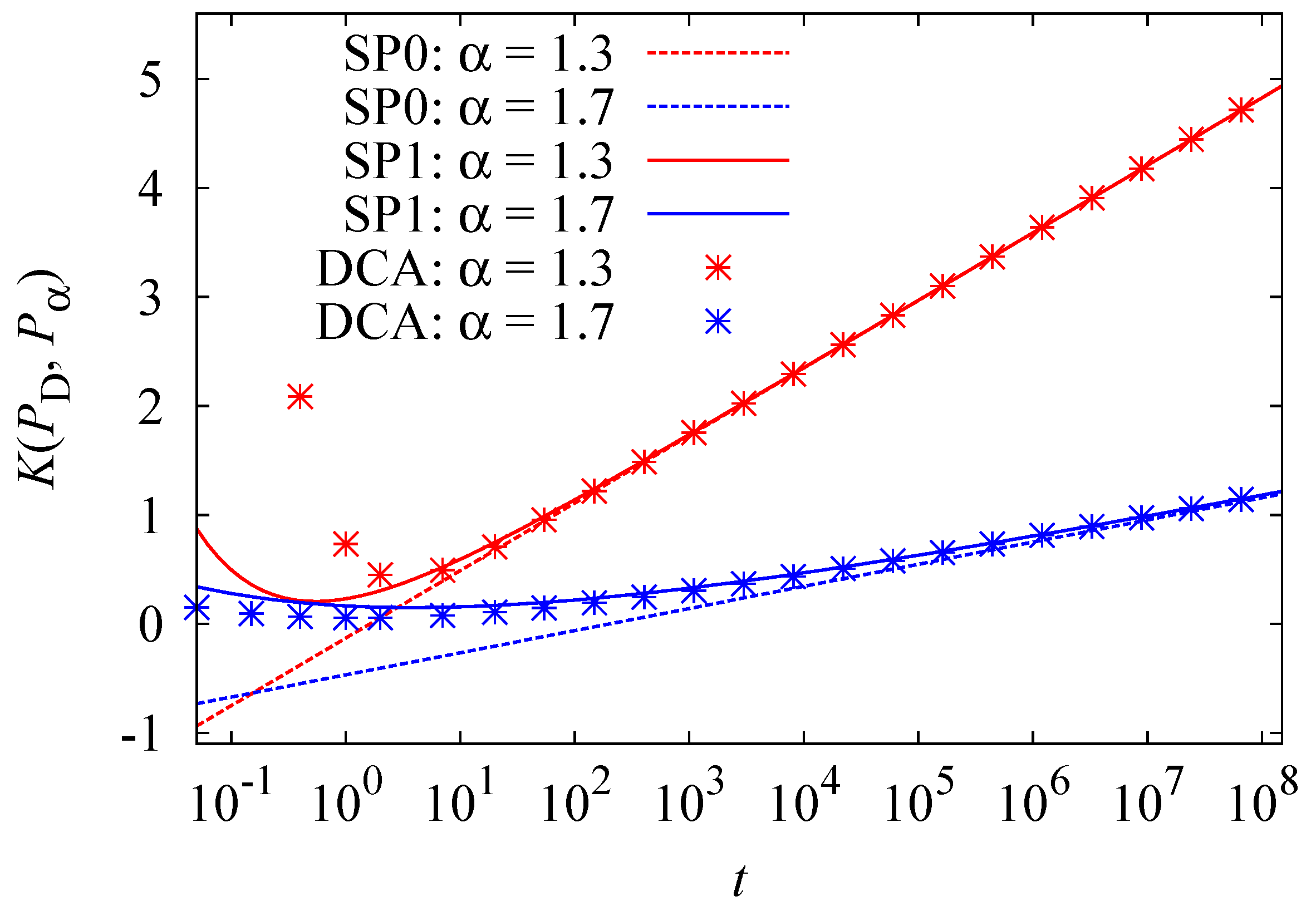
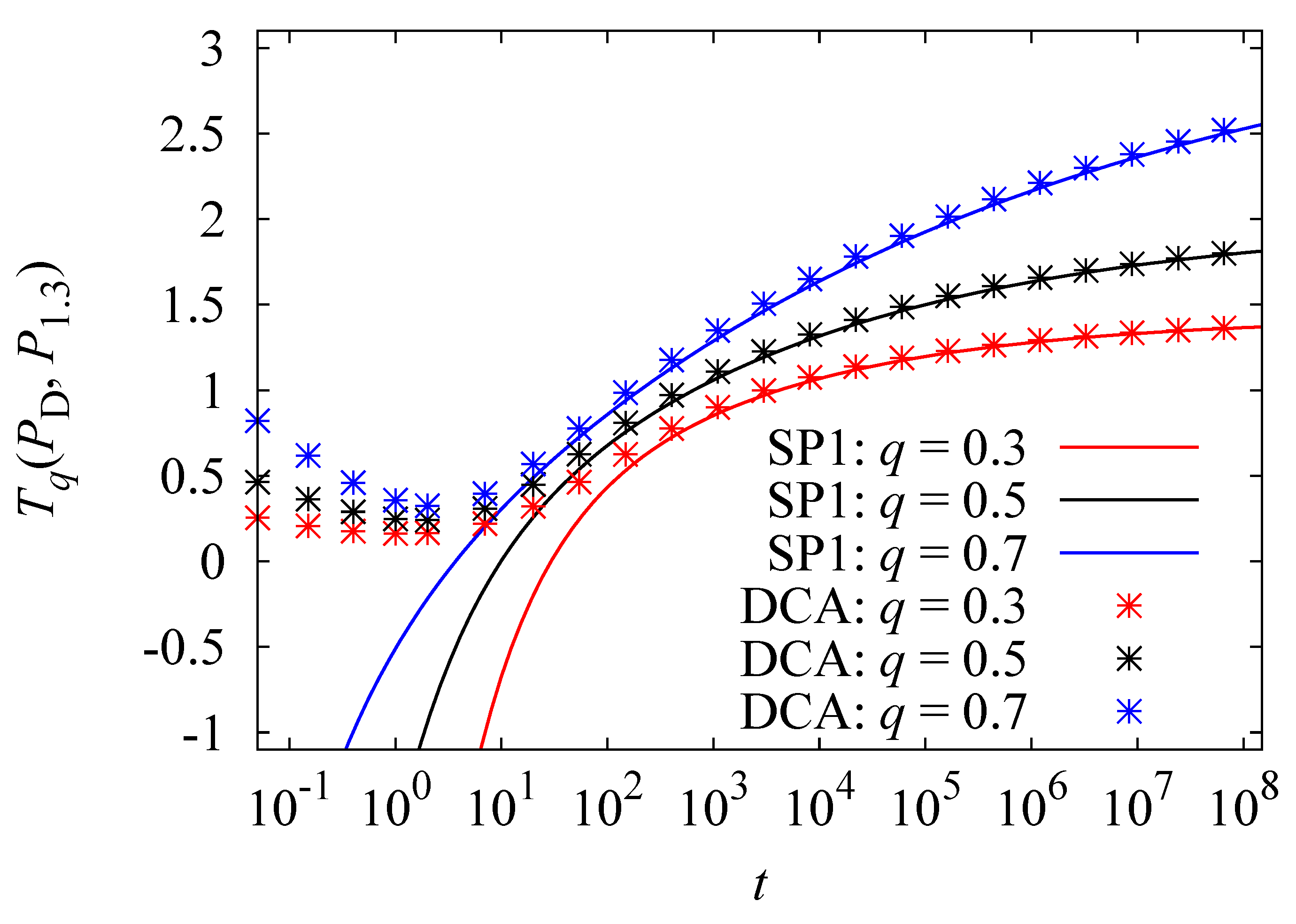
Figure 2.
A comparison between the direct numerical calculation of the Kullback-Leibler entropy, (DCA), the saddle point method of the zeroth order (SP0) and the saddle point method of first order (SP1) is shown over logarithmic time t for two different values of α. One observes that the approximations approach the DCA data points for large times and fit the data quite well already for .
Figure 2.
A comparison between the direct numerical calculation of the Kullback-Leibler entropy, (DCA), the saddle point method of the zeroth order (SP0) and the saddle point method of first order (SP1) is shown over logarithmic time t for two different values of α. One observes that the approximations approach the DCA data points for large times and fit the data quite well already for .
In
Figure 2, a comparison between the numerical evaluation of
(DCA) and its approximations SP0 and SP1 based on the saddle point method is displayed. Here, SP0 is the approximation excluding terms of
, while SP1 excludes terms of
. One sees easily how the approximations approach the data points obtained by direct numerical calculation for large times. Especially for
, that the quality increases by using the higher order SP1 is obvious. In that case, SP1 covers nearly all times
. This is not so for
, where one sees a sizable deviation for
. However, all of the asymptotic forms produce good agreement with DCA values for
.
While the long time behavior is thus understood, the short time behavior shows a surprising feature. For short times, shows an initial decay until a minimum is reached. Only then does the Kullback start to grow and approach its long time behavior.
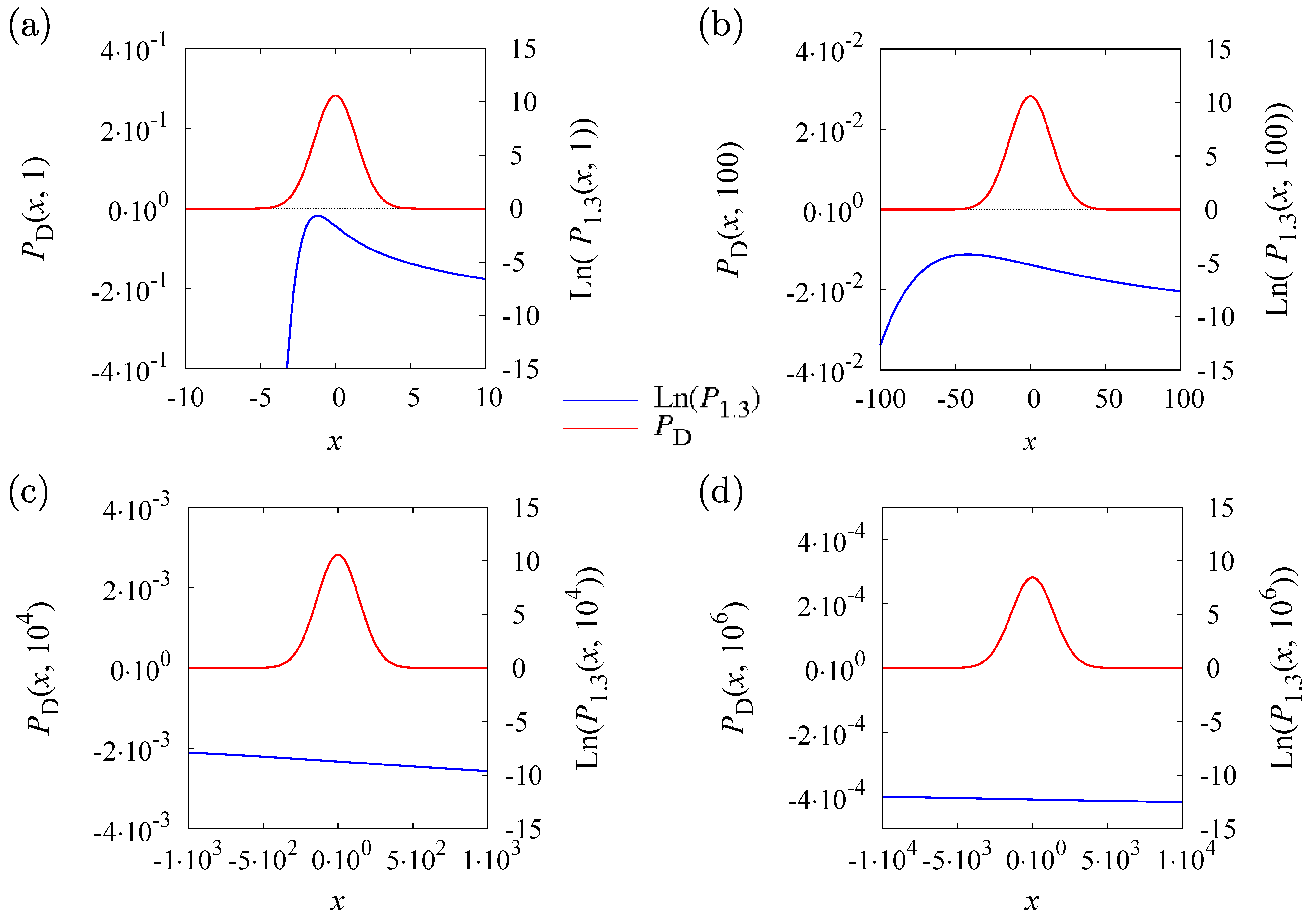
In order to understand this effect, the sequence of graphs in
Figure 3 shows how the distribution
and
change in time. The plots are for
, when
. We see that the Gaussian
acts like a window that suppresses
, where
is exponentially small. For small times,
varies considerably in that window, and thus, it cannot be approximated reasonably by its value and its first two derivatives at the peak position of the Gaussian. This changes as the time increases.
becomes flatter and flatter, and for
, the approximation works very well.
Figure 3.
Four plots of and over x are given for (a), (b), (c) and (d) for . It can be seen that within the width of , the distribution becomes flatter with increasing time. Thus, can be approximated well by its function value and its first two derivatives.
Figure 3.
Four plots of and over x are given for (a), (b), (c) and (d) for . It can be seen that within the width of , the distribution becomes flatter with increasing time. Thus, can be approximated well by its function value and its first two derivatives.
Based on the asymptotic time behavior of
, we can now see how
changes with
α at a given time
t. We do so by taking the derivative of the asymptotic form of
with respect to
α
For the different terms in Equation (
41), we get
where
Inserting Equations (
42)–(
45) into Equation (
41) and collecting all time-dependent terms leads to
For large times, this simplifies to:
From Equation (
40), we see that
in the long-time limit. Thus, the Kullback is a monotonic decreasing function of
α in the large time limit, ensuring that it retains its ordering property in
α for large times. This result anchors the ordering property at infinity, already established in the preceding sections for finite times.
7. The Tsallis Relative Entropy Time Dependence by Direct Computational Analysis
The Tsallis relative entropy provides another means to establish an ordering between
and
. Contrary to the Kullback case, both
and
exist. In [
43], we showed that these two Tsallis relative entropies are defined for
. Based on this insight, one finds an interesting relation between the two
and
from which we obtain
It thus suffices to analyze the time behavior of one of the two. Here, we choose
with
was determined for four different times
by direct computation analysis. As in the Kullback case, the data were obtained by a numerical integration procedure, which for the Tsallis case also requires a precise treatment of the known fat tail behavior of the stable distributions.
Figure 4 depicts the results for
. One can see that
decays monotonically with
α, thus showing that it provides an ordering compatible with the bridge ordering for the times presented. This figure also seems to indicate that
increases monotonically with time for fixed
α. That, however, is not true. For short times, the DCA data in
Figure 6 shows that
does not increase monotonically in time. Instead, it decreases first and then, around
, starts to increase.
Figure 4.
For the case of , the Tsallis relative entropy, , is given over α for different times . One can observe that with increasing time, the monotonic decreasing behavior is preserved, and thus, the bridge ordering property of is confirmed.
Figure 4.
For the case of , the Tsallis relative entropy, , is given over α for different times . One can observe that with increasing time, the monotonic decreasing behavior is preserved, and thus, the bridge ordering property of is confirmed.
8. Tsallis Relative Entropy for Long Times
As in the Kullback case, we want to analyze the time dependence further to show that the bridge ordering is preserved at least for large enough times. The method used is again a saddle point approximation. Using the substitution
, we get
The ratio
is the same as in the Kullback section and thus, diverges for large times. Based on Equation (
25), we make the following definitions
Again, the maximum of
is at
, and by utilizing Equation (
25), we find up to
Here,
depends on
q and takes the form
Collecting terms, we find the asymptotic time behavior for the Tsallis relative entropy for large
t
Unlike the Kullback case, this asymptotic form has a finite limit for
. The limit is
, because
, and both exponents are positive, due to
. This can be seen in the unapproximated form, too
where
. We see in the
limit that the Gaussian becomes a
δ-function. The
δ-function picks the value of
at
, making the integral finite. The prefactor is decaying towards zero, and thus, the approach of
to the limiting value
is confirmed.
Figure 5.
A comparison of direct numerical calculation of the Tsallis relative entropy, (DCA), and the saddle point method of the first order (SP1) is given over logarithmic time t for different values of q.
Figure 5.
A comparison of direct numerical calculation of the Tsallis relative entropy, (DCA), and the saddle point method of the first order (SP1) is given over logarithmic time t for different values of q.
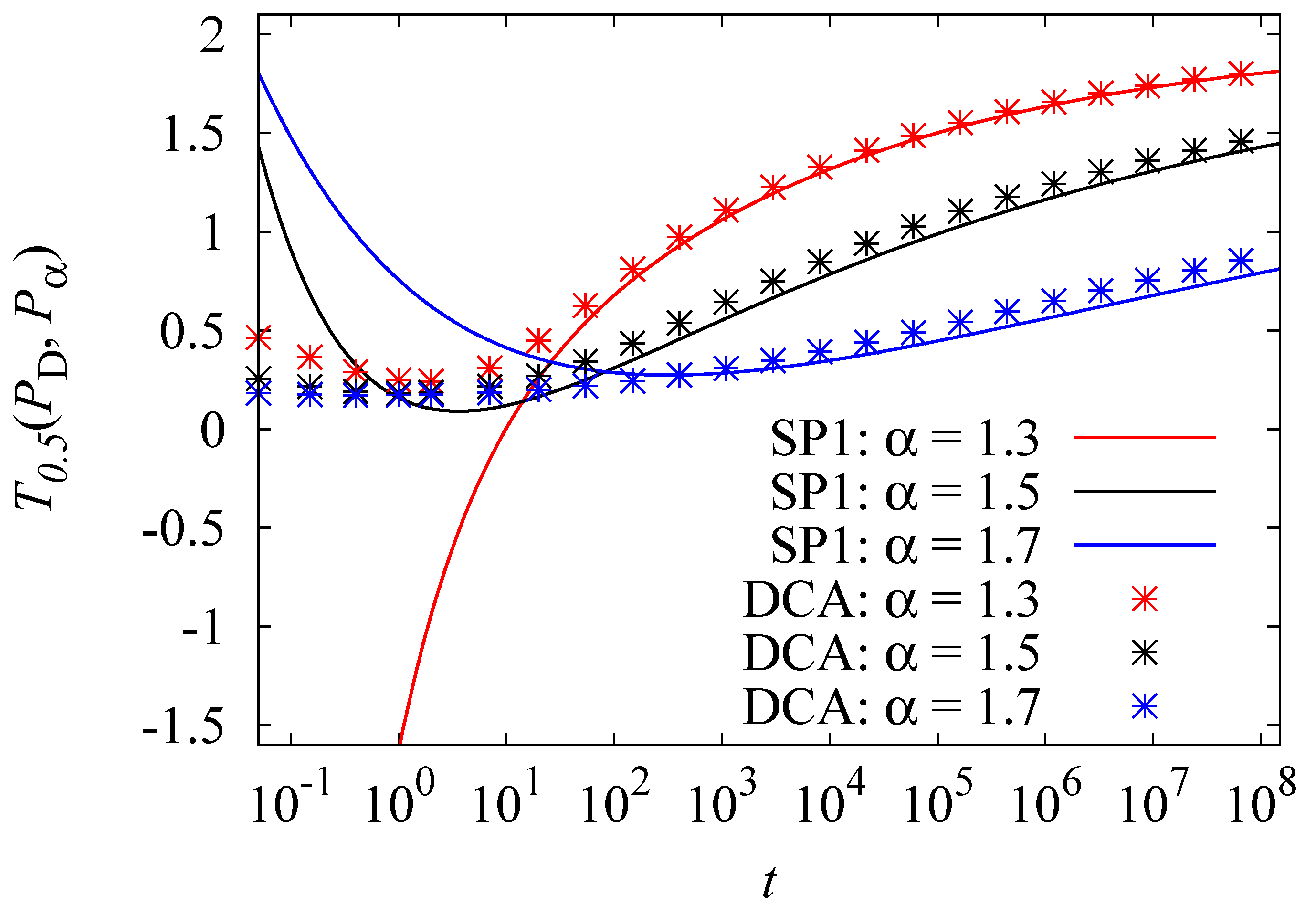
Figure 6.
A comparison of direct numerical calculation of the Tsallis relative entropy, (DCA), and the saddle point method of the first order (SP1) is given over logarithmic time t for different values of α. Note that is not monotonic in time for larger values of α, but has a clear minimum around .
Figure 6.
A comparison of direct numerical calculation of the Tsallis relative entropy, (DCA), and the saddle point method of the first order (SP1) is given over logarithmic time t for different values of α. Note that is not monotonic in time for larger values of α, but has a clear minimum around .
The quality of the saddle point approximation is shown in
Figure 5 and
Figure 6. We compare the saddle point approximations SP1 of
with the numerically obtained values (DCA) as a function of time. The approach of the approximation to the numerical data depends highly on the choice of parameters
α and
q. For small values of
α and
q, the approximation fits the numerical data relatively fast, as shown in
Figure 5. On the other hand,
Figure 6 shows that the approximations work less well for larger
α.
It can also be seen in
Figure 5 and
Figure 6 that for times
, the asymptotic approach exhibits different curve shapes depending on the choice of
α and
q. This can be understood by looking on Equation (
58) after applying Equations (
9)–(
13) and Equation (
57), which leads to
with
The first factor of Equation (
60) is always positive, but because of
,
can change sign. This depends on the parameters
α and
q, and is insignificant for large
t.
Finally, the asymptotic form shows that
decreases monotonically with
α for large times because
where the
are constants in
t. On
and
, the inequalities
hold. Thus,
will be dominated by the
term in Equation (
62) for long times, as it decays most slowly. Since
then
for large enough times. Thus, like the Kullback case, the Tsallis relative entropy remains monotonically decreasing in the infinite time limit, confirming its ordering property at both finite times and infinity. However, while signs remain fixed, the Tsallis case differs from the Kullback case in that the
α-slope goes to zero in the long-time limit, while that slope diverges in the Kullback case. Moreover, the Kullback also diverges with
t, while
approaches a constant,
, for large
t.
9. Summary
This paper is a sequel to [
43], in which relative entropies were introduced to address the physical issue of irreversibility in the mathematical context of a one-parameter bridging regime between the diffusion and wave equations. This peculiar regime represents a definitive family of processes between diffusion and waves representing a direct formal mathematical test of our understanding of the differences between the reversible and irreversible. Not only does this regime exhibit paradoxical entropy production behavior (
i.e., entropy production rates increase toward the wave limit), but entropy has a maximum in the interval, which has the consequence that one cannot determine which system is relatively “closer or further” from the pure diffusion limit by such means. However, the preceding paper showed that relative entropies could do what neither entropy nor entropy production rates could do: provide an intuitively sensible ordering, where diffusion stands at a maximum among all other bridge processes which become well ordered, due to a monotonically decreasing relationship with the parameter
α.
The goal of this paper was to extend the treatment in [
43] by addressing the issue of time. This paper asked whether the well-defined ordering produced by relative entropies was just a feature of a single time, or if the monotonic structure persist over all time. The relevant formalism was briefly set up in two parts. First, the necessary features of stable distributions, which are solutions to the dynamics in Equation (
1), were presented. Then, the appropriate asymptotic representations of integrals in terms of the saddle point method were put into place. From this foundation, the two cases of the Kullback-Leibler and Tsallis relative entropies were explored for long times. Direct numerical computation showed that both types of relative entropies preserved the
α-ordering for a wide range of time-scales. Then, asymptotic methods were compared to these direct computations, confirming that they agree well with each other for long times. It was then shown that the ordering did persist in the long-time limit in both cases. However, the Tsallis and Kullback-Leibler cases differ in that the former reached a finite limit,
, and its
α-derivative vanished in the limit of long times, while the latter diverged in both relative entropy and its
α-derivative.
Time evolution of relative entropies under a single process, particularly the Kullback-Leibler entropy, is well known to be connected to H-theorems. Thus, it would not be surprising if the time evolution of probability densities might make one think, at least initially, in terms of H-theorem questions; so, it is worth noting parenthetically that this is not an H-theorem scenario. The time evolution in this context is between pairs of processes belonging to the bridging families and not to a single process. There is no reason to expect that pairs of densities would relax to each other when subject to different processes. However, it brings back the issue of different internal quicknesses [
40,
41,
42], although now articulated from the standpoint of relative entropies. Moreover, this paper focuses on the ordering property, which ultimately is about the differences between the densities. Nonetheless, we could consider nearby processes with infinitesimal differences in families and ask whether an H-theorem-like result might hold then, but that is a topic for future work.