Efficient Approximation of the Conditional Relative Entropy with Applications to Discriminative Learning of Bayesian Network Classifiers
Abstract
:1. Introduction
2. Background
2.1. Bayesian Network Classifiers
2.2. Generative versus Discriminative Learning of Bayesian Network Classifiers
2.3. A First Approximation to the Conditional Log-Likelihood
3. Extending the Approximation to CLL
3.1. Generalizing aCLL to Multi-Classification Tasks
3.1.1. Symmetric Uniform Assumption for Multi-Classification Tasks
3.1.2. Symmetric Dirichlet Assumption for Multi-Classification Tasks
3.1.3. Estimating Parameters β and γ
| Algorithm 1 General Monte-Carlo method to estimate β and γ |
Input: number of samples, m
|
| Algorithm 2 Monte-Carlo method to estimate β and γ for Dir |
Input: number of samples, m, and hyperparameters, a and b.
|
3.2. Parameter Maximization for aCLL
4. Information-Theoretic Interpretation of the Conditional Log-Likelihood
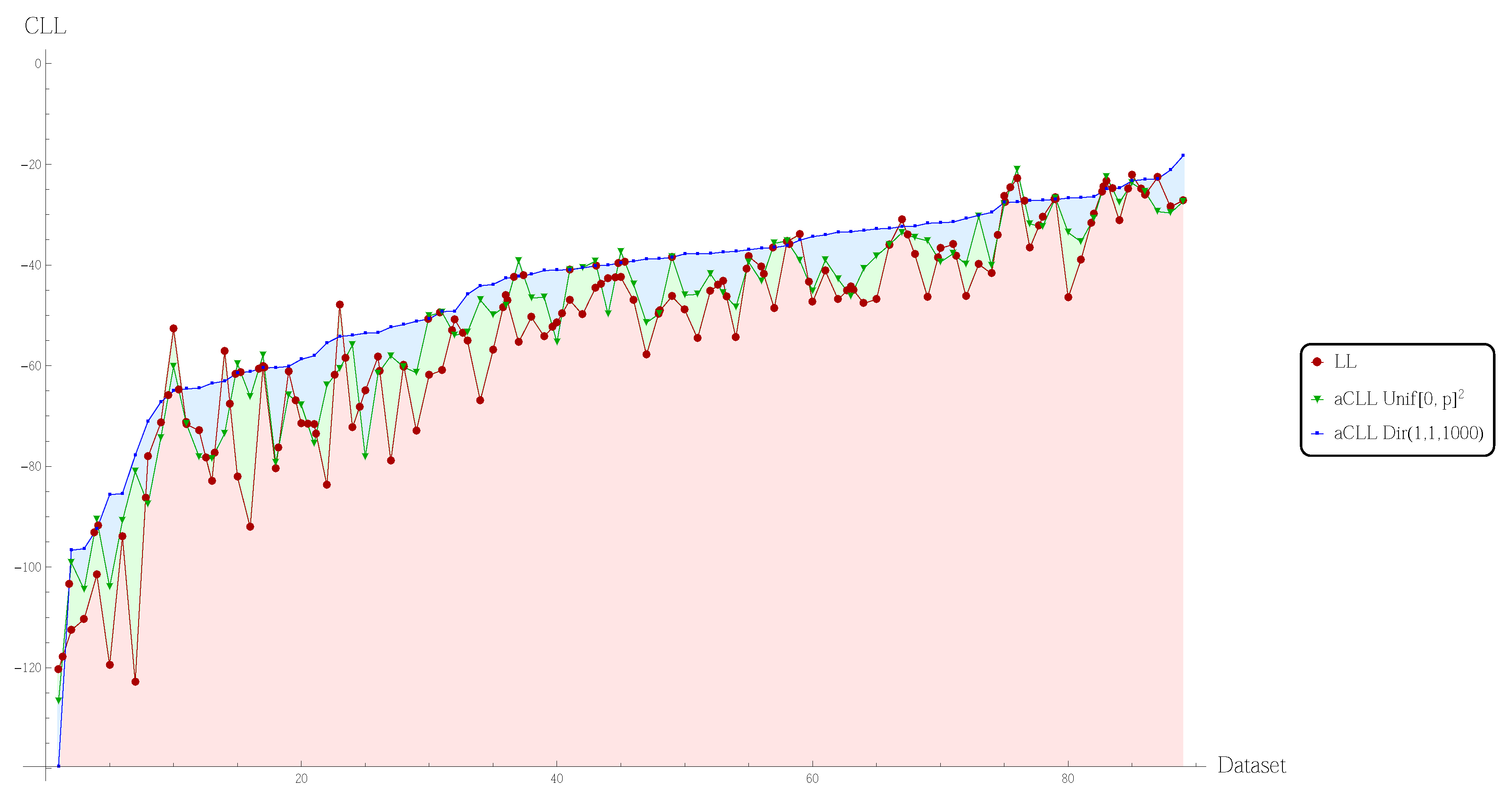
5. Experimental Results
| Searching | TAN | TAN |
|---|---|---|
| Score | LL | aCLL |
| Assumption | Unif | |
| TAN | 7.08 | 6.84 |
| aCLL | 7.21 × 10−13 | 3.96 × 10−12 |
| Dir(1, 1, 1000) | ⇐ | ⇐ |
| TAN | 3.52 | |
| aCLL | 2.15 × 10−4 | |
| Unif | ⇐ |
| Searching | TAN | TAN |
|---|---|---|
| Score | LL | aCLL |
| Assumption | Unif | |
| TAN | 6.91 | 4.07 |
| aCLL | 2.42 × 10−12 | 2.35 × 10−5 |
| Dir(1, 1, 1, 1000) | ⇐ | ⇑ |
| TAN | 7.44 | |
| aCLL | 5.03 × 10−14 | |
| Unif | ⇐ |
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Francisco, CA, USA, 1988. [Google Scholar]
- Friedman, N.; Geiger, D.; Goldszmidt, M. Bayesian network classifiers. Mach. Learn. 1997, 29, 131–163. [Google Scholar] [CrossRef]
- Grossman, D.; Domingos, P. Learning Bayesian Network Classifiers by Maximizing Conditional Likelihood. In Proceedings of the Twenty-first International Conference on Machine Learning, Banff, Alberta, Canada, 4–8 July 2004; ACM: New York, NY, USA, 2004; pp. 46–53. [Google Scholar]
- Su, J.; Zhang, H. Full Bayesian Network Classifiers. In Proceedings of the Twenty-third International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; Cohen, W.W., Moore, A., Eds.; ACM: New York, NY, USA, 2006; pp. 897–904. [Google Scholar]
- Domingos, P.; Pazzani, M.J. On the optimality of the simple Bayesian classifier under zero-one loss. Mach. Learn. 1997, 29, 103–130. [Google Scholar] [CrossRef]
- Greiner, R.; Zhou, W. Structural Extension to Logistic Regression: Discriminative Parameter Learning of Belief Net Classifiers. In Proceedings of the Eighteenth National Conference on Artificial Intelligence and Fourteenth Conference on Innovative Applications of Artificial Intelligence, Edmonton, Alberta, Canada, 28 July–2 August 2002; Dechter, R., Sutton, R.S., Eds.; AAAI/MIT: Cambridge, MA, USA, 2002; pp. 167–173. [Google Scholar]
- Su, J.; Zhang, H.; Ling, C.X.; Matwin, S. Discriminative Parameter Learning for Bayesian Networks. In Proceedings of the Twenty-fifth International Conference on Machine Learning, Helsinki, Finland, 5–9 June 2008; Cohen, W.W., McCallum, A., Roweis, S.T., Eds.; ACM: New York, NY, USA, 2008; pp. 1016–1023. [Google Scholar]
- Carvalho, A.M.; Roos, T.; Oliveira, A.L.; Myllymäki, P. Discriminative learning of Bayesian networks via factorized conditional log-likelihood. J. Mach. Learn. Res. 2011, 12, 2181–2210. [Google Scholar]
- Barash, Y.; Elidan, G.; Friedman, N.; Kaplan, T. Modeling Dependencies in Protein-DNA Binding Sites. In Proceedings of the Seventh Annual International Conference on Computational Biology, Berlin, Germany, 10–13 April 2003; ACM: New York, NY, USA, 2003; pp. 28–37. [Google Scholar]
- Carvalho, A.M.; Oliveira, A.L.; Sagot, M.F. Efficient Learning of Bayesian Network Classifiers: An Extension to the TAN Classifier. In Proceedings of the 20th Australian Joint Conference on Artificial Intelligence, Gold Coast, Australia, 2–6 December 2007; Orgun, M.A., Thornton, J., Eds.; Springer: Berlin, Germany, 2007; Volume 4830, pp. 16–25. [Google Scholar]
- Carvalho, A.M. Scoring Functions for Learning Bayesian Networks; Technical Report; INESC-ID: Lisbon, Portugal, 2009. [Google Scholar]
- Yang, S.; Chang, K.C. Comparison of score metrics for Bayesian network learning. IEEE Trans. Syst. Man. Cybern. A 2002, 32, 419–428. [Google Scholar] [CrossRef]
- Heckerman, D.; Geiger, D.; Chickering, D.M. Learning Bayesian networks: The combination of knowledge and statistical data. Mach. Learn. 1995, 20, 197–243. [Google Scholar] [CrossRef]
- De Campos, L.M. A scoring function for learning Bayesian networks based on mutual information and conditional independence tests. J. Mach. Learn. Res. 2006, 7, 2149–2187. [Google Scholar]
- Silander, T.; Roos, T.; Kontkanen, P.; Myllymäki, P. Bayesian Network Structure Learning using Factorized NML Universal Models. In Proceedings of the Fourth European Workshop on Probabilistic Graphical Models, Hirshals, Denmark, 17–19 September 2008; pp. 257–264.
- Chickering, D.M.; Heckerman, D.; Meek, C. Large-sample learning of Bayesian networks is NP-hard. J. Mach. Learn. Res. 2004, 5, 1287–1330. [Google Scholar]
- Dagum, P.; Luby, M. Approximating probabilistic inference in Bayesian belief networks is NP-hard. Artif. Intell. 1993, 60, 141–153. [Google Scholar] [CrossRef]
- Edmonds, J. Optimum branchings. J. Res. Nat. Bur. Stand. 1967, 71, 233–240. [Google Scholar] [CrossRef]
- Chow, C.K.; Liu, C.N. Approximating discrete probability distributions with dependence trees. IEEE Trans. Inform. Theory 1968, 14, 462–467. [Google Scholar] [CrossRef]
- Chickering, D.M. Learning Bayesian Networks Is NP-Complete. In Learning from Data: AI and Statistics V; Springer: Berlin, Germnay, 1996; pp. 121–130. [Google Scholar]
- Bilmes, J. Dynamic Bayesian Multinets. In Proceedings of the 16th Conference in Uncertainty in Artificial Intelligence, Stanford University, Stanford, CA, USA, 30 June–3 July 2000; Boutilier, C., Goldszmidt, M., Eds.; Morgan Kaufmann: Burlington, MA, USA, 2000; pp. 38–45. [Google Scholar]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 2007. [Google Scholar]
- Heckerman, D. A Tutorial on Learning Bayesian Networks; Technical Report MSR-TR-95-06, Microsoft Research; Microsoft: Redmond, WA, USA, 1995. [Google Scholar]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Verma, T.; Pearl, J. Equivalence and Synthesis of Causal Models. In Proceedings of the Sixth Annual Conference on Uncertainty in Artificial Intelligence, Cambridge, MA, USA, 27–29 July 1990; Bonissone, P.P., Henrion, M., Kanal, L.N., Lemmer, J.F., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 255–270. [Google Scholar]
- Chickering, D.M. Learning equivalence classes of Bayesian-network structures. J. Mach. Learn. Res. 2002, 2, 445–498. [Google Scholar]
- Lewis, P.M. Approximating probability distributions to reduce storage requirements. Inform. Control 1959, 2, 214–225. [Google Scholar] [CrossRef]
- Cover, T.; Thomas, J. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Pemmaraju, S.V.; Skiena, S.S. Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wingender, E.; Chen, X.; Fricke, E.; Geffers, R.; Hehl, R.; Liebich, I.; Krull, M.; Matys, V.; Michael, H.; Ohnhuser, R.; et al. The TRANSFAC system on gene expression regulation. Nucleic Acids Res. 2001, 29, 281–283. [Google Scholar] [CrossRef] [PubMed]
- Demsar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Carvalho, A.M.; Adão, P.; Mateus, P. Efficient Approximation of the Conditional Relative Entropy with Applications to Discriminative Learning of Bayesian Network Classifiers. Entropy 2013, 15, 2716-2735. https://doi.org/10.3390/e15072716
Carvalho AM, Adão P, Mateus P. Efficient Approximation of the Conditional Relative Entropy with Applications to Discriminative Learning of Bayesian Network Classifiers. Entropy. 2013; 15(7):2716-2735. https://doi.org/10.3390/e15072716
Chicago/Turabian StyleCarvalho, Alexandra M., Pedro Adão, and Paulo Mateus. 2013. "Efficient Approximation of the Conditional Relative Entropy with Applications to Discriminative Learning of Bayesian Network Classifiers" Entropy 15, no. 7: 2716-2735. https://doi.org/10.3390/e15072716
APA StyleCarvalho, A. M., Adão, P., & Mateus, P. (2013). Efficient Approximation of the Conditional Relative Entropy with Applications to Discriminative Learning of Bayesian Network Classifiers. Entropy, 15(7), 2716-2735. https://doi.org/10.3390/e15072716





