Improved Minimum Entropy Filtering for Continuous Nonlinear Non-Gaussian Systems Using a Generalized Density Evolution Equation
Abstract
:1. Introduction
2. Problem Formulation
2.1. System Model
2.2. Filter Dynamics
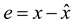 satisfies:
satisfies:
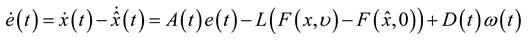
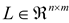 is the gain matrix to be determined and can be denoted as
is the gain matrix to be determined and can be denoted as 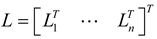 , Li is the ith row vector of L. Let
, Li is the ith row vector of L. Let 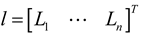 and thus
and thus 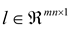 is a stretched column vector.
is a stretched column vector.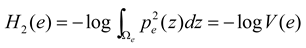
3. Formulation for the Joint PDF of Error
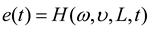
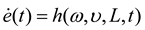
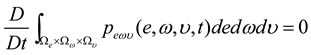
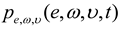 is the joint PDF of (e(t), ω, υ). It follows from Equation (7) that:
is the joint PDF of (e(t), ω, υ). It follows from Equation (7) that:
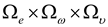 , it yields:
, it yields:
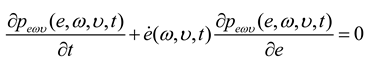
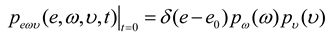
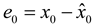 is deterministic initial value of (e(t)). Then, we have:
is deterministic initial value of (e(t)). Then, we have:
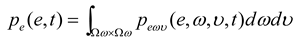
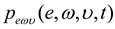 is the solution of (8), which can be obtained according to the method presented in [22].
is the solution of (8), which can be obtained according to the method presented in [22].4. Improved MEE Filtering
4.1. Performance Index
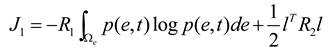
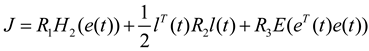
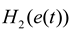 is the quadratic Renyi’s entropy given in Equation (4).
is the quadratic Renyi’s entropy given in Equation (4). 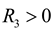 is the weight corresponding to the mean squared error. The third term on the right side of the equation is utilized to make the estimation errors approach to zero. Since Renyi’s entropy is a monotonic increasing function of the negative information potential, minimization of Renyi’s entropy is equivalent to minimizing the inverse of the quadratic information potential
is the weight corresponding to the mean squared error. The third term on the right side of the equation is utilized to make the estimation errors approach to zero. Since Renyi’s entropy is a monotonic increasing function of the negative information potential, minimization of Renyi’s entropy is equivalent to minimizing the inverse of the quadratic information potential 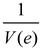 , so the performance index can be rewritten as follows:
, so the performance index can be rewritten as follows:
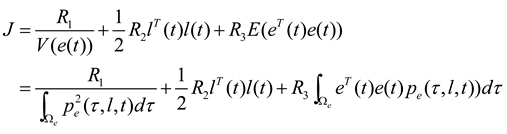
4.2. Optimal Filter Gain Matrix
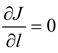 ). The elements of optimal filter gain can be solved and summarized in Theorem 1.
). The elements of optimal filter gain can be solved and summarized in Theorem 1.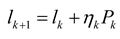
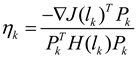 ,
, 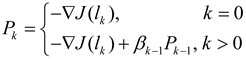 and the Hessian matrix
and the Hessian matrix 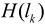 is:
is:
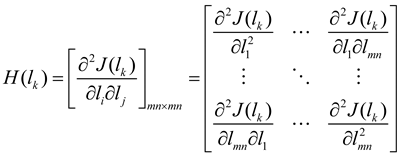
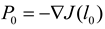 .
.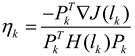 by solving
by solving 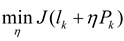 , and update the gain
, and update the gain 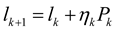 .
.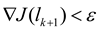 , stop, and
, stop, and 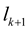 is the optimal solution; Otherwise, if
is the optimal solution; Otherwise, if 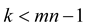 , turn to step (5), and if
, turn to step (5), and if 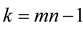 , reset
, reset 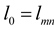 , and turn to step (2).
, and turn to step (2).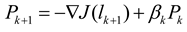 , set
, set 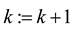 , and turn to step 3), where
, and turn to step 3), where 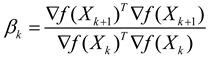 .
.4.3. Exponentially Bounded in the Mean Square
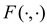 assumed to satisfy
assumed to satisfy 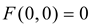 [23] and:
[23] and:
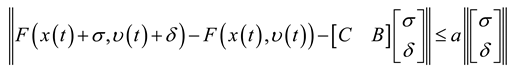
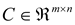 ,
, 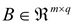 are known constant matrices,
are known constant matrices, 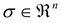 ,
, 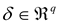 are vectors, a is known positive constant.
are vectors, a is known positive constant.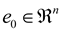 , the dynamics of the estimation error (i.e., the solution of the system (3)) is exponentially ultimately bounded in the mean square if there exist constants α > 0, β > 0 and γ > 0 such that:
, the dynamics of the estimation error (i.e., the solution of the system (3)) is exponentially ultimately bounded in the mean square if there exist constants α > 0, β > 0 and γ > 0 such that:
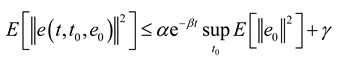
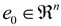 , system (3) is exponentially ultimately bounded in the mean square.
, system (3) is exponentially ultimately bounded in the mean square.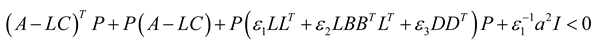
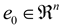 arbitrarily and denote
arbitrarily and denote 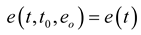 . The Lyapunov function candidate can be chosen as:
. The Lyapunov function candidate can be chosen as:
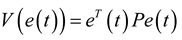
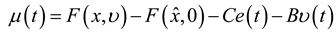
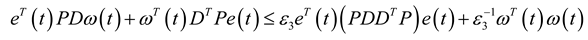
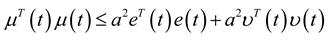
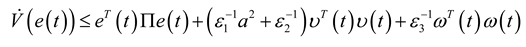
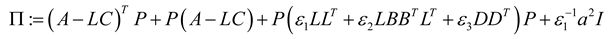
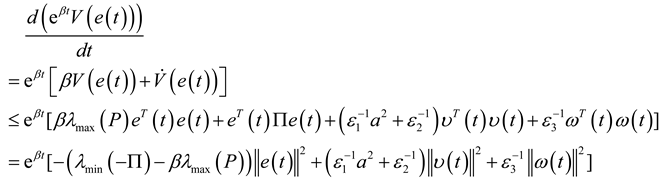
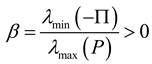 . Integrating both sides from 0 to T > 0 and taking the expectation lead to:
. Integrating both sides from 0 to T > 0 and taking the expectation lead to:
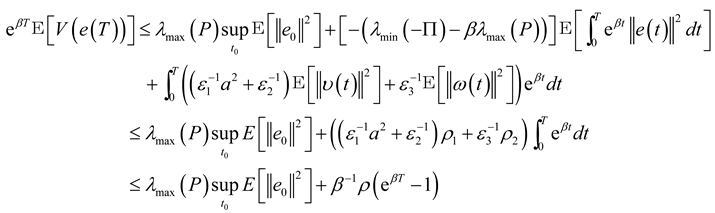
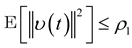 ,
, 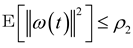 (according to Assumption 2, ω(t) and υ(t) are bounded random vectors) ,
(according to Assumption 2, ω(t) and υ(t) are bounded random vectors) , 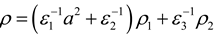 and:
and:
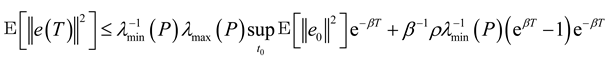
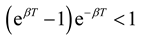 and let
and let 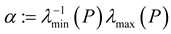 ,
, 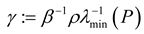 . Since T > 0 is arbitrary, the definition of exponential ultimate boundedness in (18) is then satisfied, and this completes the proof of Theorem 2.
. Since T > 0 is arbitrary, the definition of exponential ultimate boundedness in (18) is then satisfied, and this completes the proof of Theorem 2. 5. Simulation Results

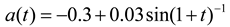 and
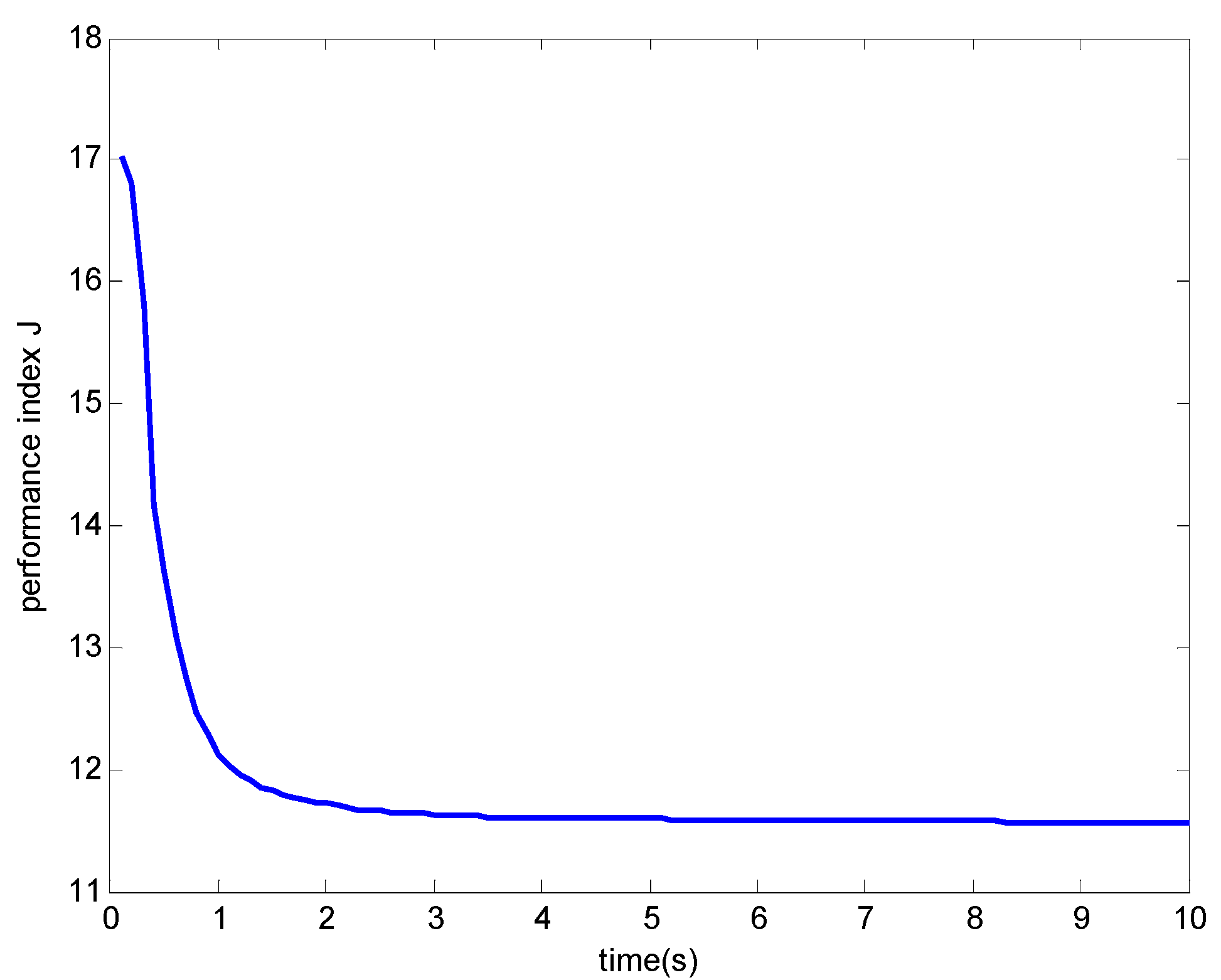
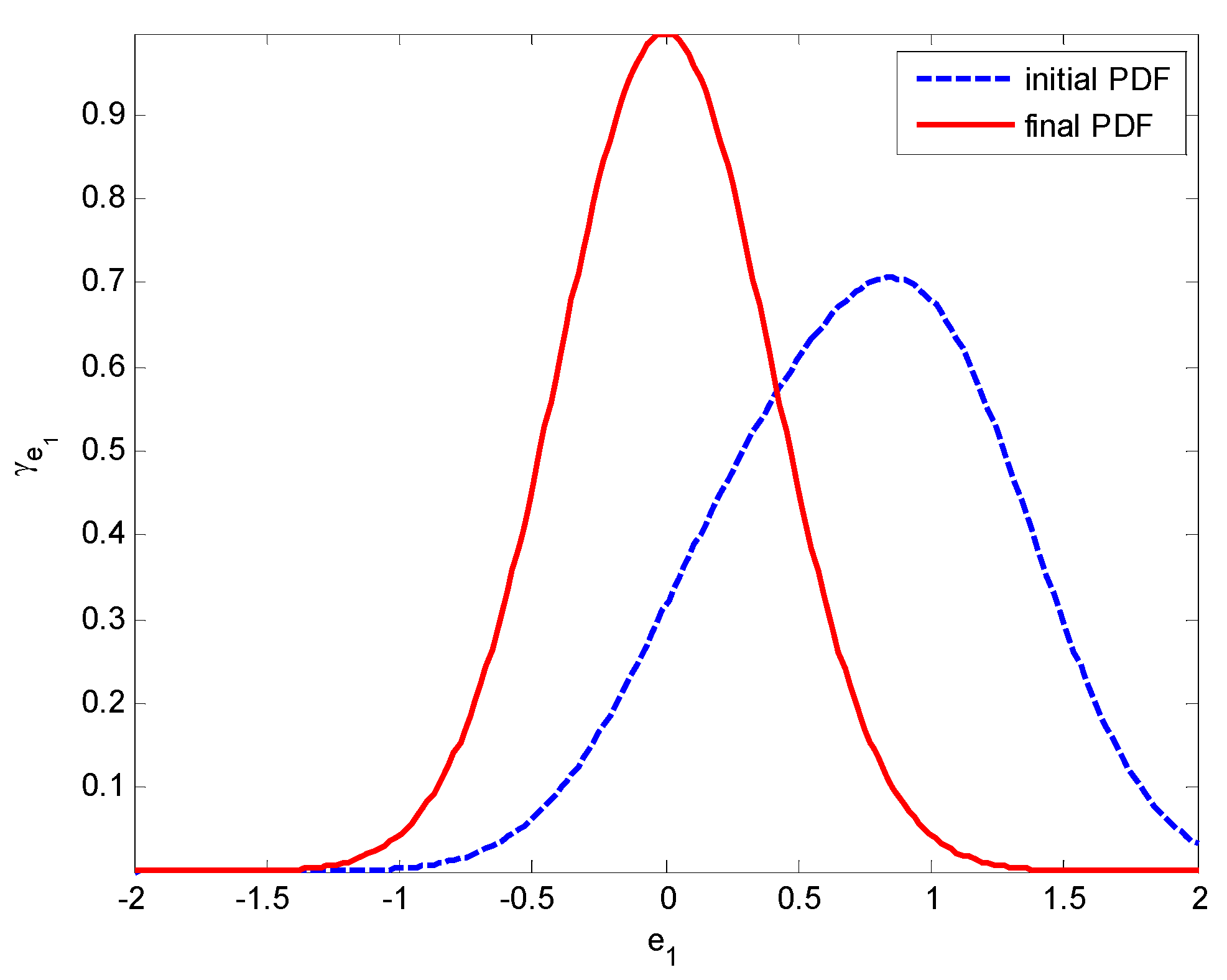
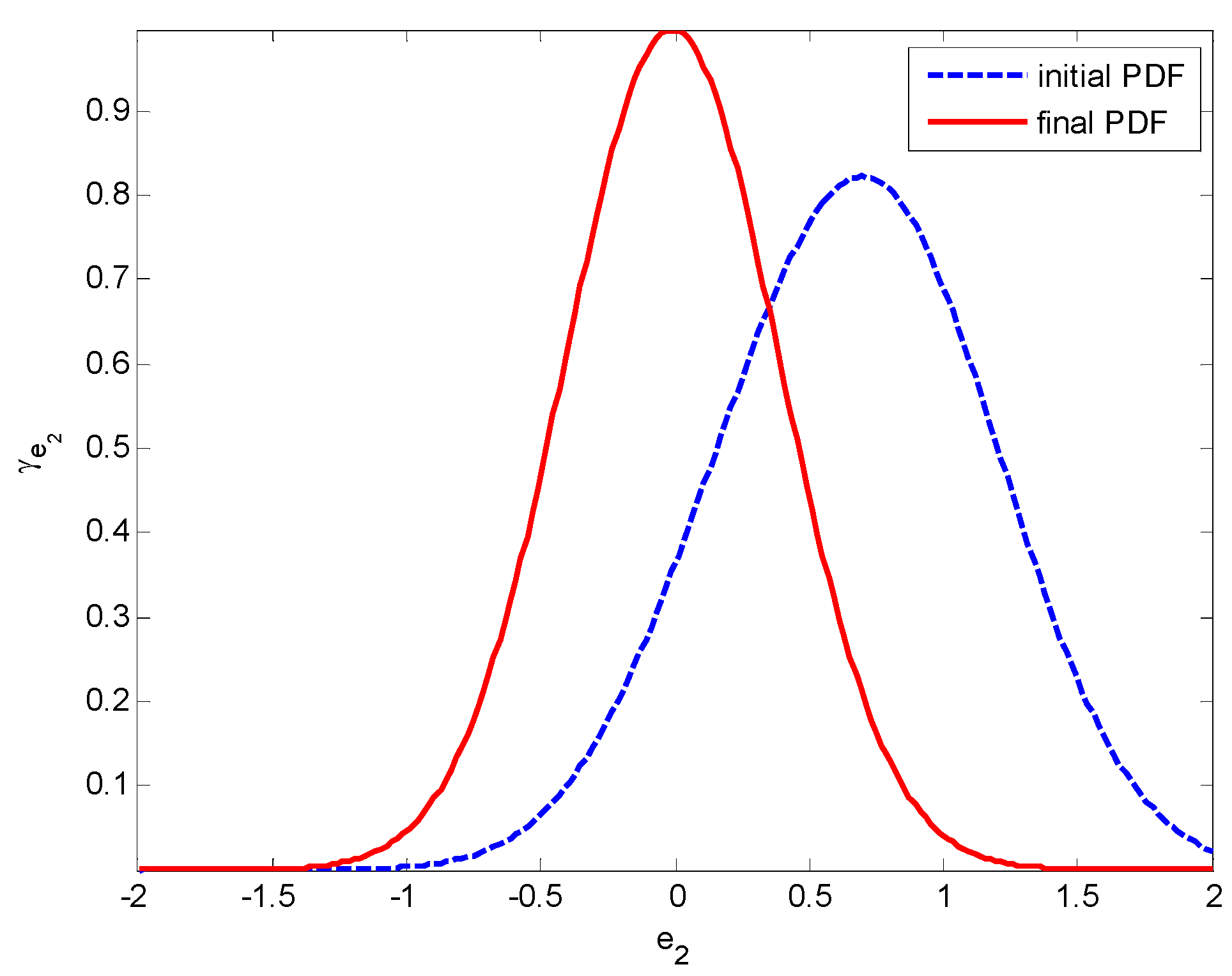
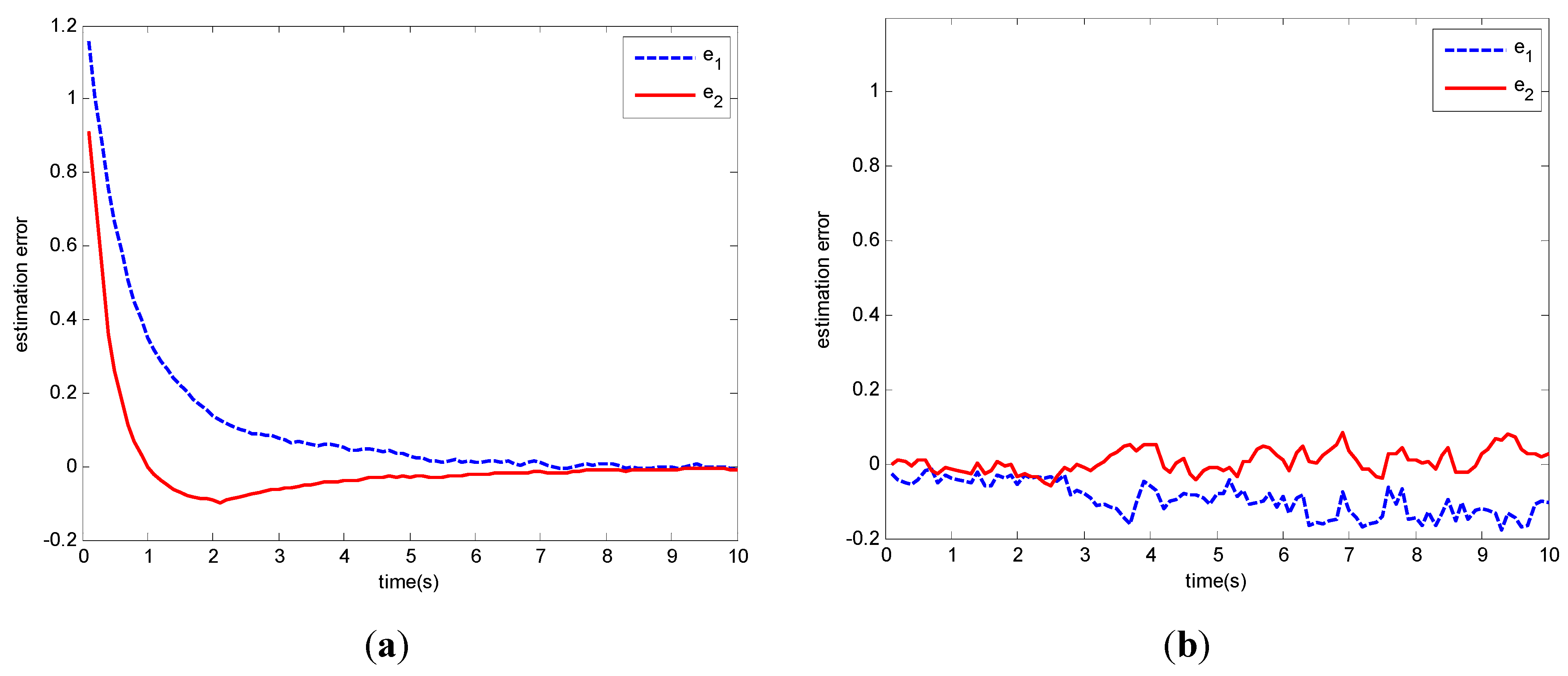
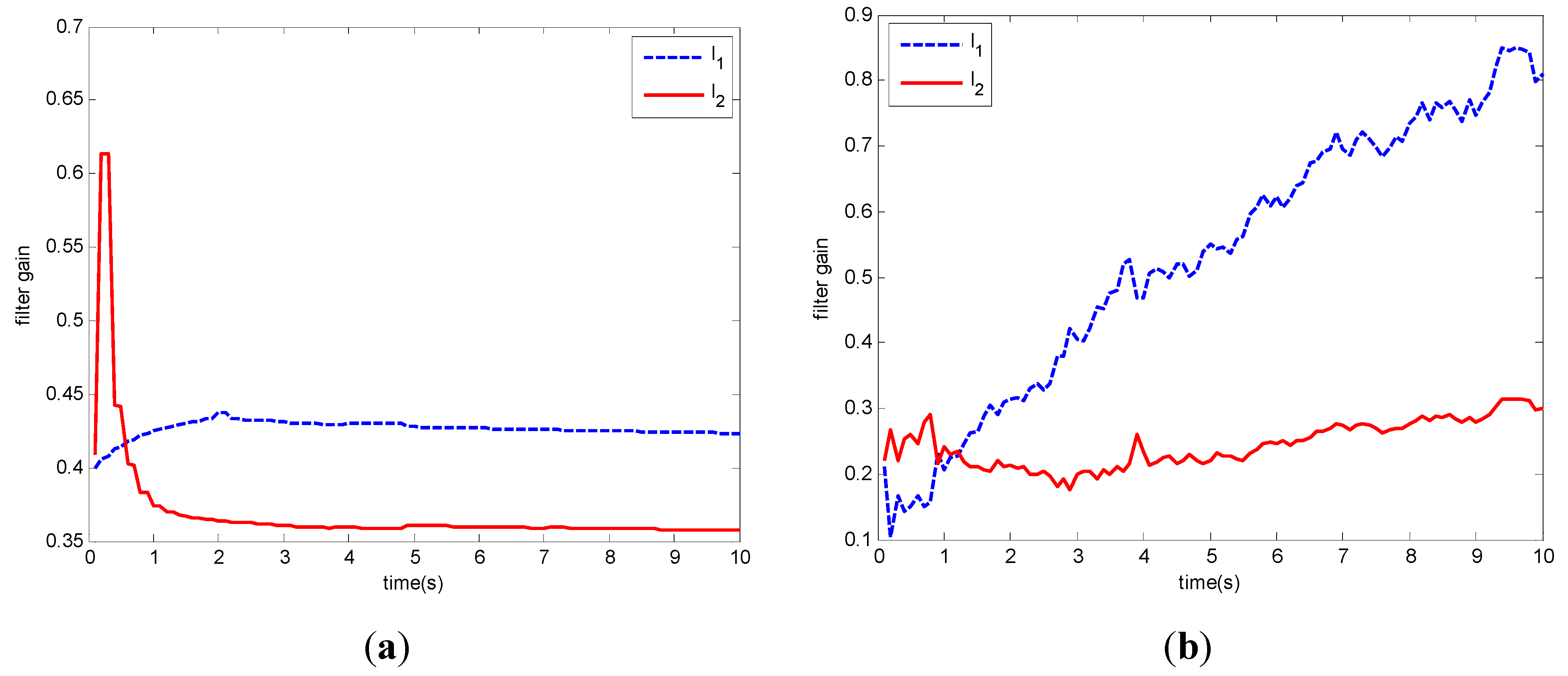
and 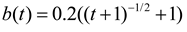 . The random disturbances ω and υ obey non-Gaussian, and their distributions are shown in Figure 1. The weights in Equation (14) are selected as R1 = 10, R2 = 2 and R3 = 10, respectively. The simulation results based on the MEE filter are shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7a and Figure 8a). And the comparative results between MEE filter and UKF are shown in Figure 7 and Figure 8.
. The random disturbances ω and υ obey non-Gaussian, and their distributions are shown in Figure 1. The weights in Equation (14) are selected as R1 = 10, R2 = 2 and R3 = 10, respectively. The simulation results based on the MEE filter are shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7a and Figure 8a). And the comparative results between MEE filter and UKF are shown in Figure 7 and Figure 8.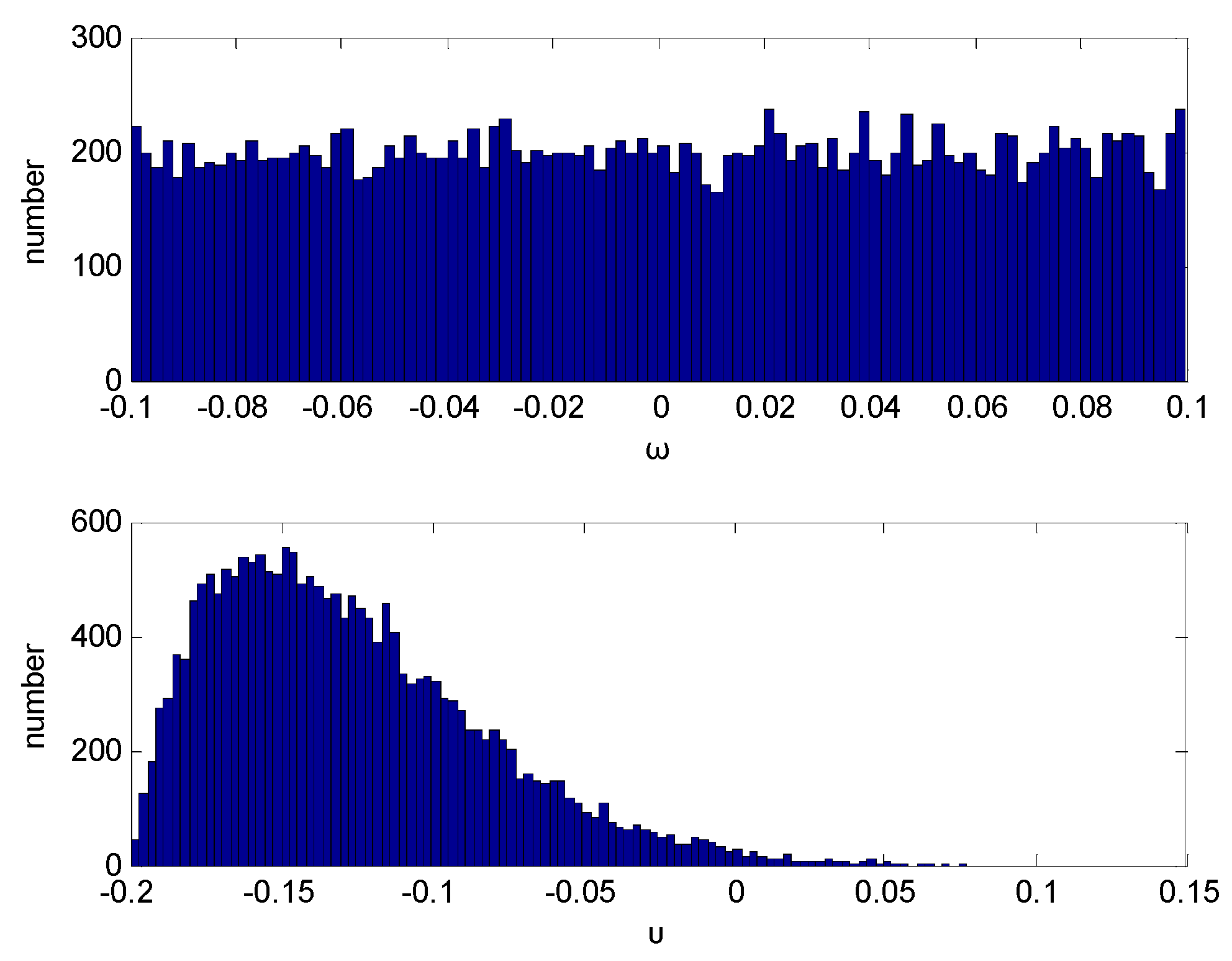
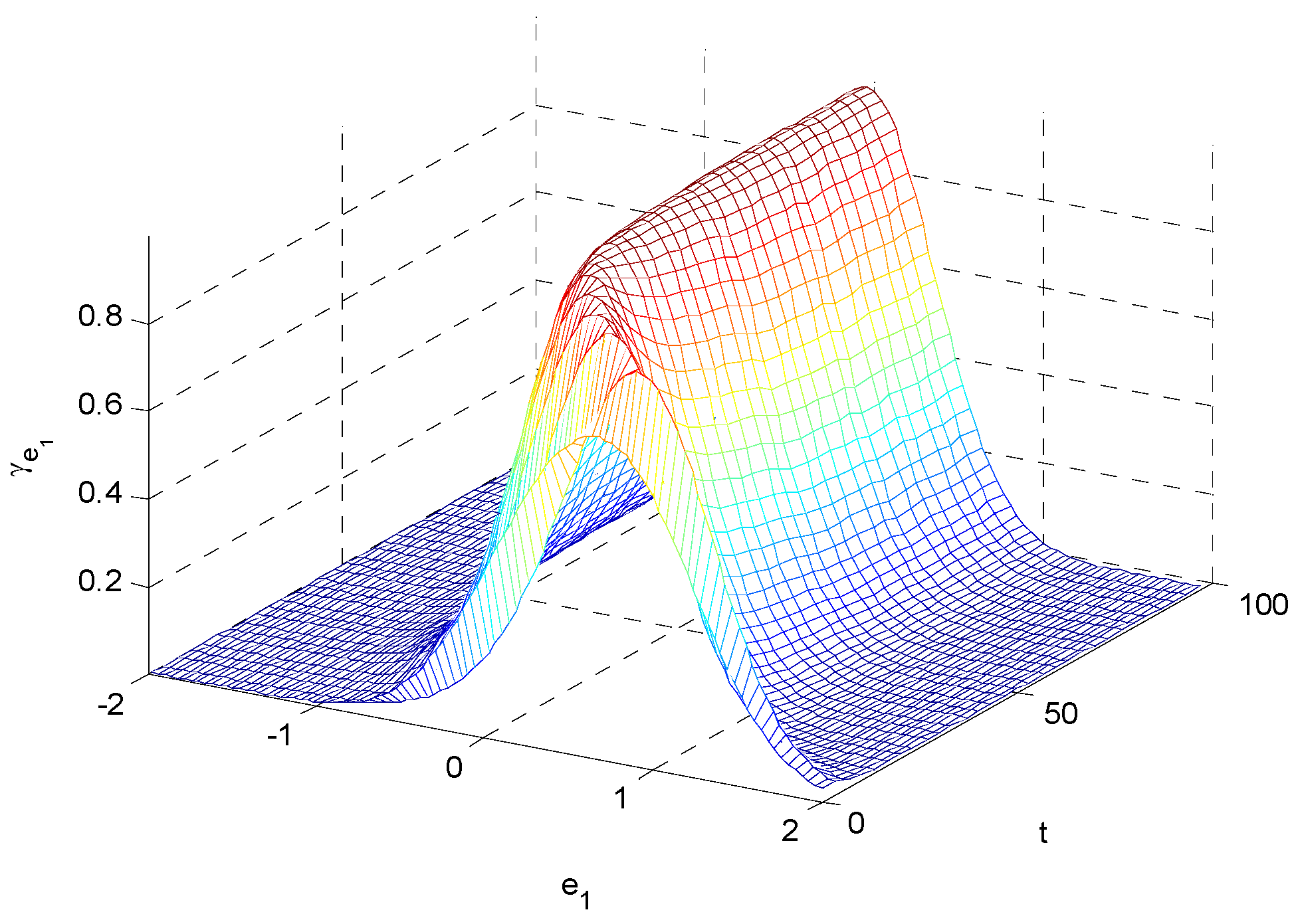
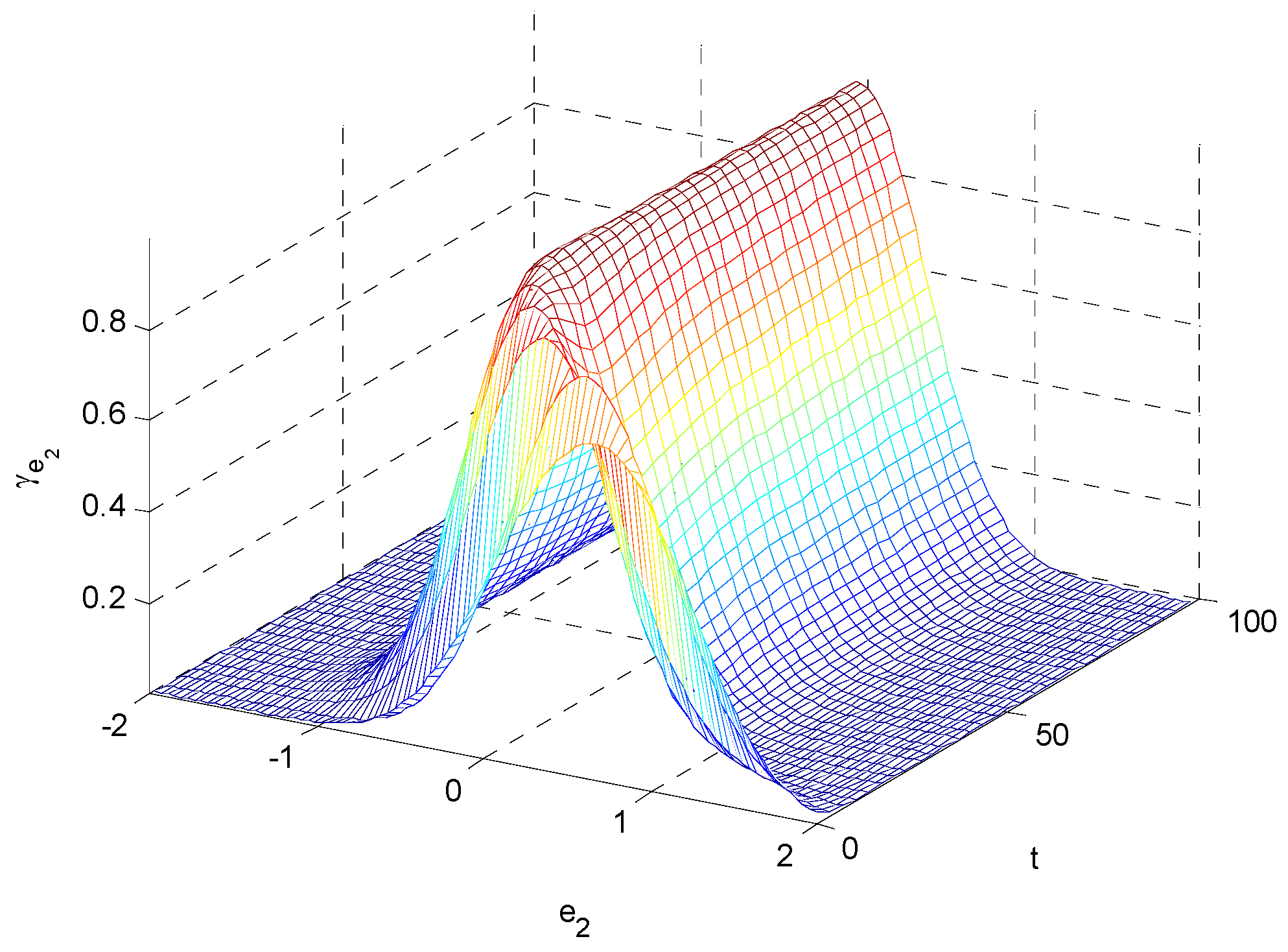
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. Trans. ASME J. Basic Eng. 1961, 83, 95–107. [Google Scholar] [CrossRef]
- Hoblos, V.G.; Chafouk, H. A gain modification form for Kalman filtering under state inequality constraints. Int. J. Adapt. Control 2010, 24, 1051–1069. [Google Scholar]
- Guo, L.; Wang, H. Fault detection and diagnosis for general stochastic systems using B-spline expansions and nonlinear filters. IEEE Trans. Circ. Syst. I 2005, 52, 1644–1652. [Google Scholar]
- Li, T.; Guo, L. Optimal fault-detection filtering for non-gaussian systems via output PDFs. IEEE Trans. Syst. Man Cybern. Syst. Hum. 2009, 39, 476–481. [Google Scholar]
- Guo, L.; Wang, H. Minimum entropy filtering for multivariate stochastic systems with non-Gaussian noises. IEEE Trans. Automat. Contr. 2006, 51, 695–700. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, D.; Wang, H.; Guo, L.; Chai, T. Distribution function tracking filter design using hybrid characteristic functions. Automatica 2010, 46, 101–109. [Google Scholar] [CrossRef]
- Kitagawa, G. Non-Gaussian state-space modeling of nonstationary time-series. J. Am. Stat. Assoc. 1987, 82, 1032–1063. [Google Scholar]
- Kramer, S.C.; Sorenson, H.W. Recursive Bayesian estimation using piece-wise constant approximations. Automatica 1988, 24, 789–801. [Google Scholar] [CrossRef]
- Tanizaki, H.; Roberto, S. Mariano, Nonlinear and Non-Gaussian State-space Modelling with Monte-Carlo Simulations. J. Econometrics 1998, 83, 263–290. [Google Scholar] [CrossRef]
- Kitagawa, G. Monte carlo filter and smoother for non-Gaussian nonlinear state space models. J. Comput. Graph. Stat. 1996, 5, 1–25. [Google Scholar]
- Cappe, O.; Godsill, S.; Moulines, E. An overview of existing methods and recent advances in sequential Monte Carlo. Proceedings of the IEEE 2007, 95, 899–924. [Google Scholar] [CrossRef]
- Vaswani, N. Particle filtering for large dimensional state spaces with multimodal observation likelihoods. IEEE Trans. Signal Proces. 2008, 56, 4583–4597. [Google Scholar] [CrossRef]
- Tang, X.; Huang, J.; Zhou, J.; Wei, P. A sigma point-based resampling algorithm in particle filter. Int. J. Adapt. Control 2012, 26, 1013–1023. [Google Scholar] [CrossRef]
- Zhao, S.Y.; Liu, F.; Luan, X.L. Risk-sensitive filtering for nonlinear Markov jump systems on the basis of particle approximation. Int. J. Adapt. Control 2012, 26, 158–170. [Google Scholar] [CrossRef]
- Erdogmus, D.; Principe, J.C. An error-entropy minimization algorithm for supervised training of nonlinear adaptive systems. IEEE Trans. Signal Proces. 2002, 50, 1780–1786. [Google Scholar] [CrossRef]
- Principe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Chen, B.; Hu, J.; Li, H.; Sun, Z. Adaptive filtering under maximum mutual information criterion. Neurocomputing 2008, 71, 3680–3684. [Google Scholar] [CrossRef]
- Li, J.; Chen, J. The principal of preservation of probability and the generalized density evolution equation. Struct. Saf. 2008, 30, 65–77. [Google Scholar]
- Peng, Y.; Li, J. Exceedance probability criterion based stochastic optimal polynomial control of Duffing oscillators. Int. J. Nonlin. Mech. 2011, 46, 457–469. [Google Scholar] [CrossRef]
- Li, J.; Peng, Y.; Chen, J. A physical approach to structural stochastic optimal controls. Probabilist. Eng. Mech. 2010, 25, 127–141. [Google Scholar] [CrossRef]
- Li, J.; Chen, J. Stochastic Dynamics of Structures; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Wang, Z.; Ho Daniel, W.C. Filtering on nonlinear time-delay stochastic systems. Automatica 2003, 39, 101–109. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications; Harwood University: New York, NY, USA, 1997. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ren, M.; Zhang, J.; Fang, F.; Hou, G.; Xu, J. Improved Minimum Entropy Filtering for Continuous Nonlinear Non-Gaussian Systems Using a Generalized Density Evolution Equation. Entropy 2013, 15, 2510-2523. https://doi.org/10.3390/e15072510
Ren M, Zhang J, Fang F, Hou G, Xu J. Improved Minimum Entropy Filtering for Continuous Nonlinear Non-Gaussian Systems Using a Generalized Density Evolution Equation. Entropy. 2013; 15(7):2510-2523. https://doi.org/10.3390/e15072510
Chicago/Turabian StyleRen, Mifeng, Jianhua Zhang, Fang Fang, Guolian Hou, and Jinliang Xu. 2013. "Improved Minimum Entropy Filtering for Continuous Nonlinear Non-Gaussian Systems Using a Generalized Density Evolution Equation" Entropy 15, no. 7: 2510-2523. https://doi.org/10.3390/e15072510
APA StyleRen, M., Zhang, J., Fang, F., Hou, G., & Xu, J. (2013). Improved Minimum Entropy Filtering for Continuous Nonlinear Non-Gaussian Systems Using a Generalized Density Evolution Equation. Entropy, 15(7), 2510-2523. https://doi.org/10.3390/e15072510





