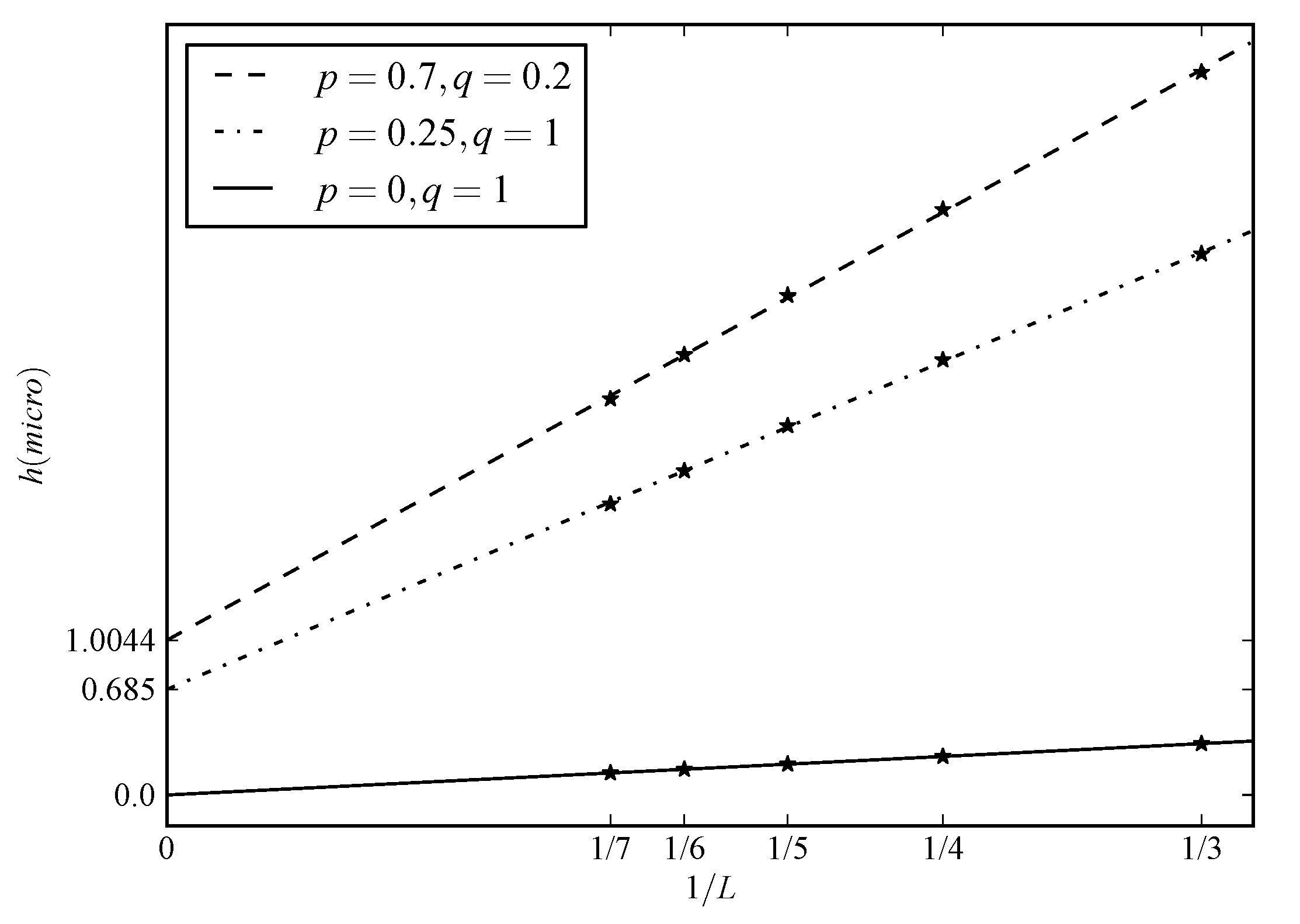1. Introduction
The time-switched dynamics of two one-dimensional, dissipative affine maps,
was studied by the authors in [
1], where they showed that the topological entropy of the resulting non-autonomous dynamical system coincides with the topological entropy of the autonomous dynamical system generating the switching (or control) sequence. In other words, the switched dynamics cannot be more complex than the switching sequence generator.
The situation envisaged in [
1] is special in several regards.
- (i)
The state space is .
- (ii)
Both the forward and backward dynamics are amenable to detailed analysis.
- (iii)
The non-autonomous pullback attractor consists of singleton component sets.
In this follow-up paper we continue studying this question in an extended setting, namely, we consider this time switching between difference equations (called constituent maps) that have pullback attractors with nontrivial component sets. Our scope is to separate the particular results from the general ones, and so better understand the intricacies of switching and non-autonomous dynamics [
2,
3,
4]. Specifically, in this paper:
- (i’)
The state space is or a proper subset of it.
- (ii’)
The constituent maps are not specified, except for the fact that they are supposed to have attractors.
- (iii’)
The component sets of the pullback attractor of the systems under switching are supposed to be uniformly bounded.
Both from an instrumental and a conceptual point of view, the main challenge is introduced by the generalization (
iii’). To begin with, working with attractors with nontrivial component sets instead of point-valued components sets requires using the Hausdorff distance. Contrarily to what happens in the latter case, the Hausdorff distance between component sets of a set-valued attractor is not continuous, in general, but only upper-continuous when a control sequence converges to another one [
2]. This technical shortcoming is behind Assumption 1 in
Section 3 (“Results using measurability”), and Assumption 3 in
Section 5 (“Results using continuity”). Also the generality of (
ii’) will be limited in different ways (injectivity of a certain map Φ in
Section 3, or Assumption 2 in
Section 4) in order to derive sharper results.
On the conceptual side, new features related to the extended geometry of set-valued attractors manifest themselves. Indeed, the observable complexity is going to be the result of two contributions. One, the “macroscopic” complexity, comes from the trajectory segments connecting different component sets of the pullback attractor (think that each component set has been lumped to a point). The other one, the “microscopic” complexity, comes from trajectory segments within the component sets. No geometrical meaning should be attached to this denomination since the (in general, uncountably many) component sets might be packed in a state space region of a size comparable to the attractor itself. The rationale for distinguishing two sorts of complexity is rather that our analytical tools will only be able to resolve the trajectories up to the precision set by the component sets. An offshoot of this picture is that the entropy of the coarse-grained dynamics (or “macroscopic entropy”) is a lower bound of the entropy of the switched dynamics. This fact will again allow us to relate the entropy of trajectories and control sequences, once we have shown that the latter coincide with the macroscopic entropy.
Thus, the main purpose of the present paper is the study of the macroscopic complexity in switched dynamics, as measured by the macroscopic topological entropy. In
Section 3 and 5 we prove that, under certain provisos, the macroscopic topological entropy coincides with the topological entropy of the switching sequence generator. In this case, the complexity of the switched dynamics (a mixture of macroscopic and microscopic complexities) is certainly greater than the complexity of the switching sequence. This result can be brought in connection with Parrondo’s paradox,
i.e., the emergence of new properties via switching [
5,
6,
7,
8]. Indeed, it suffices that the entropy of the switching sequence generator is higher than the entropies of the constituent maps for the switched dynamics to be more complex than the constituent dynamics.
This paper is organized as follows.
Section 2 sets the mathematical framework (switching systems, Hausdorff distance and pullback attractors) of the paper. Additional materials on the Hausdorff distance have been collected in the
Appendix for the reader’s convenience. A few results for further reference, but also interesting on their own, are proved as well in this section and in the
Appendix. The main theoretical results of the paper are derived in
Section 3 (Theorem 3) and
Section 5 (Theorem 4) depending on whether the switched dynamics complies with Assumption 1 (
Section 3), or with Assumption 3 (
Section 5). In between,
Section 4 scrutinizes a property needed in Theorem 3 and reformulates it as Assumption 2 to be used in the proof of Theorem 4. Some numerical simulations illustrating our theoretical results make up
Section 6. The highlights of all these sections are summarized in the Conclusion, followed by the references and the
Appendix.
3. Results Using Measurability
Remember that
is endowed with the metric (
13). Let Φ:
be the map defined by
. We show first that Φ is Borel measurable.
By definition the Borel sigma-algebras of the product spaces
and
are generated by the corresponding cylinder sets or just cylinders. If
,
, the cylinders of
have the form
where
, and the cylinders of
have the form
where
. If
, then we simplify the notation to
or
, and analogously for the cylinders of
.
If, as before,
σ is the (left) shift on
, and Σ is the shift on
, then
and, similarly,
for all
.
Lemma 1
is Borel measurable.
Proof.
Since the cylinder sets build a semi-algebra of the product sigma-algebras they generate, it suffices to prove that
is Borel measurable for every
,
, and every
(see Theorem 1.1 in [
15]). Note that
unless [see Equation (
17)]
for some
, and
for
. In any case,
Since the map
is upper semi-continuous (hence Borel measurable), the sets
,
, are Borel measurable and so is their intersection as well. □
Suppose now that Φ is one-to-one and let us explore when
is also Borel measurable, resulting in a Borel bimeasurable mapping. For
,
,
where
Note that
is an uncountable union of compact sets.
Assumption 1.
The sets and are Borel measurable for every .
Continuity or closedness of the mapping
are obvious sufficient conditions for Assumption 1 to hold. (As a matter of fact, by the closed map lemma, if
is continuous then it is closed because
is compact and
is a Hausdorff topological space.) For example, in the affine, one-dimensional case studied in [
1]
is a singleton,
i.e.,
, for all
. That all the sets
are compact (hence Borel measurable) follows in this case from the continuity of
. In
Section 5 we will study with more detail the consequences of assuming the mapping
continuous.
Lemma 2
If is one-to-one and Assumption 1 holds, then Φ is Borel bimeasurable.
Proof.
We only need to prove that Φ transforms cylinders into Borel measurable sets. In view of Equation (
21) this boils down to showing that
is Borel measurable for every
,
.
From Equation (
22) and Assumption 1, it follows that
is a finite intersection of Borel measurable sets, hence it is Borel measurable. □
Consider the diagram
then it is straightforward to check that this diagram commutes,
i.e.,
=
. In order to derive that
, it suffices that
is a bimeasurable bijection (see Corollary 8.6.1 (iv) in [
15]). This being the case, Lemma 3.2 yields the following result.
Theorem 2
Let be a bijection and suppose that Assumption 1 holds. Then .
Other conditions leading also to
will be discussed in
Section 5.
Notice that
corresponds to what we called
macroscopic entropy in the Introduction. Indeed, since (i)
is a trajectory in
, a set whose “points” are the component sets
of
; and (ii)
implies
for all
, it holds that
measures the complexity of the trajectories
up to the precision set by the distinct component sets
. To relate the macroscopic entropy,
, to the entropy of the switched dynamics (referred to as
microscopic entropy in the Introduction),
, let
be the set of entire orbits, and consider the commutative diagram
where
i is the inclusion
. Thus
is a factor of (or semi-conjugate to)
on account of
i being measure-preserving (
for all measurable
) and onto. It follows that
,
i.e.,
is a lower bound of the topological entropy of the switched dynamics
. To keep with the physical identification of entropies, set
for the topological entropy (or complexity) of the control sequence generator. From
and Theorem 2,
we conclude the following result on the relation between the topological entropies of the control sequence generator,
, and the ensuing switched dynamics,
.
Theorem 3
Under the hypotheses of Theorem 2, .
This theorem provides sufficient conditions for a complexity version of Parrondo’s paradox. Indeed, it suffices that (along with the assumptions of Theorem 2), where is the topological entropy of , for the complexity of the switched dynamics to exceed the complexity of the constituent maps.
In the special case of pullback attractors consisting of singletons, like in [
1], the inclusion
i in the diagram (
24) becomes the identity, a trivial isomorphism, and
.
4. Conditions for the Injectivity of Φ
According to Theorem 2, the injectivity of Φ (along with Assumption 1) is instrumental for and to coincide. We explore next sufficient conditions for the injectivity of Φ.
If Φ is not injective, then there are control sequences
such that
,
i.e.,
for all
. Then
and, similarly,
for all
. It follows that
for those
such that
(a nonempty set by hypothesis). This being the case, there are several conditions that prevent Equation (
27) from occurring, thus guaranteeing the injectivity of Φ.
Assumption 2.
There is no such that or, equivalently, for all .
This condition can be reworded as follows:
and
distinguish all pullback attractors of the switching dynamics.
Example 1
Let , and as in Equation (1). In this case, the pullback attractor consists of singleton sets, i.e
. , with (see [1]). Let us check whether Assumption 2 holds:but because . Since Assumption 2 holds, Φ
is injective. Example 2
Let be the attractors of , i.e., , and . If , then Assumption 2 does not hold since , and . Think, for instance, of two linear dynamics having only 0 as a fixed point. Therefore, in this case the topological entropy of the switched dynamics may be different from the topological entropy of the control sequence.
Now suppose that at least one of the maps
is invertible and define
if
is invertible, or
otherwise; if both maps are invertible, then either choice is the inverse of the other one. Then
Therefore, Assumption 2 can be particularized in the following way.
Assumption 2 for Invertible Mappings.
In case that one of the maps is invertible, there is no g-invariant .
Example 3
Suppose that are two -matrices, with being invertible, and , so that with . Thus, when applying Assumption 2 for invertible mappings, we are asking about the existence of invariant sets of known linear maps. Linear maps can be decomposed as actions of scalings (expansion/contraction, projection, reflection) and/or rotations. Therefore, the existence of G-invariant pullback attractors boils down to well-known geometrical facts.
The only invariant set of an (in general anisotropic) expansion/contraction is .
If a linear map is a projection onto a subspace V, then any set contained in V is invariant.
If a linear map is a reflection, then any set symmetric under reflections (like a star-like shaped object) is invariant.
If a linear map is a rotation by an angle α, then any set symmetric under that rotation is invariant, in particular any ball centered at the origin of radius and dimension n or if contained in the orthogonal complement of the rotation axis.
Since the origin is invariant in any case, it might happen that for some (for example, for or , since , where are the attractors of ). In this case, the version of Assumption 2 for invertible mappings would not hold.
From the preceding discussion we conclude the following result.
Lemma 3
Suppose that the maps are such that Assumption 2 holds. Then the map Φ: → defined by is one-to-one.
5. Results Using Continuity
The main technical difference between the setting of [
1] and the present general setting is that the map
is not necessarily continuous (Proposition 3). It is, however, worth following the same path as in [
1] to see how far we can go and under which conditions. The first condition is obvious.
Assumption 3.
The set-valued mapping is continuous in , i.e
., Proposition 4 provides a sufficient condition for Assumption 3 to hold.
We are going to show in this section that if Assumptions 2 (
Section 4) and 3 are fulfilled, then
is a homeomorphism.
Lemma 4
Under Assumption 3, the map Φ: defined by is uniformly continuous.
Proof.
We have to show that for any
there exists
such that
whenever
(
i.e., whenever
for
). The uniformity follows then from the compactness of
.
Consider first the second term in the decomposition
Since
for any
, we have
hence
if
We use next Assumption 1 to show that the first term in Equation (
29) with
can also be made smaller than
. Indeed, for each
n with
there exist by Equation (
28)
such that
Set
. Then
for
since
where
and
. Therefore if dist
, then
All in all, we conclude from Equation (
29), Equation (
31) and Equation (
30) with
that if dist
, then
. □
Remark.
The above proof exploits the special structure of the model and provides insight into it. The result, in fact, follows from the continuity of the mapping Φ and the compactness of the metric space .
If the correspondence
is invertible, then given a sequence
there exists a unique control sequence
such that
for every
n. Therefore,
can be determined from the knowledge of
and
.
Lemma 5
Suppose that Assumption 2 holds so that the mapping Φ is one-to-one. Then, : is continuous.
Proof.
Given
, we have to prove that there exists
such that
where
∈
, and
=
,
=
.
From
it follows
Consider now two neighboring sequences in
,
of distance
δ apart. From these sequences we determine the corresponding switching sequence under
:
Note that
, where
, and similarly
, where
.
Now suppose that, contrarily to what we need to prove, there is an
n,
, such that
. For brevity assume
,
i.e.
Then, by the triangle inequality,
We claim that the right hand side of Equation (
34) can be made arbitrarily small by choosing
δ in Equation (
32) sufficiently small.
First of all, by Proposition 2 and Equation (
32)
where
is continuous and
. As for the second term on the right hand side of Equation (
34), use Equation (
33) and Equation (
32) to derive
Therefore,
where
This proves our claim.
It follows from Equation (
35) and Equation (
36) that
, in contradiction to Assumption 2. Hence we conclude that
for
,
i.e., that dist
, where
, and
.
Notice that we did not assume Φ to be continuous in Lemma 5. With Lemmas 4 and 5 we derive a different version of Theorem 2.
Theorem 4
Suppose that Assumptions 2 and 3 hold. Then the mapping Φ: defined as is a homeomorphism, hence , i.e., .
7. Conclusions
Consider the time-switched dynamics associated with two maps
having global attractors
. In this paper we studied the relation between the topological entropy of the control sequence generator and the topological entropy of the switched dynamics. Compared with the previous paper [
1], we found some new technical obstacles.
First of all, we had to circumvent the shortcoming that the map
is not necessarily continuous in
; here
is a control sequence and
is the corresponding component set of the pullback attractor,
. To this end we assumed in
Section 3 (“Results using measurability”), (i) the measurability of certain unions of component sets (Assumption 1); and (ii) the injectivity of
. It follows then, Theorem 2, that Φ is a topological conjugacy between the shift on the control sequences,
, and the shift on the trajectories of the switched dynamics up to the precision set by the component sets,
. Being the entropy of coarse-grained trajectories,
is a lower bound of
, the topological entropy of the switched dynamics. We call
the macroscopic entropy and write
. Likewise,
is the entropy of the control sequence generator, thus we write
. In sum,
[Equation (
25) and Equation (
26)] under the hypotheses (i) and (ii).
In
Section 4 we surveyed sufficient conditions for the injectivity of Φ postulated in
Section 3. We formulated our conclusions as Assumption 2, both in a general version, and in a special version when one of the maps
is invertible.
In
Section 5 (“Results using continuity”) we hypothesized from the outset that the mapping
is continuous (Assumption 3) and paralleled the approach of [
1]. In Theorem 4 we proved that Φ is a homeomorphism (or topological conjugacy), Assumptions 2 and 3 granted. Once again we concluded that
.
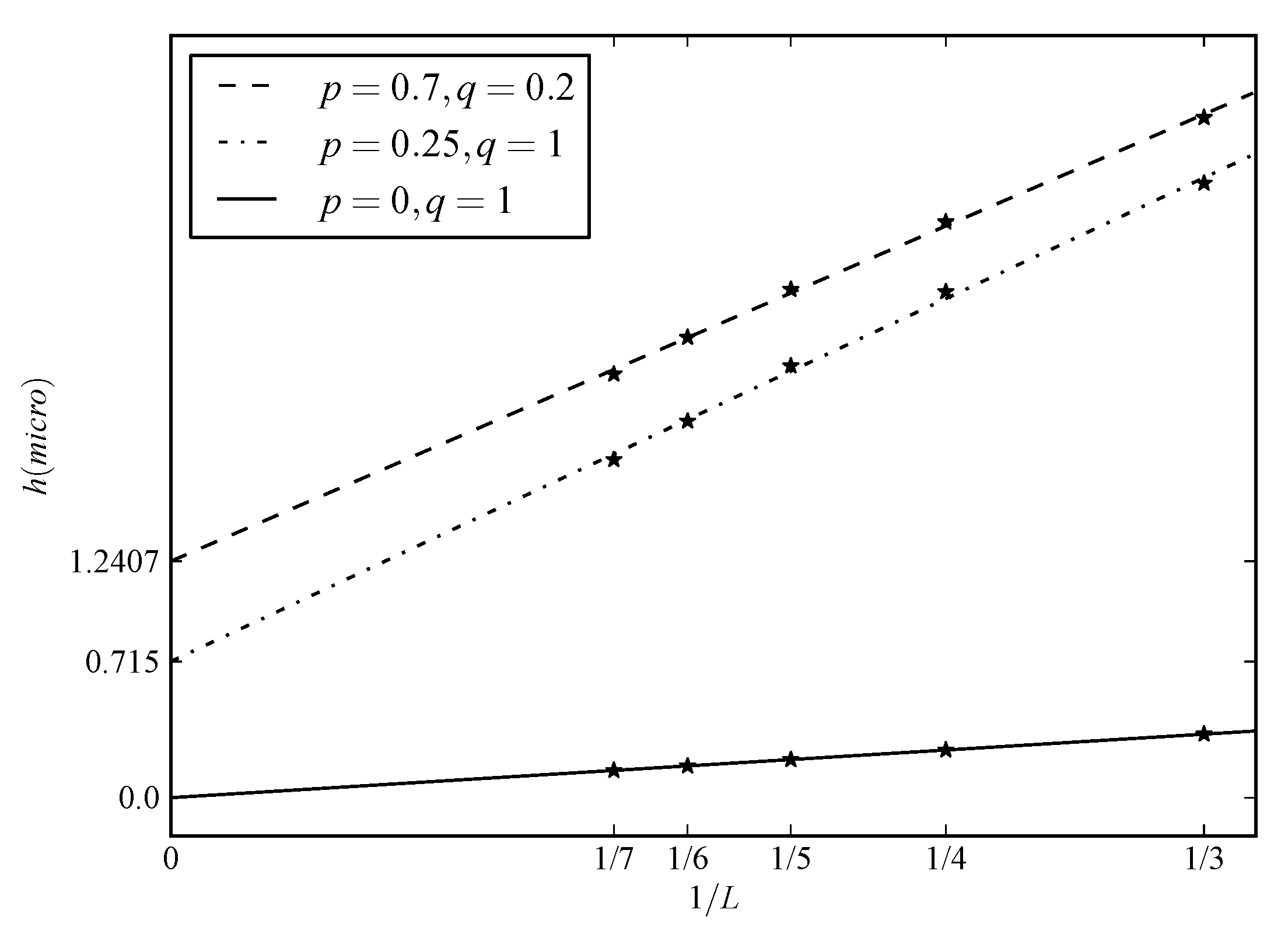
The main results of this paper, Theorems 3 and 4, are in line with what we call the complexity version of Parrondo’s paradox, namely, that the complexity of a switched dynamics may be higher than the complexity of its constituent maps. Moreover, they provide sufficient conditions as well, to wit: .
Finally, both possibilities
(Case 1) and
(Case 2) have been numerically illustrated in
Section 6.