Quantum Contextuality with Stabilizer States
Abstract
:1. Introduction
2. Mathematical Preliminaries
2.1. Stabilizer States and Clifford Gates
2.1.1. . Stabilizer States
2.1.2. . The Clifford Group
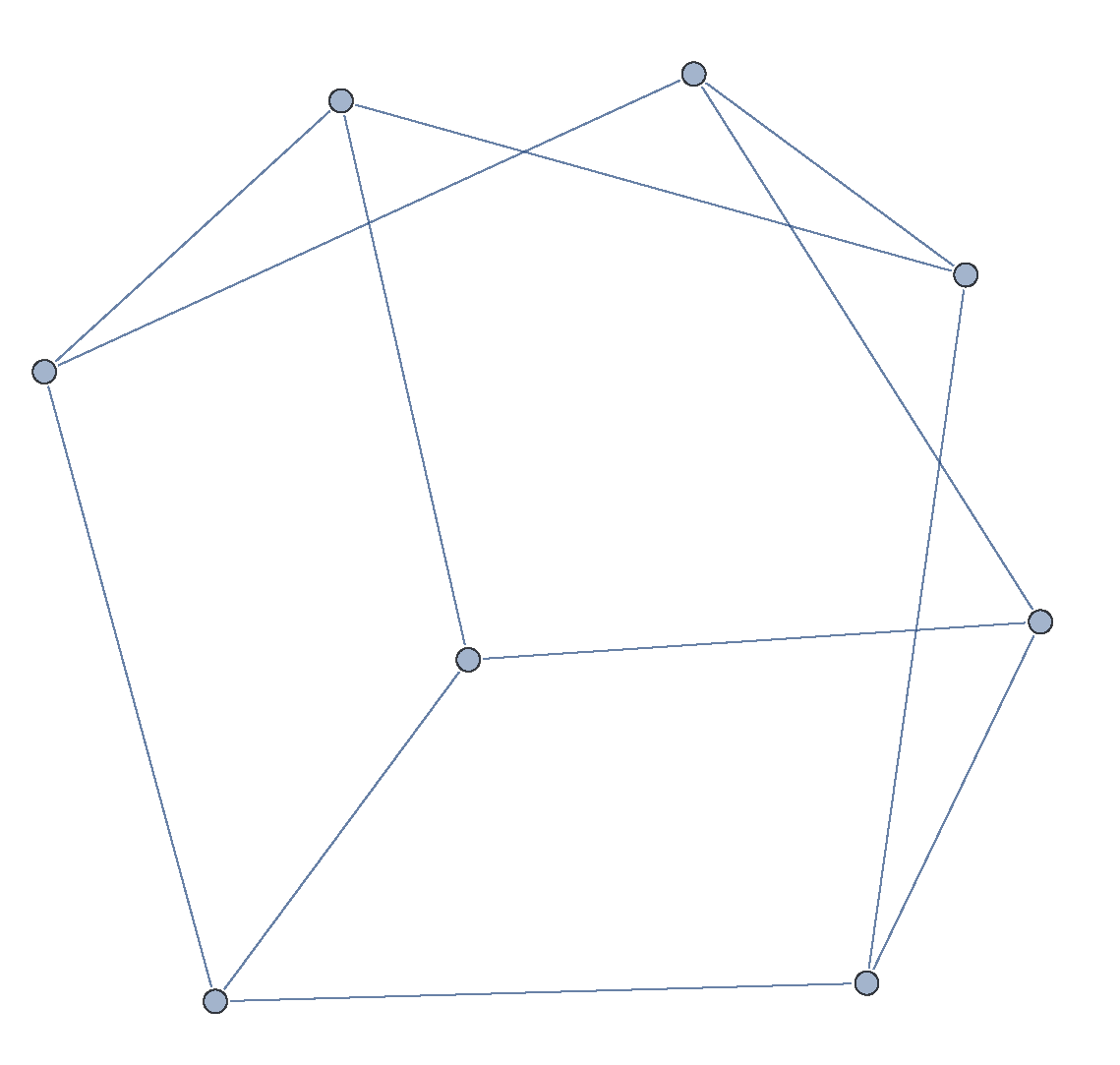
2.2. Quantum Contextuality and Graph Theory
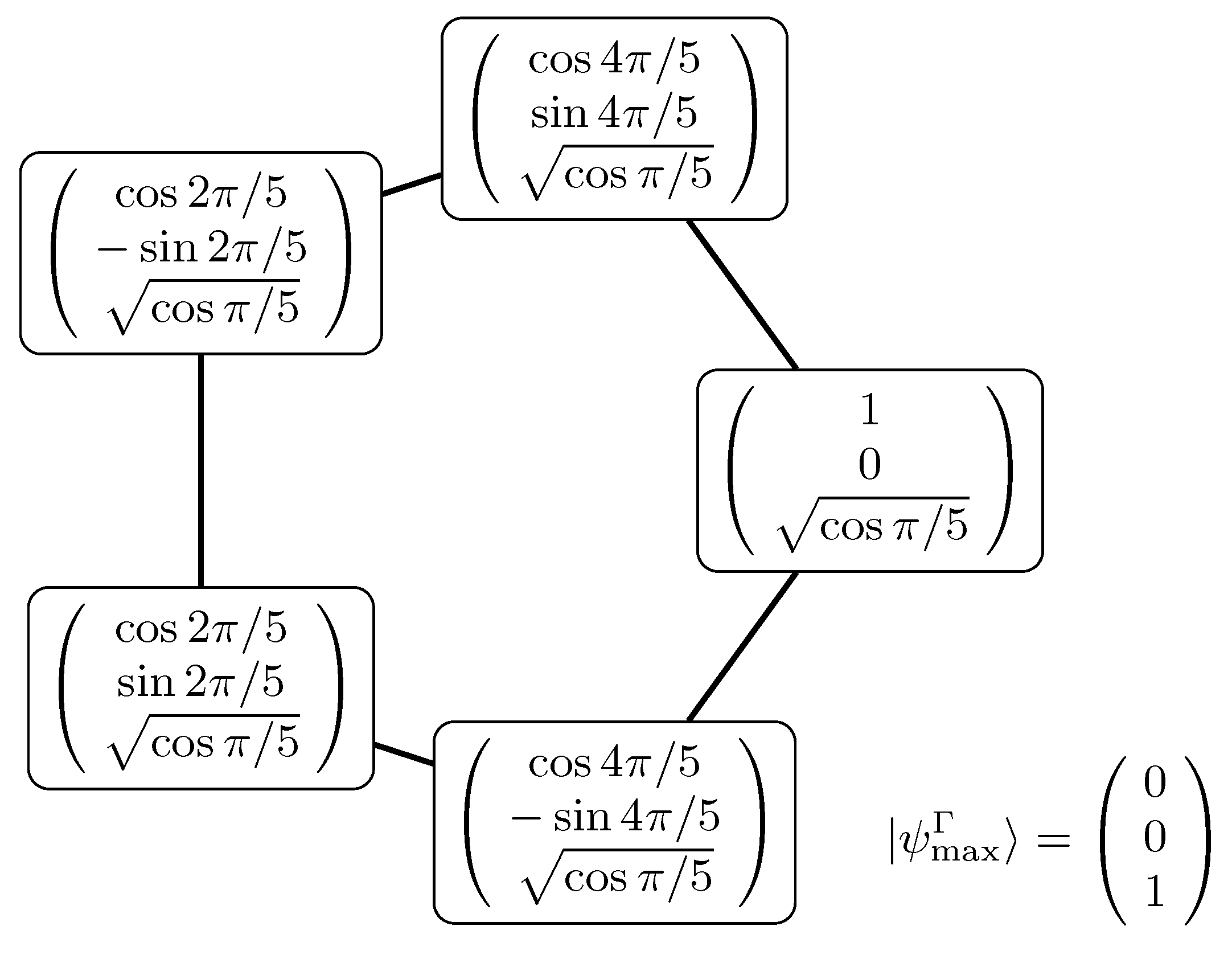
2.2.1. . Graph Theoretical Prerequisites
3. Results
3.1. State-Independent Contextuality Using Stabilizer States
| 36 | 24 | 60 | |
| 144 | 216 | 360 | |
| 900 | 3000 | 3900 | |
| d |
| 9 | |||
| 16 | 24 | 340 | |
| 36 | 120 | 156 | |
| 9 | 6 | 15 | |
| 16 | 24 | 340 | |
| 36 | 120 | 156 | |
| d |
3.1.1. . Separable Stabilizer States
3.1.2. . Entangled Stabilizer States
3.1.3. . Generic Impossibility of Qudit State-Independent Contextuality
3.2. State-Dependent Contextuality Using Bell Inequalities
| 8 | 3 | 3.414 | 3.414 | ||
| 27 | 6 | 6.412 | 7.098 | ||
| 125 | 12 | 13.090 | 18.090 | ||
| 343 | 19 | 19.411 | ? | ||
| d | ? | ? | ? | ? |
3.3. Induced Subgraphs and Equivalence of Non-Isomorphic Graphs
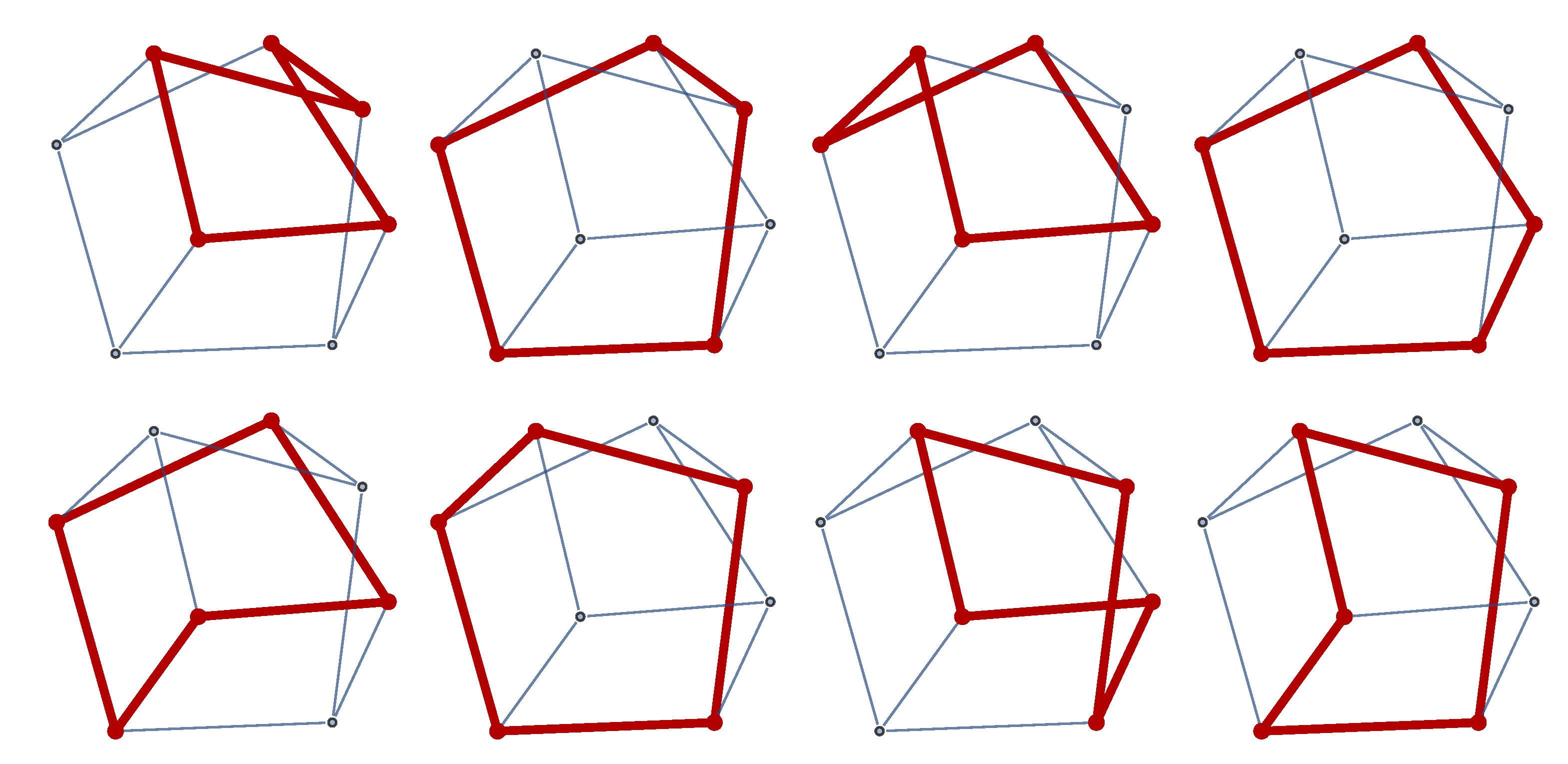
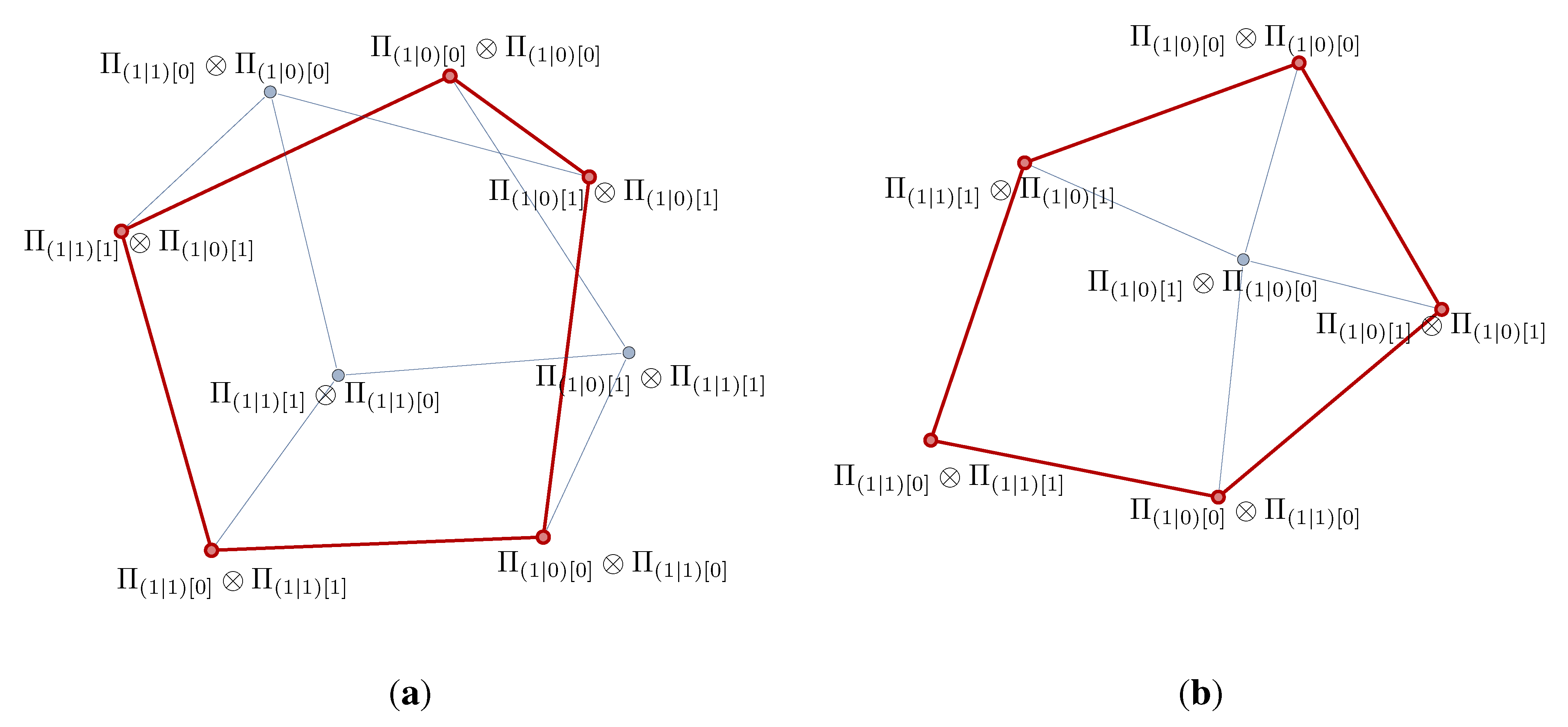
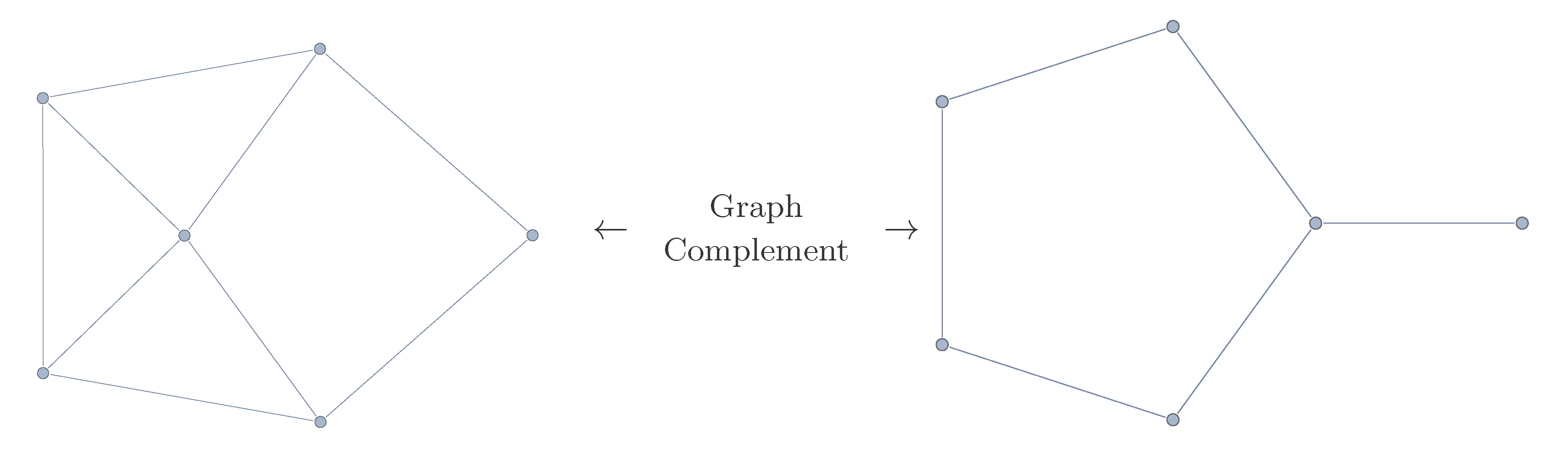
4. Summary
Acknowledgements
Conflict of Interest
References and Notes
- Bandyopadhyay, S.; Boykin, P.O.; Roychowdhury, V.; Vatan, F. A new proof for the existence of mutually unbiased bases. Algorithmica 2002, 34, 512–528. [Google Scholar]
- Lawrence, J.; Brukner, Č.; Zeilinger, A. Mutually unbiased binary observable sets on N qubits. Phys. Rev. A. 2002, 65, 032320. [Google Scholar] [CrossRef]
- Renes, J.M.; Blume-Kohout, R.; Scott, A.J.; Caves, C.M. Symmetric informationally complete quantum measurements. J. Math. Phys. 2004, 45, 2171:1–2171:10. [Google Scholar] [CrossRef]
- Scott, A.J. Optimizing quantum process tomography with unitary 2-designs. J. Phys. A: Math. Theor. 2008, 41, 055308. [Google Scholar] [CrossRef]
- Van Dam, W.; Howard, M. Bipartite entangled stabilizer mutually unbiased bases as maximum cliques of Cayley graphs. Phys. Rev. A 2011, 84, 012117. [Google Scholar] [CrossRef]
- Campbell, E.T.; Anwar, H.; Browne, D.E. Magic-state distillation in all prime dimensions using quantum reed-muller codes. Phys. Rev. X 2012, 2, 041021. [Google Scholar] [CrossRef]
- Planat, M. Twelve-dimensional Pauli group contextuality. 2012. arXiv:1201.5455 [quant-ph]. [Google Scholar]
- Gross, D. Hudson’s theorem for finite-dimensional quantum systems. J. Math. Phys. 2006, 47, 122107. [Google Scholar] [CrossRef]
- Veitch, V.; Ferrie, C.; Gross, D.; Emerson, J. Negative quasi-probability as a resource for quantum computation. New J. Phys. 2012, 14, 113011. [Google Scholar] [CrossRef]
- Ivanovic, I.D. Geometrical description of quantal state determination. J. Phys. A: Math. Gene. 1981, 14, 3241. [Google Scholar] [CrossRef]
- Appleby, D.M. Properties of the extended Clifford group with applications to SIC-POVMs and MUBs. 2009. arXiv:quant-ph/0909.5233. [Google Scholar]
- Mermin, N.D. Simple unified form for the major no-hidden-variables theorems. Phys. Rev. Lett. 1990, 65, 3373–3376. [Google Scholar] [CrossRef] [PubMed]
- Peres, A. Two simple proofs of the Kochen-Specker theorem. J. Phys. A: Math. Gene. 1991. [Google Scholar] [CrossRef]
- Aravind, P.K. Quantum kaleidoscopes and Bell’s theorem. Int. J. Mod. Phys. B 2006, 20, 1711–1729. [Google Scholar] [CrossRef]
- Cabello, A.; Severini, S.; Winter, A. (Non-)Contextuality of physical theories as an axiom. 2010. arXiv:1010.2163[quant-ph]. [Google Scholar]
- Klyachko, A.; Can, M.; Binicioğlu, S.; Shumovsky, A. Simple test for hidden variables in spin-1 systems. Phys. Rev. Lett. 2008, 101, 020403. [Google Scholar] [CrossRef] [PubMed]
- Popescu, S.; Rohrlich, D. Quantum nonlocality as an axiom. Found. Phys. 1994, 24, 379–385. [Google Scholar] [CrossRef]
- Sadiq, M.; Badziąg, P.; Bourennane, M.; Cabello, A. Bell inequalities for the simplest exclusivity graph. Phys. Rev. A 2013, 87, 012128. [Google Scholar] [CrossRef]
- Cabello, A. State-independent quantum contextuality and maximum nonlocality. 2011. arXiv:1112.5149 [quant-ph]. [Google Scholar]
- Cabello, A. Simple explanation of the quantum violation of a fundamental inequality. Phys. Rev. Lett. 2013, 110, 060402. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H. SIC POVMs and Clifford groups in prime dimensions. J. Phys. A 2010, 43, 305305. [Google Scholar] [CrossRef]
- Godsil, C.D.; Newman, M.W. Coloring an orthogonality graph. SIAM J. Discrete Math. 2008, 22, 683–692. [Google Scholar] [CrossRef]
- Östergård, P.R.J. A fast algorithm for the maximum clique problem. Disc. Appl. Math. 2002, 120, 197–207. [Google Scholar] [CrossRef]
- Niskanen, S.; Östergård, P.R.J. Cliquer User’s Guide; Version 1.0; Technical Report T48; Communications Laboratory, Helsinki University of Technology: Espoo, Finland, 2003. [Google Scholar]
- Mathematica; Version 8.0; software for technical computation; Wolfram Research Inc.: Champaign, IL, USA, 2010.
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- The 8 distinct projectors, in pairs associated with each summation in Equation (61), are equivalent to following un-normalized vectors {[(1,1,1,1),(1,-1,-1,1)],[(1,i,1,i),(1,-i,-1,i)],[(1,1,i,i),(1,-1,-i,i)],[(1,-i,i,1),(1,i,-i,1)]}.
- Ji, S.-W.; Lee, J.; Lim, J.; Nagata, K.; Lee, H.-W. Multisetting Bell inequality for qudits. Phys. Rev. A. 2008, 78, 052103. [Google Scholar] [CrossRef]
- Liang, Y.-C.; Lim, C.-W.; Deng, D.-L. Reexamination of a multisetting Bell inequality for qudits. Phys. Rev. A. 2009, 80, 052116. [Google Scholar] [CrossRef]
- In graph6 file format, ΓCHSH for d = 3 is ZznZnZWD?wBEBBDabWDZ?tk@z]?oB?WE_SBB?gWgEDb?KZ?gBZ?oDl_KBZW.
- Cabello, A.; Danielsen, L.E.; Lopez-Tarrida, A.J.; Portillo, J.R. Basic logical structures in quantum correlations. 2012. arXiv:1211.5825 [quant-ph]. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Howard, M.; Brennan, E.; Vala, J. Quantum Contextuality with Stabilizer States. Entropy 2013, 15, 2340-2362. https://doi.org/10.3390/e15062340
Howard M, Brennan E, Vala J. Quantum Contextuality with Stabilizer States. Entropy. 2013; 15(6):2340-2362. https://doi.org/10.3390/e15062340
Chicago/Turabian StyleHoward, Mark, Eoin Brennan, and Jiri Vala. 2013. "Quantum Contextuality with Stabilizer States" Entropy 15, no. 6: 2340-2362. https://doi.org/10.3390/e15062340
APA StyleHoward, M., Brennan, E., & Vala, J. (2013). Quantum Contextuality with Stabilizer States. Entropy, 15(6), 2340-2362. https://doi.org/10.3390/e15062340




