1. Introduction
The concept of energy harvesting has attracted widespread attention in the scientific and engineering communities [
1,
2,
3,
4,
5]. Energy scavenging devices are designed to capture ambient energy and convert it into usable electrical energy. The concept of power harvesting works towards developing self-powered devices that do not require replaceable power supplies. A number of sources of harvestable ambient energy exist, including waste heat, vibration, electromagnetic waves, wind, flowing water, and solar energy [
1,
2,
3,
4,
5].
Our paper introduces the concept of “entropy harvesting” in its relation to real physical systems. The notion of “entropy harvesting” has been already introduced in the fields of communication security, cryptography and data processing [
6,
7]. In our paper we revisit the idea of entropy harvesting, and implement it in physical systems, where entropy decreases as a result of naturally or artificially induced processes occurring in “open systems”. The concept of “entropy harvesting” is inspired mainly by ideas put forward by Professor Guy Deutscher in the book “
The Entropy Crisis”. G. Deutscher stated that mankind today actually faces an “entropy crisis” and not an “energy crisis” as it is commonly supposed [
8]. It takes humanity more and more energy in order to sustain an increasingly ordered environment produced by people. I quote: “What is called an energy crisis is actually an entropy crisis. It has two aspects that cannot be dissociated. The first is that the amount of energy needed to keep the entropy decrease in check may surpass the energy actually available. The second is the increasing pollution of the environment at the level of biosphere. It is precisely because we are dealing with an entropy crisis that these aspects are so intimately connected” [
8].
2. Entropic Forces and Physical Systems Suitable for Entropy Harvesting
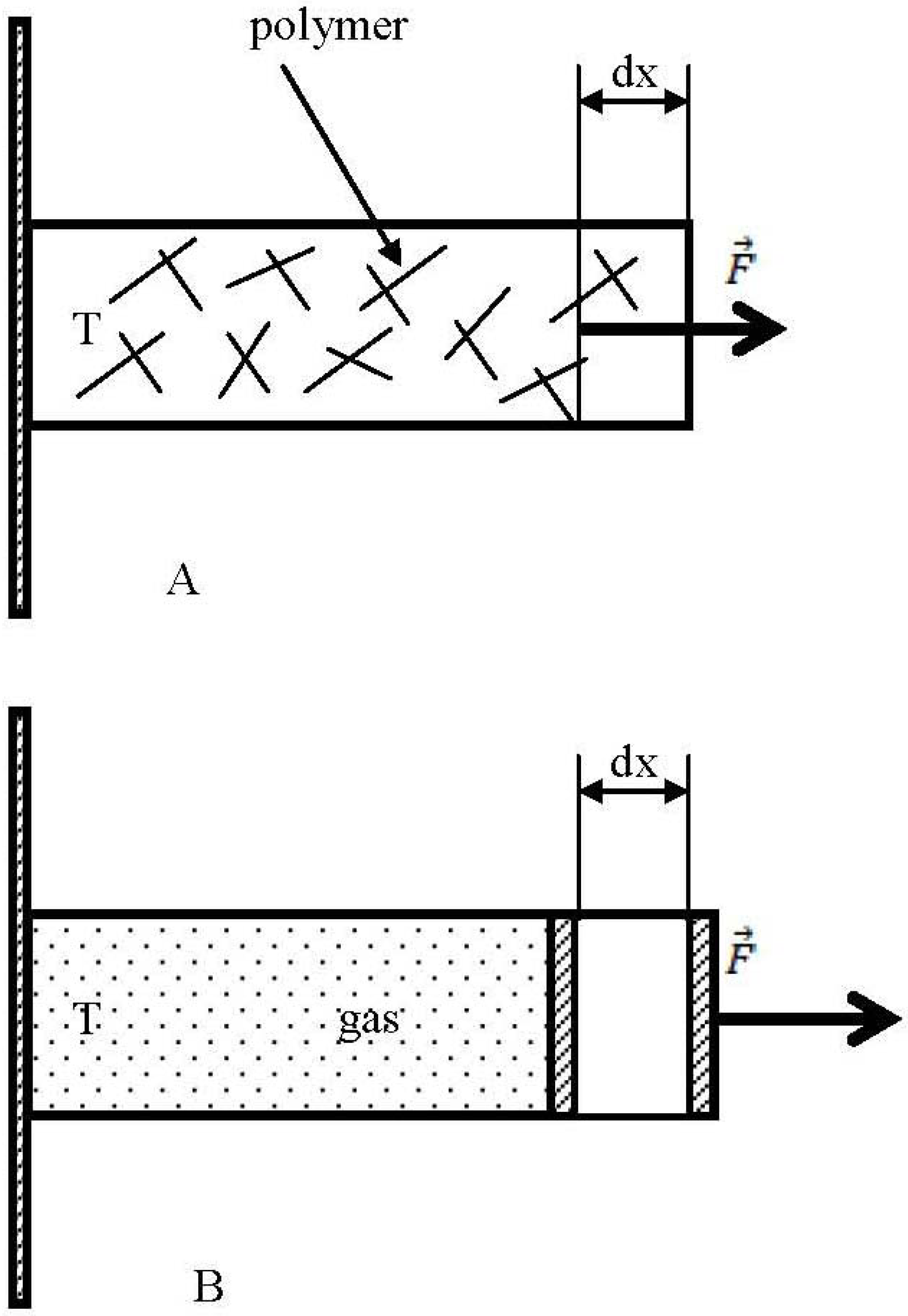
Let us start from the well-known example of an entropic harvester depicted in
Figure 1A, namely a deformed polymer (rubber) band (
is the force applied to a polymer strip,
dx is the displacement). When we stretch the rubber-band it looks from the first glance that we harvest energy (when the stretched band is released the mechanical work is done). But actually a stretched rubber-band represents an entropy harvester, exploiting so-called “entropic force”.
Figure 1.
(A) The deformed with force polymer strip—the simplest example of the “entropy harvester”.
Figure 1.
(A) The deformed with force polymer strip—the simplest example of the “entropy harvester”.
If a polymer molecule in the strip is pulled into an extended configuration, it decreases its entropy (the stretched molecule is more ordered). Randomly coiled configurations are overwhelmingly more probable;
i.e. they have greater entropy [
9]. The molecule tends to increase its entropy; this gives rise to the entropy-inspired elastic force
, given by:
where
kB is the Boltzmann constant,
T is the temperature,
N is the number of monomers,
l is the length of the monomer unit, the
is the end-to-end vector (see
Figure 2). The coefficient of proportionality
is called the entropic spring constant [
9]. Notice that the entropic elastic force given by Equation (1) is proportional to temperature; this kind of temperature dependence is typical for the other kinds of entropic forces. It has been established experimentally that when a rubber-band is stretched, the elastic force is proportional to temperature:
~
T.
Figure 2.
The model of a polymer chain. is the end-to-end vector.
Figure 2.
The model of a polymer chain. is the end-to-end vector.
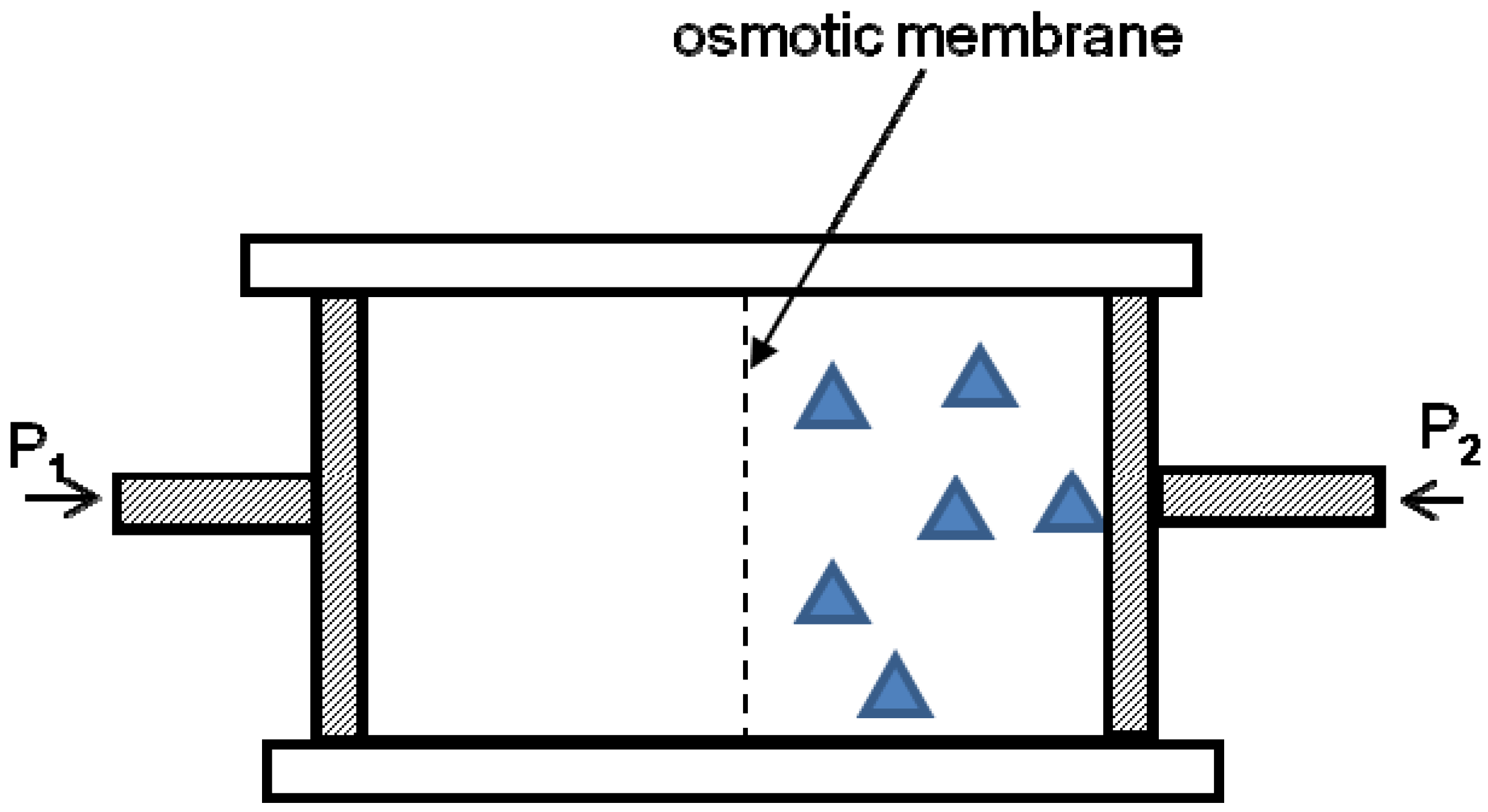
The next example of an entropic harvester is the osmotic membrane-based device, depicted in
Figure 3. Consider a solution that is separated from a pure solvent by an osmotic membrane that allows only solvent molecules, not solute (depicted with triangles in
Figure 3) to pass through. Particles of solute tend to flow from the pure solvent into the solution, in order to decrease the entropy of the system [
10]. To prevent the flow, a pressure drop should be created, as depicted in
Figure 3 (
P2 >
P1). When a pressure drop sufficient for preventing flow is applied to an osmotic system, it works as an entropy harvester. The pressure drop is given by the van’t Hoff Formula:
where
is the number of moles of solute per unit volume, and
is the gas constant [
10]. As is typical for the entropic-driven effect, the osmotic pressure drop depends linearly on the temperature (compare with Equation (1)). If we remove the pressure drop, the flow will start and the osmotic entropic harvester, shown in
Figure 3, will perform the mechanical work.
Figure 3.
To prevent osmotic flow, P2 must exceed P1. The system represents an example of an “entropy harvester”.
Figure 3.
To prevent osmotic flow, P2 must exceed P1. The system represents an example of an “entropy harvester”.
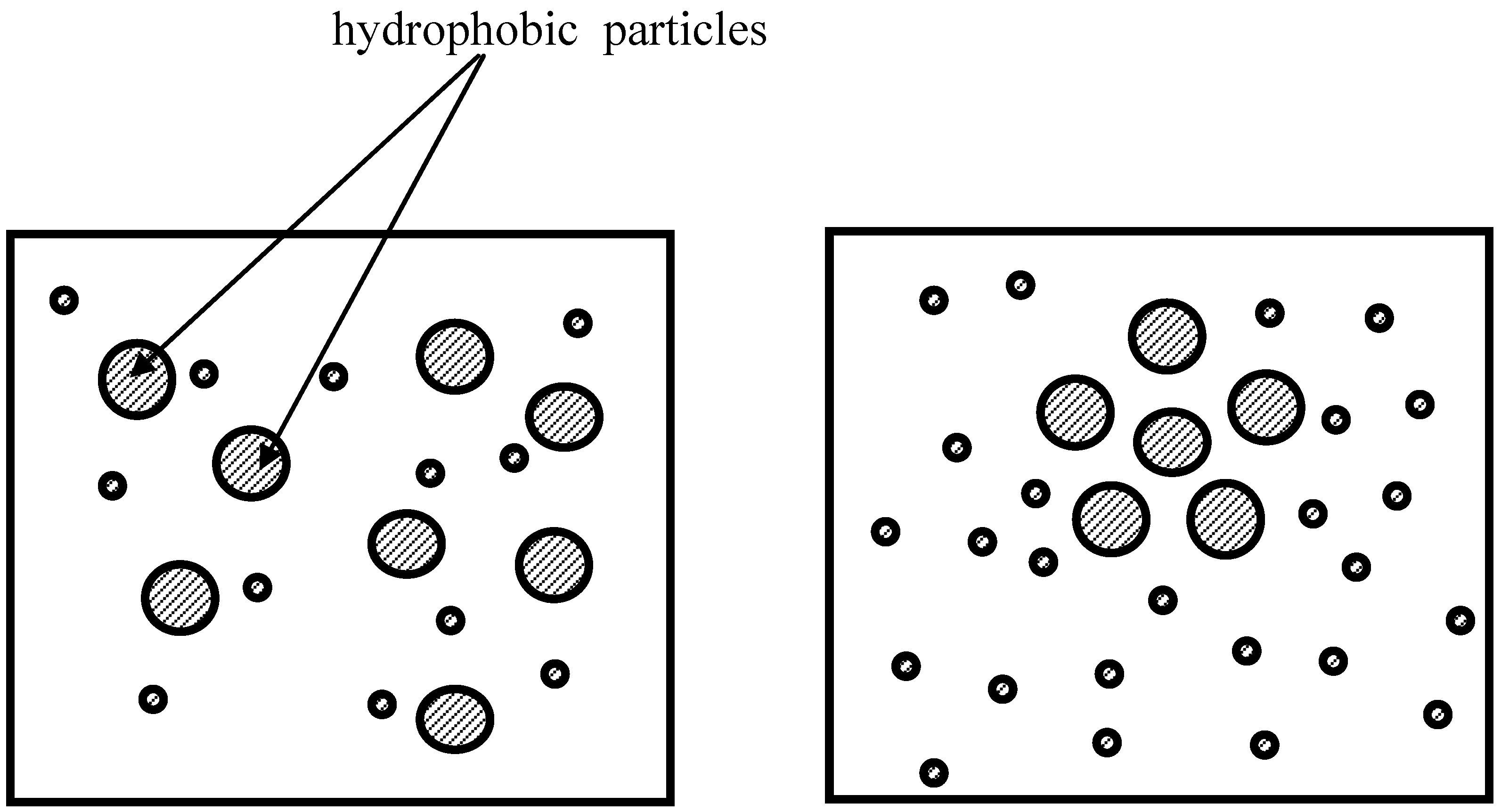
The so-called “hydrophobic effect” represents additional exemplification of the entropy-driven phenomena. The hydrophobic interaction originates from the disruption of hydrogen bonds between molecules of liquid water by the nonpolar solute [
11]. By aggregating together, nonpolar molecules reduce the surface area exposed to water and minimize this disruptive effect. This reducing of the surface is entropically favorable [
11]. This entropic effect leads also to the clustering of small hydrophobic particles, shown in
Figure 4. If we mix the suspension and increase the average distance between hydrophobic particles, the suspension will harvest entropy. Hydrophobic interactions, like other entropic effects, increase in strength with increasing temperature [
11].
Figure 4.
Clustering of hydrophobic particles dispersed in water, due to the hydrophobic effect.
Figure 4.
Clustering of hydrophobic particles dispersed in water, due to the hydrophobic effect.
We supplied a number of examples representing “entropy harvesters”, however the simplest possible entropy harvester is a box containing gas, depicted in
Figure 1B. If the gas in the container expands isothermally, the force driving the piston is given by [
12]:
This is the entropic force which is very similar to the force and pressure supplied by Equations (1) and (2). Indeed, the internal energy of a fixed quantity of an ideal gas depends only on its temperature, and not on the volume of its container, so it is not an energy effect that tends to increase the volume of the box like gas pressure does. This implies that the pressure of an ideal gas has a purely entropic origin.
4. The Efficiency of Entropy Harvesting
Consider one of the simplest possible entropy harvesters,
i.e. a box containing gas (depicted in
Figure 1B). When we cool the container isothermally, its energy decreases, and
dQ =
TdSobviously takes place, where
dQis the amount of heat taken from the system. The last expression could be re-written as:
in Equation (4) may be interpreted as the efficiency of energy harvesting (the harvested entropy per unit of withdrawn heat). It is seen that the efficiency of energy harvesting increases when the temperature is decreased. We can also re-write Equation (3) as:
It is reasonable to interpret as the efficiency of entropy harvesting related to the unit displacement of the piston. Thus, we recognize that when , the efficiency of energy harvesting increases with the temperature decreases.
5. Gravity and Entropy Harvesting
This example looks speculative compared to previous ones. Verlinde in his recent paper treated
gravity as an entropic force caused by changes in the information identified with material bodies [
15]. The positions and movements of particles in physics are related to space. According to Verlinde, “space is therefore literally a storage space for information associated with matter” [
15]. He assumed that this information is stored in discrete bits on the holographic screens [
16]. Within this approach, space is emergent and the holographic screen separates the emerged part of space, containing bodies, and stores data that describe the part of space that has not yet emerged [
15,
16].
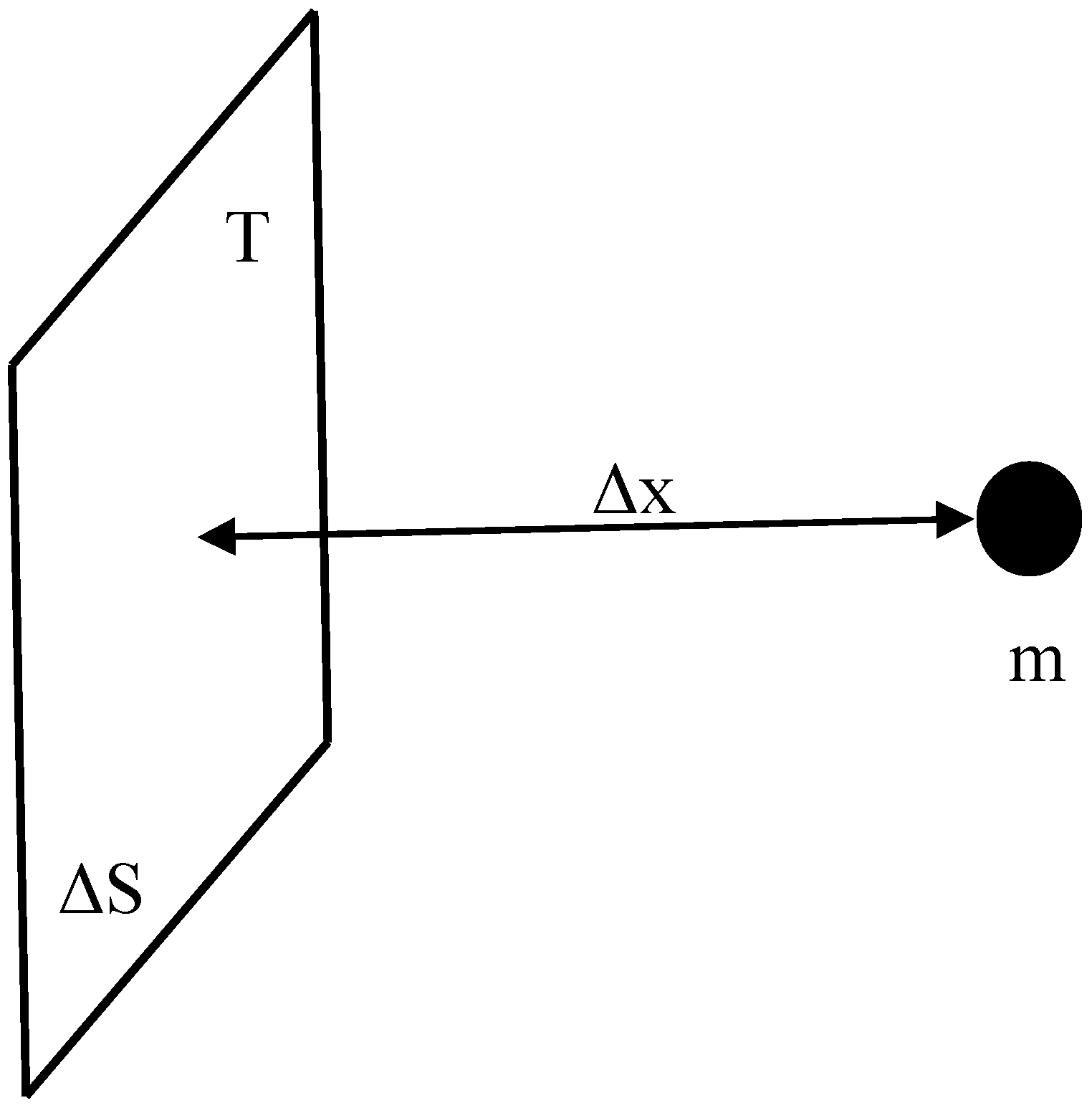
Consider a holographic screen, and a particle of mass
m that approaches from the side at which space-time already emerged, as described in
Figure 5. At this side the physics is described in macroscopic variables, such as positions of particles; on the other side it is still formulated in terms of microscopic degrees of freedom [
15]. According to the holographic principle, the information associated with the particle with the mass of
m can be mapped onto the screen that separates the two regions. Eventually the particle merges with these microscopic degrees of freedom, but beforehand it changes the amount of information associated with it. The change of entropy associated with the information drop on the boundary equals [
17]:
This information drop gives rise to the entropic force (
a is the acceleration):
Comparing Equations (6) and (7) yields for the temperature:
Figure 5.
A particle with mass m approaches the holographic screen. The screen bounds the emerged part of space which contains the particle, and stores data that describe the part of space that has not yet emerged.
Figure 5.
A particle with mass m approaches the holographic screen. The screen bounds the emerged part of space which contains the particle, and stores data that describe the part of space that has not yet emerged.
Expression (8) supplying the temperature
T coincides precisely with the so-called Unruh temperature, registered by an observer in an accelerated frame moving with acceleration
a [
18]. Verlinde proposed to treat Expression (8) as the temperature required to cause acceleration
a, and not as the temperature caused by an acceleration. In order to explain the origin of the force given by Equations (6) and (7), Verlinde likens the holographic screen to the osmotic membrane carrying temperature
T, discussed in
Section 2 [
15]. If gravitational force has an entropic origin, the displacement of physical bodies may be used for effective entropy harvesting, followed by the release of mechanical work.