1. Introduction
Information spreading and knowledge distribution are the most basic processes in the human communities all over the history that played the most important role in confederating the members into the united group [
1]. With the development of the Internet, the studies of communities were enriched by considerations of discussion groups and communities in social networks (like Twitter, groups in Facebook or communities in LiveJournal). These allowed to avoid the criterion of place and territory, and to concentrate on the pure informational interactions between the members of a community [
2]. Such interactions and dissemination of cultural entities like ideas, knowledge, or attitudes in the community certainly differ from spreading of material entities or economic behavior [
3], and in the internet social networks they form a main and in the most cases a single factor, which defines a community. Such unique property of communication as well as availability of quantitative data gave a rise to intensive studies of information diffusion in the social networks [
4,
5], and resulted in complete analysis of different aspects of information spreading and its influence on the other members of community.
In this paper, we address an opposite problem and consider the dynamics of blocks or chunks of information, as it follows from the dynamics of community. Moreover, instead of considering the complete messages referred to in communication (published in the blogs,
etc.), we deal with minimal meaningful blocks of information, which can be considered as self-representing entities commonly known as
concepts. There exist several approaches to explain general and formal properties of the concepts and their dynamics and distribution in the community [
6,
7,
8]; for the goals of this study, we use the term concept in its common sense meaning.
The study of concepts instead of messages allows using the following consideration regarding learning and forgetting processes and the observability of their results. In fact, an individual can comprehend a new concept and introduce it into the personal map by at least three different learning schemes: the first one represents learning of a new concept as a particular case of another concept comprehended earlier; the second scheme is based on the generalization of the concept(s) existing in the map; and the third scheme allows learning a concept by means of practical experience. In forgetting, the concept might either drop down from the personal map, or be substituted by another concept, or deliver its meaning to other concepts.
However, while the learning process and its results can be unambiguously observed and measured in communication, the forgetting process for the meaningful entities cannot be registered and certainly cannot be measured. The fact that the individual does not refer to a concept for some time does not necessarily indicate that the concept is forgotten, and any attempt to verify whether the individual has forgotten it or not, can make him remember. From this viewpoint, learning of concepts follows the line of the general learning processes [
9], while forgetting does not. This observation forms a basis for the suggested model and further analysis of the concepts dynamics. Notice again that such property does not hold for the meaningless chunks of symbols and for complete messages.
The rest of the paper is organized as follows:
Section 2 describes an underlying birth-death process in the community, which is used for the derivation of the concepts’ dynamics. In
Section 3, we consider the dynamics of a single concept and derive a model of informational dynamics of the community and concepts’ behavior.
Section 4 deals with the long-term behavior of concepts and considers the processes caused by introducing a new concept into the community’s maintenance.
Section 5 concludes the discourse and discusses the obtained results.
2. Underlying Birth-Death Process in the Community
The suggested model of the concept’s dynamics is based on the widely-known general birth-death process, which specifies a distribution of the members’ ages in the community. For convenience, in this section we present the main equations and terms, which will be used in the next sections.
Let be the size of the community at time , and be the number of individuals, who have been living since at least time , , and are still alive at time . It is clear that .
Denote by
a death rate function in the community, such that the value
specifies the number of individuals of age
that die in one time unit at time
. We assume that
is known. Let
be a distribution of ages in the community such that
is an amount of individuals of ages between
and
at time
. The function
satisfies the following equation:
where
is a birth rate at time
and
is an initial age distribution. The solution of this equation is the following:
where:
Denote by
a number of individuals not older than
at time
. Then:
In terms of the function
, the size
of the community is given by
and the function
is determined as:
For stationary death-birth processes, the death and birth rates
and
do not depend on time, and the Equation (1) is reduced to the following form:
The solution of this equation is:
If, in addition, the death rate
does not depend on age,
i.e.,
, then:
and the total community size is
The obtained equations define the distribution of the members’ ages in the community. In the case of natural community, such equations with the values in the scales of human life, specify real distribution of the ages; however, in the case of social networks, and corresponding communities and groups, the birth-death processes stand for the processes of joining the communities, active communication, and leaving the communities or interrupting communication in them.
3. Dynamics of a Single Concept
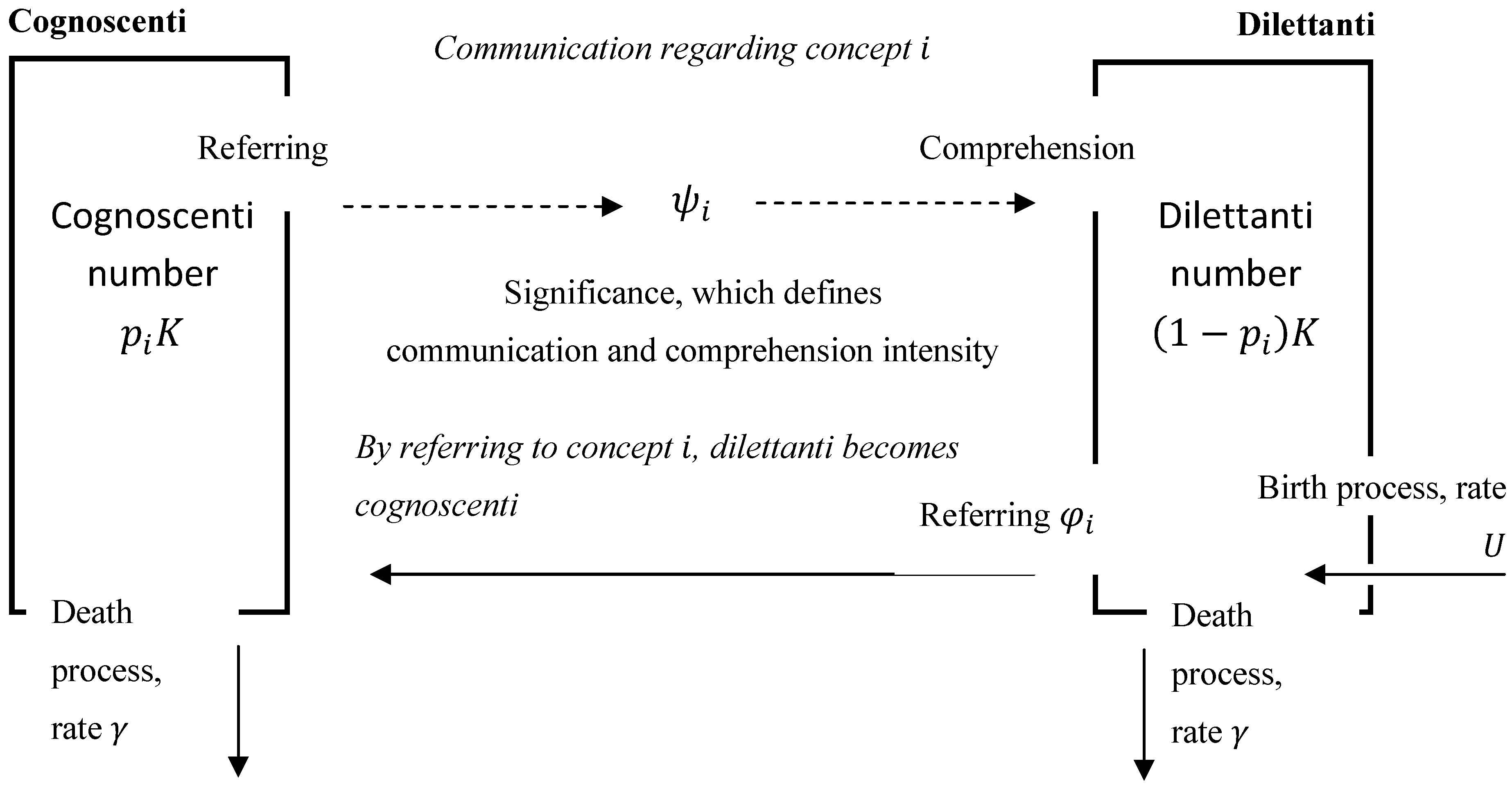
The described above dynamics of the ages’ distribution in the community forms a basis for specifying the probabilistic dynamics of concepts maintained by the community. Another necessary aspect is the concepts’ significance, which is revealed in communication and is built up from the rates of learning and forgetting of the concepts, as explained below.
Denote by
a total number of concepts, which are used in the community. Notice that here we consider a homogeneous community or a part of a social network; so it is natural to assume that the set of maintained concepts is finite (but certainly, it can be very large) and includes the terms appearing in the lexicon of the community and also can take into account the non-linguistic concepts used by the members. In
Section 4 we show how
can be estimated and its upper bound can be determined.
Denote by the probability that an individual randomly chosen from the community at time , , is aware of the concept , . The individual is believed to be aware of the concept if (s)he has referred to the concept in communication with other individuals in the community. The probability changes in time as a result of various cognitive and communication processes—personal mental activities, learning, advertisement, etc.—commonly established in the community. In order to obtain a continuous change of the probability in time, we assume that the community is quite large and that the concepts are widely known so that for any concept and time the probability is not zero, that is .
Then the value
represents a number of individuals, who are aware of the concept
at time
; we call them
cognoscenti. Similarly,
stands for a number of individuals, who are unaware of the concept
at time
; we call them
dilettanti. In both cases
stands for the size of community at time
, which is defined in
Section 2.
Next, let
be the rate the dilettanti refer to the concept
; in other words,
is a number of individuals, who have never referred to the concept
before
, and referred to it for the first time within the time interval
]. Then, the probability
can be expressed in terms of
as follows:
where
is the size of community at time
and the values
are defined by Equation (4). Consequently, in Equation (8), the expression
represents a number of cognoscenti who firstly referred to the concept
at
and are still alive at
,
. The coefficient
normalizes the indicated number over the community size.
To obtain the dynamic equation for the probability
, let us denote by
an amount of references to the concept
produced in the community per time unit. Then:
where
stands for an average amount of references to the concept
provided by a cognoscente per time unit. Therefore, each individual on average receives
references to the concept
per time unit, and the total number of references received by the dilettanti is
.
Finally, let
be a probability for a dilettante to comprehend the concept
,
i.e., to produce a reference to the concept
, while receiving a single reference from a cognoscente. Then, the average number of references to the concept
produced by the dilettanti at
per time unit is:
where the value:
specifies the communication rate between the cognoscenti and the dilettanti regarding the concept
and is referred to here as the significance of the concept. The significance
of the concept
is directly proportional to the intensity of referring
and to the probability of comprehension
. The parameters
and
represent the rates of forgetting and learning of the concept
, respectively. The simpler it is to learn the concept, the higher
should be; and the simpler to forget the concept, the smaller
should be. The introduced terms are clarified in
Figure 1.
Figure 1.
The scheme of the concept’s and community dynamics.
Figure 1.
The scheme of the concept’s and community dynamics.
The probability depends on the concept’s position in the personal concepts maps, and the number of connections that associate the concept with other concepts. The greater the average number of connections is, the greater is the number of different learning schemes, by means of which the concept is comprehended.
Now, the integral equation for the probability
is obtained by combining Equations (4), (8) and (10):
The above equation determines the dynamics of a single concept in terms of its significance
and the age structure in the community,
. To illustrate it, let us consider a stationary case, where the birth and death rate functions do not change in time. The age structure of the community and its size converge to the steady state
and
, respectively. If the concepts’ significance
is constant in time as well,
i.e., , then from Equation (12) it follows that
converges as:
where
is the average age. Notice that the limit probability
does not depend on the age distribution, but rather is specified by the average age only.
If, additionally, the death rate
does not depend on
, the Equation (12) is simplified as:
An equivalent differential equation is:
In particular, if
is constant over a time interval, then:
and:
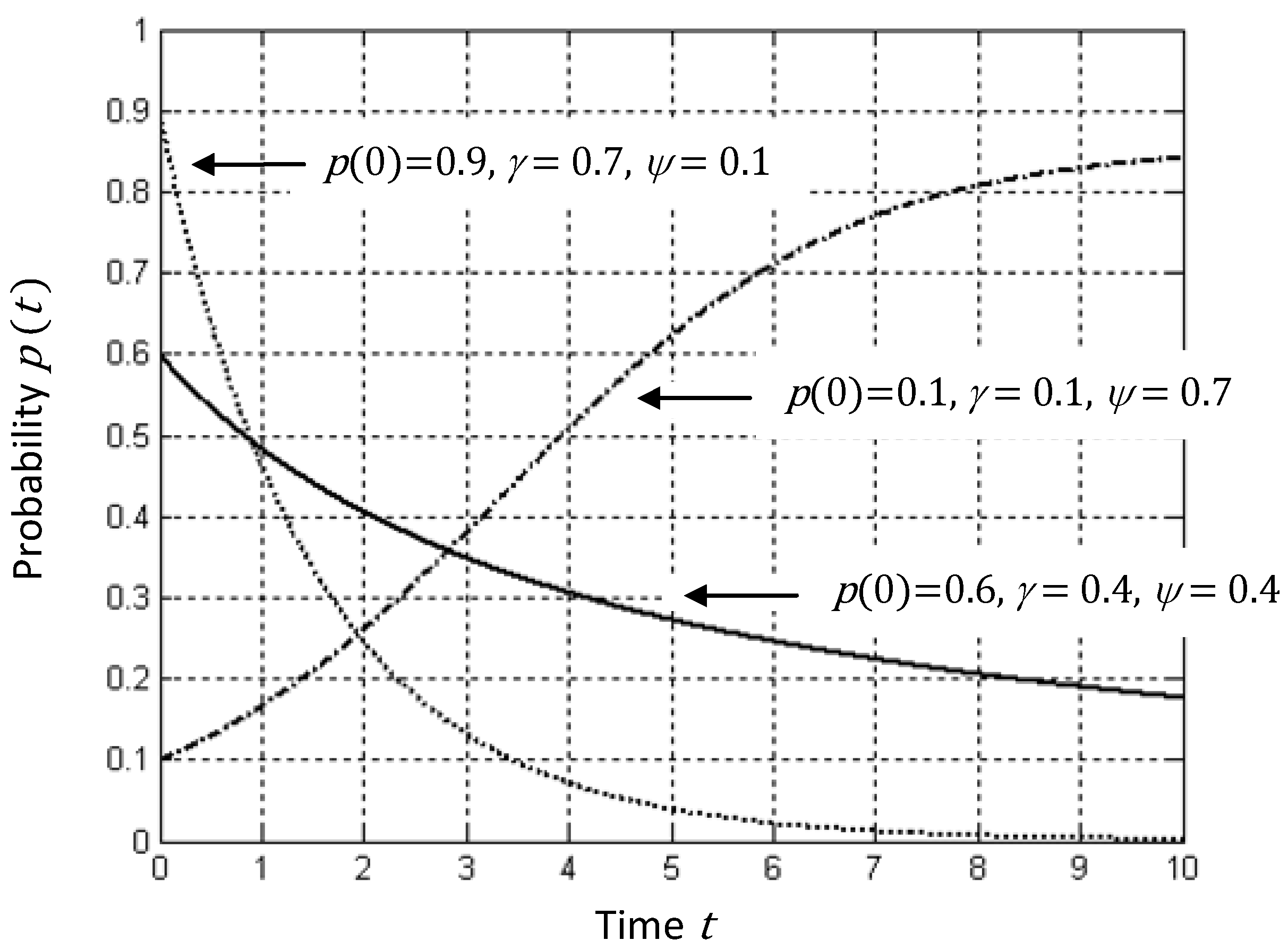
The plots of the probability
for different values of
and
are shown in
Figure 2. In the figure, the solid curve starts with
and corresponds to the values
and
. The dotted curve starts with a greater value
and presents the dynamics of the probability for
and
. In contrast, the dashed curve starts with a smaller value
and shows the probability dynamics for
and
.
Figure 2.
Probability for different values of death rate and significance .
Figure 2.
Probability for different values of death rate and significance .
The figure shows that for greater or equal , the probability decreases, as if the community “forgets” the concept, while in the opposite case the probability increases, as if the community “learns”. In this specific case, the dissemination of the awareness of concepts in the community goes in line with the way an individual learns and forgets information.
4. Long-Term Behavior of the Concepts
Both the dissemination of the awareness of a concept in the community and the vanishing of the concept are determined in Equation (12). The lower the significance of the concept,
, for the community is, the slower it disseminates. If the significance is smaller than
for a long period of time, the concept vanishes from the community [see Equation (13)]. Therefore, due to a limited communication resource, the community has to follow a certain policy to be able to maintain a set of concepts over a period of time. Each policy must satisfy the following constraint that limits the average number of references produced by an individual per time unit:
where
is the average communication capacity of an individual in the community at time
. A way to determine a meaningful policy is to follow an informational principle that requires decreasing the self-information of the set of concepts over a long-lasting time period
.
Following the information theory, the self-information of the concept
is defined as follows [
10]:
and specifies an intuitive measure of surprise that a randomly chosen individual is aware of the concept
, which goes in line with the definition of
. In a certain sense, self-information
can be considered as the complexity of the concept perceived in the community.
The policy that distributes the communication resource between the
concepts maintained in the community over the interval
, and minimizes the total complexity of the set of concepts, is the solution of the following problem:
subject to the above-obtained equation of the dynamics of
:
and the resource constraint:
To clarify the concepts’ dynamics, we consider two examples: one for a steady state solution of Equation (17) and the other for a transient solution, which connects two different steady states.
A steady state is characterized by the number
of the concepts maintained by the community, the average age
of the community, average communication capacit
, concepts’ significance
and probabilities
of the concepts’ comprehension. Notice that since
is much larger than
,
i.e.,
and since
, the constraint (18) limits the number of concepts
as:
where
is the average probability of the concept’s comprehension
.
In the steady state, Equation (17) is reduced to the minimization of the stationary self-information:
subject to
,
, and
.
The solution of this problem is given by:
where the Lagrange multiplier
satisfies the following equation:
For clarifying the transition between two steady states, let that at the community with average age be in the steady state with concepts, each with the comprehension probability , , and the average communication capacity in the community is . Then, the probabilities and the concepts’ significance can be obtained by the Equations (21) and (13), respectively.
Assume that at
a new
-th concept is introduced, and within a relatively short time period
, its probability
is increased to a certain positive value so that
. If the new concept neither improves the comprehension probability of the other concepts, nor increases the average age
and the communication capacity
of the community, it will soon vanish (or, perhaps, will substitute other concept(s) that will vanish). Otherwise, the total self-information of the set of
concepts in steady state will be higher than the self-information before introducing the
-th concept that contradicts the minimization requirement (17). Assume that the introduction of the new concept has led to increasing the comprehension probabilities
of the other concepts
by the factor
,
i.e., . Denote by
the time, at which the set of
concepts reaches a close neighborhood of the new steady state. The transition between the previous steady state and the new one satisfies the following optimal control problem:
subject to:
where
,
and
are given and the death process is defined as in Equation (14). In other words, Equations (23)–(25) require distributing the concepts’ significances
as functions of time such that the information complexity (23) is minimal.
An approximate, numerical solution of the Equations (23)–(25) for the illustration case, when
,
,
,
,
,
,
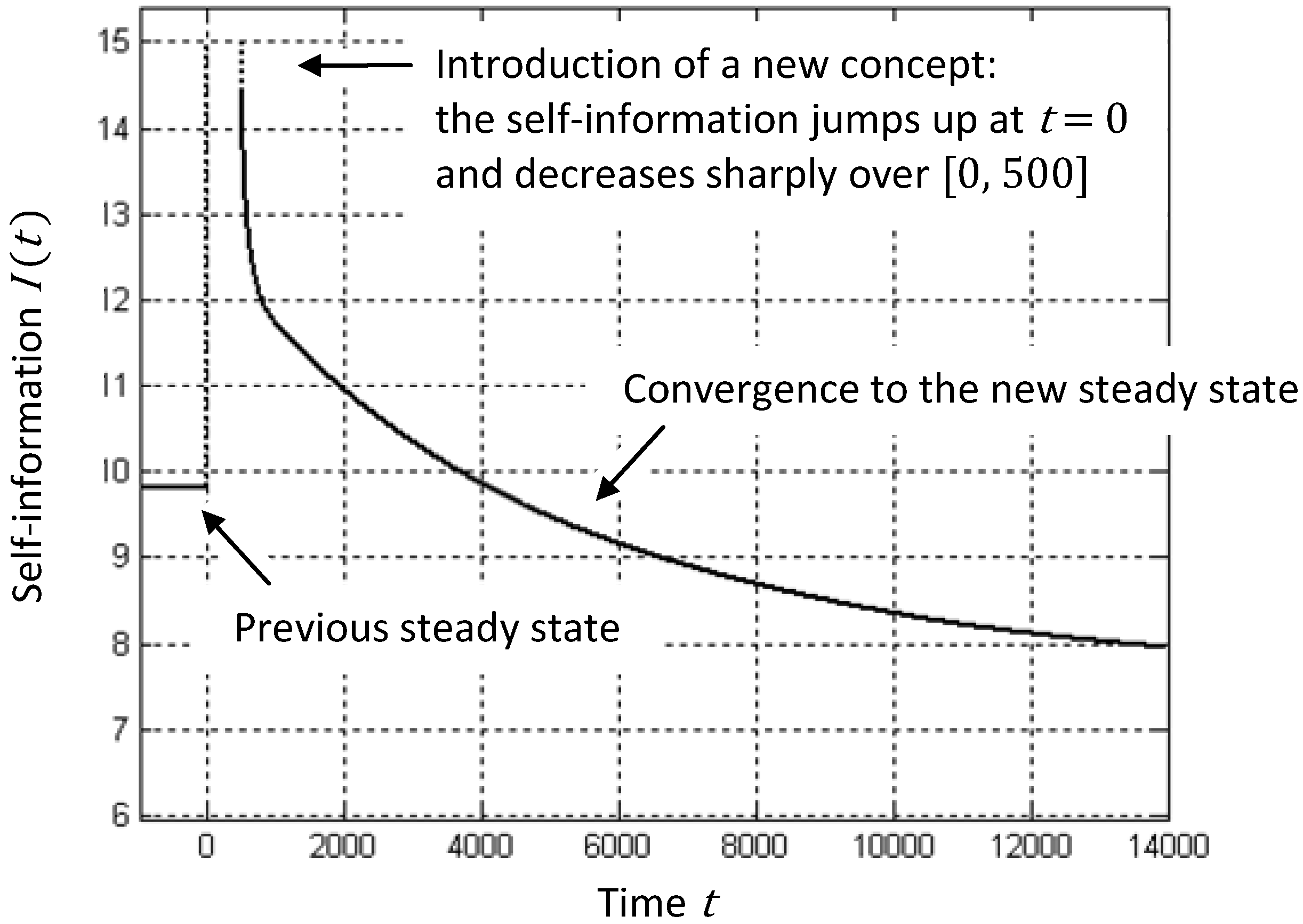
is plotted in
Figure 3. The system of
N concepts at
is characterized by the steady state probabilities,
, the concept’s significance,
,
, and the informational measure
.
Figure 3.
The self-information over the transition period.
Figure 3.
The self-information over the transition period.
The transition period, as shown in
Figure 3, consists of two arcs: at the first one, lasting about
time units, the entire communication resource is utilized by the
-th concept, while at the second, lasting up to about
time units, the resource is allocated among all the
concepts. The measure
goes down sharply over the first arc, decreases gradually over the second one and eventually converges to a new steady state with
,
and
. Thus, the introduction of a new concept, which improved the comprehension of the other concepts, has reduced the total complexity of the set of concepts. This goes in line with the long-term objective imposed by the community.
5. Discussion
The suggested approach deals with the dynamics of concepts in a homogeneous community. The assumption regarding the homogeneity allows applying average values for the comprehension probabilities and for the rates of referring the concepts in the dynamic equations. As a result, the concept’s dynamics have been developed and explained in terms of the communication channel between the group of cognoscenti and the group of dilettanti. Certainly, an enhancement of the model could consider uncertainties regarding the learning and forgetting abilities of the individuals in each group. In such a case, the comprehension and referring processes are to be modeled stochastically over the community, with the probability densities depending on time and skills of the individuals. In particular, such a model can take into account the dependences of the learning and forgetting abilities on age of the individual and the dependence of the communication rate on individual’s preferences and accessibility to communication resources.
The indicated dependences lead to the consideration of the concepts’ dynamics in a nonhomogeneous community with noisy communication channel. As a more realistic setup, such a model is expected to explain effects that can be hardly recognized within the homogeneous model. In fact, as far as the average values are concerned, the functions of time can be assumed smooth enough to provide continuous changes of the awareness probabilities. However, in some practical situations, especially for small size communities, the comprehension probabilities and referring rates can change dramatically over a very short time period. This requires use of impulse functions in the dynamic equations and may result in strongly non-linear effects in the evolution of the concepts.
These observations give rise to an unforeseen close relation between the dynamics of concepts and propagation of rumors, while, at the same time, the difference between the concepts’ dynamics and information diffusion is clearly predictable. The model of rumors propagation [
11] based on three groups of individuals: ignorants, spreaders and stifles, leads to the equations of the same kind as the equations specifying the dynamics of concepts. Such a relation can lead to a deeper understanding of the processes of collective cognition and social behavior and, with no doubt, deserves additional specific consideration. A particular example of this research direction is provided by informational bubbles that, in terms of the concept’s dynamics, are represented by a sharp rise of referring intensity followed by even more sharp (impulsive) drop in its significance.
The obtained results and possible further studies and implications, in addition to theoretical interest and input to a deeper understanding of social cognitive activities, can assist the community to make decisions regarding its financial, educational and cultural policy. Formal quantitative indicators with respect to temporary popularity of certain trademarks, university courses or genres of arts, which provide a measure of the referring rates and concepts’ significance, together with the knowledge of the concepts’ dynamics can assist in long term production planning, educational and social strategies, as well as can direct individuals in choosing labor activities. Another important application of the suggested techniques could be the analysis of impact of individual bloggers and their groups on the dissemination of knowledge in social networks.