Quantum Entanglement Concentration Based on Nonlinear Optics for Quantum Communications
Abstract
:1. Introduction
2. ECPs for Bell States
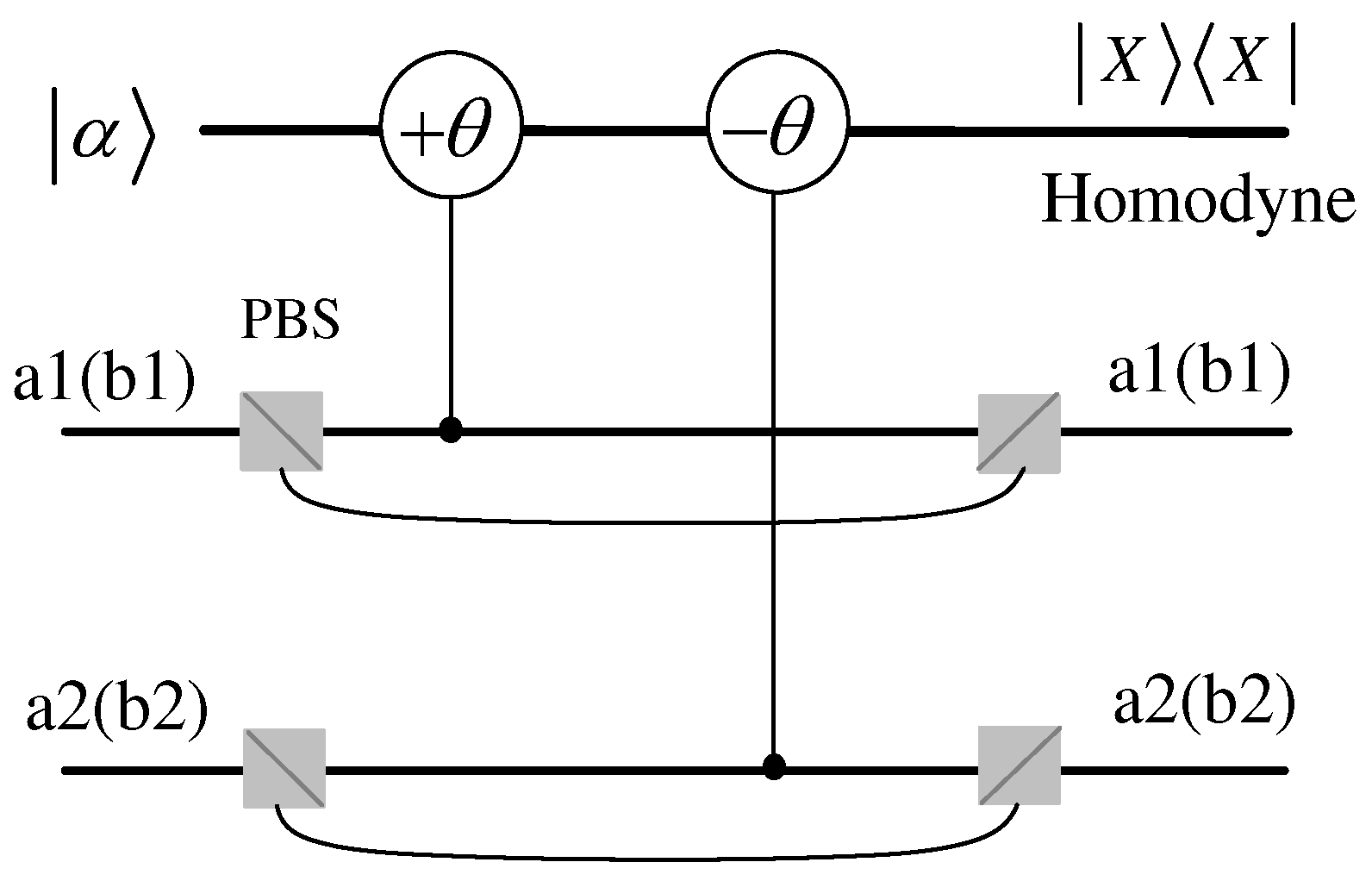
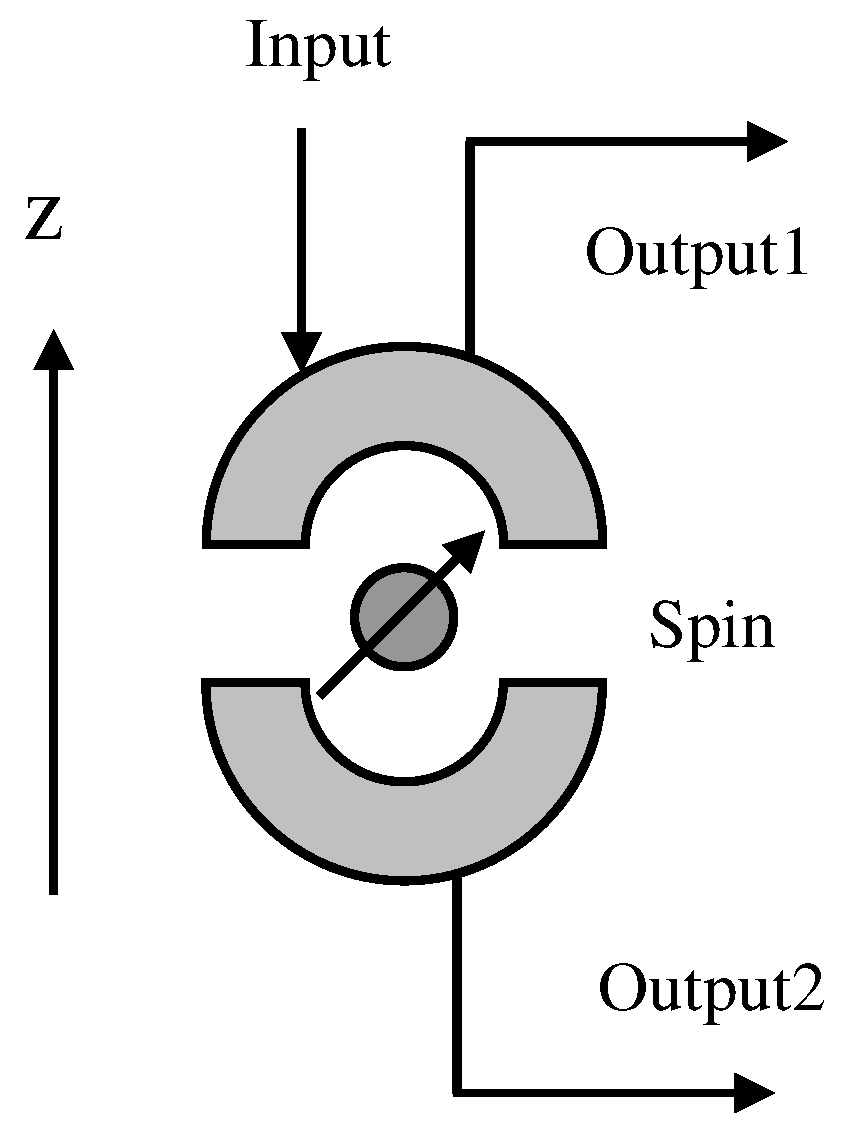
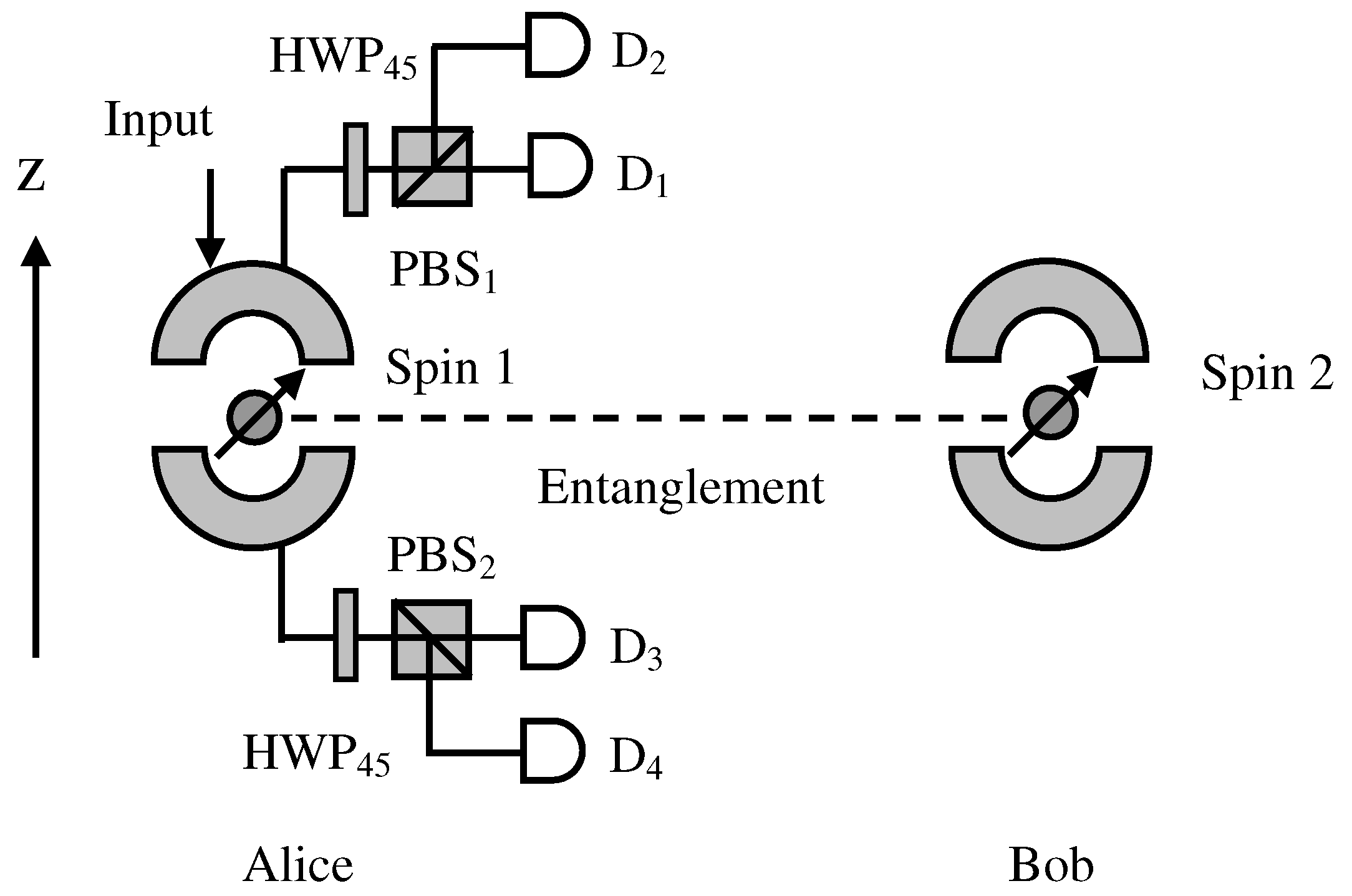
2.1. ECP with Cross-Kerr Nonlinearity
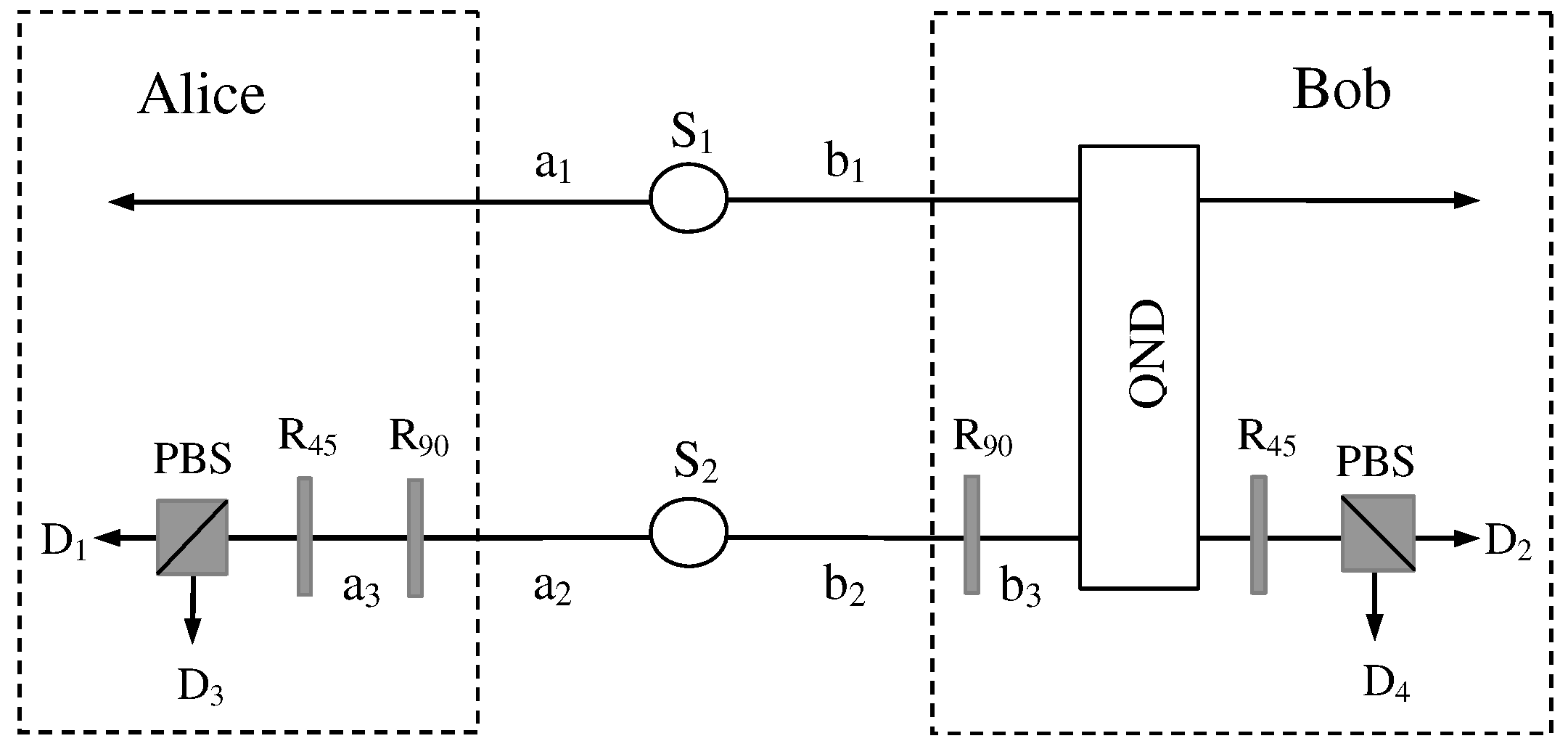
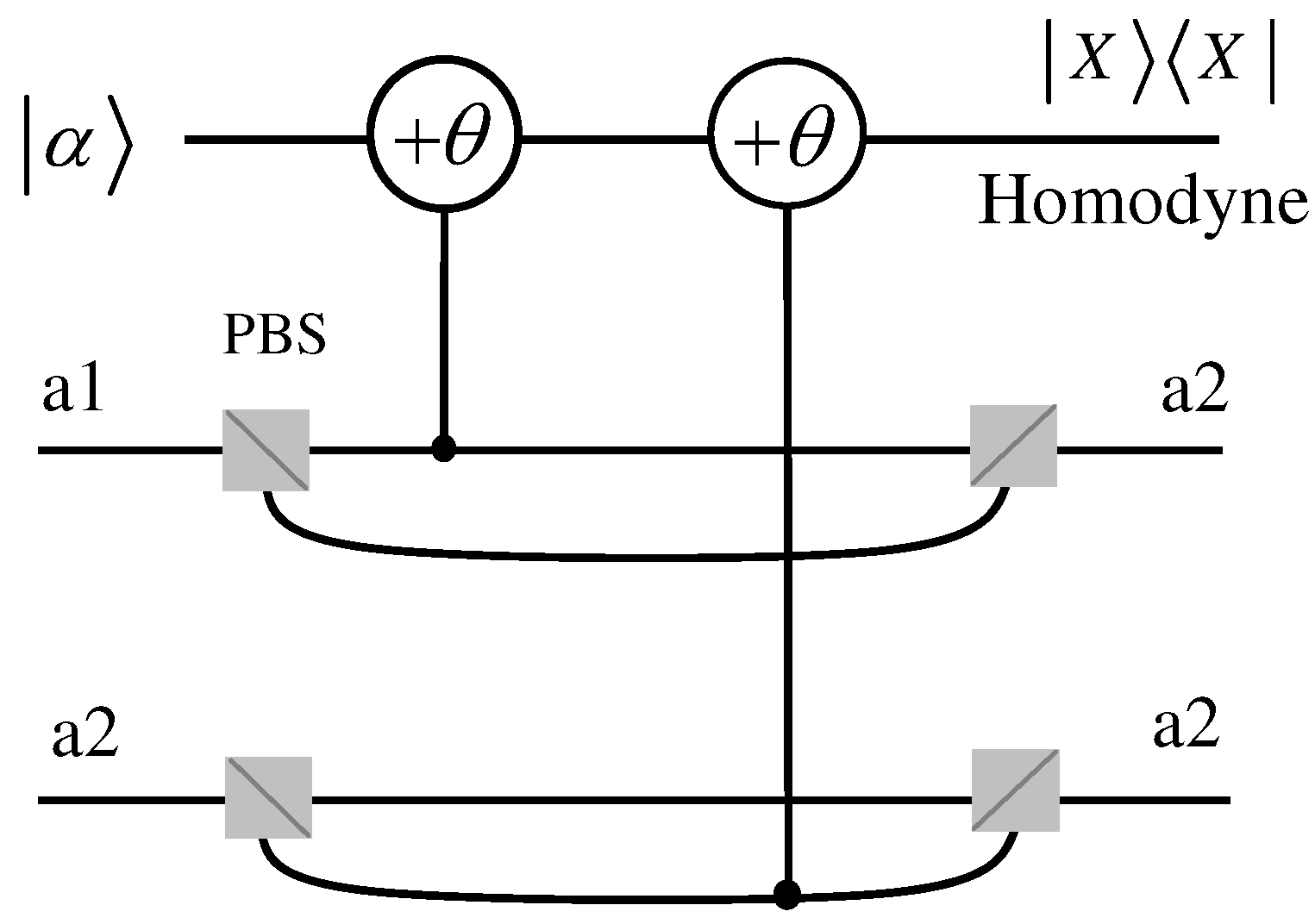
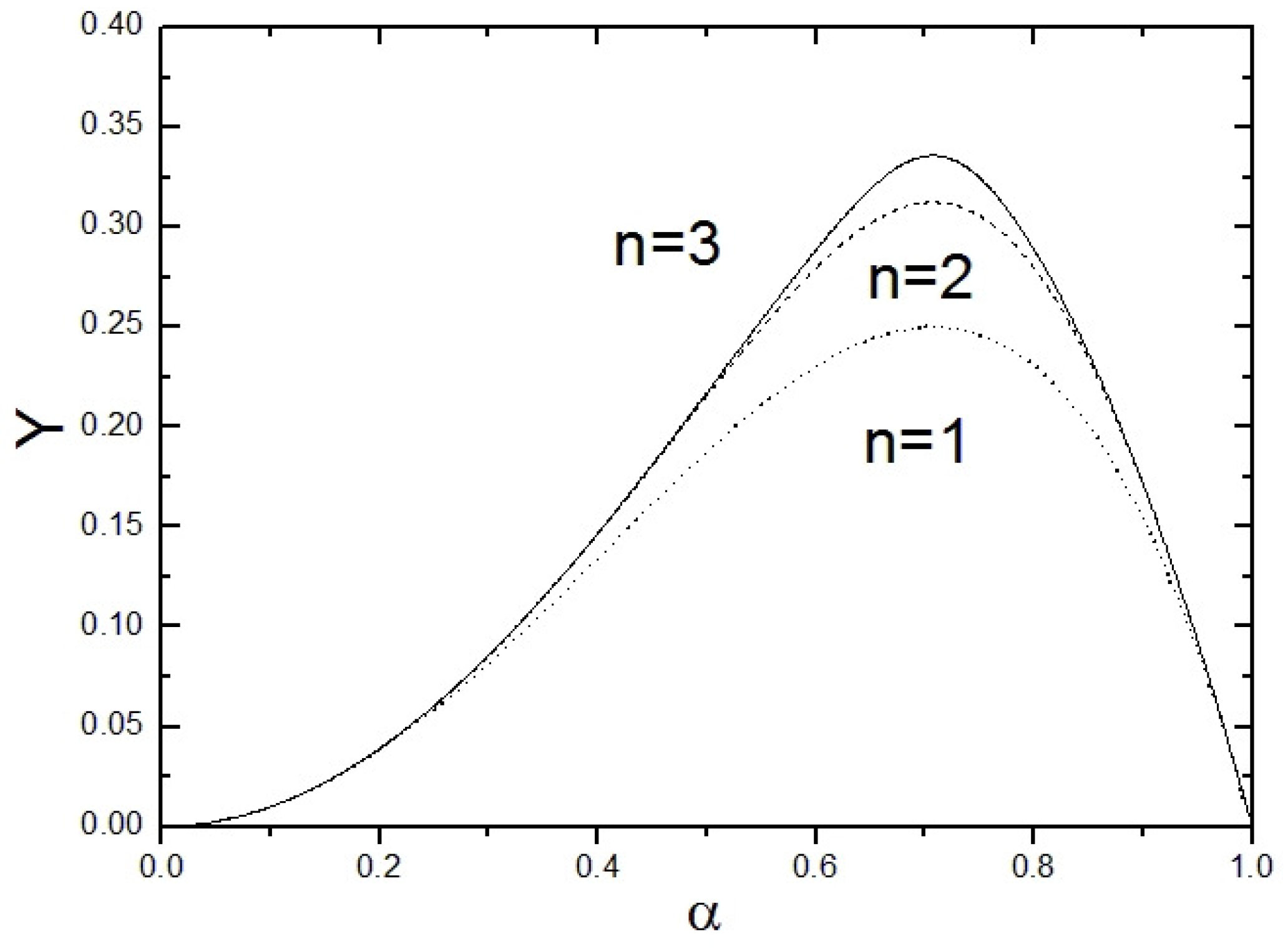
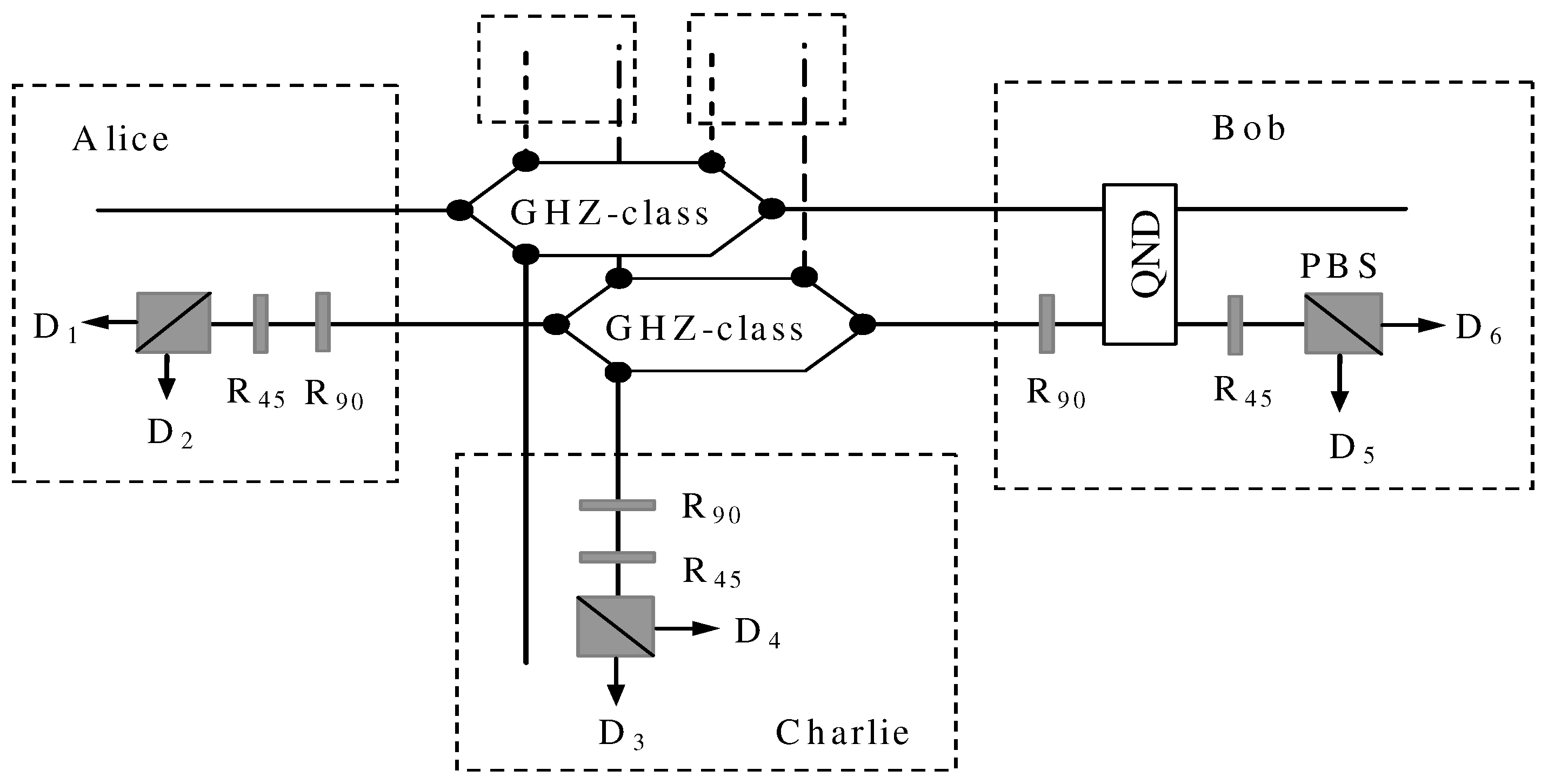
2.2. Single-Photon-Assisted Entanglement Concentration
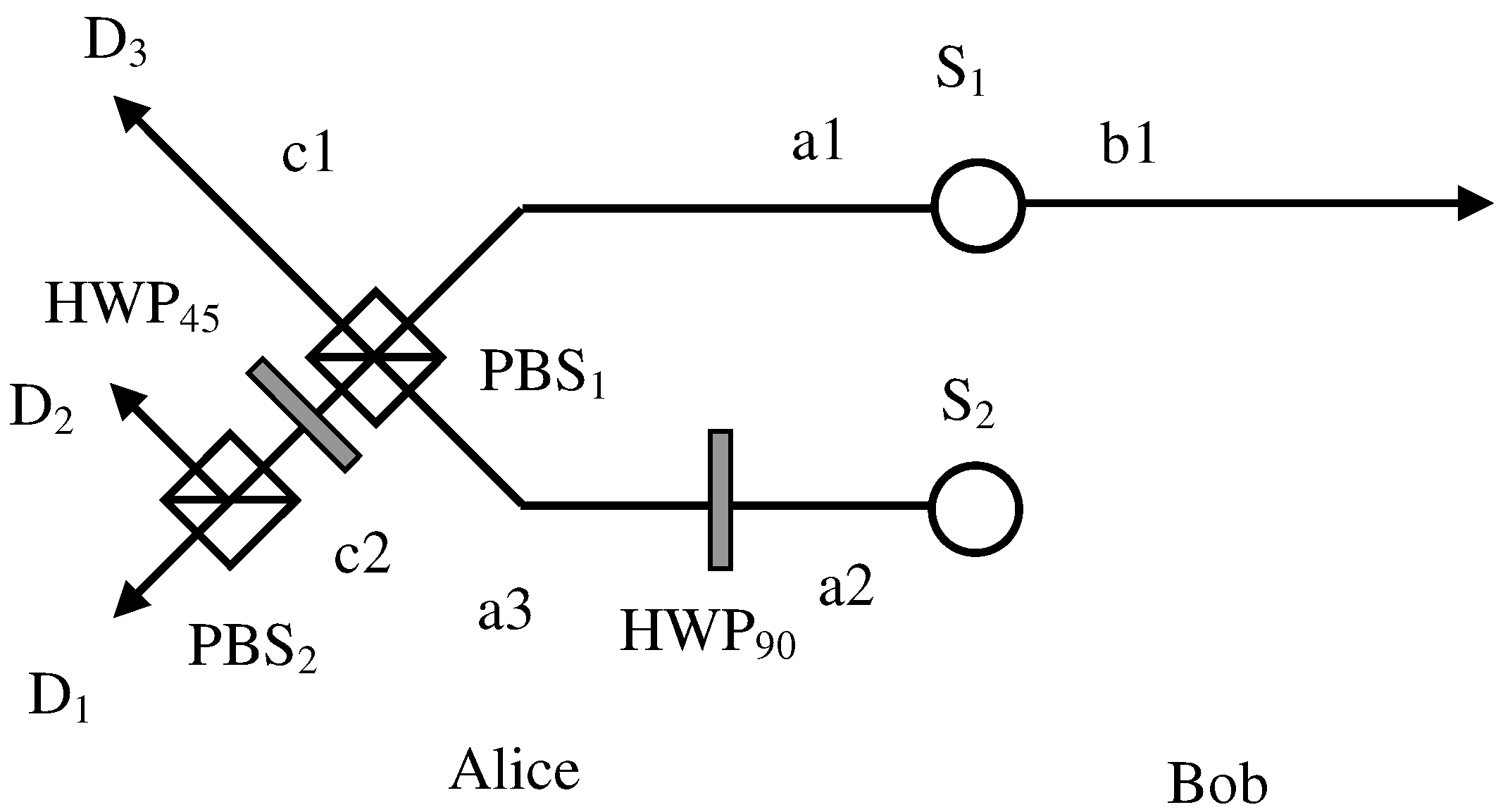
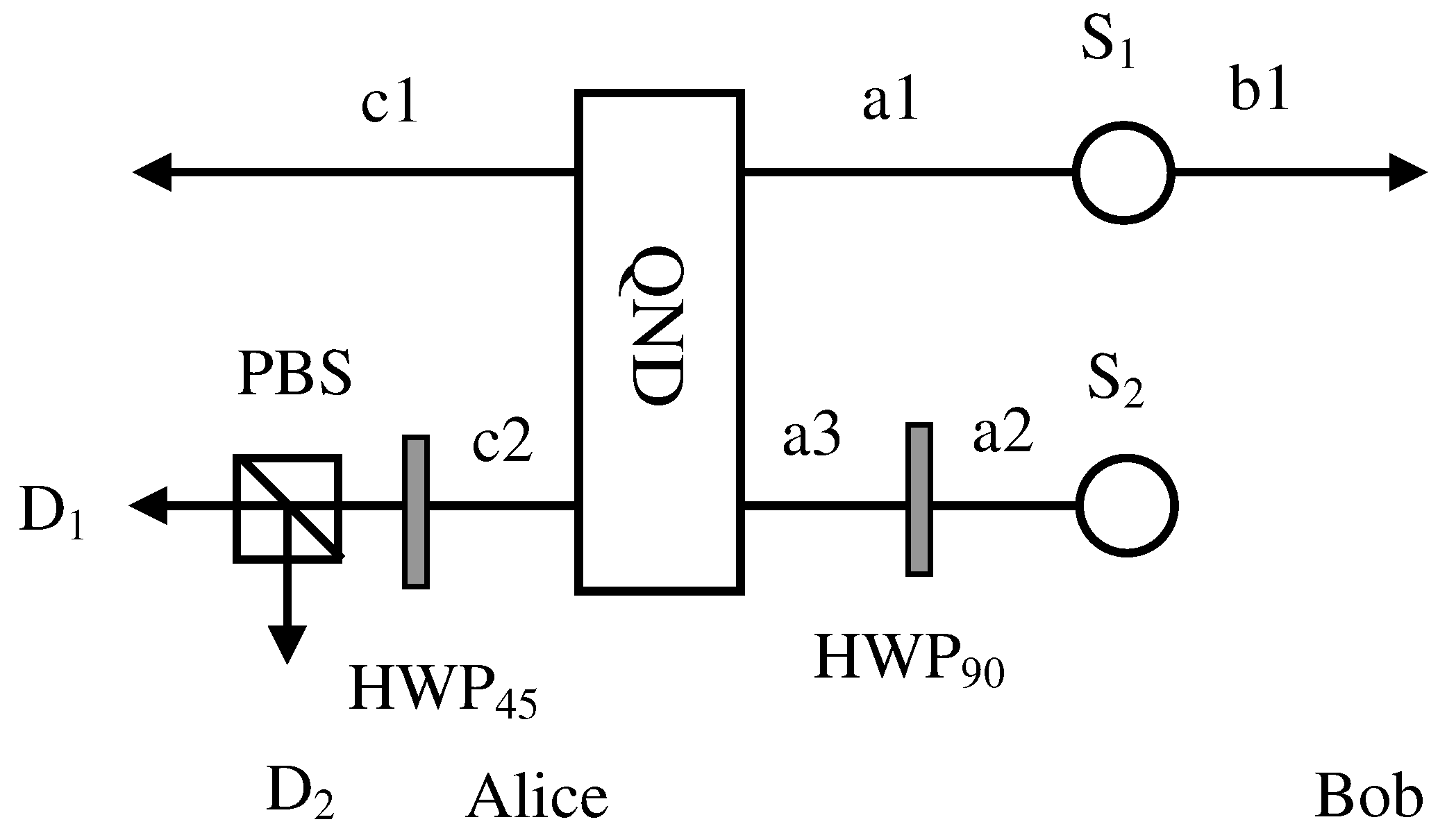
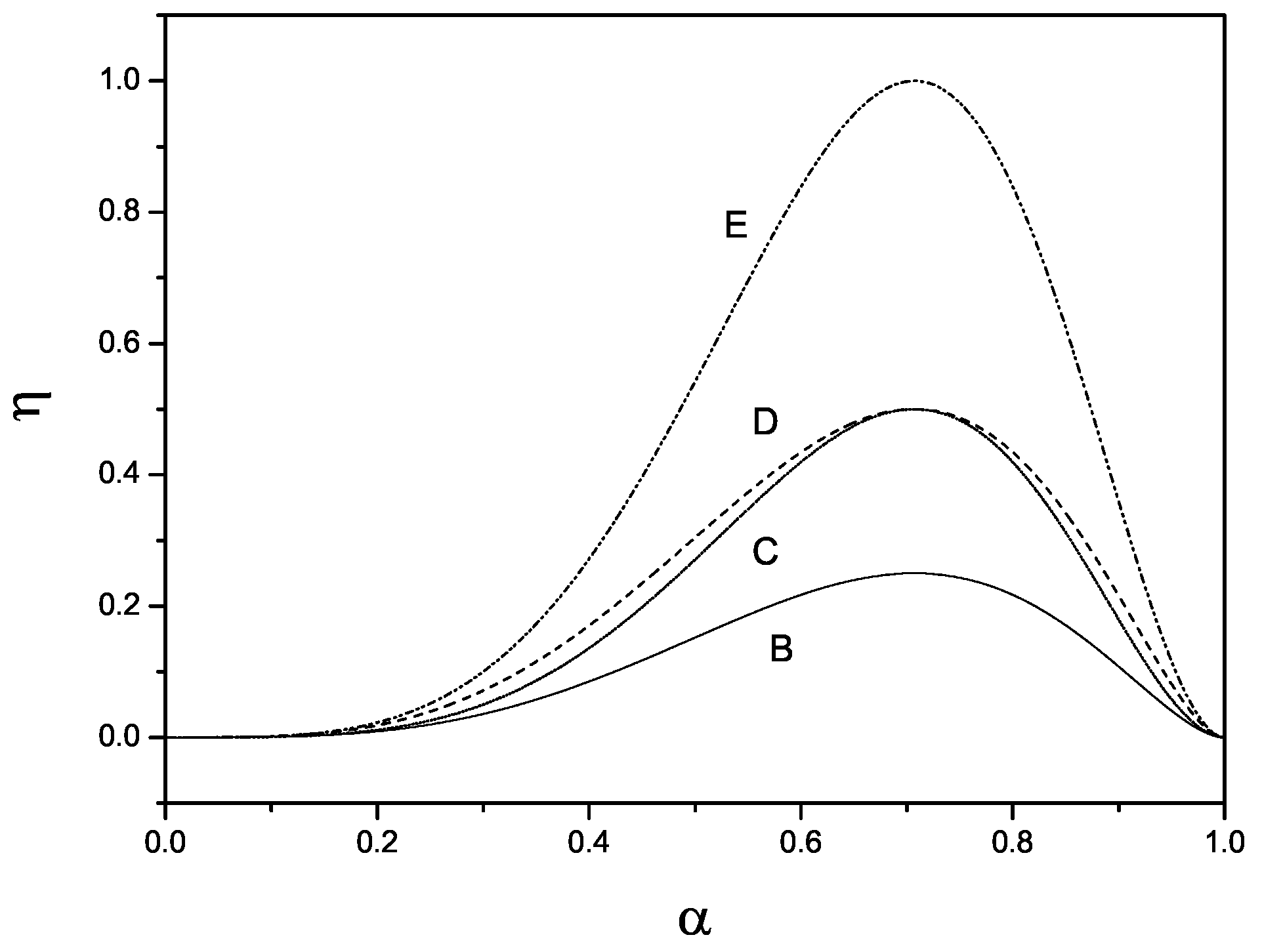
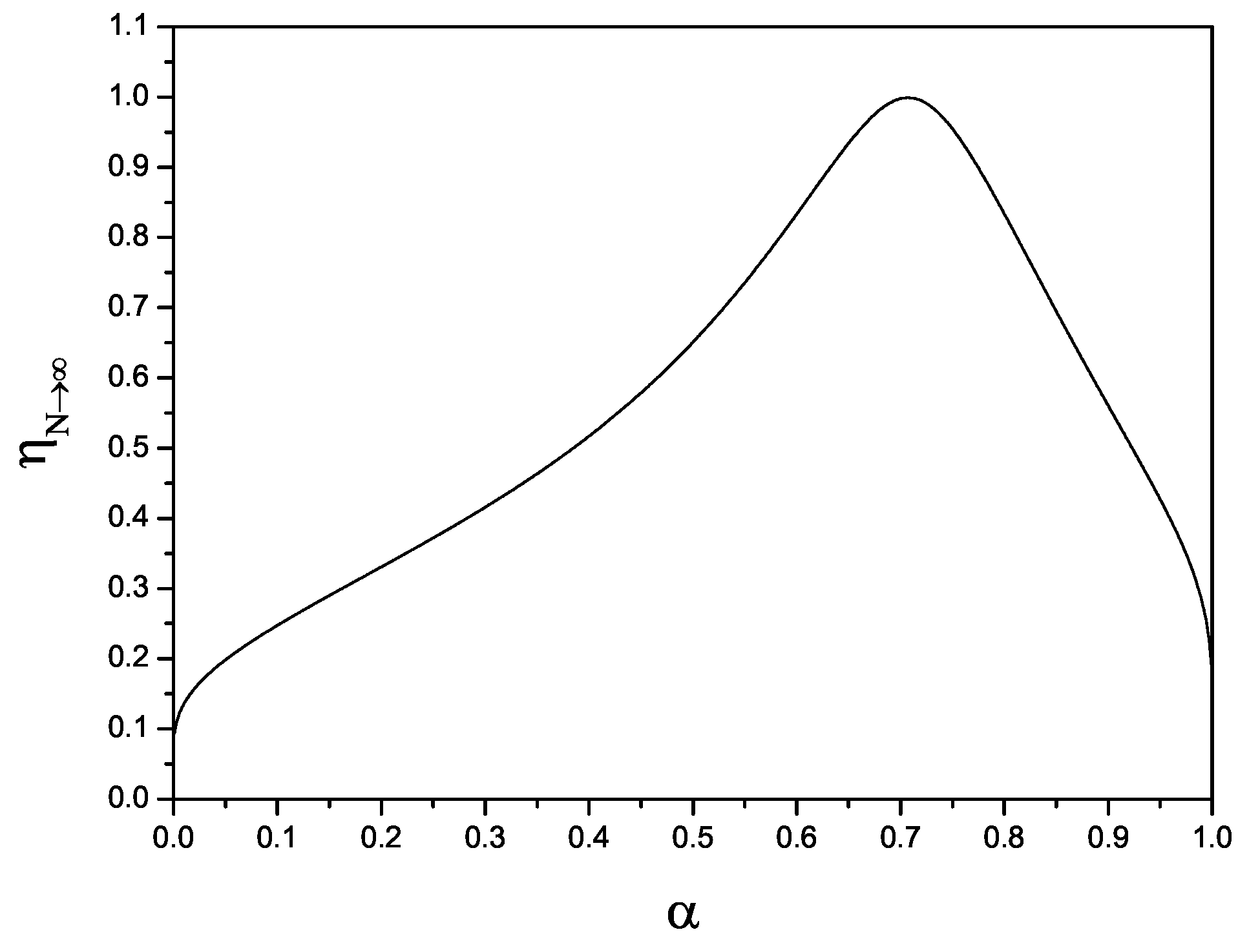
2.3. Entanglement Concentration for Single-Photon Entanglement
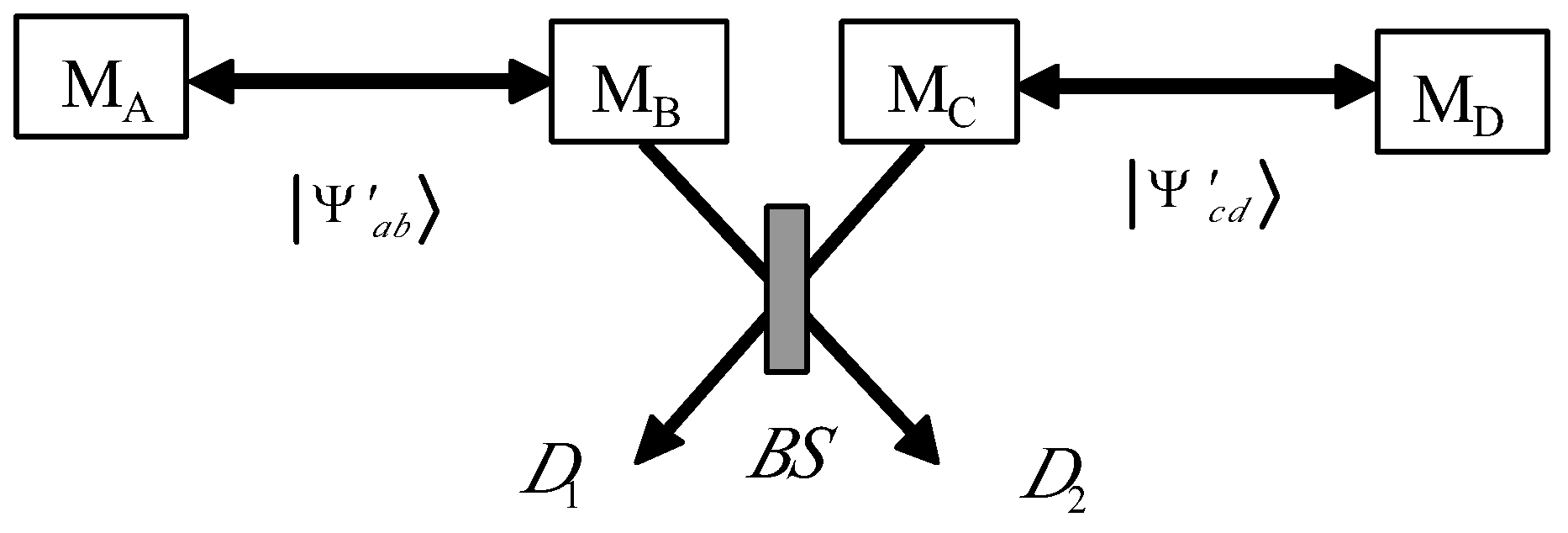
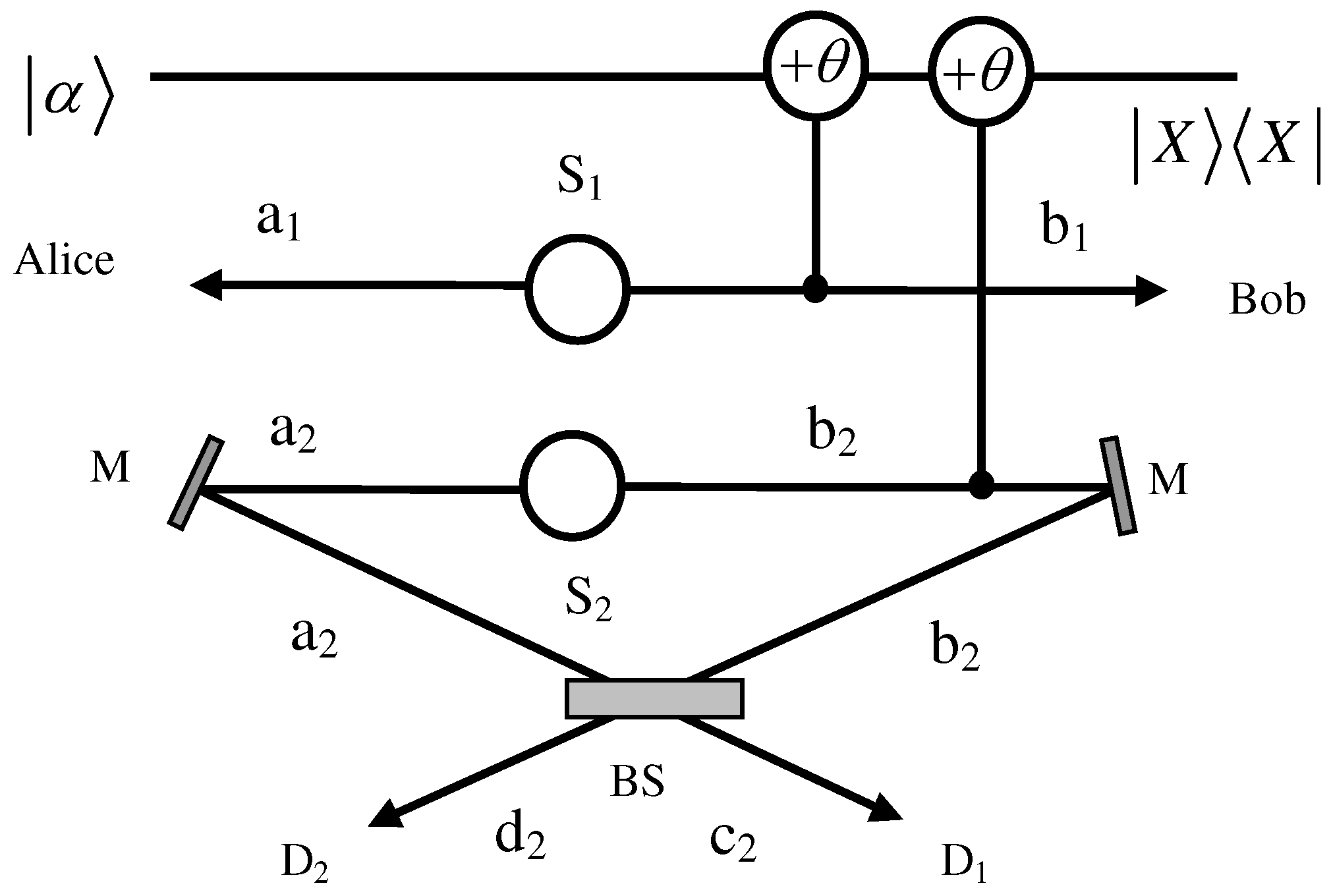
3. ECPs for W States
3.1. Two-Step Entanglement Concentration for Arbitrary W States
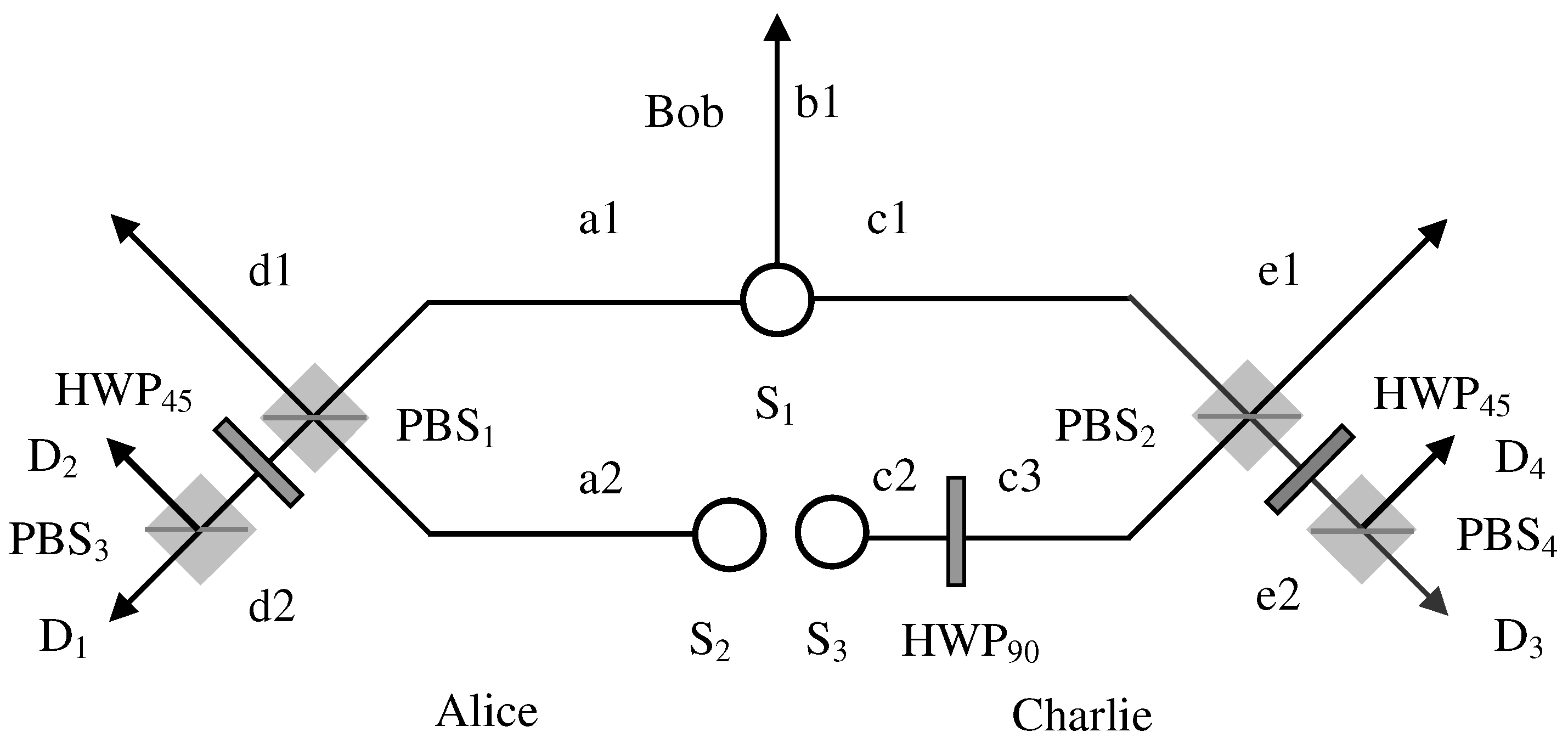
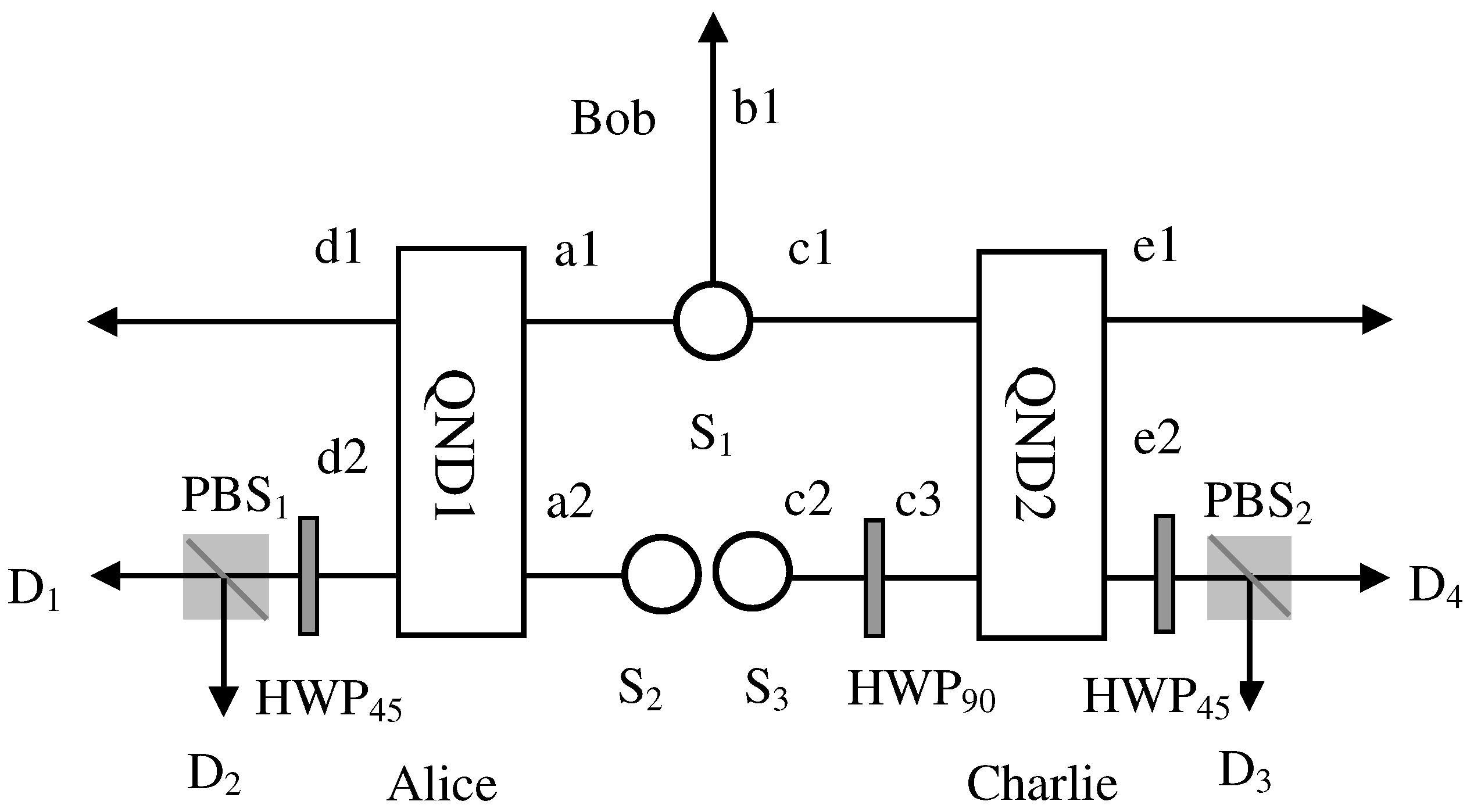
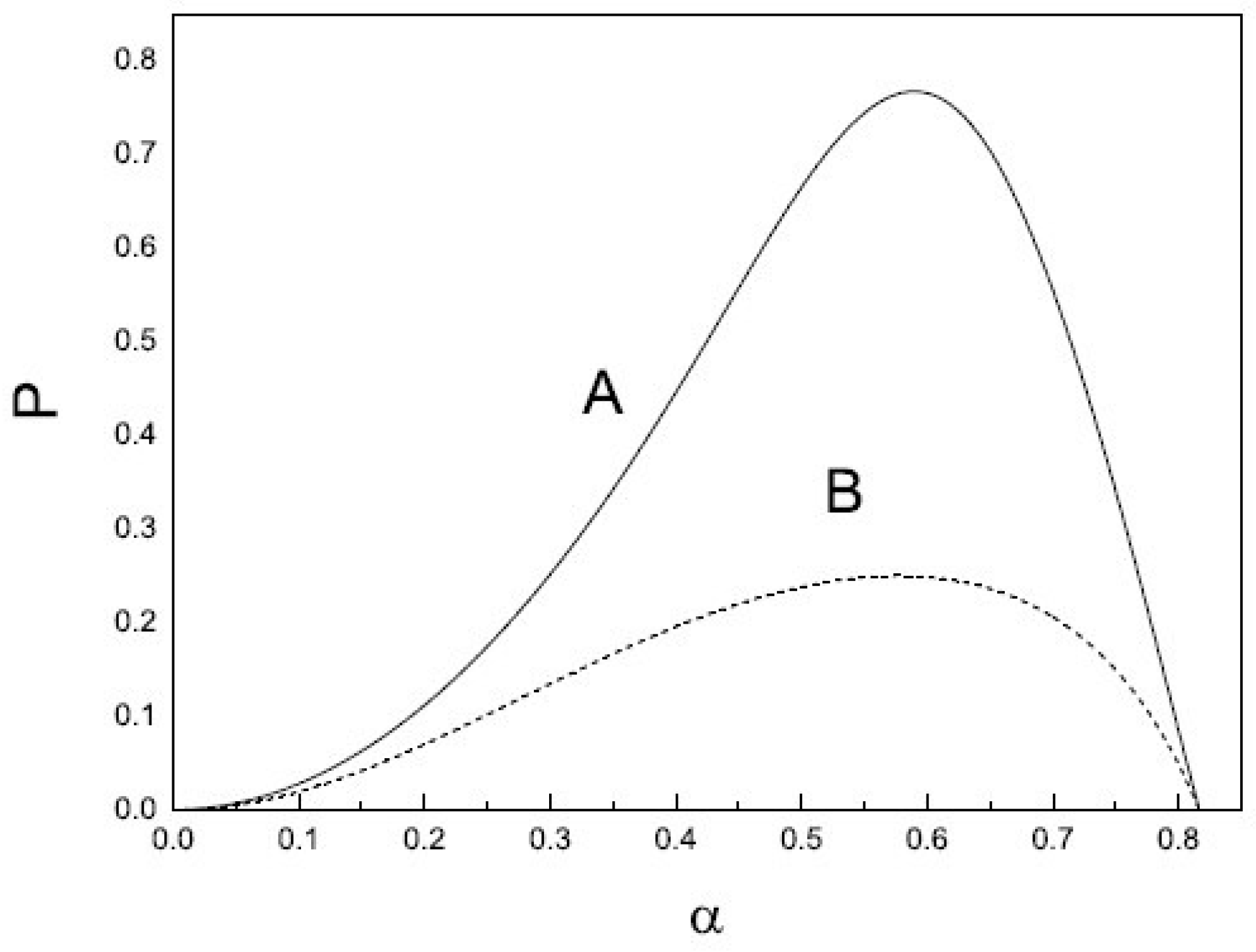
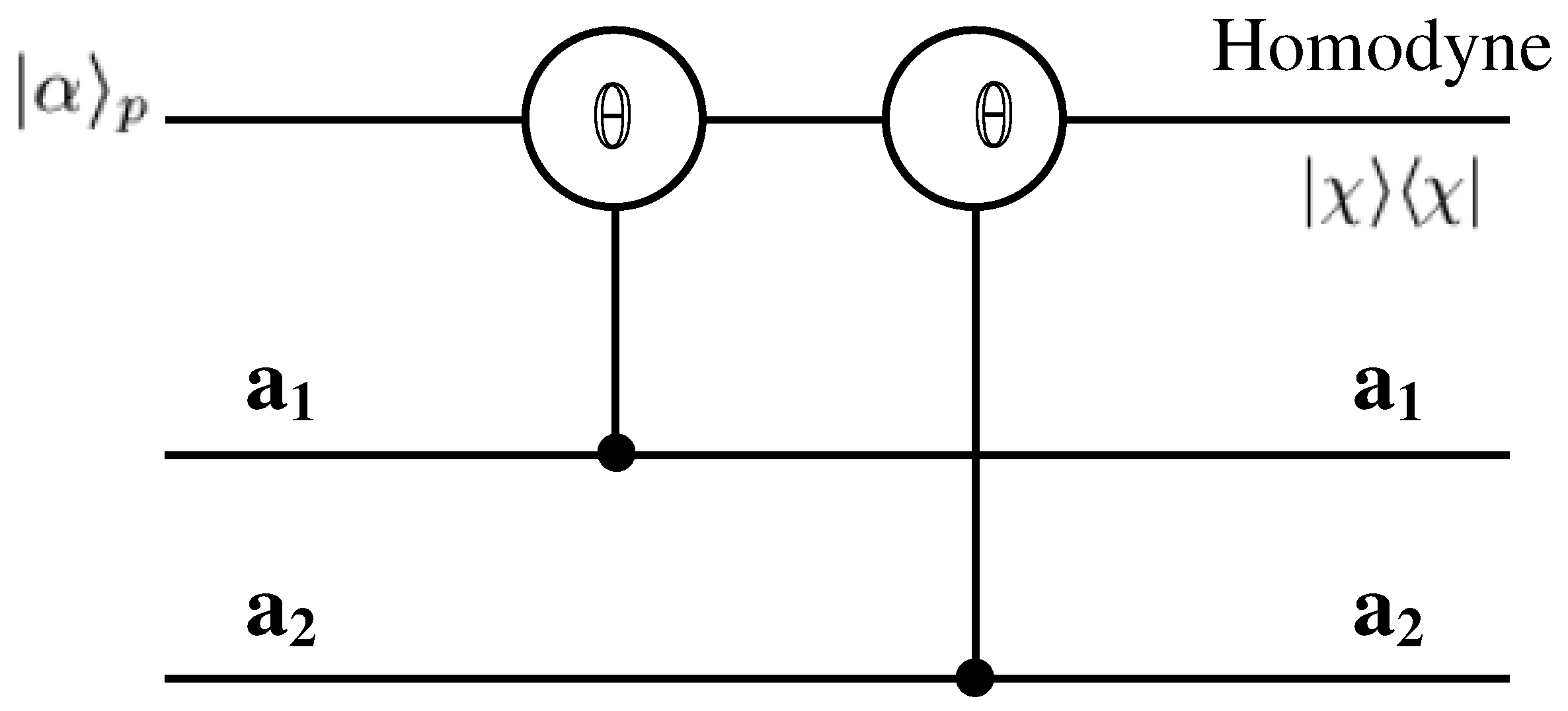
3.2. Entanglement Concentration for Single-Photon Multi-Mode W State
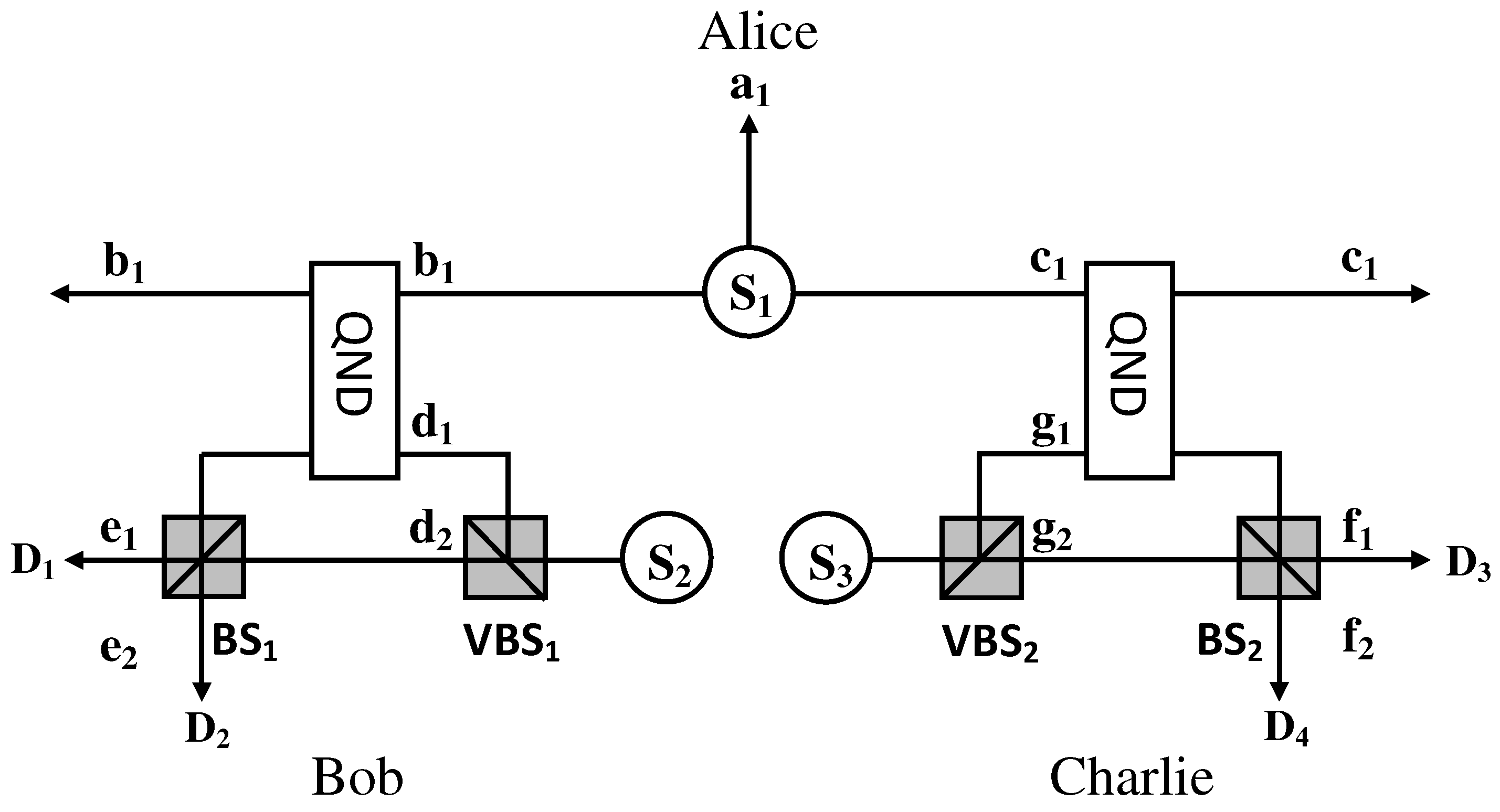
4. Some other ECPs
4.1. Entanglement Concentration for NOON State
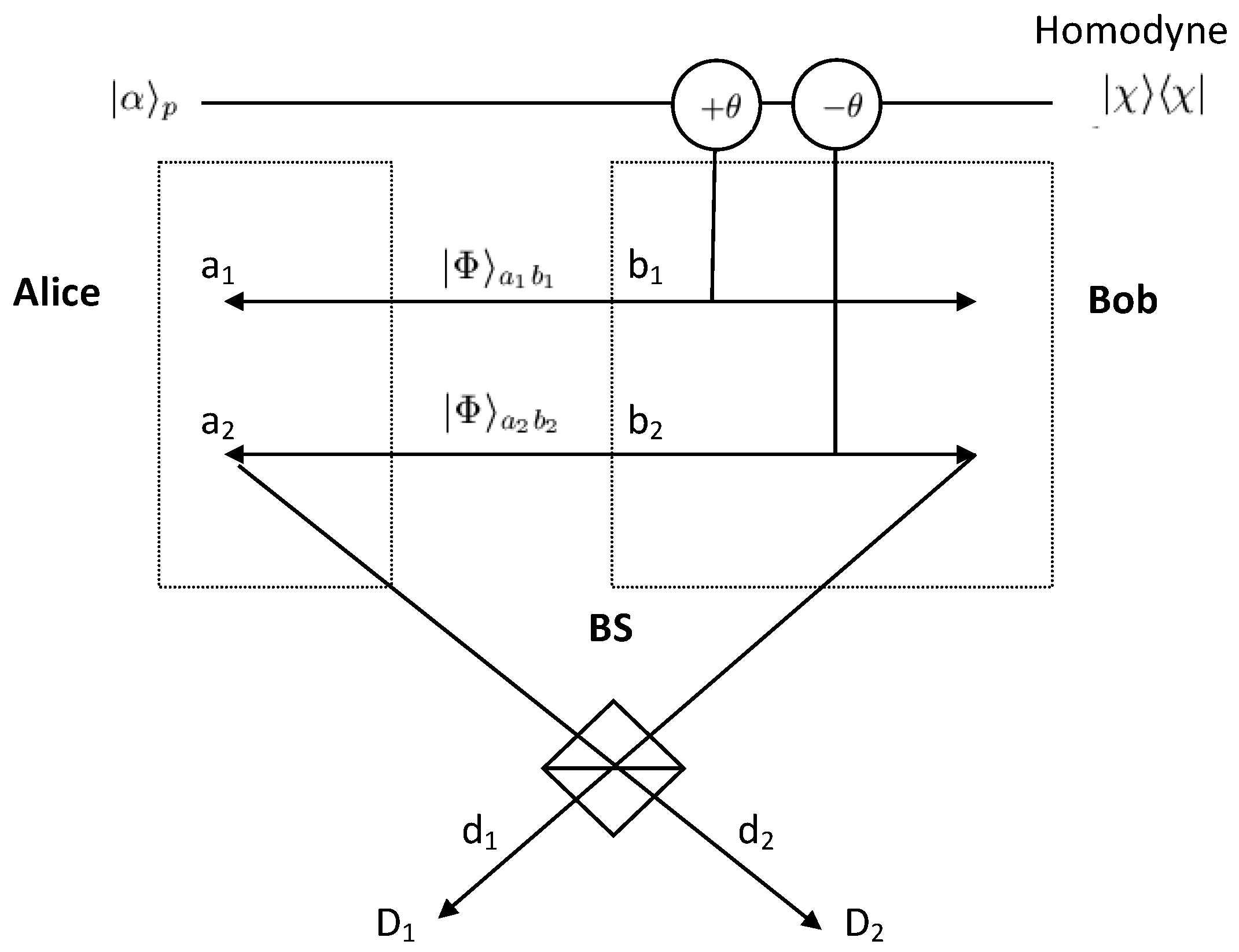
4.2. Entanglement Concentration for Electrons with Charge Detection
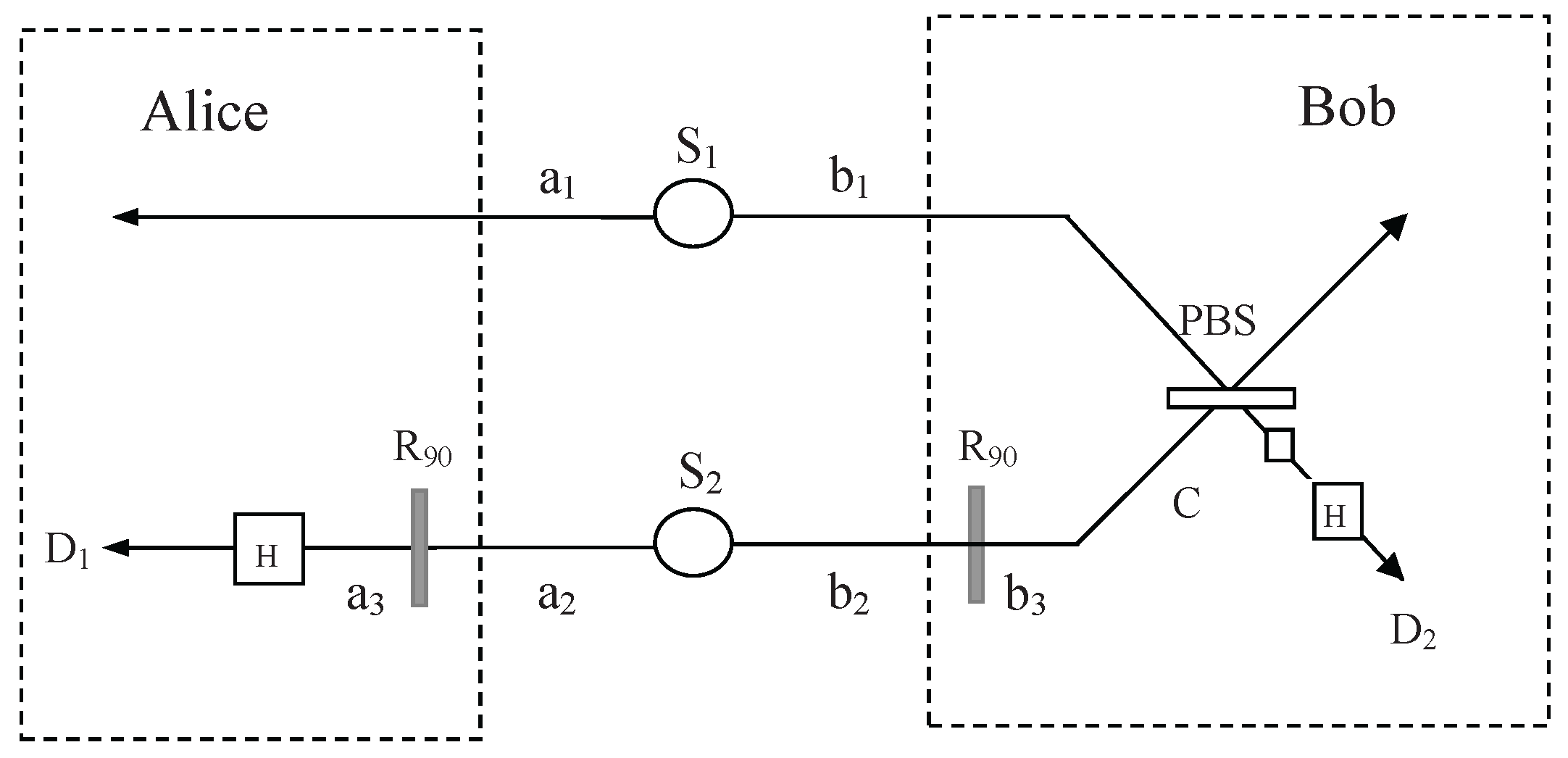
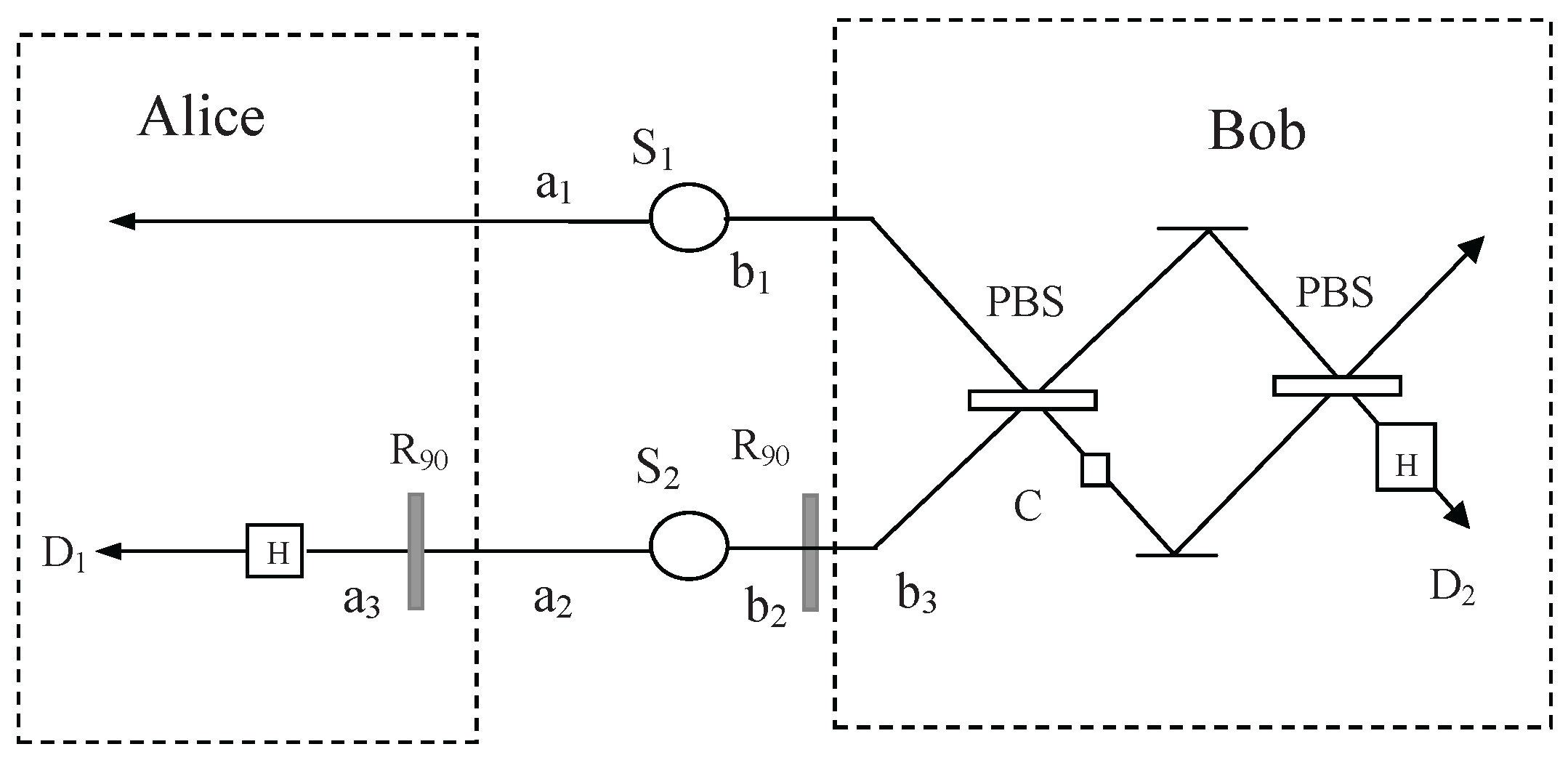
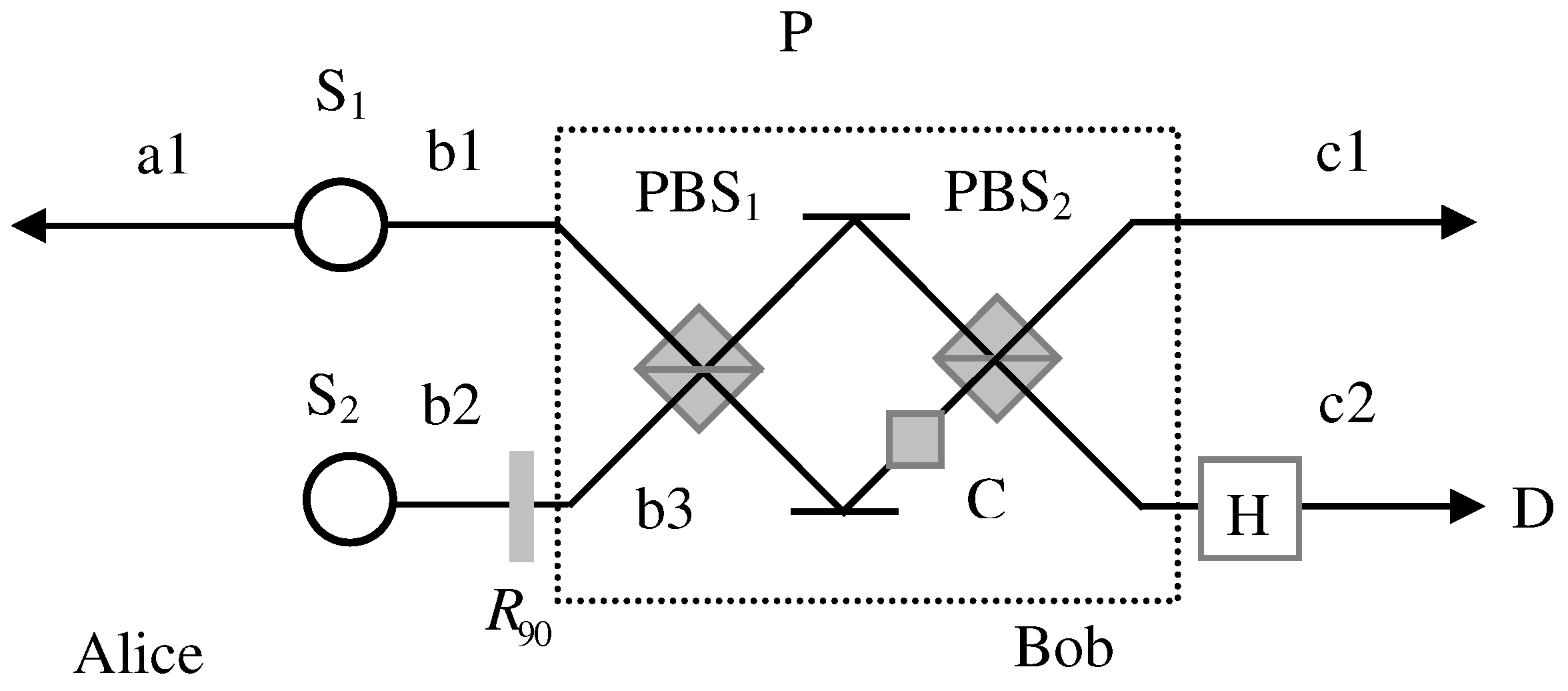
4.3. Efficient Entanglement Concentration for Quantum Dot and Optical Microcavities Systems
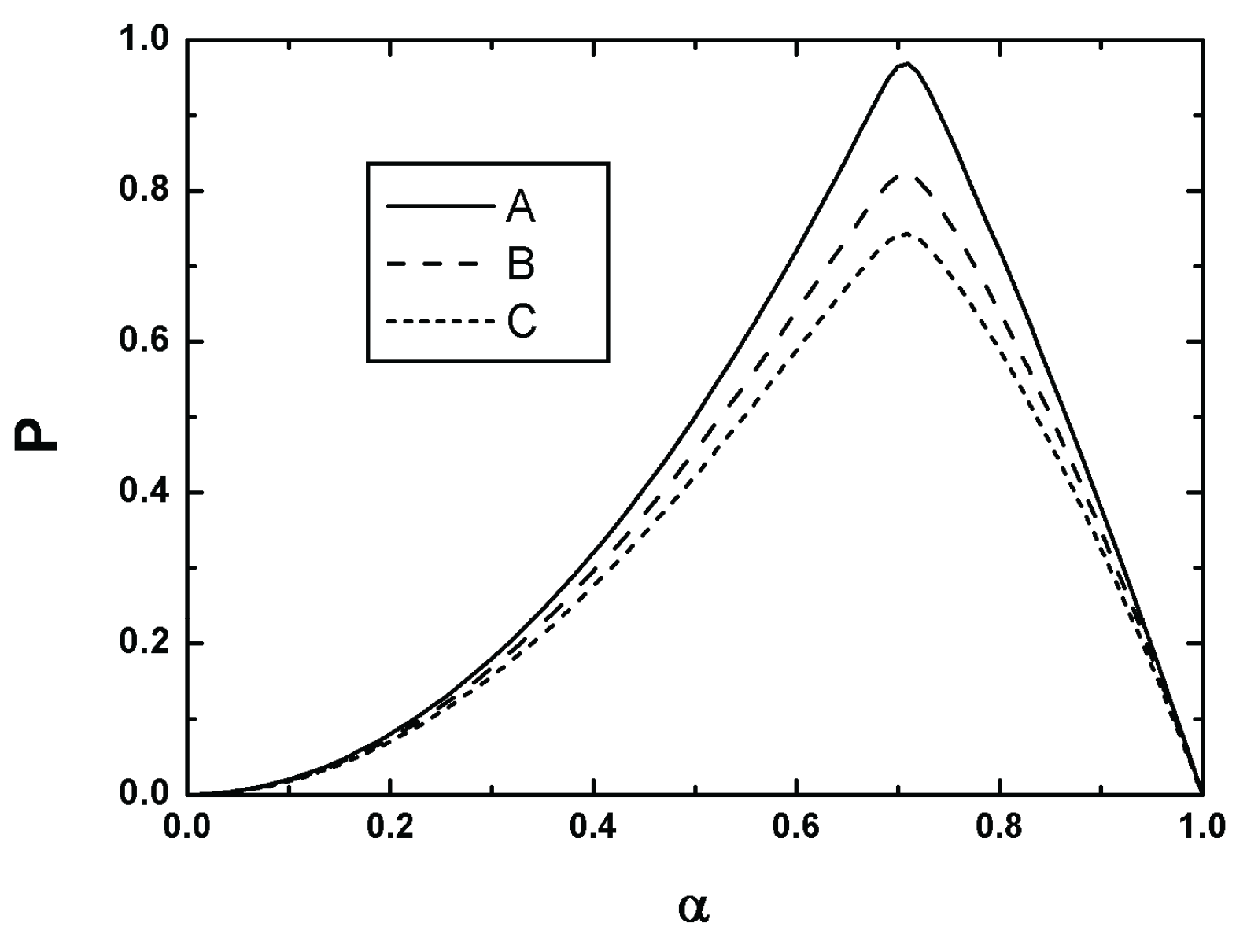
5. Discussion and Conclusion
Acknowledgments
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557–559. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of IEEE international Conference on Computers, Systems and Signal Processing, Bangalore, India, 10–19 December 1984; pp. 175–179.
- Long, G.L.; Liu, X.S. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A 2002, 65, 032302. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L.; Liu, X.S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68, 042317. [Google Scholar] [CrossRef]
- Wang, C.; Deng, F.G.; Li, Y.S.; Liu, X.S.; Long, G.L. Quantum secure direct communication with high-dimension quantum superdense coding. Phys. Rev. A 2005, 71, 044305. [Google Scholar] [CrossRef]
- Hillery, M.; Buzžek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829–1834. [Google Scholar] [CrossRef]
- Karlsson, A.; Koashi, M.; Imoto, N. Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A 1999, 59, 162–168. [Google Scholar] [CrossRef]
- Xiao, L.; Long, G.L.; Deng, F.G.; Pan, J.W. Efficient multiparty quantum-secret-sharing schemes. Phys. Rev. A 2004, 69, 052307. [Google Scholar] [CrossRef]
- Briegel, H.J.; Dür, W.; Cirac, J.I.; Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 1998, 81, 5932–5935. [Google Scholar] [CrossRef]
- Simon, C.; de Riedmatten, H.; Afzelius, M.; Sangouard, N.; Zbinden, H.; Gisin, N. Quantum repeaters with photon pair sources and multimode memories. Phys. Rev. Lett. 2007, 98, 190503. [Google Scholar] [CrossRef] [PubMed]
- Sangouard, N.; Simon, C.; de Riedmatten, H.; Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 2011, 83, 33–80. [Google Scholar] [CrossRef]
- Duan, L.M.; Lukin, M.D.; Cirac, J.T.; Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 2001, 414, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Thew, R.T.; Munro, W.J. Entanglement manipulation and concentration. Phys. Rev. A 2001, 63, 030302(R). [Google Scholar] [CrossRef]
- Thew, R.T.; Munro, W.J. Mixed state entanglement: Manipulating polarization-entangled photons. Phys. Rev. A 2001, 64, 022320. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Popescu, S.; Schumacher, B.; Smolin, J.A.; Wootters, W.K. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 1996, 76, 722–725. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.W.; Simon, C.; Zellinger, A. Entanglement purification for quantum communication. Nature 2001, 410, 1067–1070. [Google Scholar] [CrossRef] [PubMed]
- Simon, C.; Pan, J.W. Polarization entanglement purification using spatial entanglement. Phys. Rev. Lett. 2002, 89, 257901. [Google Scholar] [CrossRef] [PubMed]
- Sheng, Y.B.; Deng, F.G.; Zhou, H.Y. Efficient polarization-entanglement purification based on parametric down-conversion sources with cross-Kerr nonlinearity. Phys. Rev. A 2008, 77, 042308. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Deng, F.G. Deterministic entanglement purification and complete nonlocal Bell-state analysis with hyperentanglement. Phys. Rev. A 2010, 81, 032307. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Deng, F.G. One-step deterministic polarization-entanglement purification using spatial entanglement. Phys. Rev. A 2010, 82, 044305. [Google Scholar] [CrossRef]
- Deng, F.G. One-step error correction for multipartite polarization entanglement. Phys. Rev. A 2011, 83, 062316. [Google Scholar] [CrossRef]
- Deng, F.G. Efficient multipartite entanglement purification with the entanglement link from a subspace. Phys. Rev. A 2011, 84, 052312. [Google Scholar] [CrossRef]
- Li, X.H. Deterministic polarization-entanglement purification using spatial entanglement. Phys. Rev. A 2010, 82, 044304. [Google Scholar] [CrossRef]
- Cao, C.; Wang, C.; He, L.Y.; Zhang, R. Atomic entanglement purification and concentration using coherent state input-output process in low-Q cavity QED regime. Opt. Exp. 2013, 21, 4093–4105. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhang, Y.; Zhang, R. Entanglement purification based on hybrid entangled state using quantum-dot and microcavity coupled system. Opt. Exp. 2011, 19, 25685–25695. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Bernstein, H.J.; Popescu, S.; Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 1996, 53, 2046–2052. [Google Scholar] [CrossRef] [PubMed]
- Bose, S.; Vedral, V.; Knight, P.L. Purification via entanglement swapping and conserved entanglement. Phys. Rev. A 1999, 60, 194–197. [Google Scholar] [CrossRef]
- Shi, B.S.; Jiang, Y.K.; Guo, G.C. Optimal entanglement purification via entanglement swapping. Phys. Rev. A 2000, 62, 054301. [Google Scholar] [CrossRef]
- Zhao, Z.; Pan, J.W.; Zhan, M.S. Practical scheme for entanglement concentration. Phys. Rev. A 2001, 64, 014301. [Google Scholar] [CrossRef]
- Yamamoto, T.; Koashi, M.; Imoto, N. Concentration and purification scheme for two partially entangled photon pairs. Phys. Rev. A 2001, 64, 012304. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, T.; Chen, Y.A.; Zhang, A.N.; Pan, J.W. Experimental realization of entanglement concentration and a quantum repeater. Phys. Rev. Lett. 2003, 90, 207901. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T.; Koashi, M.; Ozdemir, S.K.; Imoto, N. Experimental extraction of an entangled photon pair from two identically decohered pairs. Nature 2003, 421, 343–346. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.B.; Heng, F. Entanglement concentration by ordinary linear optical devices without postselection. Phys. Rev. A 2003, 68, 060302. [Google Scholar]
- Boileau, J.-C.; Gottesman, D.; Laflamme, R.; Poulin, D.; Spekkens, R.W. Robust polarization-based quantum key distribution over a collective-noise channel. Phys. Rev. lett. 2004, 92, 017901. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T.; Shimamura, J.; Özdemir, S.K.; Koashi, M.; Imoto, N. Faithful qubit distribution assisted by one additional qubit against collective noise. Phys. Rev. lett. 2005, 95, 040503. [Google Scholar] [CrossRef] [PubMed]
- Li, X.H.; Deng, F.G.; Zhou, H.Y. Faithful qubit transmission against collective noise without ancillary qubits. Appl. Phys. Lett. 2007, 91, 144101. [Google Scholar] [CrossRef]
- Deng, F.G.; Li, X.H.; Deng, F.G. Passively self-error-rejecting qubit transmission over a collective-noise channel. Quant. Inf. Comput. 2011, 91, 913–924. [Google Scholar]
- Wilde, M.M. From Classical to Quantum Shannon Theory; Cambridge University Press: Cambridge, UK, 2012; in press. [Google Scholar]
- Nemoto, K.; Munro, W.J. Nearly deterministic linear optical controlled-not gate. Phys. Rev. Lett. 2004, 93, 250502. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Li, J. Quantum control gates with weak cross-Kerr nonlinearity. Phys. Rev. A 2009, 79, 022301. [Google Scholar] [CrossRef]
- Munro, W.J.; Nemoto, K.; Spiller, T.P. Weak nonlinearities: A new route to optical quantum computation. New J. Phys. 2005. [Google Scholar] [CrossRef]
- Barrett, S.D.; Kok, P.; Nemoto, K.; Beausoleil, R.G.; Munro, W.J.; Spiller, T.P. Symmetry analyzer for nondestructive Bell-state detection using weak nonlinearities. Phys. Rev. A 2005, 71, 060302(R). [Google Scholar] [CrossRef]
- Kurucz, Z.; Adam, P. Preparable ensembles for remote state preparation. J. Opt. B 2005, 7, 135–140. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Deng, F.G.; Long, G.L. Complete hyperentangled-Bell-state analysis for quantum communication. Phys. Rev. A 2010, 82, 032318. [Google Scholar] [CrossRef]
- Lin, Q.; He, B. Single-photon logic gates using minimal resources. Phys. Rev. A 2009, 80, 042310. [Google Scholar] [CrossRef]
- He, B.; Ren, Y.; Bergou, J.A. Creation of high-quality long-distance entanglement with flexible resources. Phys. Rev. A 2009, 79, 052323. [Google Scholar] [CrossRef]
- Munro, W.J.; Nemoto, K.; Beausoleil, R.G.; Spiller, T.P. High-efficiency quantum-nondemolition single-photon-number-resolving detector. Phys. Rev. A 2005, 71, 033819. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Deng, F.G. Efficient quantum entanglement distribution over an arbitrary collective-noise channel. Phys. Rev. A 2010, 81, 042332. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Deng, F.G.; Zhou, H.Y. Nonlocal entanglement concentration scheme for partially entangled multipartite systems with nonlinear optics. Phys. Rev. A 2008, 77, 062325. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Zhou, L.; Zhao, S.M.; Zheng, B.Y. Efficient single-photon-assisted entanglement concentration for partially entangled photon pairs. Phys. Rev. A 2012, 85, 012307. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Deng, F.G.; Zhou, H.Y. Single-photon entanglement concentration for long distance quantum communication. Quant. Inf. Comput. 2010, 10, 272–281. [Google Scholar]
- Munro, W.J.; Nemoto, K.; Spiller, T.P.; Beausoleil, R.G.; Kok, P.; Barrett, S.D. Optical quantum information processing utilizing weak nonlinearities: A little goes a long way. Proc. SPIE 2005, 5893. Quantum Communications and Quantum Imaging III, 58930I. [Google Scholar] [CrossRef]
- Cao, Z.L.; Yang, M. Entanglement distillation for three-particle W class states. J. Phys. B 2003, 36, 4245–4253. [Google Scholar] [CrossRef]
- Zhang, L.H.; Yang, M.; Cao, Z.L. Entanglement concentration for unknown W class states. Phys. Stat. Mech. Appl. 2007, 374, 611–616. [Google Scholar] [CrossRef]
- Yildiz, A. Optimal distillation of three-qubit W states. Phys. Rev. A 2010, 82, 012317. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Zhou, L.; Zhao, S.M. Efficient two-step entanglement concentration for arbitrary W states. Phys. Rev. A 2012, 85, 044305. [Google Scholar] [CrossRef]
- Zhou, L.; Sheng, Y.B.; Cheng, W.W.; Gong, L.Y.; Zhao, S.M. Efficient entanglement concentration for arbitrary single-photon multimode W state. J. Opt. Soc. Am. B 2013, 30, 71–78. [Google Scholar] [CrossRef]
- Furusawa, A.; Søensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional quantum teleportation. Science 1998, 282, 706–709. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Zhang, J.; Yan, Y.; Zhao, F.; Xie, C.; Peng, K. Experimental demonstration of tripartite entanglement and controlled dense coding for continuous variables. Phys. Rev. Lett. 2003, 90, 167903. [Google Scholar] [CrossRef] [PubMed]
- Aoki, T.; Takey, N.; Yonezawa, H.; Wakui, K.; Hiraoka, T.; Furusawa, A.; van Loock, P. Experimental creation of a fully inseparable tripartite continuous-variable state. Phys. Rev. Lett. 2003, 91, 080404. [Google Scholar] [CrossRef] [PubMed]
- Goöckl, O.; Lorenz, S.; Marquardt, C.; Heersink, J.; Brownnutt, M.; Silberhorn, C.; Pan, Q.; van Loock, P.; Korolkova, N.; Leuchs, G. Experiment towards continuous-variable entanglement swapping: Highly correlated four-partite quantum state. Phys. Rev. A 2003, 68, 012319. [Google Scholar]
- Sen(De), A.; Sen, U.; WieŻniak, M.; Kaszlikowski, D.; ˙ukowski, M. Multiqubit W states lead to stronger nonclassicality than Greenberger-Horne-Zeilinger states. Phys. Rev. A 2003, 68, 062306. [Google Scholar] [CrossRef]
- D¨r, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar]
- Chaves, R.; Davidovich, L. Robustness of entanglement as a resource. Phys. Rev. A 2010, 82, 052308. [Google Scholar] [CrossRef]
- Heaney, L.; Cabello, A.; Santos, M.F.; Vedral, V. Extreme nonlocality with one photon. New J. Phys. 2011, 13, 053054–053065. [Google Scholar] [CrossRef]
- Gottesman, D.; Jennewein, T.; Croke, S. Longer-Baseline Telescopes using quantum repeaters. Phys. Rev. Lett. 2012, 109, 070503. [Google Scholar] [CrossRef] [PubMed]
- Osorio, C.I.; Bruno, N.; Sangouard, N.; Zbinden, H.; Gisin, N.; Thew, R.T. Heralded photon amplification for quantum communication. Phys. Rev. A 2012, 86, 023815. [Google Scholar] [CrossRef]
- Dowling, J.P. Quantum optical metrology-the lowdown on high-N00N states. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Huelga, S.F.; Macchiavello, C.; Pellizzari, T.; Ekert, A.K. Improvement of frequency standards with quantum entanglement. Phys. Rev. Lett. 1997, 79, 3865–3868. [Google Scholar] [CrossRef]
- Mitchell, M.W.; Lundeen, J.S.; Steinberg, A.M. Super-resolving phase measurements with a multiphoton entangled state. Nature 2004, 429, 161–164. [Google Scholar] [CrossRef] [PubMed]
- Walther, P.; Pan, J.W.; Aspelmeyer, M.; Ursin, R.; Gasparoni, S.; Zeilinger, A. De Broglie wavelength of a non-local four-photon state. Natue 2004, 429, 158–161. [Google Scholar] [CrossRef] [PubMed]
- Nagata, T.; Okamoto, R.; ÓBrien, J.L.; Sasaki, K.; Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 2007, 316, 726–729. [Google Scholar] [CrossRef] [PubMed]
- Mermin, N.D. Extreme quantum entanglement in a superposition of macroscopically distinct states. Phys. Rev. Lett. 1990, 65, 1838–1841. [Google Scholar] [CrossRef] [PubMed]
- Boto, A.N.; Kok, P.; Abrams, D.S.; Braunstein, S.L.; Williams, C.P.; Dowling, J.P. Quantum interferometric optical lithography: Exploiting entanglement to beat the diffraction limit. Phys. Rev. Lett. 2000, 85, 2733–2736. [Google Scholar] [CrossRef] [PubMed]
- Bollinger, J.J.; Itano, W.M.; Wineland, D.J.; Heinzen, D.J. Optimal frequency measurements with maximally correlated states. Phys. Rev. A 1996, 54, R4649–R4652. [Google Scholar] [CrossRef] [PubMed]
- D’Angelo, M.; Chekhova, M.V.; Shih, Y. Two-photon diffraction and quantum lithography. Phys. Rev. Lett. 2001, 87, 013602. [Google Scholar] [CrossRef] [PubMed]
- Sun, F.W.; Ou, Z.Y.; Guo, G.C. Simple proof of fault tolerance in the graph-state model. Phys. Rev. A 2006, 73, 032308. [Google Scholar]
- Liu, B.; Ou, Z.Y. Feasibility of Bell tests with the W state. Phys. Rev. A 2010, 81, 033823. [Google Scholar]
- Zhou, L.; Sheng, Y.B.; Cheng, W.W.; Gong, L.Y.; Zhao, S.M. Efficient entanglement concentration for arbitrary less-entangled NOON states. Quant. Inf. Process. 2013, 12, 1307–1320. [Google Scholar] [CrossRef]
- Beenakker, C.W.J.; DiVincenzo, D.P.; Emary, C.; Kindermann, M. Charge detection enables free-electron quantum computation. Phys. Rev. Lett. 2004, 93, 020501. [Google Scholar] [CrossRef] [PubMed]
- Terhal, B.M.; DiVincenzo, D.P. Classical simulation of noninteracting-fermion quantum circuits. Phys. Rev. A 2002, 65, 032325. [Google Scholar] [CrossRef]
- Zhang, X.L.; Feng, M.; Gao, K.L. Cluster-state preparation and multipartite entanglement analyzer with fermions. Phys. Rev. A 2006, 73, 014301. [Google Scholar] [CrossRef]
- Feng, X.L.; Kwek, L.C.; Oh, C.H. Electronic entanglement purification scheme enhanced by charge detections. Phys. Rev. A 2005, 71, 064301. [Google Scholar] [CrossRef]
- Li, T.; Ren, B.C.; Wei, H.R.; Hua, M.; Deng, F.G. High-efficiency multipartite entanglement purification of electron-spin states with charge detection. Quant. Inf. Process. 2013, 12, 855–876. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Deng, F.G.; Zhou, H.Y. Multipartite electronic entanglement purification with charge detection. Phys. Lett. A 2011, 375, 396–400. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Zhou, L.; Cheng, W.W.; Gong, L.Y.; Zhao, S.M. Efficient electronic entanglement concentration assisted with single mobile electron. Chin. Phys. B 2013, accepted. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, R.; Zhang, Y.; Ma, H.Q. Multipartite electronic entanglement purification using quantum-dot spin and microcavity system. Quant. Inf. Process. 2013, 12, 525–536. [Google Scholar] [CrossRef]
- Trauzettel, B.; Jordan, A.N.; Beenakker, C.W.; Büttiker, M. Parity meter for charge qubits: An efficient quantum entangler. Phys. Rev. B 2006, 73, 235331. [Google Scholar] [CrossRef]
- Ionicioiu, R. Entangling spins by measuring charge: A parity-gate toolbox. Phys. Rev. A 2007, 75, 032339. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Deng, F.G.; Zhou, H.Y. Efficient polarization entanglement concentration for electrons with charge detection. Phys. Lett. A 2009, 373, 1823–1825. [Google Scholar] [CrossRef]
- Waks, E.; Vuckovic, J. Dipole induced transparency in drop-filter cavity-waveguide systems. Phys. Rev. Lett. 2006, 96, 153601. [Google Scholar] [CrossRef] [PubMed]
- Bonato, C.; Haupt, F.; Oemrawsingh, S.S.R.; Gudat, J.; Ding, D.; van Exter, M.P.; Bouwmeester, D. CNOT and Bell-state analysis in the weak-coupling cavity QED regime. Phys. Rev. Lett. 2010, 104, 160503. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.Y.; Munro, W.J.; Rarity, J.G. Deterministic photon entangler using a charged quantum dot inside a microcavity. Phys. Rev. B 2008, 78, 125318. [Google Scholar] [CrossRef]
- Hu, C.Y.; Munro, W.J.; ÓBrien, J.L.; Rarity, J.G. Proposed entanglement beam splitter using a quantum- dot spin in a double-sided optical microcavity. Phys. Rev. B 2009, 80, 205326. [Google Scholar] [CrossRef]
- Xu, X.; Yao, W.; Sun, B.; Steel, D.G.; Bracker, A.S.; Gammon, D.; Sham, L.J. A Jurassic ceratosaur from China helps clarify avian digital homologies. Nature 2009, 459, 940. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhang, Y.; Jin, G.S. Entanglement purification and concentration of electron-spin entangled states using quantum-dot spins in optical microcavities. Phys. Rev. A 2011, 84, 032307. [Google Scholar] [CrossRef]
- Wang, C. Efficient entanglement concentration for partially entangled electrons using a quantum-dot and microcavity coupled system. Phys. Rev. A 2012, 86, 012323. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Zhou, L.; Wang, L.; Zhao, S.M. Efficient entanglement concentration for quantum dot and optical microcavities systems. Quant. Inf. Process. 2013, 12, 1885–1895. [Google Scholar] [CrossRef]
- Shapiro, J.H. Single-photon Kerr nonlinearities do not help quantum computation. Phys. Rev. A 2006, 73, 062305. [Google Scholar] [CrossRef]
- Shapiro, J.H.; Razavi, M. Continuous-time cross-phase modulation and quantum computation. New J. Phys. 2007. [Google Scholar] [CrossRef]
- Gea-Banacloche, J. Impossibility of large phase shifts via the giant Kerr effect with single-photon wave packets. Phys. Rev. A 2010, 81, 043823. [Google Scholar] [CrossRef]
- He, B.; Lin, Q.; Simon, C. Cross-Kerr nonlinearity between continuous-mode coherent states and single photons. Phys. Rev. A 2011, 83, 053826. [Google Scholar] [CrossRef]
- Feizpour, A.; Xing, X.; Steinberg, A.M. Amplifying single-photon nonlinearity using weak measurements. Phys. Rev. Lett. 2011, 107, 133603. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Huang, G. Giant Kerr nonlinearity, controlled entangled photons and polarization phase gates in coupled quantum-well structures. Opt. Express 2011, 19, 23364–23376. [Google Scholar] [CrossRef] [PubMed]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Peng, Z.H.; Zou, J.; Liu, X.J.; Xiao, Y.J.; Kuang, L.M. Atomic and photonic entanglement concentration via photonic Faraday rotation. Phys. Rev. A 2012, 86, 034305. [Google Scholar] [CrossRef]
- Deng, F.G. Optimal nonlocal multipartite entanglement concentration based on projection measurements. Phys. Rev. A 2012, 85, 022311. [Google Scholar] [CrossRef]
- Du, F.F.; Li, T.; Ren, B.C.; Wei, H.R.; Deng, F.G. Single-photon-assisted entanglement concentration of a multi-photon system in a partially entangled W state with weak cross-Kerr nonlinearity. J. Opt. Soc. Am. B 2012, 29, 1399–1405. [Google Scholar] [CrossRef]
- Gu, B. Single-photon-assisted entanglement concentration of partially entangled multiphoton W states with linear optics. J. Opt. Soc. Am. B 2012, 29, 1685–1689. [Google Scholar] [CrossRef]
- Zhou, L. Efficient entanglement concentration for electron-spin W state with the charge detection. Quant. Inf. Process. 2013, 12, 2087–2101. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Zhou, L. Efficient W-state entanglement concentration using quantum-dot and optical microcavities. J. Opt. Soc. Am. B 2013, 30, 678–686. [Google Scholar] [CrossRef]
- Wang, H.F.; Zhang, S.; Yeon, K.H. Linear-optics-based entanglement concentration of unknown partially entangled three photon W states. J. Opt. Soc. Am. B 2010, 27, 2159–2164. [Google Scholar] [CrossRef]
- Xiong, W.; Ye, L. Schemes for entanglement concentration of two unknown partially entangled states with cross-Kerr nonlinearity. J. Opt. Soc. Am. B 2011, 28, 2030–2037. [Google Scholar] [CrossRef]
- Wang, T.J.; Long, G.L. Entanglement concentration for arbitrary unknown less-entangled three-photon W states with linear optics. J. Opt. Soc. Am. B 2013, 30, 1069–1076. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sheng, Y.-B.; Zhou, L. Quantum Entanglement Concentration Based on Nonlinear Optics for Quantum Communications. Entropy 2013, 15, 1776-1820. https://doi.org/10.3390/e15051776
Sheng Y-B, Zhou L. Quantum Entanglement Concentration Based on Nonlinear Optics for Quantum Communications. Entropy. 2013; 15(5):1776-1820. https://doi.org/10.3390/e15051776
Chicago/Turabian StyleSheng, Yu-Bo, and Lan Zhou. 2013. "Quantum Entanglement Concentration Based on Nonlinear Optics for Quantum Communications" Entropy 15, no. 5: 1776-1820. https://doi.org/10.3390/e15051776
APA StyleSheng, Y.-B., & Zhou, L. (2013). Quantum Entanglement Concentration Based on Nonlinear Optics for Quantum Communications. Entropy, 15(5), 1776-1820. https://doi.org/10.3390/e15051776



