Bayesian and Quasi-Bayesian Estimators for Mutual Information from Discrete Data
Abstract
:1. Introduction
2. Entropy and Mutual Information
3. Bayesian Entropy Estimation
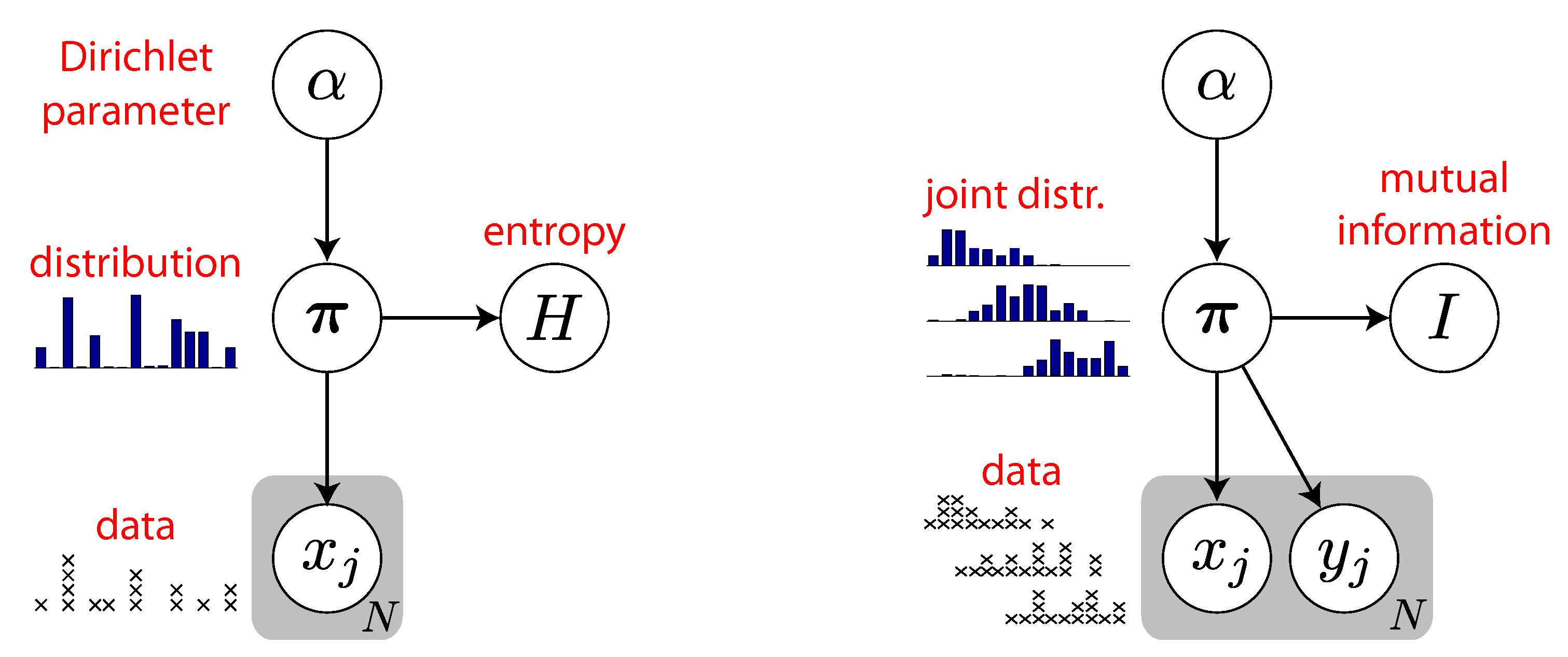
3.1. Quantifying Uncertainty
3.2. Efficient Computation
4. Quasi-Bayesian Estimation of MI
4.1. Bayesian Entropy Estimates do not Give Bayesian MI Estimates
5. Fully Bayesian Estimation of MI
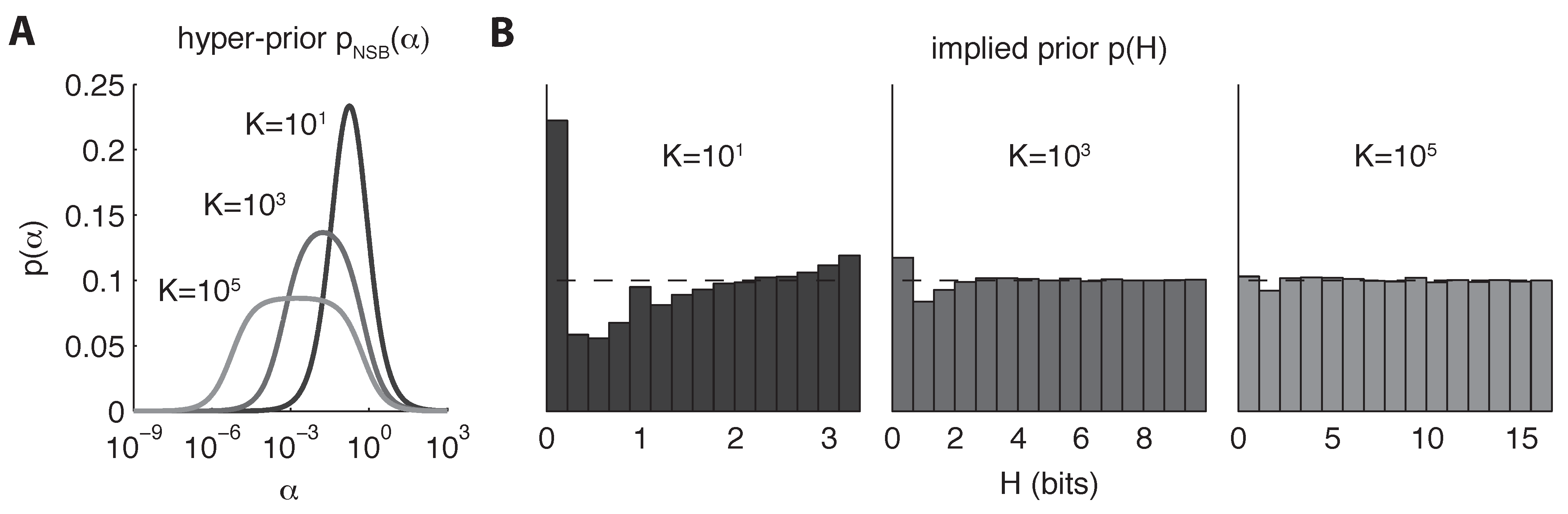
5.1. Dirichlet Prior
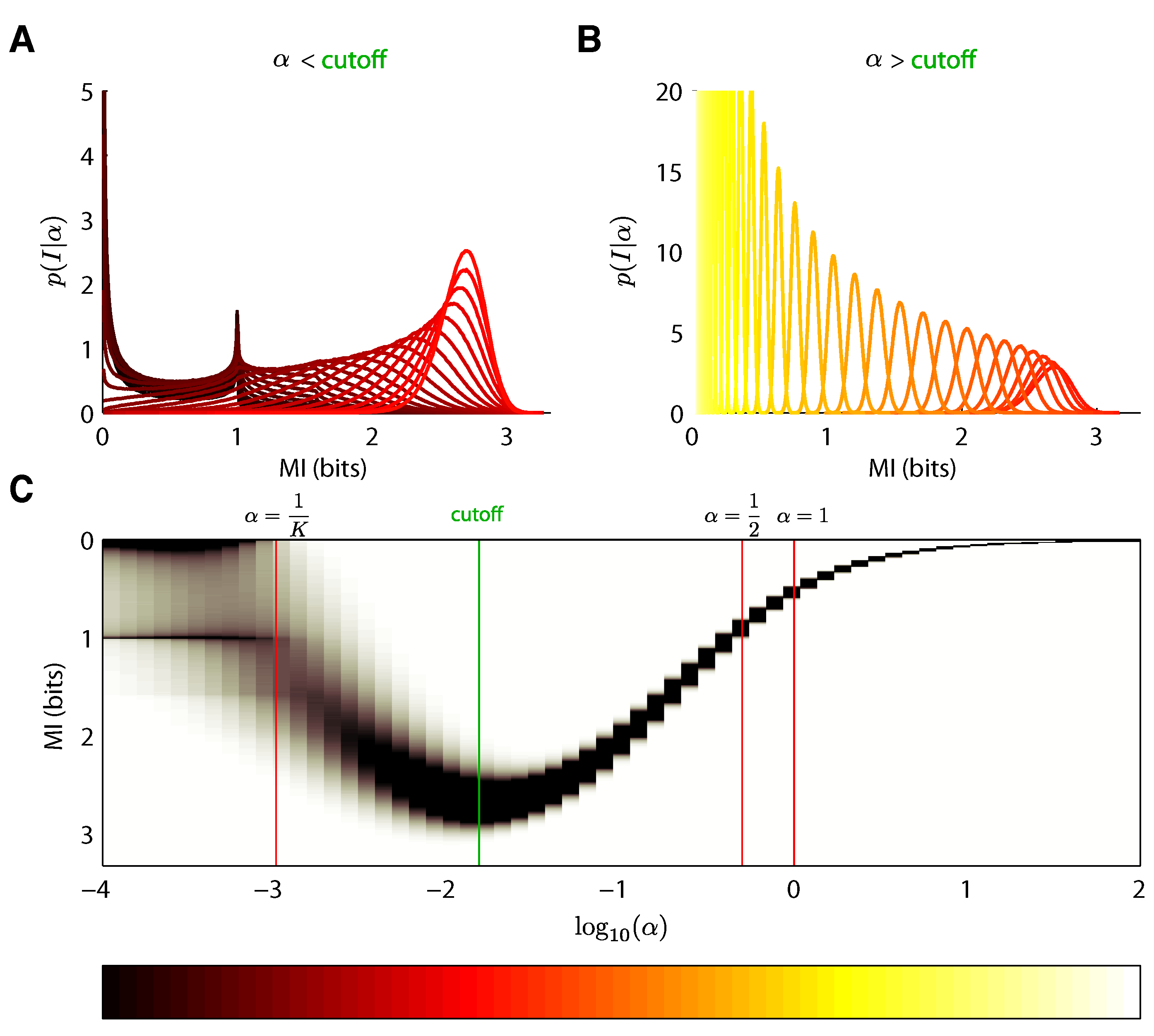
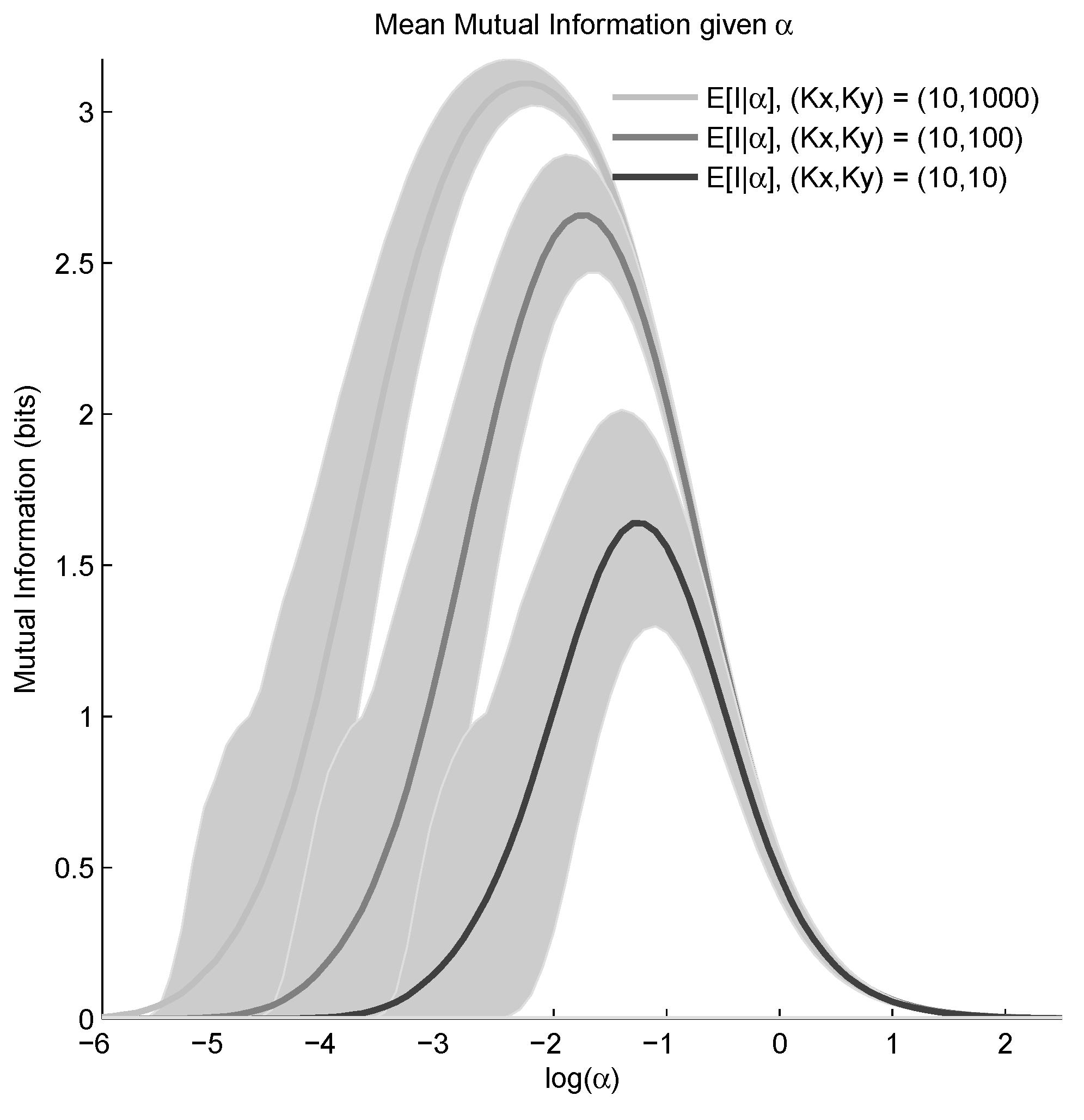
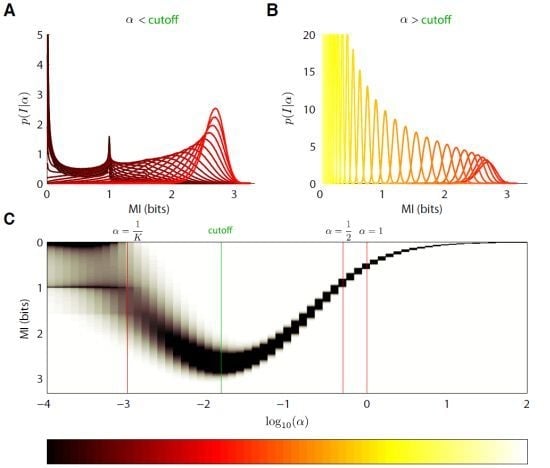
5.2. Mixture-of-Dirichlets (MOD) Prior
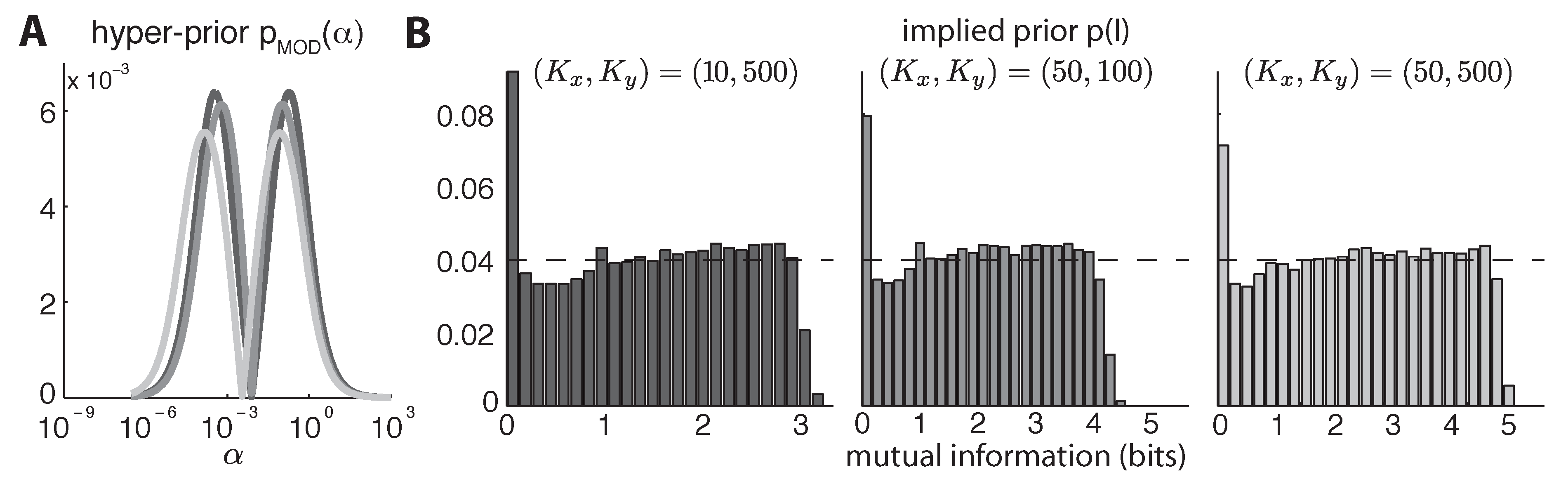
6. Results
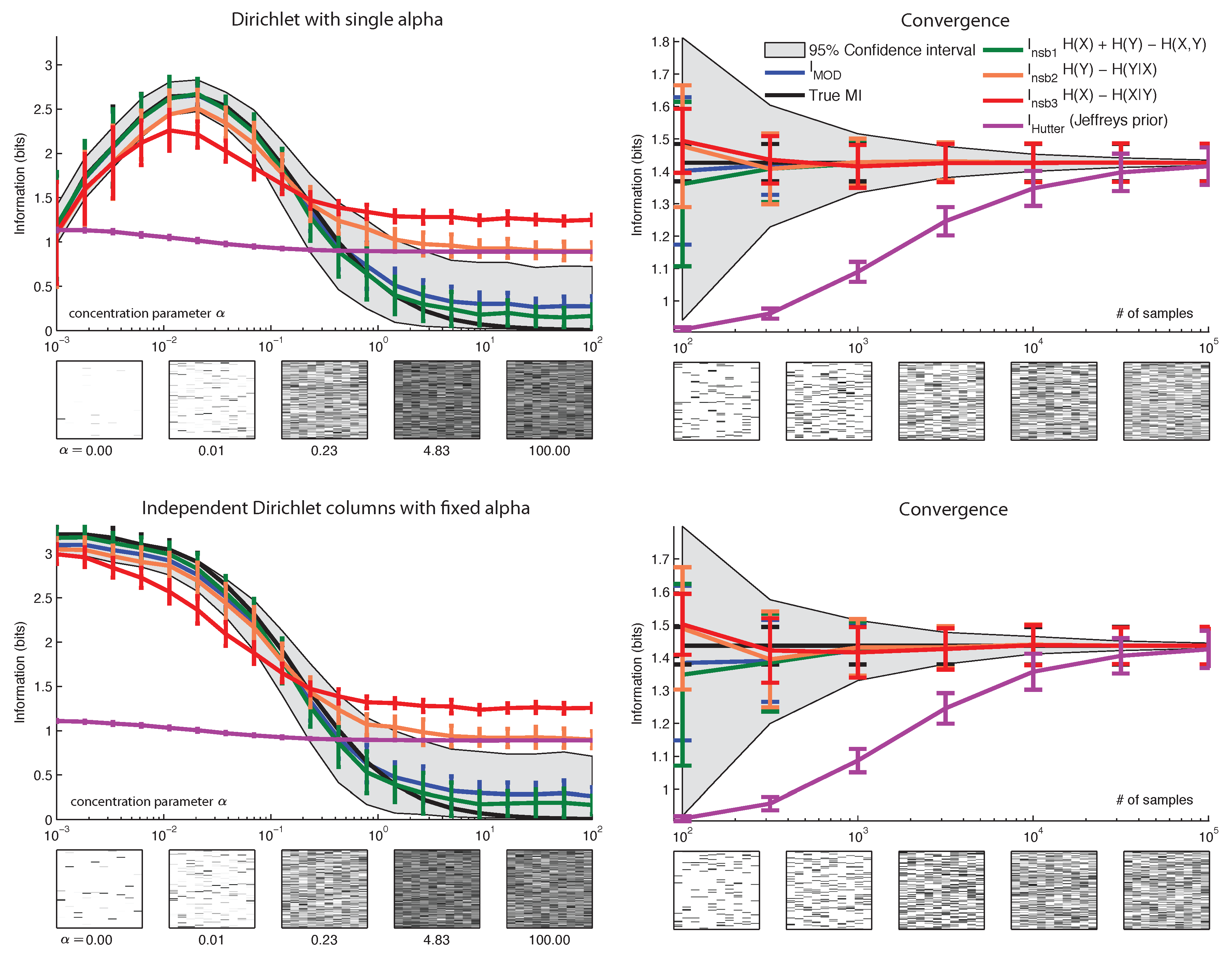
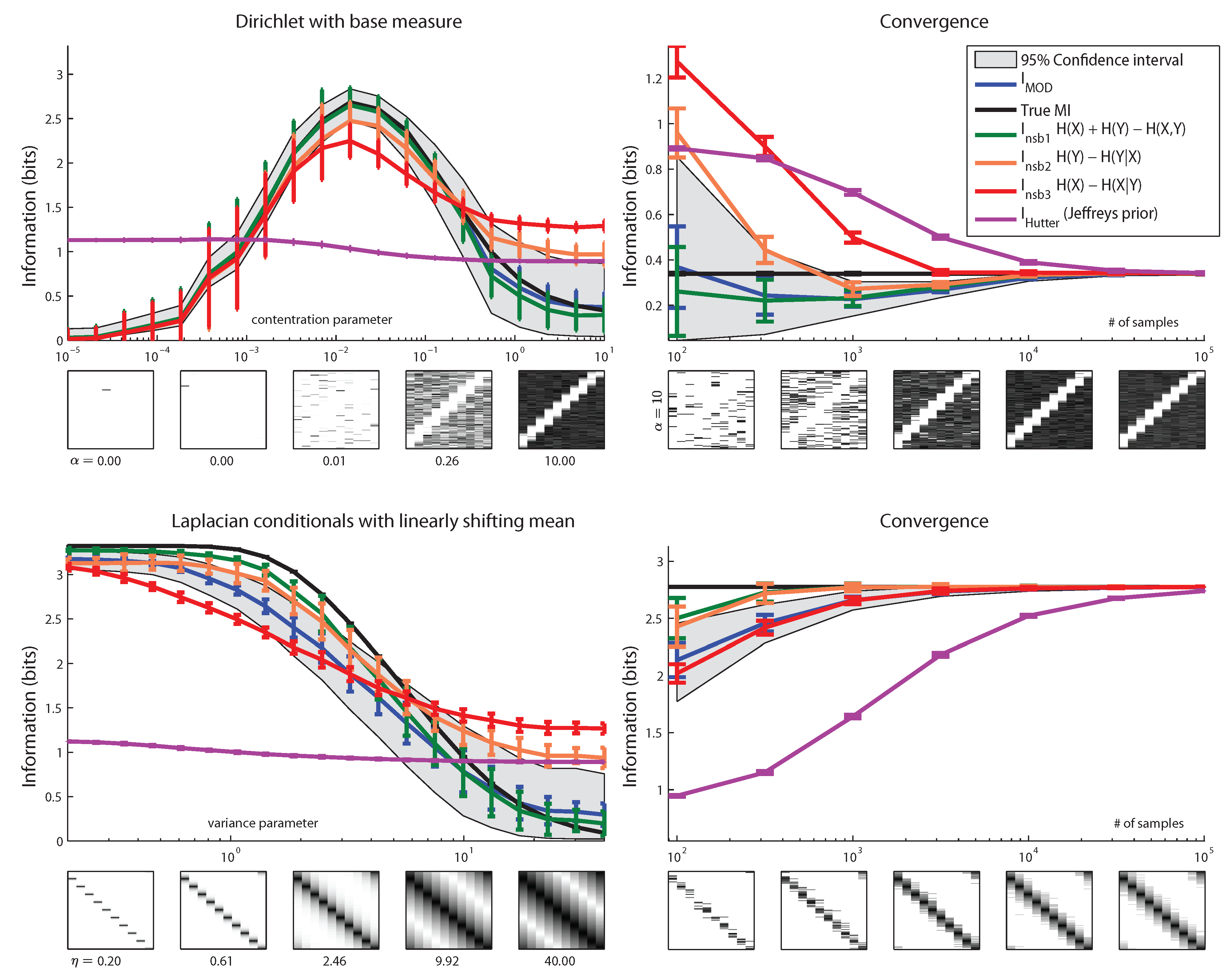
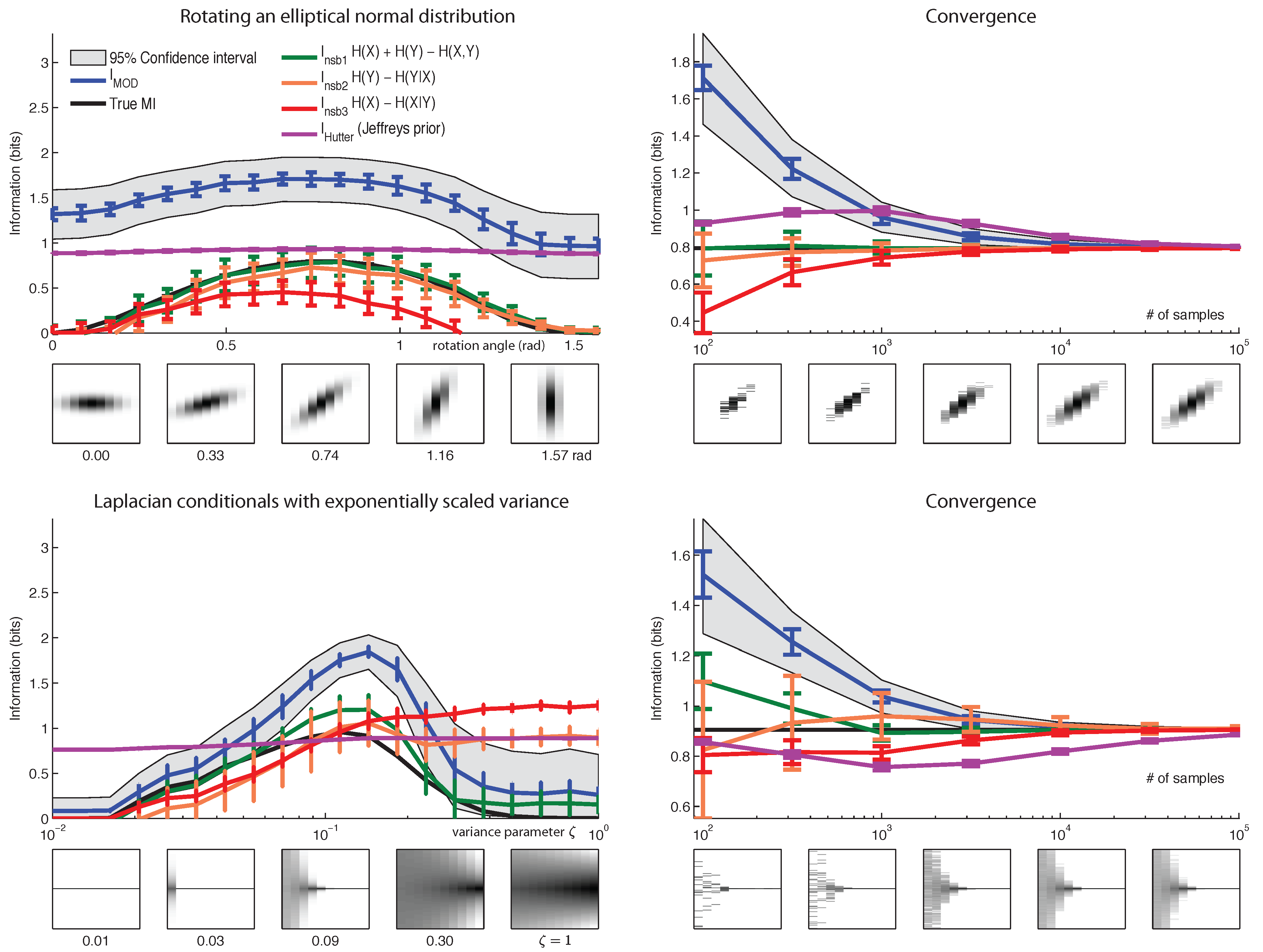
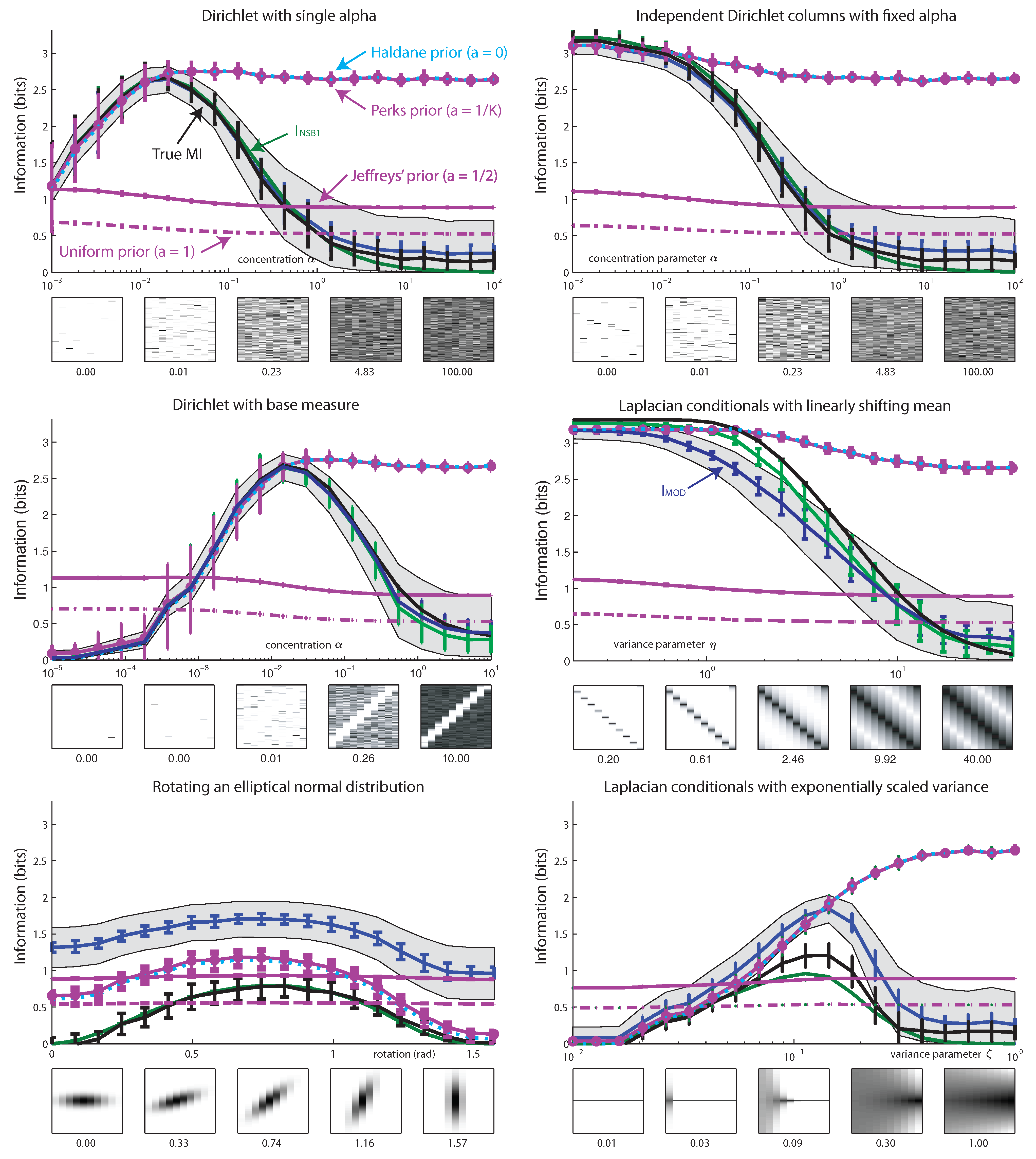
7. Conclusions
Acknowledgement
A. Derivations
A.1. Mean of Mutual Information Under Dirichlet Distribution
References
- Schindler, K.H.; Palus, M.; Vejmelka, M.; Bhattacharya, J. Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 2007, 441, 1–46. [Google Scholar]
- Rényi, A. On measures of dependence. Acta Math. Hung. 1959, 10, 441–451. [Google Scholar] [CrossRef]
- Chow, C.; Liu, C. Approximating discrete probability distributions with dependence trees. Inf. Theory IEEE Trans. 1968, 14, 462–467. [Google Scholar] [CrossRef]
- Rieke, F.; Warland, D.; de Ruyter van Steveninck, R.; Bialek, W. Spikes: Exploring the Neural Code; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Ma, S. Calculation of entropy from data of motion. J. Stat. Phys. 1981, 26, 221–240. [Google Scholar] [CrossRef]
- Bialek, W.; Rieke, F.; de Ruyter van Steveninck, R.R.; Warland, D. Reading a neural code. Science 1991, 252, 1854–1857. [Google Scholar] [CrossRef] [PubMed]
- Strong, S.; Koberle, R.; de Ruyter van Steveninck, R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998, 80, 197–202. [Google Scholar] [CrossRef]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Barbieri, R.; Frank, L.; Nguyen, D.; Quirk, M.; Solo, V.; Wilson, M.; Brown, E. Dynamic Analyses of Information Encoding in Neural Ensembles. Neural Comput. 2004, 16, 277–307. [Google Scholar] [CrossRef] [PubMed]
- Kennel, M.; Shlens, J.; Abarbanel, H.; Chichilnisky, E. Estimating Entropy Rates with Bayesian Confidence Intervals. Neural Comput. 2005, 17, 1531–1576. [Google Scholar] [CrossRef] [PubMed]
- Victor, J. Approaches to information-theoretic analysis of neural activity. Biol. Theory 2006, 1, 302–316. [Google Scholar] [CrossRef] [PubMed]
- Shlens, J.; Kennel, M.B.; Abarbanel, H.D.I.; Chichilnisky, E.J. Estimating information rates with confidence intervals in neural spike trains. Neural Comput. 2007, 19, 1683–1719. [Google Scholar] [CrossRef] [PubMed]
- Vu, V.Q.; Yu, B.; Kass, R.E. Coverage-adjusted entropy estimation. Stat. Med. 2007, 26, 4039–4060. [Google Scholar] [CrossRef] [PubMed]
- Montemurro, M.A.; Senatore, R.; Panzeri, S. Tight data-robust bounds to mutual information combining shuffling and model selection techniques. Neural Comput. 2007, 19, 2913–2957. [Google Scholar] [CrossRef] [PubMed]
- Vu, V.Q.; Yu, B.; Kass, R.E. Information in the Nonstationary Case. Neural Comput. 2009, 21, 688–703. [Google Scholar] [CrossRef] [PubMed]
- Archer, E.; Park, I.M.; Pillow, J. Bayesian estimation of discrete entropy with mixtures of stick-breaking priors. In Advances in Neural Information Processing Systems 25; Bartlett, P., Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; MIT Press: Cambridge, MA, 2012; pp. 2024–2032. [Google Scholar]
- Nemenman, I.; Shafee, F.; Bialek, W. Entropy and inference, revisited. In Advances in Neural Information Processing Systems 14; MIT Press: Cambridge, MA, 2002; pp. 471–478. [Google Scholar]
- Hutter, M. Distribution of mutual information. In Advances in Neural Information Processing Systems 14; MIT Press: Cambridge, MA, 2002; pp. 399–406. [Google Scholar]
- Hutter, M.; Zaffalon, M. Distribution of mutual information from complete and incomplete data. Comput. Stat. Data Anal. 2005, 48, 633–657. [Google Scholar] [CrossRef]
- Treves, A.; Panzeri, S. The upward bias in measures of information derived from limited data samples. Neural Comput. 1995, 7, 399–407. [Google Scholar] [CrossRef]
- Wolpert, D.; Wolf, D. Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1995, 52, 6841–6854. [Google Scholar] [CrossRef]
- Minka, T. Estimating a Dirichlet Distribution; Technical report; MIT: Cambridge, MA, USA, 2003. [Google Scholar]
- Nemenman, I.; Lewen, G.D.; Bialek, W.; de Ruyter van Steveninck, R.R. Neural coding of natural stimuli: information at sub-millisecond resolution. PLoS Comput. Biol. 2008, 4, e1000025. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Archer, E.; Park, I.M.; Pillow, J.W. Bayesian and Quasi-Bayesian Estimators for Mutual Information from Discrete Data. Entropy 2013, 15, 1738-1755. https://doi.org/10.3390/e15051738
Archer E, Park IM, Pillow JW. Bayesian and Quasi-Bayesian Estimators for Mutual Information from Discrete Data. Entropy. 2013; 15(5):1738-1755. https://doi.org/10.3390/e15051738
Chicago/Turabian StyleArcher, Evan, Il Memming Park, and Jonathan W. Pillow. 2013. "Bayesian and Quasi-Bayesian Estimators for Mutual Information from Discrete Data" Entropy 15, no. 5: 1738-1755. https://doi.org/10.3390/e15051738
APA StyleArcher, E., Park, I. M., & Pillow, J. W. (2013). Bayesian and Quasi-Bayesian Estimators for Mutual Information from Discrete Data. Entropy, 15(5), 1738-1755. https://doi.org/10.3390/e15051738