Information-Dispersion-Entropy-Based Blind Recognition of Binary BCH Codes in Soft Decision Situations
Abstract
:1. Introduction
2. Code Length Estimation and Blind Synchronization
2.1. Introduction of the Recognition Algorithm in Hard Decision Situations
2.2. Principles of the Proposed Recognition Algorithm in Soft Decision Situations
2.2.1. Calculation of pi in Soft Decision Situations
| Symbols | Polynomial expressions | Vector form |
|---|---|---|
| 1 | 1 | 001 |
| 010 | ||
| 011 | ||
| 101 | ||
| 100 | ||
| 111 | ||
| 010 | ||
| 110 |
2.2.2. Adaptive Processing of MPCM
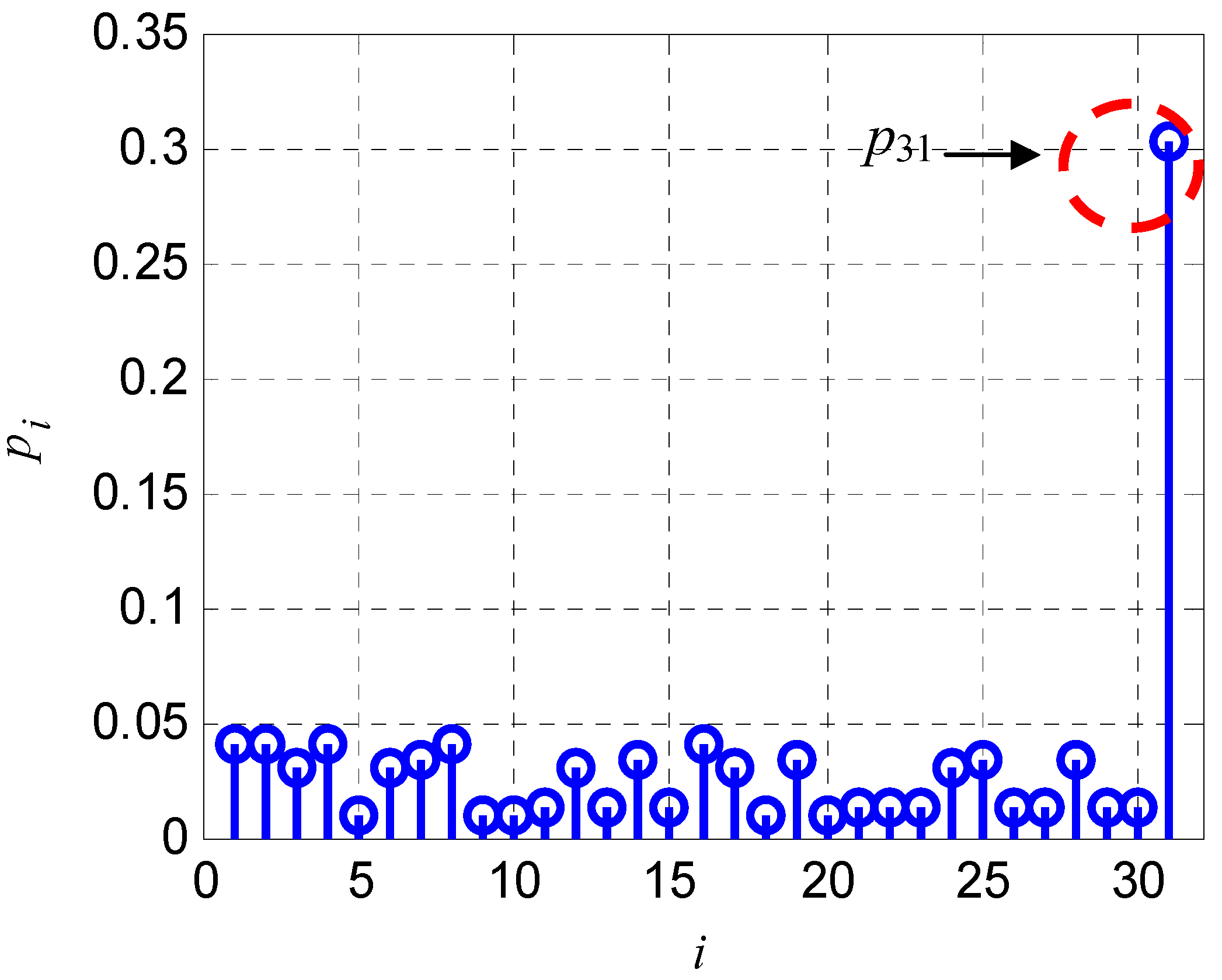
2.2.3. Summary of the Recognition Steps
3. Code Roots Recognition and Generator Polynomial Reconstruction
3.1. Principles of the Code Roots Recognition
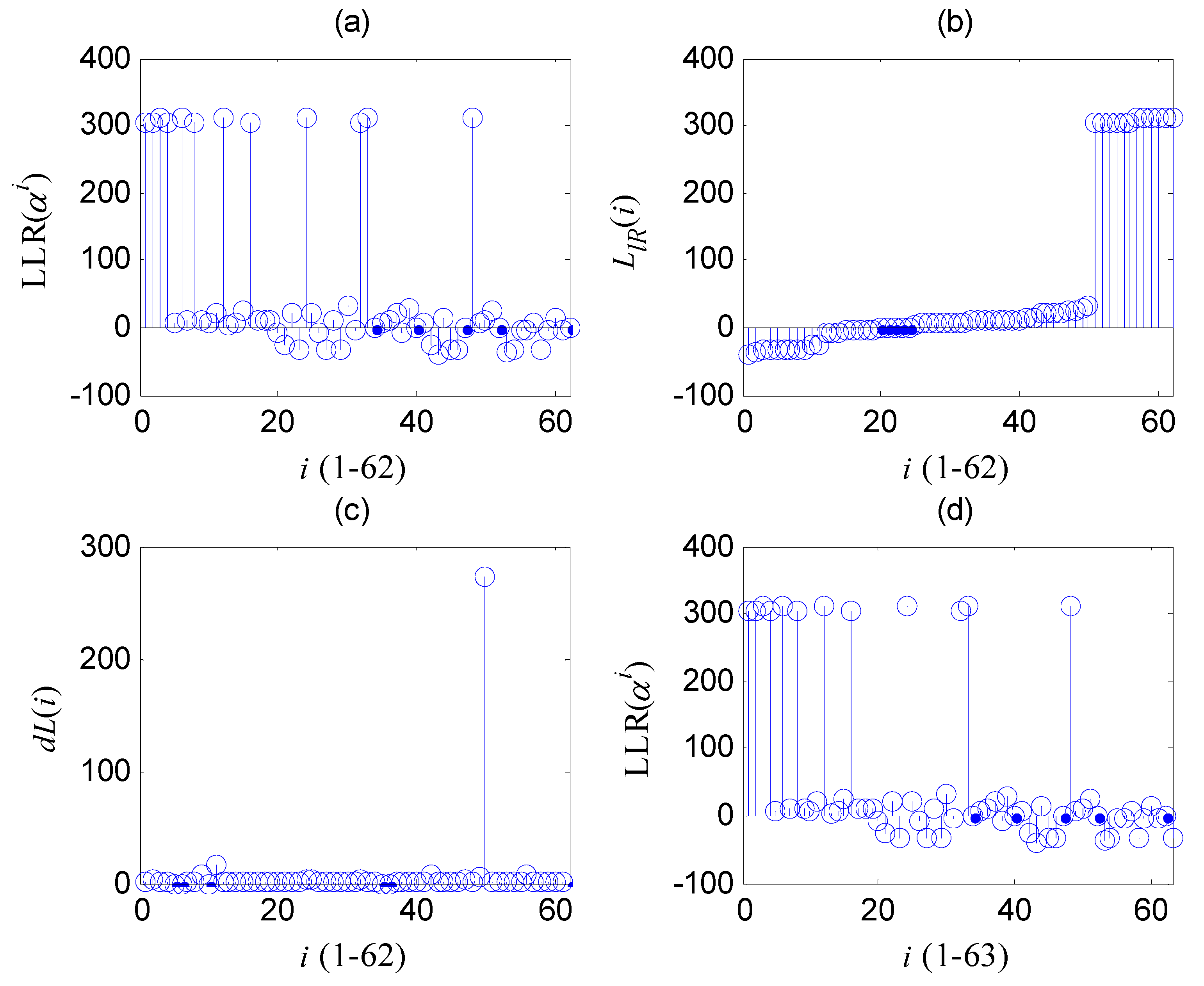
3.2. Discussion of the Element
4. Primitive Polynomial Recognition
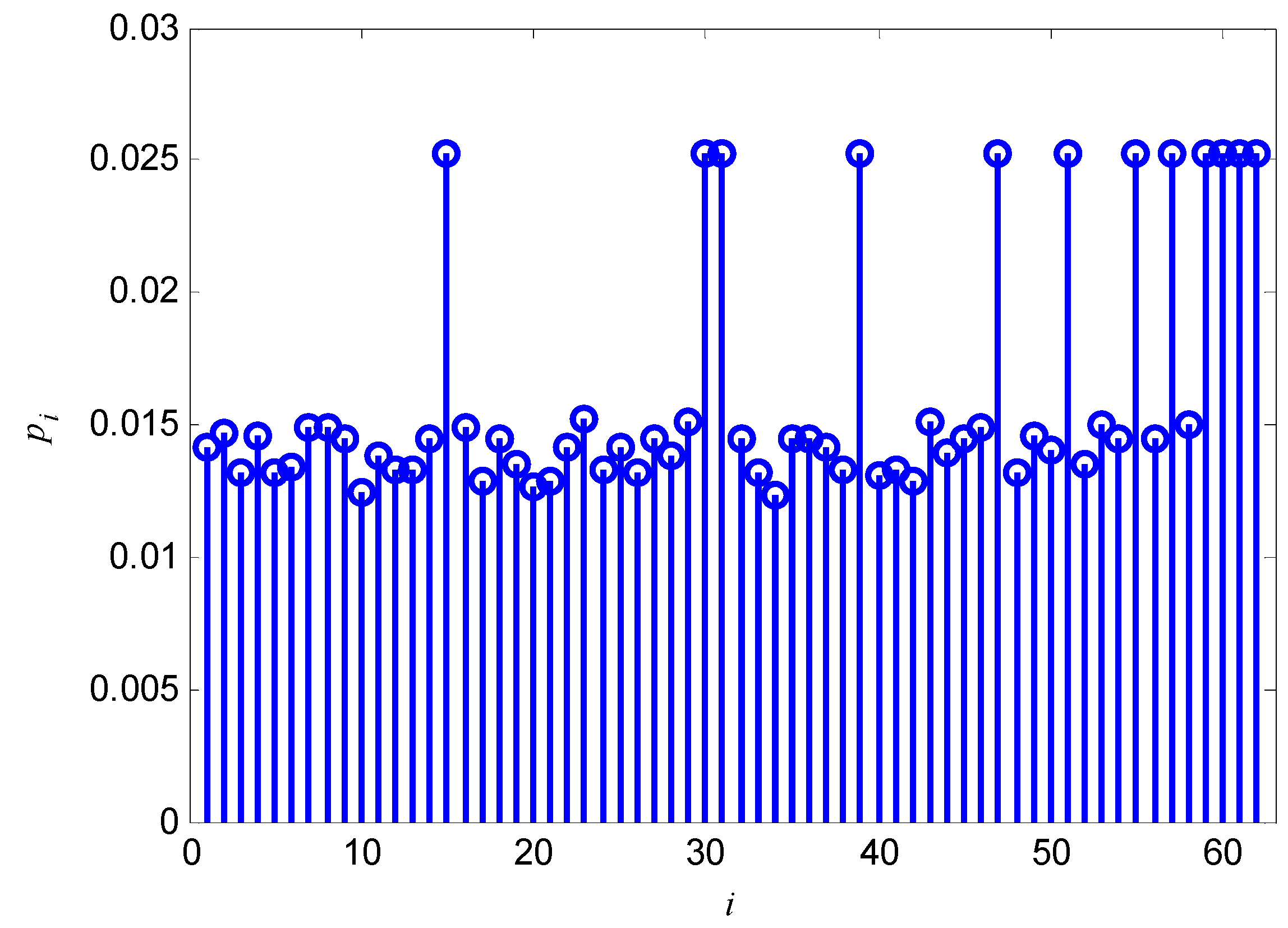
5. Computational Complexity
6. Simulations
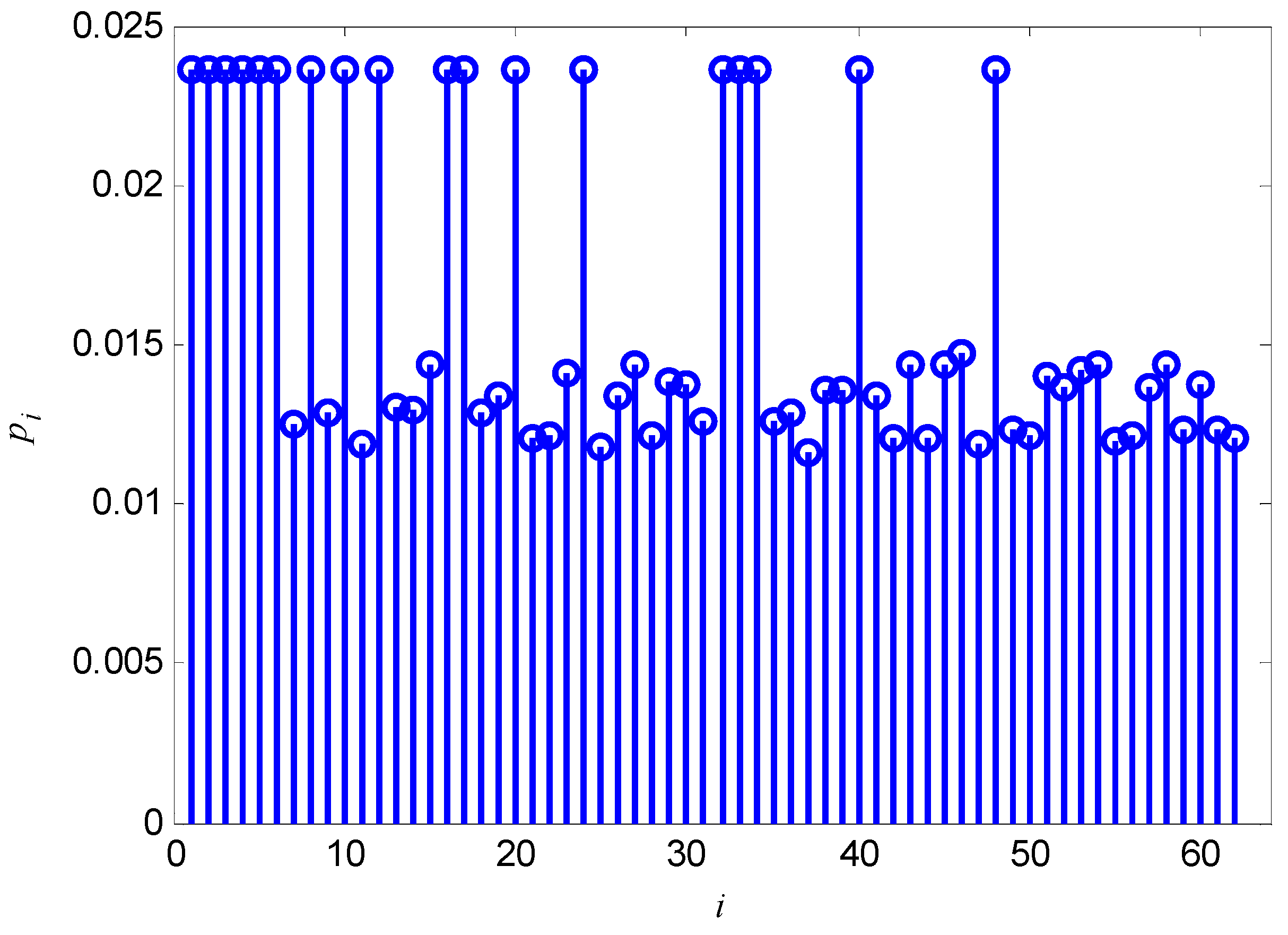
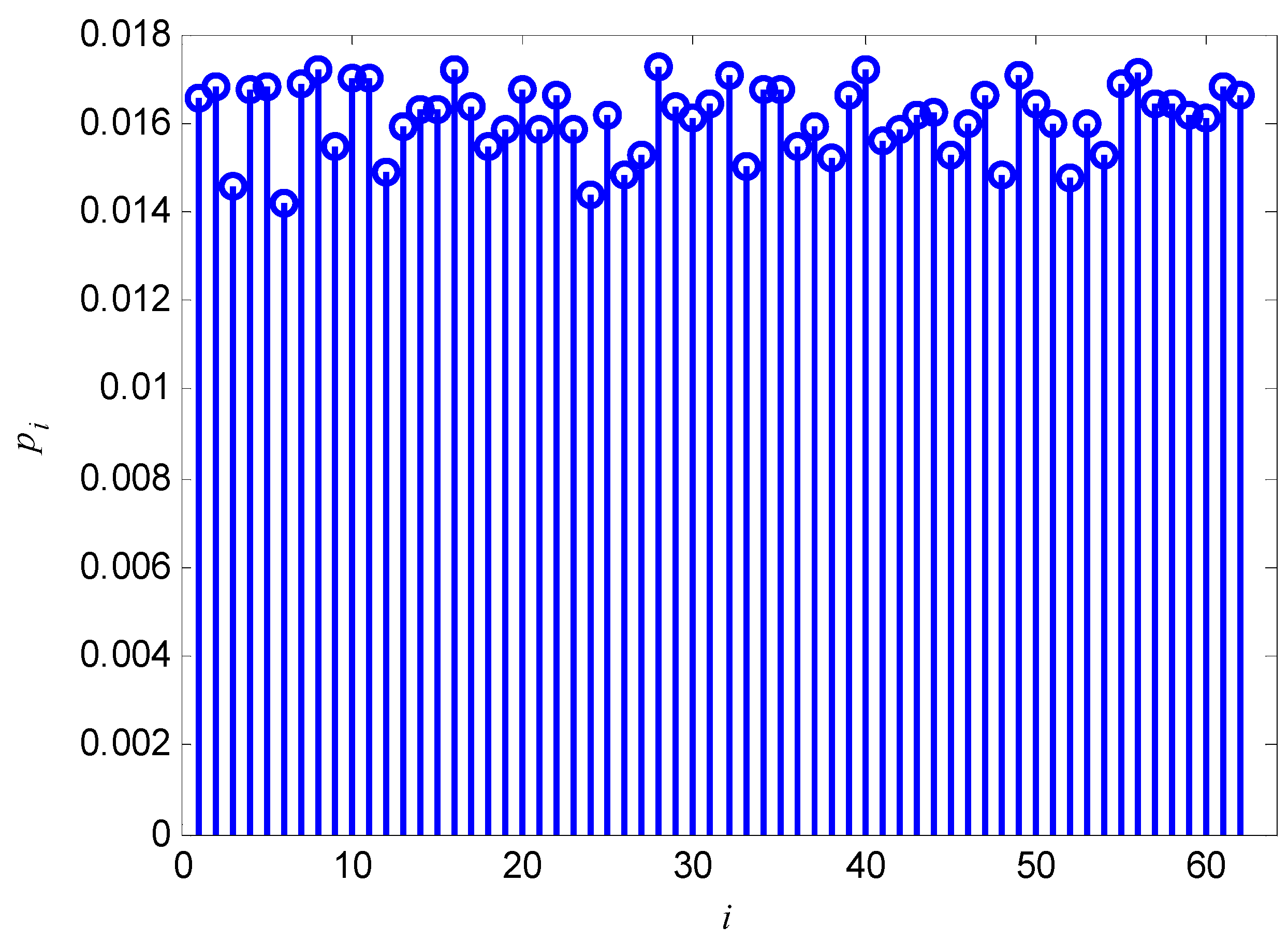
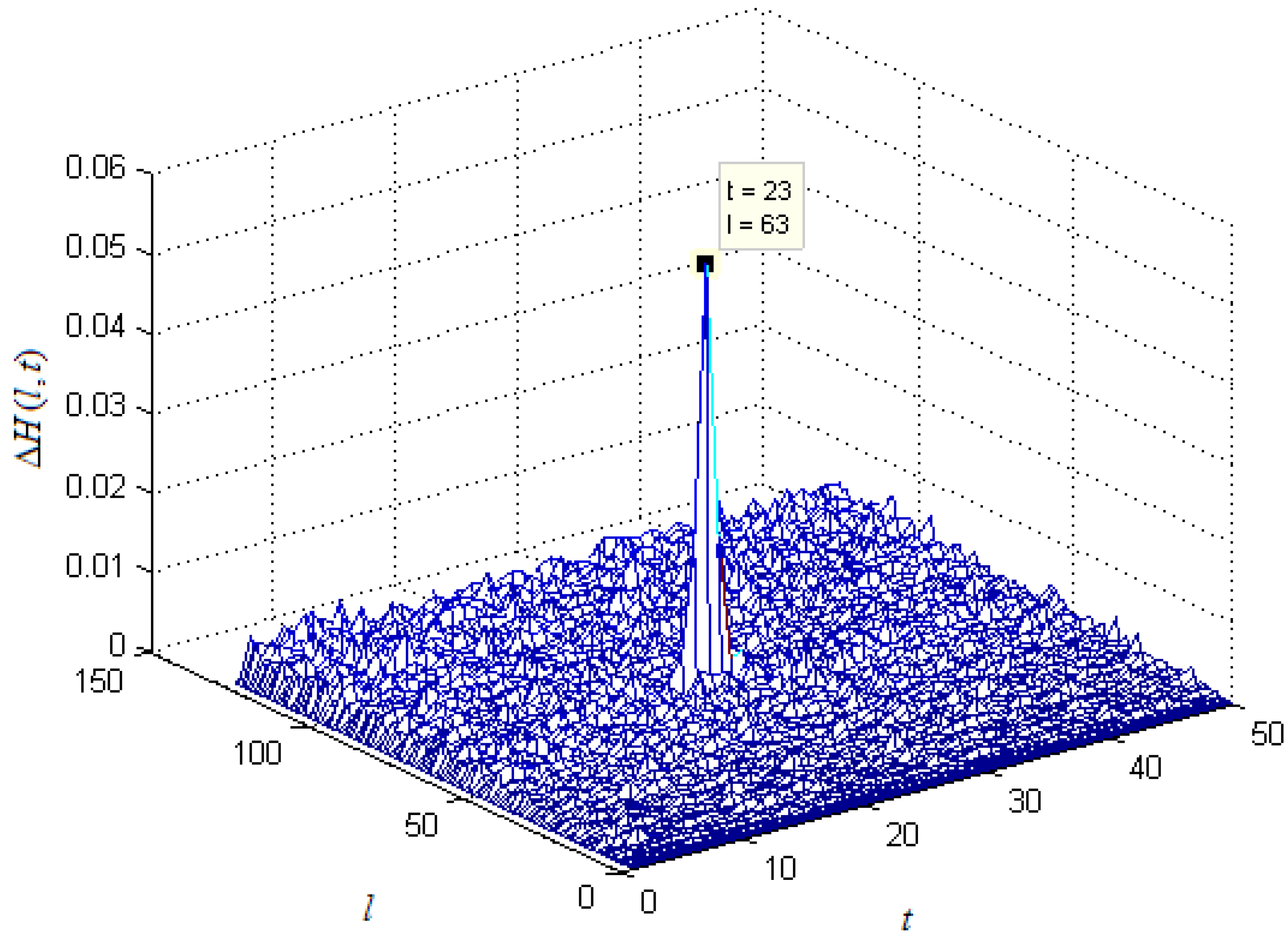
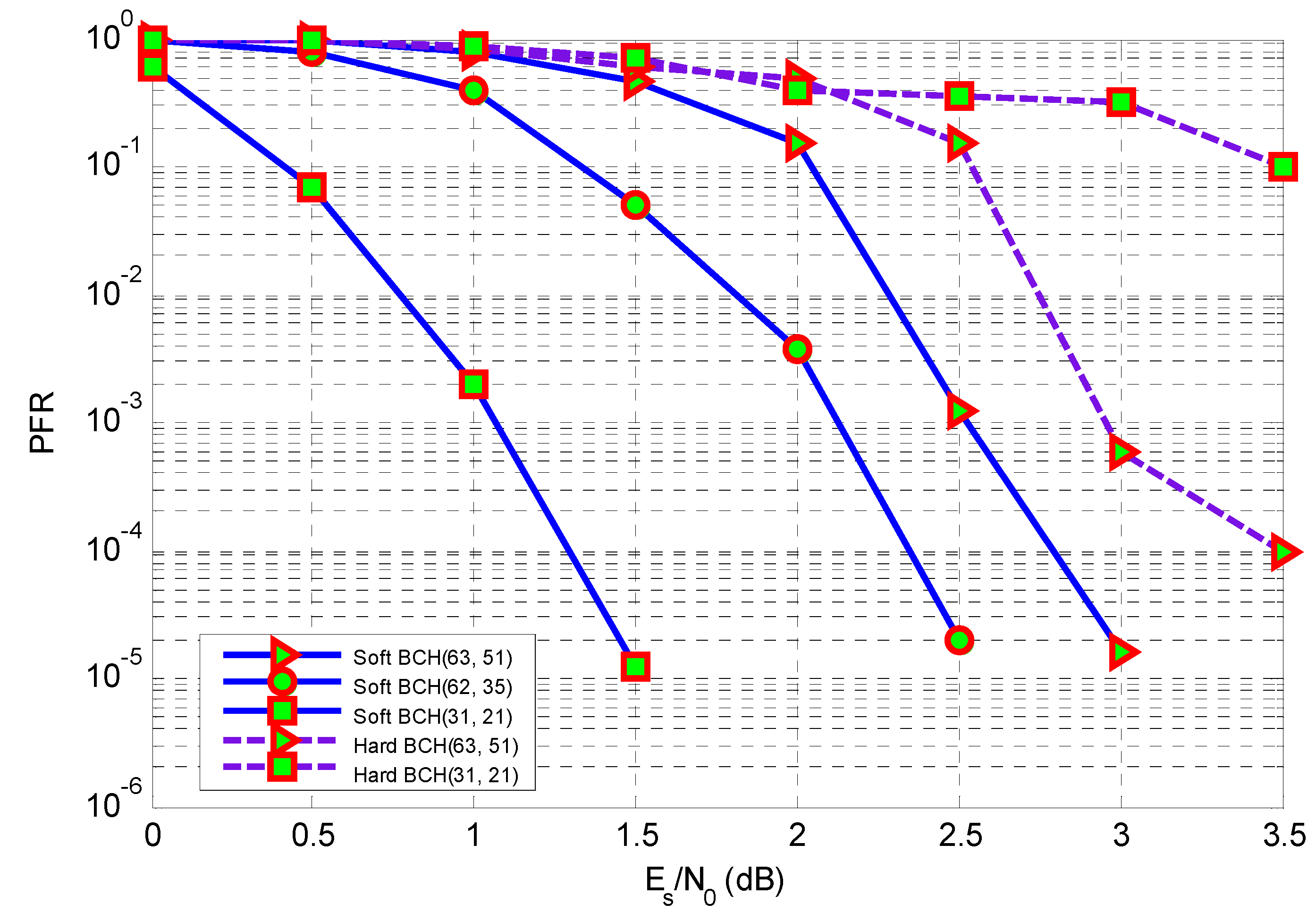

7. Conclusions
Appendix: Proof of the faultiness of the Hypothesis 1
- (1)
- The vectors in MI is linearly independent;
- (2)
- Any vector in H can be obtained by linear combinations of the vectors in MI.
References
- Lin, S.; Costello, D.J. Coding for reliable digital transmission and storage. In Error Control Coding: Fundamentals and Applications, 2nd ed.; Horton, J.M., Riccardi, D.W., Eds.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004; pp. 1–23. [Google Scholar]
- Wang, X.; Xiao, G.Z. BCH codes and Goppa codes. In Error correcting coding: principles and methods; Li, J., Ed.; Xidian University Press: Xian, China, 2001; pp. 242–317. [Google Scholar]
- Moreira, J.C.; Farrell, P.G. BCH Codes. In Essentials of Error-Control Coding; John Wiley & Sons Ltd.: Chichester, UK, 2006; pp. 97–112. [Google Scholar]
- Peterson, W.W. Encoding and error-correction procedures for Bose-Chaudhuri codes. IRE Trans. Inf. Theory 1960, 9, 459–470. [Google Scholar] [CrossRef]
- Chien, R.T. Cyclic Decoding procedure for the Bose-Chaudhuri-Hocquenghem Codes. IEEE Trans. Inf. Theory 1964, 10, 357–363. [Google Scholar] [CrossRef]
- Mitola, J.; Maguire, G.Q. Cognitive radio: making software radios more personal. IEEE Personal Commun. 1999, 6, 13–18. [Google Scholar] [CrossRef]
- Oreay, O.; Ustundag, B. A pattern construction scheme for neural network-based cognitive communication. Entropy 2011, 13, 64–81. [Google Scholar]
- Li, M.; Batalama, N.S.; Pados, A.; Melodia, T.; Medley, M.J.; Matyjas, J.D. Cognitive code-division links with blind primary-system identification. IEEE Trans. Wireless Commun. 2011, 11, 3743–3753. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, X.; Anghuwo, A.A. Joint power and spectrum allocation algorithm in cognitive radio networks. J. Syst. Eng. Electron. 2011, 4, 691–701. [Google Scholar] [CrossRef]
- Jiang, T.; Grace, D.; Mitchell, P.D. Efficient exploration in reinforcement learning-based cognitive radio spectrum sharing. IET Commun. 2011, 10, 1309–1317. [Google Scholar] [CrossRef]
- Marazin, M.; Gautier, R.; Burel, G. Algebraic method for blind recovery of punctured convolutional encoders from an errorneous bitstream. IET Signal Process. 2012, 2, 122–131. [Google Scholar] [CrossRef]
- Moosavi, R.; Larsson, E.G. A fast scheme for blind identification of channel codes. In Proceedings of 54th GLOBECOM, Houston, TX, USA, 5–9 December 2011; pp. 1–5.
- Marazin, M.; Gautier, R.; Burel, G. Dual code method for blind identification of convolutional encoder for cognitive radio receiver design. In Proceedings of IEEE Globecom Workshops, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6.
- Goldsmith, A.J.; Chua, S.G. Adaptive coded modulation for fading channels. IEEE Trans. Commun. 1998, 5, 595–602. [Google Scholar] [CrossRef]
- Burel, G.; Gautier, R. Blind estimation of encoder and interleaver characteristics in a non cooperative context. In Presented at International Conference on Communications, Internet and Information Technology, Scottsdale, AZ, USA, 17–19 November 2003.
- Choqueuse, V.; Marazin, M.; Collin, L.; Yao, K.C.; Burel, G. Blind reconstruction of linear space-time block codes: a likelihood-based approach. IEEE Trans. Signal Process. 2010, 3, 1290–1299. [Google Scholar] [CrossRef]
- Marazin, M.; Gautier, R.; Burel, G. Blind recovery of k/n rate convolutional encoders in a noisy environment. EURASIP J. Wireless Commun. Netw. 2011, 168, 1–9. [Google Scholar] [CrossRef]
- Wang, F.; Huang, Z.; Zhou, Y. A method for blind recognition of convolution code based on Euclidean algorithm. In Proceedings of IEEE WiCom, Shanghai, China, 21–25 September, 2007; pp. 1414–1417.
- Dignel, J.; Hagenauer, J. Parameter estimation of a convolutional encoder from noisy observations. In Proceedings of IEEE ISIT, Nice, France, 24–29 June 2007; pp. 1776–1780.
- Marazin, M.; Gautier, R.; Burel, G. Blind recovery of the second convolutional encoder of a turbo-code when its systematic outputs are punctured. Military Tech. Acad. Rev. 2009, 2, 213–232. [Google Scholar]
- Yongguang, Z. Blind recognition method for the Turbo coding parameters. J. Xidian Univ. 2011, 2, 167–172. [Google Scholar]
- Wen, N.; Yang, X. Recognition methods of BCH codes. Electron. Warf. 2010, 6, 30–34. [Google Scholar]
- Yang, X.; Wen, N. Recognition method of BCH codes on roots information dispersion entropy and roots statistic. J. Detect. Control. 2010, 3, 69–73. [Google Scholar]
- Lv, X.; Huang, Z.; Su, S. Fast recognition method of generator polynomial of BCH codes. J. Xidian Univ. 2011, 6, 187–191. [Google Scholar]
- Fossorier, M.; Lin, S. Bit error probability for maximum likelihood decoding of linear block codes and related soft decision decoding methods. IEEE Trans. Inf. Theory. 1998, 11, 3083–3090. [Google Scholar] [CrossRef]
- Kaneko, T.; Nishijima, T.; Inazumi, H.; Hirasawa, S. An effifient maximum likelihood decoding of linear block codes with algebraic decoder. IEEE Trans. Inf. Theory. 1994, 3, 320–327. [Google Scholar] [CrossRef]
- Sankaranarayanan, S.; Vasic, B. Iterative decoding of linear block codes: A parity-check orthogonalization approach. IEEE Trans. Inf. Theory 2005, 51, 3347–3353. [Google Scholar] [CrossRef]
- Jiang, J.; Narayanan, K.R. Iterative soft-input-soft-output decoding of Reed-Solomon codes by adapting the parity check matrix. IEEE Trans. Inf. Theory. 2006, 8, 3746–3756. [Google Scholar] [CrossRef]
- Ni, L.; Yao, F.; Zhang, L. A rotated quasi-othogonal space-time block code for asynchronous cooperative discovery. Entropy 2012, 14, 654–664. [Google Scholar] [CrossRef]
- Hagenauer, J.; Offer, E.; Papke, L. Iterative decoding of binary block and convolutional codes. IEEE Trans. Inf. Theory 1996, 2, 429–445. [Google Scholar] [CrossRef]
- Imad, R.; Sicot, G.; Houcke, S. Blind frame synchronization for error correcting codes having a sparse parity check matrix. IEEE Trans. Commun. 2009, 6, 1574–1577. [Google Scholar] [CrossRef]
- Imad, R.; Houcke, S. Theoretical analysis of a MAP based blind frame synchronizer. IEEE Trans. Wireless Commun. 2009, 11, 5472–5476. [Google Scholar] [CrossRef]
- Imad, R.; Houcke, S.; Jego, C. Blind frame synchronization of product codes based on the adaptation of the parity check matrix. In Proceedings of IEEE ICC2009, Dresden, Germany, 14–18 June, 2009; pp. 1574–1577.
- Imad, R.; Poulliat, C.; Houcke, S.; Gadat, G. Blind frame synchronization of Reed-Solomon codes: Non-binary vs. binary approach. In Proceedings of 2010 IEEE Eleventh International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Marrakech, Morocco, 20–23 June 2010; pp. 1–5.
- Moreira, J.C.; Farrell, P.G. Cyclic codes. In Essentials of Error-Control Coding; John Wiley & Sons Ltd.: Chichester, UK, 2006; pp. 81–94. [Google Scholar]
- Lin, S.; Costello, D.J. Introduction to algebra. In Error Control Coding: Fundamentals and Applications, 2nd ed.; Horton, J.M., Riccardi, D.W., Eds.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004; pp. 25–65. [Google Scholar]
© 2013 by the authors licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhou, J.; Huang, Z.; Liu, C.; Su, S.; Zhang, Y. Information-Dispersion-Entropy-Based Blind Recognition of Binary BCH Codes in Soft Decision Situations. Entropy 2013, 15, 1705-1725. https://doi.org/10.3390/e15051705
Zhou J, Huang Z, Liu C, Su S, Zhang Y. Information-Dispersion-Entropy-Based Blind Recognition of Binary BCH Codes in Soft Decision Situations. Entropy. 2013; 15(5):1705-1725. https://doi.org/10.3390/e15051705
Chicago/Turabian StyleZhou, Jing, Zhiping Huang, Chunwu Liu, Shaojing Su, and Yimeng Zhang. 2013. "Information-Dispersion-Entropy-Based Blind Recognition of Binary BCH Codes in Soft Decision Situations" Entropy 15, no. 5: 1705-1725. https://doi.org/10.3390/e15051705
APA StyleZhou, J., Huang, Z., Liu, C., Su, S., & Zhang, Y. (2013). Information-Dispersion-Entropy-Based Blind Recognition of Binary BCH Codes in Soft Decision Situations. Entropy, 15(5), 1705-1725. https://doi.org/10.3390/e15051705





