1. Introduction
Fluctuation relations (FRs) have been studied intensively over the past twenty years. Transient Fluctuation relations are the best understood. They are known to be exact for systems of arbitrary size, arbitrarily near or far from equilibrium. Previously, very few exact results were known in nonequilibrium statistical mechanics. Their application to small systems coincided with an upsurge of interest in nanotechnology and nano-biology and the study of small bio-engines. The applicability of the transient FRs far from equilibrium meant that they were an important touchstone for large deviation theory.
Asymptotic steady state fluctuation relations are far less well understood. Some such relations were known to have convergence problems close to equilibrium. In this paper we prove that for the so-called T-mixing systems, the Evans–Searles steady state fluctuation relation is free of convergence difficulties, i.e., it applies to systems of arbitrary size and applies arbitrarily near, or far from, equilibrium. This paper identifies the conditions required for the steady state FR involving the dissipation function, to be derived from the exact Evans–Searles transient fluctuation theorem, and provides an illustration of the results using numerical simulations.
In 1993 [
1], Evans, Cohen and Morriss studied the steady state fluctuations of the entropy production rate in isoenergetic SLLOD (SLLOD is the term used to refer to the standard algorithm used to model homogeneous flow [
2]) shearing systems, defined by:
where
;
N is the number of particles in a periodic system with a unit cell of volume
V;
m is the mass of each particle;
is the shear rate;
is the unit vector in the
x-direction;
is the internal force on particle
i;
is the position of each particle;
is the momentum of each particle; and
is a Lagrange multiplier that fixes the internal energy of the system,
, where
is the interparticle potential. The value of
is related to: the rate of energy dissipation under unthermostatted (adiabatic) conditions,
; the entropy production rate close to equilibrium, Σ; and the phase space expansion rate,
where
. This relationship is given by,
Here
is the off-diagonal part of the pressure tensor and
is the number of degrees of freedom. In [
1] the spatial dimension was
. In this and similar molecular dynamics models, unphysical thermostatting terms like
may be confined to arbitrarily remote boundaries. Then, the bulk properties of the systems of interest should not be affected by the thermostatting details. To set our notation, let
be a point in phase space evolved via the time evolution operator,
S, (given by the equations of motion) for a period
s from initial condition Γ. Given an observable
, let us denote its time average and integral, between times
and
, along the phase space trajectory segment with initial condition
Γ as
As the time average
over the period
τ, equals the sum of the Lyapunov exponents
for the system in the long
τ limit, Evans, Cohen and Morriss [
1] proposed and tested the asymptotic steady state relation (
)
Here
label trajectory segments generated over the period
τ and related by time reversal symmetry so that the averages of Λ over the segments
obey
. The
n-th phase space expansion rate along trajectory segment
i is given by
, and the sums run over all the positive
λ’s. The values of
and
are the probabilities of observing trajectories initially within a small volume
about
i or
[
3]. As in periodic orbit expansions [
4,
5], Equation (
4) can then be predicted to hold within a bounded range
,
. Later it was discovered that for non-isoenergetic systems, the physically relevant asymptotic limit in (4) is really
while
B was estimated to be
[
6]. These two facts can make the observability of the steady state
difficult close to equilibrium.
Evans
et al. [
1] show that if one considers Equation (
4) and sums over all
for which
(or equivalently the entropy production) takes on a particular value within some tolerance, the fluctuation relation (FR) for the entropy production rate can be obtained. However, the proportionality between Λ, the energy dissipation and the entropy production given in Equation (2) holds only for Gaussian isoenergetic systems. For instance, systems with constant kinetic energy differ from isoenergetic systems, because,
replaces
in Equation (
1), and Λ becomes the sum of two terms, only one of which is related to energy dissipated by the strain rate:
Here, the constants
depend on
N and
d.
In 1994, Evans and Searles [
7,
8] developed an alternative approach for deriving fluctuation relations for the energy dissipation that could be generalised to non-isoenergetic systems, through the introduction of the dissipation function Ω [
9]. For field-driven systems, Ω equals
[
9], which, close to equilibrium,
is the rate of entropy production [
2]. Here,
J is the dissipative flux due to the force
,
V is the volume,
is Boltzmann’s constant and
T is the temperature of the equilibrium state that the system would relax to if the driving force (strain rate) was set to zero. The numerical value of this temperature is, for this system, the kinetic temperature [
7,
8] of the nonequilibrium driven system. The first set of such relations, called transient Ω-FRs, were obtained under virtually no hypothesis, except for time reversibility and ergodic consistency; they concern phase space distributions that are not preserved by the dynamics. No bounds limit the argument values for these transient Ω-FRs. They are valid arbitrarily near or far from equilibrium. In the far from equilibrium case unlike dissipation, the entropy production cannot be defined. These transient Ω-FRs are (like related identities such as the Jarzynski equality, see e.g., [
10]) exact for all times.
Transient Ω-FRs have been verified experimentally [
11]. Many tests and laboratory experiments have also validated the extension of the transient Ω-FRs to nonequilibrium steady states [
12,
13]. This supports the use of thermostatted dynamics in this context. However, the understanding of the physical mechanisms underlying the validity of the steady state FRs is less complete [
6,
14,
15,
16]. The present paper clarifies some of these outstanding issues.
Following the approach developed by Evans and Searles, we demonstrate how time reversibility, ergodic consistency and a form of the decay of correlations, known as T-mixing [
14,
15,
17], lead to the steady state Ω-FR for systems of arbitrary size, near or far from equilibrium.
2. Calculations
For the sake of clarity, and without loss of generality, we focus our discussion and simulations on the colour conductivity model [
2] defined by:
where
is the applied colour field that is coupled to the system via the colour charges,
, and
. This model is one of the first used in nonequilibrium molecular dynamics, for calculation of the self-diffusion coefficient. It is a simplified model of an ionic liquid where the particles do not have Coulomb interactions with each other but experience a force proportional to their colour charge when subject to a field. The term
is a deterministic, time reversible term used to add or remove energy—in the form of heat—from the system [
2] in order to keep the kinetic energy fixed. If
α is set to zero, one obtains the adiabatic equations of motion, which are Hamiltonian and hence preserve phase space volumes, a condition referred to as adiabatic incompressibility of phase space, AIΓ [
2]. The thermostat might only apply to the wall particles, as discussed above. As this makes no difference for the derivation of the FRs, we employ a homogenous thermostat.
In the simulations, we choose a system in two Cartesian dimensions with
, and all results are given in Lennard-Jones reduced units. The initial distribution is taken to be the equilibrium isokinetic phase space distribution function that takes the form
where
is the total momentum of the system,
K is its kinetic energy, which is fixed at
and
. We consider a two-dimensional Gaussian isokinetic system, with kinetic energy fixed at the equipartition value
. Note that the first argument of
refers to the phase point where the distribution function is evaluated and the second argument refers to the time to which the phase space distribution function has evolved, starting from an initial distribution
.
The time integral from time 0 to time
of the dissipation function, along a trajectory originating at
Γ, is formally defined as
A key point to the definition of dissipation is that
Γ and
are the origin phases for a trajectory and its conjugate anti-trajectory respectively where
is the time reversal operator. This places constraints on the propagator
. We break the interval
into a set of symmetric subintervals:
to ensure that
is the origin of the conjugate anti-trajectory of a trajectory that starts from
Γ at
. Later we will let
so that the middle trajectory segment
approaches a steady state segment. To ensure that the dissipation function is well-defined over the ostensible phase space domain, we assume the system is ergodically consistent
i.e.,
[
18].
For our system, the instantaneous dissipation function is [
14]
where the dissipative flux,
, is obtained from the adiabatic time-derivative of the internal energy
:
while the fully thermostatted dynamics of Equation (
7) yields
by equipartition, the phase space expansion rate is
.
Time reversibility implies that for every initial condition Γ that yields a value
, there is an initial condition
yielding the value
. To obtain
the time reversal map,
, is applied to the time-evolved phase,
,
i.e.,
. We also assume that
, which guarantees that we measure properties in a co-moving frame since the average velocity of particles in the system is zero. From (8):
Substituting (13) into (9) using (11) gives,
It is very important to note that in Equation (
9) and Equation (
13), the phase point evolves but we only refer to the initial phase space distribution function. This is the Schrödinger picture.
Consider firstly the transient Ω-FR, which is just a consequence of time reversibility and ergodic consistency. In the case of the transient Ω-FR, we wish to consider evolution of the trajectory from
Γ, and therefore
t in the equations above is 0. Time reversibility implies that the coordinate transformation
has Jacobian,
i.e., the exponent involves the change in the heat. Let
and
be small intervals of width
centred in
A and
, and denote by
the set of Γ such that
where
or
. The above leads to
where
. Equation (
16) is called transient Ω-FR because the system is not time invariant as it evolves from
to
. Time reversibility is essentially the only requirement for its derivation, which is why the Ω-FR is so general and is exact.
Now, let us summarise the derivation of the steady state FR given in [
14], in the framework of our model. First of all, consider the time average of the dissipation function over the period
t to
: from Equation (
14),
. We can write,
Performing the coordinate transformation
in the denominator, noting that due to the time reversibility of the dynamics,
, and using conservation of probability in phase space, one eventually obtains [
14]:
where
is the probability distribution at time
t,
i.e., the distribution whose density
is the solution of the phase continuity equation with initial condition
.
denotes a conditional average, according to the equilibrium density
under the condition
. Taking the logarithm and dividing by
τ produces:
where
. The ensemble average is with respect to the initial distribution and
. This result is exact for all
, and observable pairs
[
14]. By “observable pairs
” we mean that, for large t,
when
.
Under the assumption of ergodic consistency, observability is clearly guaranteed at any finite time
t, for all values
A within the range allowed by the definition of Ω and by the possible constraints on the dynamics. In other words, the choice of an initial ergodically consistent state guarantees the existence of conjugate trajectory/anti-trajectory pairs in the initial distribution of phases, hence guarantees that Equation (
19) holds at all finite times
t.
One may distinguish between two types of observability. The first type is easy observability, in which one considers the time averaged dissipative flux within a few standard deviations of the mean. This is an important criterion for experiments or computer simulations. The second type is difficult observability, concerning large deviations from the mean (measured in terms of standard deviations). Of course, the probability of observing sets of trajectories with an average flux many standard deviations from the mean may be exceedingly small! However, unless precluded because of some constant of the motion or of other reasons concerning the definition of Ω, ergodic consistency implies that at any finite time t there is a nonzero probability of observing the conjugate set of anti-trajectories.
Let us begin by assuming that correlations between
and
decay instantaneously, with respect to
. The Nonequilibrium Partition Identity [
14] (which corresponds to the integral fluctuation theorem in stochastic dynamics) yields:
Therefore, , and we derive an exact steady state FR that holds for all averaging times τ.
If correlations do not decay instantaneously with respect to
, but vanish to some arbitrarily fine tolerance, for times greater than some cut-off time,
(some multiple of the Maxwell time,
, which depends on the tolerance required), one has
[
14]. Then the steady state FR is equally obtained in the
limit, but with corrections of order
, which also requires the averaging time
τ to be large.
By expanding the exponential terms and noting
, it can be seen that the decay in correlation of the two exponential terms is a special instance of the condition,
now known as T-mixing (first defined in [
17]). This guarantees the time integrability of the transient time correlations function
. Together with the dissipation theorem [
14,
19], which states that beyond some correlation time
phase variables become constant and are given by
one has that
tends to a steady state
when
and the averages of smooth phase functions according to
are given by the asymptotic statistics of single dynamical trajectories. The physical conditions for the existence and uniqueness of
are common. For example, the transport coefficients of fluids at low Reynolds or Rayleigh numbers are observed to be single valued functions of temperature, density and possibly the driving force, such as the shear rate or temperature gradient respectively. If they were not single valued functions of these state variables, then the system could not be T-mixing because correlation functions of phase space measures or order parameters for these different states would never decay in time. In T-mixing systems, the
limit of Equation (
19) turns from a statement about the time evolving ensemble
to a statement concerning also the evolution of typical single dynamical trajectories. Then, for time reversal invariant, ergodically consistent, T-mixing systems, the steady state Ω-FR holds with a correction that vanishes as
.
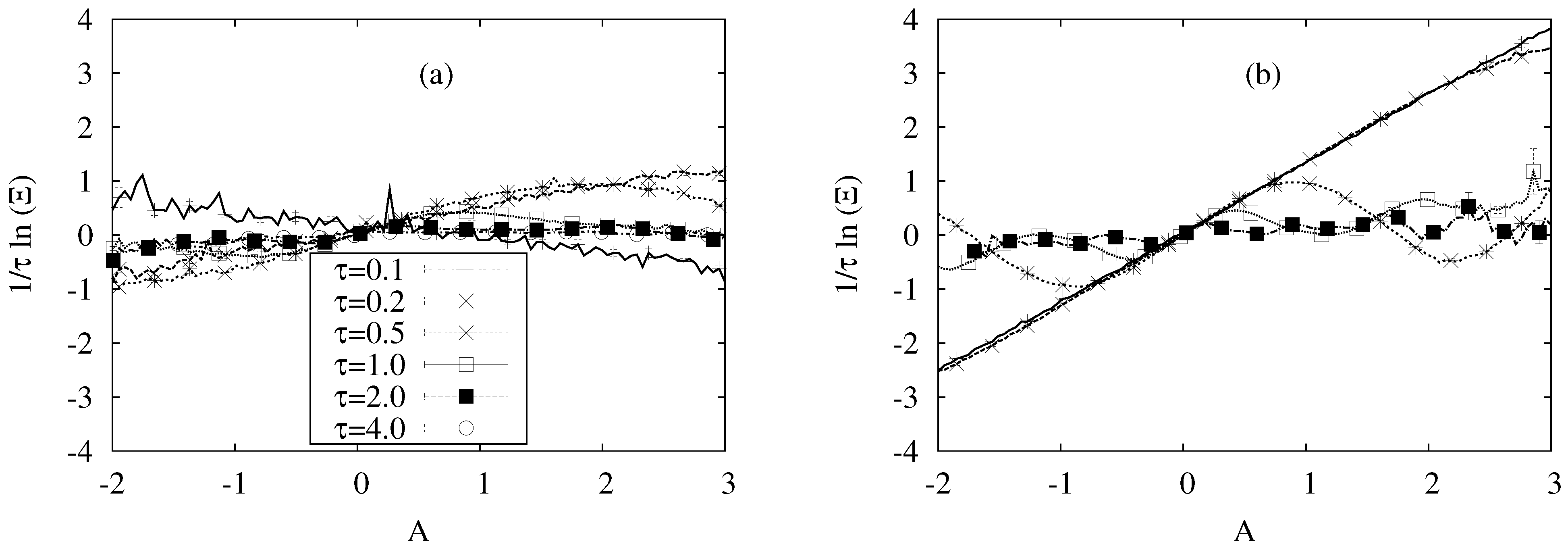
Figure 1.
Plots of the conditional ensemble average,
, which is defined in Equation (
19), as a function of
τ and
A. The systems consist of 8 particles in a periodic box undergoing colour diffusion. Here
T =1,
δ =0.048,
= 2.0,
for (
a) density = 0.8 and (
b) density = 1.0 and
τ varies between 0.1 and 4.0 for (
a) and between 0.1 and 2.0 for (
b). The error bars are one standard error in the mean of these (
a) 10 and (
b) 2 sets of data. The graphs in (
a) and in a similar system with 6 particles and density = 0.8 (not presented) are consistent with our proposal that the conditional ensemble average is bounded above and below. This may also be the case in (
b), allowing for errors in the mean for large
A (not all of which are shown), when
τ = 1.0 and 2.0.
Figure 1.
Plots of the conditional ensemble average,
, which is defined in Equation (
19), as a function of
τ and
A. The systems consist of 8 particles in a periodic box undergoing colour diffusion. Here
T =1,
δ =0.048,
= 2.0,
for (
a) density = 0.8 and (
b) density = 1.0 and
τ varies between 0.1 and 4.0 for (
a) and between 0.1 and 2.0 for (
b). The error bars are one standard error in the mean of these (
a) 10 and (
b) 2 sets of data. The graphs in (
a) and in a similar system with 6 particles and density = 0.8 (not presented) are consistent with our proposal that the conditional ensemble average is bounded above and below. This may also be the case in (
b), allowing for errors in the mean for large
A (not all of which are shown), when
τ = 1.0 and 2.0.
It is now necessary to quantify this process. In
Figure 1, we show the results of simulations of 8 WCA [
20] particle systems with densities of 0.8 and 1.0 at a temperature of 1. The ensemble averages were over a set of at least 120 million trajectories with
and
τ varying between 0.1 and 4.0. The results in
Figure 1 indicate that, indeed, the conditional ensemble average appearing in Equation (
18) and Equation (
19) is bounded. We note that at large
A the statistics are poor for
when
and 2.0, and in all cases for sufficiently large
A this will be the case, because we are sampling the tails of the probability distribution of the dissipation function. Furthermore, the value of
A at which the statistics become poor will depend on the distribution for the particular system we are considering. However, in both cases (and additional investigations with
gave similar results) the simulations suggest that there exists a constant
for our system, such that
.
If these scenarios are realised, the last term of Equation (
19) vanishes as
, as confirmed by the plots of this quantity in
Figure 2, for the same simulations as in
Figure 1. An interesting observation from
Figure 1 and
Figure 2 is the periodic nature of the quantities plotted, with the period appearing to depend both on
τ and density. For example, in
Figure 1 the period decreases as
τ increases and also as the density increases. This is likely to be related to the fact that the simulations were carried out at high densities and therefore one component of the particles’ motion involved oscillations within regions formed by the nearest neighbours. As the density decreases, the regions become larger, the periods increase and this component of the motion would diminish.
Figure 2.
Plots of
, which appears as the final term in Equation (
19), as a function of
τ and
A. The systems are the same as those described in
Figure 1, that is, in (
a) density = 0.8 and in (
b) density = 1.0. The graphs show that the final term in Equation (
19) tends to 0 as
τ increases. This was also the case for a similar system of 6 particles with density = 0.8 (not presented).
Figure 2.
Plots of
, which appears as the final term in Equation (
19), as a function of
τ and
A. The systems are the same as those described in
Figure 1, that is, in (
a) density = 0.8 and in (
b) density = 1.0. The graphs show that the final term in Equation (
19) tends to 0 as
τ increases. This was also the case for a similar system of 6 particles with density = 0.8 (not presented).
3. Discussion and Conclusions
In accord with our observations, the validity of the steady state Ω-FR,
can be attributed to the following conditions. Firstly we assume the system is time reversal invariant, ergodically consistent, and the initial distribution is even under time reversal. Then, the main technical assumptions are that the system is reversible and T-mixing. This implies that at a fixed number of standard deviations from the mean, the distribution of the dissipative flux
must be Gaussian and furthermore typical average values for the time averaged flux scale as
near the mean for weak fields. For a fixed number of samples, the easily observable range of fields goes to zero as
. However, although the easily observable range of values shrinks to zero as
, the error induced by truncating the correlation function
vanishes even faster, ensuring that the steady state Ω-FR
can be easily verified to arbitrary accuracy. By going to larger
τ, we can observe the steady state Ω-FR to arbitrarily high accuracy by taking ever more samples. Of course if the correlation time
is zero, the asymptotic limit is unnecessary since
and (24) is exact for all values of
τ.
The lack of bounds on the range of values for the argument is highly significant. It means that provided the system is T-mixing, the steady state Ω-FR is valid and verifiable outside the region of Gaussian statistics near the mean, and actually describes a symmetry of rare events in nonequilibrium steady states.
This goes to the root of the fundamental difference between the second law of thermodynamics and the fluctuation theorems. The second law says that certain probabilities are actually zero. In contradistinction, the fluctuation theorems say that certain probabilities may be exceedingly small—unobservably small for macroscopic bodies over accessible timescales—but they precisely quantify these probabilities. Thus the transient Ω-FR and the steady state Ω-FR for T-mixing systems are valid for all values of their argument that can be generated by trajectories originating in the ostensible phase space. Because of ergodic consistency, regardless of how strong or weak the field is, we can prove that the steady state Ω-FR for T-mixing systems will eventually be satisfied. The asymptotic time required for the convergence of the steady state Ω-FR does not scale with the applied field. T-mixing is to be contrasted with the mixing property of stationary measures for dynamical systems. T-mixing does not consider stationary averages but rather concerns itself with transient averages. Our approach is novel and, among other issues, identifies the physically relevant time scales (the decorrelation times with respect to
). If, on the other hand, the system is not T-mixing and a steady state is not reached, the transient relations, as well as Equation (
19), still hold for ensembles of systems at all finite times.
Previous work has also resulted in transient and steady state fluctuation relations for arbitrary odd phase variables, referred to as generalised fluctuation relations [
14,
18,
21]. These can be applied to obtain a fluctuation relation for the phase space expansion. Combining Equation (
12) and Equation (
10) gives a relationship between the instantaneous dissipation function and the phase space expansion rate for a thermostatted system. Then, using the generalised transient fluctuation relation, the transient fluctuation relation for the phase space expansion for the thermostatted system can be written as:
In the special case where there are no correlations between
and
, this will simplify to:
where the final equality is obtained by recognising that the probability ratio must be equal to unity when
. We note that this can then be used to write a fluctuation relation for joint probability distributions of
and
considered for stochastic systems in [
22,
23,
24]. In the deterministic systems studied here, these correlations will be significant, however limits under which these correlations become negligible are important to establish and will be considered in future work.
Similarly, a steady state fluctuation relation for the phase space contraction over the period of length
τ can be obtained:
In the simplistic case where there are no correlations between
and
and assuming that T-mixing holds would enable a simple form of the limiting steady state fluctuation relation for the phase space expansion to be obtained.



.jpg)




