Abstract
Several models have been proposed to explain the dark energy that is causing universe expansion to accelerate. Here the acceleration predicted by the Holographic Dark Information Energy (HDIE) model is compared to the acceleration that would be produced by a cosmological constant. While identical to a cosmological constant at low redshifts, z < 1, the HDIE model results in smaller Hubble parameter values at higher redshifts, z > 1, reaching a maximum difference of 2.6 ± 0.5% around z ~ 1.7. The next generation of dark energy measurements, both those scheduled to be made in space (ESA’s Euclid and NASA’s WFIRST missions) and those to be made on the ground (BigBOSS, LSST and Dark Energy Survey), should be capable of determining whether such a difference exists or not. In addition a computer simulation thought experiment is used to show that the algorithmic entropy of the universe always increases because the extra states produced by the accelerating expansion compensate for the loss of entropy from star formation.
Keywords:
Landauer’s principle; Holographic principle; dark energy experiments; dark energy theory; cosmological constant experiments PACS Codes:
89.70.Cf; 95.36.+x,04.70.Dy; 98.80.Es
1. Introduction
The expansion of the universe is accelerating, driven by a dark energy that presently accounts for around three quarters of the total energy of the universe. This conclusion, initially obtained using type 1a supernova as reference sources [1,2], is supported by more recent supernova measurements [3] and now confirmed by a number of independent measurements [4,5,6,7]. The large dark energy component is evident in gravitational weak lensing [4], in the projected scale of baryon acoustic oscillations [5], in the Cosmic Microwave Background radiation anisotropies [6], as well as in the growth rate of large scale structure, or clustering power spectrum of galaxies [7,8,9]. The many explanations proposed to explain dark energy include: Einstein’s cosmological constant; some form of quintessence field; and a wide range of “alternative” models [8,9].
Two properties are required for a dark energy model to fit the observations. Firstly, the model must be capable of quantitatively accounting for the dark energy density value, a high value, three times the energy density equivalence of the universe’s total mass. Secondly, at least for the recent period, redshifts z < 1, the model must provide a near constant energy density, equivalent to total dark energy increasing as ~a3 where a is the universe scale size (size relative to today, a = 1, and defined in terms of redshift, z, by a = 1/(1+z) ). For a constant energy density the dark energy equation of state parameter, w, the ratio of pressure to energy per unit volume, must take the value w = −1, since energy densities vary as a−3(1+w). Ideally we wish to find a model that satisfies these two requirements without recourse to exotic or unproven physics.
Foremost amongst likely explanations is the cosmological constant, or vacuum energy, that satisfies the second of our two requirements, by definition exhibiting a constant energy density, equivalent to the specific equation of state parameter value w = −1. In contrast, quintessence is a scalar field with a dynamic equation of state and dynamic fundamental constants that should vary over space and time. However, recent observations show that fundamental constants, for example the ratio of proton to electron masses, are constant to a high level of significance, ruling out most quintessence theories [10]. Furthermore, experimental measurements [11] at low redshifts, z < 1, limit the dark energy equation of state to lie within the narrow range w = −0.94 ± 0.09 and thus generally favour the cosmological constant explanation. Accurate measurements of dark energy at higher redshifts, z > 1, await the next generation of instruments. Unfortunately, satisfying the first requirement is more difficult as there are only two possible energy density values expected for a cosmological constant from quantum field theories [12]. The cosmological constant should either have a preferred value some 120 orders of magnitude higher than that required - a value impossible to reconcile with our universe, or it has the value zero. Then a different dark energy explanation would, if verified, enable the cosmological constant to take this second natural value: zero.
A number of holographic dark energy models attempt to account for dark energy without invoking exotic particles, exotic fields, modifications to gravity or fundamental constants, or interactions with dark matter [13,14]. The anti-de-Sitter/conformal field theory duality leads directly to considering that all of the information describing a system can be considered as being encoded on the system’s bounding surface [15,16]. Then today’s dark energy density can follow from a combination of the Planck scale with a suitable cut-off dimension, for example the infrared cut-off [17]. Holographic dark energy may also be caused by vacuum entanglement [18], effectively energy from quantum information loss via Landauer’s principle [19].
Holographic dark energy models [12,13,14,17,18] generally aim to provide an all pervading vacuum energy in the form of a cosmological constant. In contrast, the specific model considered in this paper is the Holographic Dark Information Energy, HDIE, model [20] which takes a phenomenological approach. Here dark energy is explained as the energy equivalence of the information, or entropy, associated with stars and stellar heated gas and dust. HDIE accounts for both of the required dark energy properties and, in particular, manages to satisfy the first property using well established physics (see discussion of Section 2.2). Nevertheless, HDIE is only one of the many dark energy models proposed to date and science progress requires that we eliminate all but one. With that elimination in mind, the emphasis here is on the HDIE model’s predicted signature that differentiates HDIE from other models/theories.
2. The HDIE Model
The HDIE model has been described in detail before [20] and only relevant features are recounted here. Essentially, HDIE combines Landauer’s principle [19] with the Holographic principle [15,16].
Landauer’s principle [19,21,22,23] states that any “erasure” of information, or reduction of information bearing degrees of freedom, in a system at temperature, T, requires a minimum of kBT ln2 of heat per erased bit to be dissipated into the surrounding environment. This dissipated heat increases the thermodynamic entropy of the surrounding environment to compensate for the loss of degrees of freedom and comply with the 2nd law. Information is not destroyed as the “erased” information is now effectively contained in the extra degrees of freedom created in the surrounding environment.
Heat dissipation from information erasure is comparatively weak and usually insignificant in our normal day to day experience. For example, world-wide, mankind has now accumulated some 1022 bits of stored digital data and we have the technological capacity to process a total of around 3 × 1019 instructions per second in general-purpose computers [24]. We can assume that the main information erasure that occurs during the process of computing is caused by overwriting the processor’s instruction register, when each new instruction is read from memory. In this way mankind erases some 1021 bits each second. At room temperature this rate of information erasure will generate a world-wide total of only 3W! This is insignificant, around ~10−11 of the total electronic heat dissipation (ohmic and inductive heating, etc) of the world’s ~109 computer systems that each dissipate ~102 W. Similarly, erasing the 1022 bit sum total of all man-made stored digital data would generate a world-wide total of just 3J.
Despite this low bit equivalent energy, the information-to-energy conversion process has now been demonstrated experimentally using Brownian particles under feedback control [25] and by a one-bit memory consisting of a single colloidal particle trapped in a modulated double-well potential [26]. Moreover, Landauer’s heat dissipation from information erasure is still considered the best way to reconcile Maxwell’s Demon with the second law of thermodynamics [23,27]
Landauer’s principle, while providing an information energy similar to the mc2 energy equivalence for mass, differs in that it defines an inequality, specifying a minimum equivalent energy. Experimental measurements [26] show that energy from information erasure clearly tends towards the Landauer information energy in the limit. Then, as the aim of this work is primarily to account for the high dark energy value, we assume here a direct equivalence for simplicity.
When the same degrees of freedom are considered, information entropy and thermodynamic entropy are identical. Thermodynamic entropy uses natural logarithms with units of nats, while information entropy uses base 2 logarithms with units of bits and one bit equals ln2 nats. Information entropy is used throughout this work because of its relevance to black hole entropy [28] and the Holographic principle [15,16,29]. Then every component of the universe has a (minimum) information equivalent energy of NkBT ln2 that depends on the quantity of information (or entropy), N bits, associated with the component and on the component’s temperature, T. In this way, we can consider the energy represented by information in the cosmos without requiring, or even identifying, processes whereby information may be actually “erased”.
The Holographic principle [15,16] states that the amount of information in any region, N, scales with that region’s bounding area. The Holographic Principle led directly from the discovery that the maximum entropy of a black hole is set by its surface area [28], but the principle is considered to have universal validity [29], i.e., not just limited to the maximum entropy limit of black holes.
2.1. Stellar Heated Gas and Dust
Stellar heated gas and dust and black holes have been found to make the greatest contributions to the entropy, N, of the universe [30,31,32]. Furthermore, stellar heated gas was estimated [20] to have the highest NT product, making the largest information energy contribution to the universe (see Table 1 of [20]). Black holes could make the next strongest contribution at a few percent of that level but it is doubtful whether the information within a black hole, and therefore its information energy, has any effect on the universe because of the “no hair theorem” [33]. While a black hole may exert a significant gravitational force on local objects, the only information that the universe has about it is limited to just three parameters: mass; charge; and angular momentum. From the universe’s information point of view, a black hole is no more than just another single fundamental particle, albeit a massive one! Various relics of the big bang were also considered in Table 1 of [20]. CMB photons, relic neutrinos, and relic gravitons may have high entropies, but their low temperatures result in NT products several orders of magnitude below that of stellar heated gas and dust. While there is considerable uncertainty in such entropy estimates, the decaying temperatures of these relics further excludes them from being considered as candidates to provide a constant dark energy density (see end of Section 2.5).
Since the information energy, NkBT ln2, of the universe is then primarily determined by stellar heated gas and dust, the appropriate temperature, T, will be the average temperature of baryons in the universe. Figure 1a plots average baryon temperature, T, data and the fraction of baryons in stars, f, deduced from a wide literature survey of integrated stellar density measurements, extending the earlier HDIE work [20]. Data symbols and measurement source references are listed here: open circle [34]; open squares [35]; filled rectangles [36]; diamonds [37]; upside down triangles [38]; normal triangles [39]; crosses [40]; circles with dot [41]; filled circles [42] and blue line [43].
Figure 1(a) shows that the average temperature of baryons today is T ~ 2 × 106 K, which, together with the estimate of N ~ 1086 from surveys [20,30,31], provides a quantitative estimate of the present HDIE energy value within an order of magnitude of the observed dark energy, and effectively satisfies dark energy requirement 1. Note that this is dependant on our estimate of N for stellar heated gas and dust, only accurate to a couple of orders of magnitude. We find that, despite the very low bit equivalent energy, information energy can provide a significant contribution on cosmic scales, primarily because the universe’s mass has remained constant, while both the quantity of information (entropy), N, increased continually and the average baryon temperature, T, also increased with increasing star formation.
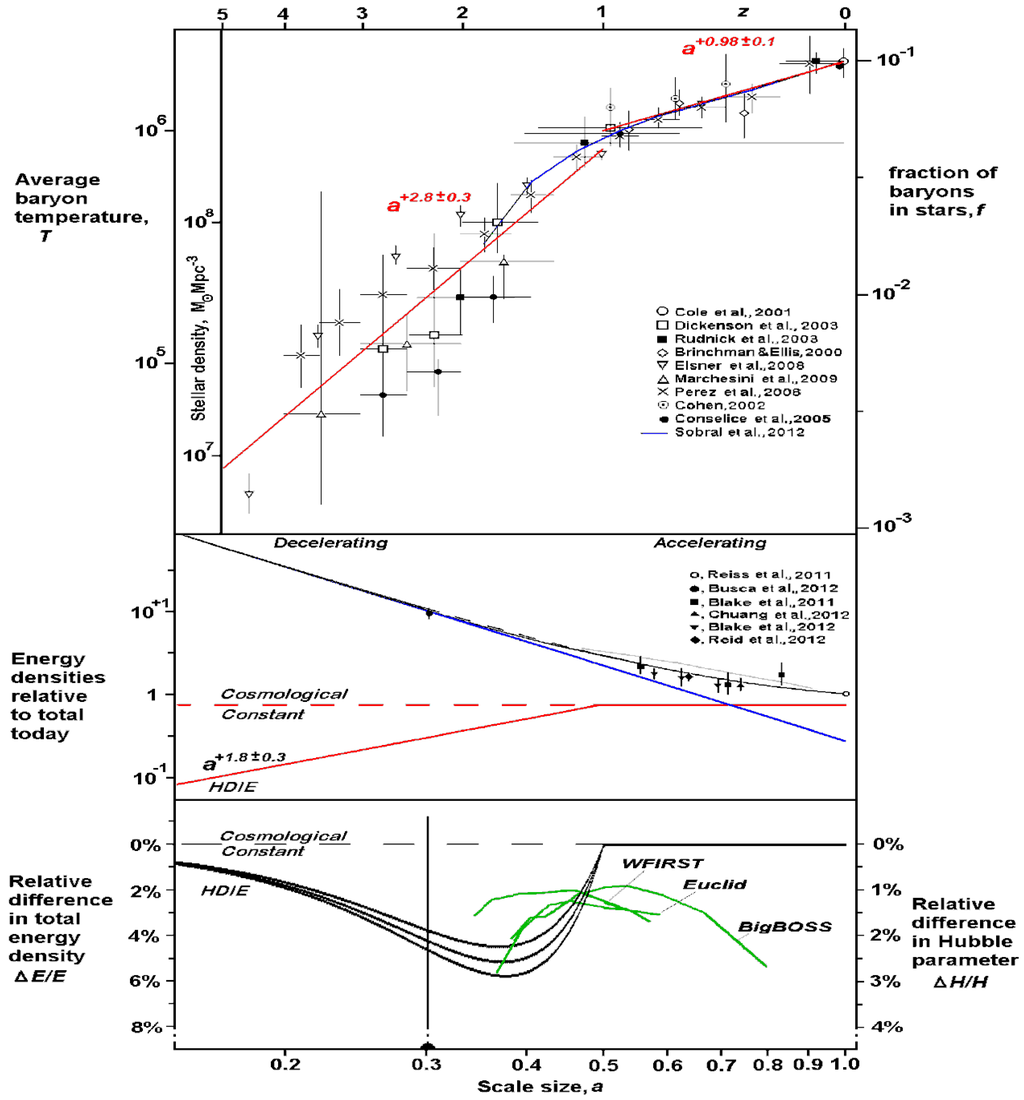
Figure 1.
Plotted against log of universe scale size, a, and redshift, z, are: (a) Upper Panel: Log plot of measured stellar densities (various symbols and blue line: see text for measurement sources) and resultant average baryon temperature, T, and the fraction of all baryons in stars, f. Red lines- best power law fits to data points are a+0.98±0.1 for z < 1, and a+2.8±0.3 for z > 1. (b) Middle Panel: Log plot of energy density contributions: red continuous line, HDIE energy density corresponding to the red line fit in the upper panel; dashed red line, cosmological constant; blue line, mass; solid black line, total for HDIE case; dashed black line, total for the case of a cosmological constant; data symbols, energy densities derived from recent Hubble parameter measurements normalised to Hubble constant measurement at a=1; grey continuous line, the gedanken experiment considered in Section 3.2. (c) Lower Panel: Linear plot of relative differences in total energy, and in Hubble parameter, between the HDIE model and a cosmological constant. The resolving thresholds of three next generation space and ground-based measurements are shown for comparison in green together with the error bar of the existing measurement at z = 2.3 (see Section 2.4).
Figure 1a shows a distinct change in power law around z ~1 and data either side of z = 1 are therefore considered separately. Applying linear least squares curve fitting to logarithmic values of the data in the redshift range z < 1, we observe a temperature gradient of a+0.98±0.1. Then, assuming the baryon information bit number, N, scales as a+2 from the holographic principle, total HDIE energy for z < 1 scales as a+2.98 ± 0.1. Since universe volume increases as a3, there is a nearly constant HDIE energy density at z < 1. The HDIE equation of state parameter lies in the narrow range −0.96 > wHDIE > −1.03 which includes the specific value, wDE = −1 and thus satisfies dark energy requirement 2. This present work improves on the earlier HDIE work [20] significantly reducing the error in the temperature gradient at z<1 from what was effectively a+0.98 ± 0.17 to a+0.98 ± 0.10.
2.2. Dependence on the Holographic Principle
HDIE can account for today’s high dark energy value (requirement 1) solely by applying proven physics, i.e., without requiring the holographic principle. Measurements of the present average baryon temperature (Figure 1a right-hand axis intercept [34,35,36,37,38,39,40,41,42,43]), are combined with estimates of the information (entropy) associated with stellar gas and dust [30,31], and experimentally proven [25,26] Landauer’s principle. However, for HDIE to account for the constant dark energy density z < 1, (requirement 2), the measured average baryon temperature relation [T α a+0.98±0.1 at z < 1, Figure 1(a)] has to be combined with the, as yet unproven, holographic principle relating information content to bounding area, N α a+2.
Now the Bekenstein-Hawking description [28] of a black hole, with entropy proportional to surface area, is widely accepted physics. But black holes exist at the maximum entropy holographic bound while the universe is some 30 orders of magnitude below the holographic bound. The holographic principle, whereby all 3-D space can be translated into a 2-D representation [15,16,44], is directly related to string theory and M-theory. Strong support for the holographic principle has been provided by a specific quantum theoretical example from string theory. The “Maldacena duality” or “anti-de-Sitter/conformal field theory” (AdS/CFT) correspondence [45] allows for a holographic translation between one particular multidimensional space with gravity and another space with one less dimension but without gravity. Another theoretical work [46] effectively combines the holographic principle with Landauer’s principle as in this present work, and suggests that gravity may emerge as an “entropic force”. Note that our present work may be thought of as considering “entropic energy”. Relevant theory in support of the holographic principle is still being developed and, as yet, there is no experimental proof of the principle. Attempts to directly verify the holographic principle by experiment are difficult and sometimes controversial [47]. Therefore the holographic principle, naturally extending the N α a+2 relation to all objects, including those well below their maximum entropy, remains an attractive but unproven hypothesis, and thus accounts for the main speculative aspect of the HDIE model.
Nevertheless, the measurements plotted in Figure 1a, showing T α a+0.98 ± 0.1 at z < 1, closely centered round the specific T α a+1 relation required to satisfy requirement 2, together with our ability above to satisfy requirement 1, provide significant support for the HDIE model. Accordingly, we continue our work below by considering HDIE primarily from a phenomenological point of view, and limit ourselves to only employing the main proposition of the holographic principle: i.e., that N α a+2.
2.3. Dark Energy Predictions for z > 1
Figure 1a shows that the temperature gradient was much steeper at redshifts z > 1, with a wider spread in measured data points and a best power law fit of a+2.8 ± 0.3. Clearly HDIE energy density was increasing in this earlier period up to the point around z ~ 1, after which there has been a near constant value that we have shown can account for both dark energy requirements from that time onwards.
In the following analysis we therefore assume that the level HDIE energy density z < 1 indeed accounts for all dark energy, and we will adopt the standard model with present energy density values: 73% dark energy, 27% matter (including dark matter) Then Figure 1b shows the mass energy density falling as a−3 (blue line), the resulting HDIE energy density contribution with the above assumption (red line), and a cosmological constant for comparison (red dashed line). The a+2.8 ± 0.3 temperature dependance, z > 1, corresponds to an HDIE energy density gradient of a+1.8 ± 0.3 when information bit quantity, N, is again assumed to scale as a2 from the Holographic principle. Then the mean a+1.8 HDIE energy density variation corresponds to an equation of state wHDIE = −1.6 for z > 1.
In Figure 1b we also compare the total energy density from HDIE plus mass (black continuous line) with the total energy density of a cosmological constant plus mass (black dashed line). At first sight, the two total energy curves lie very close together with little apparent difference because they are plotted multi-decade log versus log.
Accordingly, in Figure 1c the relative difference in total energy density, ΔE/E, between HDIE plus mass, and a cosmological constant plus mass, is shown on a linear versus log plot. The HDIE energy density gradient, a+1.8 ± 0.3, with ±1sigma upper and lower bounds from the fit to data in Figure 1a, corresponds to a relative difference in total energy, ΔE/E, in Figure 1c that peaks at −5.2 ± 1.0% near z ~1.6−1.7. Although there is a clear change in gradient around z ~ 1 evident in the data plotted in Figure 1a, our fitting to gradients that change precisely at z = 1 may provide an overemphasized sharp transition in ΔE/E at z = 1. However, this transition should not significantly affect the size or the location of the predicted negative peak in ΔE/E at z ~1.7. At earlier times, z > 4, the higher mass density swamps any difference between HDIE and a cosmological constant. Later, as the mass density falls ΔE/E begins to reflect the difference in the energy densities of the two dark energy components, peaking at z ~ 1.7 as HDIE energy density rapidly increases as a+1.8 ± 0.3 towards z ~ 1, after which time there is no difference between models.
While the Hubble constant, H0, is the fundamental ratio between the recessional velocities of objects in the universe and their distance from us today, H0 is just the present value of the more general Hubble parameter, H. The Hubble parameter, H, varies with changes in universe expansion rate over time and is therefore a function of universe scale factor, a. Since total energy density, E, is proportional to H2, (from the Friedmann equation, [48]) the HDIE model thus predicts that the Hubble parameter around z ~ 1.7 should be 2.6 ± 0.5% less than that expected for a cosmological constant explanation for dark energy.
2.4. Measurement Capabilities of Next Generation Instruments
The HDIE predicted ~2.6% difference in the Hubble parameter cannot be resolved by today’s instruments which still have typical resolutions >5%. In Figure 1b the total energy density data points plotted are derived from recent experimental measurements of the Hubble parameter [49,50,51,52,53,54] and normalised to the Hubble Constant measurement [50] at a = 1. Despite some considerable spread in error bars, the data points clearly support the change from deceleration to acceleration. In particular, the one measurement above z = 1, that at z = 2.3 [49], is relevant to the HDIE discussion and is replotted in Figure 1c. While the data point is clearly below the dashed cosmological constant line, as expected for the HDIE model, the error bar, which necessarily includes both the measurement errors of [49] and [50], is large and includes the expected values of both dark energy explanations.
Fortunately, the next generation of space and ground-based dark energy instruments should be capable of making measurements at sufficient resolution to distinguish between a cosmological constant and the HDIE model. The future European Space Agency Euclid spacecraft [55], and the planned NASA WFIRST spacecraft [56], will both cover the redshift range 0.7 < z < 2.0, while the ground-based BigBOSS [57], LSST [58] and Dark Energy Survey [59] measurement campaigns will measure z < 1.7, z < 5 and z < 2, respectively. These experiments employ a combination of techniques: weak gravitational lensing to measure the growth of structure; supernova distances at low z; and baryon acoustic oscillations at higher z. The expected mission resolution of three of these dark energy experiments are shown in Figure 1c (green lines) for comparison. The 2%–3% difference in Hubble parameter around z ~ 1.7 should be resolved by all three experiments. At the time of writing these next generation measurement development timescales are: Dark Energy Survey starting a five year survey in 2012, BigBOSS first light 2016 with full science starting 2017; ESA Euclid launch 2019; LSST first light 2020 with full science starting 2022; and NASA WFIRST launch 2022.
Note that HDIE effectively provides a dynamic equation of state but, rather than a smooth variation, there are two distinct regimes: wHDIE = −1 for z < 1; and wHDIE ~−1.6 for z >1. Now it is usual when designing these experiments to characterise any dynamic equation of state parameter, w(a), by a smoothly varying two parameter model, typically given as: w(a) = wp + wa(1 − a) , where wp is the present value, the early value was wp + wa, and the mid-point transition occurs at a = 0.5, or z = 1. The experimental figure of merit is then determined by how small the error ellipse is in the wp − wa plane. For example, the ESA Euclid measurement accuracies equivalent to 1 sigma error are expected to be 0.02 in wp, and 0.1 in wa up to z ~ 2 [55]. These accuracies are clearly sufficient to falsify HDIE where the nearest equivalent parameter values are wp = −1 and wa = −0.6, as compared to the cosmological constant values of wp = −1 and wa = 0. The expected difference between HDIE and the cosmological constant is small and peaks over a narrow predicted range of redshifts. A more appropriate way to identify the signature of HDIE is by a determination of the Hubble parameter, H, or total energy density as a function of scale factor, a, or redshift, z (as in Figure 1b,c). The HDIE model is therefore falsifiable [60], since a failure to observe this specific signature would clearly exclude this model.
2.5. Characteristic Energy
The characteristic energy of HDIE, the energy equivalence of a bit of information, kBT ln2, depends solely on temperature, T. Today, some 10% of the baryons are located in stars at temperatures ~2 × 107 K with characteristic energies ~103eV. As the remaining 90% of baryons exist at very much lower temperatures the average baryon temperature of baryons is ~2 × 106 K, one tenth of stellar temperatures, and corresponds to an average characteristic energy ~102eV.
It is interesting here to consider the characteristic bit energy of the 90% of baryons not involved in star formation and thus we need to associate a representative temperature. We can consider the radiation temperature, T’, that would have the same energy density as matter: ρc2 = σT’4, where ρ is the universe total mass density (including dark matter), and σ the radiation constant. Substituting σ and kB by their definitions in terms of fundamental constants, we obtain the characteristic bit energy, Echar = kBT’ ln2 = (15ρћ3c5/π2)1/4 ln2.
This definition was previously identified [61,62] as being identical to the characteristic energy of a cosmological constant (taking ln2 ~ 1, identical to equation 17:14 of [63]). In this way we obtain a value T’~ 35K, corresponding to a characteristic energy of ~3 × 10−3 eV. Note that we expect a temperature around 10 times the temperature of the cosmic microwave background, CMB, since present matter energy density is ~104 times the CMB energy density.
Previously it was difficult to account for the low characteristic milli-eV energy usually associated with the cosmological constant [63]. Here it may be explained as an information bit equivalent energy. While the characteristic energy of HDIE corresponds to information concerning stars and star formation, the characteristic energy of the cosmological constant corresponds to information concerning the colder parts of the universe not involved in star formation. In recent times, z < 1, HDIE characteristic bit energy has increased as a+1 with increasing star formation while the cosmological constant characteristic energy always falls as ρ+1/4, or a−3/4, with the cooling universe majority. Then it is difficult to see how the cosmological constant, with a characteristic energy falling as a−3/4, can produce a total energy that increases as a+3 as required for a constant dark energy density. Similarly, the relics of the big bang, CMB, relic neutrinos, and relic gravitons, all exhibit decaying temperatures, and thus decaying characteristic energies, effectively discounting them from making a significant information energy contribution to a constant dark energy density.
In contrast, HDIE from stellar heated gas and dust has a characteristic bit energy that increases as a+1 and, with total bit number, N, increasing as a+2 by the holographic principle, provides the required a+3 total energy variation.
3. Gedanken Experiment
We have shown that the HDIE model, incorporating Landauer’s principle, may be considered a serious contender to explain dark energy. Landauer’s principle also provides an explanation for Maxwell’s Demon, the famous gedanken (thought) experiment of physics [23,27]. We continue here with what might be considered a less serious thought experiment, but one that nevertheless provides an interesting, information related, aspect to the universe’s accelerating expansion.
3.1. Hypothetical Computer Simulation
Consider the amount of information that a hypothetical super computer located outside the universe would need to fully simulate the universe’s baryons. We conveniently ignore how such a computer can be located outside the universe, how this information would be gathered, and any measurement limitations imposed by the uncertainty principle. For a full physics simulation we require that each spatial parameter of every baryon be registered to the maximum physically meaningful accuracy, i.e., at the resolution of the Planck length, lp = 1.6 × 10−35 m. Intergalactic baryons in the present universe, size lu~1027 m, then require an accuracy of one part in 6 × 1061 (~2205) and hence require 205 bits per spatial parameter. Similarly baryons located in giant molecular clouds, size lgmc ~1018 m, and baryons located in typical stars, e.g. the sun size ls ~109 m, require ~175 bits and ~145 bits respectively per spatial parameter.
Rather than consider the total information required for our simulation it is more convenient to limit ourselves to estimating the average number of bits per spatial parameter per baryon. We assume that the 10% of baryons presently located in stars that now require ~145 bits per parameter were, at earlier times, located in giant molecular clouds that required ~30 bits more at ~175 bits per parameter. We model this change from giant molecular clouds to stars from the variation of the fraction, f(a), of baryons in stars as a function of scale size using the power law fits to the measurements plotted in Figure 1a. Meanwhile the remaining 90% of baryons, intergalactic baryons not involved in star formation, increased as log2(a) up to their present 205 bits per parameter. The average number of bits per parameter per baryon, nav, is a function of scale size, a, and is then given by:
.
nav(a) = (1 − f(1)) log2(a lu/lp) + (f(1) − f(a)) log2(lgmc/lp) + f(a) log2(ls/lp)
Inserting values of f(a) from Figure 1a we find that nav increased with intergalactic baryons but reached a peak value of 200.03 bits at a ~ 0.32, but then decreased due to increasing star formation to today’s value of 199.02 bits, almost exactly one bit below the peak value. This one bit loss can be simply explained by the 10% of baryons that formed stars lost 30 bits per spatial parameter, contributing a loss of 3 bits to nav, while the 90% intergalactic baryons only added 2 bits to nav between a = 1/4 and the present, a = 1.
The amount of information required to simulate an isolated system should never decrease, otherwise it must imply a decrease in that system’s number of states or information, which would be contrary to the 2nd law. Now, if the universe expanded faster to double its expected size over the recent period, this would increase the contribution of the 90% intergalactic baryons to nav by a further 1 bit. Then we could effectively compensate for our loss of one bit in nav and satisfy the 2nd law again. Interestingly, dark energy has indeed doubled the size of the universe, exactly as we require, since it has increased the energy density by a factor of four, corresponding to a doubling of the Hubble parameter. Figure 1b grey continuous line, uses the above relation and assumptions to show the minimum variation in total energy density that is required to ensure there is no decrease in the amount of information needed as input to our simple computer simulation during this period. This variation can be seen to lie close to that deduced from the effects of dark energy (whether due to HDIE or a cosmological constant).
It is a surprise to find that the accelerating expansion was necessary for the universe to comply with the 2nd law and ensure that there was no decrease in the amount of information required for input to our simple thought experiment! Note that while the approach here is based on just a few simple assumptions, they are all, none the less, quite reasonable. For example, many of the 90%, intergalactic baryons, not involved in star formation, do not move freely throughout the whole universe, but are probably constrained to intergalactic filaments, whose dimensions presumably stretch with the increasing space between galaxies, and hence still have dimensions that scale with a. We have ignored the information represented by CMB, as it has remained near constant since decoupling, with CMB wavelength increasing in proportion to universe size. We have also ignored those baryons still in giant molecular clouds, yet to take part in star formation, but these will just add a constant amount to nav. If we had used a different minimum resolution, for example the Fermi length, 10−15 m, the above bit numbers would be 66 bits less but, without the doubling of universe size from dark energy, there would still have been the same reduction of 1 bit in nav. So, although there is considerable uncertainty in absolute quantity of information required for our simulation, we can reasonably say that the doubling in universe size due to dark energy was just what was required to ensure that the amount of information needed as input to our computer simulation did not decrease.
Of course it is still possible that our requirement for about one bit is just a coincidence, perhaps because we chose giant molecular clouds (size ~1018m) as the starting points for star formation. For comparison, at the two extremes of starting point either side, we would have obtained a value close to two bits drop in nav if we had considered star formation as starting all the way from the parent galaxies (size ~1021 m). Alternatively we would obtain a value close to zero change in nav if we had considered that star formation only started much later, at the final pre-stellar stage of proto-stellar nebula (size ~1015 m). However, given the typical star formation sequence and the timescale considered in Figure 1, it seems most reasonable to consider pre-existing giant molecular clouds as the effective beginning points for star formation.
3.2. Algorithmic Information Content
The relation between the above computer simulation information and the actual information intrinsic to the universe is analogous to the relation between the algorithmic information content (algorithmic entropy or Kolmogorov complexity), the size of the smallest algorithm that can generate a dataset and the actual amount of information contained within that dataset [64,65]. For non-random datasets algorithmic information is always less than the information in the dataset. For a truly random dataset, i.e. one that cannot be calculated by an algorithm, the algorithmic information is always equal to, or just slightly greater than, the amount of information in the dataset by the size of the small program required to access the random dataset. That dataset must then be completely included as data, constituting the bulk of program code.
At ~200 bits per spatial parameter each of the ~1080 baryons in the universe requires ~103 bits, giving a total baryon simulation requirement ~1083 bits. This value is not very dependent on simulation resolution, whether at Planck or Fermi lengths. Then, by analogy to algorithmic information content, we see that this simulation requirement is, as expected, less than the above N~1086 bits of HDIE, because significant structure, or non-randomness, exists today in the form of galaxies, stars etc.
Before structure began to form the algorithmic and actual entropies would have been equal since the universe was effectively random. At 3.8 × 105 years, the time of decoupling, the irregularities that eventually formed today's galaxies and stars were still insignificant at the level of 10−5, as evidenced in CMB today. Significant structure only began with the first stars at ~108 years. Between 108 years (a ~ 10−2) and today, 1.37 × 1010 years (a = 1), the required simulation information increased at the rate of log2 a, while holographic information increased at the faster rate of a2, to explain the above difference of ~103 between these two entropies today.
4. Implications for the cosmos
Our gedanken experiment above suggests that the universe, as a whole, still manages to satisfy the 2nd law when degrees of freedom are lost as interstellar clouds collapse to form stars. The extra expansion from dark energy acceleration provides enough of an increase in inter-galactic states to compensate for those states lost during star formation. Interestingly, with the HDIE explanation for dark energy, the extra expansion is itself a direct result of star formation. Note that previously, it was suggested [66] that the loss of thermodynamic entropy due to structure and star formation is counteracted by a gain in gravitational entropy.
We have shown that the energy represented by HDIE makes a significant contribution to the overall universe energy density and can quantitatively account for the observed dark energy. Our use of the HDIE energy density equivalence of information is similar to the use of ρc2 for the energy density equivalence of the matter contribution to the universe total energy density budget.
There are four implications for the cosmos that will follow if the predicted HDIE model signature is observed, and HDIE thus found to be the correct explanation for dark energy:
The first implication concerns the reason why the temperature variation a+0.98±0.1 so closely follows a+1 since z ~ 1 to provide the near constant HDIE energy density, −0.96 < wHDIE < −1.03. If star formation had continued to proceed at the earlier faster rate, then it would have continued the steep a+2.8 ± 0.3 average baryon temperature increase after z ~ 1. This would have increased HDIE dark energy well above its present value, lead to much greater acceleration and greater expansion, but in turn, would have resulted in much less star formation. It would appear that since z ~ 1 there has been a balance, or feedback, between expansion acceleration and star formation. This has naturally maintained the star formation rate close to a+1 for a constant dark energy density. Note that the reduced rate of star and structure formation starting at z~1 was previously attributed to the onset of acceleration [67]. Thus HDIE can provide a natural explanation for the reason why wDE = −1 since z ~1.
The second implication concerns the cosmic coincidence problem. Our existence just now in the era dominated by dark energy is considered an unlikely coincidence. However, HDIE dark energy density increased with increasing entropy and increasing baryon temperature with increasing star formation, while mass density decreased with increasing universe scale size. There had to be a time when HDIE energy density reached a level comparable to mass energy density to initiate acceleration (provided that time was reached before f(a) = 1). Similarly, the likelihood of our existence also increased as overall star formation increased, and thus likely to occur after HDIE started to make a significant contribution to the energy budget, effectively removing the cosmic coincidence problem.
The third implication concerns how long the present period of accelerating expansion will last. Acceleration will continue provided the overall universe equation of state parameter is limited to w < −1/3 [9]. This threshold corresponds to HDIE energy density falling off as a−2, and, assuming the total information, N, continues to follow the Holographic principle as a+2, provides a limiting average baryon temperature, T, variation of a−1. Thus, acceleration due to HDIE will continue, providing T does not fall off more steeply than a−1. Computer simulations of future average baryon temperatures, T, up to a = 200 [68], predict a levelling off of T since f(a) is limited by definition to f(a) < 1, with a slow eventual fall as star formation ceases, but falling less steeply than the threshold gradient of a−1. Thus acceleration should continue, until at least the universe has increased in size by a factor of 200.
Clearly the final implication is that, should the predicted signature of HDIE be observed, it would provide very strong support for the holographic principle (see Section 2.2).
5. Summary
Computer scientist Landauer [69] emphasized that “Information is Physical” and astrophysicist Wheeler [70] went further, declaring with his famous slogan “It from Bit”, that information may be more fundamental than matter. All of the arguments put forward in this paper for the HDIE dark energy explanation, as well as those used in the above thought experiment, also combine to point to the importance of considering information as one of the fundamental properties of the universe.
Most importantly, we have shown that HDIE can account for dark energy both qualitatively and quantitatively, accounting for both key dark energy properties in the redshift range z < 1: the constant dark energy density and that energy density value. Furthermore, with the HDIE explanation for dark energy, we no longer have the coincidence problem.
At higher redshifts, HDIE should produce a clear signature, predicting that at z ~ 1.7 the Hubble parameter will have a value 2.6 ± 0.5% less than that expected for a cosmological constant. Then the HDIE model is falsifiable, as the size and location of this predicted signature lies within the resolvable ranges of the next generation of dark energy measurements.
Finally, the accelerating expansion appears to have been necessary in order for there to be no decrease in the universe's algorithmic entropy.
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.-G.; Castertano, S.; Ferguson, H.C.; Mobasher, B.; Gold, B.; Challis, P.J.; Filippenko, A.V.; Jha, S.; Li, W.; et al. New Hubble space telescope discoveries of type 1a supernovae at z ≥ 1; narrowing constraints on the early behaviour of dark energy. Astrophys. J. 2007, 659, 98–121. [Google Scholar] [CrossRef]
- Bacon, D.J.; Refregier, A.R.; Ellis, R.S. Detection of weak gravitational lensing by large-scale structure. Mon. Not. R. Astron. Soc. 2000, 318, 625–640. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF galaxy survey: Baryon acoustic oscillations and the local Hubble constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Sherwin, B.D; Dunkley, J.; Das, S.; Appel, J.W.; Bond, J.R.; Carvalho, C.S.; Delvin, M.J.; Dunner, R.; Essinger-Hileman, T.; et al. Evidence for dark energy from the cosmic microwave background alone using the Atacama Cosmology Telescope lensing measurements. Phys. Rev. Lett. 2011, 107, 021302. [Google Scholar] [CrossRef] [PubMed]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Davis, T.; Drinkwater, M.J.; Forster, K.; Gilbank, D.; et al. The WiggleZ dark energy survey: The growth rate of cosmic structure since z = 0.9. Mon. Not. R. Astron. Soc. 2011, 415, 2876–2891. [Google Scholar] [CrossRef]
- Carroll, S.M. Why is the universe accelerating? In Carnegie Observatories Astrophysics Series, Vol. 2, Measuring and Modeling the Universe; Freedmann, W.L., Ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark energy and the accelerating universe. Ann. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Thompson, R.I.; Martins, C.J.A.P.; Vielveuf, P.E. Constraining cosmologies with fundamental constants I. quintessence and K-essence. Mon. Not. R. Astron. Soc. 2013, 428, 2232–2240. [Google Scholar] [CrossRef]
- Tegmark, M.; Eisenstein, D.J.; Strauss, M.A.; Weinberg, D.H.; Blanton, M.R.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Hamilton, A.J.S.; Knapp, G.R.; et al. Cosmological constraints from the SDSS luminous red galaxies. Phys. Rev. D 2006, 74, 123507. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Li, M. A model of holographic dark energy. Phys. Lett. B 2004, 603, 1–5. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, B.; Zhang, Y.-Z. Holographic dark energy reexamined. Phys. Rev. D 2005, 72, 043510. [Google Scholar] [CrossRef]
- Fischler, W.; Susskind, L. Holography and cosmology. 1998. [Google Scholar]
- Hooft, G. Obstacles on the way towards the quantization of space, time and matter- and possible solutions. Stud. Hist. Phil. Mod. Phys. 2001, 32, 157–180. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, Y.-Z. Holography and holographic dark energy model. Class. Quantum Grav. 2005, 22, 4895–4901. [Google Scholar] [CrossRef]
- Lee, J.W.; Lee, J.; Kim, H.-C. Dark energy from vacuum entanglement. J. Cosmol. Astropart. P. 2007, 08, 005. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 3, 183–191. [Google Scholar] [CrossRef]
- Gough, M.P. Holographic Dark Information Energy. Entropy 2011, 13, 924–935. [Google Scholar] [CrossRef]
- Piechocinska, B. Information erasure. Phys. Rev. A 2000, 61, 062314. [Google Scholar] [CrossRef]
- Landauer, R. Dissipation and noise immunity in computation and communication. Nature 1988, 335, 779–784. [Google Scholar] [CrossRef]
- Maxwell’s Demon 2: Entropy. In Classical and Quantum Information; Leff, H.S.; Rex, A.F. (Eds.) Computing IOP Publishing Ltd: London, UK, 2003.
- Hilbert, M.; López, P. The world’s technological capacity to store, communicate, and compute information. Science 2011, 332, 60–65. [Google Scholar] [CrossRef] [PubMed]
- Toyabe, S.; Sagawa, T.; Ueda, M.; Muneyuki, E.; Sano, M. Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality. Nat. Phys. 2010, 6, 988–992. [Google Scholar] [CrossRef]
- Berut, A.; Arakelyan, A.; Petrosyan, A.; Ciliberto, S.; Dillenschneider, R.; Lutz, E. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature 2012, 483, 187–189. [Google Scholar] [CrossRef] [PubMed]
- Maruyama, K.; Nori, F.; Vlatko, V. The physics of Maxwell’s demon and information. Rev. Mod. Phys. 2009, 81, 1–23. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Frampton, P.H.; Hsu, S.D.H.; Kephart, T.W.; Reeb, D. What is the entropy of the universe? Classical Quant. Grav. 2009, 26, 145005. [Google Scholar] [CrossRef]
- Egan, C.A.; Lineweaver, C.H. A larger estimate of the entropy of the universe. Astrophys. J. 2010, 710, 1825–1834. [Google Scholar] [CrossRef]
- Buosso, R.; Harnik, R.; Kribs, G.D.; Perez, G. Predicting the cosmological constant from the causal entropic principle. 2007. [Google Scholar]
- Ruffini, R.; Wheeler, J.A. Introducing the black hole. Phys. Today 1971, 24, 30–41. [Google Scholar] [CrossRef]
- Cole, S.; Norberg, P.; Baugh, C.M.; Frenk, C.S.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Colless, M.; Collins, C.; Couch, W.; et al. The 2dF galaxy redshift survey. Mon. Not. R. Astron. Soc. 2001, 326, 255–273. [Google Scholar] [CrossRef]
- Dickinson, M.; Papovich, C.; Ferguson, H.C.; Budavari, T. The evolution of the global stellar mass density at 0 < z < 3. Astrophys. J. 2003, 587, 25–40. [Google Scholar]
- Rudnick, G.; Rix, H-W.; Franx, M.; Labbe, I.; Blanton, M.; Daddi, E.; Schreiber, N.M.F.; Moorwood, A.; Rottgering, H.; Trujillo, I.; et al. The rest-frame optical uminosity density, color, and stellar mass density of the universe from z = 0 to z = 3. Astrophys. J. 2003, 599, 847–864. [Google Scholar] [CrossRef]
- Brinchmann, J.; Ellis, R.S. The mass assembly and star formation characterisatics of field galaxies of known morphology. Astrophys. J. 2000, 536, L77–L80. [Google Scholar] [CrossRef] [PubMed]
- Elsner, F.; Feulner, G.; Hopp, U. The impact of Spitzer infrared data on stellar mass estimates. Astron. Astrophys. 2008, 477, 503–512. [Google Scholar] [CrossRef]
- Marchesini, D.; Van Dokkum, P.G.; Schreiber, N.M. F.; Franx, M.; Labbe, I.; Wuyts, S. Evolution of the stellar mass function of galaxies from z = 4.0. Astrophys. J. 2009, 701, 1765–1796. [Google Scholar] [CrossRef]
- Perez-Gonzalez, P.G.; Rieke, G.H.; Villar, V.; Barro, G.; Blaylock, M.; Egami, E.; Gallego, J.; Gil de Paz, A.; Pascual, S.; Zamorano, J.; et al. The stellar mass assembly of galaxies from z = 0 to z = 4.0. Astrophys. J. 2008, 675, 234–261. [Google Scholar] [CrossRef]
- Cohen, J.G. Caltech faint galaxy redshift survey. Astrophys. J. 2002, 567, 672–701. [Google Scholar] [CrossRef]
- Conselice, C.J.; Blackburne, J.A.; Papovich, C. The luminosity, stellar mass, and number density evolution of field galaxies. Astrophys. J. 2005, 620, 564–583. [Google Scholar] [CrossRef]
- Sobral, D.; Smail, I.; Best, P.N.; Geach, J.E.; Matsuda, Y.; Stott, J.P.; Cirasuolo, M.; Kurk, J. A large Hα survey at z=2.23, 1.47, 0.84 & 0.40: The 11 Gyr evolution of star-forming galaxies from HiZELS. 2012. [Google Scholar]
- Buosso, R. The holographic principle. Rev. Mod. Phys. 2002, 74, 825–874. [Google Scholar] [CrossRef]
- Maldacena, J. The large N limit of superconformal field theories and supergravity. 1998. [Google Scholar]
- Verlinde, E. On the origin of gravity and the laws of Newton. 2010. [Google Scholar]
- Cho, A. Sparks fly over shoestring test of the holographic principle. Science 2012, 336, 147–149. [Google Scholar] [CrossRef] [PubMed]
- Friedman, A. On the curvature of space. Gen. Relat. Gravit. 1999, 31, 1991–2000. [Google Scholar] [CrossRef]
- Busca, N.G.; Delubac, T.; Rich, J.; Bailey, S.; Font-Ribera, A.; Kirkby, D.; Le Goff, J.M.; Pieri, M.M.; Slosar, A.; Auborg, E.; et al. Baryon acoustic oscillations in the Lyα forest of Boss quasars. 2012. [Google Scholar]
- Reiss, A.G.; Macri, L.; Casertano, S.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R. A 3% solution: Determination of the Hubble constant with the Hubble Space Telescope and wide field camera. Astrophys. J. 2011, 730, 119. [Google Scholar] [CrossRef]
- Blake, C.; Glazebrook, K.; Davis, T.M.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Drinkwater, M.J.; Forster, K; et al. The WiggleZ dark energy survey: Measuring the cosmic expansion history using the Alcock-Paczynski test and distant supernovae. Mon. Not. R. Astron. Soc. 2011, 418, 1725–1735. [Google Scholar] [CrossRef]
- Chuang, C.-H.; Wang, Y. Measurements of H(z) and Da(z) from the two-dimensional two-point correlation function of Sloan Digital Sky Survey luminous red galaxies. Mon. Not. R. Astron. Soc. 2012, 426, 226–236. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ dark energy survey: Joint measurements of the expansion and growth history at z <1. Mon. Not. R. Astron. Soc. 2012, 425, 405–414. [Google Scholar]
- Reid, B.A.; Samushia, L.; White, M.; Percival, W.J.; Manera, M.; Padmanabhan, N.; Ross, A.J.; Sanchez, A.G.; Bailey, S.; Bizyaev, D.; et al. The clustering of galaxies in the SDSS-III Baryon oscillation spectroscopic survey. 2012. [Google Scholar]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Augueres, J.L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; et al. Euclid definition study report. 2011. [Google Scholar]
- NASA WFIRST Final Report. Available online: http://www.wfirst.gsfc.nasa.gov/science/sdt_public/WFIRST_SDT_Final_Report.pdf (accessed on 26 November 2012).
- Schlegel, D.J.; Bebek, C.; Heetderks, H.; Ho, S.; Lampton, M.; Levi, M.; Mostek, N.; Padmanabhan, N.; Perlmutter, S.; Roe, N.; et al. The ground-based StageIV BAO Experiment. 2009. [Google Scholar]
- Ivezic, Z.; Tyson, J.A.; Acosta, E.; Allsman, R.; Anderson, S.F.; Andrew, J.; Axelrod, T.; Barr, J.D.; Becker, A.C.; et al. LSST: From science drivers to reference design and anticipated data products. 2011. [Google Scholar]
- Dark Energy Survey proposal. Available online: http://www.darkenergysurvey.org/reports/proposal-standalone.pdf (accessed on 15 January 2013).
- Popper, K. The Logic of Scientific Discovery; Routledge: London, UK, 1959. [Google Scholar]
- Gough, M.P.; Carozzi, T.; Buckley, A.M. On the similarity of information energy to dark energy. 2006. [Google Scholar]
- Gough, M.P. Information equation of state. Entropy 2008, 10, 150–159. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Principles of Physical Cosmology; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Zurek, W.H. Thermodynamic cost of computation, algorithmic complexity and the information metric. Nature 1989, 341, 119–124. [Google Scholar] [CrossRef]
- Devine, S. The insights of Algorithmic Entropy. Entropy 2009, 11, 85–110. [Google Scholar] [CrossRef]
- Penrose, R. The Road to Reality; Jonathan Cape: London, UK, 2004. [Google Scholar]
- Guzzo, L.; Pierleoni, M.; Meneux, B.; Branchini, E.; Le Fevre, O.; Marinoni, C.; Garilli, B.; Blaizot, J.; De Lucia, G.; Pollo, A.; et al. A test of the nature of cosmic acceleration using galaxy redshift distortions. Nature 2008, 451, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Nagamine, K.; Loeb, A. Future evolution of the intergalactic medium in a universe dominated by a cosmological constant. New Astron. 2004, 9, 573–583. [Google Scholar] [CrossRef]
- Landauer, R. Information is physical. Phys. Today. 1991, 44, 23. [Google Scholar] [CrossRef]
- Wheeler, J.A. Information, physics, quantum: The search for links. Zurek, W., Ed.; In Complexity, Entropy, and the Physics of Information; Addison-Wesley: Redwood City, California, USA, 1990. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).