1. Introduction
Particle swarm optimization (PSO) is a metaheuristic algorithm based on social species behavior. PSO is a popular method that has been used successfully to solve a myriad of search and optimization problems [
1]. The PSO is inspired in the behavior of bird blocking or fish schooling [
2]. Each bird or fish is represented by a particle with two components, namely by its position and velocity. A set of particles forms the swarm that evolves during several iterations giving rise to a powerful optimization method.
The simplicity and success of the PSO led the algorithm to be employed in problems where more than one optimization criterion is considered. Many techniques, such as those inspired in genetic algorithms (GA) [
3,
4], have been developed to find a set of non-dominated solutions belonging to the Pareto optimal front. Since the multi-objective particle swarm optimization (MOPSO) proposal [
5], the algorithm has been used in a wide range of applications [
1,
6]. Moreover, a considerable number of variants of refined MOPSO were developed in order to improve the algorithm performance, e.g., [
7].
In single objective problem the performance of the algorithms can be easily evaluated by comparing the values obtained by each one. Moreover, when the performance over time is required the evolution of the best fitness value of the population is normally used. Advanced studies can be accomplished by means of the dynamic analysis [
8,
9] of the evolution. Many indexes were introduced to measure the performance of multi-objective algorithms according to the solution set produced by them [
10,
11,
12]. In those cases, when is difficult to identify the best algorithm, nonparametic statistical tests are crucial [
13,
14].
Shannon entropy has been applied in several fields, such as communications, economics, sociology, and biology among others, but in evolutionary computation it has not been fully explored. For an example of research work in this area we can refer to Galaviz-Casas [
15], which studies the entropy reduction during the GA selection at the chromosome level. Masisi
et al. [
16] used the (Renyi and Shannon) entropy to measure the structural diversity of classifiers based in neural networks. The measuring index is obtained by evaluating the parameter differences and the GA optimizes the accuracy of 21 classifiers ensemble. Myers and Hancock [
17] predict the behavior of GA formulating appropriate parameter values. They suggested the population Shannon entropy for run-time performance measurement, and applied the technique to labeling problems. Shannon entropy provides useful information about the algorithm state. The entropy is measured in the parameter space. It was shown that populations with entropy smaller than a given threshold become saturated and the population diversity disappears. Shapiro and Bennett [
18,
19] adopted the maximum entropy method to find out equations describing the GA dynamics. Kita
et al. [
20] proposed a multi-objective genetic algorithm (MOGA) based on a thermodynamical GA. They used entropy and temperature concepts in the selection operator.
Farhang-Mehr and Azarm [
21] formulated an entropy based MOGA inspired by the statistical theory of gases, which can be advantageous in improving the solution coverage and uniformity along the front. Indeed, in a enclosed environment, when an ideal gas undergoes an expansion, the molecules move randomly, archiving a homogeneous and uniform equilibrium stated with maximum entropy. This phenomenon occurs regardless of the geometry of the closed environment.
Qin
et al. [
22] presented an entropy based strategy for maintaining diversity. The method maintains the non-dominated number of solutions by deleting those with the worst distribution, one by one, using the entropy based strategy. Wang
et al. [
23] developed an entropy-based performance metric. They pointed out several advantages, namely that (i) the computational effort increases linearly with the solution number, (ii) the metric qualifies the combination of uniformity and coverage of Pareto set and (iii) it determines when the evolution has reached maturity.
LinLin and Yunfang [
24] proposed a diversity metric based on entropy to measure the performance of multi-objective problems. They not only show when the algorithm can be stopped, but also compare the performance of some multi-objective algorithms. The entropy is evaluated from the solution density of a grid space. These researchers compare a set of MOGA algorithms performance with different optimization functions.
In spite of having MOPSO used in a wide range of applications, there are a limited number of studies about its dynamics and how particles self-organize across the Pareto front. In this paper the dynamic and self-organization of particles along MOPSO algorithm iterations is analyzed. The study considers several optimization functions and different population sizes using the Shannon entropy for evaluating MOPSO performance.
Bearing these ideas in mind, the remaining of the paper is organized as follows.
Section 2 describes the MOPSO adopted in the experiments.
Section 3 presents several concepts related with entropy.
Section 4 addresses five functions that are used to study the dynamic evolution of MOPSO using entropy. Finally,
Section 5 outlines the main conclusions and discusses future work.
2. Multiobjective Particle Swarm Optimization
The PSO algorithm is based on a series of biological mechanisms, particularly in the social behavior of animal groups [
2]. PSO consists of particles movement guided by the most promising particle and the best location visited by each particle. The fact that particles work with stochastic operators and several potential solutions, provides PSO the ability to escape from local optima and to maintain a population with diversity. Moreover, the ability to work with a population of solutions, introduces a global horizon and a wider search variety, making possible a more comprehensive assessment of the search space in each iteration. These characteristics ensure a high ability to find the global optimum in problems that have multiple local optima.
Most real world applications have more than a single objective to be optimized, and therefore, several techniques were proposed to solve those problems. Due to these reasons, in the last years many of the approaches and principles that were explored in different types of evolutionary algorithms have been adapted to the MOPSO [
5].
Multi-objective optimization problem solving aims to find an acceptable set of solutions, in contrast with uni-objective problems where there is only one solution (except in cases where uni-objective functions have more than one global optimum). Solutions in multi-objective optimization problems intend to achieve a compromise between different criteria, enabling the existence of several optimal solutions. It is common to use the concept of dominance to compare the various solutions of the population. The final set of solutions may be represented graphically by one or more fronts.
Algorithm 1 illustrates a standard MOPSO algorithm. After the swarm initialization, several loops are performed in order to increase the quality of both the population and the archive. In iteration loop t, each particle in the population selects a particle guide from the archive . Based on the guide and personal best, each particle moves using simple PSO formulas. At the end of each loop (Line 12) the archive is updated by selecting the non-dominant solutions among the population, , and the archive . When the non-dominant solution number is greater than the size of the archive, the solutions with best diversity and extension are selected. The process comes to an end, usually after a certain number of iterations.
| Algorithm 1: The Structure of a standard MOPSO Algorithm |
- 1:
- 2:
Random initialization of - 3:
Evaluate - 4:
=Selection of non-dominated solutions - 5:
while the process do - 6:
for Each particle do - 7:
Select - 8:
Change position - 9:
Evaluate particle - 10:
Update p - 11:
end for - 12:
= Selection - 13:
- 14:
end while - 15:
Get results from A
|
3. Entropy
Many entropy interpretations have been suggested over the years. The best known are
disorder,
mixing,
chaos,
spreading,
freedom and
information [
25]. The first description of entropy was proposed by Boltzmann to describe systems that evolve from ordered to disordered states.
Spreading was used by Guggenheim to indicate the diffusion of a energy system from a smaller to a larger volume. Lewis stated that, in a spontaneous expansion gas in an isolated system,
information regarding particles locations decreases while, the missing information or,
uncertainty increases.
Shannon [
26] developed the information theory to quantify the information loss in the transmission of a given message. The study was carried out in a communication channel and Shannon focused in physical and statistical constraints that limit the message transmission. Moreover, the measure does not addresses, in this way, the meaning of the message. Shannon defined
H as a measure of information, choice and uncertainty:
The parameter
K is a positive constant, often set to value 1, and is used to express
H in an unit of measure. Equation (
1) considers a discrete random variable
characterized by the probability distribution
.
Shannon entropy can be easily extended to multivariate random variables. For two random variables
entropy is defined as:
4. Simulations Results
This section presents five functions to be optimized with 2 and 3 objectives, involving the use of entropy during the optimization process. The optimization functions
to
, defined by Equation (
3) to Equation (
6), are known as Z2, Z3, DTLZ4 and DTLZ2 [
27,
28], respectively, and
is known as UF8, from CEC 2009 special session competition [
29].
These functions are to be optimized using a MOPSO with a constant inertia coefficient and acceleration coefficients and . The experiments adopt iterations and the archive has a size of 50 particles. Furthermore, the number of particles is maintained constant during each experiment and its value is predefined at the begging of each execution.
To evaluate the Shannon entropy the objective space is divided into cells forming a grid. In the case of 2 objectives, the grid is divided into 1024 cells,
, where
is the number of cells in objective
i. On the other hand, when 3 objectives are considered the grid is divided in 1000 cells, so that
. The size in each dimension is divided according to the maximum and minimum values obtained during the experiments. Therefore, the size
of dimension
i is given by:
The Shannon entropy is evaluated by means of the expressions:
where
is the number of solutions in the range of cell with indexes
.
The dynamical analysis considers only the elements of the archive and, therefore, the Shannon entropy is evaluated using that set of particles.
4.1. Results of Optimization
The first optimization function to be considered is
, with 2 objectives, represented in Equation (
3). For measuring the entropy, Equation (
9) is adopted (
i.e.,
). The results depicted in
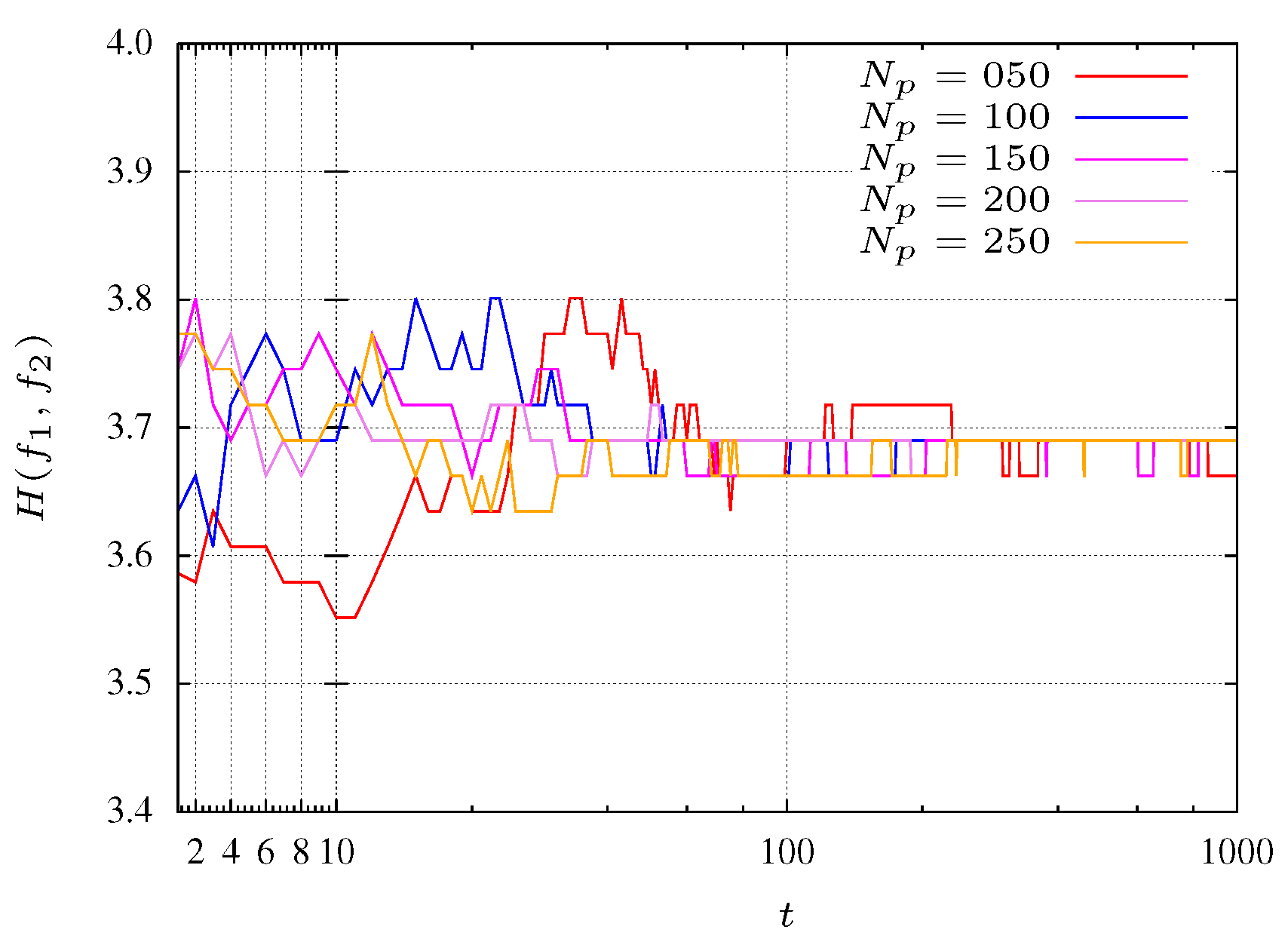
Figure 1 illustrate several experiments with different population sizes
. The number of parameters is maintained constant, namely with value
.
Figure 1.
Entropy during the MPSO evolution for function.
Figure 1.
Entropy during the MPSO evolution for function.
In
Figure 1 it is verified that, in general, entropy has a value that hardly varies over the MOPSO execution. At the beginning, outside the transient, the entropy measure is
. This transient tends to dissipate as the PSO converges and the particles became organized. Additionally, from
Figure 1 it can be seen that the archive size does not influence the PSO convergence rate. Indeed, MOPSO is an algorithm very popular to find optimal Pareto fronts in multi-objective problems, particularly with two objectives.
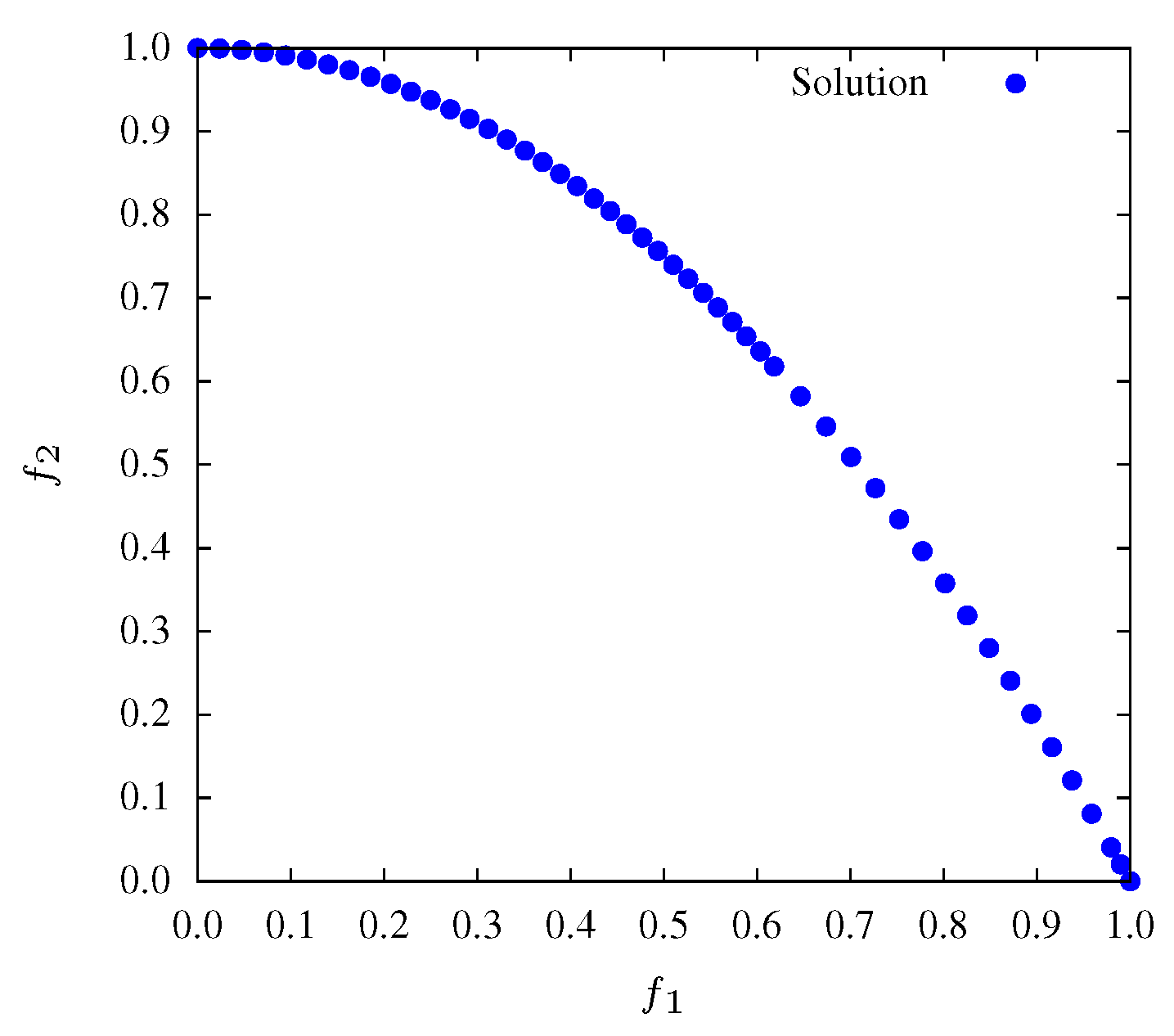
Figure 2,
Figure 3 and
Figure 4 show that during all the evolution process the MOPSO presents a good diversity. Therefore, is expected that entropy has a small variation throughout iterations. Moreover, after generation 90, entropy presents minor variations revealing the convergence of the algorithm.
Figure 2.
Non-dominated solutions at iteration for function and .
Figure 2.
Non-dominated solutions at iteration for function and .
Figure 3.
Non-dominated solutions at iteration for function and .
Figure 3.
Non-dominated solutions at iteration for function and .
Figure 4.
Non-dominated solutions at iteration for function and .
Figure 4.
Non-dominated solutions at iteration for function and .
4.2. Results of Optimization
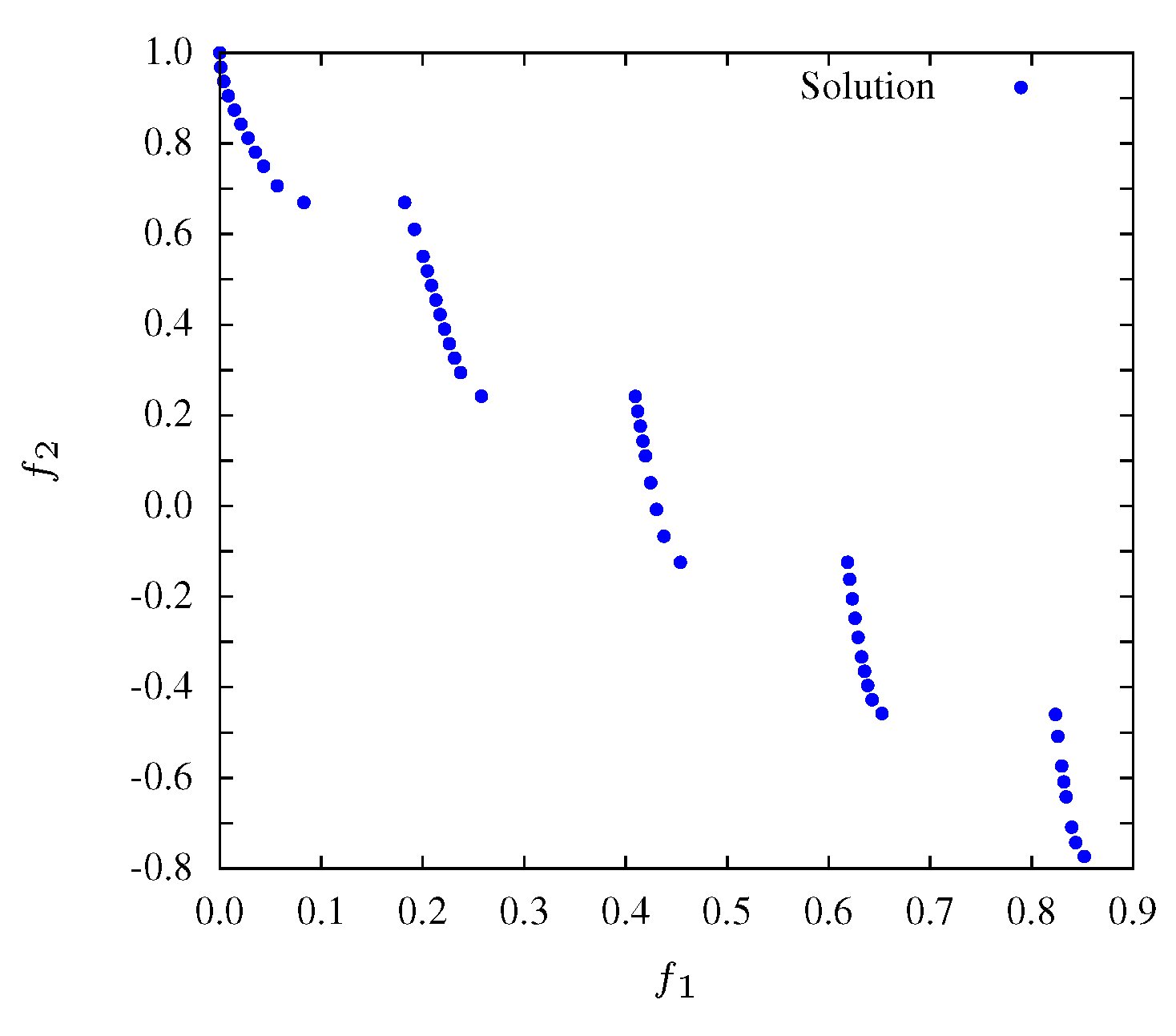
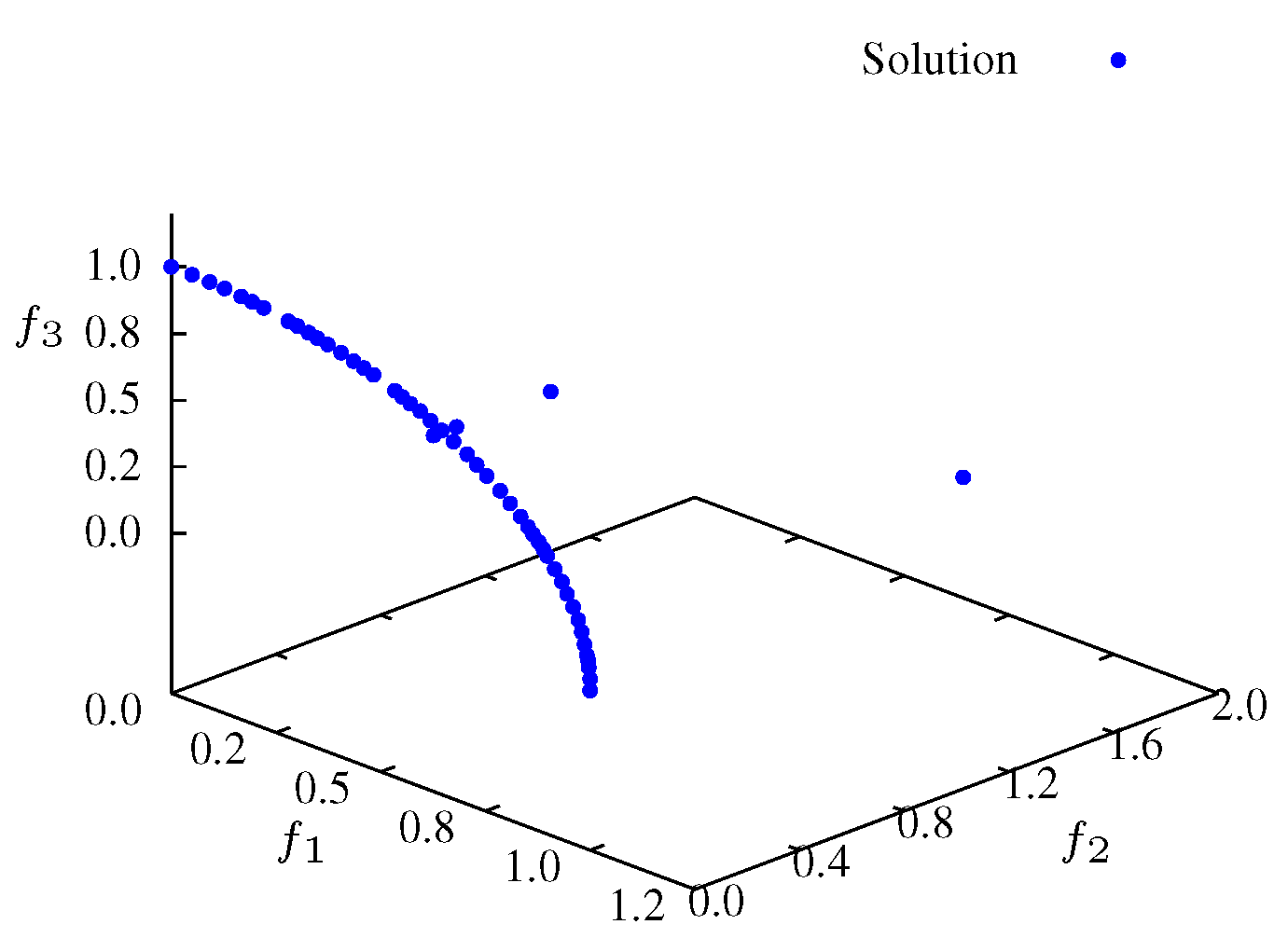
Figure 5 illustrates the entropy evolution during the optimization of
. This function includes 2 objectives and leads to a discontinuous Pareto front represented in
Figure 6. The experiments were executed with the same population sizes as for
. It was verified that experiments with a low number of population solutions have a poor (low) initial entropy, revealing a nonuniform front solution at early iterations.
Figure 5.
Entropy during the MPSO evolution for function.
Figure 5.
Entropy during the MPSO evolution for function.
Figure 6.
Non-dominated solutions at iteration for .
Figure 6.
Non-dominated solutions at iteration for .
4.3. Results of Optimization
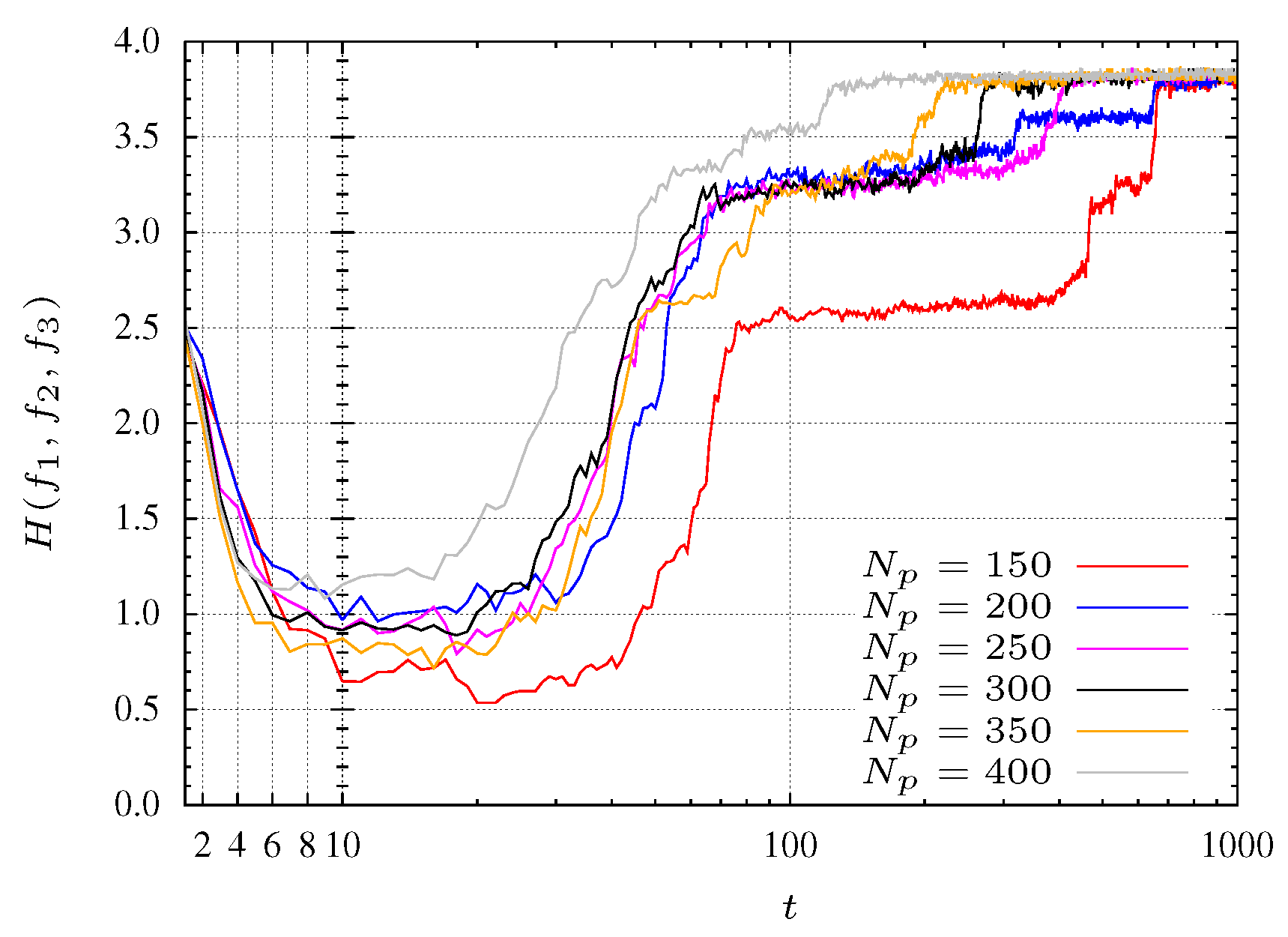
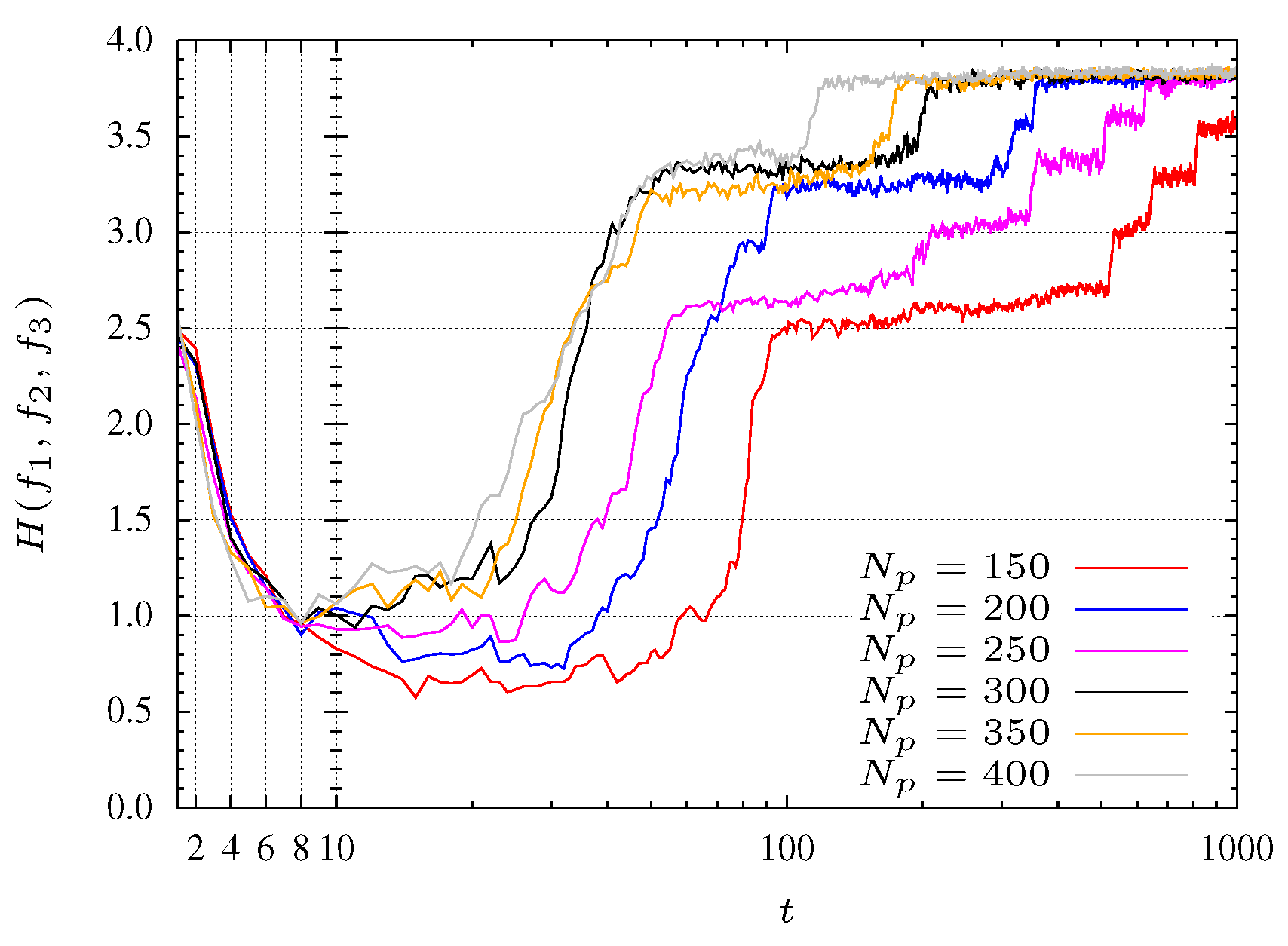
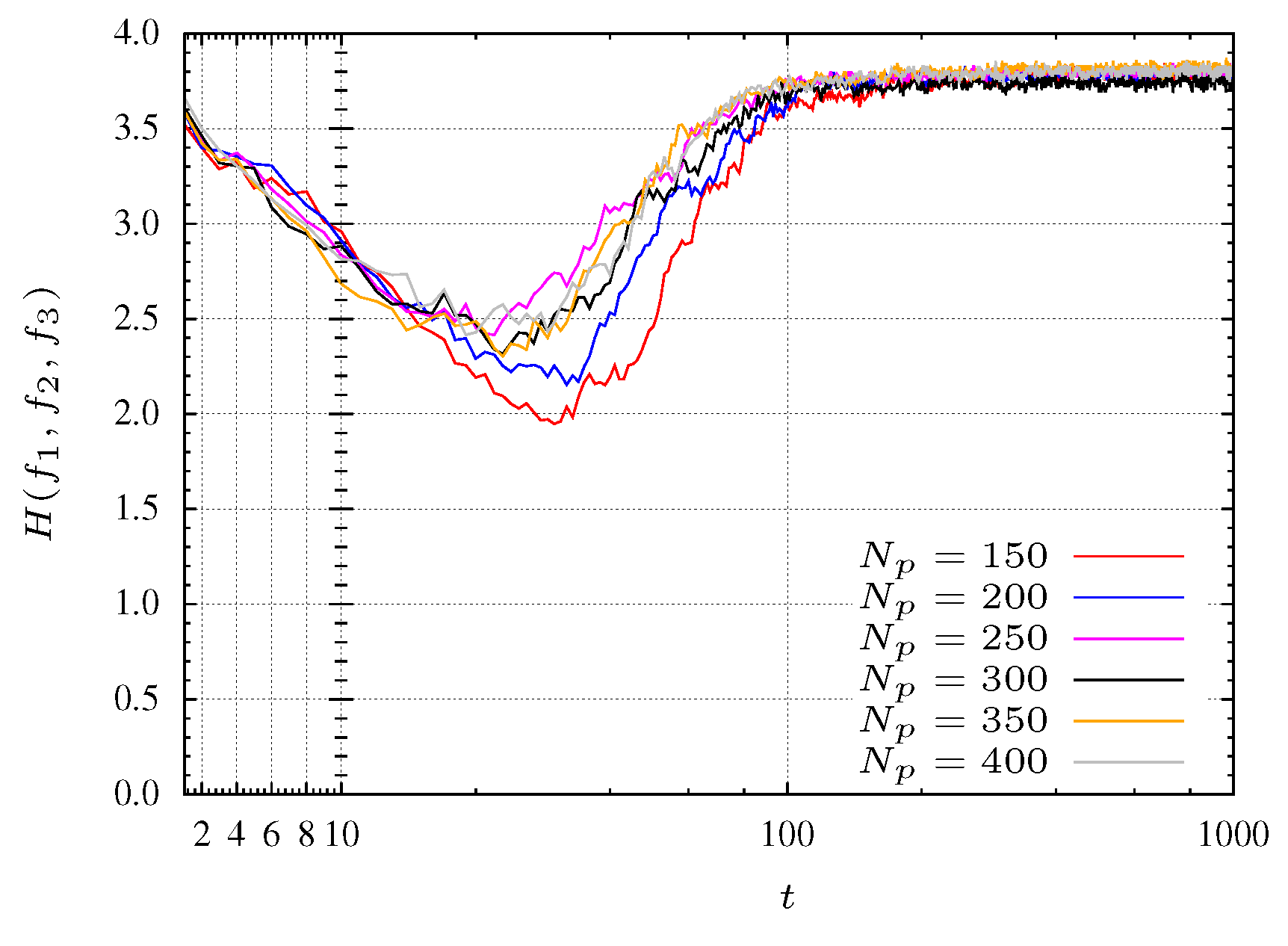
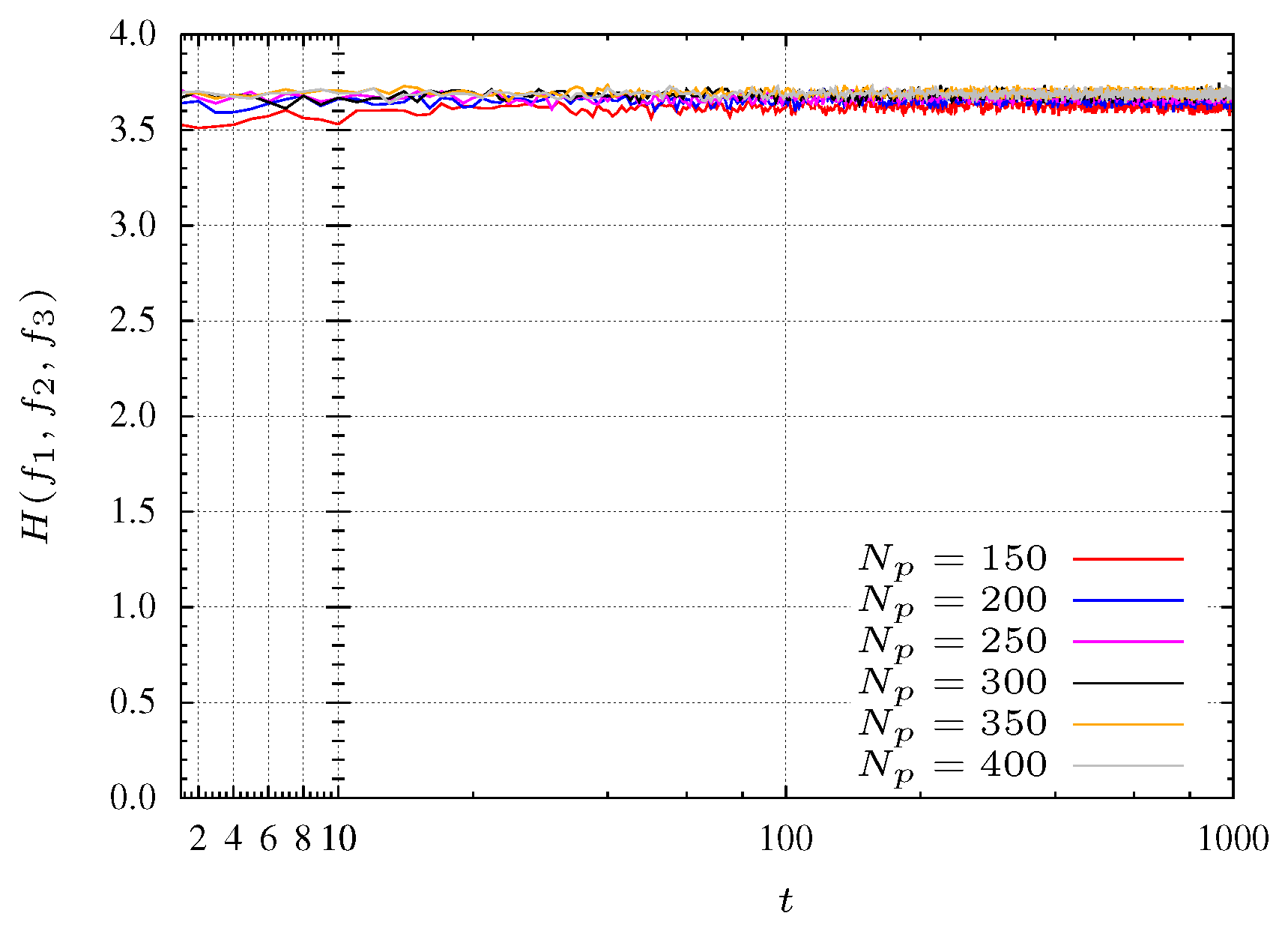
In the case of the optimization of function
in Equation (
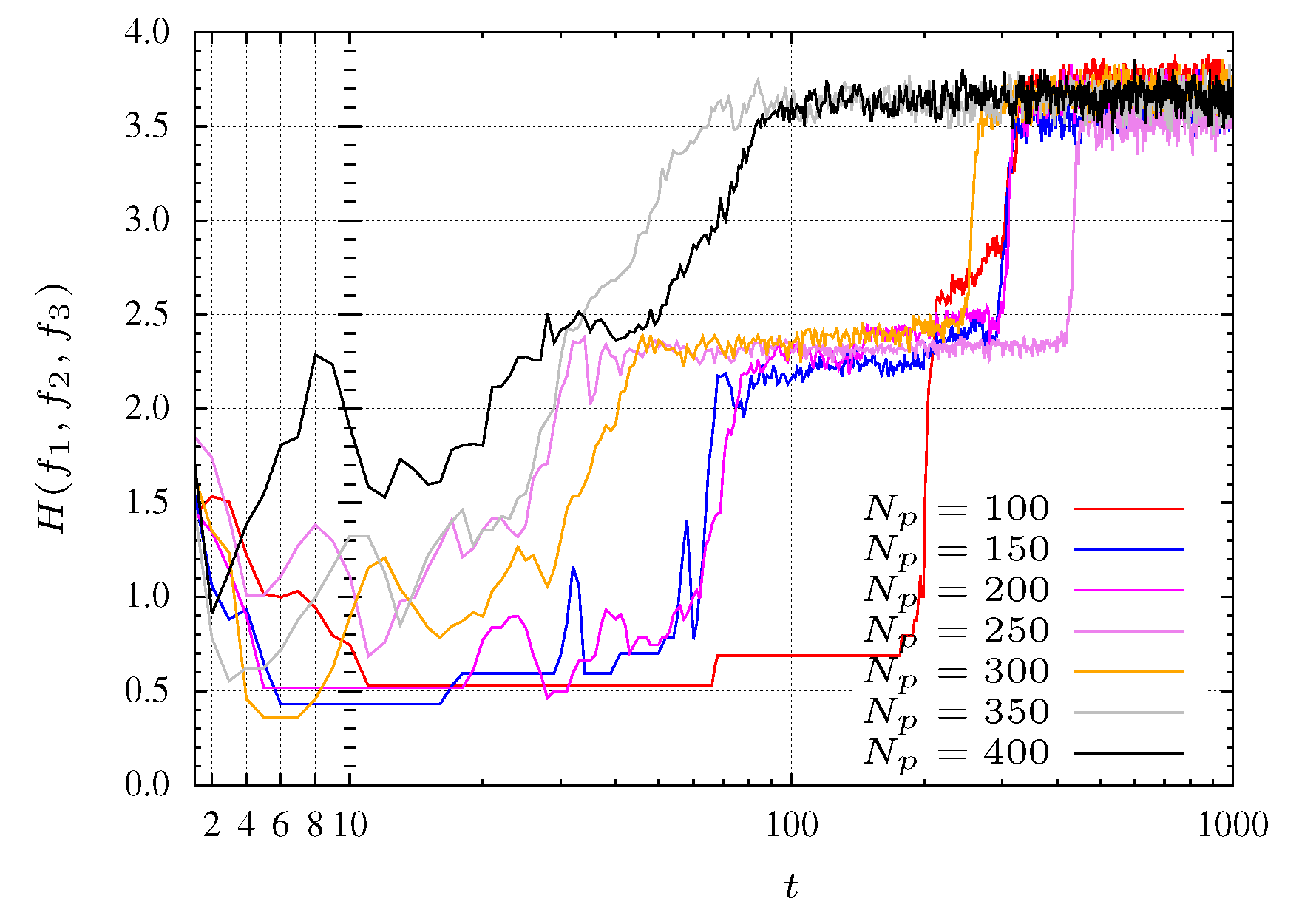
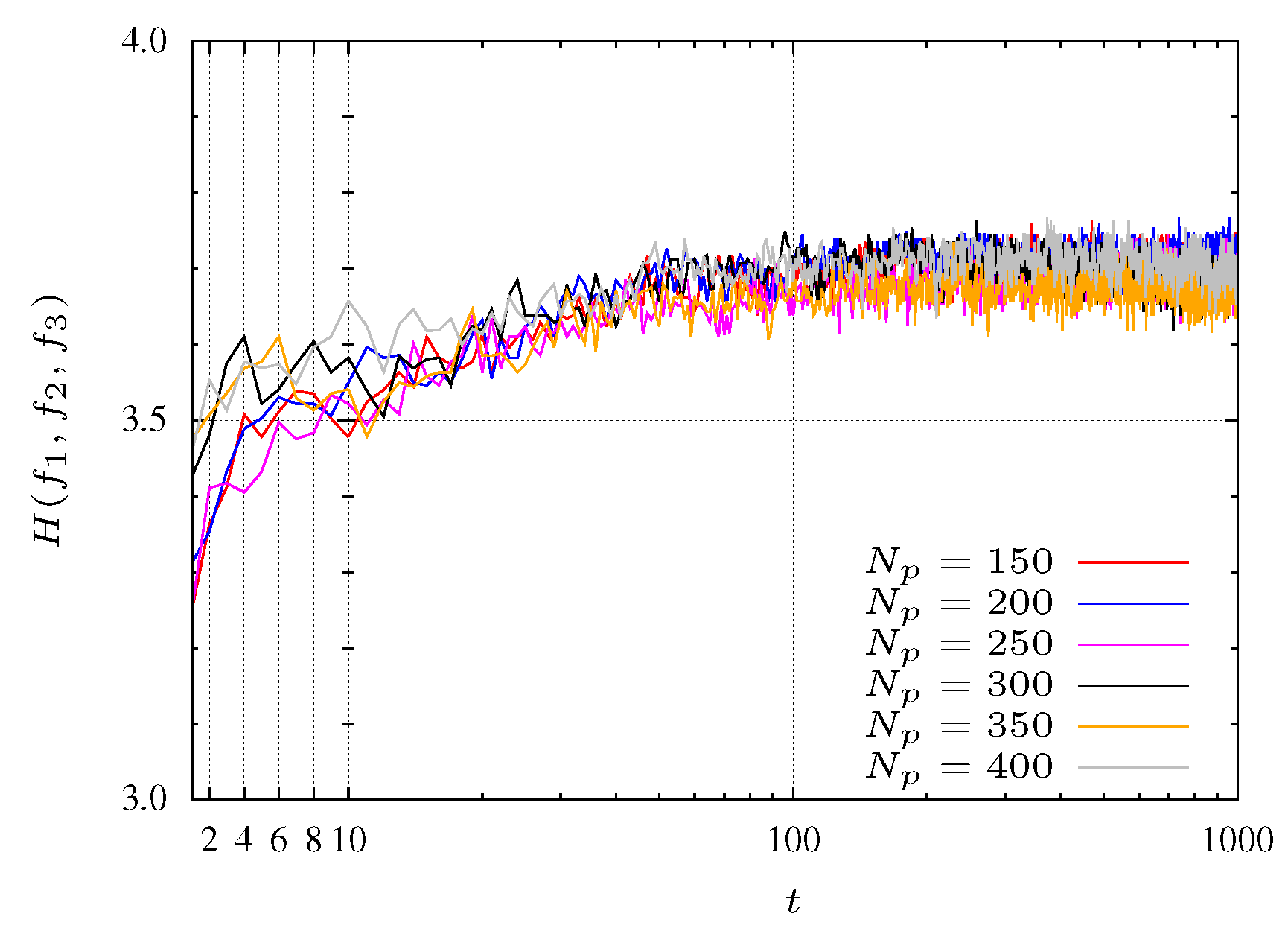
5), three objectives are considered. The entropy evolution is plotted in
Figure 7 for
. Moreover, is considered
and
.
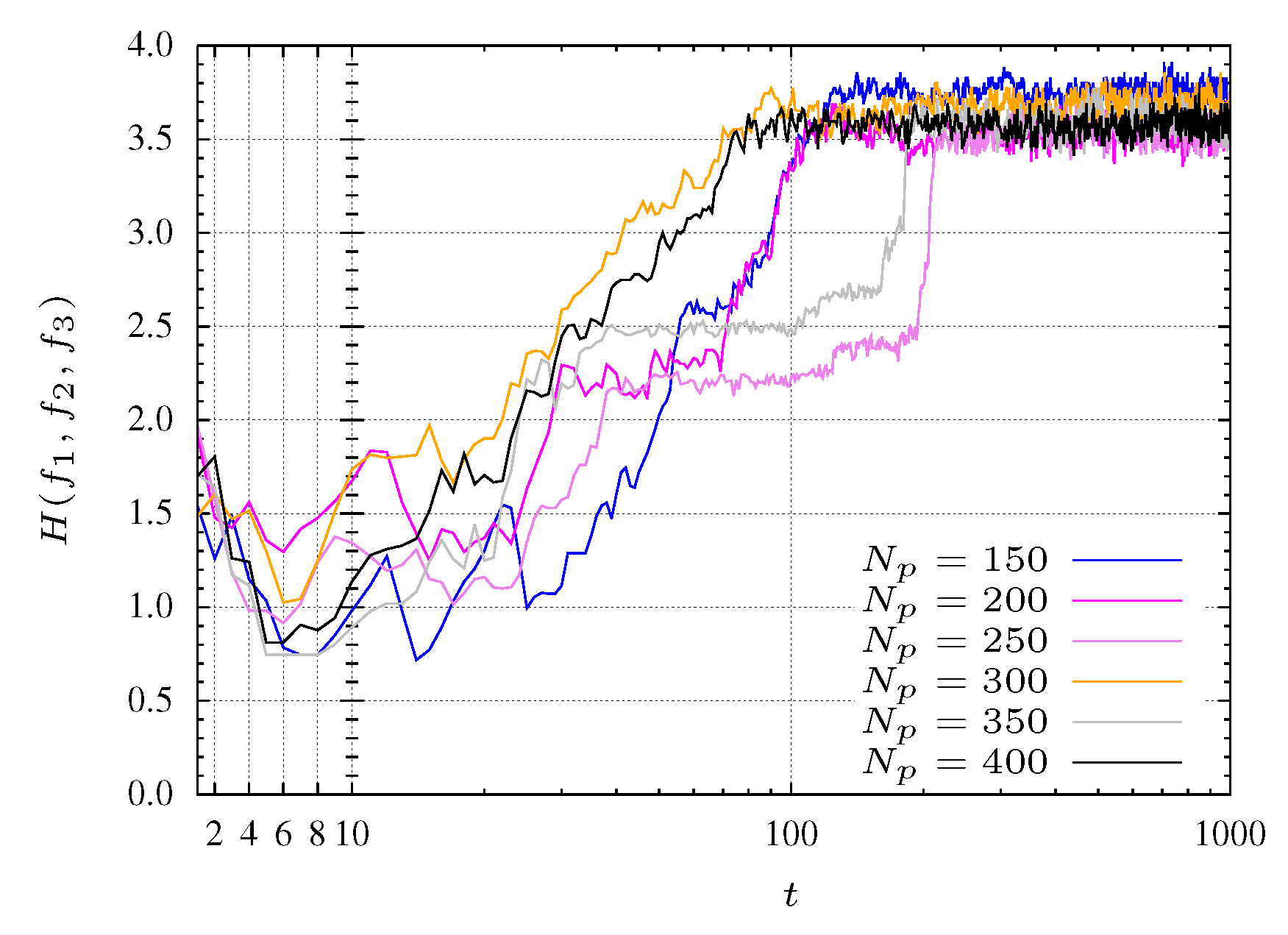
For experiments with a small population size, the convergence of the algorithm reveals some problems. Indeed, for populations with
particles the algorithm does not converge to the Pareto optimal front. With
particles the algorithm takes some time to start converging. This behavior is shown in
Figure 7 where pools with many particles (
i.e., 350 and 400 particles) reach faster the maximum entropy. In other words, a maximum entropy corresponds to a maximum diversity.
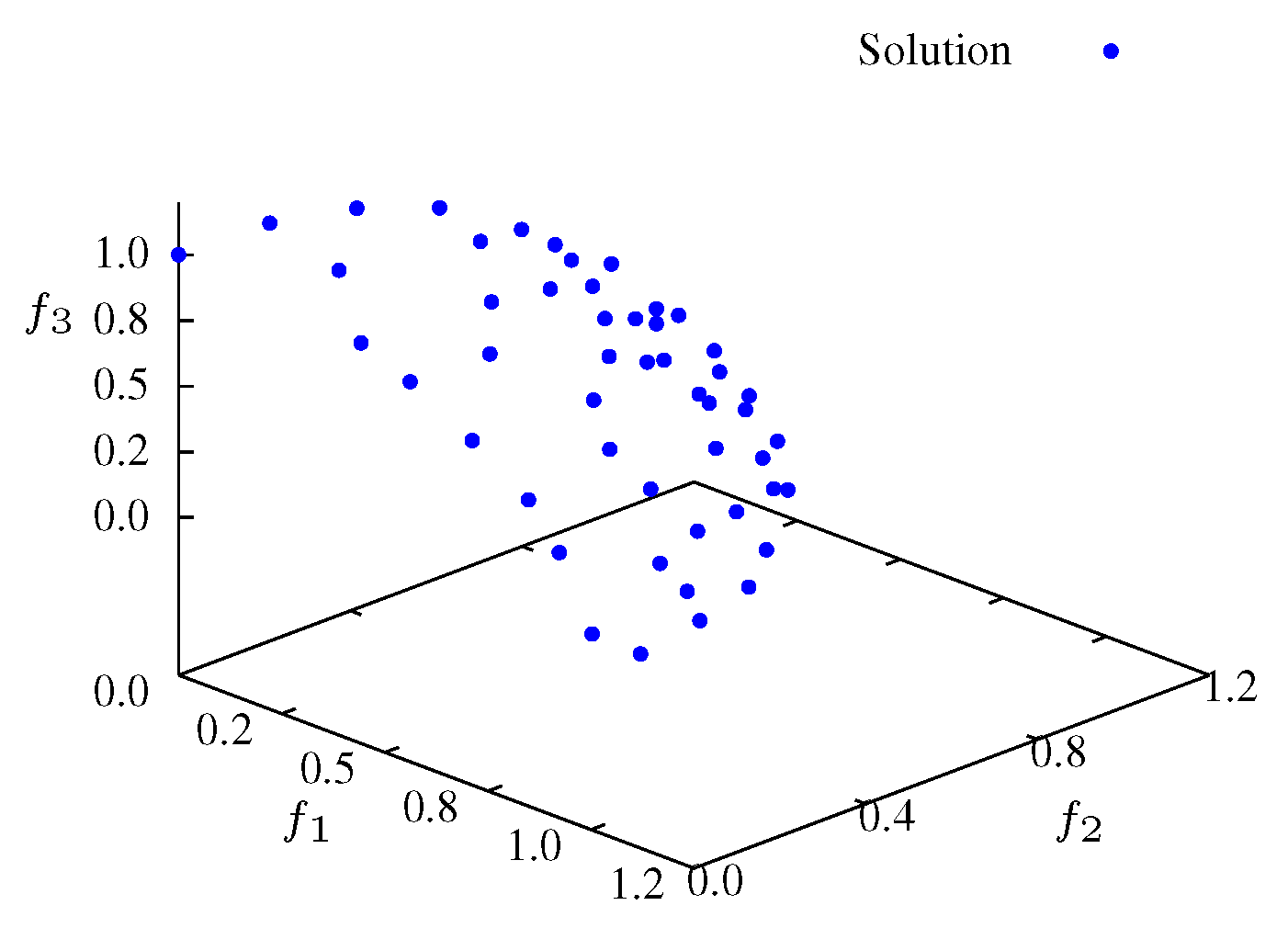
In
Figure 7 three search phases are denoted by SP1, SP2 and SP3. The SP1 phase corresponds to a initial transient where the particles are spread for all over the search space with a low entropy. For the experiment with
, phase SP1 corresponds to the first 30 iterations (see
Figure 8 and
Figure 9). The second phase, SP2, occurs between iterations 40 and 200, where the particles search the
plane, finding mainly a 2-dimensional front (
Figure 10 and
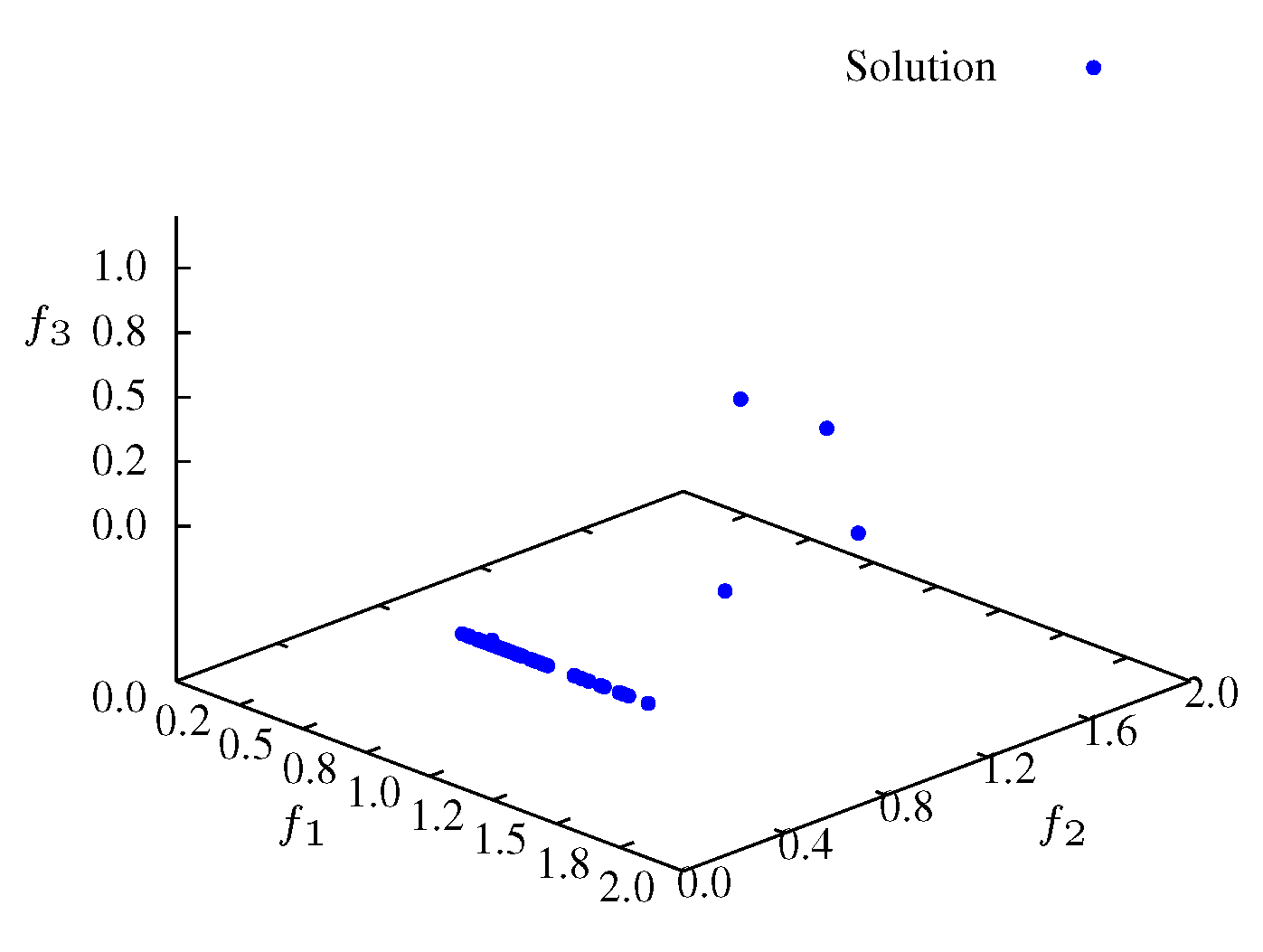
Figure 11). Finally, in the SP3 phase (e.g., steady state) the algorithm approaches the maximum entropy. In this phase, particles move in the entire front and are organized in order to give a representative front with good diversity (see
Figure 12 and
Figure 13).
Figure 7.
Entropy during the MPSO evolution for function.
Figure 7.
Entropy during the MPSO evolution for function.
For experiments considering populations with more particles, these phases are not so clearly defined. This effect is due to the large number of particles that allows the algorithm to perform a more comprehensive search. In other words, the MOPSO stores more representative space points helping, in this way, the searching procedure.
Figure 8.
Non-dominated solutions at iteration for .
Figure 8.
Non-dominated solutions at iteration for .
Figure 9.
Non-dominated solutions at iteration for .
Figure 9.
Non-dominated solutions at iteration for .
Figure 10.
Non-dominated solutions at iteration for .
Figure 10.
Non-dominated solutions at iteration for .
Figure 11.
Non-dominated solutions at iteration for .
Figure 11.
Non-dominated solutions at iteration for .
Figure 12.
Non-dominated solutions at iteration for .
Figure 12.
Non-dominated solutions at iteration for .
Figure 13.
Non-dominated solutions at iteration for .
Figure 13.
Non-dominated solutions at iteration for .
4.4. Results of Optimization
The results for the optimization function
are depicted in
Figure 14. The function has 3 objectives and the Pareto front is similar to the one for function
. It can be observed that optimization with a larger number of solutions presents a regular convergence, as was verified for
.
Figure 14.
Entropy during the MPSO evolution for function.
Figure 14.
Entropy during the MPSO evolution for function.
4.5. Results of the , and Medians
MOPSO is a stochastic algorithm and each time it is executed is obtained a different convergence path for the best particle. In this line of thought, for each test group, 22 distinct simulations were performed and the median taken as representing the entropy evolution. This section presents the entropy evolution for 12 cases test set, 6 for and 6 for , with population sizes of particles.
Figure 15 and
Figure 16 show evolution of the median of the 6 cases test sets for
and
, respectively. It can be seen that the larger the population size, the faster the convergence of the algorithm in finding an uniform spreading covering the Pareto front. The only exception is the case of
particles and
function, that leads to a faster convergence than the case with
particles.
Figure 15.
Median entropy during the MPSO evolution for function.
Figure 15.
Median entropy during the MPSO evolution for function.
Figure 16.
Median entropy during the MPSO evolution for function.
Figure 16.
Median entropy during the MPSO evolution for function.
Figure 17 presents the evolution of the median of 6 cases test sets for
. It can also be observed that population size affects the diversity, and consequently the space exploration, of the algorithm at early iterations.
Figure 17.
Median entropy during the MPSO evolution for function.
Figure 17.
Median entropy during the MPSO evolution for function.
At initial iterations, it is natural to observe a entropy peak because the particles are scattered throughout the objective space, and it is difficult to find near particles among the others. In these stages spread was not maximum (entropy) because the distribution is not uniform.
4.6. Results of the , and Medians for MSPSO Algorithm
In this section, the functions
,
and
are optimized using the Spreed-constrained Multi-Objective PSO (SMPSO) [
30]. The algorithm was downloaded from jMetal website [
31]. The algorithm was slightly modified in order to save the archive solutions during the algorithm evolution. This SMPSO has the particularity of producing new effective particles positions in cases where the velocity becomes too high and uses a polynomial mutation as a turbulence factor.
Figure 18 and
Figure 19 present the evolution of the median of the 12 cases test sets, 6 for
and 6 for
, with population sizes of
particles. From these functions it can be seen that the algorithm maintains a good spreed during its entire evolution, even in initial iterations. This is due to the polynomial mutation and velocity effect.
Figure 18.
Median entropy during the MSPSO evolution for function.
Figure 18.
Median entropy during the MSPSO evolution for function.
Figure 19.
Median entropy during the MSPSO evolution for function.
Figure 19.
Median entropy during the MSPSO evolution for function.
When optimizing
(
Figure 20) it can be observed a low entropy at early iterations that increases over the iterations, meaning that the spread also improves throughout the execution of the algorithm.
Figure 20.
Median entropy during the MSPSO evolution for function.
Figure 20.
Median entropy during the MSPSO evolution for function.
The MSPSO maintains a good diversity during the search process. This phenomena, does not occur in the standard MOPSO used previously, where diversity decreases in initial stages of the algorithm.
5. Conclusions and Future Work
This paper addressed the application of the entropy concept for representing the evolution behavior of a MOPSO. One interpretation of entropy is to express the spreading of a system energy from a small to a large state. This work adopted this idea and transposed it to measure the diversity during the evolution of a multi-objective problem. Moreover, this measure is able to capture the convergence rate of the algorithm. The optimization of four functions was carried-out. According to the entropy index, the and functions, with two objectives, are easily and early reached, independently of the number of population particles. When three objectives are considered, for functions , and , the number of population particles has an important role during the algorithm search. It was verified that entropy can be used to measure the convergence and the MOPSO diversity during the algorithm evolution. On the other hand, when using the MSPSO algorithm an high entropy / diversity was observed during the entire evolution. Therefore, the deployed entropy based index can be used to compare the solution diversity during evolution among different algorithms.
In conclusion, the entropy diversity can be used as a evolution index for multi-objective algorithms in the same way the best swarm element is used in single objective optimization problems.
Future work will be devoted to incorporating entropy based indexes to evaluate the swarm diversity in the algorithm run time. Indeed, as the analysis results presented in this paper confirm, swarm diversity can be evaluated along evolution time, and if the entropy index is lower than a problem function specific threshold, then measures can be adopted to reverse the diversity population decrease. The use of online entropy based indexes can also be applied to the swarm population as well as to the non-dominated archive. This will allow evaluate both populations diversity in order to prevent the MOPSO premature convergence. The former research lines are currently under research and their results will be submitted for another publication soon.