Core-Based Dynamic Community Detection in Mobile Social Networks
Abstract
:1. Introduction
2. Preliminary
3. Cumulative Stable Link
3.1. Dataset
3.2. Stable Link Extraction
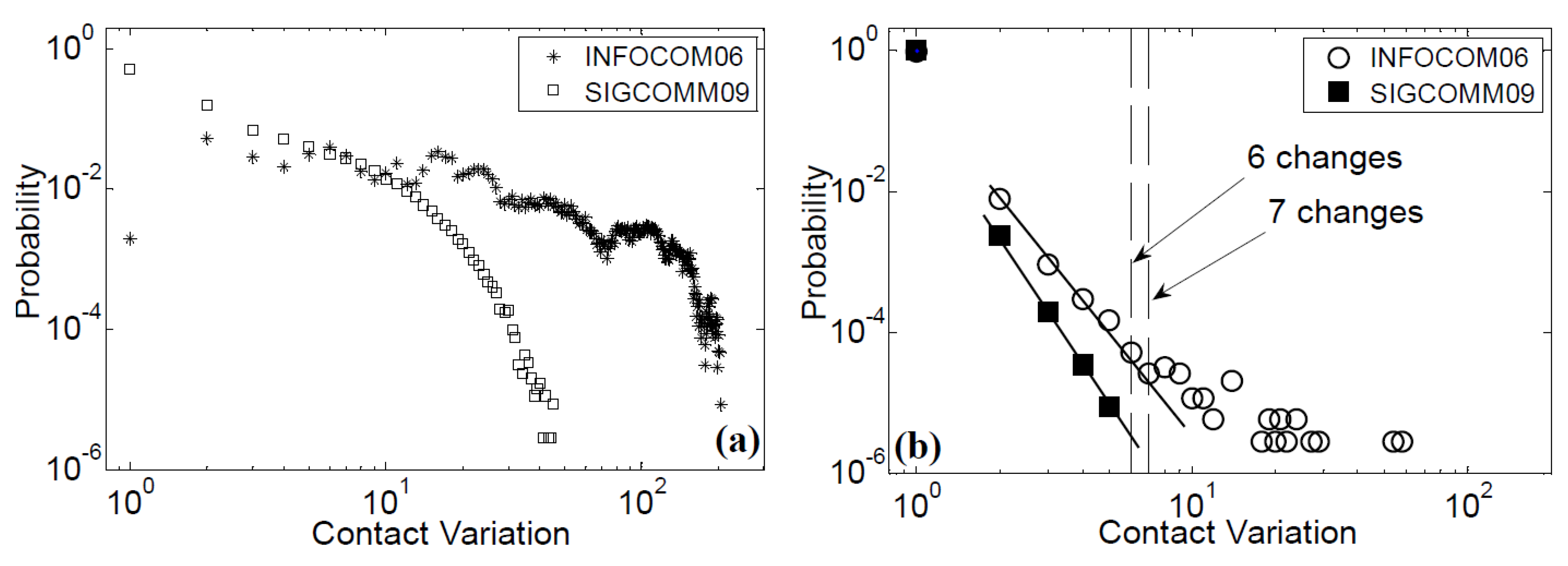
3.3. Distribution of CCSC
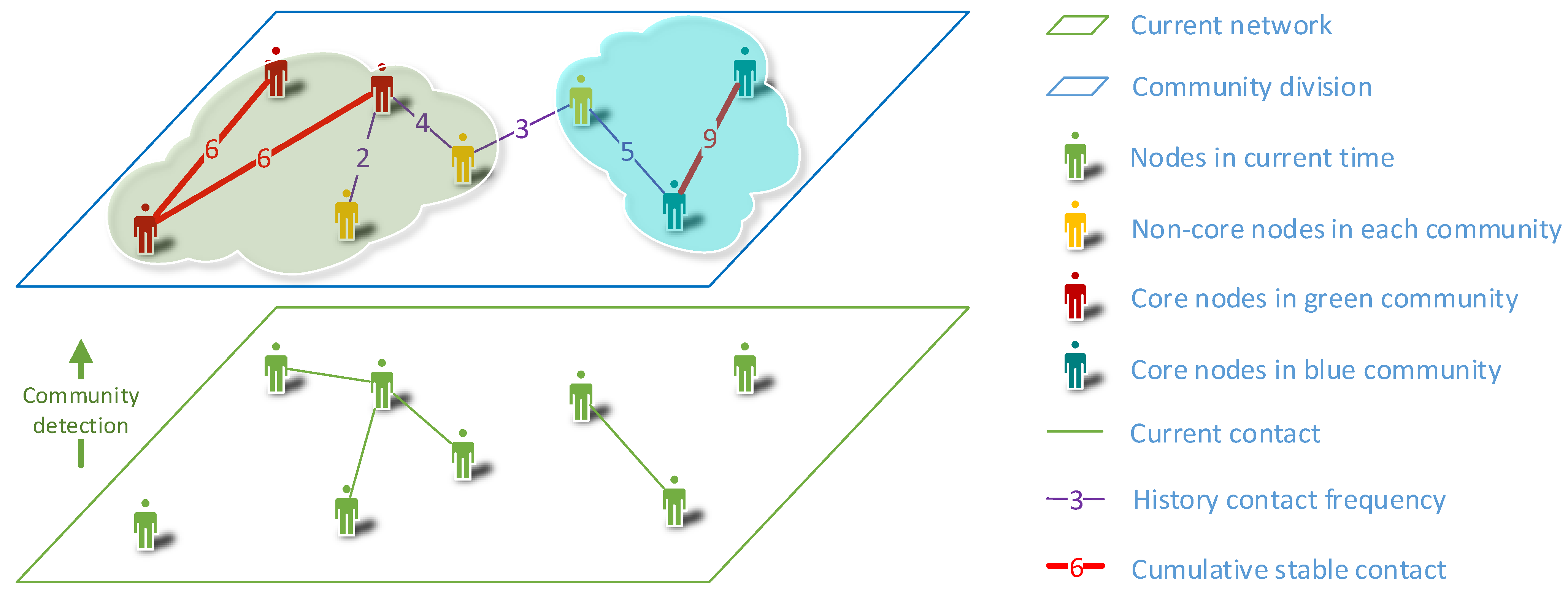
4. Core-based Community Evolution
4.1. Core based Community Detection
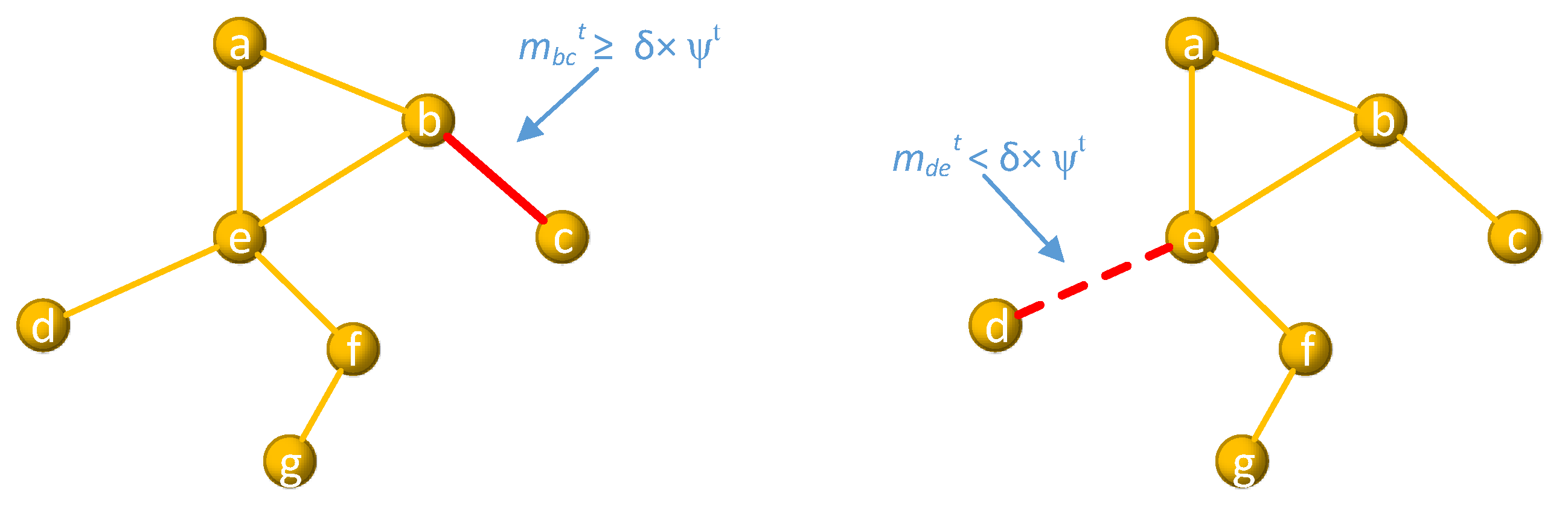
| Algorithm 1: Link Removal |
| While link removal set ≠ Ø |
| Extract linkij from link removal set. |
| If vi and vj in the same core Then |
| If vi and vj have a stable cumulative contact Then |
| Remove linkij from existing community cores. |
| If vi and vj connect with any other nodes Then |
| If there is a path connects vi and vj Then |
| Split the core into two parts, including vi and vj separately. (Splitting) |
| Else If vi and vj don’t connect with any other nodes Then |
| Remove vi and vj from cores. (Contraction or Death) |
| Else If vi or vj doesn’t connect with any nodes Then |
| Remove vi or vj which doesn’t connect with any nodes. (Contraction) |
| Algorithm 2: Link Addition |
| While link addition set ≠ Ø |
| Extract linkij from link addition set. |
| If vi and vj have a stable cumulative contact Then |
| If vi and vj not in the same core Then |
| If vi and vj have only one neighbor Then |
| Create a new community core. (Birth) |
| Else If vi or vj have one neighbor Then |
| Merge the two cores. (Merging) |
| Else |
| Add linkij from existing community cores. (Growth) |
| Algorithm 3: Remaining Node Addition |
| While remaining node set ≠ Ø |
| Extract vi from remaining node set. |
| If there is only one path from vi to any cores Then |
| vi join into the connected core. |
| Else If there are multiple paths from vi to any cores Then |
| vi join into the core which has the shortest distance to it. |
| Else |
| A community is created including vi and nodes connected with vi. |
4.2. Community Evolution
4.2.1. Model
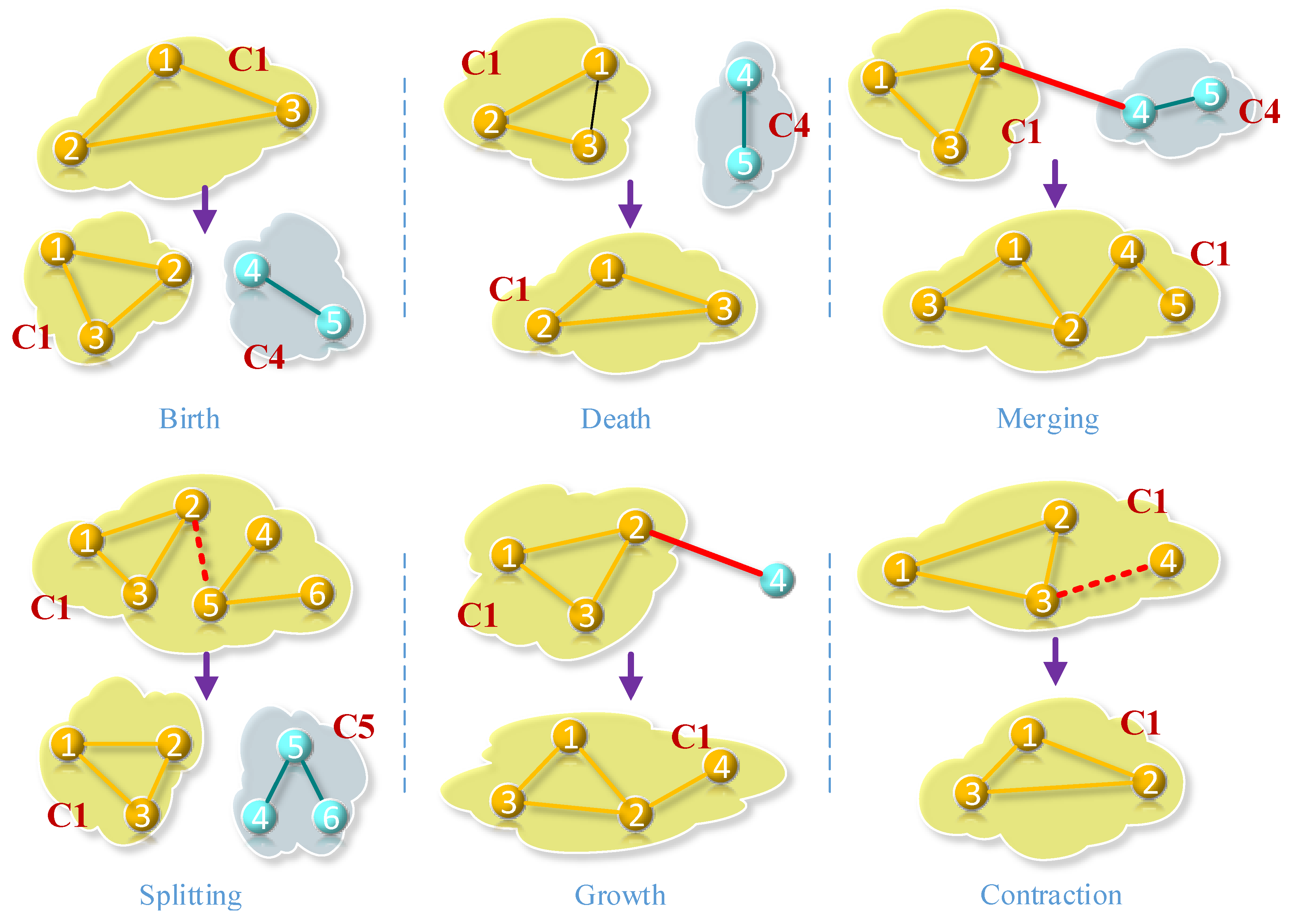
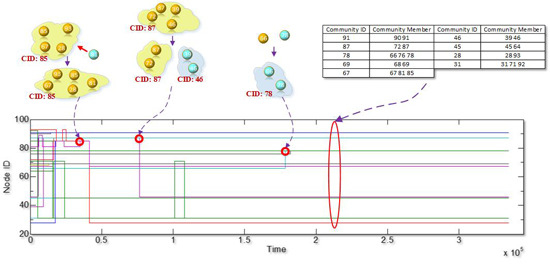
4.2.2. Tracking Communities
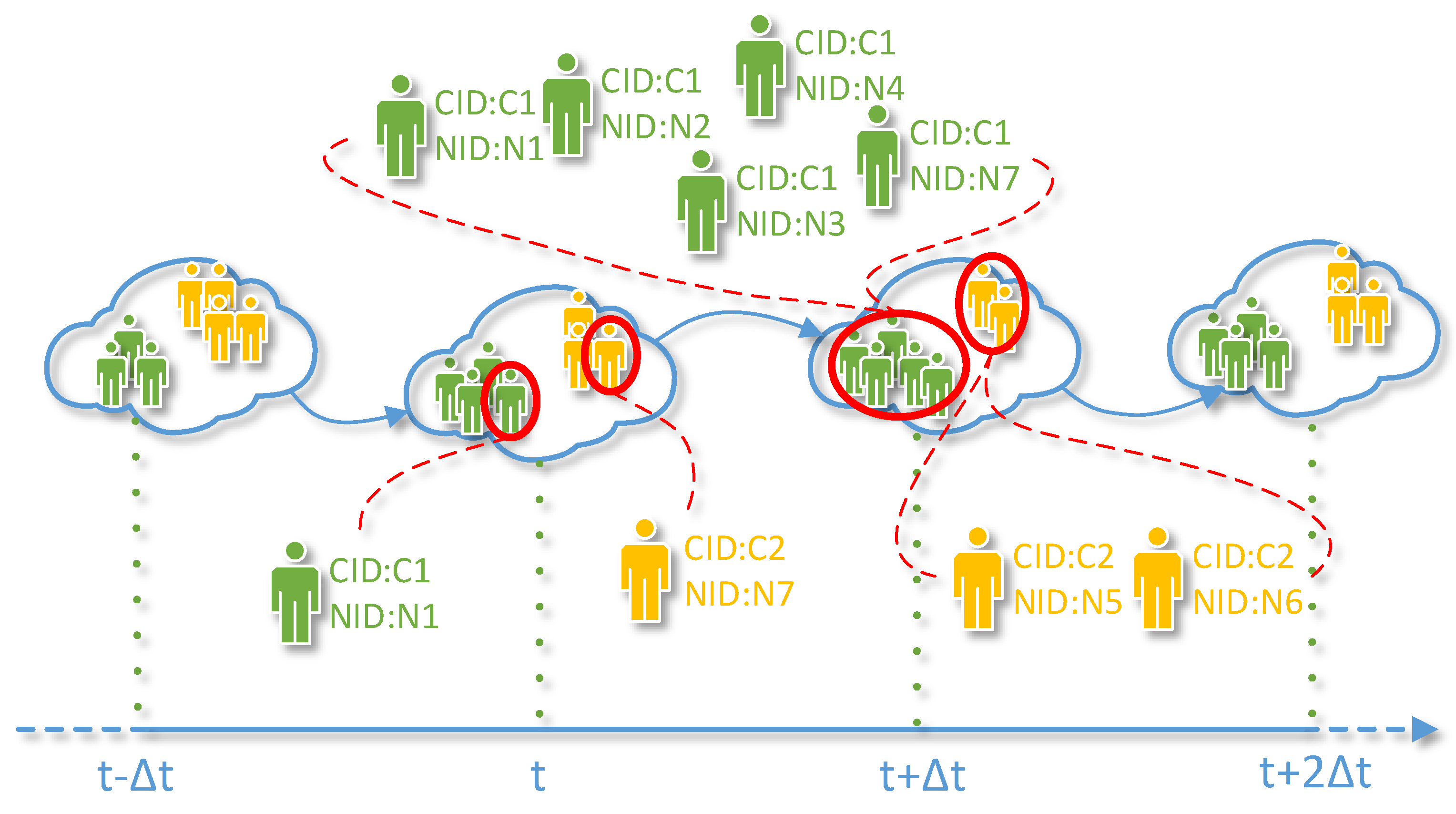
- Any nodes’ community ID at any timestamps can be retrieved.
- Members in any communities at any timestamps can be obtained.
5. Evaluation
5.1. Contact Variation
5.2. Change of 0–1 Contact Matrix
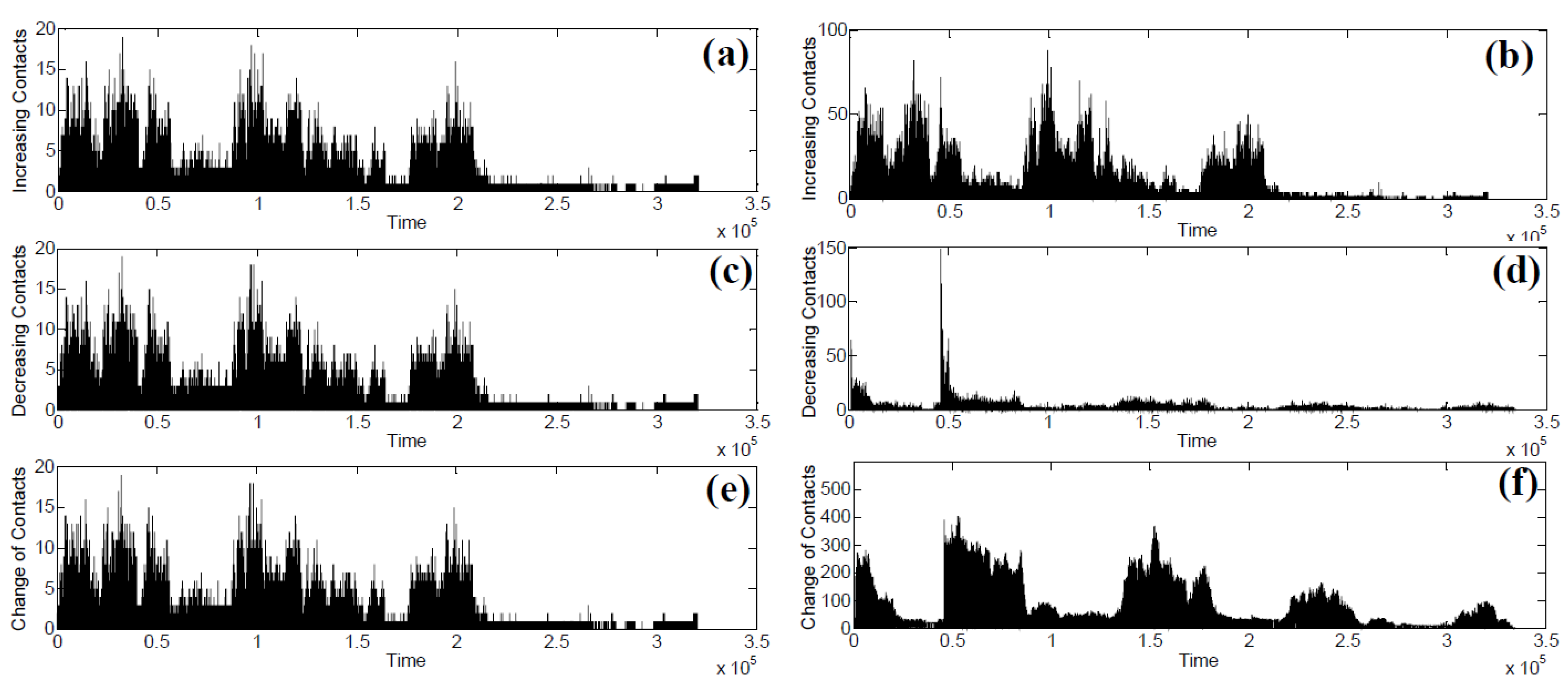

5.3. Selected Node Count

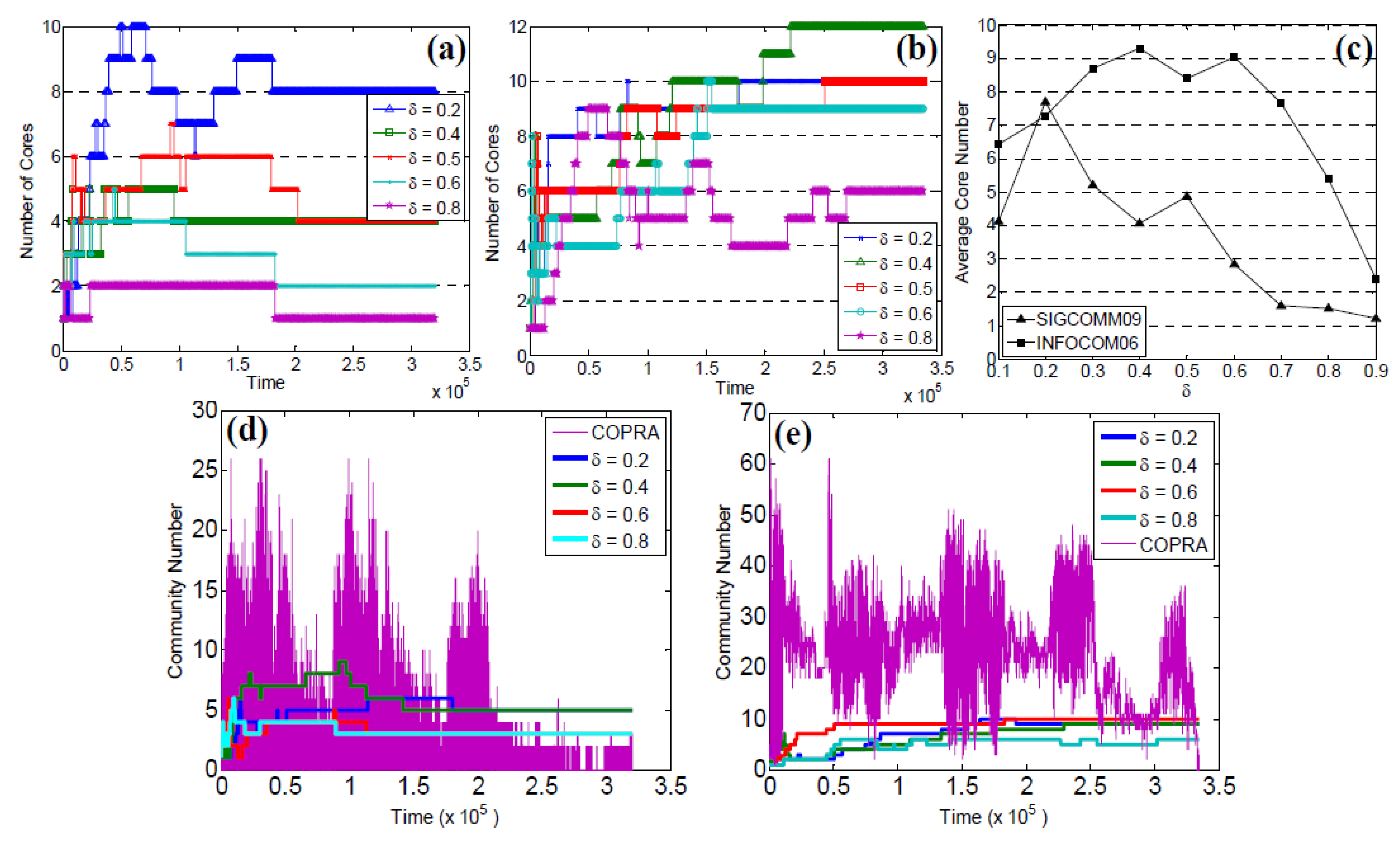
5.4. Community Core Tracking
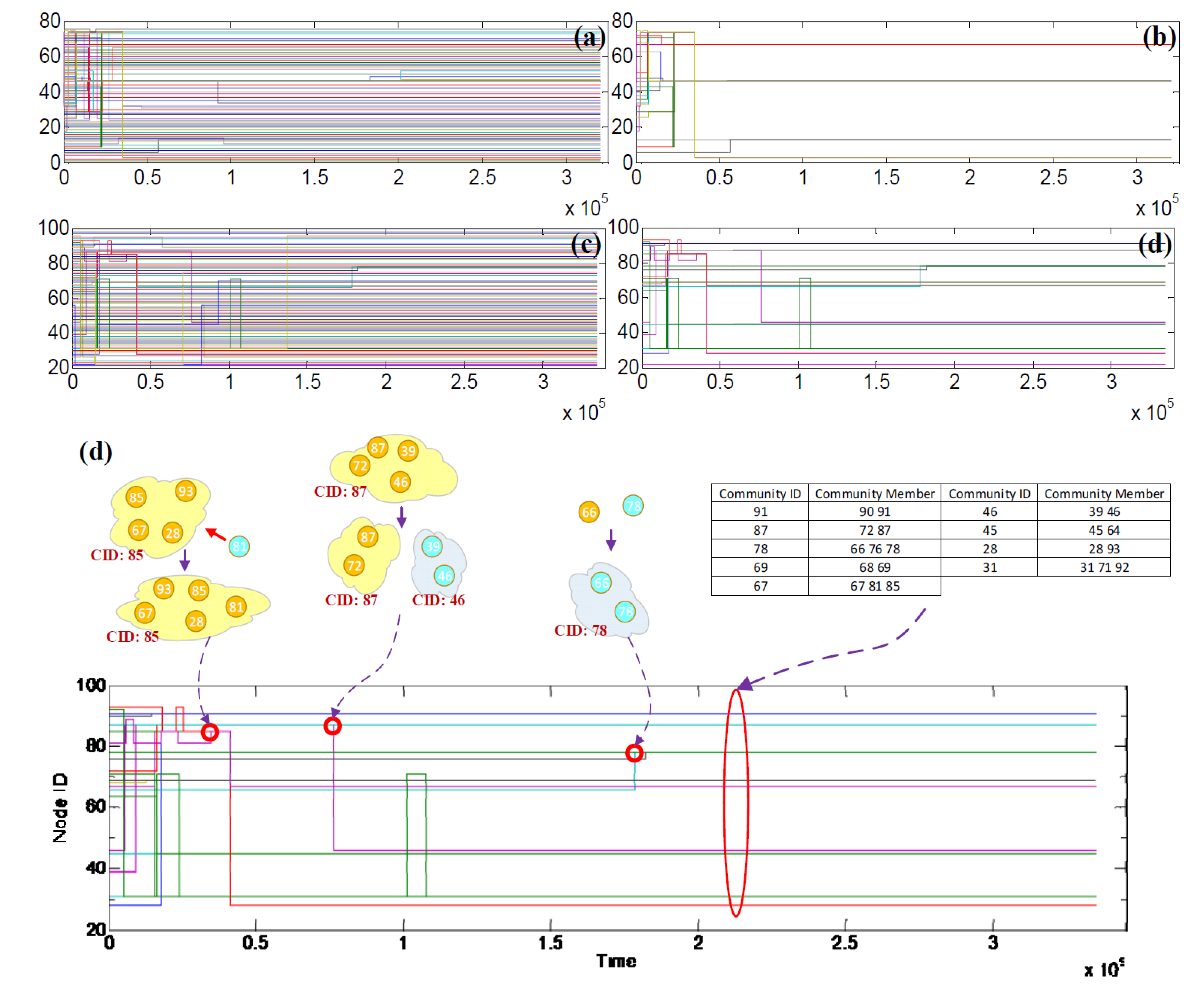
5.5. Number of Communities
5.6. Normalized Mutual Information

5.7. Scalability


6. Conclusions
Conflict of Interest
Acknowledgments
References
- Zhang, Y.; Yeung, D-.Y. Overlapping Community Detection via Bounded Nonnegative Matrix Tri-factorization. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 606–614.
- Lin, W.; Kong, X.; Yu, P.S.; Wu, Q.; Jia, Y.; Li, C. Community Detection in Incomplete Information Networks. In Proceedings of International Conference on World Wide Web (WWW), Lyon, France, 16–20 April 2012; pp. 341–350.
- Bródka, P.; Saganowski, S.; Kazienko, P. Group Evolution Discovery in Social Networks. In Proceedings of the International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Kaohsiung, Taiwan, 25–27 July 2011; pp. 247–253.
- Cazabet, R.; Amblard, F.; Hanachi, C. Detection of Overlapping Communities in Dynamical Social Networks. In Proceedings of IEEE International Conference on Social Computing (SocialCom), Minneapolis, MN, USA, 20–22 August 2010; pp. 309–314.
- Seifi, M.; Guillaume, J.-L. Community Cores in Evolving Networks. In Proceedings of International Conference companion on World Wide Web (MSND), Lyon, France, 16–20 April 2012.
- Hui, P.; Crowcroft, J.; Diot, C.; Gass, R.; Scott, J. Impact of human mobility on opportunistic forwarding algorithms. IEEE Trans. Mobile Comput. 2007, 6, 606–620. [Google Scholar]
- Nguyen, N.P.; Dinh, T.N.; Xuan, Y.; Thai, M.T. Adaptive Algorithms for Detecting Community Structure in Dynamic Social Networks. In Proceedings of the IEEE Conference on Computer Communications (INFOCOM), Shanghai, China, 10–15 April 2011; pp. 2282–2290.
- Hui, P. People are the Network: Experimental Design and Evaluation of Social-Based Forwarding Algorithms. Technical Report UCAM-CL-TR-713; University of Cambridge Computer Laboratory: Cambridge, UK, 2008. [Google Scholar]
- Xu, H.; Xiao, W.; Tang, D.; Tang, J.; Wang, Z. Community core evolution in mobile social networks. Sci. World J. 2013, 2013, 781281. [Google Scholar] [CrossRef] [PubMed]
- Holme, P.; Saramaki, J. Temporal Networks. Phys. Rep. 2012, 519, 97–125. [Google Scholar] [CrossRef]
- Chakrabarti, D.; Kumar, R.; Tomkins, A. Evolutionary Clustering. In Proceedings of 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, Pennsylvania, PA, USA, 20–23 August 2006.
- Kim, M.-S.; Han, J. A Particle-and-Density Clustering Method for Dynamic Networks. In Proceedings of VLDB, Lyon, France, 24–28 August 2009.
- Chi, Y.; Song, X.; Zhou, D.; Hino, K.; Tseng, B.L. Evolutionary Spectral Clustering by Incorporating Temporal Smoothness. In Proceedings of 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007.
- Yang, T.; Chi, Y.; Zhu, S.; Gong, Y.; Rong, J. Detecting communities and their evolutions in dynamic social networks—a Bayesian approach. Mach. Learn. 2011, 82, 157–189. [Google Scholar] [CrossRef]
- Tang, X.; Yang, C.C. Dynamic Community Detection with Temporal Dirichlet Process. In Proceedings of 3rd International Conference on Social Computing (SocialCom), Boston, MA, USA, 9–11 October 2011.
- Lin, Y.-R.; Chi, Y.; Zhu, S.; Sundaram, H.; Tseng, B.L. FacetNet: A Framework for Analyzing Communities and Their Evolutions in Dynamic Networks. In Proceedings of the 23rd International World Wide Web Conference, Beijing, China, 21–25 April 2008.
- Nguyen, N.P.; Dinh, T.N.; Tokala, S.; Thai, M.T. Overlapping Communities in Dynamic Networks: Their Detection and Mobile Applications. In Proceedings of the 17th Annual International Conference on Mobile Computing and Networking (MobiCom), Las Vegas, CA, USA, 19–23 September 2011.
- Hui, P.; Yoneki, E.; Chan, S.-Y.; Crowcroft, J. Distributed Community Detection in Delay Tolerant Networks. In Proceedings of 2nd ACM/IEEE International Workshop on Mobility in the Evolving Internet Architecture (MobiArch), Kyoto, Japan, 27 August 2007.
- Chan, S.-Y.; Hui, P.; Xu, K. Community Detection of Time-Varying Mobile Social Networks. In Proceedings of The 1st International Conference on Complex Sciences: Theory and Applications (Complex), Shanghai, China, 23–25 February 2009.
- Greene, D.; Doyle, D.; Cunningham, P. Tracking the Evolution of Communities in Dynamic Social Networks. In Proceedings of International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Odense, Denmark, 9–11 August 2010.
- Bródka, P.; Saganowski, S.; Kazienko, P. Group Evolution Discovery in Social Networks. In Proceedings of International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Kaohsiung, Taiwan, 25–27 July 2011.
- Pietiläinen, A.-K.; Oliver, E.; LeBrun, J.; Varghese, G.; Diot, C. MobiClique: Middleware for Mobile Social Networking. In Proceedings of the 2nd ACM Workshop on Online Social Networks (WOSN), Barcelona, Spain, 17 August 2009; pp. 49–54.
- Wang, D.; Pedreschi, D.; Song, C.; Giannotti, F.; Barabási, A.-L. Human Mobility, Social Ties, and Link Prediction. In Proceedings of 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011.
- Bródka, P.; Saganowski, S.; Kazienko, P. GED: The method for group evolution discovery in social networks. Soc. Netw. Anal. Min. 2013, 3, 1–14. [Google Scholar] [CrossRef]
- Gliwa, B.; Bródka, P.; Zygmunt, A.; Saganowski, S.; Kazienko, P.; Koźlak, J. Different Approaches to Community Evolution Prediction in Blogosphere. In Proceedings of SNAA 2013 at ASONAM, Niagara Falls, Canada, 25–28 August 2013.
- Gliwa, B.; Saganowski, S.; Zygmunt, A.; Bródka, P.; Kazienko, P.; Koźlak, J. Identification of Group Changes in Blogosphere. In Proceedings of International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Istanbul, Turkey, 26–29 August 2012.
- Gregory, S. Finding overlapping communities in networks by label propagation. New J. Phys. 2011, 12, 103018. [Google Scholar] [CrossRef]
- Meila, M. Comparing clusterings—An information based distance. J. Multivar. Anal. 2007, 98, 873–895. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S.; Kertesz, J. Detecting the overlapping and hierarchical community structure in complex networks. New J. Phys. 2009, 11, 033015. [Google Scholar] [CrossRef]
- Isella, L.; Stehle, J.; Barrat, A.; Cattuto, C.; Pinton, J.-F.; vanden Broeck, W. What’s in a crowd? Analysis of face-to-face behavioral networks. J. Theor. Biol. 2011, 271, 166–180. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xu, H.; Hu, Y.; Wang, Z.; Ma, J.; Xiao, W. Core-Based Dynamic Community Detection in Mobile Social Networks. Entropy 2013, 15, 5419-5438. https://doi.org/10.3390/e15125419
Xu H, Hu Y, Wang Z, Ma J, Xiao W. Core-Based Dynamic Community Detection in Mobile Social Networks. Entropy. 2013; 15(12):5419-5438. https://doi.org/10.3390/e15125419
Chicago/Turabian StyleXu, Hao, Yanli Hu, Zhenwen Wang, Jianwei Ma, and Weidong Xiao. 2013. "Core-Based Dynamic Community Detection in Mobile Social Networks" Entropy 15, no. 12: 5419-5438. https://doi.org/10.3390/e15125419
APA StyleXu, H., Hu, Y., Wang, Z., Ma, J., & Xiao, W. (2013). Core-Based Dynamic Community Detection in Mobile Social Networks. Entropy, 15(12), 5419-5438. https://doi.org/10.3390/e15125419