1. Introduction: Mini-Review of -Entropy
In their seminal works, Shannon and Khinchin showed that, assuming four information theoretic axioms, the entropy must be of the Boltzmann–Gibbs type,
. In many physical systems, one of these axioms may be violated. For non-ergodic systems, the so-called separation axiom (Shannon–Khinchin Axiom 4) is not valid. We show that whenever this axiom is violated, the entropy takes a more general form,
, where
c and
d are scaling exponents and
is the incomplete gamma function. These exponents
define equivalence classes for
all, interacting and non-interacting, systems and unambiguously characterize any statistical system in its thermodynamic limit. The proof is possible because of two newly discovered scaling laws, which exist for any entropic form, given the first three Shannon–Khinchin axioms hold [
1].
can be used to define equivalence classes of statistical systems. A series of known entropies can be classified in terms of these equivalence classes. We show that the corresponding distribution functions are special forms of Lambert-
exponentials containing, as special cases, Boltzmann, stretched exponential and Tsallis distributions (power-laws). We go on by showing how the dependence of phase space volume
of a classical system on its size
N uniquely determines its extensive entropy and, in particular, the requirement extensively fixes the exponents
[
2]. We give a concise criterion when this entropy is not of the Boltzmann–Gibbs–Shannon type, but has to assume a
generalized (non-additive) form. We showed that generalized entropies can only exist when the dynamically (statistically) relevant fraction of degrees of freedom in the system vanishes in the thermodynamic limit [
2]. These are systems where the bulk of the degrees of freedom is frozen and is practically statistically inactive. Systems governed by generalized entropies are therefore systems whose phase space volume effectively collapses to a lower-dimensional “surface”. We explicitly illustrated the situation for binomial processes and argue that generalized entropies could be relevant for self-organized critical systems, such as sand piles, for spin systems that form meta-structures, such as vortices, domains, instantons,
etc., and for problems associated with anomalous diffusion [
2]. In this contribution, we largely follow the lines of thought presented in [
1,
2,
3].
Theorem 2 in the seminal 1948 paper,
The Mathematical Theory of Communication [
4], by Claude Shannon, proves the existence of the one and only form of entropy, given that three fundamental requirements hold. A few years later, A.I. Khinchin remarked in his
Mathematical Foundations of Information Theory [
5]: “However, Shannon’s treatment is not always sufficiently complete and mathematically correct so that, besides having to free the theory from practical details, in many instances I have amplified and changed both the statement of definitions and the statement of proofs of theorems.” Khinchin adds a fourth axiom. The three fundamental requirements of Shannon, in the “amplified” version of Khinchin, are known as the Shannon–Khinchin (SK) axioms. These axioms list the requirements needed for an entropy to be a reasonable measure of the “uncertainty” about a finite probabilistic system. Khinchin further suggests to also use entropy as a measure of the information
gained about a system when making an “experiment”,
i.e., by observing a realization of the probabilistic system.
Khinchin’s first axiom states that for a system with W potential outcomes (states), each of which is given by a probability, , with , the entropy, , as a measure of uncertainty about the system must take its maximum for the equi-distribution , for all i.
Khinchin’s second axiom (missing in [
4]) states that any entropy should remain invariant under adding zero-probability states to the system,
i.e.,
.
Khinchin’s third axiom (separability axiom) finally makes a statement of the composition of two finite probabilistic systems, A and B. If the systems are independent of each other, entropy should be additive, meaning that the entropy of the combined system, , should be the sum of the individual systems, . If the two systems are dependent on each other, the entropy of the combined system, i.e., the information given by the realization of the two finite schemes, A and B, , is equal to the information gained by a realization of system A, , plus the mathematical expectation of information gained by a realization of system B, after the realization of system A, .
Khinchin’s fourth axiom is the requirement that entropy is a continuous function of all its arguments, , and does not depend on anything else.
Given these axioms, the
Uniqueness Theorem [
5] states that the one and only possible entropy is
where
k is an arbitrary positive constant. The result is, of course, the same as Shannon’s. We call the combination of four axioms the Shannon–Khinchin (SK) axioms.
From information theory, we now move to physics, where systems may exist that violate the separability axiom. This might especially be the case for non-ergodic, complex systems exhibiting long-range and strong interactions. Such complex systems may show extremely rich behavior in contrast to simple ones, such as gases. There exists some hope that it should be possible to understand such systems also on a thermodynamical basis, meaning that a few measurable quantities would be sufficient to understand their macroscopic phenomena. If this were possible, through an equivalent to the second law of thermodynamics, some appropriate entropy would enter as a fundamental concept relating the number of microstates in the system to its macroscopic properties. Guided by this hope, a series of so-called generalized entropies have been suggested over the past few decades; see [
6,
7,
8,
9,
10,
11] and
Table 1. These entropies have been designed for different purposes and have not been related to a fundamental origin. Here, we ask how generalized entropies can look if they fulfill some of the Shannon–Khinchin axioms, but explicitly violate the separability axiom. We do this axiomatically, as first presented in [
1]. By doing so, we can relate a large class of generalized entropies to a single fundamental origin.
The reason why this axiom is violated in some physical, biological or social systems is
broken ergodicity,
i.e., that not all regions in the phase space are visited, and many microstates are effectively “forbidden”. Entropy relates the number of microstates of a system to an
extensive quantity, which plays the fundamental role in the systems thermodynamical description. Extensive means that if two initially isolated,
i.e., sufficiently separated systems,
A and
B, with
and
the respective numbers of states, are brought together, the entropy of the combined system,
, is
.
is the number of states in the combined system,
. This is not to be confused with
additivity, which is the property that
. Both extensivity and additivity coincide if the number of states in the combined system is
. Clearly, for a non-interacting system, Boltzmann–Gibbs–Shannon entropy,
, is extensive
and additive. By “non-interacting” (short-range, ergodic, sufficiently mixing, Markovian,
etc.) systems, we mean
. For interacting statistical systems, the latter is in general not true; the phase space is only partly visited, and
. In this case, an additive entropy, such as Boltzmann–Gibbs–Shannon, can no longer be extensive and
vice versa. To ensure the extensivity of entropy, an entropic form should be found for the particular interacting statistical systems at hand. These entropic forms are called
generalized entropies and usually assume trace form [
6,
7,
8,
9,
10,
11]
W being the number of states. Obviously not all generalized entropic forms are of this type. Rényi entropy, for example, is of the form,
, with
G a monotonic function. We use trace forms Equation (
2) for simplicity. Rényi forms can be studied in exactly the same way, as will be shown, however, at more technical cost.
Table 1.
Order in the zoo of recently introduced entropies for which SK1–SK3 hold. All of them are special cases of the entropy given in Equation (
3), and their asymptotic behavior is uniquely determined by
c and
d. It can be seen immediately that
,
and
are asymptotically identical; so are
and
, as well as
and
.
Table 1.
Order in the zoo of recently introduced entropies for which SK1–SK3 hold. All of them are special cases of the entropy given in Equation (3), and their asymptotic behavior is uniquely determined by c and d. It can be seen immediately that , and are asymptotically identical; so are and , as well as and .
| Entropy | | c | d | Reference |
|---|
| | c | d | |
| | 1 | 1 | [5] |
| | | 0 | [6] |
| () | | 0 | [8] |
| | 1 | 0 | [6] |
| | 1 | 0 | [9] |
| | 1 | 0 | [10] |
| | 1 | | [7] |
| | 1 | | [12,13] |
| | | 1 | [14] |
Let us revisit the Shannon–Khinchin axioms in the light of generalized entropies of trace form Equation (
2). Specifically, Axioms SK1–SK3 (now re-ordered) have implications on the functional form of
g.
SK1: The requirement that S depends continuously on p implies that g is a continuous function.
SK2: The requirement that the entropy is maximal for the equi-distribution (for all i) implies that g is a concave function.
SK3: The requirement that adding a zero-probability state to a system, with , does not change the entropy implies that .
SK4 (separability axiom): The entropy of a system, composed of sub-systems A and B, equals the entropy of A plus the expectation value of the entropy of B, conditional on A. Note that this also corresponds exactly to Markovian processes.
As mentioned, if SK1 to SK4 hold, the only possible entropy is the Boltzmann–Gibbs–Shannon (BGS) entropy. We are now going to derive the extensive entropy when separability Axiom SK4 is violated. Obviously, this entropy will be more general and should contain BGS entropy as a special case.
We now assume that Axioms SK1, SK2, SK3 hold,
i.e., we restrict ourselves to trace form entropies with
g continuous, concave and
. These systems we call
admissible systems. Admissible systems when combined with a maximum entropy principle show remarkably simple mathematical properties [
15,
16].
This generalized entropy for (large) admissible statistical systems (SK1–SK3 hold) is derived from two hitherto unexplored fundamental scaling laws of extensive entropies [
1]. Both scaling laws are characterized by exponents
c and
d, respectively, which allow one to uniquely define equivalence classes of entropies, meaning that two entropies are equivalent in the thermodynamic limit if their exponents
coincide. Each admissible system belongs to one of these equivalence classes
, [
1].
In terms of the exponents
, we showed in [
1] that all generalized entropies have the form
with
the incomplete Gamma-function.
Special Cases of Equivalence Classes
Let us look at some specific equivalence classes
.
Boltzmann–Gibbs entropy belongs to the
class. One gets from Equation (
3)
Tsallis entropy belongs to the
class. From Equation (
3) and the choice
(see below), we get
Note, that although the
pointwise limit,
, of Tsallis entropy yields BG entropy, the asymptotic properties,
, do
not change continuously to
in this limit! In other words, the thermodynamic limit and the limit,
, do not commute.
The entropy related to stretched exponentials [
7] belongs to the
classes; see
Table 1. As a specific example, we compute the
case
leading to a superposition of two entropy terms, the asymptotic behavior being dominated by the second.
Other entropies that are special cases of our scheme are found in
Table 1.
Inversely, for any given entropy, we are now in the remarkable position to characterize
all large SK1–SK3 systems by a pair of two exponents
; see
Figure 1.
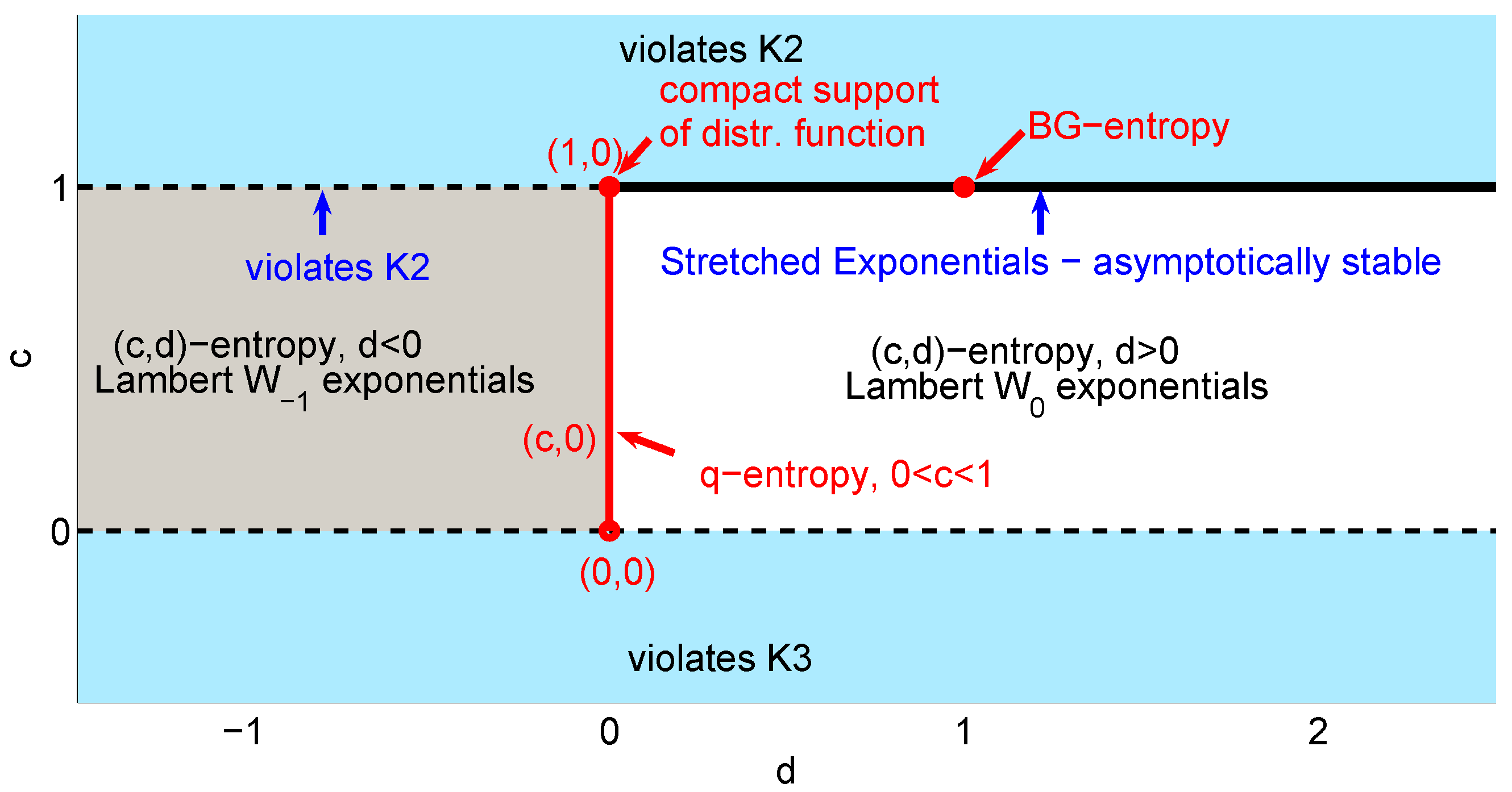
Figure 1.
Entropies parametrized in the
-plane, with their associated distribution functions. Boltzmann–Gibbs–Shannon (BGS) entropy corresponds to
, Tsallis entropy to
and entropies for stretched exponentials to
. Entropies leading to distribution functions with compact support belong to equivalence class
. Figure from [
3].
Figure 1.
Entropies parametrized in the
-plane, with their associated distribution functions. Boltzmann–Gibbs–Shannon (BGS) entropy corresponds to
, Tsallis entropy to
and entropies for stretched exponentials to
. Entropies leading to distribution functions with compact support belong to equivalence class
. Figure from [
3].
For example, for
, we have
, and
.
, therefore, belongs to the universality class
. For
(Tsallis entropy) and
, one finds
and
, and Tsallis entropy,
, belongs to the universality class
. Other examples are listed in
Table 1.
The universality classes are equivalence classes with the equivalence relation given by: and . This relation partitions the space of all admissible g into equivalence classes completely specified by the pair .
1.1. Distribution Functions
Distribution functions associated with
-entropy, Equation (
3), can be derived from so-called generalized logarithms of the entropy. Under the maximum entropy principle (given ordinary constraints) the inverse functions of these logarithms,
, are the distribution functions,
, where, for example,
r can be chosen
. One finds [
1]
with the constant
. The function,
, is the
k-th branch of the Lambert-
function, which, as a solution to the equation
, has only two real solutions,
, the branch
and branch
. Branch
covers the classes for
, branch
those for
.
Special Cases of Distribution Functions
It is easy to verify that the class leads to Boltzmann distributions, and the class yields power-laws or, more precisely, Tsallis distributions, i.e., q-exponentials. All classes associated with for are associated with stretched exponential distributions. Expanding the branch of the Lambert- function for , the limit, , is shown to be a stretched exponential. It was shown that r does not affect its asymptotic properties (tail of the distributions), but can be used to incorporate finite size properties of the distribution function for small x.
1.2. How to Determine the Exponents, c and d.
In [
2], we have shown that the requirement of extensivity determines uniquely both exponents,
c and
d. What does extensivity mean? Consider a system with
N elements. The number of system configurations (microstates) as a function of
N are denoted by
. Starting with SK2,
(for all
i), we have
. As mentioned above, extensivity for two subsystems,
A and
B, means that
Using this equation, one can straight forwardly derive the formulas (for details, see [
2])
Here,
means the derivative with respect to
N.
1.3. A Note on Rényi-type Entropies
Rényi entropy is obtained by relaxing SK4 to the unconditional additivity condition. Following the same scaling idea for Rényi-type entropies,
, with
G and
g being some functions, one gets
where
. The expression
provides the starting point for deeper analysis, which now gets more involved. In particular, for Rényi entropy with
and
, the asymptotic properties yield the class
, (BGS entropy), meaning that Rényi entropy is additive. However, in contrast to the trace form entropies used above, Rényi entropy can be shown to be
not Lesche stable, as was observed before [
17,
18,
19,
20,
21]. All of the
entropies can be shown to be Lesche stable; see [
3].
3. Conclusions
Based on recently discovered scaling laws for trace form entropies, we can classify all statistical systems and assign a unique system-specific (extensive) generalized entropy. For non-ergodic systems, these entropies may deviate from the Shannon form. The exponents for BGS systems are
; systems characterized by stretched exponentials belong to the class
, and Tsallis systems have
. A further interesting feature of all admissible systems is that they are all
Lesche-stable, and that the classification scheme for generalized entropies of type
can be easily extended to entropies of the Rényi type,
i.e.,
. For proofs, see [
3].
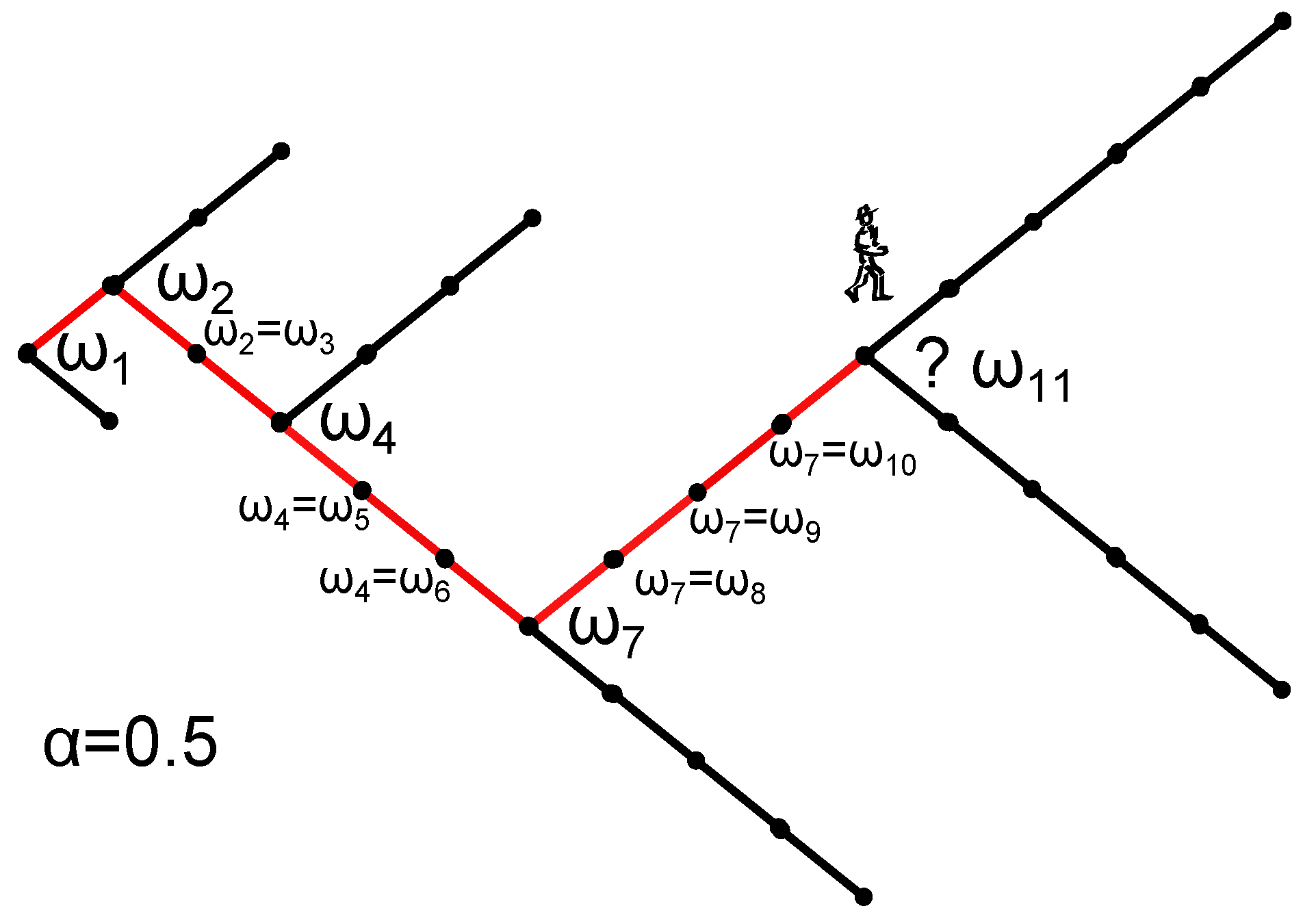
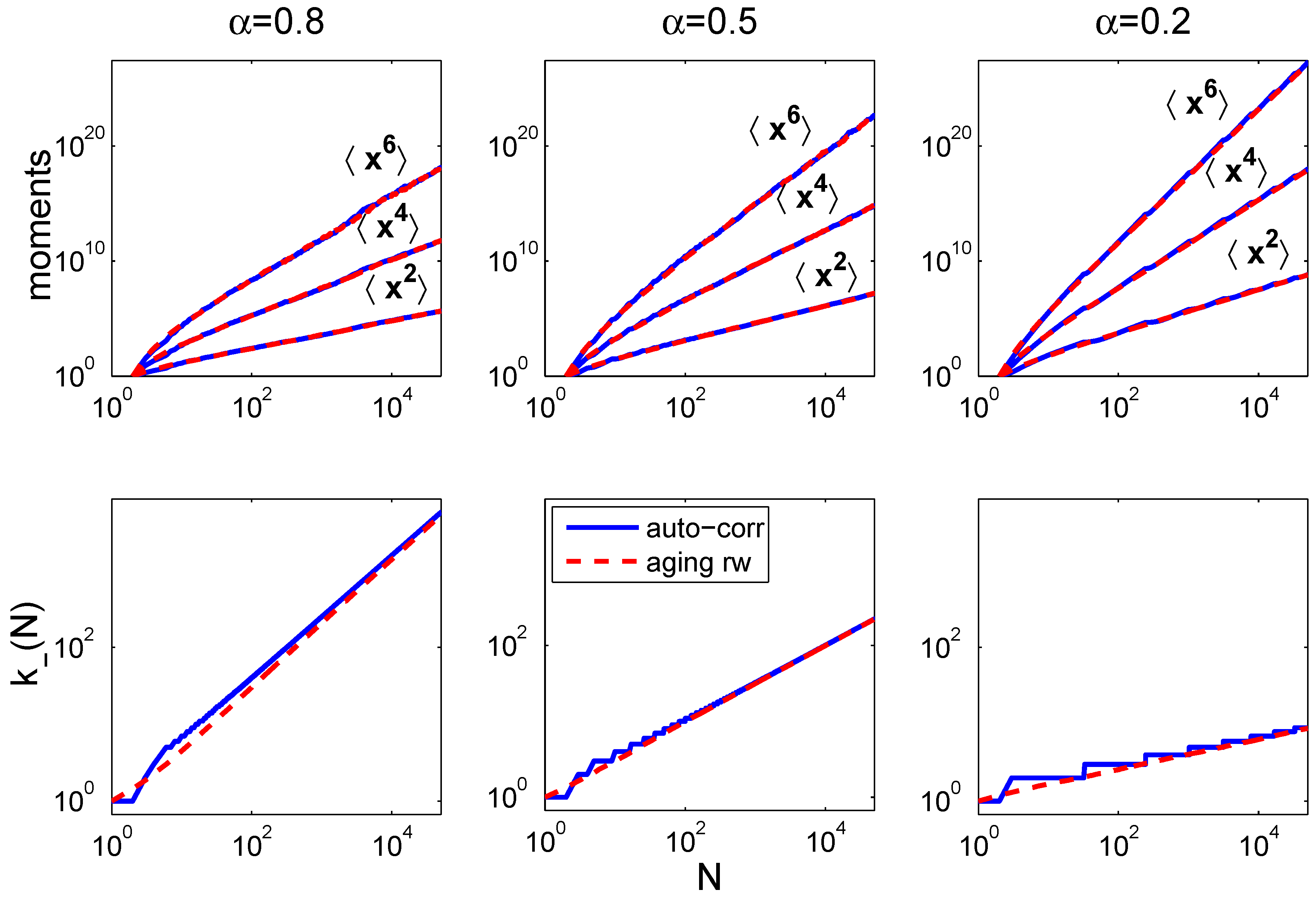
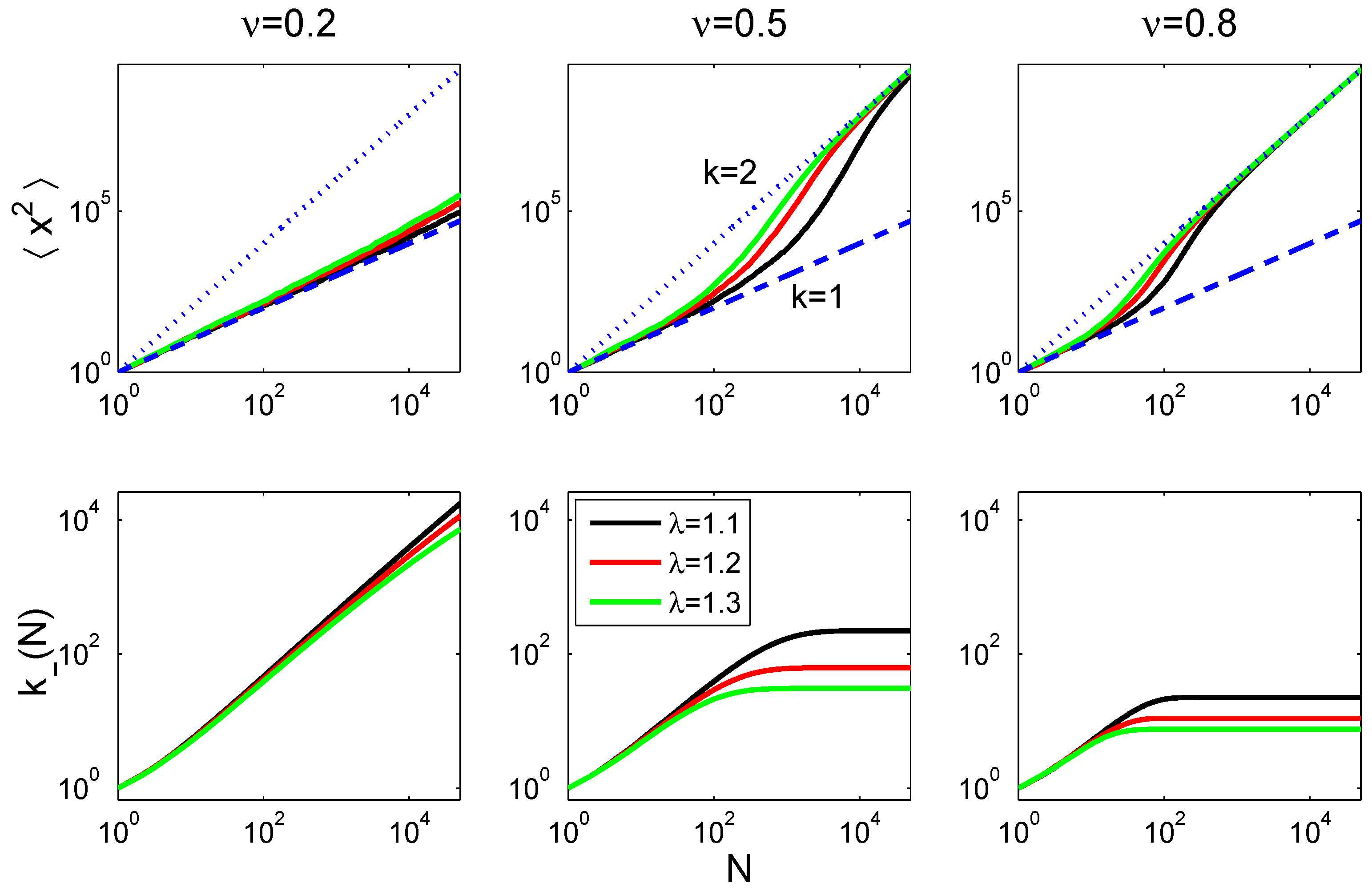
We demonstrated that the auto-correlated random walk characterized by
introduced in [
2] cannot be distinguished from accelerating random walks in terms of distribution functions. Although the presented auto-correlated random walk is of entropy class
, and the accelerated random walk is of class
, both processes have the same distribution function, since all moments,
, are identical. We have shown that other classes of random walks can naturally be obtained, including those belonging to the
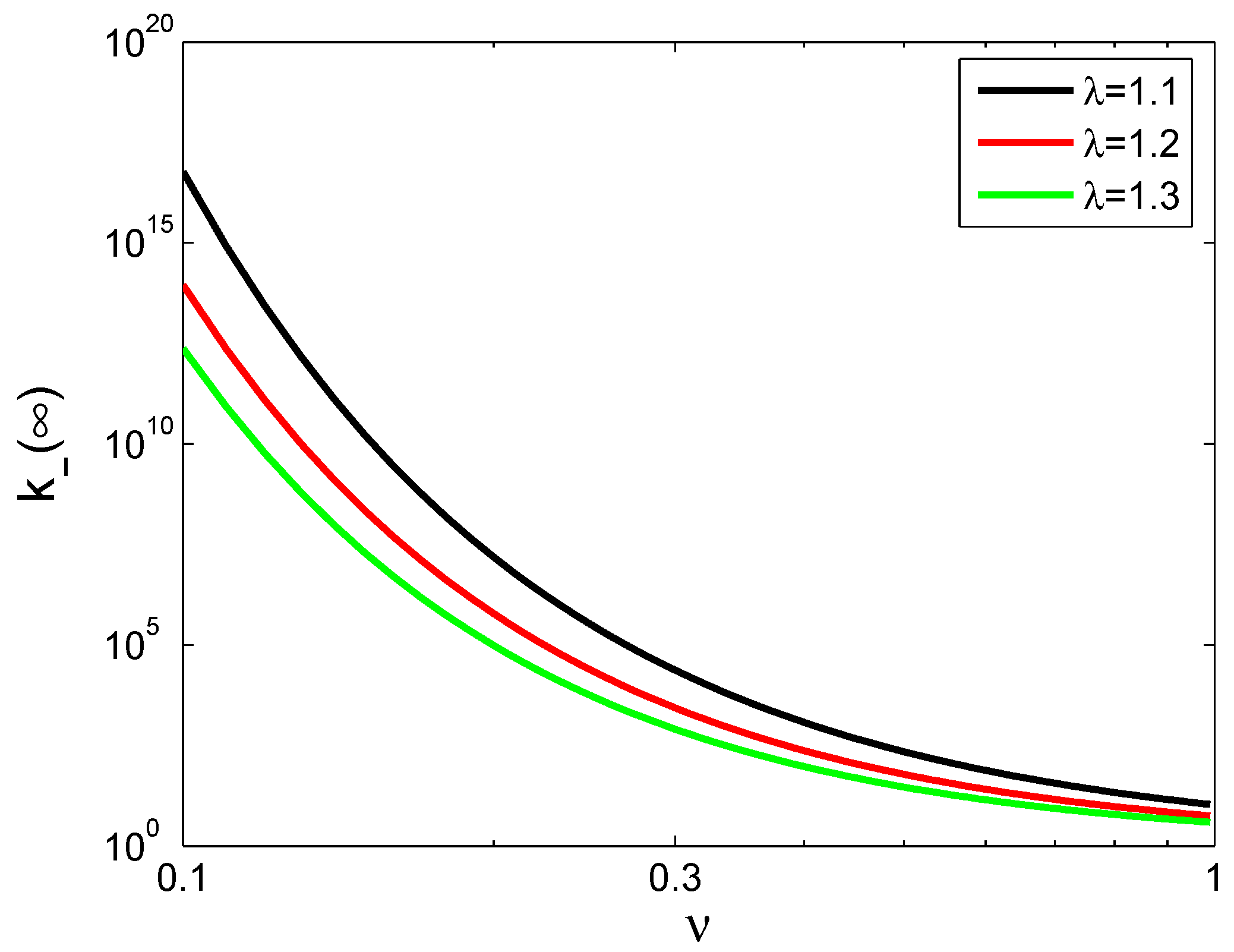
(Tsallis) equivalence class. Moreover, we showed numerically that the auto-correlated random walk is asymptotically equivalent to a particular
aging random walk, where the probability of a decision to reverse the direction of the walk depends on the path the random walk has taken. This concept of aging can easily be generalized to different forms of aging, and it can be expected that many of the admissible systems can be represented by a specific type of aging that is specified by the aging function,
g. Finally, we have seen that different equivalence classes
can be realized by specifying an aging function,
g. The effective number of direction reversal decisions corresponding to the aging function remains finite, and therefore, the associated generalized entropy requires a class
with
. We believe that it should be possible that the scheme of aging random walks can be naturally extended to aging processes in physical, biological and social systems.