1. Introduction
The measure of multivariate association, that is, of the association between groups of components of a general
d-dimensional random vector
, is a topic of increasing interest in a series of application contexts. Among the information measures, the mutual information, a special case of relative entropy or Kullback-Leibler distance [
1], is a quantity that measures the mutual dependence between the variables considered. Unlike the measures of linear dependency between random variables, such as the correlation coefficient, the mutual information is particularly interesting as it is sensitive also to dependencies that are not codified in the covariance. Although this is one of the most popular dependency measures, it is only one of the many other existing ones, see for example [
2].
The extension of mutual information to
d–dimensional random vectors is not trivial [
3,
4,
5]. Considering the distance between the joint distribution of the random vector and the joint distribution of the random vector with independent univariate components gives the so called total mutual information. However, in many instances, it is more interesting to study the distance between groups of components of the random vector, which are again multivariate random vectors of different dimensions. Hence the mutual information, in its general
d–dimensional definition, is a distance of the joint distribution of the random vector to the joint distribution of groups of components considered independent from each other. We consider here this general framework with the aim of introducing a good estimator for the multivariate mutual information.
The problem of statistical estimation of mutual information has been considered by various authors. Optimized estimators that use adaptive bin sizes have been developed in [
6,
7]. A very good estimator based on
k–nearest neighbor statistics is proposed in [
8]. A computationally efficient modification of this method appeared recently in [
9]. The estimation of mutual information sets in the broader context of the estimation of information–type measures such as entropy, Kullback–Leibler distance, divergence functionals, Rényi entropy. The
k–nearest neighbor statistics are used to build an estimator for entropy in [
10] and for the more general Rényi entropy in [
11,
12]. An overview of nonparametric entropy estimators can be found in [
13]. For the case of discrete random variables, see for example [
14]. A variational characterization of divergences allows the estimation of Kullback–Leibler divergence (and more generally any
f–divergence) to turn into a convex optimization problem [
15,
16,
17]. An interesting application of information–type quantities to devise a measure of statistical dispersion can be found in [
18].
We propose here a new and simple estimator for the mutual information in its general multidimensional definition. To accomplish this aim, we first deduce an equation that links the mutual information between groups of components of a
d-dimensional random vector to the entropy of the so called linkage function [
19], that reduces to the copula function [
20] in dimension
. In this way the problem of estimating mutual information is reduced to the estimation of the entropy of a suitably transformed sample of the same dimensions as the original random vector. This topic is hence closely related to the estimation of the Shannon entropy.
The structure of the paper is as follows: Notation and mathematical background are introduced in
Section 2, where a brief survey on copula function and linkage function is also provided. In
Section 3 we expose the method proposed to estimate the mutual information, providing also some details on the resulting algorithm and on the implementation care required.
Section 4 contains some examples where the estimator is applied to simulated data and its performances are compared with some other estimators in literature. Conclusions are drawn in
Section 5.
2. Notations and Mathematical Background
Given a dimensional random vector , let us denote , for , the joint cumulative distribution function (c.d.f.) and , for and , the marginal c.d.f. of the th component. When X is absolutely continuous, for is the joint probability density function (p.d.f.) and for and the corresponding marginal p.d.f. of the th component. Furthermore, and , where each assumes a different value ranging from 1 to d and , denote respectively the conditional c.d.f. and the conditional p.d.f. of the variable with respect to the variables . For the sake of brevity, when is any multi–index of length n we use the following notation denoting the c.d.f. of the random vector and denoting the p.d.f. of . Furthermore, when not necessary, we omit the argument of the functions, i.e., we may write in spite of .
The mutual information (MI) of a 2-dimensional random vector
is given by
If
and
are independent
.
The relative entropy (or Kullback-Leibler distance)
D between the p.d.f.’s
f and
g is defined by
Hence, MI can be interpreted as the Kullback-Leibler distance of the joint p.d.f.
from the p.d.f.
of a vector with independent components,
i.e., it is a measure of the distance between
and the random vector with the same marginal distributions but independent components.
The differential entropy of the absolutely continuous random vector
is defined as
MI and entropy in the case
are related through the well known equation [
1]
The generalization of MI to more than two random variables is not unique [
3]. Indeed different definitions can be given according to different grouping of the components of the random vector
. More precisely, for any couple of multi-indices
of dimensions
h and
k respectively, with
and partitioning the set of indices
, the
can be defined as the
, where
and
. Therefore we have
More generally, for any
n multi-indices
of dimensions
respectively, such that
and partitioning the set of indices
the following quantities
are all
d–dimensional extensions of Equation (
1). In the particular case
where all the multi-indices have dimension 1, Equation (
6) gives the so called total MI, a measure of the distance of the distribution of the given random vector to the one with the same marginal distributions but mutually independent components.
Equation (
6) can be rewritten as
and then, integrating each term, it is is easy to prove the following generalization to the
d–dimensional case of Equation (
4)
Another approach to the study of dependencies between random variables is given by copula functions (for example [
20]). A
dimensional copula (or
copula) is a function
with the following properties:
- (1)
for every , if at least one coordinate is null and if all coordinates are 1 except ;
- (2)
for every and such that , .
Here
is the so called
volume of
,
i.e., the
th order difference of
C on
where
Hence, a copula function is a non–decreasing function in each argument.
A central result in the theory of copulas is the so called Sklar’s theorem, see [
20]. It captures the role that copulas play in the relationship between joint c.d.f.’s and their corresponding marginal univariate distributions. In particular it states that for any
dimensional c.d.f.
of the random vector
there exists a
copula
C such that for all
where
are the univariate margins. If the margins are continuous, then the copula
C is uniquely determined. Otherwise,
C is uniquely determined over Ran
Ran
, where Ran
is the range of the function
. Conversely, if
C is a copula and
,
are one-dimensional distribution functions, then the function
defined in Equation (
11) is a
d-dimensional distribution function with margins
,
.
In particular, a copula
C can be interpreted as the joint c.d.f. of the random vector
, where each component is obtained through the transformation
Indeed
Moreover, as each component is obtained with Equation (
12), the univariate marginal distributions of the random vector
U are all uniform on
. An important property that is tightly bound to MI is that copula functions are invariant under strictly increasing transformations of the margins, see [
20].
If a copula
C is differentiable, the joint p.d.f. of the random vector
X can be written as
where
is the so called density of the copula
C.
As illustrated in [
21], it is not possible to use copula functions to handle multivariate distribution with given marginal distributions of general dimensions, since the only copula that is compatible with any assigned multidimensional marginal distributions is the independent one. To study dependencies between multidimensional random variables we resort to a generalization of copula notion. It relies on the use of the so-called linkage functions introduced in [
19].
Let us consider the d-dimensional random vector X and any n multi-indices of dimensions respectively, such that and partitioning the set . For , let be the -dimensional c.d.f. of and let be the joint c.d.f. of , which is of dimension d as the multi–indices are partitioning the set .
Define the transformation
,
as
for all
in the range of
.
Then the vectors
are
-dimensional vectors of independent uniform
random variables, see [
19].
The linkage function corresponding to the
d-dimensional random vector
is defined as the joint p.d.f.
L of the vector
Notice that for
the linkage function reduces to the copula function. Analogously to the two–dimensional case, linkages are invariant under strictly increasing functions, that is a
d–dimensional function with components strictly increasing real univariate functions, see Theorem 3.4 in [
19].
The information regarding the dependence properties between the multivariate components of the random vector is contained in the linkage function, that is independent from the marginal c.d.f.’s. Linkage functions can then be successfully employed when one is interested in studying the dependence properties between the random vectors disregarding their single components. On the other hand, linkage functions allow to study the interrelationships not only between all the components of a random vector, but also between given chosen sets of not overlapping random components of the vector. They contain the information regarding the dependence structure among such marginal vectors, while the dependence structure within the marginal vectors is not considered explicitly. It must be underlined that different multivariate c.d.f.’s can have the same linkage function but different marginal distributions.
In the next Section we will discuss the use of linkage functions for the computation of the MI between random vectors.
4. Examples and Simulation Results
In this Section we show the results obtained with the estimator proposed in
Section 3. The examples cover the cases
. We choose cases for which the MI can be computed either in a closed form expression or numerically, so that we can easily compare our results with the exact ones.
Several methods have been already proposed in the literature to estimate the MI between multivariate random vectors from sample data. One of the most efficient seems to be the binless method exposed in [
8], based on estimates from
k–nearest neighbor statistics. We refer from now on to this method as “KSG” from the names of the authors. On the other hand, a straightforward way to estimate MI could be to estimate separately the entropy terms in Equation (
8) by means of a suitable estimator as the one proposed in [
10,
32] and sum them up. Let us notice that this procedure is not recommended as the errors made in the individual estimates of each entropy term would presumably not cancel. We refer to this methodology as the “plain entropy” method. The results obtained with our estimator are here compared both to the KSG and to the “plain entropy”.
As mutual information is a particular case of Kullback–Leibler divergence, we could use the estimators proposed in [
15,
17]. However let us remark that our estimator is based on one single sample of size
N drawn from
, the multivariate joint law of the random vector
. On the other side, the estimators proposed in [
15,
17] and adapted to the case of mutual information are based on two samples: one drawn from the multivariate joint law and the other from
, the product of the
n marginal laws. We could build the missing sample from the given one, but it is not obvious that the estimators will keep their good properties. Indeed in our setting the samples are no more independent as some resampling procedure should be devised to make the method suitable for our particular case. From a preliminary numerical study it seems that the performances of the estimators proposed in [
15,
17] are not comparable to the performances of our estimator. Hence we skip this comparison.
The examples illustrated in the next two Subsections are chosen to test our approach on distributions that could be troublesome for our approach. Following the discussion introduced in the previous Section, the delicate point of the method is the estimation of the (conditional) cumulative distribution functions in Equation (
20). Hence we consider an example where the density to be estimated has bounded support as for the Uniform r.v. (Example 2) and an example where the density is positive valued and with an early steep peak as for the Exponential r.v. (Example 3). To address the problem of tails in estimation of information–theoretic quantities, we present two examples of heavy-tailed distributions: the lognormal (Example 4) and the Levy (Example 5). Note that the lognormal distribution is heavy tailed but with finite all order moments, while the Levy is an alpha–stable distribution with power law tail probability and no finite moments.
We rely on simulated data, while we reserve to a future work the application of the estimator to data coming from real experiments. For each example we perform simulation batches of the random vectors involved for each of the following sample sizes .
4.1. Two-Dimensional Vectors
Let us consider the following five cases of two-dimensional random vectors .
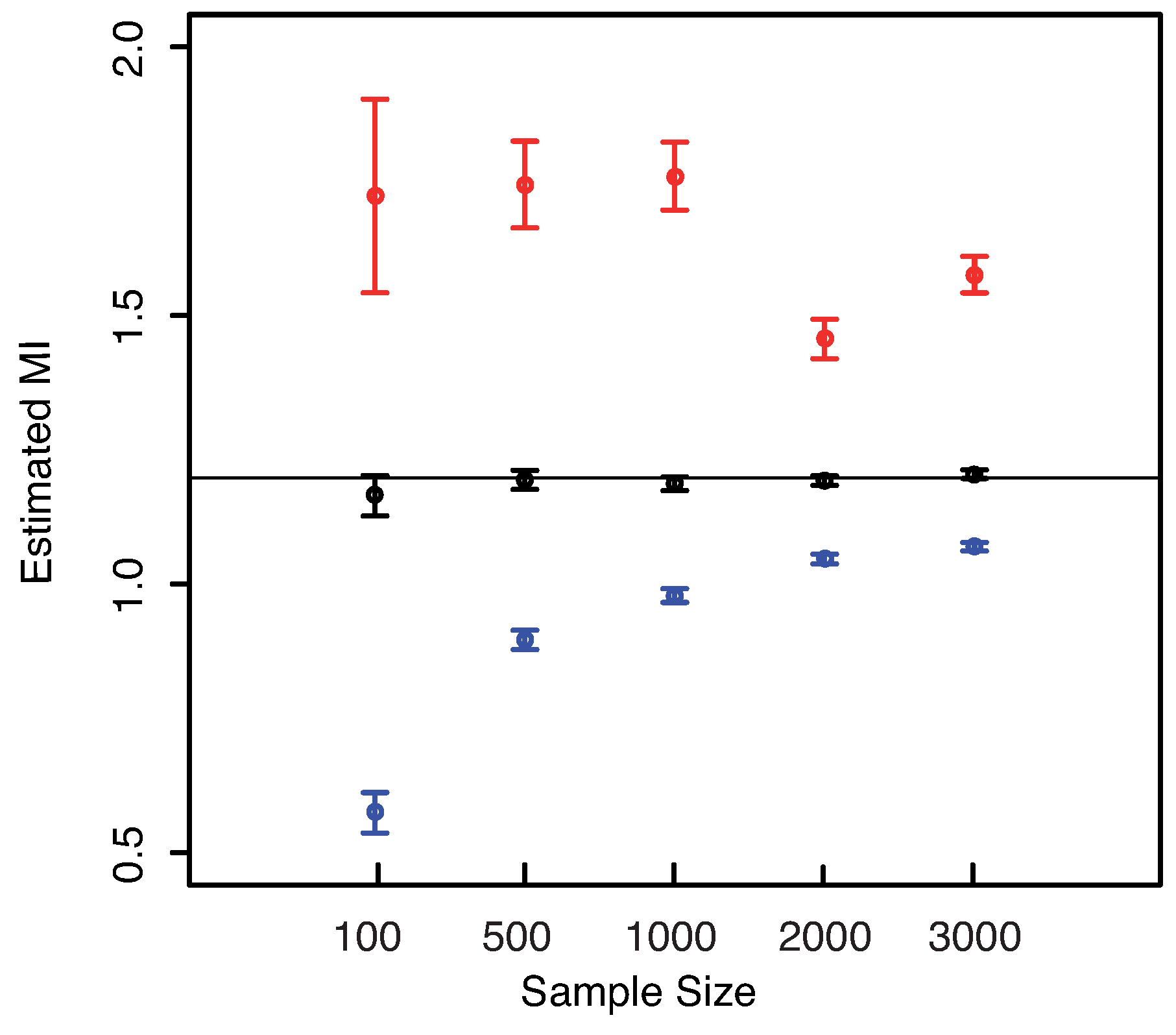
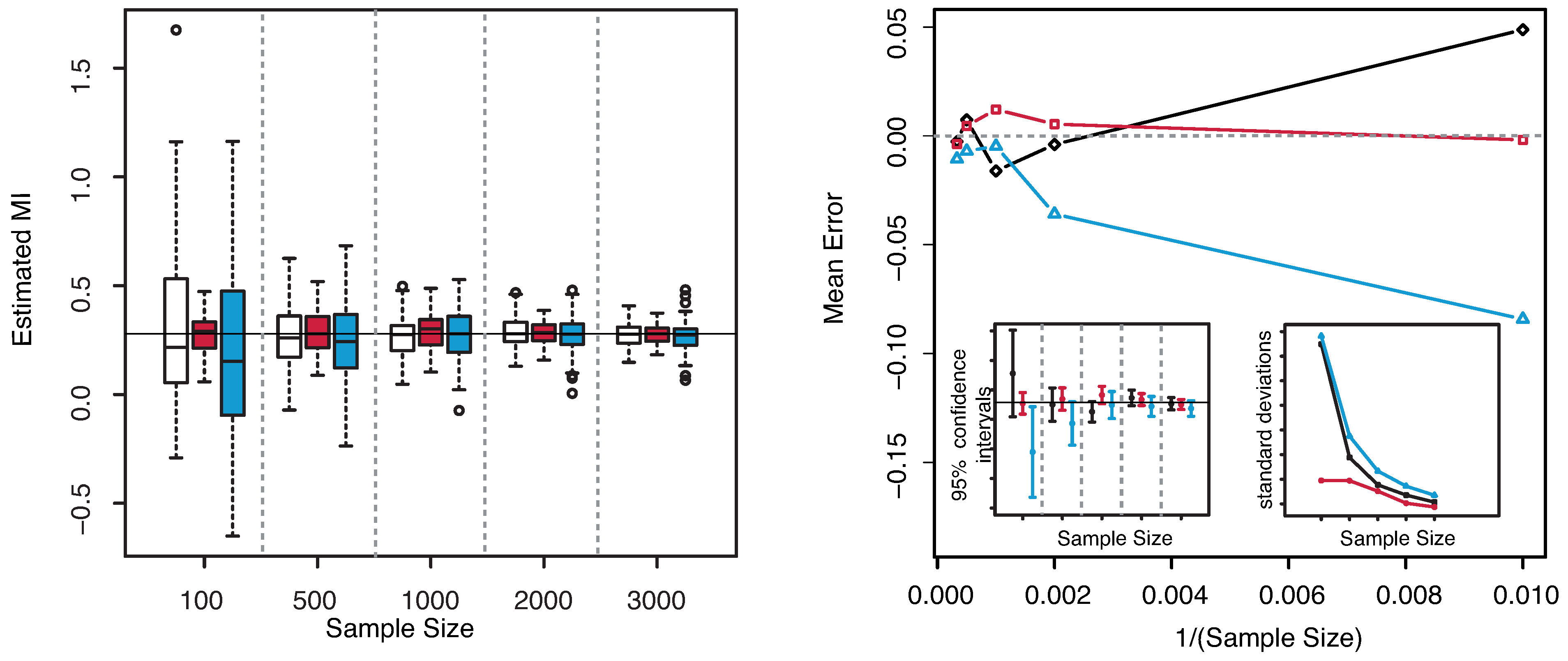
Example 1. Let
be a gaussian random vector with standard normal components and correlation coefficient
. Denoting as
σ the covariance matrix of
X, the MI between
and
is given as
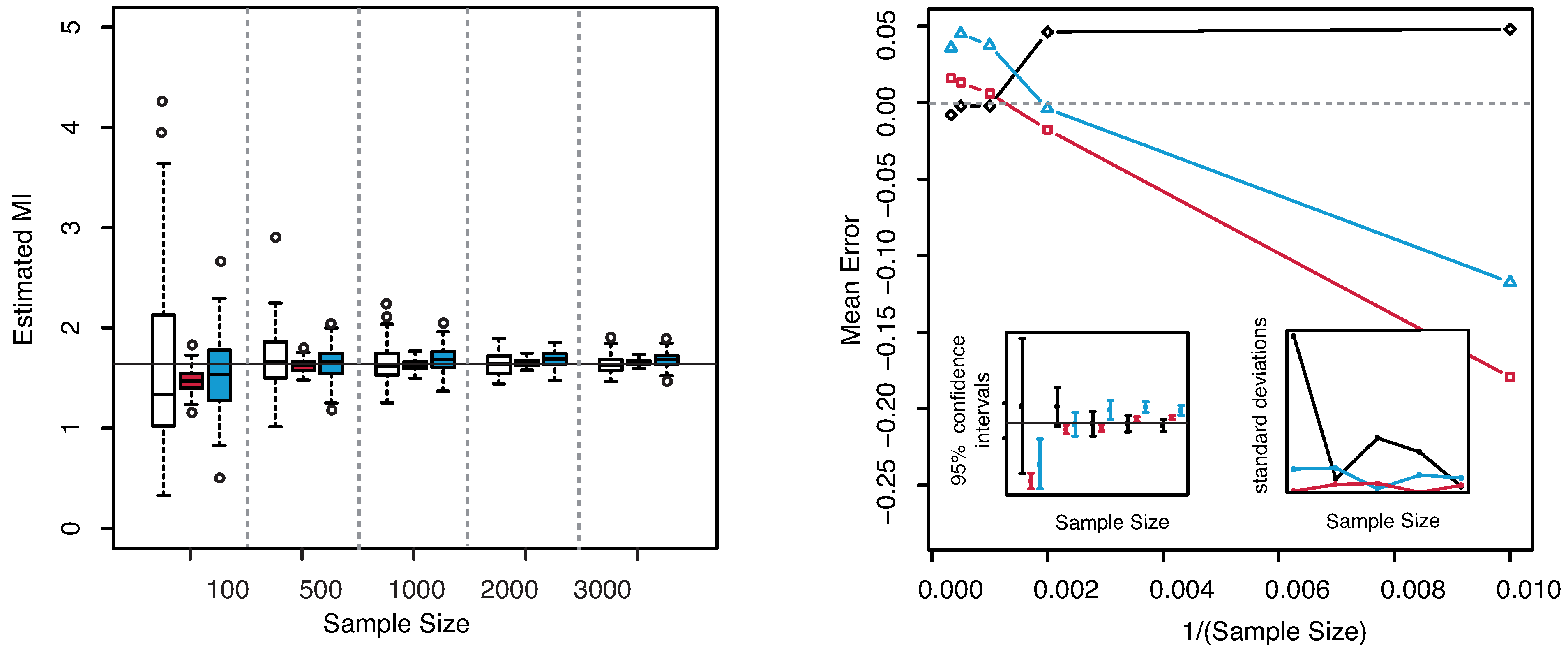
The numerical results are illustrated in
Figure 3. The horizontal line indicates the exact value
. Both plots reveal that our estimator of the MI is centered around its true value. The interquartile range considerably decreases with increasing sample size, becoming minimal for
. The comparison of the performances with the KSG and “plain entropy” estimators shows that our method performs comparably with KSG except for very small sample sizes (
), where it has a larger dispersion, see
Figure 3—right panel—bottom right inset. It results even better for the highest sample sizes. However its variance quickly decreases to the values attained by the KSG estimator that are sensibly smaller that the variances of the “plain entropy” method. Actually, the “plain entropy” estimator leads to poorer performances such as larger interquartile range and less marked centering of the confidence interval around the true value.
Figure 3.
(Example 1) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
Figure 3.
(Example 1) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
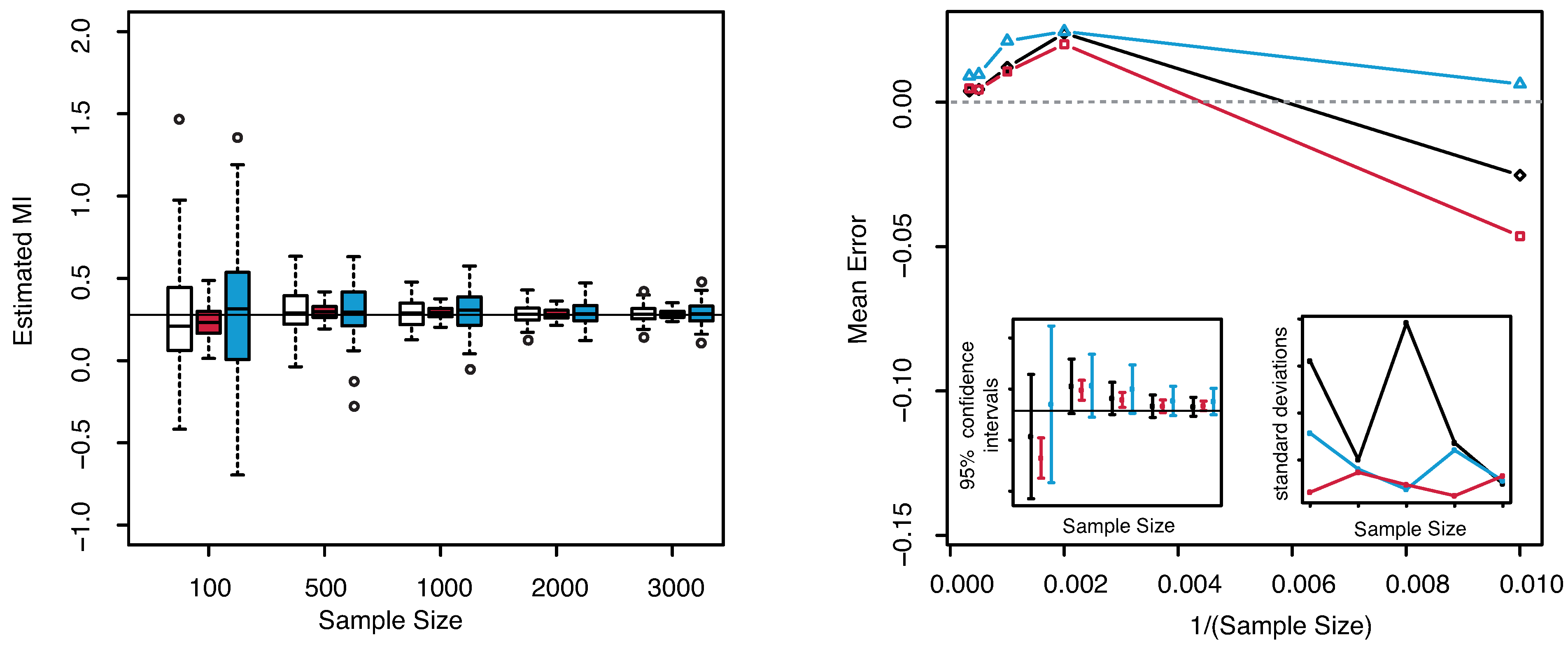
Example 2. Let
and
be linearly dependent random variables, related through the following equation
where
is uniformly distributed on the interval
and
is a standard gaussian random variable. In this case the mutual information is proved to be
bit, see [
33].
The numerical results are illustrated in
Figure 4. Similar observations as for the previous example can be deduced for this case. The dispersion is clearly highly reduced as the sample size increases, but the estimated MI is always centered with respect to the true value. The “plain entropy” method is again less performing with respect to the others both in terms of dispersion and of centering the true value. The standard deviations of the estimates obtained with our method appear always lower than the ones obtained with the “plain entropy” method and comparable with those obtained by KSG method except for very small sample sizes
.
Figure 4.
(Example 2) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
Figure 4.
(Example 2) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
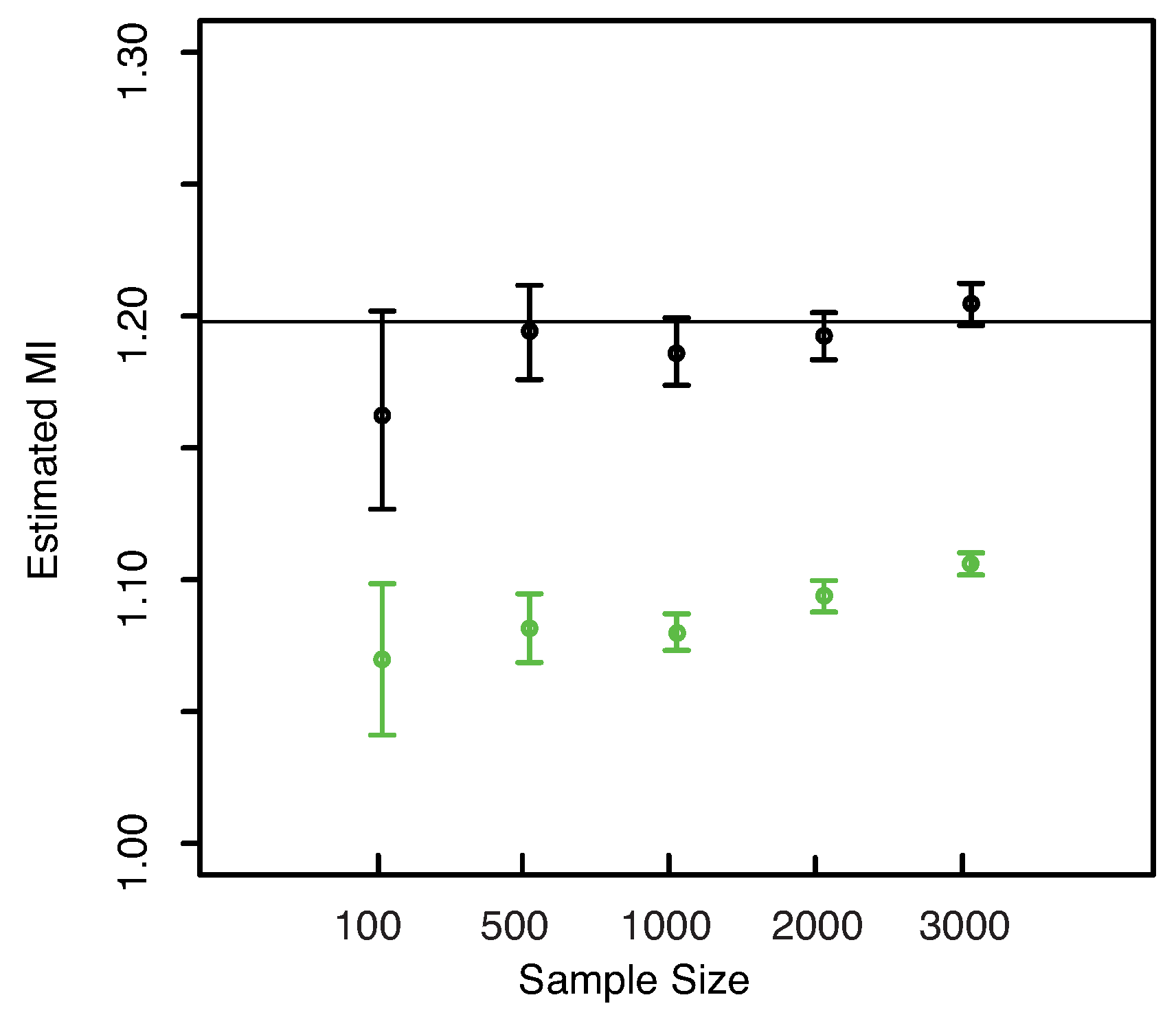
Example 3. Let
,
have joint c.d.f. given in the following equation
with components that are respectively a uniform random variable on the interval
and an exponential random variable with unitary parameter. In this case the copula function can be obtained in closed form (see [
20])
which corresponds to the copula density function
A numerical integration then allows to obtain the mutual information
bit.
Both the boxplots and the confidence intervals in
Figure 5 show that the values of MI obtained with our estimator are centered around the true value even for the smallest sample sizes
and
. The comparison with KSG and “plain entropy” methods in
Figure 5—right panel shows that the method proposed allows to obtain results that are comparable with the first one apart only for
and is always better performing than the second one. This last method produces not centered estimates for small sample sizes such as
and
. The standard deviations behave as in the previous example.
Figure 5.
(Example 3) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
Figure 5.
(Example 3) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
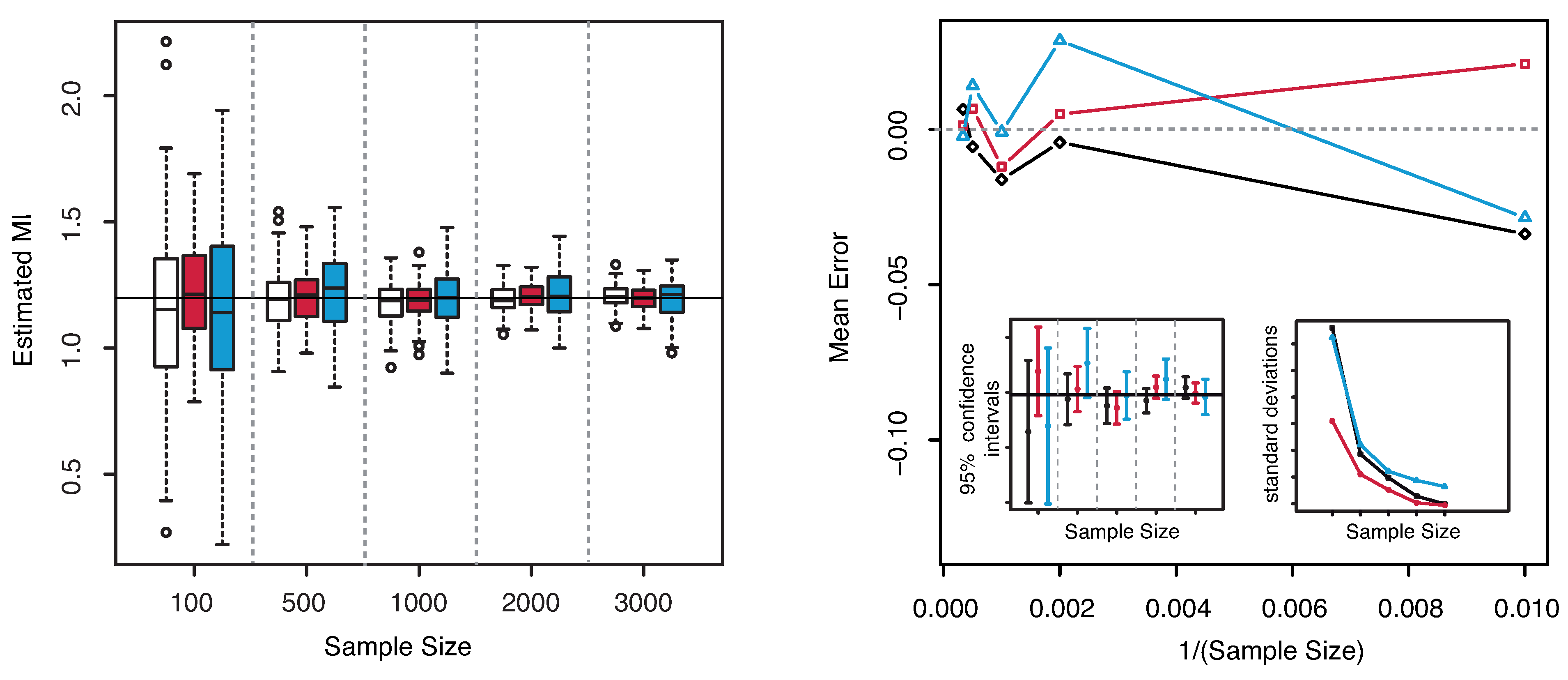
Example 4. Let
be a bivariate lognormal random vector with zero mean and covariance matrix given by
with
and
. Let us notice that the random vector
can be interpreted as a two–dimensional geometric Ornstein–Uhlenbeck (OU) process at the time
, see [
34]. The numerical value of the mutual information in this case is again
bit, as in the Example 1. Indeed the random vector
can be obtained as the exponential of the bivariate OU process at time
, that is a Gaussian random vector. As MI is invariant under reparametrization of the marginal distributions and in the Gaussian case (with components with equal variances) depends only on the covariance structure, we get the same value as in the previous example.
The results are illustrated in
Figure 6. The methods are applied to samples drawn from the joint distribution of
with no pre–processing. Our approach gives good results both in terms of centered confidence intervals and standard deviations. Hence the method is robust to this kind of heavy–tailed distributions. The KSG estimator gives bad results for smaller sample sizes (
) as the corresponding confidence intervals do not include the true value of MI. The “plain entropy” method seems to behave perfectly in this case.
Figure 6.
(Example 4) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
Figure 6.
(Example 4) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
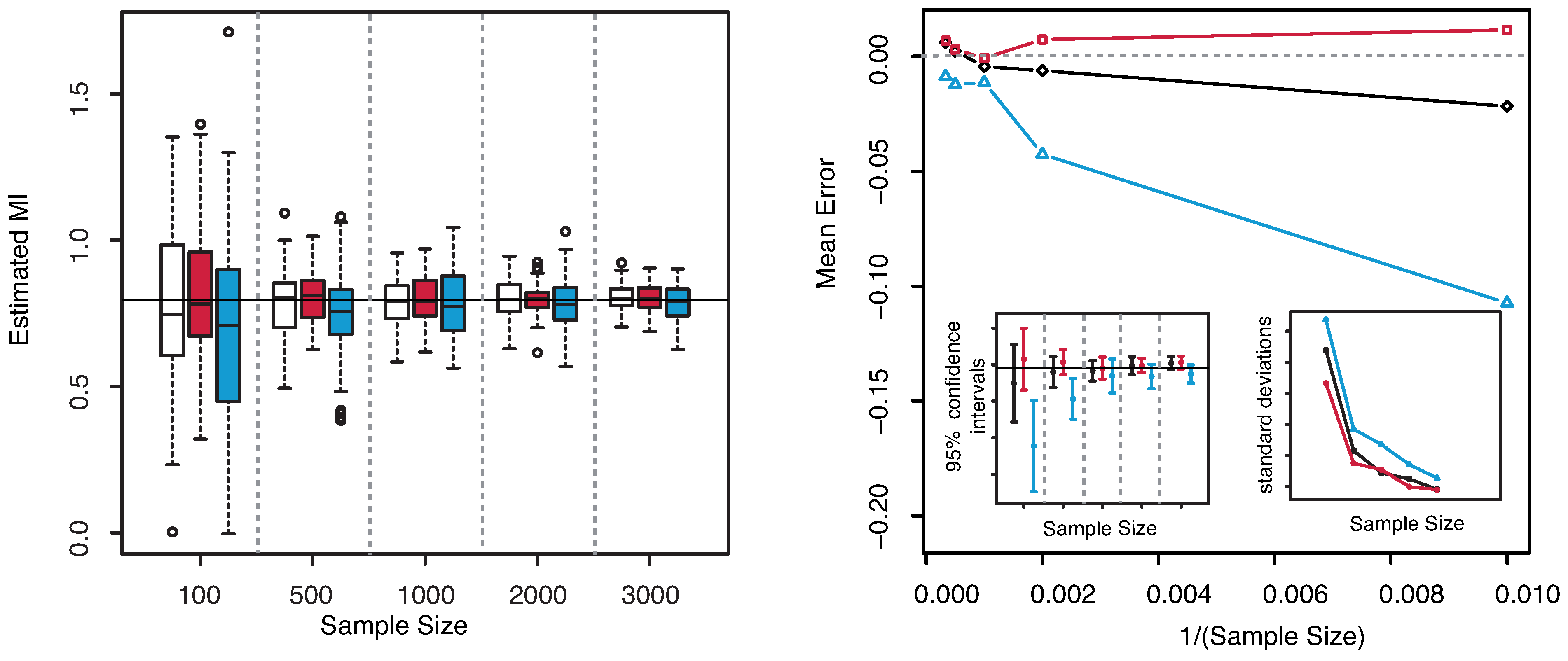
Example 5. Let
be a random vector with Levy distributed margins,
i.e., with p.d.f. given by
with
and
and coupled by the same copula function introduced in Equation (
40). Hence the mutual information is again
bit.
All the three methods fail in estimating MI in this case. The results are totally unreliable. The errors are very large even for larger sample sizes. Concerning our method the problem relies in the estimation of the density of the margins when the tail has strongly power law behavior. In this very ill–served example, the tails are so heavy that it is frequent to have values very far from those corresponding to the largest part of the probability mass and the kernel estimate is poor as it would need too many points. The kernel method fails and so the estimation of MI.
However we propose here to exploit the property of MI of being invariant under reparametrization of the margins. This trick allows to get rid of the heavy tail problems at least in some cases. For example, when the random variables are positive valued, we could apply a sufficiently good transformation of the values in order to improve the estimates. Such a transformation should be strictly monotone and differentiable and able to lighten and shorten the tails of the distribution, as the logarithm function. In
Figure 7 we illustrate the results obtained on samples drawn from the couple
with Levy margins and pre–processed applying a log–transformation to the values. Such a procedure will not affect the estimated value, as it can be seen in the figure. All the three methods now give correctly estimated values.
Figure 7.
(Example 5) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
Figure 7.
(Example 5) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
Hence the method is shown to be only partly robust to heavy–tailed distributions, as KSG and “plain entropy”. In particular it succeeds when applied to distributions with tail behavior as in the log–normal case and fails on strong power law tailed distributions as the Levy one. However, in the latter case, our proposal is to take advantage of the invariance property of MI and to pre–process data in order to reduce the importance of the tails. This comment holds good for any dimension , as the examples shown in the next section.
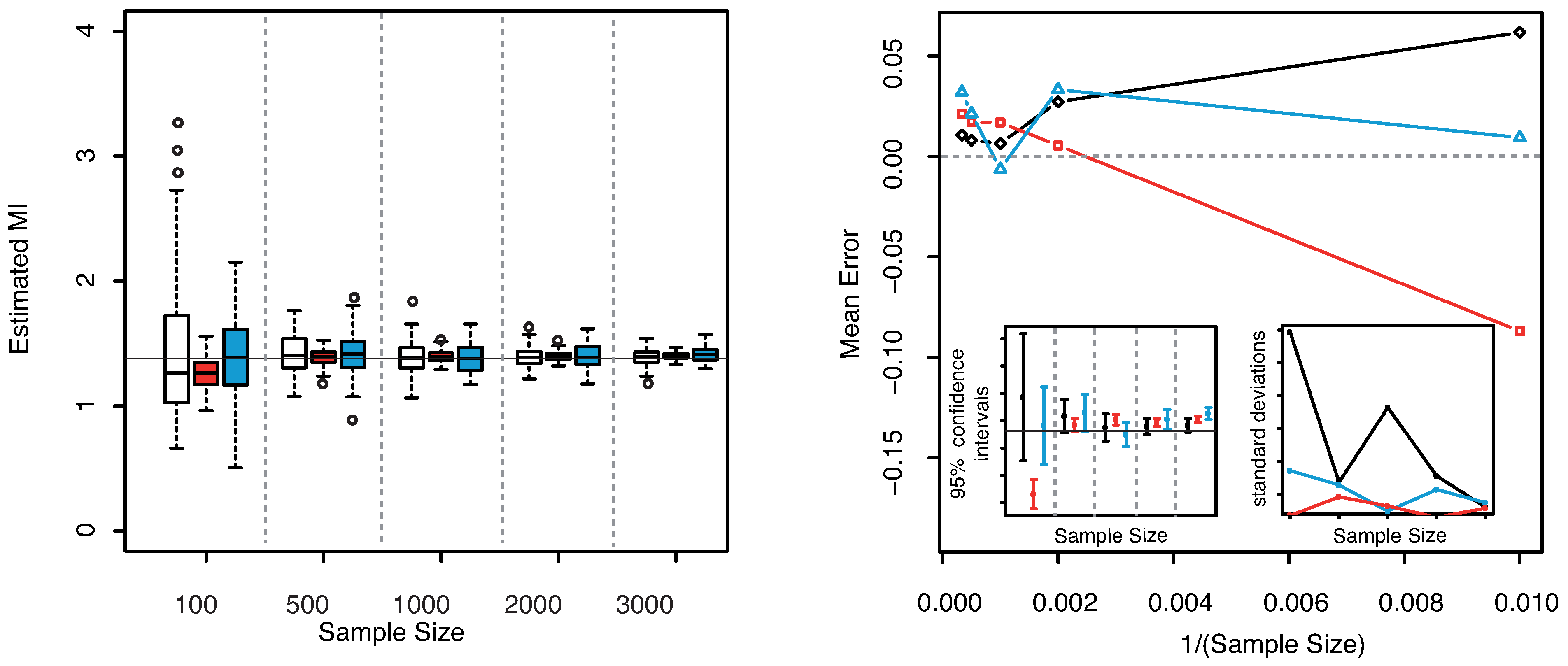
4.2. Three-Dimensional Vectors
We tested our estimator also in the case
, considering the multi–indices given in Equation (
31). Let
be a gaussian random vector with standard normal components and pair correlation coefficients
. The exact MI can be evaluated by means of the following equation
where
denotes the covariance matrix of the random vector
Y. In the specific case we get
bit.
In
Figure 8—left panel we show the boxplots of the estimated MI values as the sample size increases. From both plots the unbiasedness of the estimator even for small sample sizes can be clearly detected. Our estimator always leads to better results than the others both for unbiasedness and for the dispersion, cf.
Figure 8—right panel. Both the KSG and the “plain entropy” estimator do not center the exact value of the MI for the largest sample sizes (
and
), even though the standard deviations are comparable with the ones obtained with our method.
Figure 8.
(Gaussian
) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
Figure 8.
(Gaussian
) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
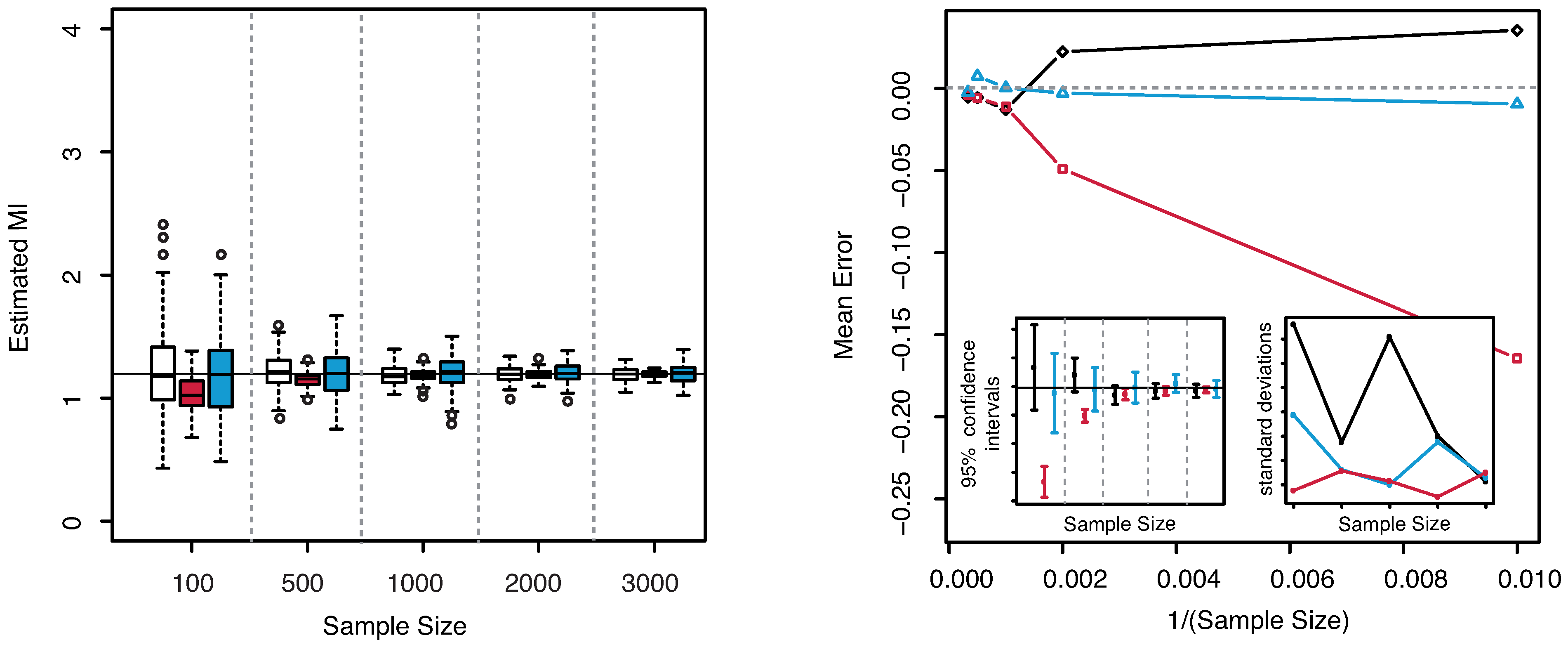
4.3. Four-Dimensional Vectors
For the case
we considered a multivariate Gaussian random vector with mean and covariance matrix given as
We chose the following multi–indices to group the components:
and
. The results are illustrated in
Figure 9. As already noticed for the three dimensional Gaussian case, the KSG and “plain entropy” estimators seems biased while the estimator here presented centers the true value for all the explored sample sizes.
Figure 9.
(Gaussian
) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.
Figure 9.
(Gaussian
) Left panel: Boxplots of the estimated MI grouped according to different sample sizes. Right panel: mean error as a function of
(Sample Size). Insets to the right panel: 95% confidence interval for the estimated MI (bottom left) and standard deviations (bottom right) versus Sample Size. Color map: black and white for the estimator we propose in
Section 3.2, red for KSG and blue for “plain entropy”.