1. Introduction
Wireless broadband has become an integral part of work, as well as daily life, because of the challenge of dealing with large amounts of Internet data. Although broadband access is very common on the land, maritime networks still need attention in this area. Due to their heterogeneous, low bandwidth and dynamic connectivity, maritime networks are difficult to manage [
1]. Nowadays, communication systems based on narrow ultra-high frequency band (UHF, 300MHz–3GHz) and very high frequency band (VHF, 30–300MHz) are used for close water ports’ ship-to-shore communication. On the other hand, satellite communication is used for long range ship-to-shore and ship-to-ship communication [
2]. Satellite links are very expensive for voice calls and Internet access, to and from the ship, when compared to land communication. Improvements in existing techniques, as well as new research, are required in order to reduce the cost of communication and provide high speed data rates at sea.
Using a dedicated spectrum in maritime networks is difficult, due to congested bandwidth allocation [
3]. The network devices on the shore may need to coexist with other radio devices installed on the land. Moreover, it is also necessary to synchronize the frequency bands around the world, as ships may travel between different countries and continents. Zhou
et al. showed that spectrum issues in maritime networks can be alleviated by incorporating cognitive radio (CR) technology [
3]. In this regard, they have also found that much of the spectrum is underutilized at sea. CR is a key technology that can help to mitigate the scarcity of the spectrum by using licensed spectrum bands opportunistically for unlicensed users. CR’s advantages associated with the opportunistic access of unused the licensed band are the alleviation of spectrum scarcity, the large bandwidth, long-range communication using TV band and reduced cost for communication.
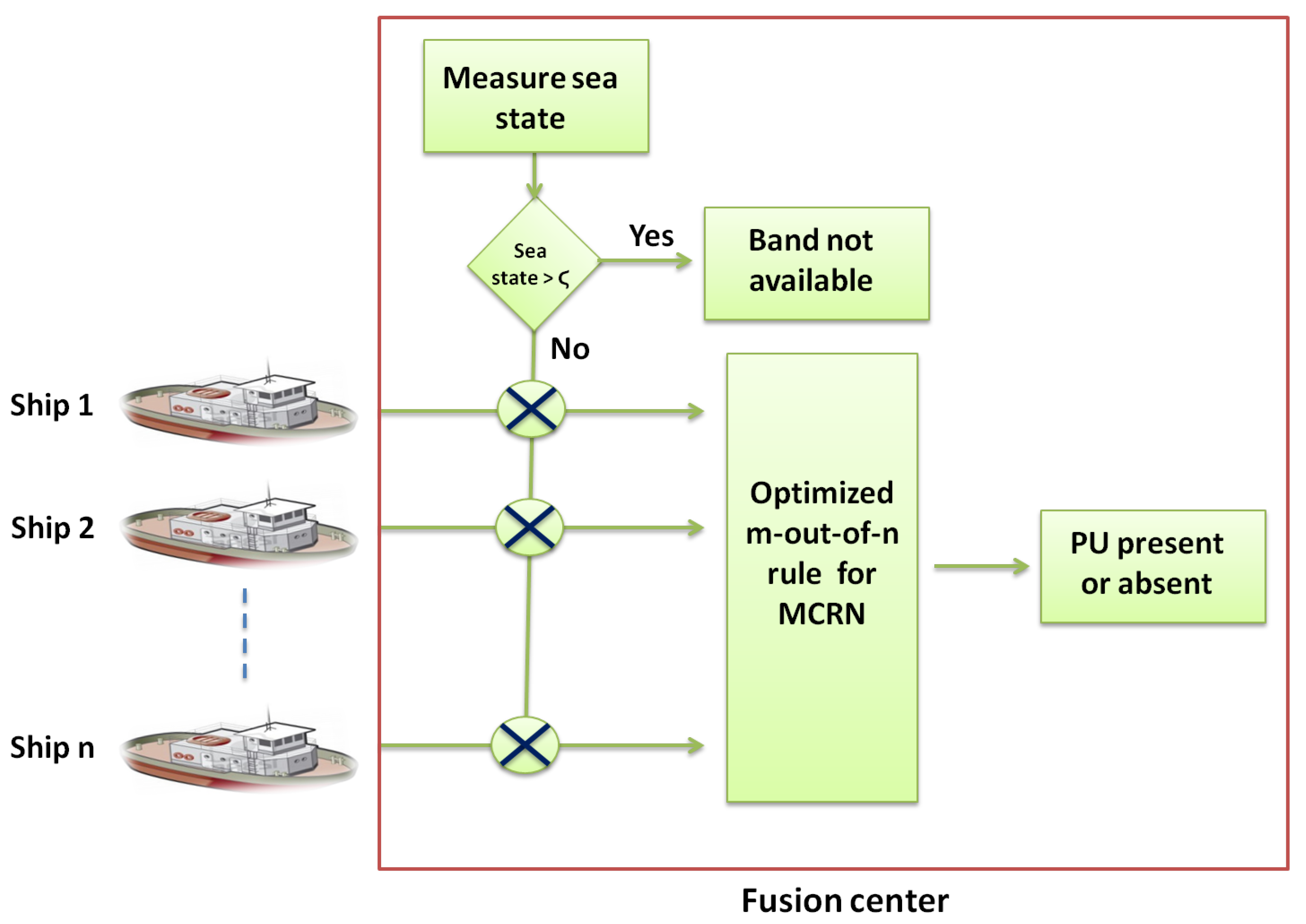
The most essential task for CR is the detection of the licensed/primary user (PU), which is achieved by sensing the radio environment. This process is called spectrum sensing. If the PU is absent, its spectrum is available for a cognitive radio/secondary user (SU) and is called the spectrum hole/white space. The spectrum sensing requirements for maritime cognitive radio networks (MCRN) have to face unique challenges in the sea environment because of the following reasons: (1) radio wave propagation over water; (2) surface reflection; and (3) wave occlusions. Therefore, to achieve a higher detection probability, CR may need a longer sensing time or some advances in the existing spectrum sensing schemes. In cooperative spectrum sensing, the local decision of multiple SUs is fused to get the final decision. Cooperative spectrum sensing seems to be an effective method to improve detection performance and to mitigate the impact of the unique challenges mentioned earlier.
Researchers have been focused on improving the sensing accuracy with minimum sensing time to avoid interference. The most renowned local spectrum sensing schemes are energy detection, entropy detector, matched filter and cyclostationary feature detection [
4]. There are many improved local sensing schemes [
5,
6] and advanced cooperative spectrum sensing schemes [
7,
8] proposed in the literature. However, none of them has been effective at overcoming the unique challenges associated with MCRN, which includes radio wave propagation over water, surface reflection and wave occlusions.
Entropy is the measure of uncertainty in random variables [
9]. Under a fixed-dimension probability space, the entropy of a signal is independent of noise power. Therefore, entropy-based detection can be used to cancel out the effect of noise uncertainty in MCRN. Entropy-based spectrum sensing can be used to counteract the unique challenges associated with the MCRN.
In this paper, we investigated entropy-based detection to counteract sea state effects. The path loss model for maritime communication during shadowing is considered, and the model is close to the real channel model. The optimal number of samples are found and used to calculate the entropy of the sensed signal as the measure of information of the received PU signal for the test statistic. We proposed a cooperative spectrum sensing scheme for MCRN, which considers the conditions of the sea environment and uses the entropy-based detector with the optimal number of samples as a local detector. The throughput optimization of the m-out-of-n rule is also considered with respect to the sea conditions. The optimal m and n are derived for the throughput optimization setup.
The rest of the paper is organized as follows. Related work is discussed in
Section 2, while
Section 3 gives a brief overview of maritime cognitive radio network and channel modeling. A system model, the optimization problem of a number of samples in the entropy-based detection scheme and centralized cooperative spectrum sensing are discussed in
Section 4 Section 5 demonstrates the simulation results, and finally, conclusions are drawn in
Section 6.
2. Related Work
The MCRN was first proposed by Zhou
et al. [
3]. The authors analyzed and presented the design requirements of the MCRN to enable cognitive operations and be suitable for the sea environment. Moreover, they investigated the possible available spectrum in the sea, the requirements that follow and the standards available. The challenges associated with MCRN, including movement on the sea surface and channel characterization, were addressed. A medium access control (MAC) protocol and a routing protocol were also presented to meet the challenges associated with MCRN.
In [
10], we presented performance analysis for spectrum sensing in MCRN. In which existing fusion rules for cooperative spectrum sensing were compared to highlight the need for a unique cooperative spectrum sensing scheme for MCRN. We investigated entropy-based spectrum sensing for local spectrum sensing in MCRN in [
11]. However, a cooperative spectrum sensing scheme that is unique to MCRN is not discussed in [
10,
11].
Recently, some new communication systems, particularly for maritime networks, have been proposed. In Singapore, WISE-PORT (Wireless-broadband-access for Seaport) provides IEEE802.16e-based wireless broadband access up to 5 Mbps, with a coverage distance of 15 km [
12]. However, it still requires improvements. The first digital VHF network with a data rate of 21 and 133 kbps with a coverage range of 130 km was developed in Norway [
13]. This system operates in the licensed VHF channel, which results in a narrow bandwidth and slow communication speed. To provide high speed and low cost ship-to-shore and ship-to-ship communication, the mesh/
ad hoc network based on IEEE 802.16d mesh technology was proposed in a project called TRITON [
14]. The authors developed a prototype that operates at 2.3 and 5.8 GHz.
Each ship is required to be capable of sensing the spectrum for MCRN. Moreover, the maritime environment has challenges, like the channel model, link quality, due to the sea movement, and so on. Television spectrum, cellular band and maritime spectrum holes are available at sea, which may range between tens of MHz to several GHz. Each ship in the MCRN needs to sense the spectrum according to its capability and change its operational frequency to achieve the best communication quality.
Currently, the main focus of research in spectrum sensing for cognitive radio is divided into two main streams: (i) improving local sensing; and (ii) enhancing cooperative spectrum sensing for better data fusion results. The major local sensing techniques considered for cognitive radios are energy detection, matched filter detection and cyclostationary detection. Energy detection is the simplest technique, which has a short sensing time, but its performance is comparatively poor under low signal-to-noise ratio (SNR) conditions. Matched filter detection is another simple technique, but it requires prior knowledge about the waveform of the PU. Cyclostationary detection provides reliable spectrum sensing, but it is computationally complex and requires a long sensing time [
4]. In cooperative spectrum sensing, all the local sensing observations made by SUs are reported to a fusion center, and a final decision about the presence or absence of the PU is conducted at the fusion center [
7]. Based on the final decision received by the fusion center, each SU reconfigures its operating parameters. Spectrum sensing must produce a high probability of detection and a low probability of false alarms to achieve better network performance.
The sea environment is divided into 10 different sea states, depending on the wave height, the average period of waves and the average wavelength of waves [
15]. The higher probability of detection can be achieved by a longer sensing time [
3]. Moreover, for relatively calm sea (e.g., sea state 3), the usual spectrum sensing schemes may be used. However, relatively advanced spectrum sensing schemes and cooperative fusion rules are required for higher sea states.
The idea of entropy-based spectrum sensing was proposed by Nagraj [
16], in which the information entropy is estimated from the output of a matched filter. The entropy of the received signal is reduced if it contains a modulated PU signal. However, it requires perfect knowledge of the PU waveform and synchronization.
The received signal is transformed in the frequency domain, and the spectrum magnitude is regarded as a random variable [
17]. The probability space is partitioned into fixed dimensions, and the Shannon entropy is calculated as an information measure of the received PU signal for test statistics. It is demonstrated that under a fixed-dimension probability space, the entropy is independent of noise power. The authors concluded that their proposed scheme has better performance and is more robust against noise uncertainty in comparison with energy detectors and cyclostationary detectors [
17].
Sabat
et al. proposed a spectrum sensing scheme based on the entropy estimation of the cyclostationary features of the received PU [
18]. To improve the spectrum sensing performance, the proposed scheme was extended to centralized spectrum sensing using soft and hard decision fusion rules. The results revealed that the proposed scheme outperforms the cyclostationary detection based on the spectral coherence function (SCF) and energy detection.
A spectral entropy-based PU detection scheme performs better than energy detection without any prior knowledge of the PU waveform [
19]. It is highlighted that the optimal threshold and the optimal number of samples should be studied for entropy-based spectrum sensing.
Zhang
et al. [
20] proposed a frequency-domain entropy-based spectrum sensing scheme for CR, which proved to be independently robust against noise uncertainty, as the entropy of noise is constant. It is concluded that the sensing time is reduced to about 75% in comparison with the energy detector under the same detection performance. Moreover, the results proved that the frequency-domain entropy-based detector outperforms the time-domain entropy-based detector.
All the existing entropy-based detectors do well under low SNR conditions, but none of them has considered sea state distribution. MCRNs should be intelligent enough to switch their operating parameters to suit the sea state, geographic location/region and communication range in order to achieve better throughput and quality of service (QoS). UHF is used in the USA for maritime navigation services, and therefore, it is important to protect the primary band. To achieve this, a high probability of detection and a low probability of false alarms are required for precise detection of PU and for efficient utilization of bandwidth, respectively.
5. Simulation Results
The simulation has been carried out to investigate the performance of spectrum sensing in the MCRN. The simulation consists of the sea wave movement model and the path loss model as discussed in
Section 3.1 and
Section 3.2. We assumed that there are fifteen SUs, and all of them experience additive white Gaussian noise (AWGN) with the same variance; the path loss depends on the radio environment during communication. Each SU uses the entropy-based detection scheme with the optimal number,
N, and the energy detector for its local observation having an average SNR
. We also assumed that SUs are unaware of relevant PU information, such as the position, moving direction and velocity.
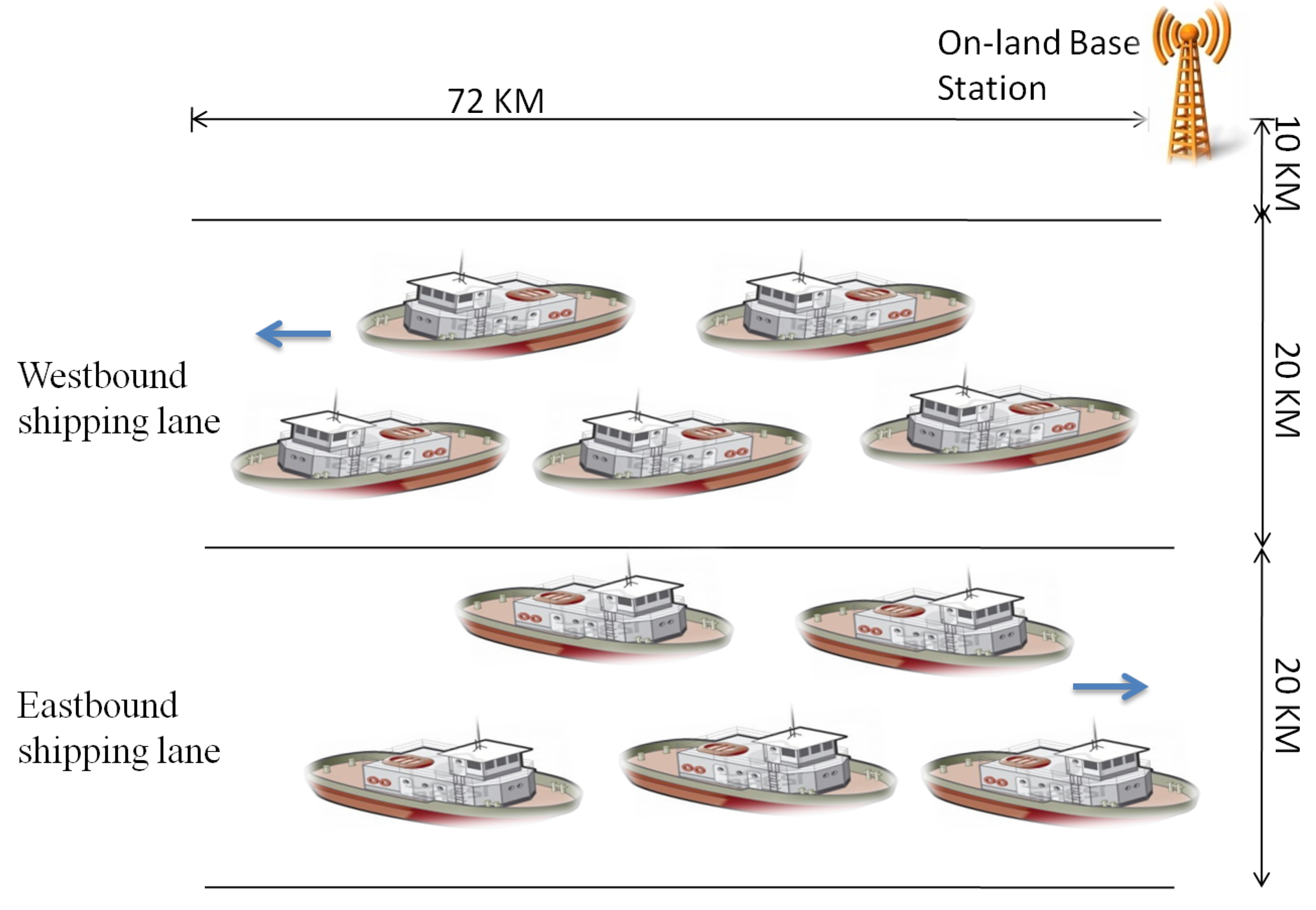
Figure 3.
A simulation model of the MCRN in a narrow navigation channel.
Figure 3.
A simulation model of the MCRN in a narrow navigation channel.
The network model considered for the simulations is a general maritime wireless network, as shown in
Figure 3. It covers a narrow navigation channel with the traffic separation scheme defined by the International Maritime Organization (IMO). The network consists of one westbound and one eastbound shipping lane in parallel, each with a width of
, and it has a land station, which acts as a central entity in cooperative spectrum sensing. A similar type of network model was also considered earlier for simulations [
3]. The sea states simulated in this paper are 4, 6 and 7, and
Table 1 shows the parameters that these three sea states have.
Table 1.
Parameters of sea states 4, 6 and 7.
Table 1.
Parameters of sea states 4, 6 and 7.
| 4 | 6 | 7 |
|---|
| 18 | 27 | 37 |
| | | |
| | | |
| 5 | | 10 |
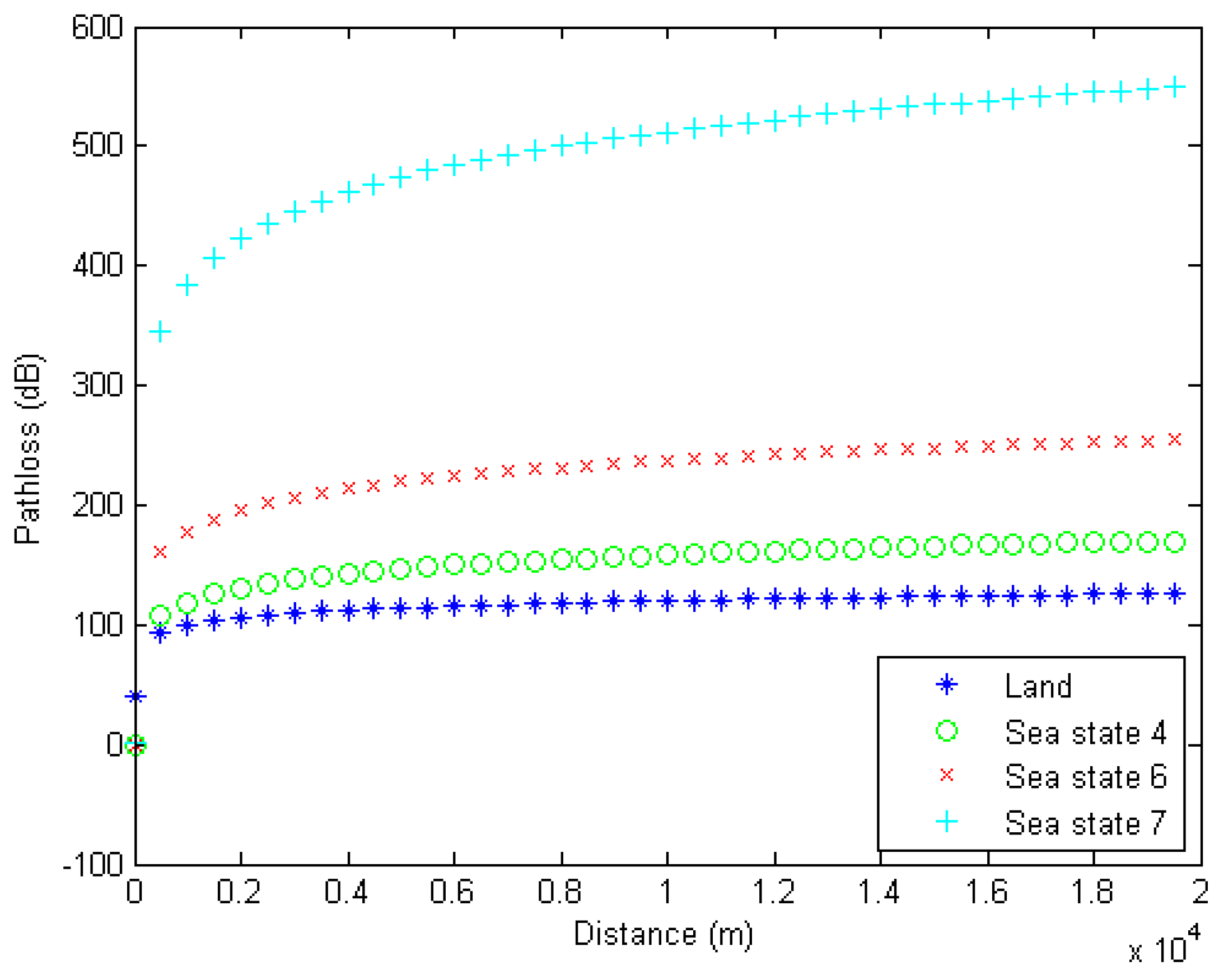
Figure 4 shows the path loss for
GHz for different radio environments, including land and sea environments. The sea states considered for measuring the path loss are 4, 6 and 7, for which wind speed, significant wave height, average wavelength and average wave period are given in
Table 1. The physical distance between the transmitter and the receiver varies from zero to 20 km, and its reference distance is 1 m. Results show that path loss in the maritime environment is comparable to one in the land environment up to sea state 4 (
Figure 4). Severe path loss is observed at sea states higher than 4. Path loss almost gets doubled at sea state 6 in comparison with sea state 4. For sea state 7, path loss is almost five-times as compared to either sea state 4 or the land environment. It becomes worse at higher sea states.
Figure 4.
Comparison of the path loss model on land and different sea states.
Figure 4.
Comparison of the path loss model on land and different sea states.
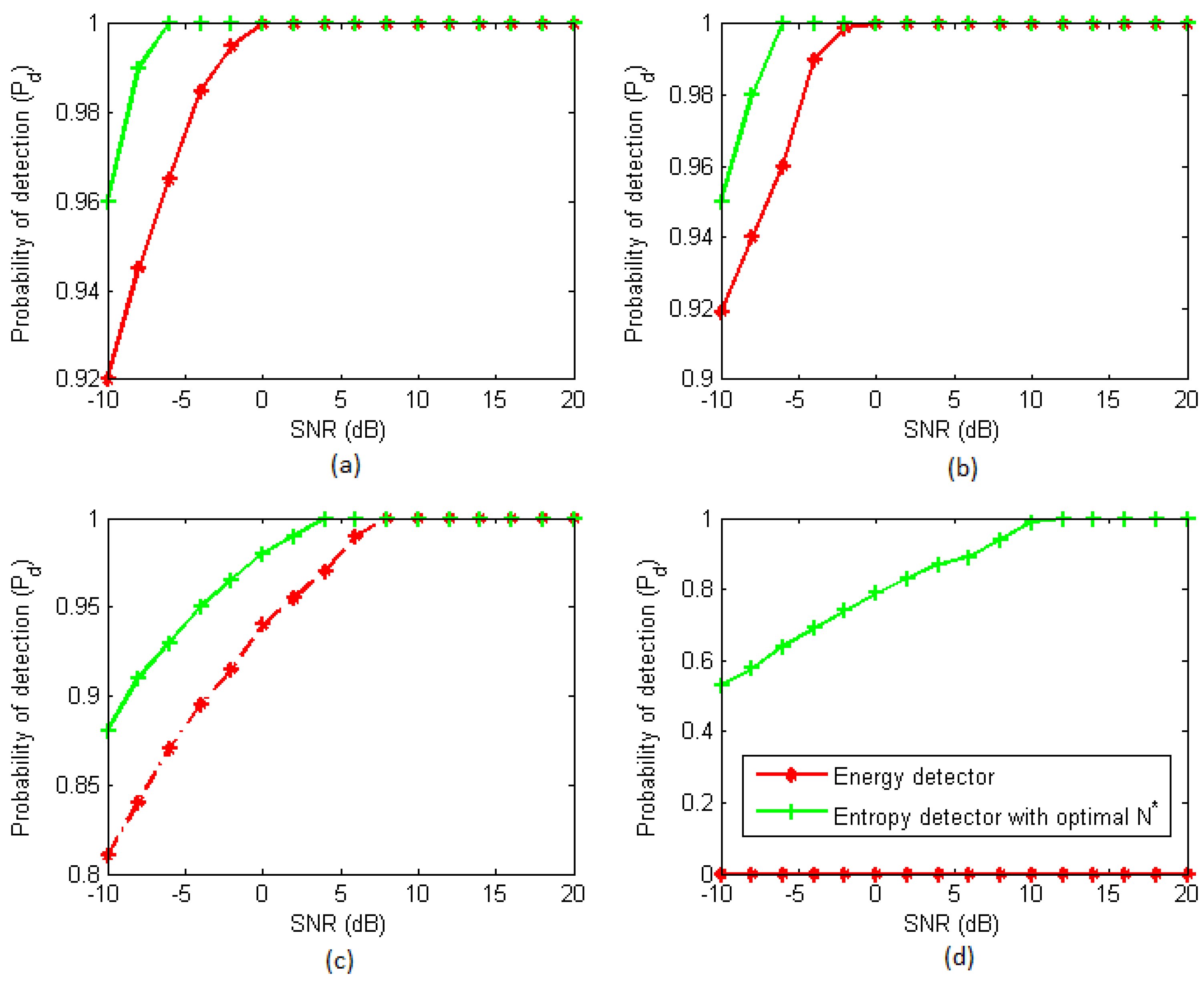
Figure 5.
The impact of the signal-to-noise ratio (SNR) on the probability of detecting: (a) the land network; (b) sea state 4; (c) sea state 6; and (d) sea state 7.
Figure 5.
The impact of the signal-to-noise ratio (SNR) on the probability of detecting: (a) the land network; (b) sea state 4; (c) sea state 6; and (d) sea state 7.
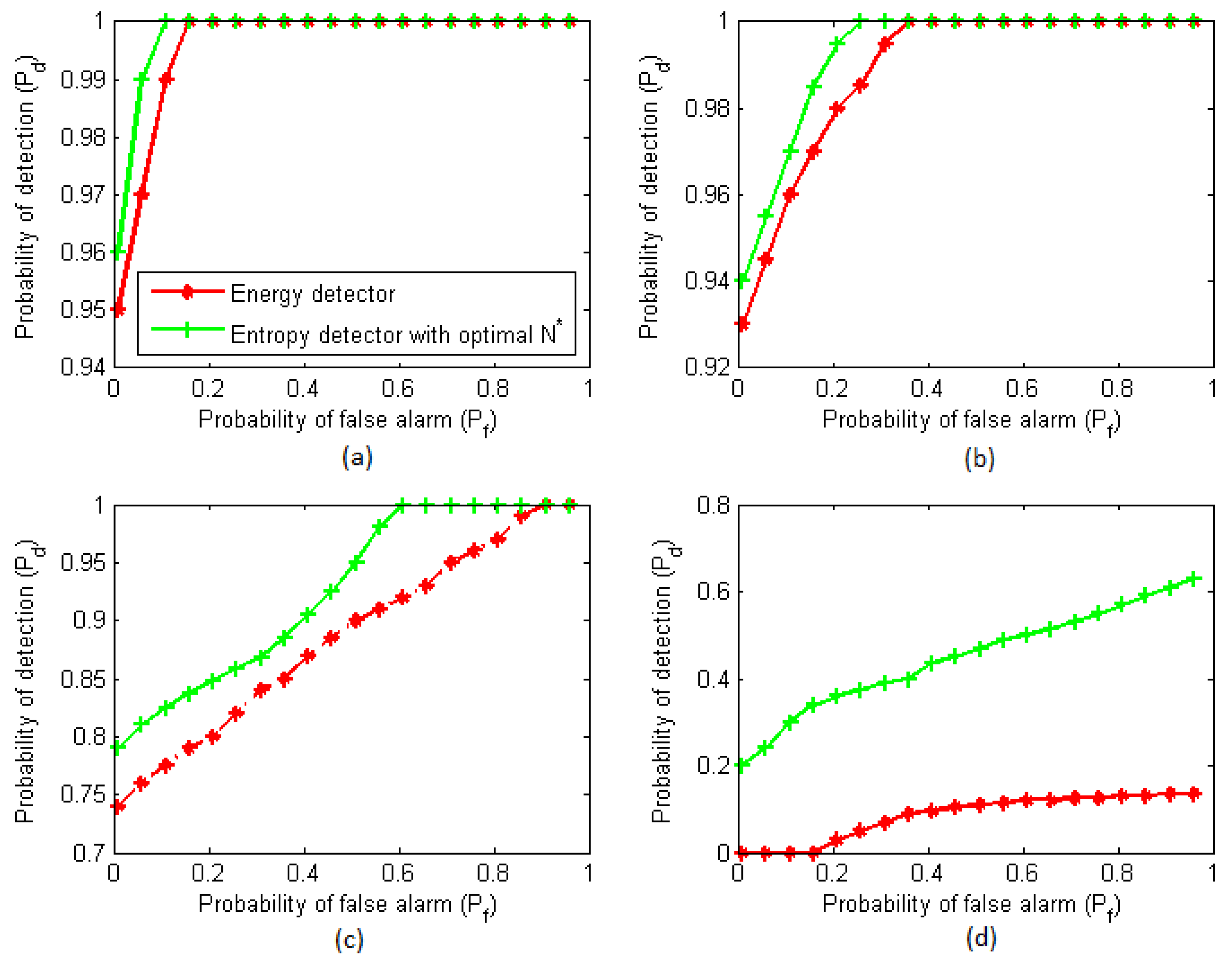
Figure 6.
Probability of detection vs. the probability of a false alarm at (a) the land network; (b) sea state 4; (c) sea state 6; and (d) sea state 7.
Figure 6.
Probability of detection vs. the probability of a false alarm at (a) the land network; (b) sea state 4; (c) sea state 6; and (d) sea state 7.
The probability of detection using energy detection and optimal entropy-based detection with the same number of samples was investigated to determine its sensitivity for detecting a PU’s presence for a range of SNR from –10 dB to 20 dB. According to the draft IEEE 802.22 standard [
26], the probability of a false alarm should be less than or equal to
. Therefore, the decision threshold,
, was set to maintain
.
Figure 5 (a) and (b) shows that the probabilities of detection at the land and sea state 4 are similar to each other, because both of them suffer almost the same path loss. In
Figure 5 (c), when the sea state is 6, the probability of detection in the case of the entropy-based detector is a little higher than the energy detection, even under low SNR conditions. However, for sea state 7, the probability of detection in the case of the energy detector is near zero over the entire range of SNR, because of severe path loss. However, the entropy-based detector can still detect the PU signal under good SNR conditions, as shown in
Figure 5 (d).
The practical interest of MCRN is to determine the relationship between
or
and
. Complementary receiver operation characteristic (ROC) curves can be obtained from the plot of
against
for a given average SNR and the time bandwidth product,
, with varying thresholds [
27]. The complementary ROC curves at the land, sea state 4, sea state 6 and sea state 7, when using the energy detector and entropy-based detector with the optimal number of samples,
, as local detectors, are shown in
Figure 6. Here, we assumed that the average SNR of SU is
dB. The result shows that the complementary ROC performance of the entropy-based detector with optimal
N is better than that of the energy detector in the above-mentioned four cases. However, for sea state 6 and higher, it cannot detect the primary user with a high probability under low
. Therefore, the cooperative spectrum sensing proposed in
Section 4.3 helps to achieve better detection performance for higher sea states.
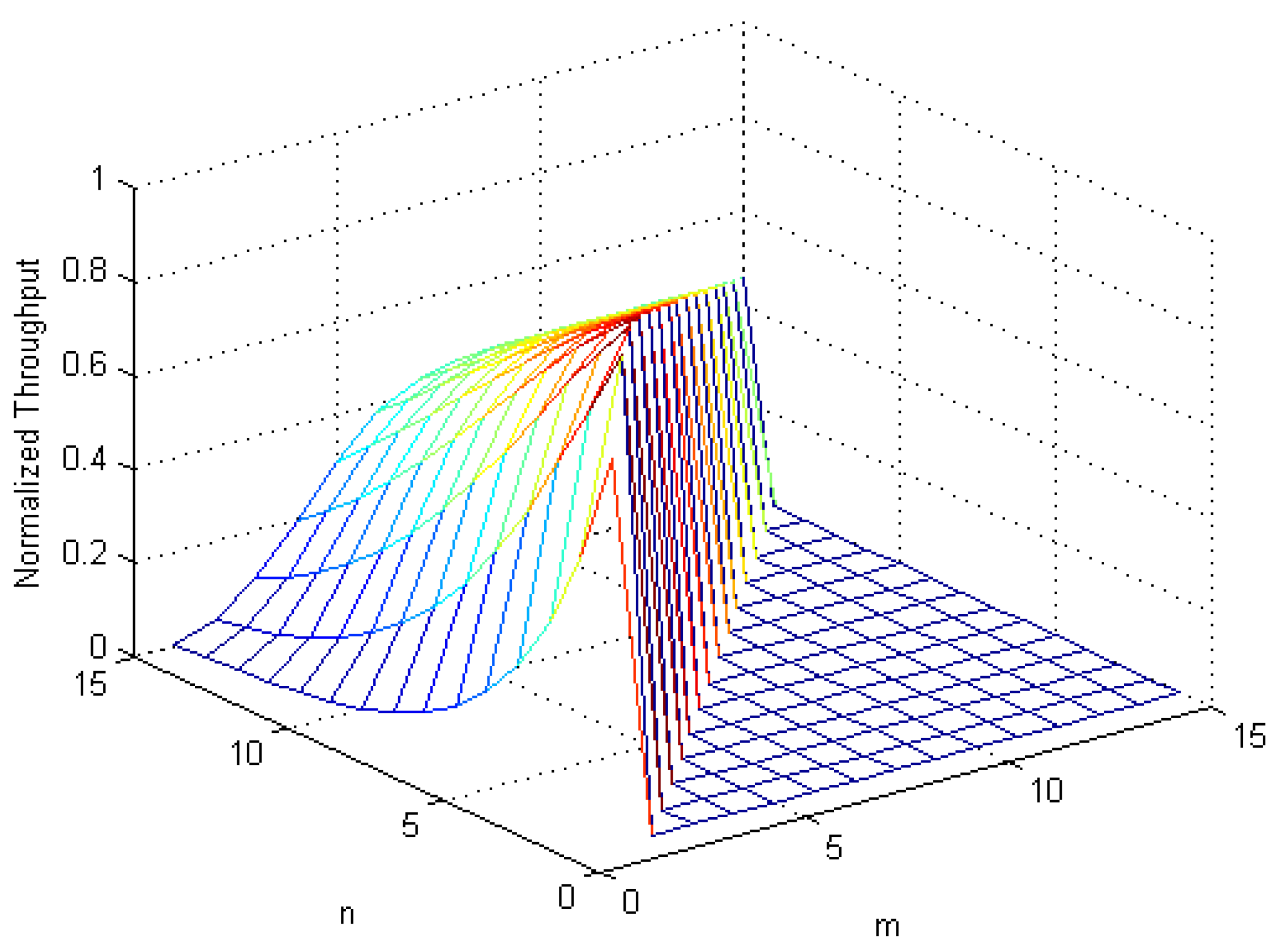
Figure 7.
Normalized throughput versus n and m.
Figure 7.
Normalized throughput versus n and m.
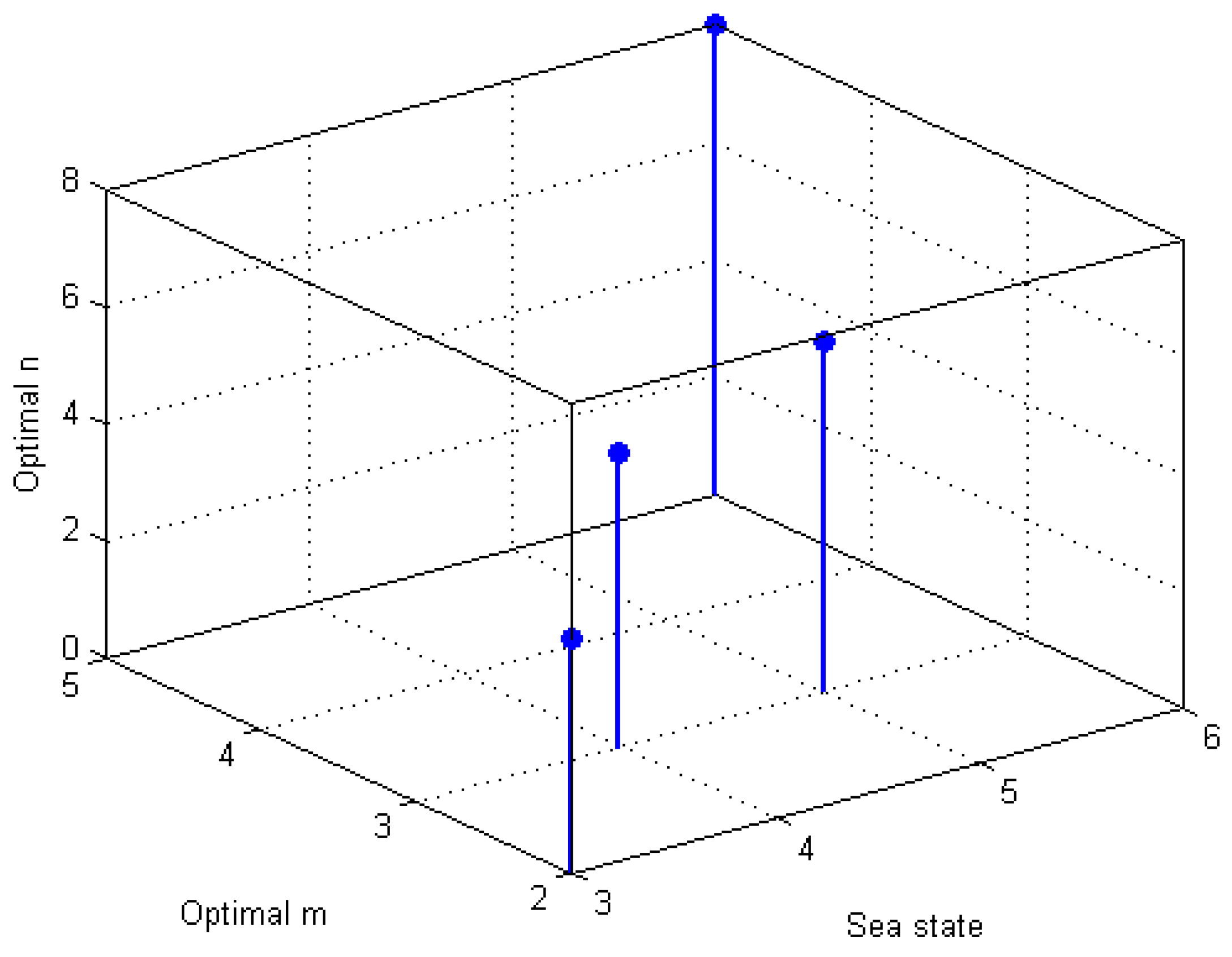
Figure 8.
Optimal n and m versus the sea state.
Figure 8.
Optimal n and m versus the sea state.
The normalized throughput
versus n and
m for the detection constraint equal to
is shown in
Figure 7. It is evident from the
Figure 7 that the choice of
m and
n has a huge impact on the throughput of MCRN. Moreover, there is a unique optimal point where the throughput of the MCRN is maximal.
The optimal
n and
m to maximize the achievable throughput
versus the sea state are shown in
Figure 8. For the simulations,
and
are taken as
and
, respectively. We found that for the different sea states, ranging from 3 to 6, majority rule is either optimal or near optimal.
The complementary ROC curves for the land, sea state 4 and sea state 6 for the optimized
m-out-of-
n rule (discussed in
Section 4.4), when using the energy detector and entropy-based detector with optimal
N as local detectors, are shown in
Figure 9. The proposed cooperative spectrum sensing scheme is used with the sea state threshold
. There are a total of fifteen SUs participating in cooperation, and the SNRs of the SUs vary from –10 dB to 10 dB. The distance from the PU varies from zero to 20 km for each SU randomly.
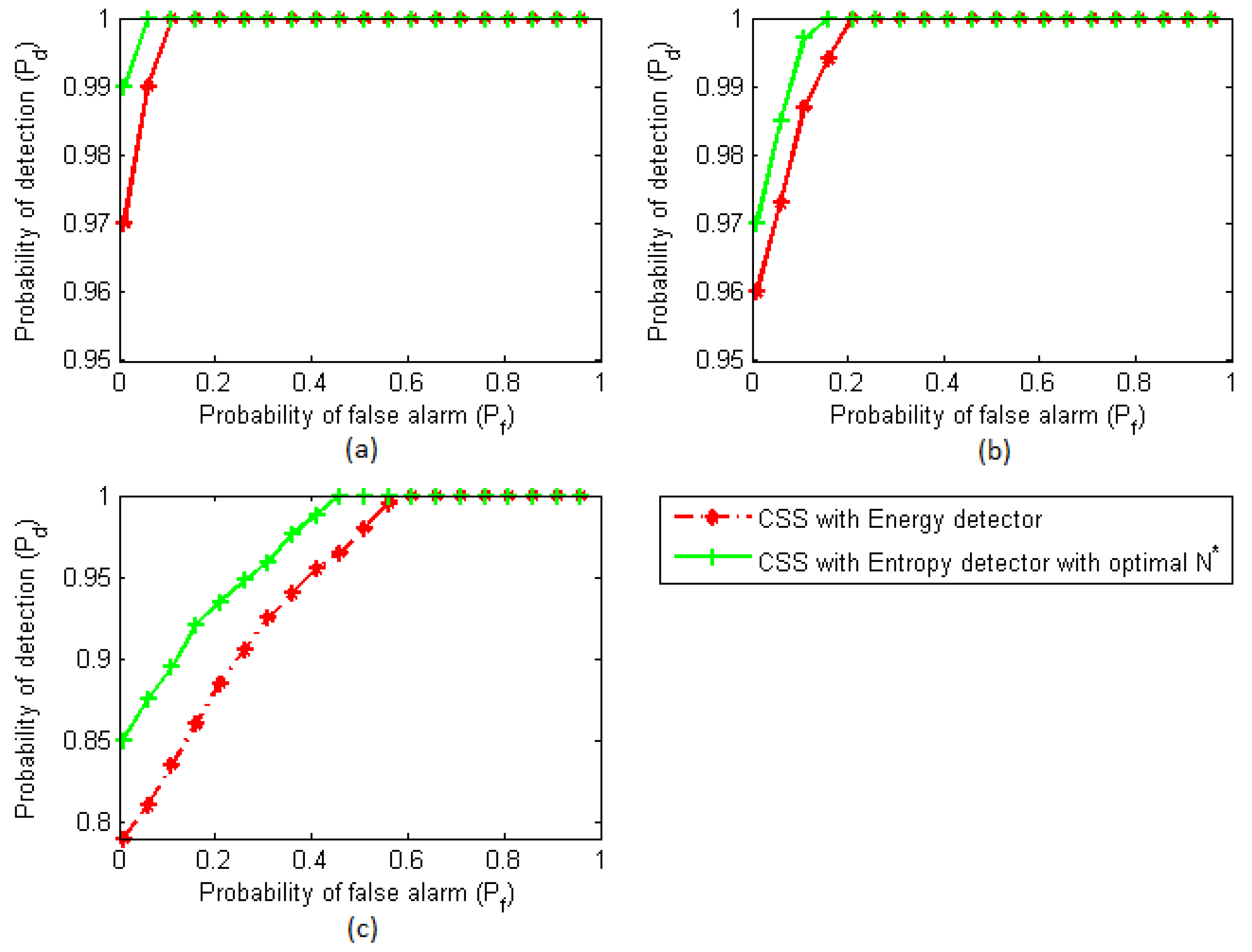
Figure 9(a) shows the ROC curves for the land environment in which the probability of detection is high for both the energy detector and entropy-based detector. Thus, our results indicated that both detectors with an optimized
m-out-of-
n fusion rule in cooperative spectrum sensing work reasonably well for the land environment.
Figure 9(b) shows the ROC for the sea environment having sea state 4. The probability of detection is still good in the case of the energy detection and entropy-based detector with the same number of samples as the local detector. The complementary ROC for sea state 6 is shown in
Figure 9(c). In the case of energy detection with the optimized
m-out-of-
n rule, the probability of detection for sea state 6 does not satisfy the requirement of IEEE 802.22, with the same number of samples as used for entropy-based detection. However, the entropy-based detector with the optimal number of samples,
, works reasonably well under sea state 6.
Figure 9.
Probability of detection vs. Probability of detection vs. the probability of a false alarm with 15 SUs participating in cooperative spectrum sensing at; (a) the land network; (b) sea state 4; and (c) sea state 6.
Figure 9.
Probability of detection vs. Probability of detection vs. the probability of a false alarm with 15 SUs participating in cooperative spectrum sensing at; (a) the land network; (b) sea state 4; and (c) sea state 6.
6. Conclusions
In this paper, we have proposed a cooperative spectrum sensing scheme, while considering the sea environment. The optimal number of samples for entropy-based detection for MCRN has been calculated. A cooperative spectrum sensing scheme has been proposed while considering the sea environment. In addition, throughput optimization of the m-out-of-n rule for MCRN has also been considered. Simulation results showed that the performance of the energy detector and entropy-based detector is almost same for the land environment. However, for sea states 4, 6 and 7, the entropy-based detector with the optimal number of samples, , performs better than the energy detector. In the case of cooperative spectrum sensing with the optimized m-out-of-n rule, the entropy-based detector and energy detector are used as local detection schemes. We showed further that for the desired range of sea states, the majority fusion rule is either optimal or near optimal in terms of the throughput of the MCRN.
For sea state 7 and higher, although the entropy-based detector could detect PUs with a high probability in comparison with the energy detector, still, the constraints of the probability of detection and false alarms are not satisfied. One way to improve the sensing performance at higher sea states is to design a new advanced signal processing algorithm in order to detect a distorted signal. An advanced algorithm, like cyclostationary feature detection, needs a relatively long time for sensing in comparison with the energy detector and entropy-based detector.
The advanced sensing algorithms should be investigated in the future for efficient spectrum sensing in the MCRN. Moreover, the multi-path effect, due to the reflections of the signal on the sea surface, is also a good direction to be considered in the future.