Applications of Entropy in Finance: A Review
Abstract
:1. Introduction
2. Concepts of Entropy Used in Finance
2.1. The Shannon Entropy
2.2. The Tsallis Entropy
2.3. The Kullback Cross-entropy
2.4. The Tsallis Relative Entropy
2.5. The Fuzzy Entropy
2.6. Other Kinds of Entropy
2.7. Generalised Entropy
3. Principles of Entropy Used in Finance
3.1. Jaynes’ Maximum Entropy Principle
- (1)
- has the maximum uncertainty; or
- (2)
- is least committed to the information not given to us; or
- (3)
- is most random; or
- (4)
- is most unbiased (any deviation from the maximum entropy results in a bias).
3.2. Kullback’s Minimum Cross-Entropy Principle
4. Applications of Entropy in Portfolio Selection
4.1. Entropy as a Measure of Risk
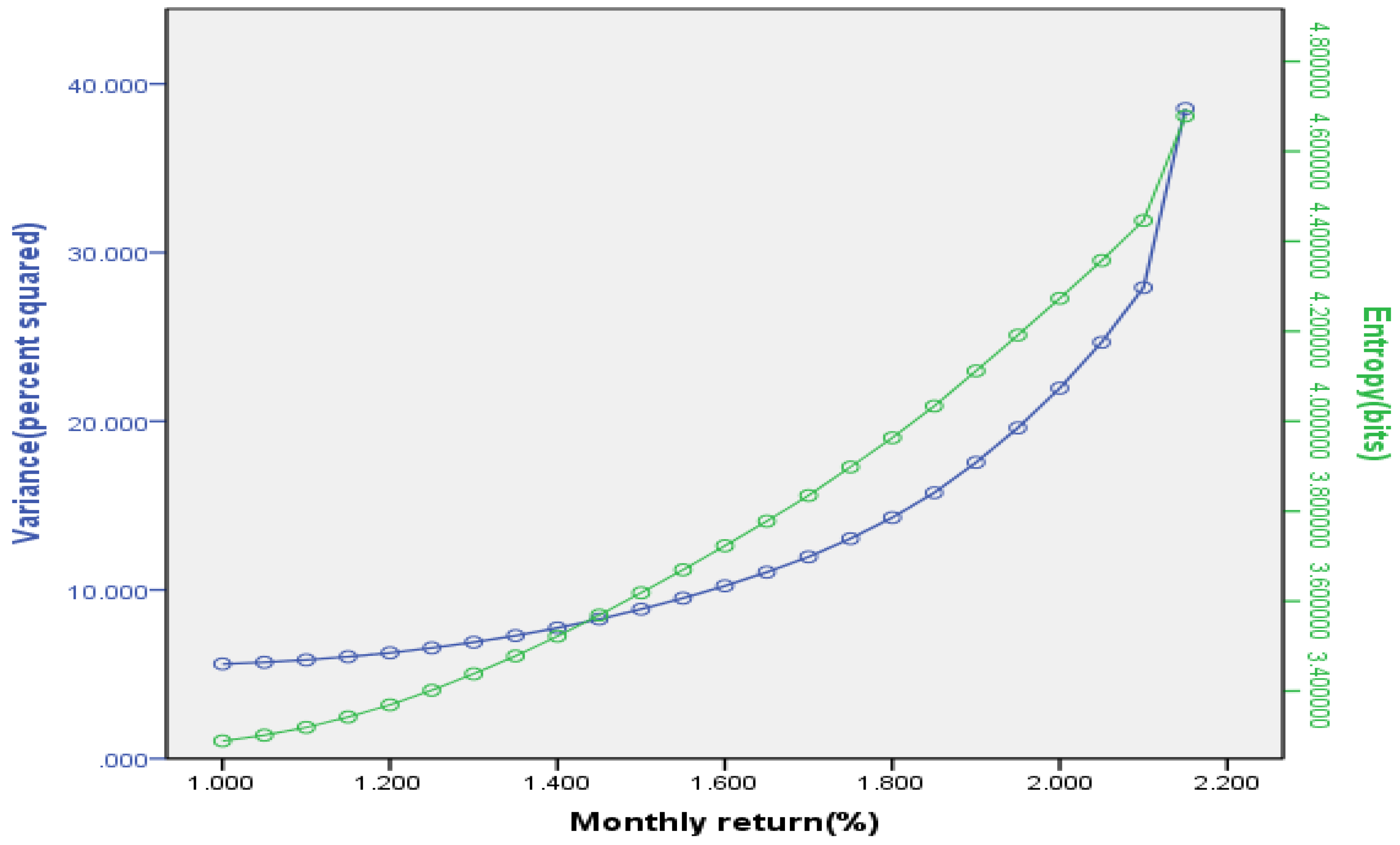
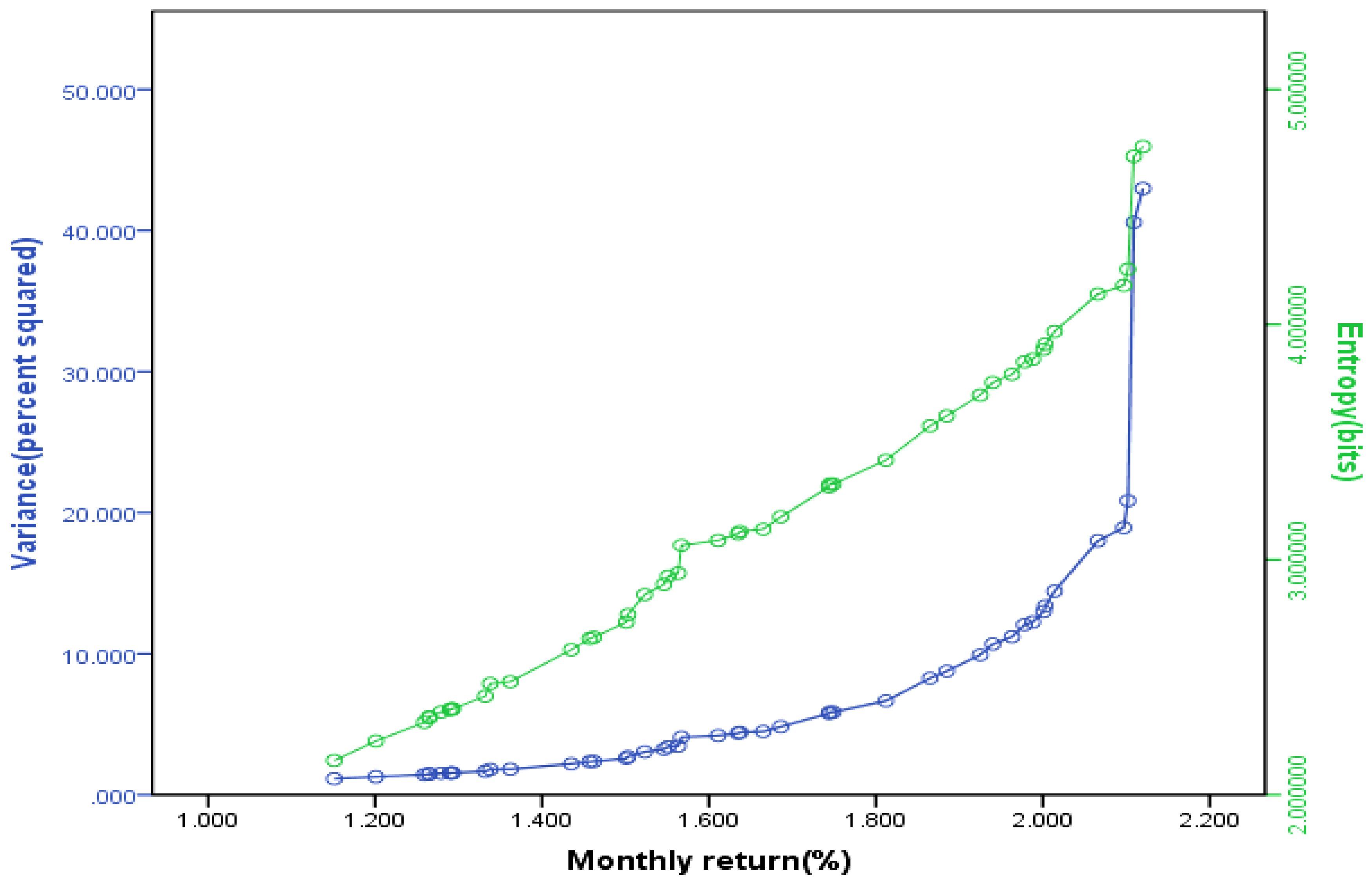
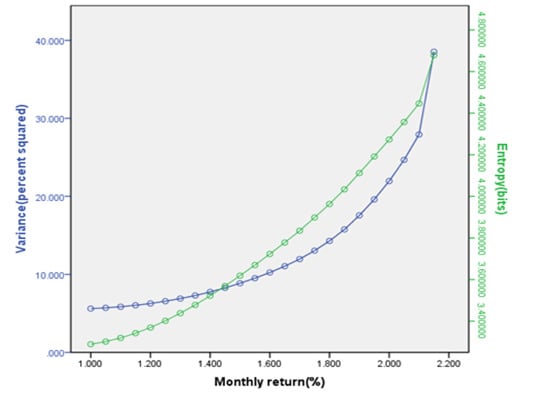
4.2. Entropy as a Measure of Capital Increment
4.3. Entropy as a Measure of Portfolio Diversification
5. Applications of Entropy in Asset Pricing
5.1. Entropy in Option Pricing
5.2. Entropy in Other Derivative Securities Pricing
6. Applications of Entropy in Other Fields of Finance
- (1)
- The process ε(L)q is a supermartingale;
- (2)
- There exists a predictable increasing process h(q) such that h0(q) = 0 andis a martingale.
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Laidler, K.J. Thermodynamics. In The World of Physical Chemistry; Oxford University Press: New York, NY, USA, 1995; pp. 156–240. [Google Scholar]
- Clausius, R. Ueber verschiedene für die Anwendung bequeme formen der Hauptgleichungen der mechanischen Wärmetheorie. Ann. Phys. Chem. 1865, 125, 53–400. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.J.; Wang, D.H. Understanding atmospheric behaviour in terms of entropy: a review of applications of the second law of thermodynamics to meteorology. Entropy 2011, 13, 211–240. [Google Scholar] [CrossRef]
- Brissaud, J.B. The meanings of entropy. Entropy 2005, 7, 68–96. [Google Scholar] [CrossRef]
- Philippatos, G.C.; Wilson, C.J. Entropy, market risk, and the selection of efficient portfolios. Appl. Econ. 1972, 4, 209–220. [Google Scholar] [CrossRef]
- Ou, J.S. Theory of portfolio and risk based on incremental entropy. J. Risk Finance 2005, 6, 31–39. [Google Scholar] [CrossRef]
- Xu, J.P.; Zhou, X.Y.; Wu, D.D. Portfolio selection using λ mean and hybrid entropy. Ann. Oper. Res. 2011, 185, 213–229. [Google Scholar] [CrossRef]
- Usta, I.; Kantar, Y.M. Mean-variance-skewness-entropy measures: a multi-objective approach for portfolio selection. Entropy 2011, 13, 117–133. [Google Scholar] [CrossRef]
- Jana, P.; Roy, T.K.; Mazumder, S.K. Multi-objective possibilistic model for portfolio selection with transaction cost. J. Comput. Appl. Math. 2009, 228, 188–196. [Google Scholar] [CrossRef]
- Zhang, W.G.; Liu, Y.J.; Xu, W.J. A possibilistic mean-semivariance-entropy model for multi-period portfolio selection with transaction costs. Eur. J. Oper. Res. 2012, 222, 341–349. [Google Scholar] [CrossRef]
- Zhou, R.X.; Wang, X.G.; Dong, X.F.; Zong, Z. Portfolio selection model with the measures of information entropy-incremental entropy-skewness. Adv. Inf. Sci. Service Sci. 2013, 5, 853–864. [Google Scholar]
- Smimoua, K.; Bector, C.R.; Jacoby, G. A subjective assessment of approximate probabilities with a portfolio application. Res. Int. Bus. Finance 2007, 21, 134–160. [Google Scholar] [CrossRef]
- Huang, X.X. Mean-entropy models for fuzzy portfolio selection. IEEE Tran. Fuzzy Syst. 2008, 16, 1096–1101. [Google Scholar] [CrossRef]
- Rödder, W.; Gartner, I.R.; Rudolph, S. An entropy-driven expert system shell applied to portfolio selection. Expert Syst. Appl. 2010, 37, 7509–7520. [Google Scholar] [CrossRef]
- Gulko, L. Dart boards and asset prices introducing the entropy pricing theory. Adv. Econom. 1997, 12, 237–276. [Google Scholar]
- Gulko, L. The entropy theory of stock option pricing. Int. J. Theoretical Appl. Finance 1999, 2, 331–355. [Google Scholar] [CrossRef]
- Gulko, L. The entropy theory of bond option pricing. Int. J. Theoretical Appl. Finance 2002, 5, 355–383. [Google Scholar] [CrossRef]
- Buchen, P.W.; Kelly, M. The maximum entropy distribution of an asset inferred from option prices. J. Financ. Quant. Anal. 1996, 31, 143–159. [Google Scholar] [CrossRef]
- Neri, C.; Schneider, L. Maximum entropy distributions inferred from option portfolios on an asset. Finance Stochast. 2012, 16, 293–318. [Google Scholar] [CrossRef]
- Krishnan, H.; Nelken, L. Estimating implied correlations for currency basket options using the maximum entropy method. Derivatives Use Trading Regul. 2001, 7, 1–7. [Google Scholar]
- Rompolis, L.S. Retrieving risk neutral densities from European option prices based on the principle of maximum entropy. J. Empir. Finance 2010, 17, 918–937. [Google Scholar] [CrossRef]
- Guo, W.Y. Maximum entropy in option pricing: a convex-spline smoothing method. J. Futures Markets 2001, 21, 819–832. [Google Scholar] [CrossRef]
- Borwein, J.; Choksi, R.; Maréchal, P. Probability distributions of assets inferred from option prices via the principle of maximum entropy. J. Soc. Ind. Appl. Math. 2003, 14, 464–478. [Google Scholar] [CrossRef]
- Stutzer, M. A simple nonparametric approach to derivative security valuation. J. Finance 1996, 51, 1633–1652. [Google Scholar] [CrossRef]
- Hawkins, R.J. Maximum entropy and derivative securities. Adv. Econometrics 1997, 12, 277–300. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Frittelli, M. The minimal entropy martingale measure and the valuation problem in incomplete markets. Math. Finance 2000, 10, 39–52. [Google Scholar] [CrossRef]
- Benth, F.E.; Groth, M. The minimal entropy martingale measure and numerical option pricing for the Barndorff-Nielsen-Shephard stochastic volatility model. Stoch. Anal. Appl. 2009, 27, 875–896. [Google Scholar] [CrossRef]
- Hunt, J.; Devolder, P. Semi-Markov regime switching interest rate models and minimal entropy measure. Phys. A 2011, 390, 3767–3781. [Google Scholar] [CrossRef]
- Grandits, P. The p-optimal martingale measure and its asymptotic relation with the minimal entropy martingale measure. Bernoulli 1999, 5, 225–247. [Google Scholar] [CrossRef]
- Branger, N. Pricing derivative securities using cross-entropy an economic analysis. Int. J. Theor. Appl. Finance 2004, 7, 63–81. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Havrda, J.; Charvát, F. Quantification method of classification processes: concept of structural α-entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Patil, G.P.; Taillie, C. Diversity as a concept and its measurement. J. Am. Stat. Assoc. 1982, 77, 548–561. [Google Scholar] [CrossRef]
- Tsallis, C. Generalized entropy-based criterion for consistent testing. Phys. Rev. E 1998, 58, 1442–1445. [Google Scholar] [CrossRef]
- Luca, A.D.; Termini, S. A definition of non-probabilistic entropy in the setting of fuzzy sets theory. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Bhandari, D.; Pal, N.R. Some new information measures for fuzzy sets. Inf. Sci. 1993, 67, 209–228. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy entropy and conditioning. Inf. Sci. 1986, 40, 165–174. [Google Scholar] [CrossRef]
- Pal, N.R.; Bezdek, J.C. Measuring fuzzy uncertainty. IEEE Trans. Fuzzy Syst. 1994, 2, 107–118. [Google Scholar] [CrossRef]
- Yager, R.R. On the entropy of fuzzy measures. IEEE Trans. Fuzzy Syst. 2000, 8, 453–461. [Google Scholar] [CrossRef]
- Li, X.; Liu, B. Maximum entropy principle for fuzzy variable. Int. J. Uncertain. Fuzz. 2007, 15, 43–52. [Google Scholar] [CrossRef]
- Li, P.; Liu, B. Entropy and credibility distributions for fuzzy variables. IEEE Trans. Fuzzy Syst. 2008, 16, 123–129. [Google Scholar]
- Brody, D.C.; Buckley, I.R.C.; Constantinou, I.C. Option price calibration from Rényi entropy. Phys. Lett. 2007, 366, 298–307. [Google Scholar] [CrossRef]
- Liese, F.; Vajda, I. On divergences and informations in statistics and information theory. IEEE Trans. Inform. Theor. 2006, 52, 4394–4412. [Google Scholar] [CrossRef]
- Balestrino, A.; Caiti, A.; Crisostomi, E. Generalised entropy of curves for the analysis and classification of dynamical systems. Entropy 2009, 11, 249–270. [Google Scholar] [CrossRef]
- Csiszár, I. Eine Informationstheoretische Ungleichung und ihre Anwendung auf den Beweis der Ergodizität on Markoffschen Ketten. Publ. Math. Inst. Hungar. Acad. Sci. 1963, 8, 84–108. [Google Scholar]
- Ali, M.S.; Silvey, D. A general class of coefficients of divergence of one distribution from another. J. Roy. Stat. Soc. B 1966, 28, 131–140. [Google Scholar]
- Kapur, J.N.; Kesavan, H.K. Jaynes’ Maximum Entropy Principle. In Entropy Optimization Principles with Applications; Academic Press: San Diego, CA, USA, 1992; pp. 23–151. [Google Scholar]
- Markowitz, H. Portfolio selection. J. Finance 1952, 7, 77–91. [Google Scholar]
- White, D.J. Entropy, market risk and the selection of efficient portfolios: comment. Appl. Econ. 1974, 6, 73–75. [Google Scholar] [CrossRef]
- Philippatos, G.C.; Wilson, C.J. Entropy, market risk and the selection of efficient portfolios: reply. Appl. Econ. 1974, 6, 77–81. [Google Scholar] [CrossRef]
- Hoskisson, R.E.; Hitt, M.A.; Johnson, R.H.; Moesel, D. Construct validity of an objective (entropy) categorical measure of diversification strategy. Strat. Manag. J. 2006, 14, 215–235. [Google Scholar] [CrossRef]
- Dionísio, A.; Menezes, R.; Mendes, D.A. Uncertainty Analysis in Financial Markets: Can Entropy be a Solution? In Proceedings of the 10th Annual Workshop on Economic Heterogeneous Interacting Agents, University of Essex, Colchester, UK, 13 June 2005.
- Philippatos, G.C.; Gressis, N. Conditions of equivalence among E-V, SSD and E-H portfolio selection criteria: The case for uniform, normal and lognormal distributions. Manag. Sci. 1975, 21, 617–625. [Google Scholar] [CrossRef]
- Bera, A.K.; Park, S.Y. Optimal Portfolio Diversification Using the Maximum Entropy Principle. In Proceedings of the Second Conference on Recent Developments in the Theory, Method, and Applications of Information and Entropy Econometrics, Washington DC, WA, USA, 23 September 2009.
- Usta, I.; Kantar, Y.M. Analysis of Multi-objective Portfolio Models for the Istanbul Stock Exchange. In Proceedings of the 2nd International Workshop on Computational and Financial Econometrics, Neuchatel, Switzerland, 19 June 2008.
- Jana, P.; Roy, T.K.; Mazumder, S.K. Multi-objective mean-variance-skewness model for portfolio optimization. Appl. Math. Optim. 2007, 9, 181–193. [Google Scholar]
- Samanta, B.; Roy, T.K. Multi-objective portfolio optimization model. Tamsui Oxf. J. Math. Sci. 2005, 21, 55–70. [Google Scholar]
- Bera, A.K.; Park, S.Y. Optimal portfolio diversification using the maximum entropy principle. Economet. Rev. 2008, 27, 484–512. [Google Scholar] [CrossRef]
- Kapur, J.N. Maximum-Entropy Probability Distributions: Principles, Formalism and Techniques. In Maximum Entropy models in Science and Engineering; Wiley Eastern Limited: New Delhi, India, 1990; pp. 1–146. [Google Scholar]
- Csiszár, I. I-divergence geometry of probability distributions and minimization problems. Ann. Probab. 1975, 3, 146–158. [Google Scholar] [CrossRef]
- Zhou, R.X.; Chen, L.M.; Qiu, W.H. The entropy model of American bond option pricing. Math. Pract. Theor. 2006, 36, 59–64. [Google Scholar]
- Zhou, R.X.; Sun, J.; Xu, J.R. Valuation of interest rate options based on the entropy pricing method under incomplete market. J. Beijing Univ. C.T. 2008, 35, 101–103. [Google Scholar]
- Zhou, R.X.; Wang, X.G. Study of hedging parameters based on the entropy model of stock option pricing. J. Beijing Univ. C. T. 2009, 36, 100–104. [Google Scholar]
- Trivellato, B. The minimal k-entropy martingale measure. Int. J. Theor. Appl. Finance 2012, 15, 1–22. [Google Scholar] [CrossRef]
- Trivellato, B. Deformed exponentials and applications to finance. Entropy 2013, 15, 3471–3489. [Google Scholar] [CrossRef]
- Kaniadakis, G. Non-linear kinetics underlying generalized statistics. Phys. A 2001, 296, 405–425. [Google Scholar] [CrossRef]
- Kaniadakis, G. H-theorem and generalized entropies within the framework of nonlinear kinetics. Phys. Lett. A 2001, 288, 283–291. [Google Scholar] [CrossRef]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. Phys. Rev. E 2002, 66, 056125. [Google Scholar] [CrossRef]
- Kaniadakis, G.; Scarfone, A.M. Lesche stability of kappa-entropy. Phys. Stat. Mech. Appl. 2004, 340, 102–109. [Google Scholar] [CrossRef]
- Choulli, T.; Hurd, T.R. The role of Hellinger Processes in mathematical finance. Entropy 2001, 3, 150–161. [Google Scholar] [CrossRef]
- Hackworth, J.F. Uncertainty and the yield curve. Econ. Lett. 2008, 98, 259–268. [Google Scholar] [CrossRef]
- Zhou, R.X.; Xiong, M.H. Treasury Risk Measurement and Empirical Comparison-based on Information Entropy. In Proceedings of World Automation Congress, Puerto Vallarta, Jalisco, Mexico, 24 June 2012.
- Candeal, J.C.; De Miguel, J.R.; Indur, A.E. Utility and entropy. Econ. Theor. 2001, 17, 233–238. [Google Scholar] [CrossRef]
- Abbas, A.E. Entropy methods for adaptive utility elicitation. IEEE Trans on Systems 2004, 34, 169–178. [Google Scholar] [CrossRef]
- Abbas, A.E. Maximum entropy utility. Oper. Res. 2006, 54, 277–290. [Google Scholar] [CrossRef]
- Yang, J.P.; Qiu, W.H. A measure of risk and a decision making model based on expected utility and entropy. Eur. J. Oper. Res. 2005, 164, 792–799. [Google Scholar] [CrossRef]
- Zhou, R.X.; Liu, S.C.; Qiu, W.H. Survey of applications of entropy in decision analysis. Control Decis. 2008, 23, 361–371. [Google Scholar]
- Li, J.S. Pricing longevity risk with the parametric bootstrap: A maximum entropy approach. Insur. Math. Econ. 2010, 47, 176–186. [Google Scholar] [CrossRef]
- Mistrulli, P.E. Assessing financial contagion in the interbank market: Maximum entropy versus observed interbank lending patterns. J. Bank. Finance 2011, 35, 1114–1127. [Google Scholar] [CrossRef]
- Ortiz-Cruz, A.; Rodriguez, E.; Ibarra-Valdez, C.; Alvarez-Ramirez, J. Efficiency of crude oil markets: Evidences from informational entropy analysis. Energ. Pol. 2012, 41, 365–373. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhou, R.; Cai, R.; Tong, G. Applications of Entropy in Finance: A Review. Entropy 2013, 15, 4909-4931. https://doi.org/10.3390/e15114909
Zhou R, Cai R, Tong G. Applications of Entropy in Finance: A Review. Entropy. 2013; 15(11):4909-4931. https://doi.org/10.3390/e15114909
Chicago/Turabian StyleZhou, Rongxi, Ru Cai, and Guanqun Tong. 2013. "Applications of Entropy in Finance: A Review" Entropy 15, no. 11: 4909-4931. https://doi.org/10.3390/e15114909
APA StyleZhou, R., Cai, R., & Tong, G. (2013). Applications of Entropy in Finance: A Review. Entropy, 15(11), 4909-4931. https://doi.org/10.3390/e15114909