Synchronization of a Novel Hyperchaotic Complex-Variable System Based on Finite-Time Stability Theory
Abstract
:1. Introduction
2. Basic Conception of Finite-Time Stability Theory and System Description
3. Finite-Time Synchronization of a Novel Hyperchaotic Complex-Variable System
4. Numerical Simulations
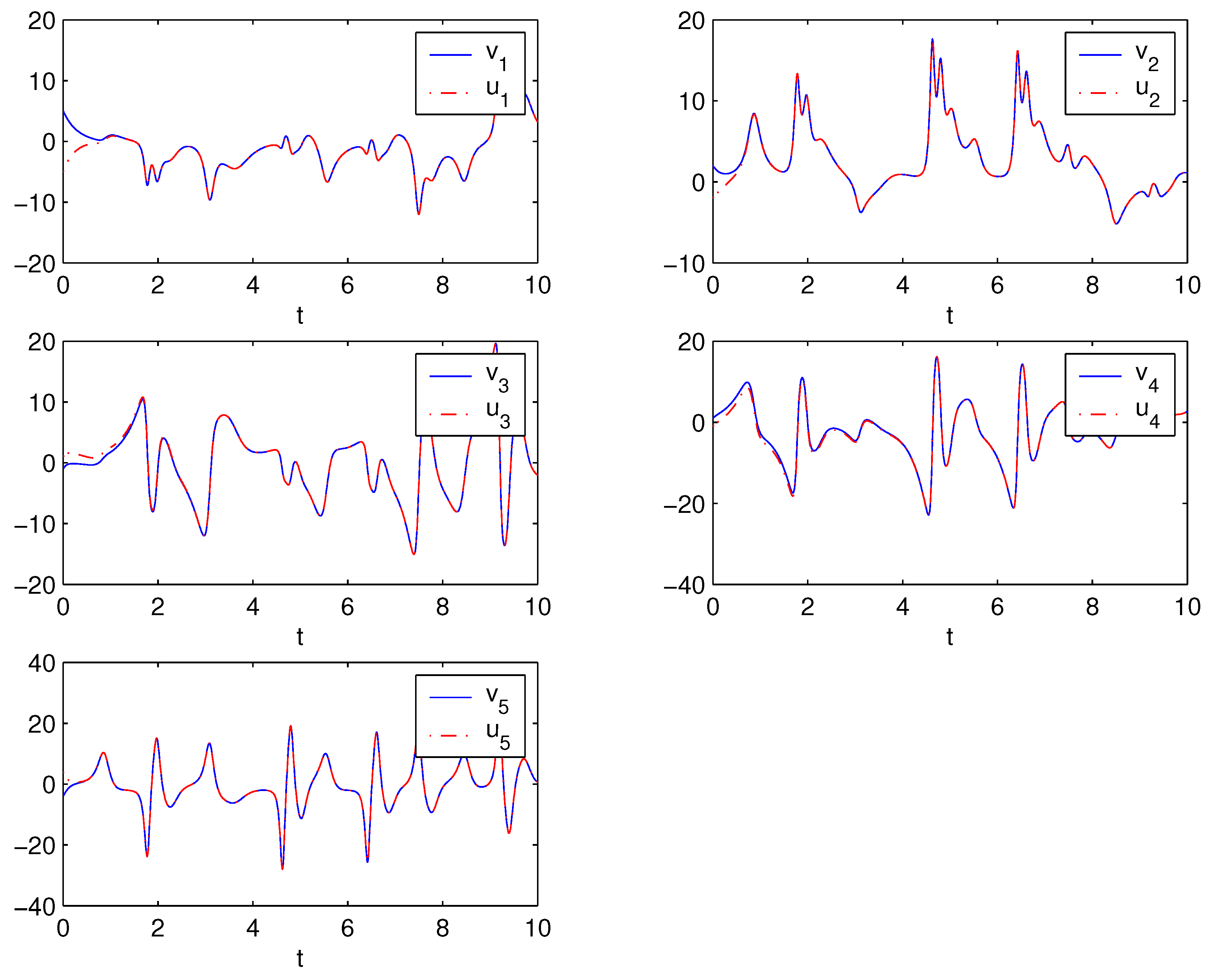
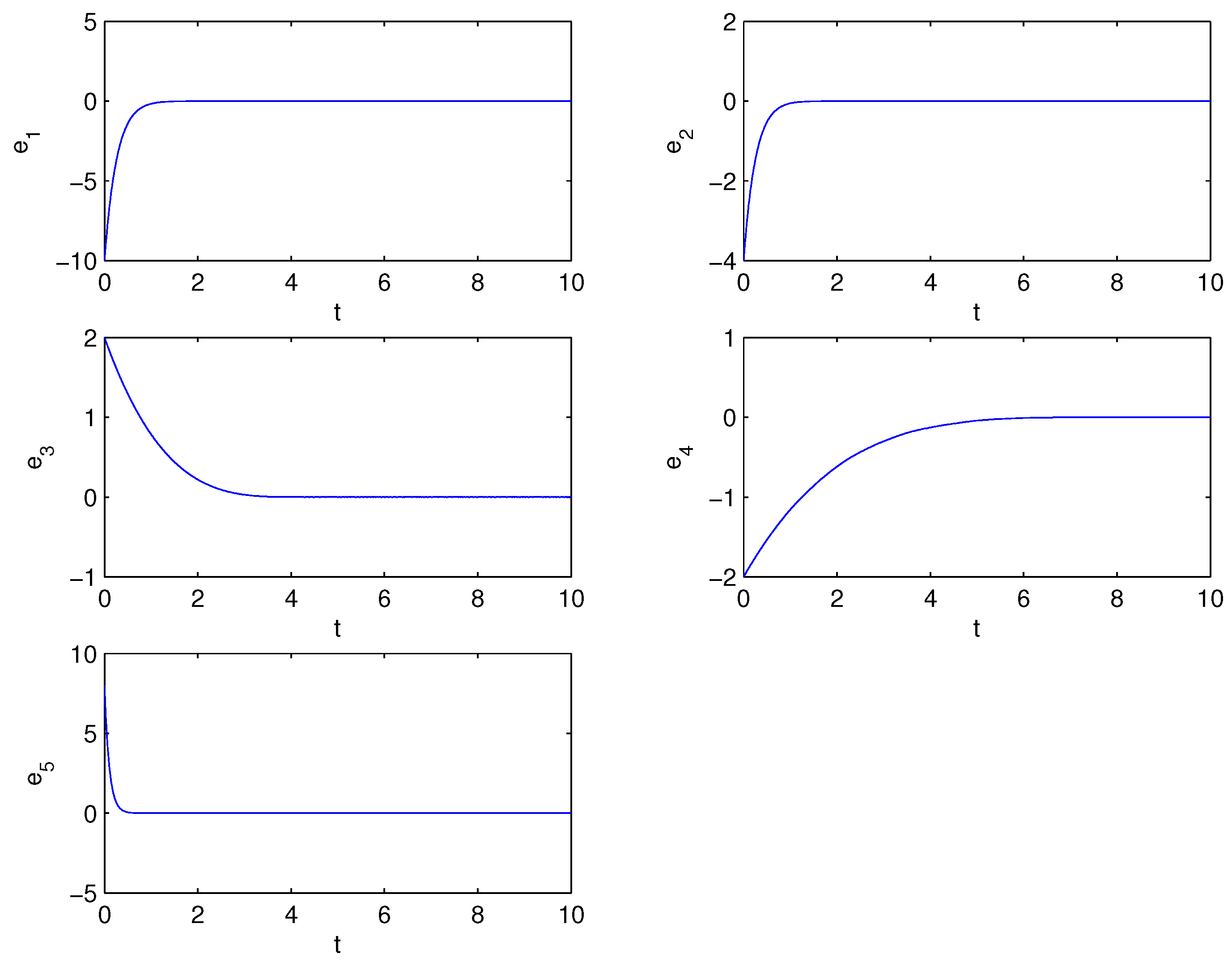
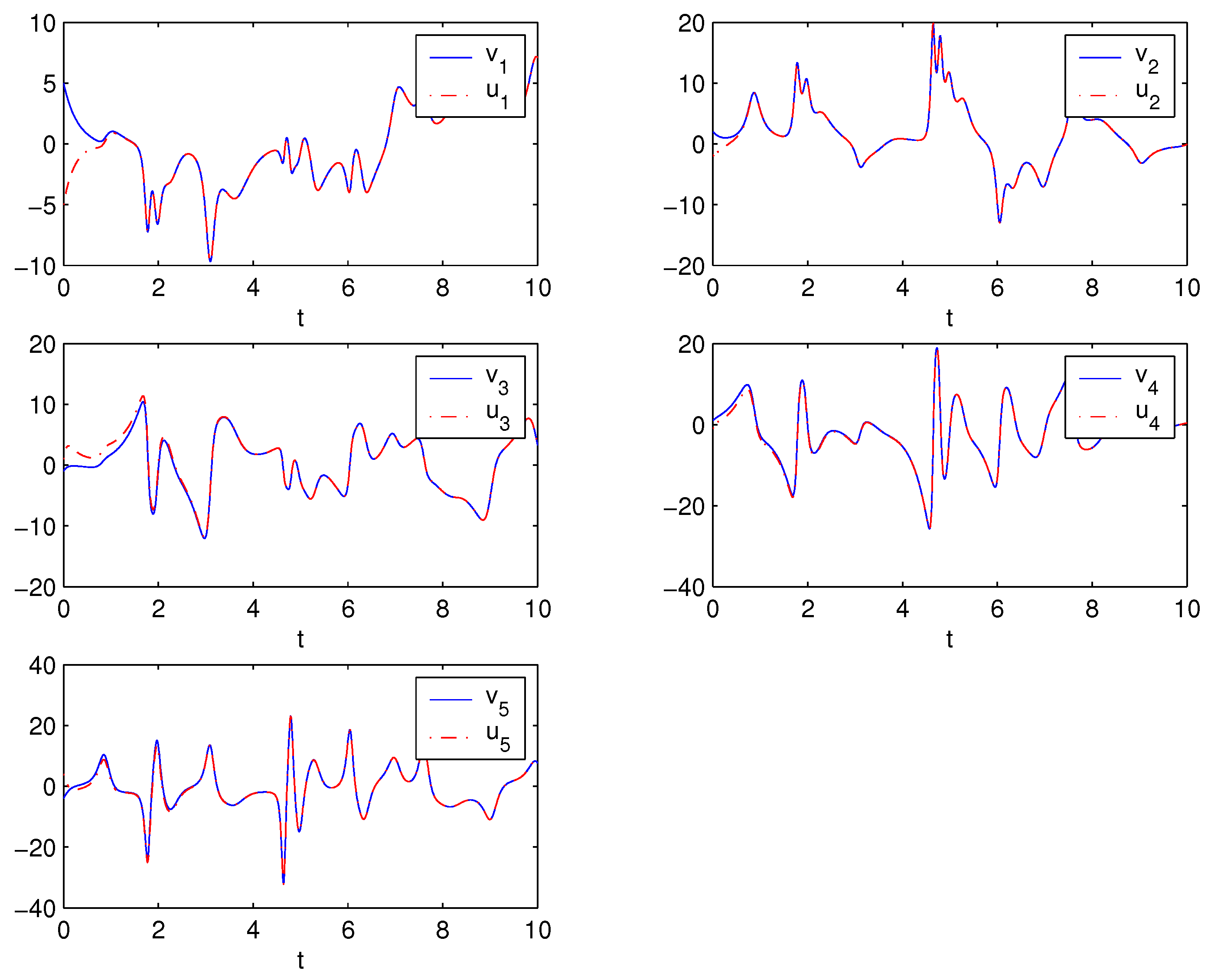

5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Rössler, O.E. An equation for hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar] [CrossRef]
- Matsumoto, T.; Chua, L.O.; Kobayashi, K. Hyperchaos: Laboratory experiment and numerical confirmation. IEEE Trans. Circuits Syst. 1986, 33, 1143–1149. [Google Scholar] [CrossRef]
- Grassi, G.; Mascolo, S. A system theory approach for designing cryptosystems based on hyperchaos. IEEE Trans. Circuits Syst. I 1999, 46, 1135–1138. [Google Scholar] [CrossRef]
- Yin, H.; Chen, Z.; Yuan, Z. A blind watermarking algorithm based on hyperchaos and coset by quantizing wavelet transform coefficients. Int. J. Innov. Comput. Inf. Control 2007, 3, 1635–1643. [Google Scholar]
- Zhu, C.X. A novel image encryption scheme based on improved hyperchaotic sequences. Opt. Commun. 2012, 285, 29–37. [Google Scholar] [CrossRef]
- Fowler, A.C.; Gibbon, J.D.; McGuinness, M.J. The complex Lorenz equations. Physica D 1982, 4, 139–163. [Google Scholar] [CrossRef]
- Ning, C.Z.; Haken, H. Detuned lasers and the complex Lorenz equations: Subcritical and supercritical Hopf bifurcations. Phys. Rev. A 1990, 41, 3826–3837. [Google Scholar] [CrossRef] [PubMed]
- Gibbon, J.D.; McGuinness, M.J. The real and complex Lorenz equations in rotating fluids and lasers. Physica D 1983, 5, 108–122. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Bountis, T.; Mahmoud, E.E. Active control and global synchronization of the complex Chen and Lü systems. Int. J. Bifurc. Chaos 2007, 17, 4295–4308. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Bountis, T.; Al-Kashif, M.A.; Aly, S.A. Dynamical properties and synchronization of complex non-linear equations for detuned lasers. Dyn. Syst. 2009, 24, 63–79. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Ahmed, M.E.; Sabor, N. On autonomous and nonautonomous modified hyperchaotic complex Lü systems. Int. J. Bifurc. Chaos 2011, 21, 1913–1926. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Ahmed, M.E. A hyperchaotic complex system generating two-, three-, and four-scroll attractors. J. Vib. Control 2012, 18, 841–849. [Google Scholar] [CrossRef]
- Chen, G.; Dong, X. From Chaos to Order: Methodologies, Perspectives and Applications; World Scientific: Singapore, Singapore, 1998. [Google Scholar]
- Liao, T.; Huang, N. An observer-based approach for chaotic synchronization with applications to secure communications. IEEE Trans. Circuits Syst. I 1999, 46, 1144–1150. [Google Scholar] [CrossRef]
- Boccaletti, S.; Grebogi, C.; Lai, Y.C.; Mancini, H.; Maza, D. The control of chaos: Theory and applications. Phys. Rep. 2000, 329, 103–197. [Google Scholar] [CrossRef]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhou, C.S. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Hu, M.; Yang, Y.; Xu, Z.; Guo, L. Hybrid projective synchronization in a chaotic complex nonlinear system. Math. Comput. Simul. 2008, 79, 449–457. [Google Scholar] [CrossRef]
- Liu, S.; Liu, P. Adaptive anti-synchronization of chaotic complex nonlinear systems with unknown parameters. Nonlinear Anal. RWA 2011, 12, 3046–3055. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E.; Arafa, A.A. On projective synchronization of hyperchaotic complex nonlinear systems based on passive theory for secure communications. Phys. Scr. 2013, 87, 055002. [Google Scholar] [CrossRef]
- Liu, P.; Liu, S. Robust adaptive full state hybrid synchronization of chaotic complex systems with unknown parameters and external disturbances. Nonlinear Dyn. 2012, 70, 585–599. [Google Scholar] [CrossRef]
- Haimo, V.T. Finite time controllers. SIAM J. Control Optim. 1986, 24, 760–770. [Google Scholar] [CrossRef]
- Vincent, U.E.; Guo, R. Finite-time synchronization for a class of chaotic and hyperchaotic systems via adaptive feedback controller. Phys. Lett. A 2011, 375, 2322–2326. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Huang, X.Q.; Lin, W.; Yang, B. Global finite-time stabilization of a class of uncertain nonlinear systems. Automatica 2005, 41, 881–888. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhou, X.; Jiang, M.; Cai, X. Synchronization of a Novel Hyperchaotic Complex-Variable System Based on Finite-Time Stability Theory. Entropy 2013, 15, 4334-4344. https://doi.org/10.3390/e15104334
Zhou X, Jiang M, Cai X. Synchronization of a Novel Hyperchaotic Complex-Variable System Based on Finite-Time Stability Theory. Entropy. 2013; 15(10):4334-4344. https://doi.org/10.3390/e15104334
Chicago/Turabian StyleZhou, Xiaobing, Murong Jiang, and Xiaomei Cai. 2013. "Synchronization of a Novel Hyperchaotic Complex-Variable System Based on Finite-Time Stability Theory" Entropy 15, no. 10: 4334-4344. https://doi.org/10.3390/e15104334
APA StyleZhou, X., Jiang, M., & Cai, X. (2013). Synchronization of a Novel Hyperchaotic Complex-Variable System Based on Finite-Time Stability Theory. Entropy, 15(10), 4334-4344. https://doi.org/10.3390/e15104334



