On a Generalized Entropy Measure Leading to the Pathway Model with a Preliminary Application to Solar Neutrino Data
Abstract
:1. Introduction
2. A Generalized Measure of Entropy
2.1. Another Method
3. A Generalized Model
4. Generalization to the Matrix Case
5. Standard Deviation Analysis and Diffusion Entropy Analysis
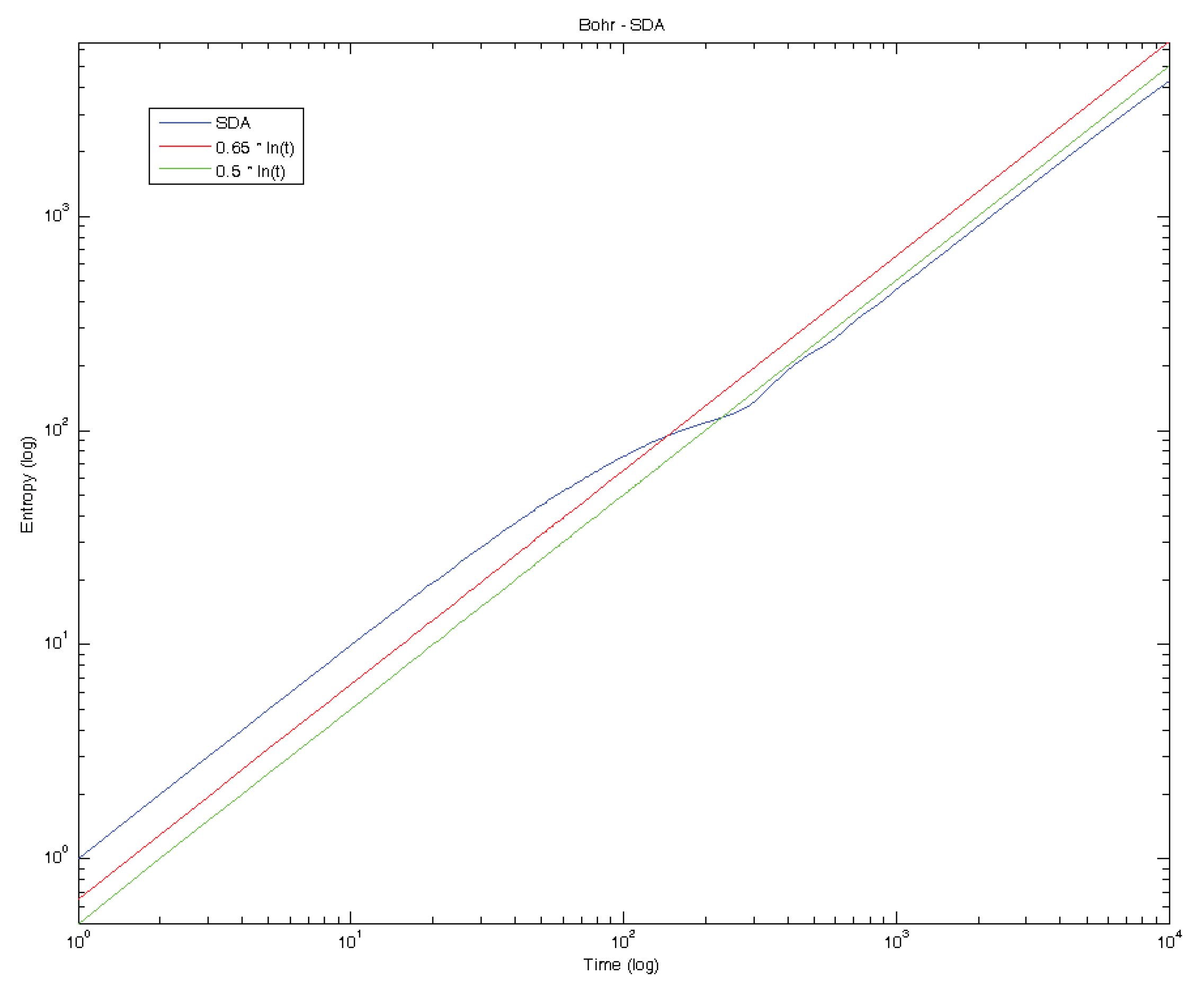
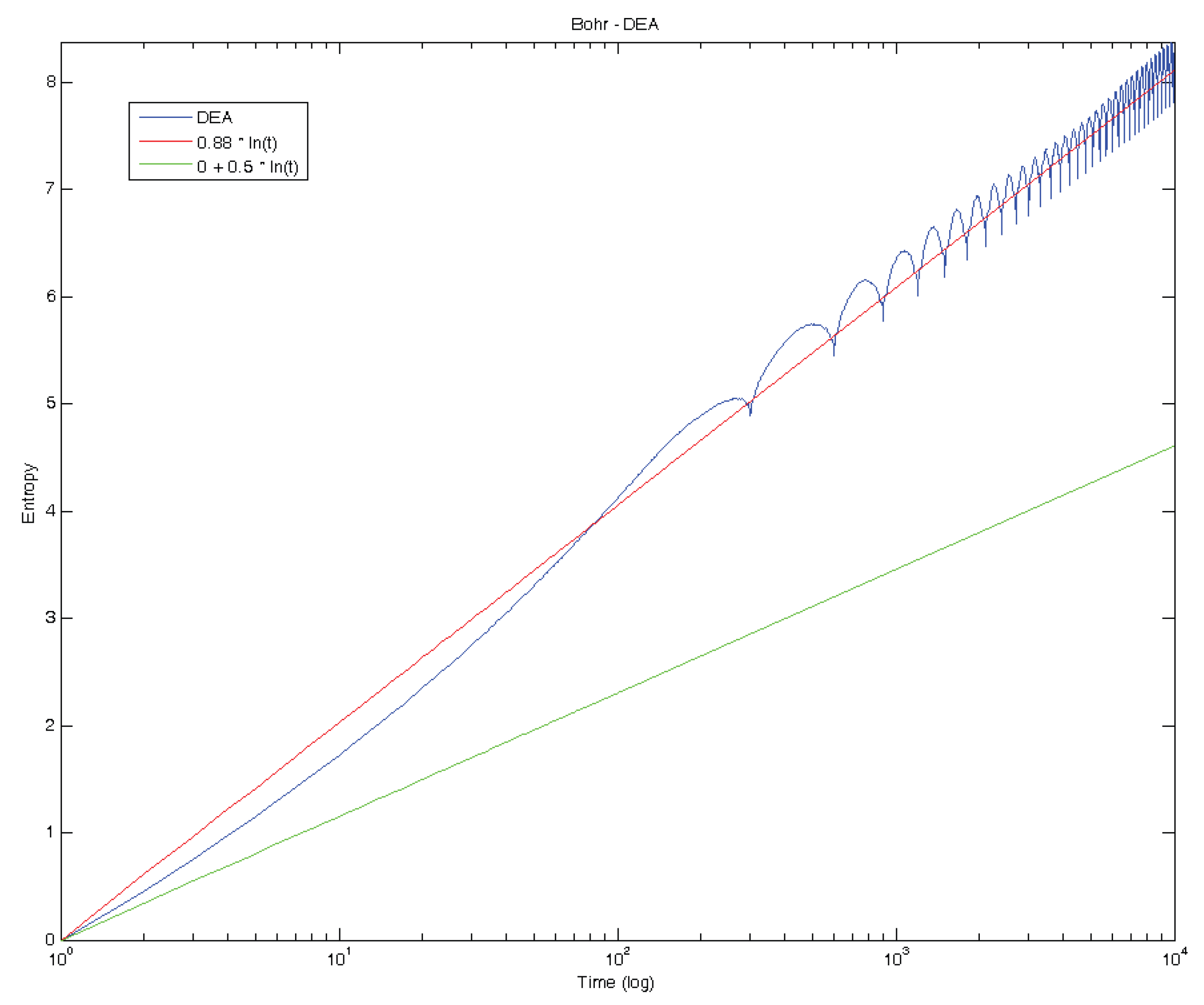
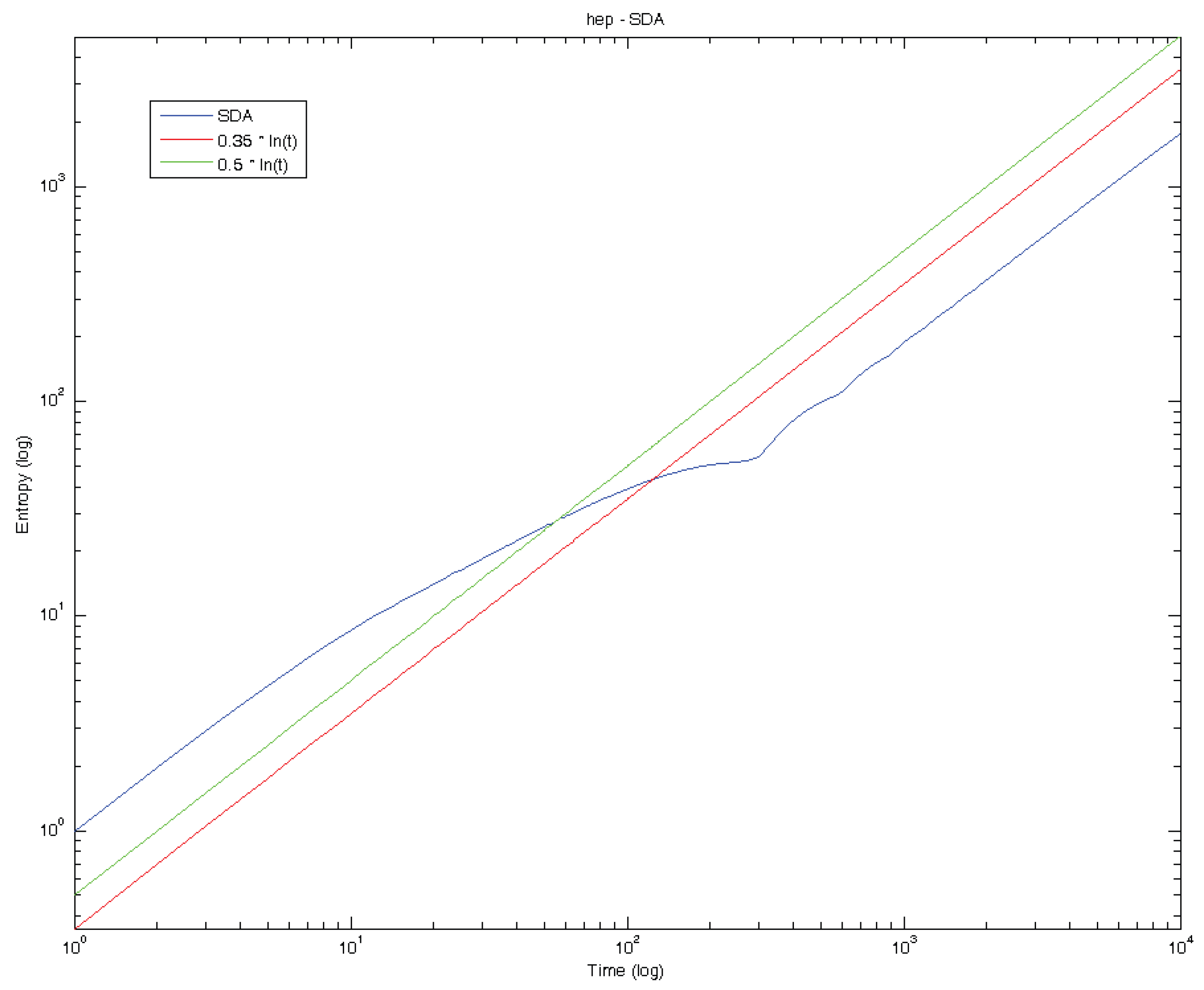
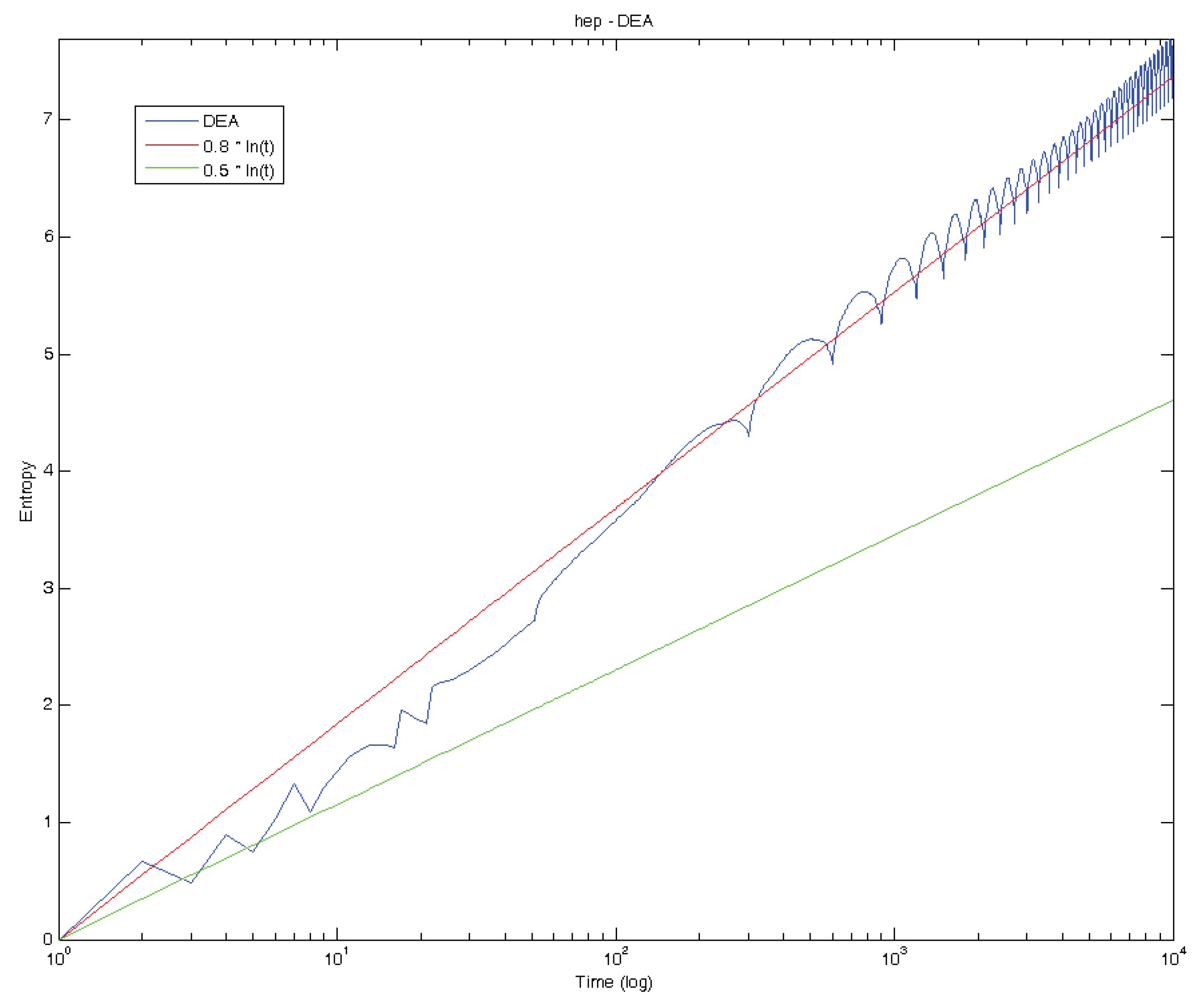
6. Conclusions
Acknowledgements
Conflicts of Interest
References
- Greven, A.; Keller, G.; Warnecke, G. Entropy; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Penrose, R. Cycles of Time: An Extraordinary New View of the Universe; The Bodley Head: London, UK, 2010. [Google Scholar]
- Mathai, A.M. A pathway to matrix variate gamma and normal densities. Linear Algebra Appl. 2005, 396, 317–328. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalizations of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Beck, C. Stretched exponentials from superstatistics. Physica A 2006, 365, 96–101. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G.D. Superstatistics. Physica A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Mathai, A.M.; Rathie, P.N. Basic Concepts in Information Theory and Statistics: Axiomatic Foundations and Applications; Wiley Eastern: New Delhi, India; Wiley Halsted: New York, NY, USA, 1975. [Google Scholar]
- Gell-Mann, M.; Tsallis, C. Nonextensive Entropy: Interdisciplinary Applications; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Mathai, A.M. Jacobians of Matrix Transformations and Functions of Matrix Argument; World Scientific Publishing: New York, NY, USA, 1997. [Google Scholar]
- Mathai, A.M. Some properties of Mittag-Leffler functions and matrix-variate analogues: A statistical perspective. Fract. Calc. Appl. Anal. 2010, 13, 113–132. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. Pathway model, superstatistics, Tsallis statistics and a generalized measure of entropy. Physica A 2007, 375, 110–122. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Special Functions for Applied Scientists; Springer: New York, NY, USA, 2008. [Google Scholar]
- Mathai, A.M.; Provost, S.B.; Hayakawa, T. Bilinear Forms and Zonal Polynomials; Springer: New York, NY, USA, 1995. [Google Scholar]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1995, 49, 1685–1689. [Google Scholar] [CrossRef]
- Scafetta, N.; Grigolini, P. Scaling detection in time series: Diffusion entropy analysis. Phys. Rev. E 2002. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1983. [Google Scholar]
- Haubold, H.J.; Mathai, A.M. A heuristic remark on the periodic variation in the number of solar neutrinos detected on Earth. Astrophys. Space Sci. 1995, 228, 113–134. [Google Scholar] [CrossRef]
- Sakurai, K.; Haubold, H.J.; Shirai, T. The variation of the solar neutrino fluxes over time in the Homestake, GALLEX(GNO), and the Super-Kamiokande experiments. Space Radiat. 2008, 5, 207–216. [Google Scholar]
- SuperKamiokande. Available online: http://www-sk.icrr.u-tokyo.ac.jp/sk/index-e.html (accessed on 20 September 2013).
- Sebastian, N.; Joseph, D.P.; Nair, S.S. Overview of the pathway idea in statistical and physical sciences. arXiv:1307.793 [math-ph].
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mathai, A.M.; Haubold, H.J. On a Generalized Entropy Measure Leading to the Pathway Model with a Preliminary Application to Solar Neutrino Data. Entropy 2013, 15, 4011-4025. https://doi.org/10.3390/e15104011
Mathai AM, Haubold HJ. On a Generalized Entropy Measure Leading to the Pathway Model with a Preliminary Application to Solar Neutrino Data. Entropy. 2013; 15(10):4011-4025. https://doi.org/10.3390/e15104011
Chicago/Turabian StyleMathai, Arak M., and Hans J. Haubold. 2013. "On a Generalized Entropy Measure Leading to the Pathway Model with a Preliminary Application to Solar Neutrino Data" Entropy 15, no. 10: 4011-4025. https://doi.org/10.3390/e15104011
APA StyleMathai, A. M., & Haubold, H. J. (2013). On a Generalized Entropy Measure Leading to the Pathway Model with a Preliminary Application to Solar Neutrino Data. Entropy, 15(10), 4011-4025. https://doi.org/10.3390/e15104011



