Moving Frames of Reference, Relativity and Invariance in Transfer Entropy and Information Dynamics
Abstract
:1. Introduction
- (1)
- a space-time interpretation for the relevant variables in the system; and
- (2)
- some frame of reference for the observer, which can be moving in space-time in the system while the measures are computed.
2. Dynamics of Computation in Cellular Automata
- blinkers as the basis of information storage, since they periodically repeat at a fixed location;
- particles as the basis of information transfer, since they communicate information about the dynamics of one spatial part of the CA to another part; and
- collisions between these structures as information modification, since collision events combine and modify the local dynamical structures.
3. Information-theoretic Quantities
4. Framework for Information Dynamics
4.1. Information Storage
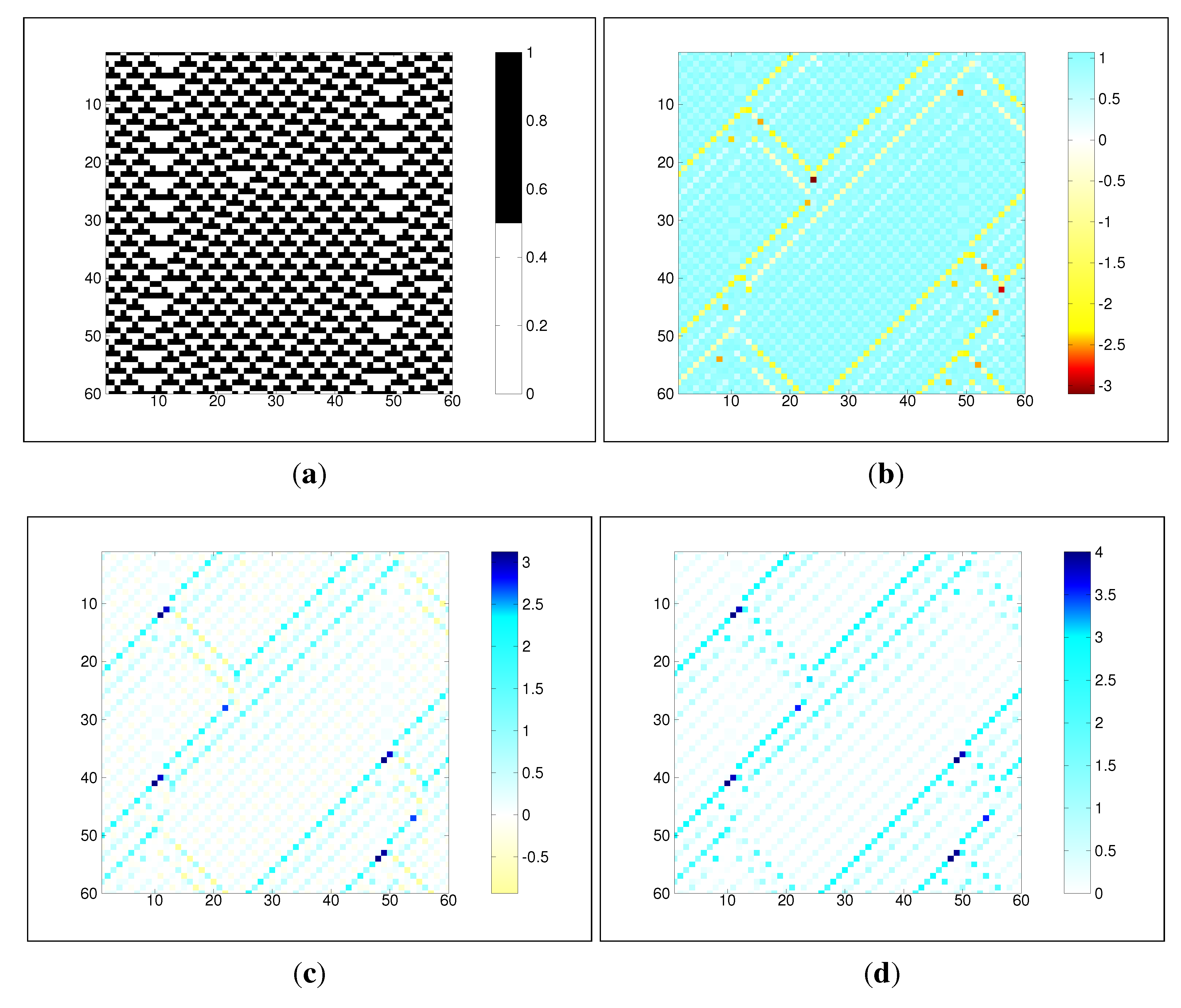
4.2. Information Transfer
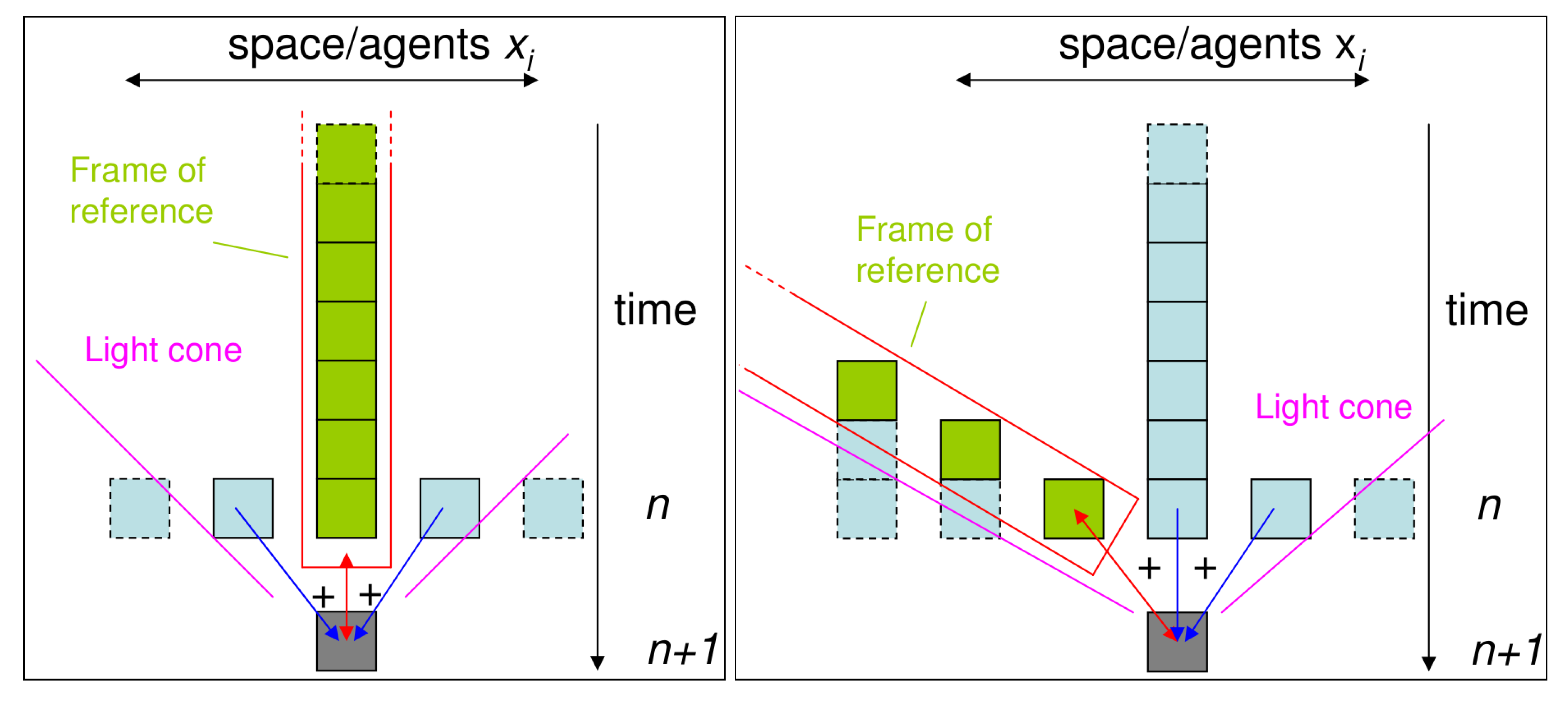
5. Information Dynamics for a Moving Observer
5.1. Meaning of the Use of the Past State
- (1)
- To separate information storage and transfer. As described above, we know that provides information storage for use in computation of the next value . The conditioning on the past state in the transfer entropy ensures that none of that information storage is counted as information transfer (where the source and past hold some information redundantly) [5,6].
- (2)
- To capture the state transition of the destination variable. We note that Schreiber’s original description of the transfer entropy [9] can be rephrased as the information provided by the source about the state transition in the destination. That (or including redundant information ) is a state transition is underlined in that the are embedding vectors [35], which capture the underlying state of the process.
- (3)
- To examine the information composition of the next value of the destination in the context of the past state of the destination. With regard to the transfer entropy, we often describe the conditional mutual information as “conditioning out” the information contained in , but this nomenclature can be slightly misleading. This is because, as pointed out in Section 4.2, a conditional mutual information can be larger or smaller than the corresponding unconditioned form, since the conditioning both removes information redundantly held by the source variable and the conditioned variable (e.g., if the source is a copy of the conditioned variable) and adds information synergistically provided by the source and conditioned variables together (e.g., if the destination is an XOR-operation of these variables). As such, it is perhaps more useful to describe the conditioned variable as providing context to the measure, rather than “conditioning out” information. Here then, we can consider the past state as providing context to our analysis of the information composition of the next value .
5.2. Information Dynamics with a Moving Frame of Reference
5.3. Invariance
5.4. Hypotheses and Expectations
- The two contexts or frames of reference in fact provide the same information redundantly about the next state (and in conjunction with the sources for transfer entropy measurements).
- Neither context provides any relevant information about the next state at all.
- Regular background domains appearing as information storage regardless of movement of the frame of reference, since their spatiotemporal structure renders them predictable in both moving and stationary frames. In this case, both the stationary and moving frames would retain the same information redundantly regarding how their spatiotemporal pattern evolves to give the next value of the destination in the domain;
- Gliders moving at the speed of the frame appearing as information storage in the frame, since the observer will find a large amount of information in their past observations that predict the next state observed. In this case, the shift of frame incorporates different information into the new frame of reference, making that added information appear as information storage;
- Gliders that were stationary in the stationary frame appearing as information transfer in the channel when viewed in moving frames, since the source will add a large amount of information for the observer regarding the next state they observe. In this case, the shift of frame of reference removes relevant information from the new frame of reference, allowing scope for the source to add information about the next observed state.
6. Results and Discussion
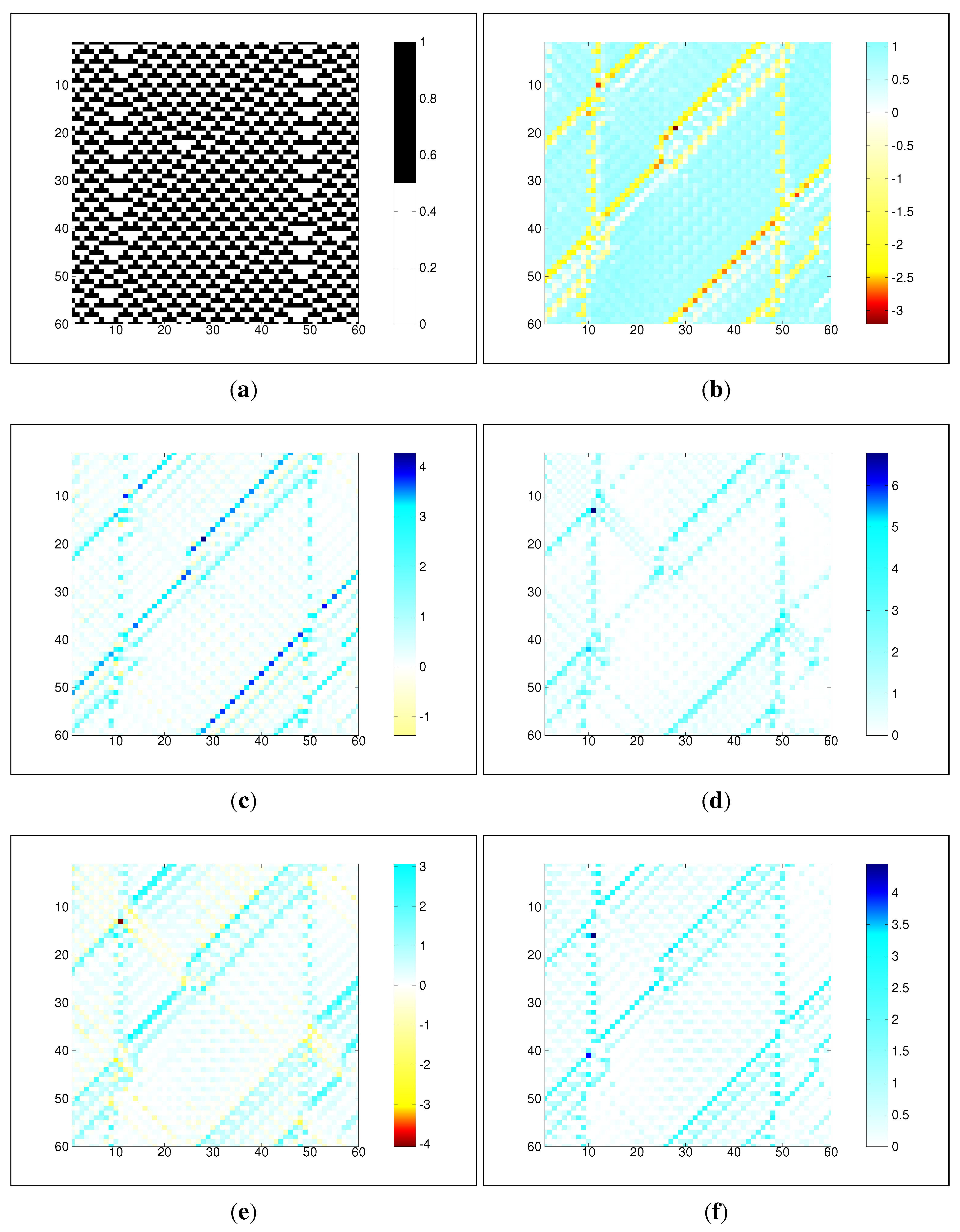
7. Conclusions
Acknowledgements
References
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics, 4th ed.; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- MacKay, D.J. Information Theory, Inference, and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Detecting Non-trivial Computation in Complex Dynamics. In Proceedings of the 9th European Conference on Artificial Life (ECAL 2007), Lisbon, Portugal, 10–14 September 2007; Almeidae Costa, F., Rocha, L.M., Costa, E., Harvey, I., Coutinho, A., Eds.; Springer: Berlin / Heidelberg, 2007; Vol. 4648, Lecture Notes in Computer Science. pp. 895–904. [Google Scholar]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 2008, 77, 026110+. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Information modification and particle collisions in distributed computation. Chaos 2010, 20, 037109+. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local measures of information storage in complex distributed computation. Inform. Sciences 2012, 208, 39–54. [Google Scholar] [CrossRef]
- Lizier, J.T. The local information dynamics of distributed computation in complex systems; Springer Theses, Springer: Berlin / Heidelberg, Germany, 2013. [Google Scholar]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.A. Cellular automata methods in mathematical physics. PhD thesis, Massachusetts Institute of Technology, 1994. [Google Scholar]
- Mitchell, M. Computation in Cellular Automata: A Selected Review. In Non-Standard Computation; Gramss, T., Bornholdt, S., Gross, M., Mitchell, M., Pellizzari, T., Eds.; VCH Verlagsgesellschaft: Weinheim, Germany, 1998; pp. 95–140. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Hanson, J.E.; Crutchfield, J.P. The Attractor-Basin Portait of a Cellular Automaton. J. Stat. Phys. 1992, 66, 1415–1462. [Google Scholar] [CrossRef]
- Grassberger, P. New mechanism for deterministic diffusion. Phys. Rev. A 1983, 28, 3666. [Google Scholar] [CrossRef]
- Grassberger, P. Long-range effects in an elementary cellular automaton. J. Stat. Phys. 1986, 45, 27–39. [Google Scholar] [CrossRef]
- Hanson, J.E.; Crutchfield, J.P. Computational mechanics of cellular automata: An example. Physica D 1997, 103, 169–189. [Google Scholar] [CrossRef]
- Wuensche, A. Classifying cellular automata automatically: Finding gliders, filtering, and relating space-time patterns, attractor basins, and the Z parameter. Complexity 1999, 4, 47–66. [Google Scholar] [CrossRef]
- Helvik, T.; Lindgren, K.; Nordahl, M.G. Local information in one-dimensional cellular automata. In Proceedings of the International Conference on Cellular Automata for Research and Industry, Amsterdam; Sloot, P.M., Chopard, B., Hoekstra, A.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Vol. 3305, Lecture Notes in Computer Science. pp. 121–130. [Google Scholar]
- Helvik, T.; Lindgren, K.; Nordahl, M.G. Continuity of Information Transport in Surjective Cellular Automata. Commun. Math. Phys. 2007, 272, 53–74. [Google Scholar] [CrossRef]
- Shalizi, C.R.; Haslinger, R.; Rouquier, J.B.; Klinkner, K.L.; Moore, C. Automatic filters for the detection of coherent structure in spatiotemporal systems. Phys. Rev. E 2006, 73, 036104. [Google Scholar] [CrossRef]
- Langton, C.G. Computation at the edge of chaos: phase transitions and emergent computation. Physica D 1990, 42, 12–37. [Google Scholar] [CrossRef]
- Mitchell, M.; Crutchfield, J.P.; Hraber, P.T. Evolving Cellular Automata to Perform Computations: Mechanisms and Impediments. Physica D 1994, 75, 361–391. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Regularities unseen, randomness observed: Levels of entropy convergence. Chaos 2003, 13, 25–54. [Google Scholar] [CrossRef] [PubMed]
- Prokopenko, M.; Gerasimov, V.; Tanev, I. Evolving Spatiotemporal Coordination in a Modular Robotic System. In Ninth International Conference on the Simulation of Adaptive Behavior (SAB’06); Nolfi, S., Baldassarre, G., Calabretta, R., Hallam, J., Marocco, D., Meyer, J.A., Parisi, D., Eds.; Springer Verlag: Rome, Italy, 2006; Volume 4095, Lecture Notes in Artificial Intelligence; pp. 548–559. [Google Scholar]
- Prokopenko, M.; Lizier, J.T.; Obst, O.; Wang, X.R. Relating Fisher information to order parameters. Phys. Rev. E 2011, 84, 041116+. [Google Scholar] [CrossRef]
- Mahoney, J.R.; Ellison, C.J.; James, R.G.; Crutchfield, J.P. How hidden are hidden processes? A primer on crypticity and entropy convergence. Chaos 2011, 21, 037112+. [Google Scholar] [CrossRef] [PubMed]
- Crutchfield, J.P.; Ellison, C.J.; Mahoney, J.R. Time’s Barbed Arrow: Irreversibility, Crypticity, and Stored Information. Phys. Rev. Lett. 2009, 103, 094101. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Bialek, W.; Nemenman, I.; Tishby, N. Complexity through nonextensivity. Physica A 2001, 302, 89–99. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63, 105. [Google Scholar] [CrossRef] [PubMed]
- Shalizi, C.R. Causal Architecture, Complexity and Self-Organization in Time Series and Cellular Automata. PhD thesis, University of Wisconsin-Madison, 2001. [Google Scholar]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605–615. [Google Scholar] [CrossRef]
- Shalizi, C.R.; Shalizi, K.L.; Haslinger, R. Quantifying Self-Organization with Optimal Predictors. Phys. Rev. Lett. 2004, 93, 118701. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. 2010. arXiv:1004.2515. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Rand, D., Young, L.S., Eds.; Springer: Berlin / Heidelberg, Germany, 1981; Vol. 898, Lecture Notes in Mathematics, chapter 21; pp. 366–381. [Google Scholar]
- Lizier, J.T. JIDT: An information-theoretic toolkit for studying the dynamics of complex systems. Available online: https://code.google.com/p/information-dynamics-toolkit/ (accessed on 15 November 2012).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lizier, J.T.; Mahoney, J.R. Moving Frames of Reference, Relativity and Invariance in Transfer Entropy and Information Dynamics. Entropy 2013, 15, 177-197. https://doi.org/10.3390/e15010177
Lizier JT, Mahoney JR. Moving Frames of Reference, Relativity and Invariance in Transfer Entropy and Information Dynamics. Entropy. 2013; 15(1):177-197. https://doi.org/10.3390/e15010177
Chicago/Turabian StyleLizier, Joseph T., and John R. Mahoney. 2013. "Moving Frames of Reference, Relativity and Invariance in Transfer Entropy and Information Dynamics" Entropy 15, no. 1: 177-197. https://doi.org/10.3390/e15010177
APA StyleLizier, J. T., & Mahoney, J. R. (2013). Moving Frames of Reference, Relativity and Invariance in Transfer Entropy and Information Dynamics. Entropy, 15(1), 177-197. https://doi.org/10.3390/e15010177




