1. Introduction
The “understanding of computational processes in nature and in the human mind” [
1] has been central in the development of the Memory Evolutive Neural System (or MENS), a mathematical brain/mind-inspired model of a cognitive system, allowing for the emergence of higher order cognitive processes, up to thought, consciousness and creativity.
MENS proposes a common frame accounting for the functioning of the neural and of the mental and cognitive system at different levels of description and across different timescales. It is not intended as a model of the
invariant structure of the neuro-cognitive system, but as a
dynamic model sizing up the system ‘in the making’, with the variation over time of its configuration and of its information processing. It describes how various brain areas interact as hybrid systems and generate an “algebra of mental objects” (in the terms of Changeux [
2]) through iterative ‘binding’ of more and more complex synchronous assemblies of neurons. In its frame mental objects are treated as ‘conceptual higher level’ neurons (called
category-neurons) on which to compute how cognitive processes of increasing complexity can emerge.
The bio-inspired development of MENS has followed the two directions proposed by Dodig‐Crnkovic: “analyzing living organisms as info‐computational systems/agents, and implementing natural computation strategies” [
1]. Indeed, first we characterize the properties of the human brain/mind at the root of cognitive processes; then we ‘abstract’ them in MENS. A third step would be to develop an adequate kind of (probably unconventional) computation to simulate them
MENS is an application of the Memory Evolutive Systems (MES), developed with Vanbremeersch [
3] which gives a model, based on Category Theory, for complex multi-scale, multi-agent self-organized systems, such as biological, social or cognitive systems.
In
Section 2, we recall some features of MES, indicating the role of Category Theory in them.
Section 3 emphasizes the neural basis of MENS. A description of the structure and of the local/global dynamic of MENS is given in
Section 4 and
Section 5, while
Section 6 deals with the emergence of higher cognitive processes. The conclusion proposes an extension of MENS to artificial cognitive systems, and emphasizes the computational problems which it raises.
2. Why Category Theory in Memory Evolutive Systems?
Category Theory has a unique status at the border between mathematics, logic, and meta-mathematics. Introduced by Eilenberg and Mac Lane [
4] in the early forties, its development (e.g., by Kan [
5], Ehresmann [
6], Lawvere [
7]) has provided a setting in which a general concept of structure is possible, and essential mathematical constructions are unified thanks to a capture of their common roots in the ways of thinking of the “working mathematician”. As these ways reflect some of the main mental operations at the basis of science, it is natural that categories have begun to be applied to other scientific domains, in particular computer science, physics, complexity theory and biology.
Different kinds of graphs are extensively used to represent networks of any nature. Here graph always denotes the data of a set of objects and a set of oriented edges (called arrows or links) between them, denoted by a: A → B; several arrows may go from A to B, and closed links are accepted. A path of a graph is a sequence of successive arrows.
A
category [
4] is such a graph equipped with an internal composition associating to a pair (
a, b) of successive arrows
a: A → B and
b: B → C, an arrow from A to C denoted
ab, and called its
composite; this composition is associative (meaning that
a(bc) = (ab)c ) and each object A has an
identity.Each graph generates the category of its paths: the objects are the same, the links are the paths of the graph, and the composition is the convolution of paths; in it, two paths cannot have the same composite. On the opposite in a category which is not the category of paths of a graph, two different paths with the same extremities may have the same composite.
This property is the reason for which we use categories rather than simple graphs in our study of complex systems; indeed we need to distinguish which paths play the same functional role, and the composition will be defined so that they have the same composite (we then say that they are functionally equivalent). In particular it opens the way to important “universal constructions”, such as the colimit operation which will model the ‘binding’ of a pattern P of linked objects.
A
pattern (or diagram) P in a category is a family of objects P
i with some distinguished links
f: P
i → P
j. A
collective link from P to an object N is a family (
si) of links
si from the different P
i to N, such that
fsj = si for each distinguished link
f: P
i → P
j of P. The pattern admits a
colimit (or inductive limit [
5]) M if there is a collective link (
li) from P to M which factorizes any other collective link, so that the collective links (
si) from P to any N are in 1-1 correspondence with the links
s: M → N binding them; formally, for each
i, we have the equation
si =
lis. (cf.
Figure 1)
Figure 1.
Collective link and colimit of a pattern P.
Figure 1.
Collective link and colimit of a pattern P.
Remark. Collective links and, a fortiori, colimits make an essential use of the composition of the category (via the above equations, as seen on the figure) and could not be defined in simple graphs. Category theory extensively uses diagrams, in particular commutative diagrams (in which two paths with the same extremities have the same composite). Proofs are often made more intuitive by reasoning on figures rather than writing the corresponding long sequences of equations; it is what is called the “diagram chasing” process, ubiquitous in articles using categories.
The Memory Evolutive Systems give a model based on a ‘dynamic’ Category Theory, incorporating time and durations, for complex multi-scale systems, with the following characteristics:
- (i)
The structure of the system is changing, its components and their links varying over time. The few models of complex systems using category theory (e.g., inspired by [
8]) only consider one category representing the invariant structure of system. On the contrary, in MES the system is not represented by a unique category but by what we call [
9] an
Evolutive System; it consists of a family of categories K
t, representing the successive configurations of the system at each time
t, and partial transition functors from K
t to K
t' accounting for the change from
t to
t' (a functor [
4] is a map between categories which preserves their composition and identities.)
- (ii)
The system is hierarchical, with a tangled hierarchy of components varying over time. A component C of a certain level ‘binds’ at least one pattern P of interacting components of lower levels so that C, and P acting collectively, have the same functional role. Modelling this hierarchy raises the
Binding Problem: how do simple objects bind together to form “a whole that is greater than the sum of its parts” [
10] and how can such “wholes” interact? In the categorical setting, the ‘whole’ C is represented by the colimit of the pattern P of interacting simple objects; and the interactions between wholes are described in terms of simple links and complex links (cf. [
3] and
Section 4).
- (iii)
There is emergence of complex multiform components, with development of a
flexible central memory. Whence the
Emergence Problem: how to measure the ‘real’ complexity of an object and what is the condition making possible the emergence over time of increasingly complex structures and processes? We characterize this condition as the
Multiplicity Principle [
3], a kind of ‘flexible redundancy’ which ensures the existence of components which binds various lower level patterns which are not isomorphic nor even well connected; such components are said to be
multiform. And we prove that the Multiplicity Principle is necessary for the emergence of increasingly complex objects and processes with multiform presentations, constructed by iterated
complexification processes. The complexification of a category K describes the ‘universally constructed’ category K' deduced from K after changes of the following kinds: addition of given new objects, formation (or preservation, if it exists) of a new object which becomes the colimit of some given pattern, suppression or decomposition of some objects. K' has been explicitly constructed in [
9] and [
3] (its links are both simple and complex links, cf.
Section 4), and the construction is amenable to usual computations.
- (iv)
The system has a multi-agent self-organization. Its global dynamic is modulated by the cooperation/competition of a network of internal functional subsystems, called the co-regulators, acting as agents with the help of a long-term memory. Each co-regulator operates locally with its own rhythm, procedures and complexity, but the commands of the different co-regulators can be conflicting and must be harmonized. While the local dynamics are amenable to conventional computations, the problem is different for the global one.
MENS is a MES the level 0 of which represents the ‘physical’ neural system (neurons and synapses), while its higher level components are ‘conceptual’ objects (called category-neurons) which represent mental objects as the binding of synchronous (hyper-)assemblies of neurons.
3. Properties of the Neural System
Despite the huge progress of brain research in the last 20 years, we still do not understand the brain's large-scale organizational principles allowing for the emergence of higher order cognitive processes. Interesting mathematical models of a local nature have been developed for particular processes in specialized brain areas; as the different brain areas are heterogeneous both anatomically and functionally, such models cannot be extended to other areas or processes.
However, there are some general properties, and MENS relies on them:
- (i)
The graph of neurons at an instant t: Its objects represent the states Nt of the neurons N existing at t (measured by their activity around t), its links from Nt to N't represent the states of the synapses from N to N', weighted by their propagation delay around t and by their strength (to transmit an activation of N to N'). A synapse can be active or passive at t. The activity of N at t is a sum of the activities of the neurons connected to N by an active link, pondered by the strength of this link. The graph changes over time: some neurons ‘die’, new neurons are formed, and the same for synapses; the activity of a neuron varies, delays and strengths of synapses may also slowly change.
- (ii)
The structural core. The graph of neurons has a central sub-graph, called its
structural core, discovered by Hagmann
et al. [
11] in 2008: “Our data provide evidence for the existence of a structural core in human cerebral cortex. This complex of densely connected regions in posterior medial cortex is both spatially and topologically central within the brain <….> the core may be an important structural basis for shaping large-scale brain dynamics <...> linked to self-referential processing and consciousness.” Recently (2011) it has been found that this core is a sub-graph with several hubs (e.g., the precuneus and the cingulated cortex) forming a “rich club” [
12].
- (iii)
Synchronous assemblies of neurons. Already in the forties Hebb [
13] has noted the formation, persistence and intertwining of more or less complex and distributed assemblies of neurons whose synchronous activation is associated to specific mental processes: “Any frequently repeated, particular stimulation will lead to the slow development of a ‘cell-assembly’ as a close system”. And he gives the
Hebb rule for synaptic plasticity: “When an axon of cell A is near enough to excite B and repeatedly or persistently takes part in firing it <…> A’s efficiency, as one of the cells firing B, is increased.” This rule has been experimentally verified in different brain areas.
- (iv)
Degeneracy property of the neural code. Emphasized by Edelman, it says that: “more than one combination of neuronal groups can yield a particular output, and a given single group can participate in more than one kind of signaling function.” [
14]. Thus the mental representation of a stimulus should be the common ‘binding’ of the more or less different neural patterns which it can synchronously activate in different contexts or at different times.
- (v)
Modular organization. The brain has a modular organization, with a variety of ‘modules’ or areas of the brain with a specific function, from small specialized parts (the “treatment units” of Crick [
15]) such as visual centres processing colour, to large areas such as the visual or motor areas, or nuclei of the emotive brain (brain stem and limbic system) or the associative cortex
. These modules interact to direct the self-organized dynamic of the system.
The neural system will be represented by an
Evolutive System [
Section 2(i)], denoted by NEUR: it has for configuration at
t the
category of neurons NEUR
t, which is the category of paths of the graph of neurons at
t: its objects model the states of the neurons N existing at
t, the links model the
synaptic paths between them, labelled by their propagation delay and strength (defined as the sum of those of their factors).
The transition from t to a later time t' associates to the state Nt at t of a neuron N its new state Nt' at t' provided that N still exists at t', and similarly for the links. The transitions describe what has changed, but they do not indicate the kind of computation (as processing of information) which is internally responsible for the change. A component of NEUR models a neuron through the sequence of its successive states; it is still called neuron, or cat-neuron of level 0. NEUR constitutes the level 0 of MENS, from which higher levels are constructed by iterated complexification processes.
4. Category-Neurons and Their Links
As said above, a mental object (e.g., the mental image of a simple stimulus) synchronously activates an assembly of neurons P, and possibly several ones in different contexts. In simple cases, there is a neuron N ‘binding’ the assembly, which becomes the colimit of P in NEUR and will represent the mental object; for instance there are neurons representing a segment or an angle [
16], or more complex but very familiar objects.
However, generally there is no “grand-mother neuron” [
17] in NEUR. A mental object S which activates an assembly of neurons P having no colimit in NEUR will be represented by a conceptual object M, called a
category-neuron (abbreviated in
cat-neuron) of level 1, which will become the colimit of P in the larger system MENS, and act as a memory of S. The construction of M (by a
complexification process) will determine what are the good links between M and other (cat-)neurons, and will guarantee that M also becomes the colimit of the other assemblies of neurons which S can synchronously activate. Having thus constructed cat-neurons of level 1 and their links, we can speak of
assemblies of cat-neurons of level 1, and iterate the construction to obtain a hierarchy of cat-neurons of increasing levels, representing more and more complex mental objects binding together assemblies of simpler ones. Let us explicit the construction.
Formally, any assembly of (cat-)neurons is modelled by a pattern P in MENS. For the assembly to synchronously activate a (cat-)neuron N, there must exist a collective link (si) from P to N, allowing that all the si transmit an activation of Pi to N at the same time; in particular this imposes that all the zigzags of links between Pi and Pj have the same propagation delay. A pattern with this property is said to be polychromous.
If such a pattern P is repeatedly activated, its distinguished links are strengthened (via Hebb rule), and there is formation of a mental object. This object will be represented by a higher level cat-neuron M, which becomes the
colimit of P in MENS (cf.
Figure 1). It is important to note that the activation of P precedes that of its colimit M.
The degeneracy property asserts that the mental object can also activate (simultaneously or at different times) other patterns Q, not necessarily connected to P by a cluster of links. The representing cat-neuron M must also be the colimit of Q, so that M is a
multiform cat-neuron [
3], which can be activated by anyone of its different decompositions P, Q, …, with possibility of switches between them. The existence of cat-neurons which are multiform signifies that MENS satisfies the
Multiplicity Principle [
3]. Once formed the cat-neuron M preserves its identity up to its ‘death’ though its lower level decompositions can vary more or less quickly over time. The
stability span of M at an instant
t is the longest period during which M admits a decomposition P at
t whose successive states remain a decomposition of M.
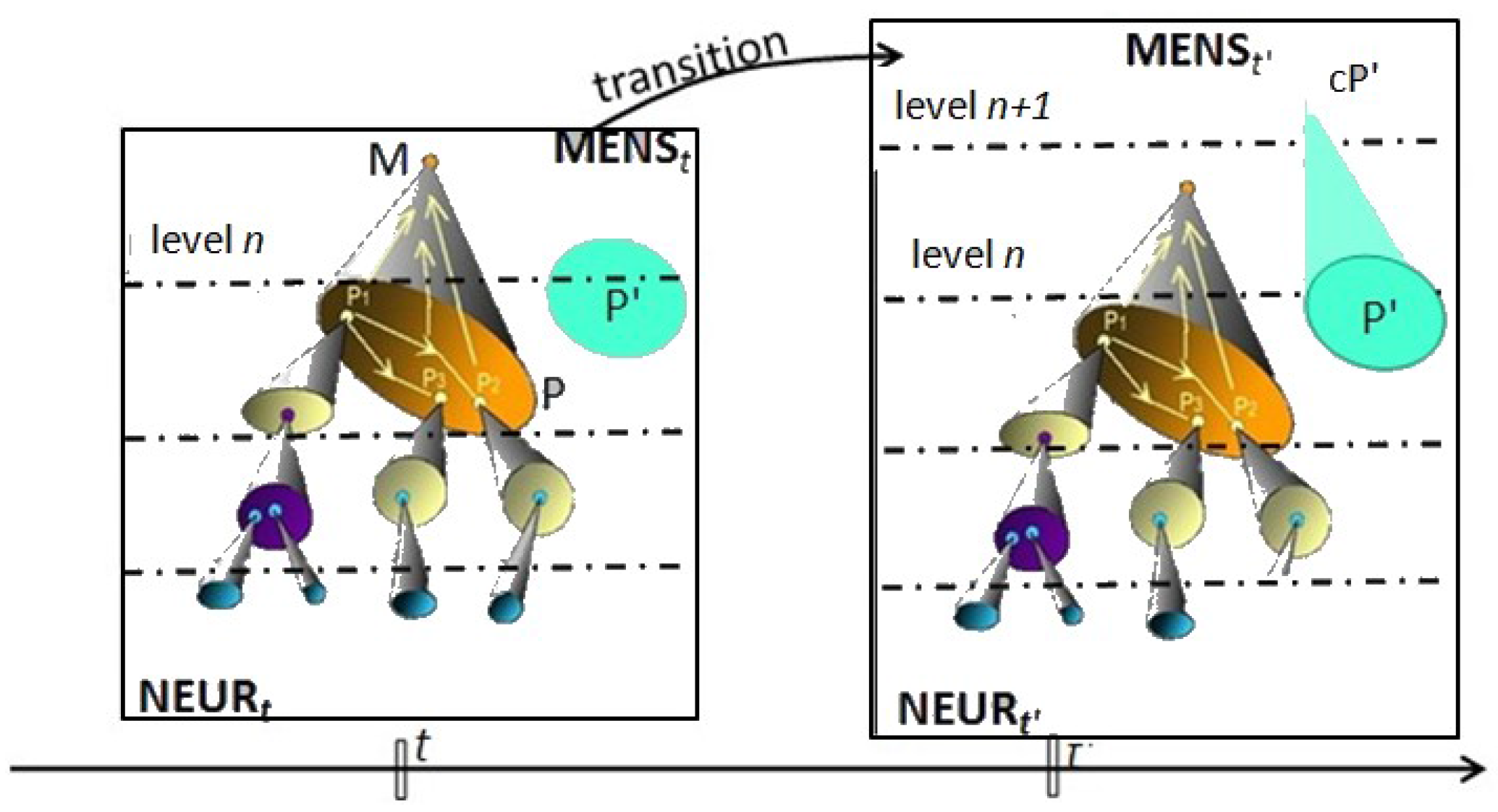
MENS is an Evolutive System. At an instant t of the life of the individual, the configuration category MENSt models the present state of the neural, mental and cognitive system; its objects are the cat-neurons of any level (from the level 0 of neurons up) existing at t with their activity, and their links with their propagation delay and strength; a link is active or not at t.
The transition from
t to
t' points out the structural changes without accounting for the information processing at their origin (to be considered in
Section 5). The changes are events of the following kinds: formation (or preservation if it exists) of a new cat-neuron binding some pattern P' of already existing lower level cat-neurons, possibly loss or decomposition of some cat-neurons. In the categorical setting, the new configuration MENS
t' at
t' is obtained as the
complexification of MENS
t [cf.
Section 2(iii)] with respect to a procedure Pr having objectives of the preceding kinds (cf.
Figure 2). Such a complexification is solution of the "universal problem" of constructing a category in which the objectives of Pr are satisfied in the ‘best’ way. We have given an explicit construction of the complexification, in particular of the links between cat-neurons; and we have shown in [
18] how, using its universal property, the propagation delays and strengths of synaptic paths (at the level 0) can be extended to the links of any level, as well as the
Hebb rule.
Figure 2.
Complexification process.
Figure 2.
Complexification process.
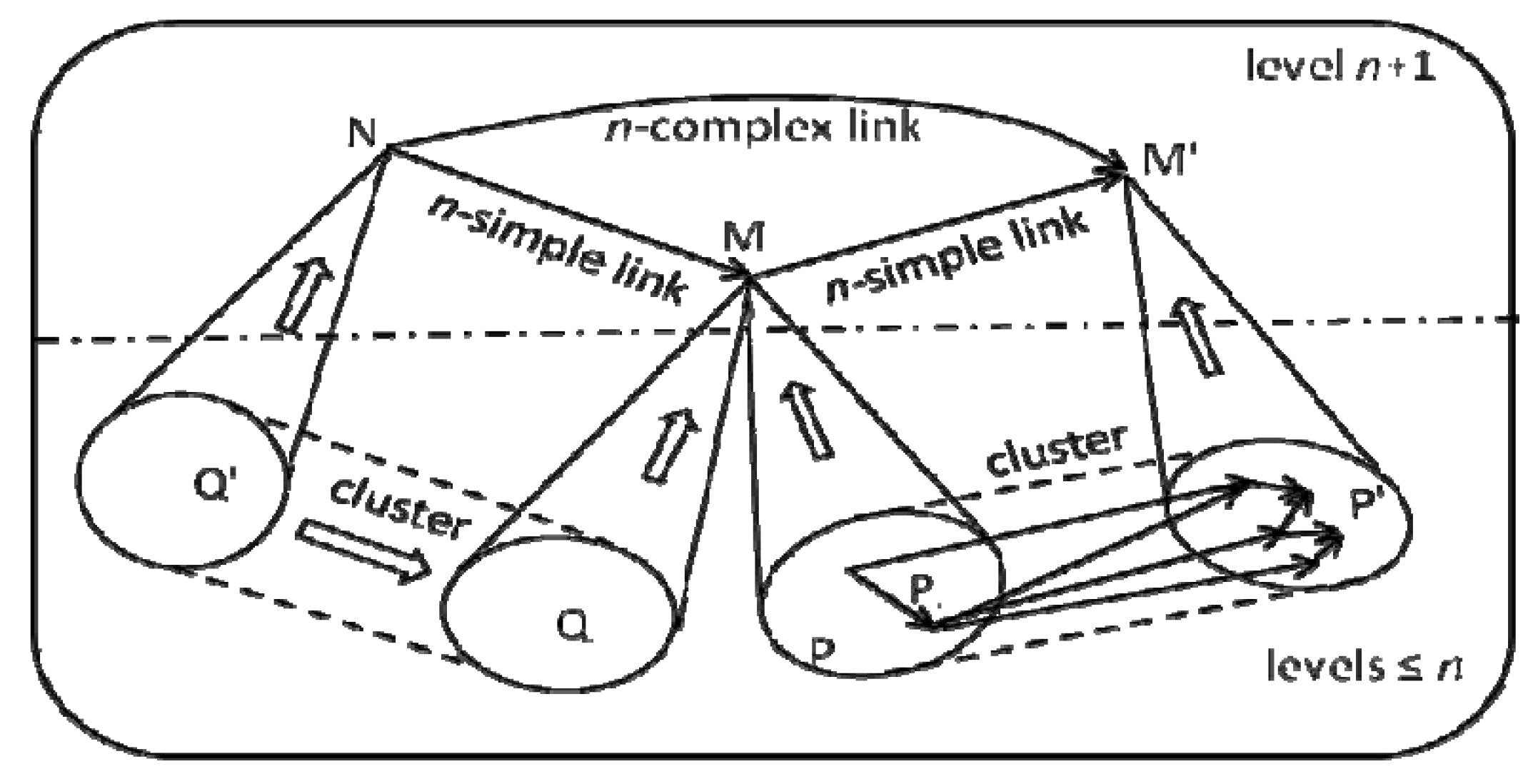
More explicitly, the construction distinguishes two kinds of links (
Figure 3):
- (i)
Simple links. They ‘bind’ clusters of lower level links as follows. Let M and M' be 2 cat-neurons binding lower level patterns P and P' respectively. If we have a cluster G of links from P to P' well correlated by the distinguished links of P and P', this cluster binds into a link from M to M', called a (P, P')-simple link (or n-simple link if P and P' are of level ≤ n). Such a link just translates at the level n+1 the information that P can coherently activate components of P' through the links of G; and this information is computable at the lower levels. A composite of n-simple links binding adjacent clusters is n-simple.
- (ii)
Complex links. They emerge at a higher level, as composites of
n-simple links binding non-adjacent clusters. Their existence is possible because of the existence of cat-neurons M which are multiform.
Figure 3 presents a complex link from N to M' composite of a (Q', Q)-simple link with a (P, P')-simple link, where P and Q are non-connected decompositions of the multiform cat-neuron M. Such a link represents information
emerging at the level
n+1 by integration of the global structure of the lower levels, and not locally computable through lower level decompositions of N and M'; indeed the fact that the cat-neuron M is multiform imposes global conditions, calling out all its lower decompositions and their collective links; could it be amenable to some kind of unconventional computation?
Figure 3.
Cluster, simple and complex links.
Figure 3.
Cluster, simple and complex links.
Remark. Here we only speak of cat-neurons constructed by colimits. In fact there are also cat-neurons obtained by projective limits [
5], which arise for instance in the construction of a semantic memory. When the procedure asks also for the formation of such ‘classifying’ cat-neurons, we speak of a
mixed complexification; its construction is more complicated [
3].
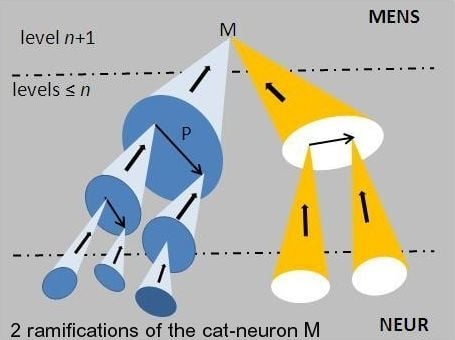
The construction of cat-neurons of higher levels allows making more precise the brain/mind correlation. A cat-neuron M of level >0 represents a mental object and not a physical neuron. However the
activation or the
recall of M has neurophysiological consequences; indeed, it consists in the unfolding of one of the ramifications of M down to the neural level 0 (cf.
Figure 2): first activation of one of its decompositions P into a synchronous assembly of cat-neurons of lower levels, then a decomposition of each component of P, and so on down to the
physical activation of synchronous assemblies of neurons. Because of the propagation delays of the links, the unfolding has a certain duration.
At each step, there is a choice between various (possibly non-connected) decompositions, so that the activation of M has several freedom degrees leading to multiple physical realizabilities into hyper-assemblies (i.e., assemblies of assemblies of … assemblies) of neurons. The ramifications of M have not all the same length. The complexity order of M is the smallest length of a ramification; it is less or equal to the level of M. The level indicates the number of steps in which M has been constructed, while the complexity order measures the smallest number of steps sufficient for its later activation.
Using deep results on complexifications of categories satisfying the Multiplicity Principle, and in particular the
Iterated Complexification Theorem proved in [
3] (Chapter 4, Section 6.1), we deduce the following:
Emergence Theorem. Iterated complexifications preserve the Multiplicity Principle and lead to the emergence in MENS of cat-neurons of increasing complexity order, representing more and more complex mental objects or cognitive processes.
5. Local and Global Dynamic of MENS
As any Memory Evolutive System, MENS has a multi-scale self-organization; it is modulated by a network of co-regulators which rely on the modular organization of NEUR and help developing a central long-term memory.
The Memory is a hierarchical sub-system Mem of MENS, which develops over time; it models the innate or acquired knowledge of any modality and the information of any kind which the individual can store and later recognize and/or recall. A cat-neuron M in Mem, called record, represents the mental object associated to an item S (external object, signal, past event, internal state, sensory-motor or cognitive processes, …). Initially S activates a particular pattern P of cat-neurons, if the corresponding neural activity persists, the links of P are strengthened (by Hebb rule) and P binds into a cat-neuron M which becomes its colimit in MENS; over time M takes its own identity as a multiform cat-neuron and can even disassociate from P at a later time to adapt to changing situations (as long as the change is progressive enough). S can be recognized and M recalled through the activation of any of the ramifications of M down to the neural level, with possibility of switches between them; so M is a robust memory but not a rigid one (as in a computer) since it remains flexible and can be constantly revised to account for changes.
Mem contains a sub-system Proc, the
Procedural Memory in which the records, called
procedures, have links (or ‘commands’) toward the pattern of their effectors (e.g., motor commands of a specific movement); these cat-neurons are based on multiple brain regions (e.g., frontal and parietal regions, cerebellum). Mem also contains a sub-system Sem, the
Semantic Memory, in which records are classified into invariance classes with respect to some attributes (for the formation of Sem, cf. [
3], Chapter 10).
The memory plays an important role in the dynamic of MENS which is modulated by the cooperative/competitive interactions between functional sub-systems, the co-regulators, related to the modular organization of the brain. A co-regulator is based on a specific module of the brain, meaning that its cat-neurons have ramifications down to this module (so that they model hyper-assemblies of neurons of the module). It has its own differential access to Mem, in particular to Proc, to recall its ‘admissible procedures’ specific of its function.
The dynamic of MENS must account for both the local information processing of each co-regulator, which operates with its own rhythm and function, and the global dynamic which results from an ‘interplay’ among these co-regulators. While the local dynamics are amenable to conventional computations, their merging in the global one raises computational problems.
First we analyze the local dynamic: A co-regulator CR operates stepwise as a hybrid system; a step from
t to
t' is divided into more or less intermingled phases:
- (i)
Formation of the landscape at t. It is a category Lt which models the partial information accessible to CR through active links: its objects are clusters G from a cat-neuron B to CR with at least one link activating a cat-neuron in CR around t. It plays the role of a working memory for CR during the step.
- (ii)
Selection of an admissible procedure Pr to respond to the situation with adequate structural changes. It is done through the landscape, using the access of CR to Mem to recall how the information has been processed in preceding analogue events. For instance in presence of an object S, a CR treating colours will retain only information on the colour of S, and the objective of Pr could be to bind the pattern P of neurons activated by the colour to memorize the colour or, if already known, recall it.
- (iii)
Commands of the procedure are sent to its effectors in MENS. In the above example, the binding of P into a CR-record of S consists in strengthening the distinguished links of P using Hebb rule. The dynamic by which the effectors should realize the commands during the continuous time of the step is computable, using differential equations (for instance of the “Cohen-Grossberg-Hopfield with delays” type) in the phase space of the landscape whose coordinates are the activities of the cat-neurons and the strengths of the links between them; we refer to [
18] for more details.
- (iv)
Evaluation at the beginning of the next step, by comparison of the anticipated landscape (which should be the complexification of Lt with respect to Pr) with the new landscape; then Pr and its result are recorded. If the commands of Pr have not entirely succeeded, we say that there is a fracture for CR.
The global dynamic must take account of the different local dynamics of the co-regulators. At a given time the commands sent by the various co-regulators should all be realized by the effectors of the system. Since the co-regulators have different functions and rhythms, these commands can be conflicting, and there is need of an equilibration process to ensure the correlation of the different commands, possibly neglecting some of them. For instance to seize an object, the visual and motor commands should fit together. This process, called the interplay among the co-regulators, leads to the operative procedure Pr° which will be implemented on the system.
The interplay searches for a best compromise between the more or less conflicting commands, keeping as much of them as possible. In particular it takes advantage of the degrees of freedom of a multiform command which can be activated through anyone of its lower level decompositions, with possible switches between them: the decompositions allowing for a better coordination are selected through a kind of Darwinian selection process; for instance, depending on the context, we can seize an object in the right or left hand.
The operative procedure Pr° actually carried out can by-pass the procedures of some co-regulators thus causing dysfunction (temporary fracture or longer
de-synchrony) to them. A main cause of fractures is the non-respect of the structural temporal constraints (or
synchronicity laws) imposed on a co-regulator CR by the propagation delays and stability spans in its landscape [
3]. Fractures may backfire between co-regulators with heterogeneous complexity levels and temporalities. In the interplay, an important role is played by
evaluating co-regulators, based on parts of the emotive brain which evaluate the procedures in function of their consequences on the well-being of the person.
A standing problem is to determine what kind of computation could help model the interplay among the co-regulators. Since it makes use of the flexibility of the commands as multiform cat-neurons, it is probably not amenable to conventional computations (cf.
Section 4).
6. AC and Higher Cognitive Processes
The co-regulators jointly participate in the development over time of an important functional sub-system of the memory Mem, the Archetypal Core AC which will act as an internal model, essential for the emergence of higher cognitive processes.
In
Section 3 we have said that the brain has a structural core which plays a main role in the shaping of large-scale brain dynamic. A cat-neuron in AC is a higher order cat-neuron, often activated and with ramifications down to the structural core; thanks to the "rich club" organization of this core, the hyper-assemblies of neurons which it binds are largely distributed in different brain areas. Thus an archetypal record integrates and intertwines recurring memories and experiences of different modalities (sensory-motor, proprioceptive, affective, …) as well as notable events with their emotive undertones. Archetypal records are connected by complex links which become stronger and faster (thanks to Hebb rule) along time. These links form
archetypal loops which propagate very quickly the activation of an archetypal record A back to itself, thus maintaining it for a long time; the activation of A resonates to lower levels via the unfolding of ramifications of A and switches between different decompositions (cf.
Figure 4).
It follows that an activation of part of AC extends to a larger domain D of MENS, both in depth (lower level decompositions P are activated) and in duration: if A is activated at
t, it means that P has been activated earlier (cf.
Section 4), and, since the activation of A is self-maintained by the loops, the activation of P will be maintained in the near future: the ‘present’ of D has some extent, as proposed by Husserl: “Il y a dans le présent une
rétention du passé (rétention primaire si c’est un passé immédiat, rétention secondaire si c’est un souvenir plus lointain) et une
protention du futur (de ce qui va immédiatement arriver)” [
19].
Figure 4.
Archetypal Core at the basis of GL.
Figure 4.
Archetypal Core at the basis of GL.
AC represents an internal model of the Self, reflecting a personal vision of the world since each ramification of an archetypal record represents a specific association of mental objects dependent on the former experiences of the person. It plays a motor role in the development of higher cognitive processes, through information processing by higher level co-regulators based on associative brain areas and directly linked to AC; these co-regulators, called
intentional co-regulators, can be compared to the “conscious units” of Crick [
15]. An arousing situation or a non-expected event S (such as a fracture in a higher co-regulator) leads to the activation of some archetypal cat-neurons. As explained above, it triggers, through archetypal loops, an extension of the activated domain D. This activation is transmitted back to the intentional co-regulators, which can cooperate to construct a
global landscape GL uniting their respective landscapes and extending them in depth and duration (cf.
Figure 4). GL assembles information related to the present state, reinforces evanescent traces recently accumulated in lower levels of the working memory, and even anticipates some future trends. Successive global spaces partially overlap each other.
The global landscape GL can be compared to the “global workspace” proposed by different authors (e.g., [
20]), and to the “theatre of consciousness” of Baars [
21]. It gives a frame for the development of higher cognitive processes, in particular
conscious processes characterized by an integration of the time dimension through 2 possibly alternative and/or intermingled processes which extend Husserl’s retention and pretention:
- (i)
A
retrospection process (toward the past) proceeds by abduction (in the sense of Pierce [
22]) to recollect information back in time thanks to its reinforcement in GL. Processing this information allows for analyzing the event S which has triggered the formation of GL and finding its possible causes, thus “sensemaking” of the present.
- (ii)
A prospection process (toward the future) is then developed in GL, to try and select long term strategies. It is done through the formation, inside GL, of local ‘virtual’ landscapes (representing “mental spaces”), where successive procedures can be tried by internally constructing the corresponding complexifications, with evaluation of their benefits and of the risk of dysfunction. A sequence of alternating retrospection and prospection processes thus leads to various ‘scenarios’. Once a scenario is selected, the retrospection process allows back-casting to find sequences of procedures (implicating co-regulators of various levels) able to realize this long term program.
The formation of scenarios is at the root of anticipation and creativity. Scenarios directly inspired by the contextual environment and current trends are obtained by simple complexifications of successive virtual landscapes that add, delete and/or combine components (examples: “combinational” and “exploratory” creativity [
23]; metaphors and “conceptual blending” [
24]). More innovative scenarios (“transformational creativity” [
23]) make use of iterated complexifications which (as asserted by the “Iterated complexification Theorem” [
3]) are not reducible to a unique complexification and lead to the emergence of mental objects of increasing complexity, so that these scenarios transcend the current situation.
Successive global spaces can ‘consciously’ process information coming from higher-order cat-neurons, while they ‘automatically’ keep traces of the operations of lower level co-regulators (recruited by retrospection). It explains how a creative process can go through an ‘incubation period’ during which the person consciously performs unrelated operations, followed by an “insight” with emergence in the global space of new ideas for the creative scenario.
7. Conclusions and Future Work
This paper shows how to model a “theory of mind”, in which a hierarchy of mental objects and processes emerges from the functioning of the brain, through the iterative binding of neuronal (hyper-)assemblies. We show that
the degeneracy property of the neural code is the characteristic which makes this emergence possible, and we explain how it allows the development of a flexible memory, with a central part, the Archetypal Core AC at the basis of the Self and of the formation of higher cognitive processes up to consciousness and creativity. The info-computational model MENS is an application of the Memory Evolutive Systems [
3], based on a ‘dynamic’ Category Theory.
The same constructions could lead to the development of a multi-scale
artificial cognitive system capable of higher cognitive processes, provided that it has for level 0 a system satisfying the assumptions of
Section 3 (existence of a structural core, reinforcement of active assemblies of objects, degeneracy property). Or to the development of Neuro-Bio-ICT systems enlarging MENS, obtained by connecting, to the neural system, an artificial cognitive system acting as an “exocortex” to monitor dysfunctions and/or enhance human abilities [
25].
In any case, the local dynamics should be computable, but the problem remains to study how the interplay between them leading to the global dynamic could be amenable to some kind of (hyper-) computation.