Thermodynamic Geometry and Topological Einstein–Yang–Mills Black Holes
Abstract
:1. Introduction
2. Thermodynamic Geometry
3. Ruppeiner Geometry
3.1. Five Dimensional Black Holes

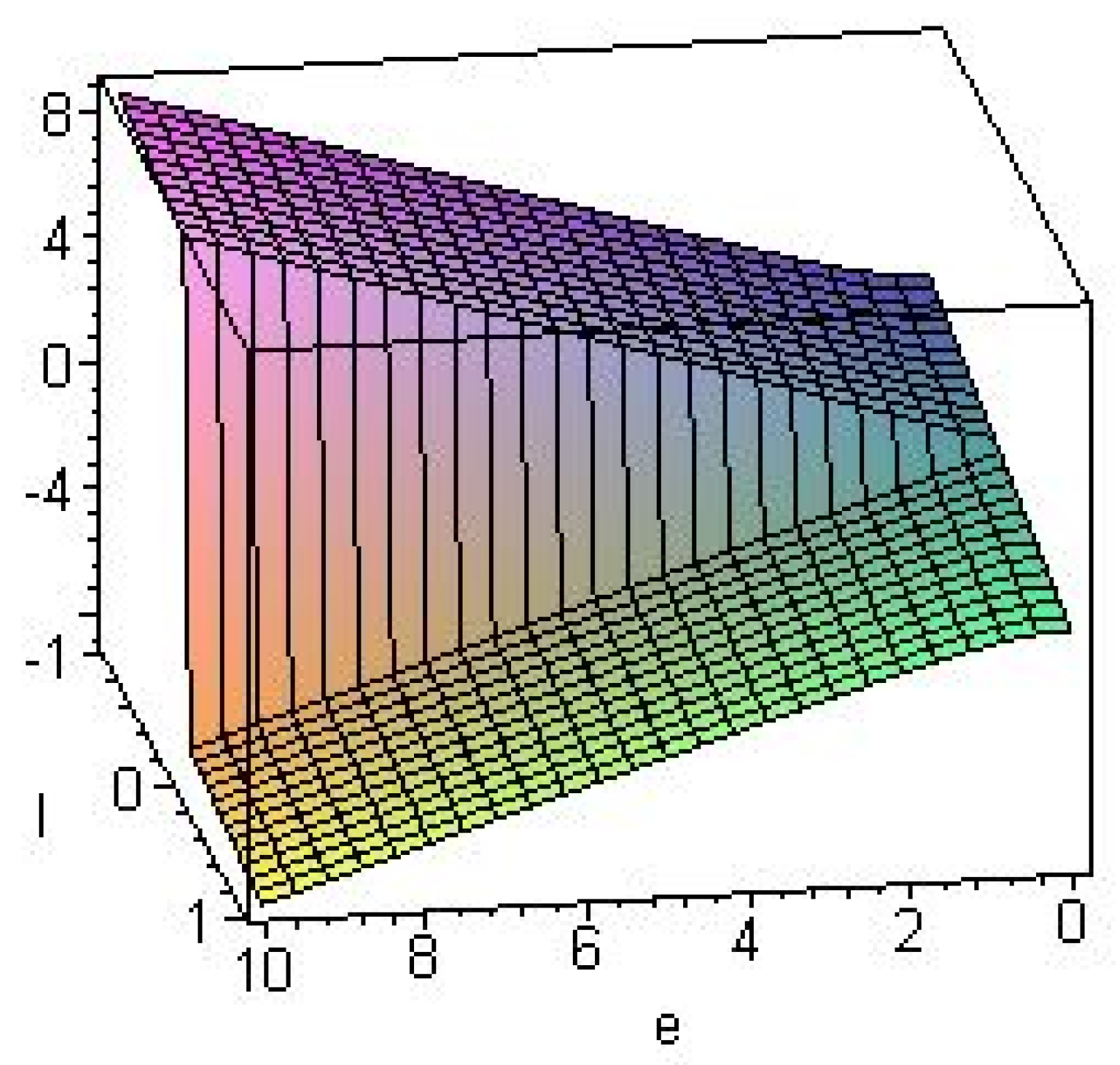
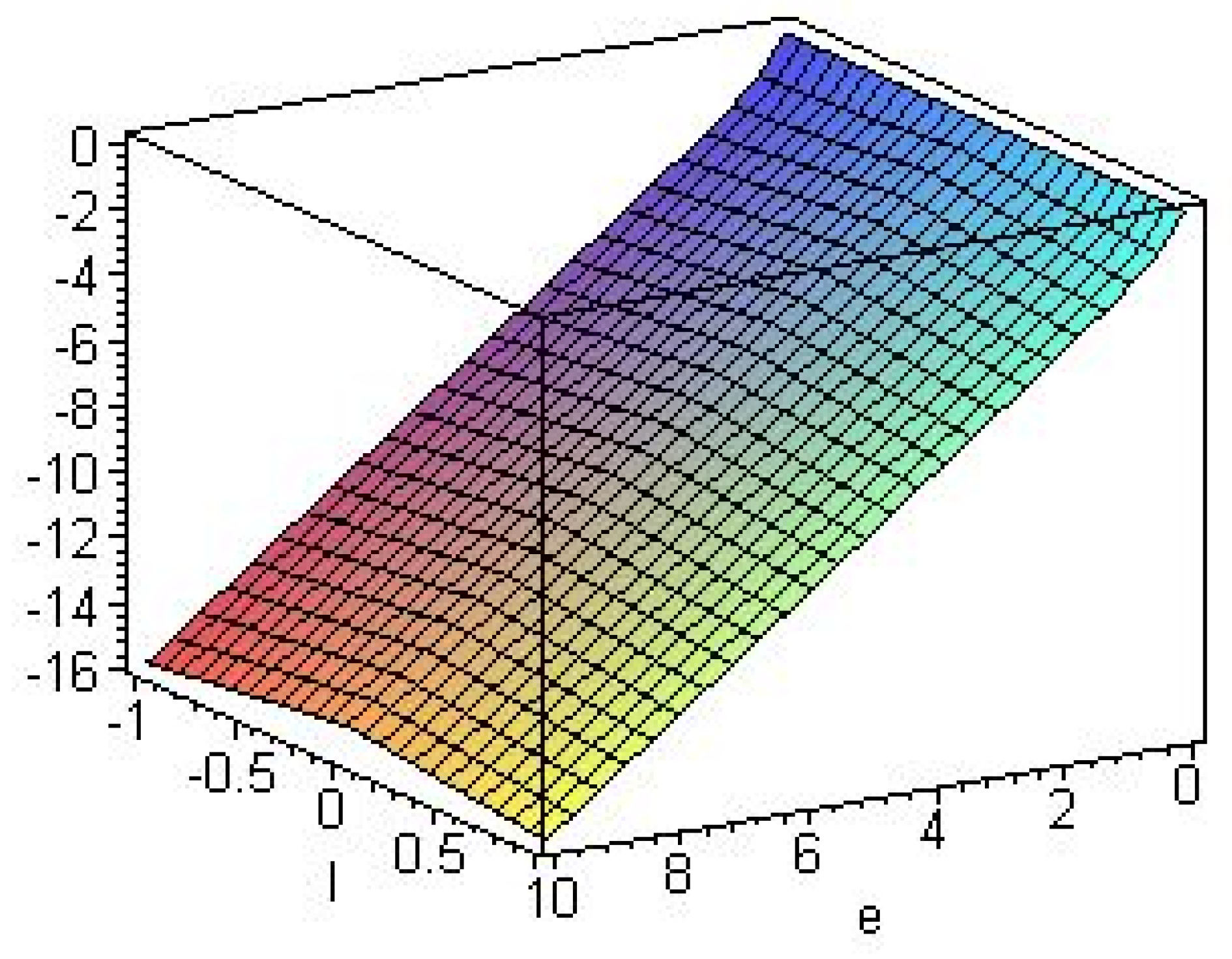
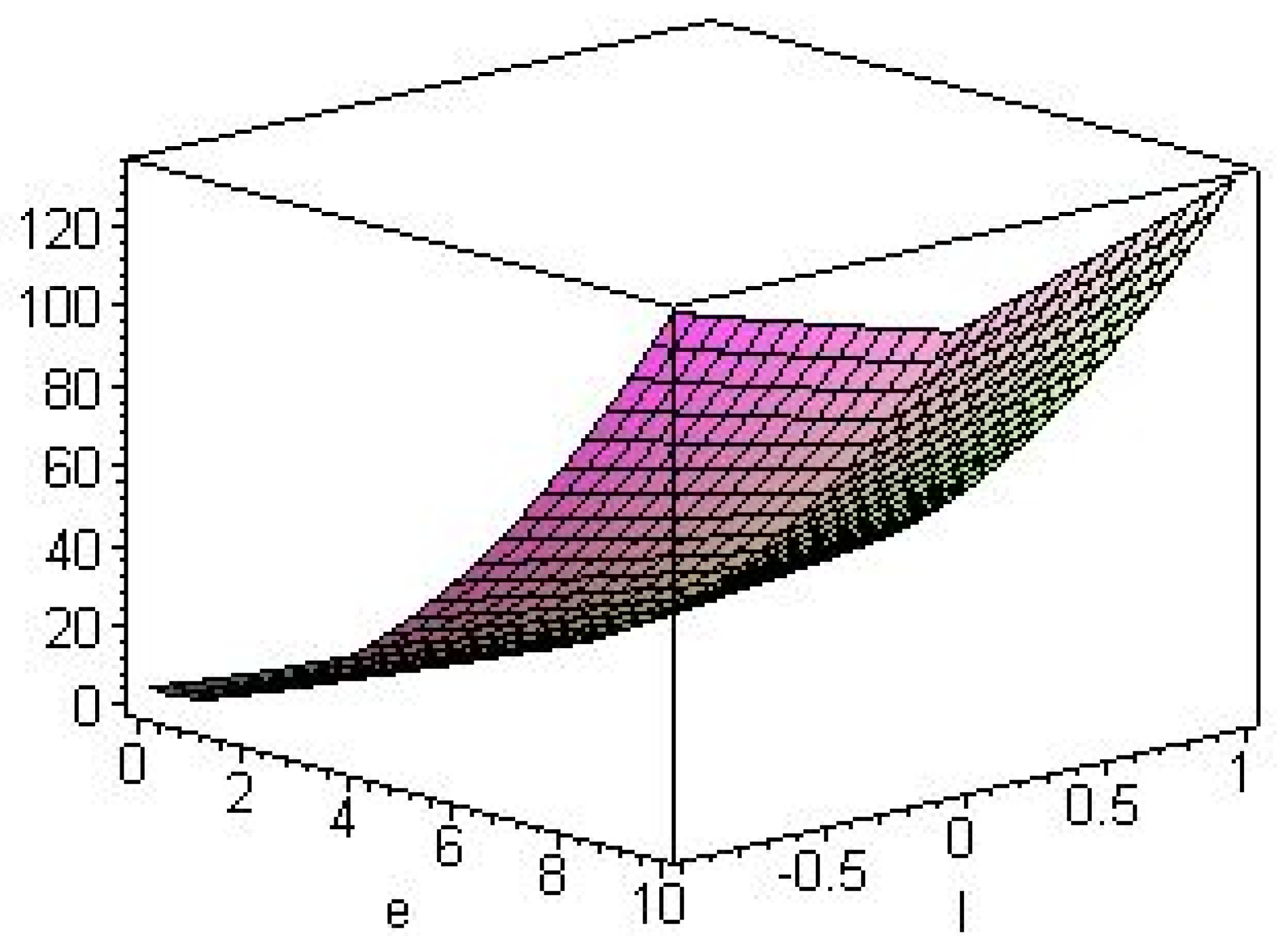
3.2. Higher Dimensional Black Holes
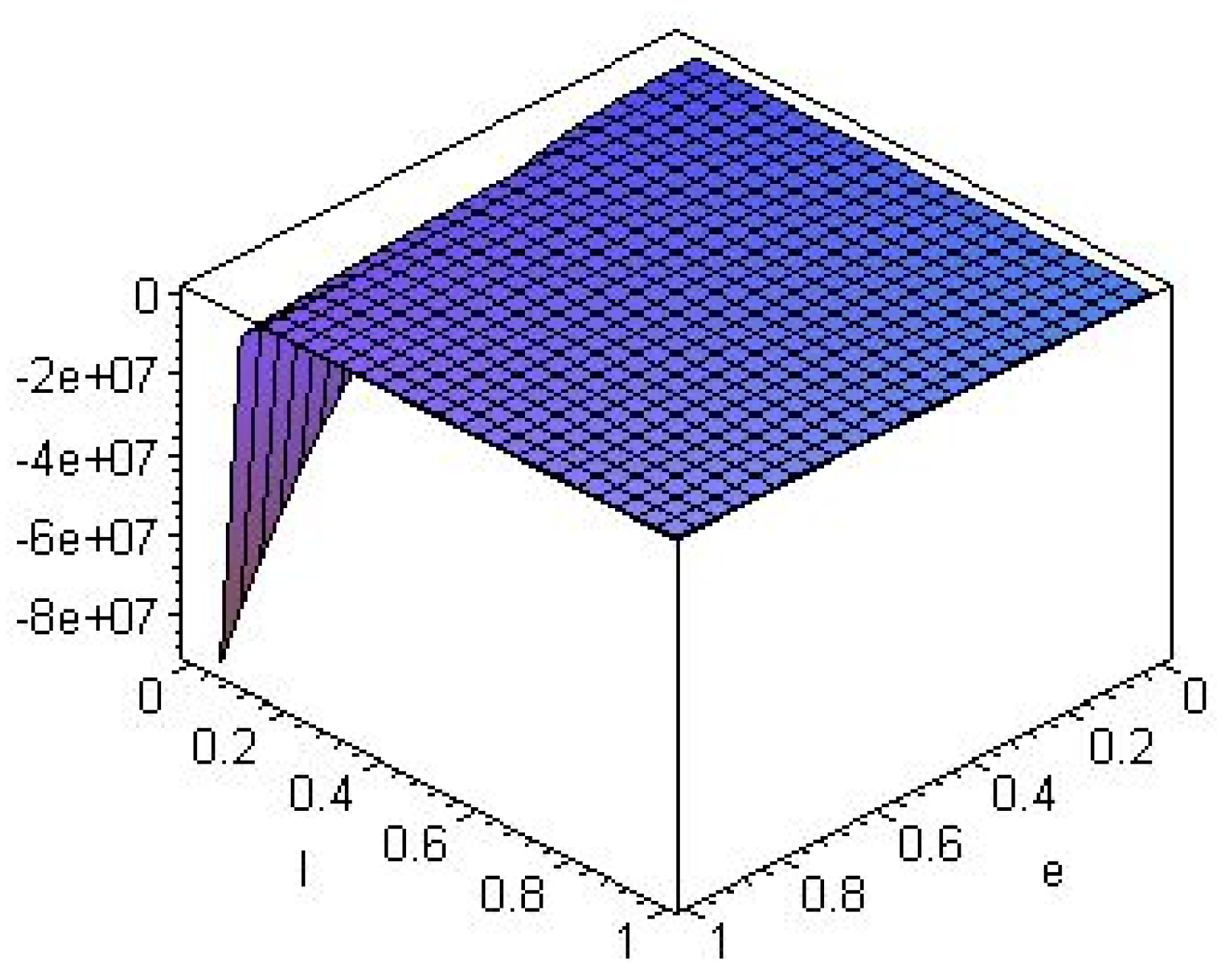
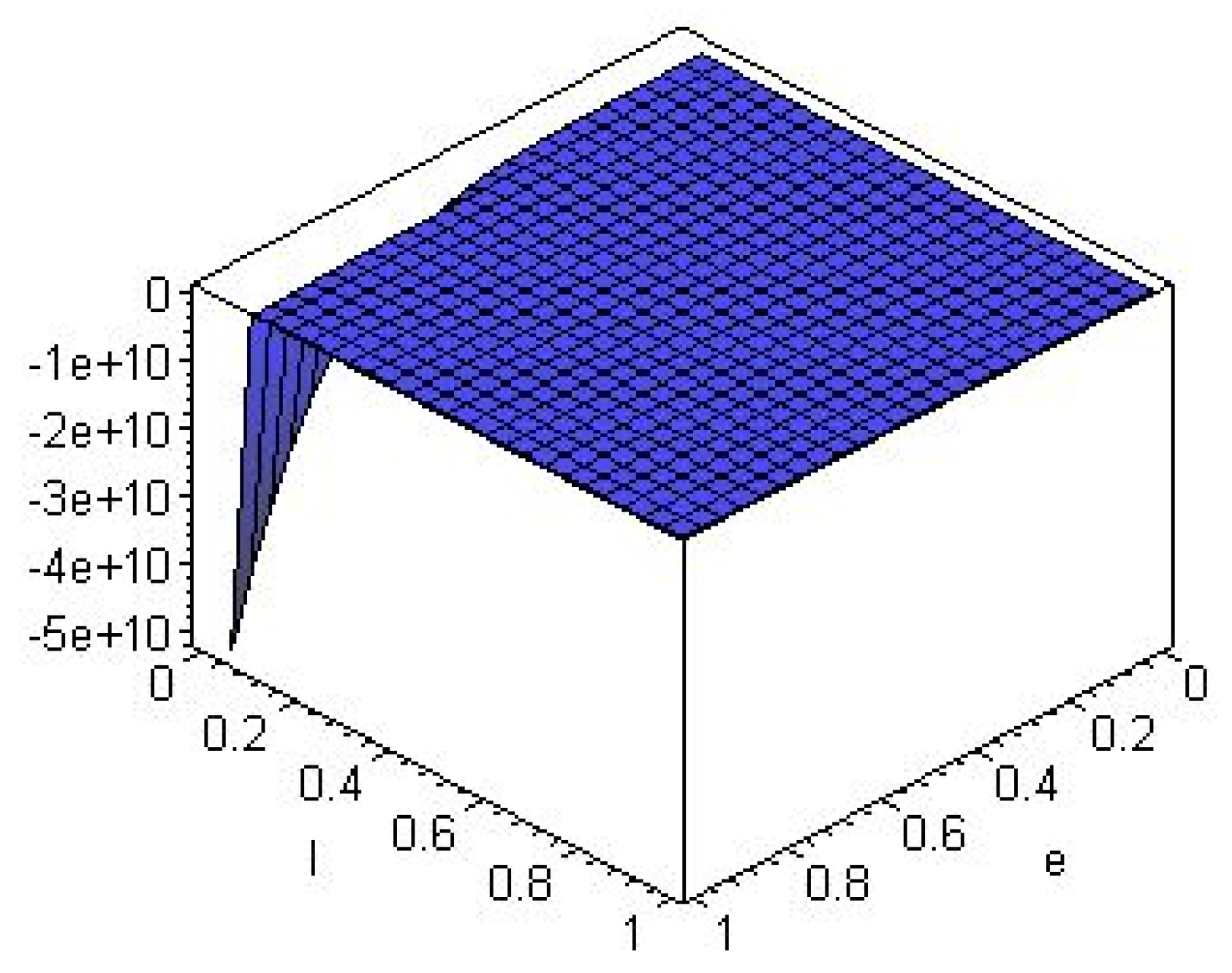
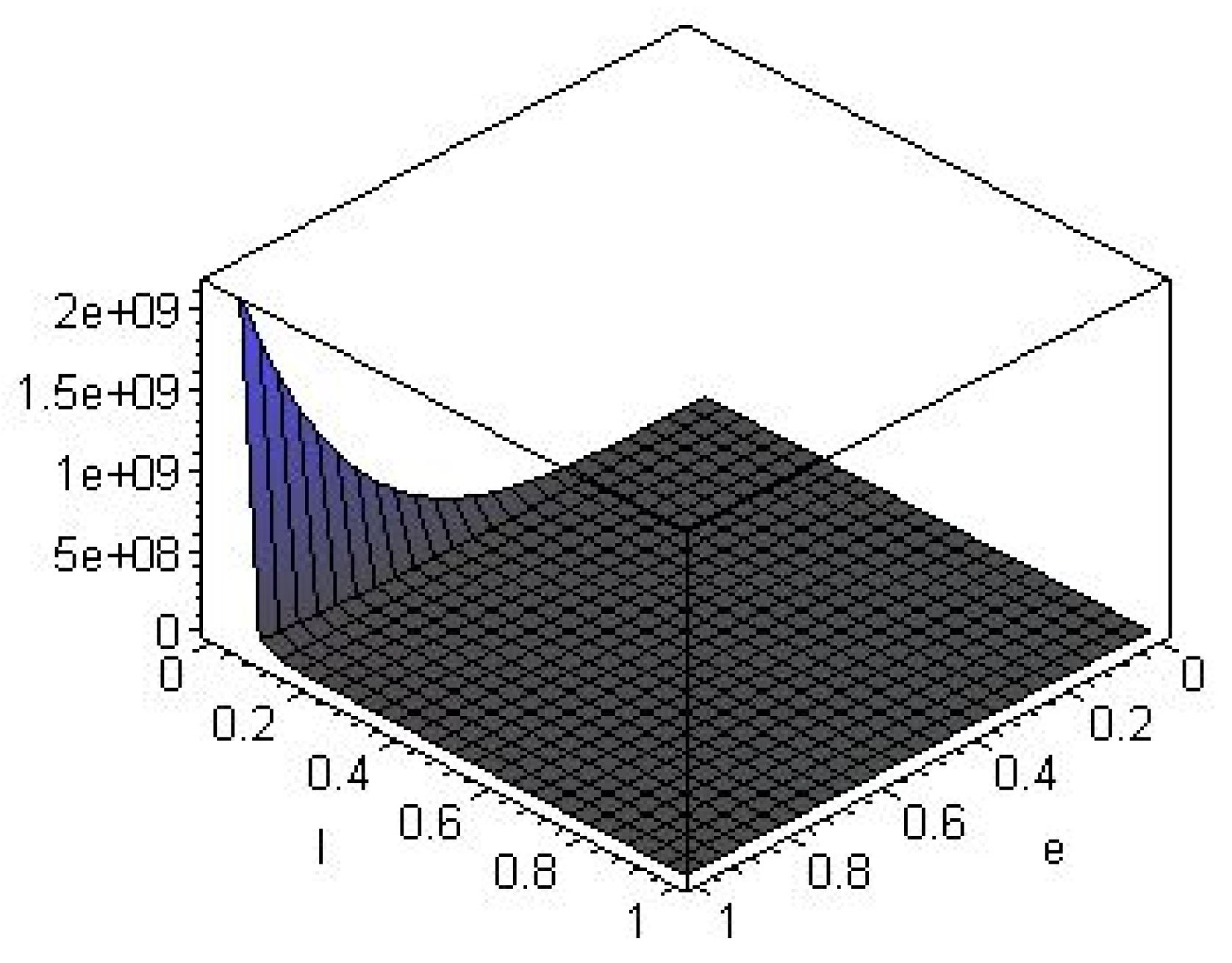
4. Weinhold Geometry
4.1. Five Dimensional Black Holes
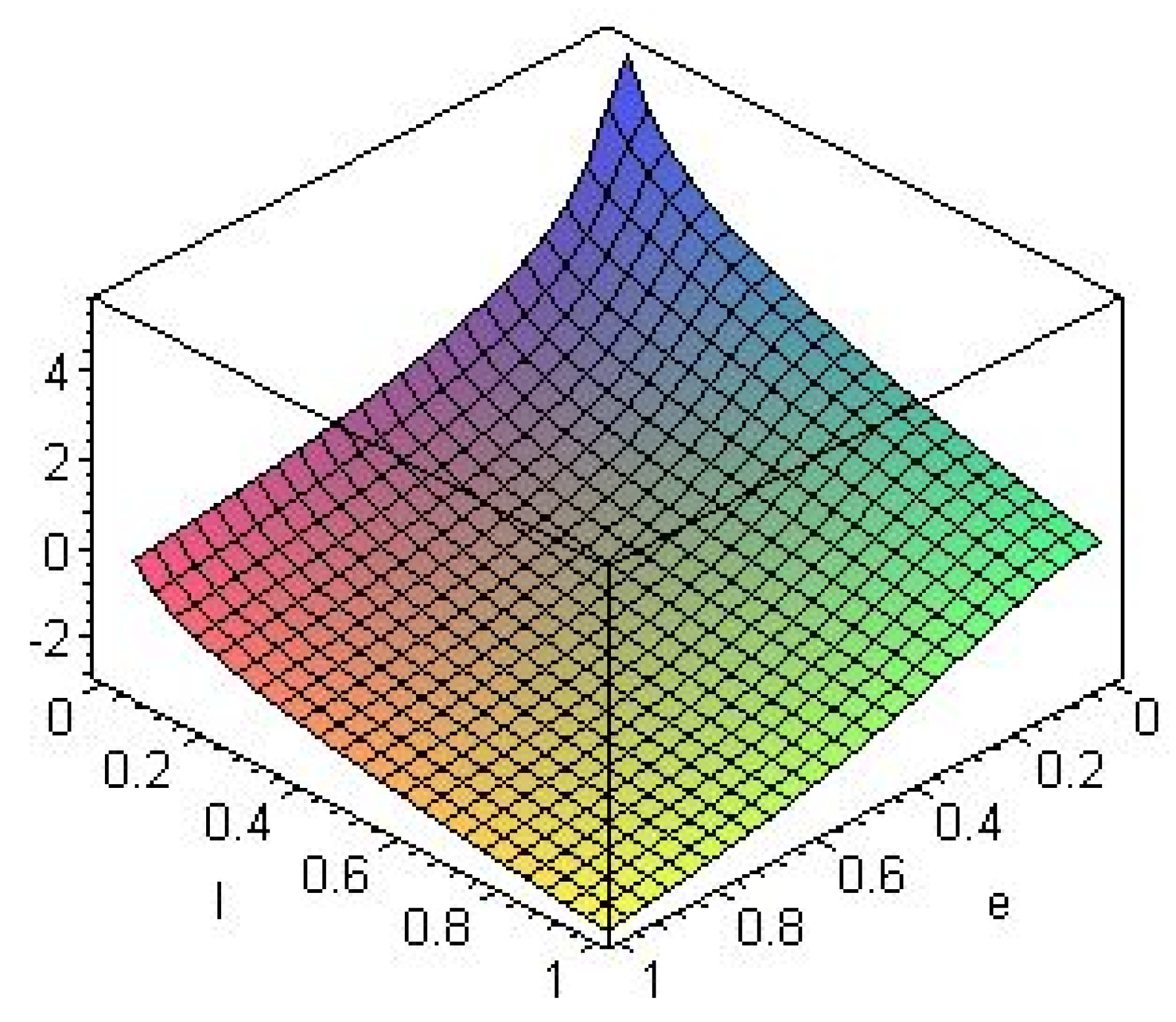
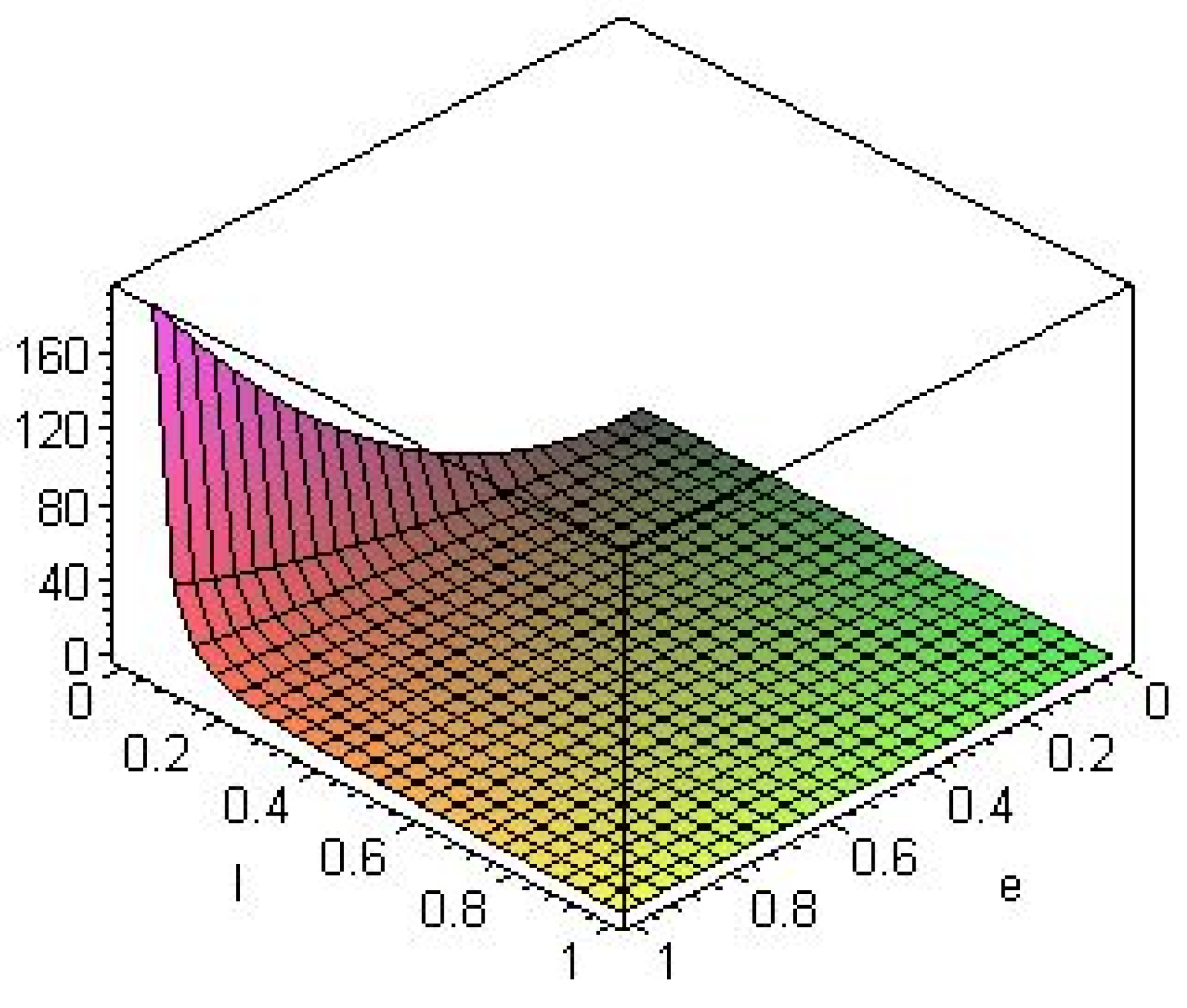
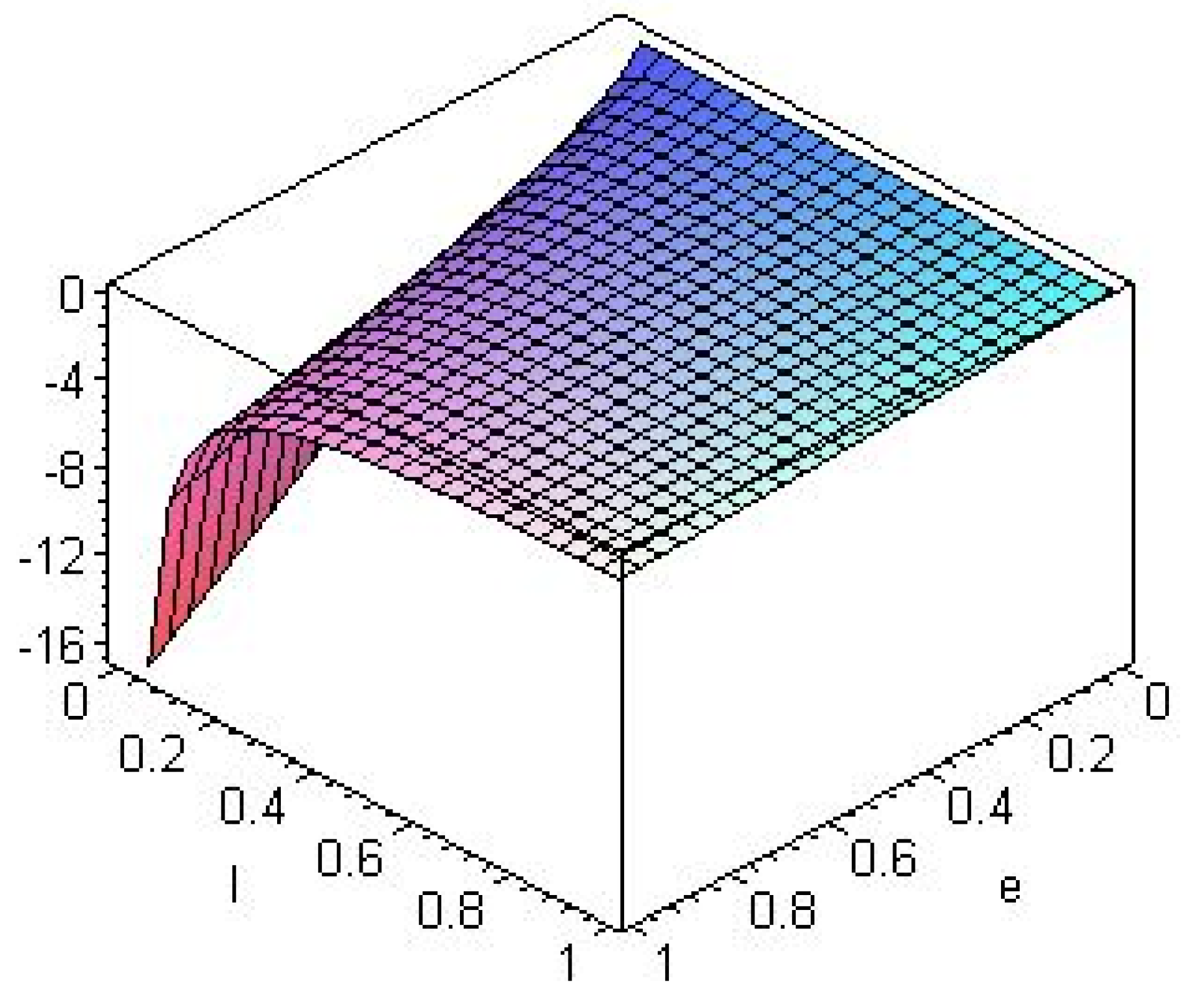
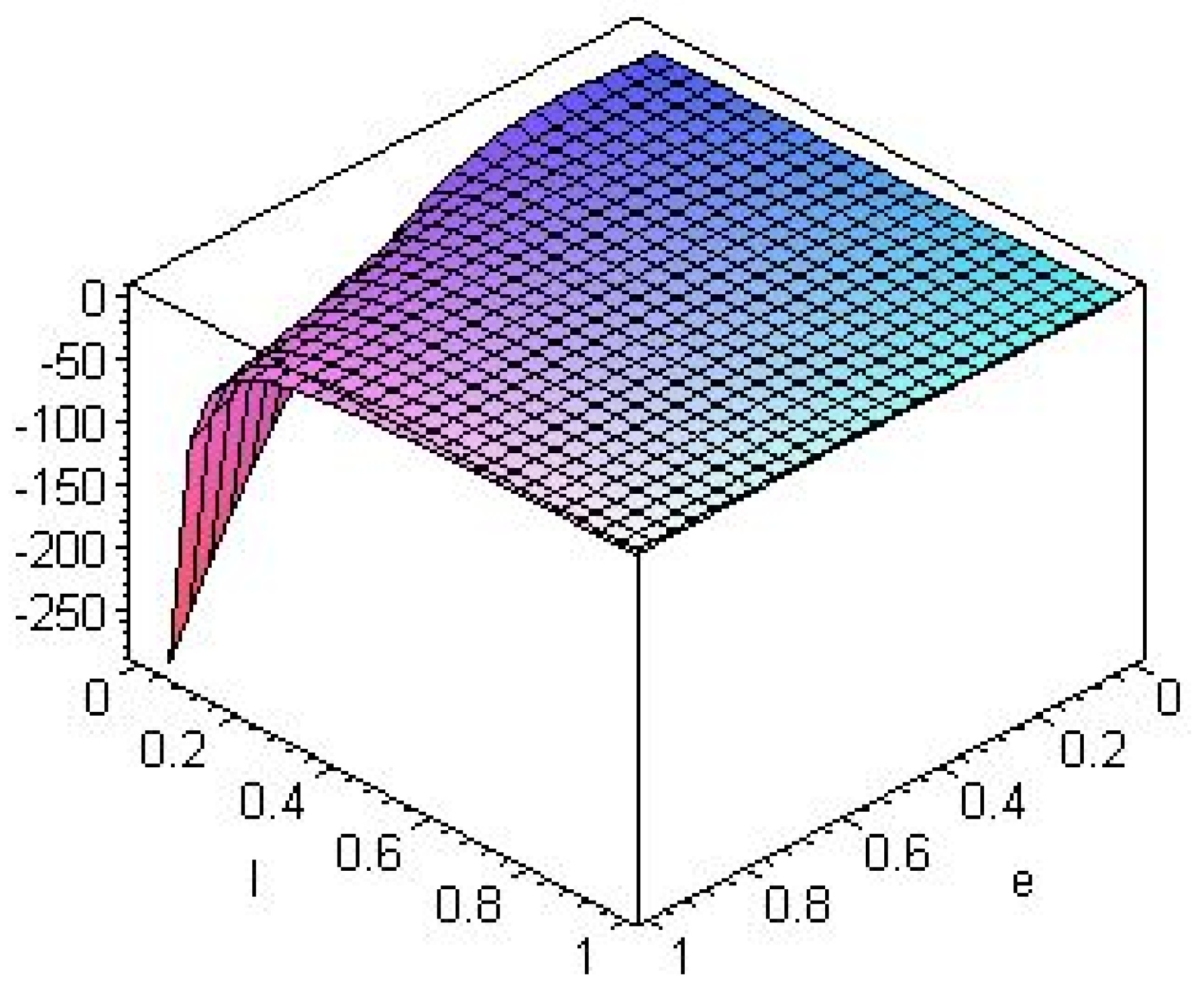
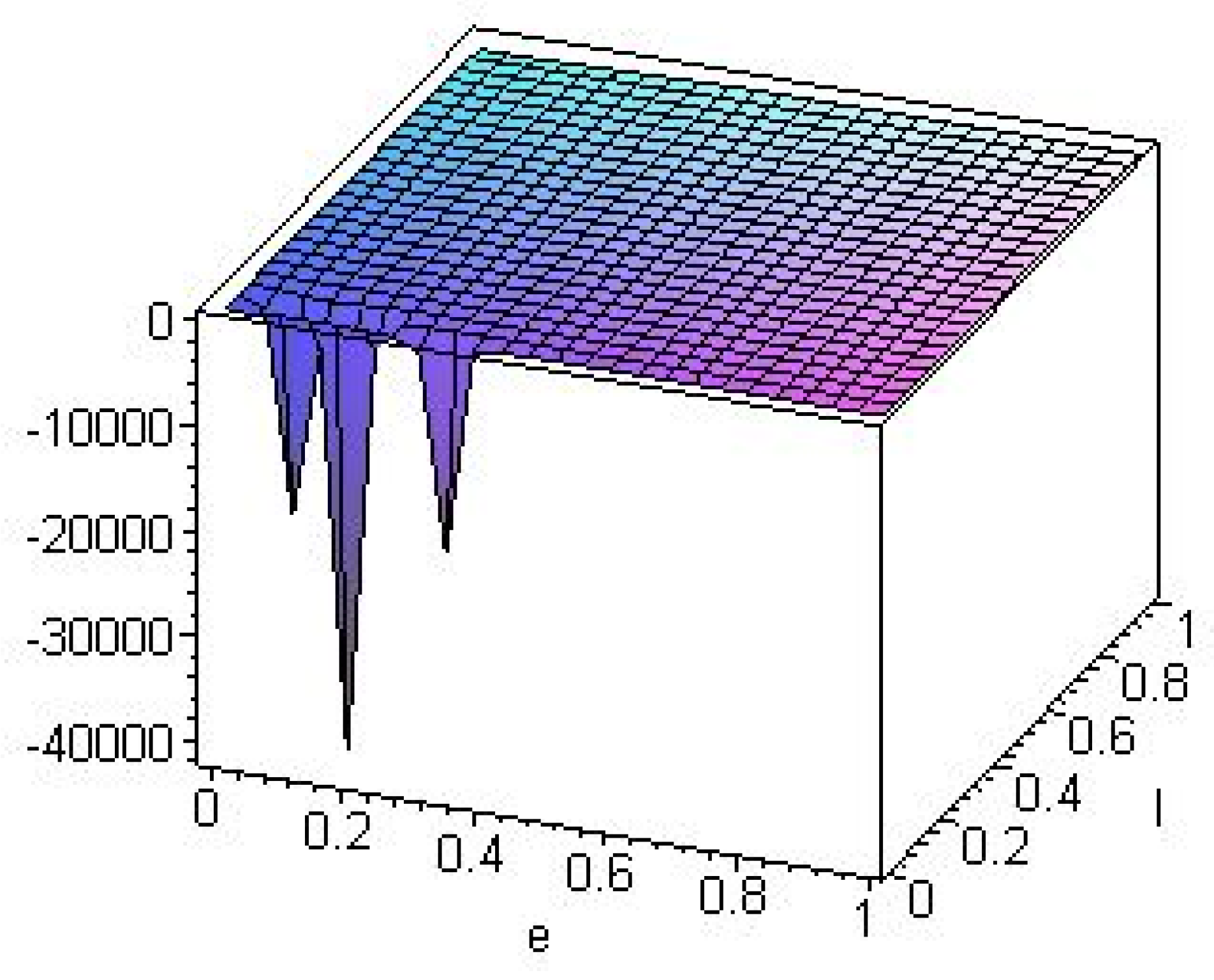
4.2. Higher Dimensional Black Holes

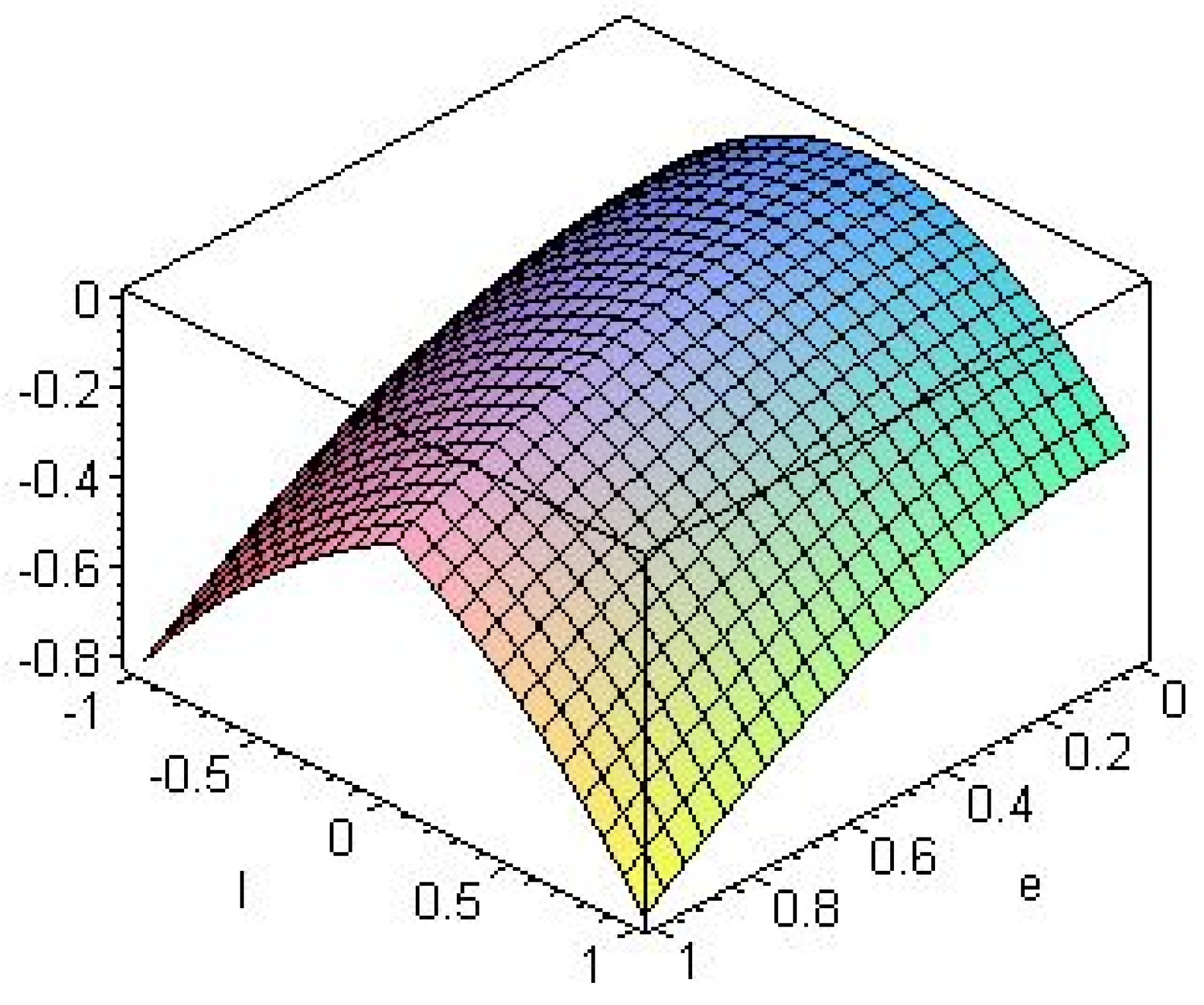
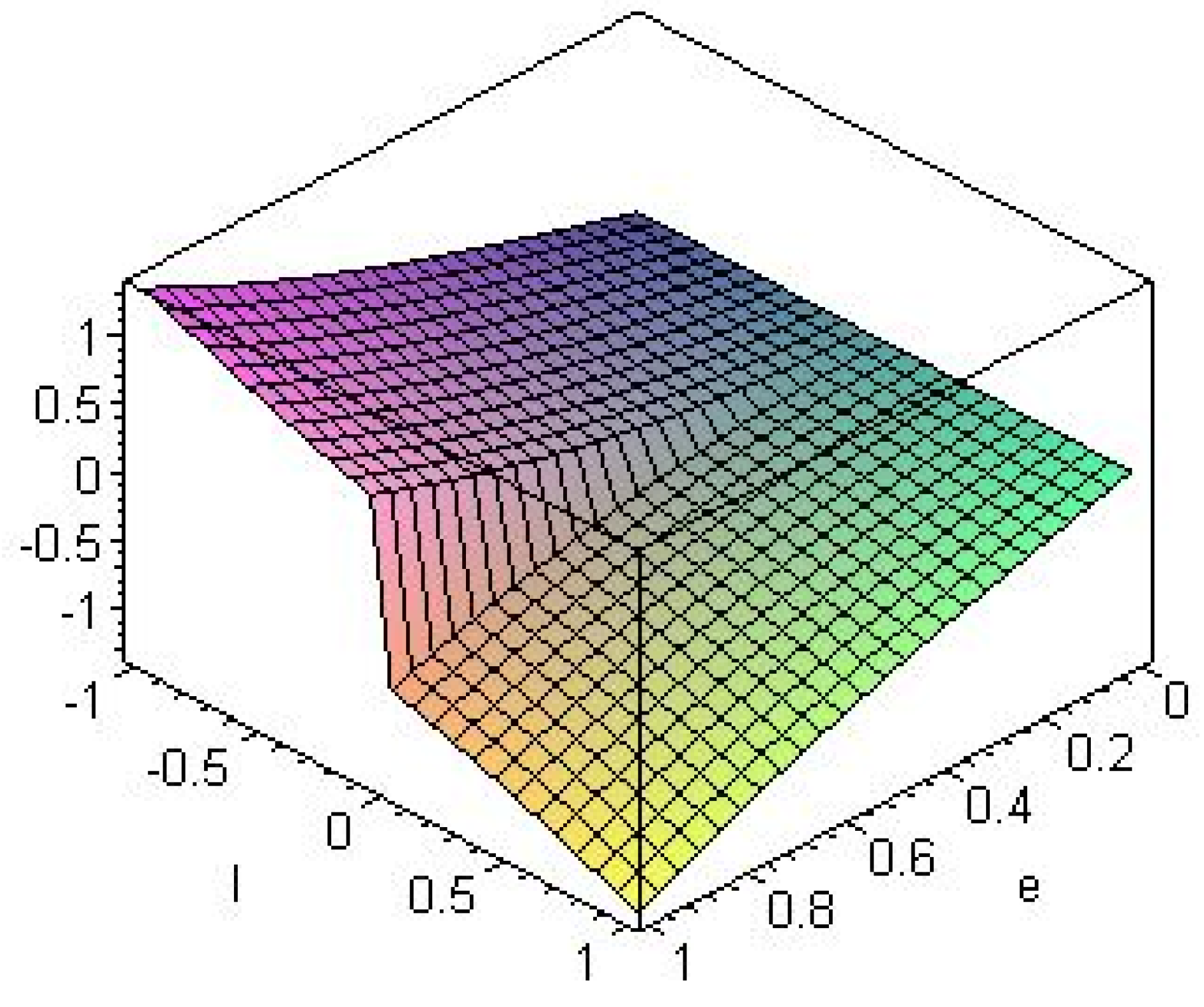
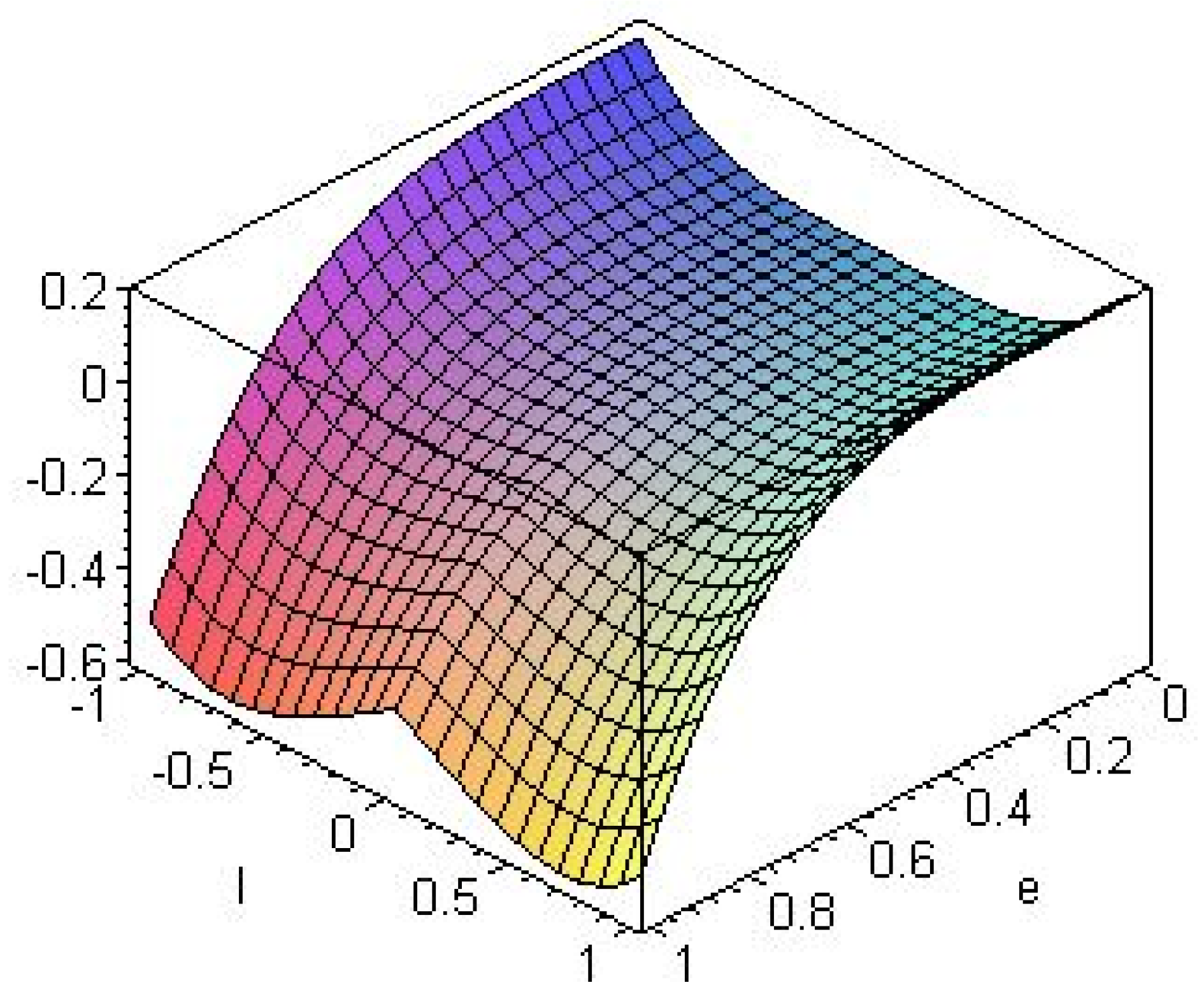
5. Conclusions
Acknowledgements
References
- Ruppeiner, G. Riemannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys. 1995, 67, 605, Erratum 1996, 68, 313. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamic curvature and phase transitions in Kerr–Newman black holes. Phy. Rev. D 2008, 78, 024016. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamics: A Riemannian geometric model. Phys. Rev. A 1979, 20, 1608–1613. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamic critical fluctuation theory? Phys. Rev. Lett. 1983, 50, 287–290. [Google Scholar] [CrossRef]
- Ruppeiner, G. New thermodynamic fluctuation theory using path integrals. Phys. Rev. A 1983, 27, 1116–1133. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamic curvature of the multicomponent ideal gas. Phys. Rev. A 1990, 41, 2200–2202. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, B.N. On Generalized Uncertainty Principle; LAP Academic Publication: Saarbrücken, Germany, 2011. [Google Scholar] [Green Version]
- Tiwari, B.N. Sur les corrections de la géométrie thermodynamique des trous noirs; Éditions Universitaires Européennes: Saarbrücken, Germany, 2011. [Google Scholar] [Green Version]
- Sarkar, T.; Sengupta, G.; Tiwari, B.N. On the thermodynamic geometry of BTZ black holes. J. High Energ. Phys. 2006, 2006, 15. [Google Scholar] [CrossRef]
- Sarkar, T.; Sengupta, G.; Tiwari, B.N. Thermodynamic geometry and extremal black holes in string theory. J. High Energ. Phys. 2008, 2008, 76. [Google Scholar] [CrossRef]
- Bellucci, S.; Tiwari, B.N. On the microscopic perspective of black branes thermodynamic geometry. Entropy 2010, 12, 2096. [Google Scholar] [CrossRef]
- Bellucci, S.; Tiwari, B.N. An exact fluctuating 1/2-BPS configuration. J. High Energ. Phys. 2010, 2010, 23. [Google Scholar] [CrossRef]
- Bellucci, S.; Tiwari, B.N. State-space correlations and stabilities. Phys. Rev. D 2010, 82, 084008. [Google Scholar] [CrossRef]
- Bellucci, S.; Tiwari, B.N. Thermodynamic geometry and Hawking radiation. J. High Energ. Phys. 2010, 2010, 30. [Google Scholar] [CrossRef]
- Bellucci, S.; Tiwari, B.N. Black strings, black rings and state-space manifold. Int. J. Mod. Phys. A 2011, 26, 5403–5464. [Google Scholar] [CrossRef]
- Bellucci, S.; Tiwari, B.N. State-space manifold and rotating black holes. J. High Energ. Phys. 2011, 2011, 118. [Google Scholar] [CrossRef]
- Aman, J.E.; Bengtsson, I.; Dokrajt, N. Flat information geometries in black hole thermodynamics. Gen. Rel. Grav. 2006, 38, 1305–1315. [Google Scholar] [CrossRef]
- Shen, J.; Cai, R.G.; Wang, B.; Su, R.K. Thermodynamic geometry and critical behavior of black holes. Int. J. Mod. Phys. A 2007, 22, 11–27. [Google Scholar] [CrossRef]
- Aman, J.E.; Bengtsson, I.; dokrajt, N. Geometry of black hole thermodynamics. Gen. Rel. Grav. 2003, 35, 1733–1743. [Google Scholar] [CrossRef]
- Aman, J.E.; Pidokrajt, N. Geometry of higher-dimensional black hole thermodynamics. Phys. Rev. D 2006, 73, 024017. [Google Scholar] [CrossRef]
- Tiwari, B.N. Geometric Perspective of Entropy Function: Embeddings, Spectrum and Convexity; LAP Academic Publication: Saarbrücken, Germany, 2011. [Google Scholar] [Green Version]
- Weinhold, F. Metric geometry of equilibrium thermodynamics. J. Chem. Phys. 1975, 63, 2479–2484. [Google Scholar] [CrossRef]
- Weinhold, F. Metric geometry of equilibrium thermodynamics. II. Scaling, homogeneity, and generalized Gibbs-Duhem relations. J. Chem. Phys. 1975, 63, 2484–2488. [Google Scholar] [CrossRef]
- Bellucci, S.; Chandra, V.; Tiwari, B.N. On the thermodynamic geometry of hot QCD. Int. J. Mod. Phys. A 2011, 26, 43–70. [Google Scholar] [CrossRef]
- Bellucci, S.; Chandra, V.; Tiwari, B.N. A geometric approach to correlations and quark number susceptibilities. Mod. Phys. Lett. A 2010, 27(10), 1250055–1250061. [Google Scholar] [CrossRef]
- Bellucci, S.; Chandra, V.; Tiwari, B.N. Thermodynamic stability of Quarkoniumn bound states. Int. J. Mod. Phys. A 2011, 26, 2665–2724. [Google Scholar] [CrossRef]
- Bartnik, R.; McKinnon, J. Particlelike solutions of the Einstein–Yang–Mills equations. Phys. Rev. Lett. 1988, 61, 141–144. [Google Scholar] [CrossRef] [PubMed]
- Yasskin, P.B. Solutions for gravity coupled to massless gauge fields. Phys. Rev. D 1975, 12, 2212–2217. [Google Scholar] [CrossRef]
- Winstanley, E. Physics of black holes. Lect. Notes Phys. 2009, 769, 49–87. [Google Scholar]
- Okuyama, N.; Maeda, K. I. Five-dimensional black hole and particle solution with a non-Abelian gauge field. Phys. Rev. D 2003, 67, 104012–104030. [Google Scholar]
- Mazharimousavi, S. H.; Halilsoy, M. Einstein–Yang–Mills black hole solution in higher dimensions by the Wu–Yang Ansatz. Phys. Lett. B 2008, 659, 471–475. [Google Scholar] [CrossRef]
- Brihaye, Y.; Chakrabarti, A.; Tchrakian, D.H. Particle-like solutions to higher-order curvature Einstein–Yang–Mills systems in d dimensions. Classical Quant. Grav. 2003, 20, 02765–02784. [Google Scholar] [CrossRef]
- Brihaye, Y.; Chakrabarti, A.; Hartmann, B.; Tchrakian, D.H. Higher order curvature generalizations of Bartnick–McKinnon and coloured black hole solutions in d=5. Phys. Lett. B 2003, 561, 161–173. [Google Scholar] [CrossRef]
- Torii, T.; Maeda, K.I.; Tachizawa, T. Cosmic colored black holes. Phys. Rev. D 1995, 52, R4272–R4276. [Google Scholar] [CrossRef]
- Volkov, M. S.; Straumann, N.; Lavrelashvili, G.; Heusler, M.; Brodbeck, O. Cosmological analogues of the Bartnik–McKinnon solutions. Phys. Rev. D 1996, 54, 7243–7251. [Google Scholar] [CrossRef]
- Mann, R.B.; Radu, E.; Tchrakian, D.H. Non-Abelian solutions in AdS4 and d=11 supergravity. Phys. Rev. D 2006, 74, 064015–064039. [Google Scholar] [CrossRef]
- Bjoraker, J.; Hosotani, Y. Stable monopole and Dyon solutions in the Einstein–Yang–Mills theory in asymptotically anti-de Sitter space. Phys. Rev. Lett. 2000, 84, 1853–1856. [Google Scholar] [CrossRef] [PubMed]
- Baxter, J.E.; Winstanley, E. On the existence of soliton and hairy black hole solutions of su(N) Einstein–Yang–Mills theory with a negative cosmological constant. Classical Quant. Grav. 2008, 25, 245014–245044. [Google Scholar] [CrossRef]
- Brodbeck, O.; Heusler, M.; Lavrelashvili, G.; Straumann, N.; Volkov, M.S. Stability analysis of new solutions of the EYM system with a cosmological constant. Phys. Rev. D 1996, 54, 7338–7352. [Google Scholar] [CrossRef]
- Winstanley, E. Existence of stable hairy black holes in su(2) Einstein–Yang–Mills theory with a negative cosmological constant. Classical Quant. Grav. 1999, 16, 1963–1978. [Google Scholar] [CrossRef]
- Wu, T.T.; Yang, C.N. Properties of Matter under Unusual Conditions; Mark, H., Fenbach, S., Eds.; Interscience: New York, NY, USA, 1969; pp. 349–354. [Google Scholar] [Green Version]
- Bostani, N.; Dehghani, M.H. Topological black holes of (n+1)-dimensional Einstein–Yang–Mills gravity. Mod. Phys. Letts. A 2010, 25(18), 1507–1519. [Google Scholar] [CrossRef]
- Cvetic, M.; Lu, H.; Pope, C.N. Non-Abelian black holes in D=5 maximal gauged supergravity. Phys. Rev. D 2010, 81, 044023–044030. [Google Scholar] [CrossRef]
- Hubeny, V.E.; Minwalla, S.; Rangamani, M. The fluid/gravity correspondence. arXiv 2011. [Google Scholar] [Green Version]
- Banerjee, N.; Bhattacharya, J.; Bhattacharyya, S.; Jain, S.; Minwalla, S.; Sharma, T. Constraints on fluid dynamics from equilibrium partition functions. arXiv 2012. [Google Scholar] [CrossRef]
Appendix A: Ruppeiner Geometry of Higher Dimensional Topological Einstein–Yang–Mills Black Holes
Appendix B: Weinhold Geometry of Five Dimensional Topological Einstein–Yang–Mills Black Holes
Appendix C: Weinhold Geometry of Higher Dimensional Topological Einstein–Yang–Mills Black Holes
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bellucci, S.; Tiwari, B.N. Thermodynamic Geometry and Topological Einstein–Yang–Mills Black Holes. Entropy 2012, 14, 1045-1078. https://doi.org/10.3390/e14061045
Bellucci S, Tiwari BN. Thermodynamic Geometry and Topological Einstein–Yang–Mills Black Holes. Entropy. 2012; 14(6):1045-1078. https://doi.org/10.3390/e14061045
Chicago/Turabian StyleBellucci, Stefano, and Bhupendra Nath Tiwari. 2012. "Thermodynamic Geometry and Topological Einstein–Yang–Mills Black Holes" Entropy 14, no. 6: 1045-1078. https://doi.org/10.3390/e14061045
APA StyleBellucci, S., & Tiwari, B. N. (2012). Thermodynamic Geometry and Topological Einstein–Yang–Mills Black Holes. Entropy, 14(6), 1045-1078. https://doi.org/10.3390/e14061045



