Entropy-Based Block Processing for Satellite Image Registration
Abstract
:1. Introduction
2. Scale-invariant Feature Transform
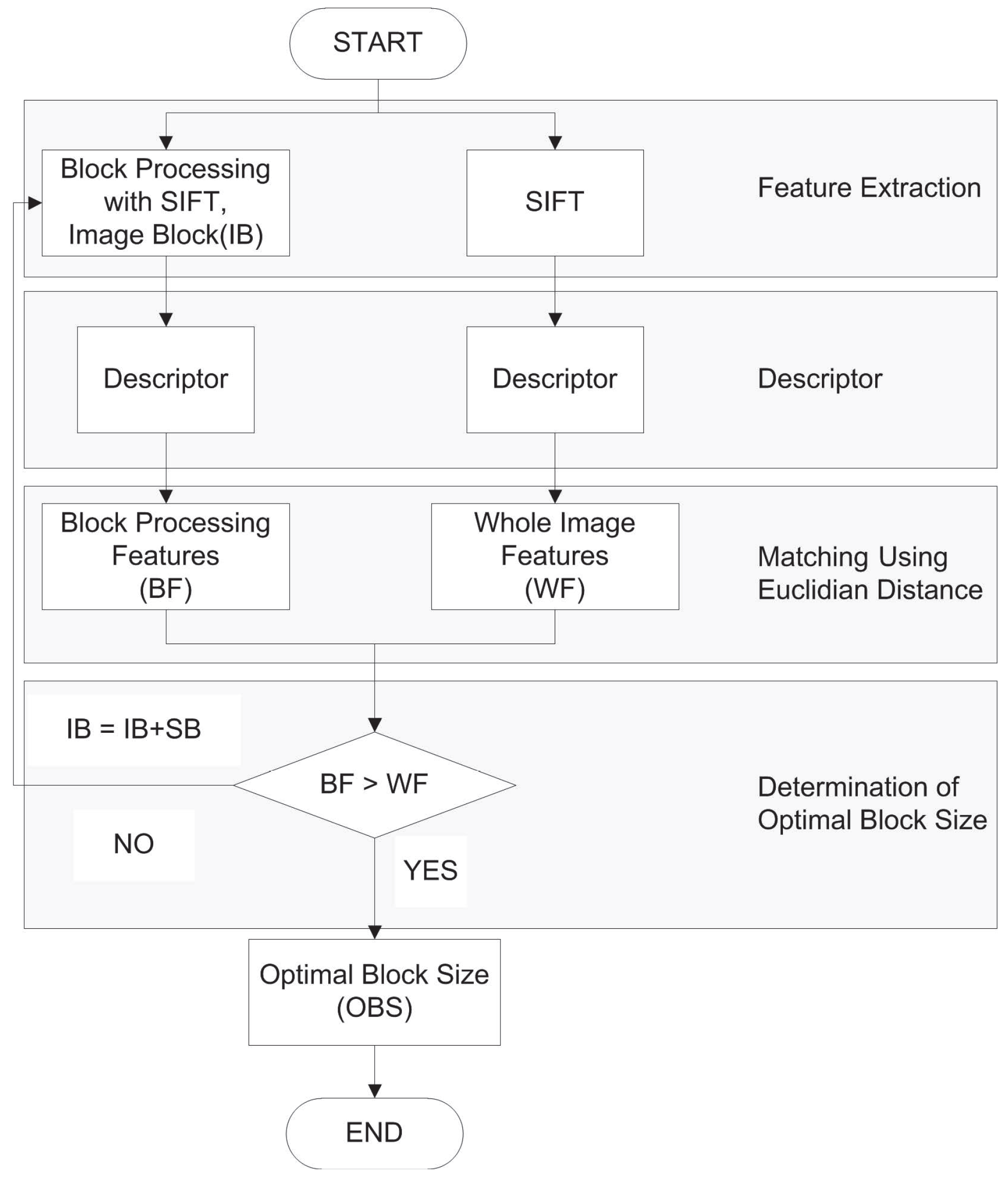
3. Proposed Method
| Step | Process | Time Consumed |
|---|---|---|
| Detector | Scale space | 96.64 |
| Difference of Gaussian (DoG) | ||
| DoG extrema | ||
| Localization: Filter edge and low contrast responses | ||
| Descriptor | Assign keypoints orientations | 114.17 |
| Histogram, Normalization, Gaussian weighting | ||
| Matching | Feature matching | 102.42 |
3.1. Block Processing

| Block size | Non-block | |||
|---|---|---|---|---|
| The number of features | 5532 | 3361 | 5756 | 6987 |
| Processing time(s) | 9531.3993 | 436.4116 | 497.1570 | 520.8296 |
3.2. Determination of Optimal Block Size

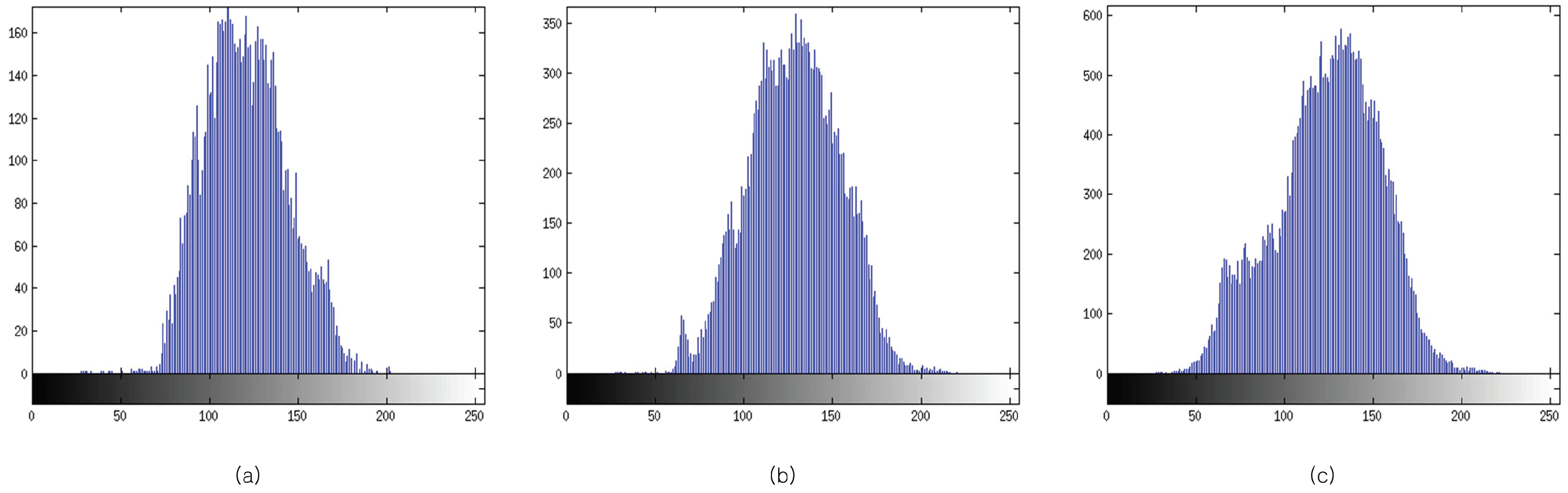
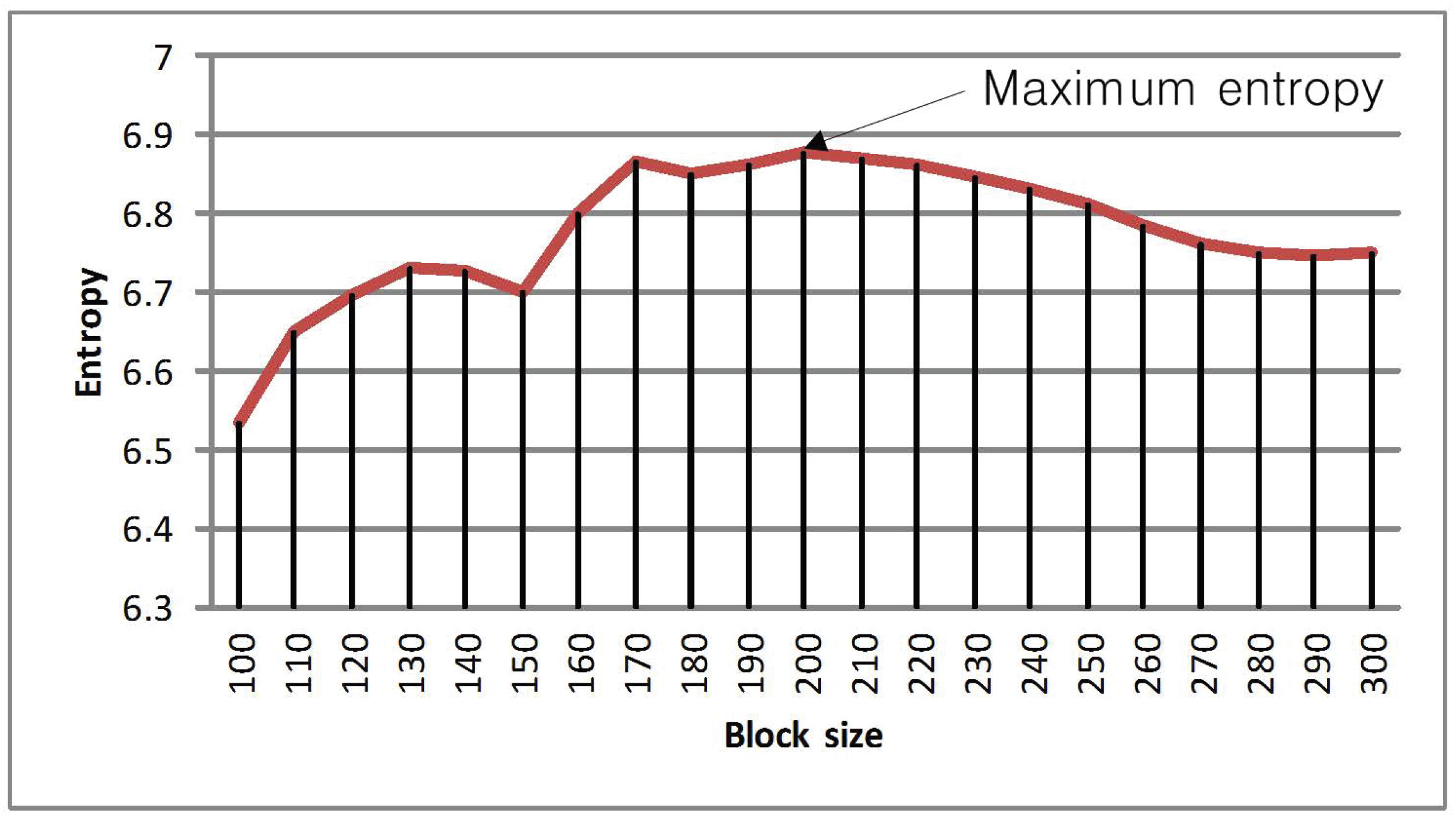
4. Experimental Results

| Parameter | Value |
|---|---|
| (a) Scale space | |
| Number of octaves in scale space | 9 |
| Number of scale per octave | 3 |
| Nominal pre-smoothing | 0.05 |
| (b) Detector | |
| Local extrema threshold | 0.001 |
| Local extrema localization threshold | 2 |
| (c) Descriptor | |
| Descriptor window magnification | 3.0 |
| Number of spatial bins | 4 |
| Number of orientation bins | 8 |

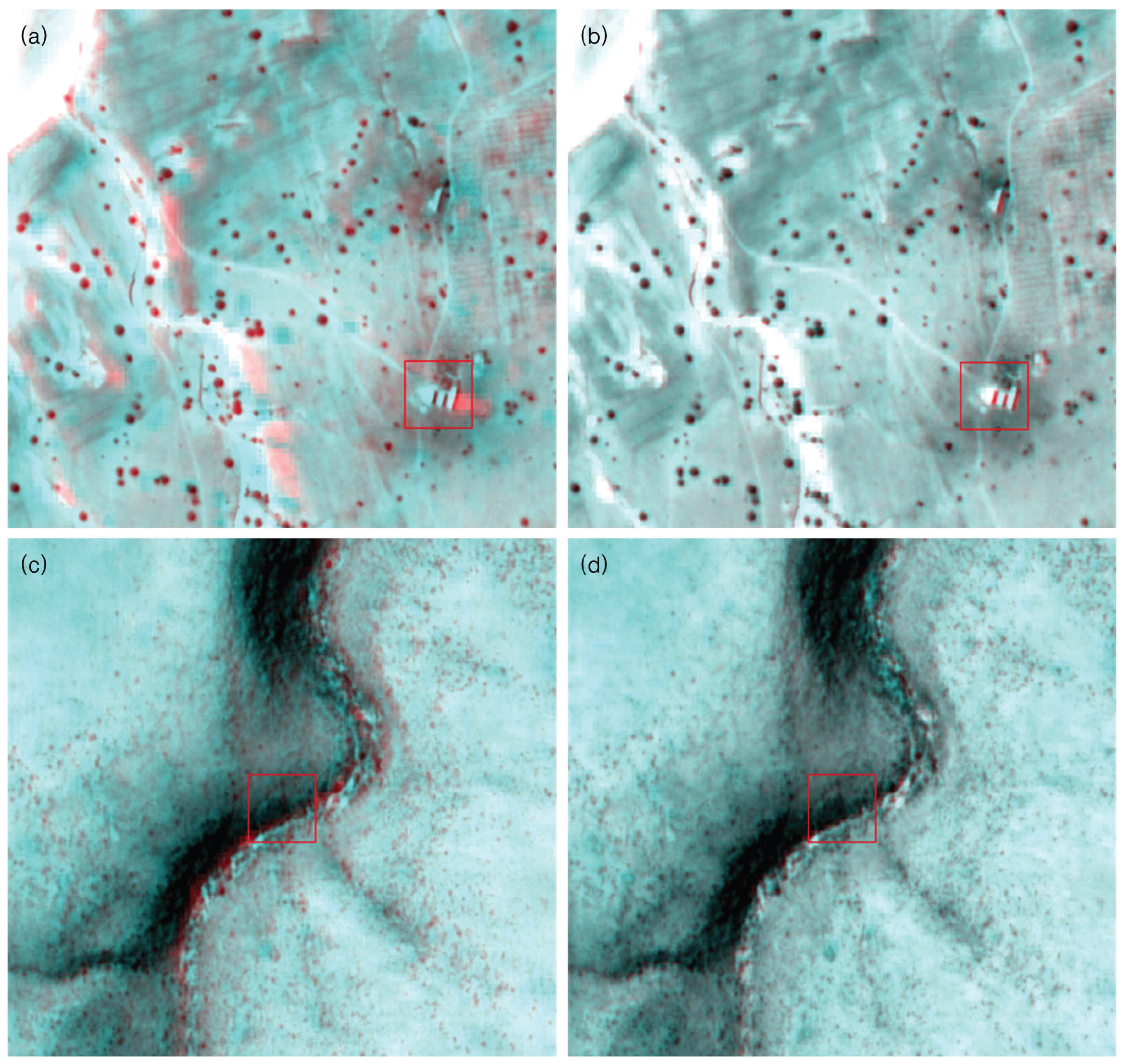
| Block size | Non-block | |||
|---|---|---|---|---|
| (a) Sample 1 | ||||
| Total matching points | 5532 | 3361 | 5756 | 6987 |
| Processing time(s) | 9531.3993 | 436.4116 | 497.1570 | 520.8296 |
| RMSE | 0.3760 | 0.3536 | 0.3010 | 0.3075 |
| (a) Sample 2 | ||||
| Total matching points | 1742 | 1206 | 2062 | 2351 |
| Processing time(s) | 8404.5322 | 295.9979 | 322.8102 | 338.1715 |
| RMSE | 0.7987 | 0.5963 | 0.4597 | 0.4830 |
5. Conclusions
Acknowledgment
References
- Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1615–1630. [Google Scholar] [CrossRef] [PubMed]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Freeman, W.; Adelson, E. The design and use of steerable filters. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 891–906. [Google Scholar] [CrossRef]
- Koenderink, J.; van Doorn, A. Representation of local geometry in the visual system. Biol. Cybern. 1987, 55, 367–375. [Google Scholar] [CrossRef] [PubMed]
- Lazebnik, S.; Schmid, C.; Ponce, J. A sparse texture representation using affine-invariant regions. In Proceedings of the Computer Vision and Pattern Recognition, IEEE Computer Society Conference, Madison, USA, 18-20 June 2003; Volume 2, pp. 319–324.
- Lowe, D. Object Recognition From Local Scale-Invariant Features. In Proceedings of the Computer Vision and Pattern Recognition, IEEE Computer Society Conference, Ft. Collins, USA, 23-25 June 1999; Volume 2, pp. 1150–1157.
- Lowe, D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Ke, Y.; Sukthankar, R. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors. In Proceedings of the Computer Vision and Pattern Recognition, IEEE Computer Society Conference, Washington, D.C., USA, 27 June - 2 July, 2004; Volume 2, pp. 506–513.
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Computer vision and image understanding 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Juan, L.; Gwun, O. A comparison of sift, pca-sift and surf. Int. J. Image Process. 2009, 3, 143–152. [Google Scholar]
- Friedman, J.; Bentley, J.; Finkel, R. An algorithm for finding best matches in logarithmic expected time. ACM Trans. Math. Softw 1977, 3, 209–226. [Google Scholar] [CrossRef]
- Vila, M.; Bardera, A.; Feixas, M.; Sbert, M. Tsallis mutual information for document classification. Entropy 2011, 13, 1694–1707. [Google Scholar] [CrossRef]
- Koenderink, J. The structure of images. Biol. Cybern. 1984, 50, 363–370. [Google Scholar] [CrossRef] [PubMed]
- Lindeberg, T. Scale-space Theory in Computer Vision; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Bernstein, R. Image geometry and rectification. Man. Remote Sens. 1983, 1, 873–922. [Google Scholar]
- Chen, H.; Arora, M.; Varshney, P. Mutual information-based image registration for remote sensing data. Int. J. Remote Sens. 2003, 24, 3701. [Google Scholar] [CrossRef]
- Hong, G.; Zhang, Y. Wavelet-based image registration technique for high-resolution remote sensing images. Comput. Geosci. 2008, 34, 1708–1720. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lee, I.; Seo, D.-C.; Choi, T.-S. Entropy-Based Block Processing for Satellite Image Registration. Entropy 2012, 14, 2397-2407. https://doi.org/10.3390/e14122397
Lee I, Seo D-C, Choi T-S. Entropy-Based Block Processing for Satellite Image Registration. Entropy. 2012; 14(12):2397-2407. https://doi.org/10.3390/e14122397
Chicago/Turabian StyleLee, Ikhyun, Doo-Chun Seo, and Tae-Sun Choi. 2012. "Entropy-Based Block Processing for Satellite Image Registration" Entropy 14, no. 12: 2397-2407. https://doi.org/10.3390/e14122397
APA StyleLee, I., Seo, D.-C., & Choi, T.-S. (2012). Entropy-Based Block Processing for Satellite Image Registration. Entropy, 14(12), 2397-2407. https://doi.org/10.3390/e14122397





