Today, it can be safely said that the code-script has been fully decoded, yet we are incapable of arbitrary prediction. This is not a problem having to do with DNA conceived as a program, but a property of computational irreducibility, as stressed by Wolfram [
4]. Wolfram shows that simple computer programs are capable of producing apparently random (not
algorithmically random) behavior. Wolfram’s cellular automaton Rule 30 is the classic example, as it is by most standards the simplest possible cellular automaton, yet we know of no way to shortcut its evolution other than by running the rule step by step. This was already known for some mathematical objects, such as the mathematical constant
π or
, which have simple representations, as they are computable numbers (one can algorithmically produce any arbitrary number of digits) the digits of whose decimal expansions look random. However, a formula has been found to shortcut the digits of
π in bases that are powers of
, where one does not need to compute the first digits in order to calculate a digit in any position of its
-ary expansion [
33].
Biological evolution and ecology are intimately linked, because the reproductive success of an organism depends crucially on its reading of the environment. If we assume that the environment is modeled as a Markov chain, we can map the organism’s sensors with a Hidden Markov Model (HMM). In such models, the state of the world is not directly observable. Instead, the sensors are a probabilistic function of the state. HMM techniques can solve a variety of problems: filtering (i.e., estimating the current state of the world), prediction (i.e., estimating future states), smoothing (i.e., estimating past states), and finding the most likely explanation (i.e., estimating the sequence of environmental states that best explains a sequence of observations according to a certain optimality criterion). HMMs have become a popular computational tool for the analysis of sequential data.
Following standard mathematical terminology, let us identify the environment as an HMM denoted by , a sequence of t random variables partially accessed by an organism using the sequence of observables , with corresponding to the hidden states. There are t states of the environment (e.g., “sunny”, “predator nearby”, “cold”, etc.), but organisms can only have partial access to them through . For every state there is a chance that an organism will perform one of a number of possible activities depending on the state of the environment.
In the simulation of a stochastic process, we attempt to generate information about the future based on the observation of the present and eventually of the past. However, implicit in the Markov model is the notion that the past and the future are independent. Particularly from the perspective of an observer, the model is memoryless. In this case it is said that the HMM is of the order
, which simply means that
,
i.e., the probability of the random variable
X being
x at time
t depends only on
at time
t. If the distribution of the states at time
is the same as that at time
t, the Markov process is called stationary [
34]. The stationary Markov process then has a stationary probability distribution, which we will assume throughout the paper in the interests of mathematical simplicity (without loss of generalization). An
m-order HMM is an HMM that allows transitions with probabilities among at most
states before the source state, which means that one can take advantage of correlations among these states for learning and predicting. In linguistics, for example, a 0-order HMM allows the description of a single gram distribution of letters (e.g., in several languages “e" is the most common letter), versus a 1-order HMM that provides information about bigrams, determining with a certain probability the letter that precedes or follows another letter (in English, for example, “h" following “t" is among the most common bigrams, so once a “t" is spotted one can expect an “h" to follow, and the probability of its so doing is high compared with, say, the probability of an "h" following a “z".) In a 2-HMM one can rule out the trigram “eee" in English, assigning it a probability 0 because it does not occur, while “ee" can be assigned a reasonable non-zero probability. In what follows we will use the HMM model to discuss potential energy extraction from a string.
4.1. Simulation of Increasingly Predictable Environments
There are distinct binary strings of length n. The probability of picking 1 among the is . We are interested in converting information (bits) into energy, but putting bits together means working with strings. Every bit in a string represents a state in the HMM; it will be 0 or 1 according to a probability value (a belief). So in this example, the organism processes information by comparing every possible outcome to the actual outcome, starting with no prior knowledge (the past is irrelevant). We know that for real organisms, the (evolutionary) past is very relevant, and it is often thought of in terms of a genetic history. This is indeed how we will conceptualize it. We will take advantage of what an HMM allows us to describe in order to model this “past".
Landauer’s Principle [
11,
12] states that erasing (or resetting) one bit produces
joules of heat, where
T is the ambient temperature and
k is Boltzmann’s constant (
J K
). Then it follows that an organism with finite storage memory updates its state
according to a series of
n observations at time
by a process of comparison. And if
differs from
by
j bits, then at least
joules will be spent, according to Landauer’s Principle, to reset the bits of
to
.
Pollination, for example, is the result of honeybees’ ability to remember foraging sites, and is related to the honeybee memory endurance, hence its learning and storing capabilities. Honeybees use landmarks, celestial cues and path integration to forage for pollen and nectar and natural resources like propolis and water [
35].
But and can only differ by at most n bits, and they may do so by chance at most on average, in a random environment modeled by a 0-order HMM (a system with no memory). If every bit is equally likely, the probability of occurrence of any string of length n is .
Each of the strings can have different i bits, with . This difference can be measured by the Hamming distance d between strings of the same size.
4.2. Energy Groups
It follows that the number of “energy" groups according to the number of bits is precisely
n. This is because if one arbitrarily chooses “1" as a bit that will reconfigure a tape (see
Section 3.2) to produce energy, one can extract
k bits of energy out of a string of length
n given by the binomial formula:
For example, from a one bit binary string, 0 or 1 unit of energy can be extracted, depending on whether the string is 0 or 1 (in the simulations below we will actually assume that 0 returns
of energy, which is a fair assumption according to the one-dimensional random walk behavior of a Turing machine equipped with a piston, as described in
Section 3.2).
For length
we have the possible binary strings 00, 01, 10 and 11. If 1 is the energy returning bit, we have it that 00 returns no energy, 01 and 10 each provides 1 unit of energy, and 11 provides 2 units of energy, that is 1, 2, 1. For
, the energy distribution among all the
strings is 1, 3, 3, 1, and for
, the distribution is 1, 4, 6, 4, 1 (see
Figure 2). Evidently the maximum energy return of a binary string is bounded by the length of the string, that is
. The minimum energy return is always 0 for any
n (the string
, that is the repetition of
n 0s).
For random strings one would produce on average
joules, but to reach thermodynamic equilibrium one can take “0" as a negative return of energy, hence “-1" for these purposes. Thus from a random string one would get 0 units of energy on average. Strings like 01 and 10 are considered
energetically equivalent, given that each bit is independent in the stochastic environment, and the organism may expect one or another bit. In other words, if the organism expects a 1 in a string of 2 bits, the position of the bit in the string is irrelevant. It can come in first or second place in the 2 bit string; only when it occurs for the first time will it produce energy (compare again to the piston scenario in
Section 3.2).
There are
energy groups from the
strings of length
n (see
Figure 2 and
Figure 3). One can see then how
energy groups can form, each representing the possible amount of energy extracted from a sequence configuration (fixing the expected configuration). In such a case, a string like 0101 produces the same amount of energy as 1010, but also as 110 and 101. In general, for strings of length
n, the maximum amount of energy one can extract is
n, but with different probabilities (depending on the number of energy groups) one can actually get any integer value in the interval [
,
n]. Among the
strings of length
n, there are the energy groups
and
, each returning a different amount of free energy. For strings of 2 bits we have
and
, with −1, 0 and 2 as possible energy returns, hence only 3 groups. Therefore, the number of groups is given by the number of different energy returns. This probability can be calculated from
C as follows:
which is the probability of extracting
i joules out of string
s. Better said, it is the probability of getting a string with
i joules. If looking to produce negative work out of zeroes, then the probability of getting
i joules can be calculated by:
Figure 2.
Energy groups: Possible extraction values from the different energy groups among all the strings of increasing length . Each figure can be read as follows: Taking the first plot (top left), there is 1 string that has an energy return of 0 units of energy (0000); 4 strings that return 1 unit of energy (e.g., 0100); 6 strings that return 2 units of energy (e.g., 1100); 4 other strings that return 3 units of energy (e.g., 0111) and finally 1 string that can return the maximum energy (1111).
Figure 2.
Energy groups: Possible extraction values from the different energy groups among all the strings of increasing length . Each figure can be read as follows: Taking the first plot (top left), there is 1 string that has an energy return of 0 units of energy (0000); 4 strings that return 1 unit of energy (e.g., 0100); 6 strings that return 2 units of energy (e.g., 1100); 4 other strings that return 3 units of energy (e.g., 0111) and finally 1 string that can return the maximum energy (1111).
By turning from a 0-order (
Figure 2) to an
m-order HMM, one can model the organism’s ability to capture patterns of up to length
(by assigning probabilities based on a distribution of frequencies from experience, or learning). The energy one can extract from the environment is statistically described by the skewness of the probability distribution for energy extraction from strings decreasingly random in nature. For a 0-order HMM, the skewness (the degree of asymmetry of a distribution) of the normal distribution for
is evidently 0 (symmetric, evenly distributed, see
Figure 2), but as soon as the HMM is of order 1 (see
Figure 3) probabilities among states can have values different from
, and the skewness is negative for
, which means that the bulk of the distribution has shifted to the right and one can have a positive exchange of energy in an environment with some predictability.
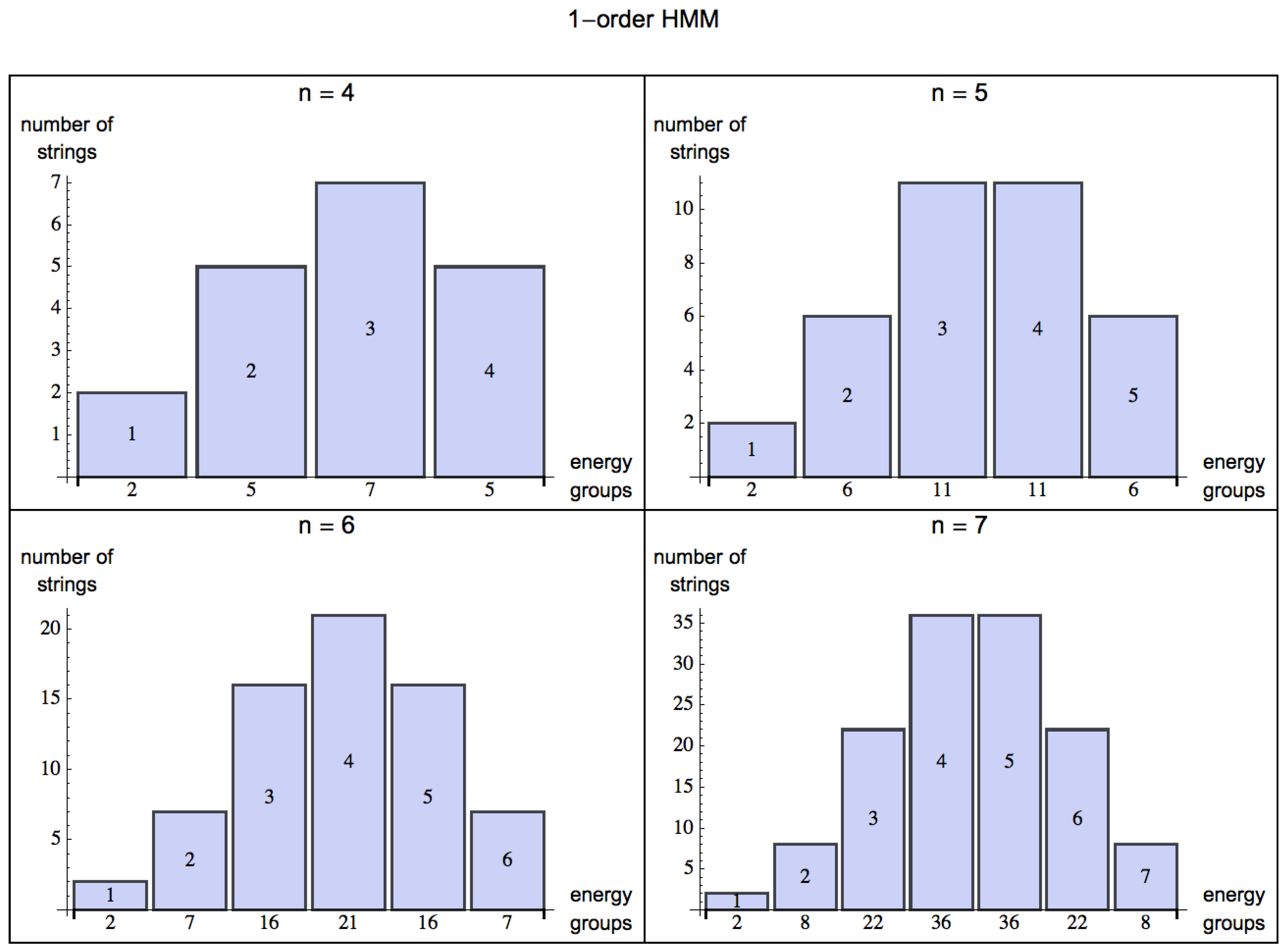
Figure 3.
Shift of the distributions of energy groups for strings of increasing length
, modeling a very simple potential predictable environment represented by a 1-order HMM (compared with a 0-order HMM in
Figure 2) in a scenario for
, where given a state, an organism can potentially make an optimal choice based on the transition value of the next state according to
p. The bulk of the values, measured by a negative skewness, clearly lie to the right of the mean, indicating the predictability of the environment (mirrored by the learning capabilities of living organisms) and therefore a possible positive energy extraction.
Figure 3.
Shift of the distributions of energy groups for strings of increasing length
, modeling a very simple potential predictable environment represented by a 1-order HMM (compared with a 0-order HMM in
Figure 2) in a scenario for
, where given a state, an organism can potentially make an optimal choice based on the transition value of the next state according to
p. The bulk of the values, measured by a negative skewness, clearly lie to the right of the mean, indicating the predictability of the environment (mirrored by the learning capabilities of living organisms) and therefore a possible positive energy extraction.
It is clear that different energy groups grow at different rates for increasing string length n (one way to visualize this is by plotting the Pascal triangle using the binomial formula). The number of strings of length n grows at while the number of strings from which energy can be extracted grows at a slower rate than (for example, the number of strings that provide maximum energy is always 1, and hence remains constant—the strings of n 1s). Thus, one can see how the equilibrium of energy returns pulls the distribution to the mean average, having as a consequence no positive energy return. The possibility of modeling transitions with probability , however, increases the number of strings with a positive energy return.
In other words, if an organism S is a finite state automaton able to make predictions about binary strings of at most length n (hence with memory capacity of length n) and the environment E is another finite-state automaton capable of generating strings of length m, if then S can predict any pattern produced by E. However if then S will be able to predict only patterns of length smaller than n and will miss those greater than m, potentially . Taken to the limit, if n is too short, or m too large compared with n, then S will miss most patterns in E.
4.3. Organisms Survive (only) in Predictable Environments
It is clear how living organisms convert information into energy by using information in locating food, for example, or in figuring out how to navigate within a habitat, in learning how to hunt, in securing a mate,
etc. As we argue, however, the extent to which an organism is adapted to or is able to produce offspring in a particular environment depends on a positive exchange ratio between information and energy. For an organism to make use of acquired information (e.g., for learning) it must be able to store it. In the context of biological systems, upon making an observation an organism must record both the stimulus and its appropriate response (e.g., Pavlov’s dog). Memory is a vital characteristic for many organisms (such as honeybees, which develop memory through learning gradually over time [
36,
37]) and therefore requires the persistence of periodic structures.
The previous rationale allows us to describe how an organism with finite memory will use and convert energy at an abstract fundamental thermodynamic level to keep up with the information from its environment and update its current state. For example, when foraging, honeybees form simple associations between landmarks in order to navigate along their flight path. Honeybees also use the direction of sunlight as an indication when traveling along familiar routes during the process of path integration. For these reasons [
38,
39], honeybees can fly back to their hives in complicated situations.
Natural selection has equipped organisms to cope with trade-offs involving memory capabilities, time spent and energy return, enabling them to take these into account when deciding whether to undertake certain actions in return for spending resources. Take cheetahs, for example, who spend most of their energy in the very first instants of a hunt. Because they are not able to keep up the speed of pursuit for longer periods, they have to size up a situation and hit upon the near optimal starting point for a chase.
So what does the existence of living organisms tell us about structure versus randomness in nature? That one would need to attribute incredible power to living organisms, power to overcome a random environment having no structure, or alternatively, to accept that a stochastic environment in which living organisms can survive and reproduce needs a degree of structure.
What computational thermodynamics tells us about nature is that organisms cannot survive in a random world, because in order to exchange energy for information about the world, the organism needs a minimum degree of predictability, or else it will not be able to take advantage of the information it has acquired and stored. Hence, an organism in a random world cannot survive due to fundamental thermodynamic limits.
4.4. DNA, Memory in Simple Organisms and Reactive Systems
Our argument might seem to depend on the physical memory of an organism, but it has been shown that reactive systems, for example, can exhibit non-trivial behavior without need of an explicit memory. A classical example is the kind of “vehicle" proposed by Braitenberg [
40]. These vehicles make simple, direct connections between sensors and actuators. For example, a vehicle with two photosensors on its sides (left and right) connected to opposing wheel motors (left sensor to right motor, right sensor to left motor) exhibits phototaxis. This is because the sensor closer to the light will cause the opposing motor to spin faster, turning the vehicle towards the light. If the vehicle turns too much, the other sensor will counteract this movement, and both sensors and motors will coordinate until the light source is reached. This behavior does not require an explicit memory, but it does require information stored in the design details of the system, perhaps mirroring what happens in very simple living organisms (such as insects, or simpler organisms such as bacteria), where DNA is the result of the state of the world acting directly on the information stored and codified by genes, as explained by Fisher [
6], and hence just another type of memory.
The difference between a reactive system—such as a Braitenberg vehicle—and a representational system (where bits in a memory represent aspects of the environment) is at the level of the location of the relevant information of the system. On the one hand, representational systems can store information in a specific location, generally updated many times during the lifespan of an organism. This is useful when the sensor channel capacity (maximum information that can be transmitted over a communications channel) is low compared with the environmental complexity, since not all of the relevant information can be sensed at once. On the other hand, reactive systems do not store information. Nevertheless, relevant information is required for computation to take place. In principle, a reactive system could perform tasks of the same complexity as a representational system [
41], but the reactive system would require a sensor channel capacity equal to or greater than the memory size of the representational system. For example, if an environment requires 4 bits of relevant information to be processed by an organism to survive, this could be achieved by a reactive system with four 1-bit sensors (each sensor having a 1-bit channel capacity), or by a representational system with a single 1-bit sensor and a 4-bit memory. The trade-off is similar to that of storing everything about the environment in the DNA or letting organisms evolve brains capable of storing information that is more volatile.
Given the fact that reactive systems also need to process relevant information from their environment, as stated by Ashby’s law of requisite variety [
14], our argument applies to both representational and reactive systems. These are finite, in memory and channel capacity, so the predictability of their environment is also limited. Representational systems are useful for prediction, while reactive systems are useful for adaptation. But computationally, either system requires the same environmental predictability in order to survive, independent of the particular strategy or mechanism used. How to balance memory and channel capacity is certainly an interesting topic, mirrored in the trade-off aforementioned (DNA storage versus brain storage), but it is beyond the scope of this paper.