Programming Unconventional Computers: Dynamics, Development, Self-Reference
Abstract
:1. Introduction
2. Classical History and Unconventional Futures
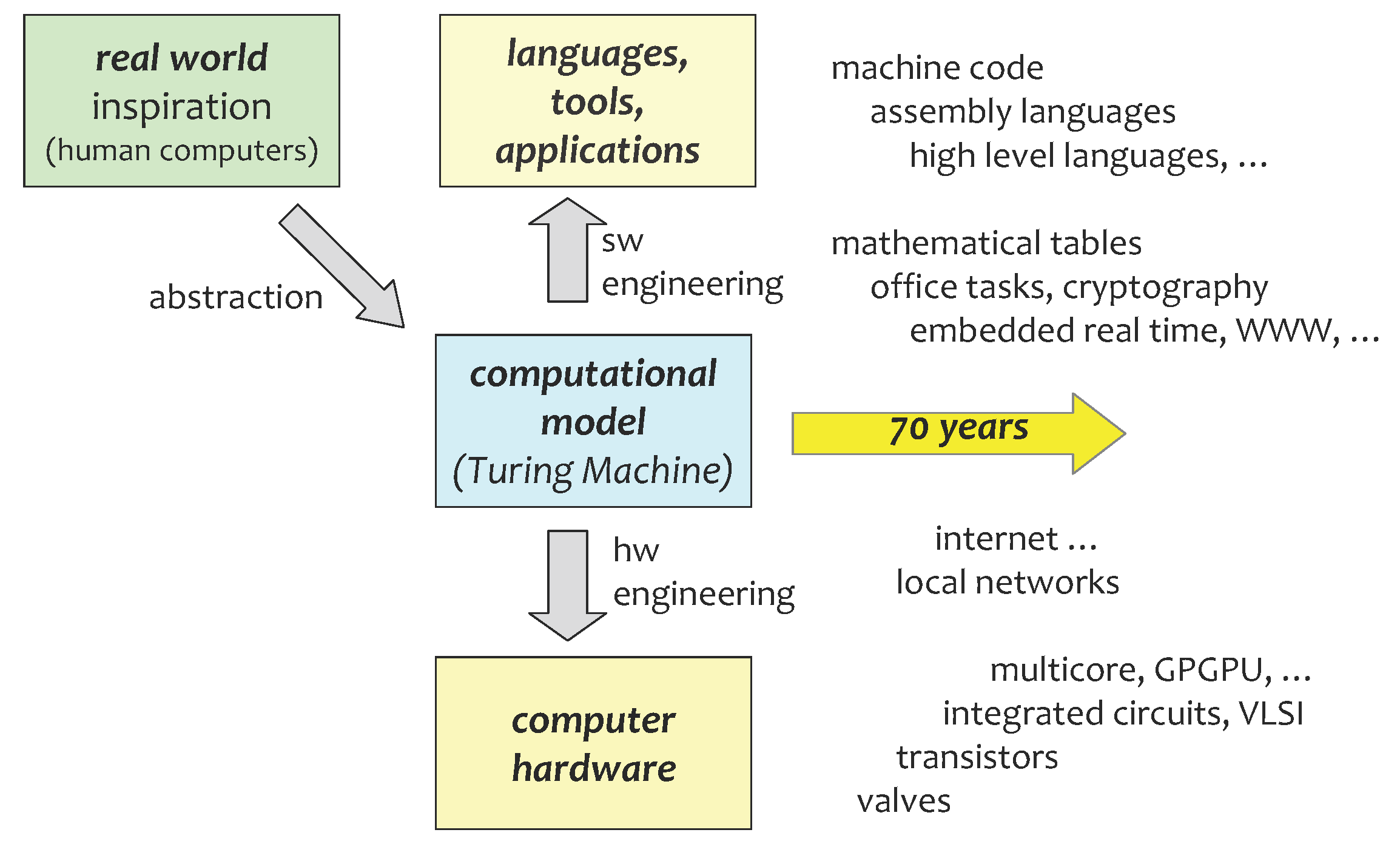
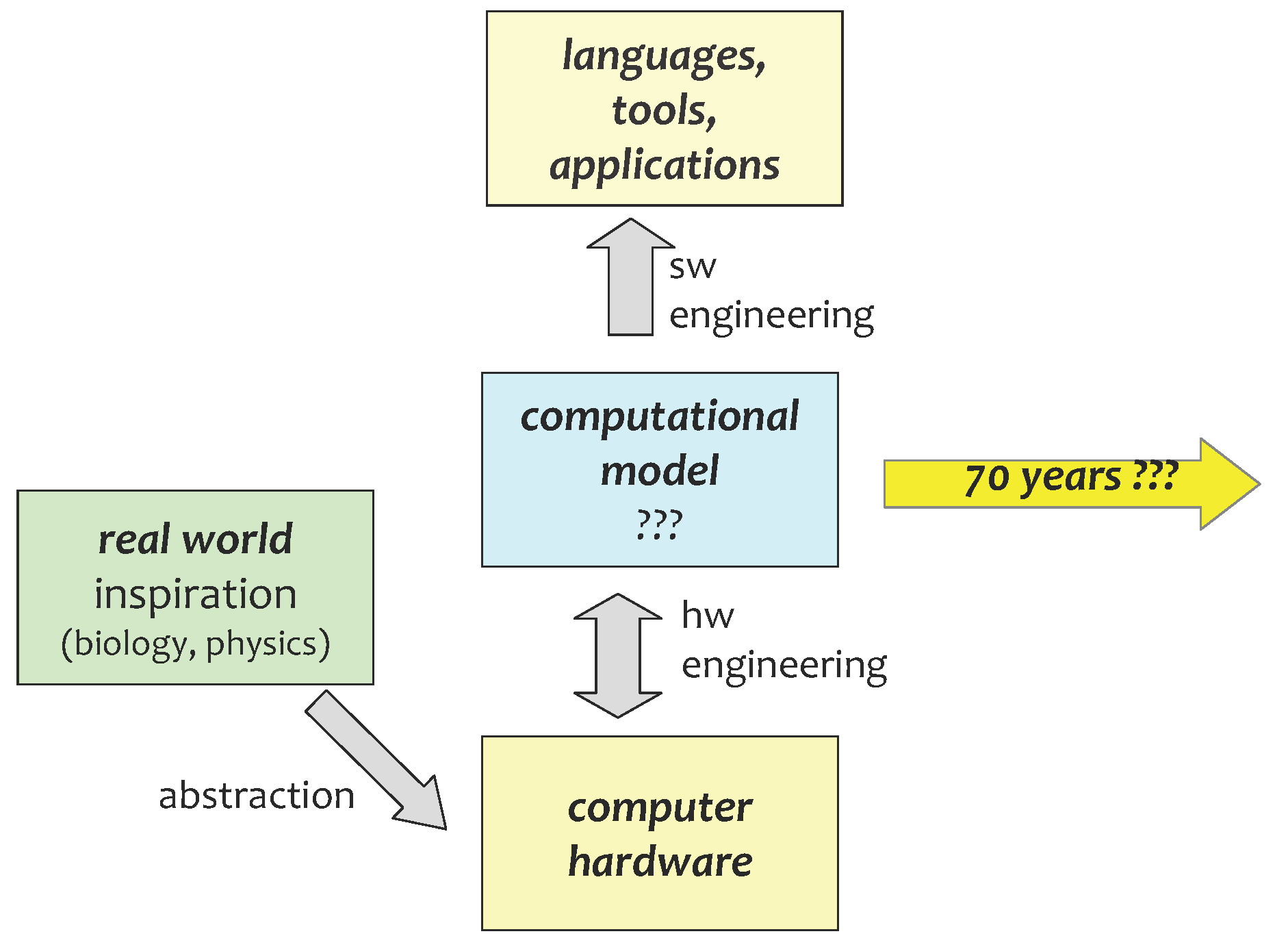

3. Computational Models as Abstractions of Physics
4. Inspired by Biological Modelling
Organic life exists only so far as it evolves in time. It is not a thing but a process—a never-resting continuous stream of events— Cassirer [18]
A process-centric description is arguably also needed in the context of emergence [20]. To summarise these ideas: “Life is a verb, not a noun.” [21].It must be a biology that asserts the primacy of processes over events, of relationships over entities, and of development over structure.— Ingold [19]
4.1. Process
4.2. Dynamics
4.3. Development
4.4. Self-reference
5. Conclusions
Acknowledgments
References
- Copeland, B.J. The Modern History of Computing. In The Stanford Encyclopedia of Philosophy, 2008 ed.; Zalta, E.N., Ed.; Archived online: http://plato.stanford.edu/archives/fall2008/entries/ computing-history/ (accessed on 6 August 2012).
- Turing, A.M. On computable numbers, with an application to the entscheidungsproblem. Proc. Lond. Math. Soc. 1937, S2–S42, 230–265. [Google Scholar] [CrossRef]
- Adamatzky, A. Physarum Machines: Computers From Slime Mould; World Scientific: Singapore, 2010. [Google Scholar]
- Tóth, Á.; Showalter, K. Logic gates in excitable media. J. Chem. Phys. 1995, 103, 2058–2066. [Google Scholar]
- Adamatzky, A.; de Lacy Costello, B.; Asai, T. Reaction-Diffusion Computers; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Miller, J.F.; Downing, K. Evolution in materio: Looking Beyond the Silicon Box. In Proceedings of NASA/DoD Conference on Evolvable Hardware, Washington D.C., USA, 15–18 July 2002; pp. 167–176.
- Stepney, S. The neglected pillar of material computation. Phys. D: Nonlinear Phenom. 2008, 237, 1157–1164. [Google Scholar] [CrossRef]
- Enz, C.C.; Vittoz, E.A. CMOS Low-power Analog Circuit Design. In Emerging Technologies, Tutorial for 1996 International Symposium on Circuits and Systems; IEEE Service Center: Piscataway, NJ, USA, 1996; pp. 79–133. [Google Scholar]
- Conrad, M. The Price of Programmability. In The Universal Turing Machine; Herken, R., Ed.; Oxford University Press: Oxford, UK, 1988; pp. 285–307. [Google Scholar]
- Sloman, A. The Irrelevance of Turing Machines to Artificial Intelligence. In Computationalism: New Directions; Scheutz, M., Ed.; MIT Press: Cambridge, MA, USA, 2002; pp. 87–127. [Google Scholar]
- Copeland, B.J. Accelerating turing machines. Minds Mach. 2002, 12, 281–300. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A Math. Phys. Sci. 1985, 400, 97–117. [Google Scholar] [CrossRef]
- Hogarth, M. Does general relativity allow an observer to view an eternity in a finite time? Found. Phys. Lett. 1992, 5, 173–181. [Google Scholar] [CrossRef]
- NIST. The NIST Reference on Constants, Units, and Uncertainty, 2011. Available online: http://physics.nist.gov/cuu/Constants/ (accessed on 6 August 2012).
- NPL. What is the most accurate measurement known? 2010. Available online: http://www.npl.co.uk/reference/faqs/what-is-the-most-accurate-measurement-known-(faq-quantum) (accessed on 6 August 2012).
- Arndt, J.; Haenel, C. π Unleashed; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Yee, A.J.; Kondo, S. Round 2 …10 Trillion Digits of Pi. 2011. Available online: http://www.numberworld.org/misc_runs/pi-10t/details.html (accessed on 6 August 2012).
- Cassirer, E. An Essay on Man; Yale University Press: New Haven, CT, USA, 1944. [Google Scholar]
- Ingold, T. An anthropologist looks at biology. Man 1990, 25, 208–229. [Google Scholar] [CrossRef]
- Stepney, S.; Polack, F.; Turner, H. Engineering Emergence. In Proceedings of the ICECCS 2006: 11th IEEE International Conference on Engineering of Complex Computer Systems, Stanford, CA, USA, 15–17 August 2006; pp. 89–97.
- Gilman, C.P. Human Work; McClure, Philips and Co: New York, NY, USA, 1904. [Google Scholar]
- Hoare, C.A.R. Communicating Sequential Processes; Prentice Hall: Upper Saddle River, NJ, USA, 1985. [Google Scholar]
- Milner, R. A Calculus of Communicating Systems; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Milner, R. Communication and Concurrency; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Milner, R. Communicating and Mobile Systems: The π-Calculus; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Milner, R. The Space and Motion of Communicating Agents; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Cardelli, L.; Gordon, A.D. Mobile ambients. Theor. Comput. Sci. 2000, 240, 177–213. [Google Scholar] [CrossRef]
- Hillston, J. A Compositional Approach to Performance Modelling; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Baeten, J.C.M.; Weijland, W.P. Process Algebra; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Ciocchetta, F.; Hillston, J. Process Algebras in Systems Biology. In Formal Methods for Computational Systems Biology; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5016, pp. 265–312. [Google Scholar]
- Calder, M.; Hillston, J. Process Algebra Modelling Styles for Biomolecular Processes; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5750, pp. 1–25. [Google Scholar]
- Schumann, A.; Adamatzky, A. Logical Modelling of Physarum Polycephalum. CoRR 2011. [Google Scholar]
- Aczel, P. Non-well-founded Sets; CSLI: Stanford, CA, USA, 1988. [Google Scholar]
- Sangiorgi, D. On the origins of bisimulation and coinduction. ACM Trans. Progr. Lang. Syst. 2009, 31, 15:1–15:41. [Google Scholar] [CrossRef]
- Hawking, S.W. A Brief History of Time; Bantam Dell: New York, NY, USA, 1988. [Google Scholar]
- Barwise, J.; Etchemendy, J. The Liar: An Essay on Truth and Circularity; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Jacobs, B. Introduction to Coalgebra. Towards Mathematics of States and Observations. draft v2.00. Available online: http://www.cs.ru.nl/B.Jacobs/CLG/JacobsCoalgebraIntro.pdf (accessed on 8 October 2012).
- Maes, P. Concepts and Experiments in Computational Reflection; ACM Press: New York, NY, USA, 1987; pp. 147–155. [Google Scholar]
- Hickinbotham, S.; Stepney, S.; Nellis, A.; Clarke, T.; Clark, E.; Pay, M.; Young, P. Embodied Genomes and Metaprogramming. In Advances in Artificial Life, ECAL 2011, Proceedings of the Eleventh European Conference on the Synthesis and Simulation of Living Systems, Paris, France, August 2011; MIT Press: Cambridge, MA, USA, 2011; pp. 334–341. [Google Scholar]
- Stepney, S.; Hoverd, T. Reflecting on Open-Ended Evolution. In Advances in Artificial Life, ECAL 2011, Proceedings of the Eleventh European Conference on the Synthesis and Simulation of Living Systems, Paris, France, August 2011; MIT Press: Cambridge, MA, USA, 2011; pp. 781–788. [Google Scholar]
- Cuesta, C.; de la Fuente, P.; Barrio-Solórzano, M.; Beato, E. Coordination in a Reflective Architecture Description Language. In Coordination Models and Languages; Arbab, F., Talcott, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2315, pp. 479–486. [Google Scholar]
- Cuesta, C.; Romay, M.; de la Fuente, P.; Barrio-Solórzano, M. Reflection-Based, Aspect-Oriented Software Architecture. In Software Architecture; Oquendo, F., Warboys, B., Morrison, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3047, pp. 43–56. [Google Scholar]
- Alligood, K.T.; Sauer, T.D.; Yorke, J.A. Chaos : An Introduction to Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos; Westview Press: Boulder, CO, USA, 1994. [Google Scholar]
- Beer, R.D. A dynamical systems perspective on agent-environment interaction. Artif. Intell. 1995, 72, 173–215. [Google Scholar] [CrossRef]
- Stepney, S. Nonclassical Computation: A Dynamical Systems Perspective. In Handbook of Natural Computing; Rozenberg, G., Bäck, T., Kok, J.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 4, Chapter 59; pp. 1979–2025. [Google Scholar]
- Pask, G. The Natural History of Networks. In Self-Organzing Systems; Yovits, M.C., Cameron, S., Eds.; Pergamon Press: Oxford, UK, 1960. [Google Scholar]
- Cariani, P. To evolve an ear: Epistemological implications of Gordon Pask’s electrochemical devices. Syst. Res. 1993, 10, 19–33. [Google Scholar] [CrossRef]
- Thompson, A.; Layzell, P.J.; Zebulum, R.S. Explorations in design space: Unconventional electronics design through artificial evolution. IEEE Trans. Evol. Comput. 1999, 3, 167–196. [Google Scholar] [CrossRef]
- Harding, S.L.; Miller, J.F.; Rietman, E.A. Evolution in Materio: Exploiting the physics of materials for computation. IJUC 2008, 4, 155–194. [Google Scholar]
- Goldstein, J. Emergence as a construct: History and issues. Emergence 1999, 1, 49–72. [Google Scholar] [CrossRef]
- Abraham, R.H. Dynamics and Self-Organization. In Self-organizing Systems: The Emergence of Order; Yates, F.E., Ed.; Plenum: New York, NY, USA, 1987; pp. 599–613. [Google Scholar]
- Baguelin, M.; LeFevre, J.; Richard, J.P. A Formalism for Models with a Metadynamically Varying Structure. In Proceedings of the European Control Conference, Cambridge, UK, 1–4 September 2003.
- Moulay, E.; Baguelin, M. Meta-dynamical adaptive systems and their application to a fractal algorithm and a biological model. Phys. D 2005, 207, 79–90. [Google Scholar] [CrossRef]
- Kuan, C.Y.; Roth, K.A.; Flavell, R.A.; Rakic, P. Mechanisms of programmed cell death in the developing brain. Trends Neurosci. 2000, 23, 291–297. [Google Scholar] [CrossRef]
- Pajni-Underwood, S.; Wilson, C.P.; Elder, C.; Mishina, Y.; Lewandoski, M. BMP signals control limb bud interdigital programmed cell death by regulating FGF signaling. Development 2007, 134, 2359–2368. [Google Scholar] [CrossRef] [PubMed]
- Fontana, W. Algorithmic Chemistry. In Artificial Life II; Addison-Wesley: Boston, MA, USA, 1991; pp. 159–209. [Google Scholar]
- Fontana, W.; Buss, L.W. The Barrier of Objects: From Dynamical Systems to Bounded Organizations. In Boundaries and Barriers; Casti, J.L., Karlqvist, A., Eds.; Addison-Wesley: Boston, MA, USA, 1996; Chapter 4; pp. 56–116. [Google Scholar]
- Bagley, R.J.; Farmer, J.D. Spontaneous Emergence of a Metabolism. In Artificial Life II; Addison-Wesley: Boston, MA, USA, 1991; pp. 93–140. [Google Scholar]
- Simons, P. Reasoning on a tight budget: Lesniewski’s nominalistic metalogic. Erkenntnis 2002, 56, 99–122. [Google Scholar] [CrossRef]
- Prusinkiewicz, P.; Lindenmayer, A. The Algorithmic Beauty of Plants; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Păun, G. Computing with membranes. J. Comput. Syst. Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef]
- Giavitto, J.L.; Michel, O. Data Structure as Topological Spaces. In Proceedings of the 3nd International Conference on Unconventional Models of Computation UMC02, Kobe, Japan, 15–19 October 2002; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2509, pp. 137–150. [Google Scholar]
- Giavitto, J.L.; Spicher, A. Topological rewriting and the geometrization of programming. Phys. D 2008, 237, 1302–1314. [Google Scholar] [CrossRef]
- Michel, O.; Banâtre, J.P.; Fradet, P.; Giavitto, J.L. Challenging questions for the rationale of non-classical programming languages. Int. J. Unconv. Comput. 2006, 2, 337–347. [Google Scholar]
- Doursat, R. Organically Grown Architectures: Creating Decentralized, Autonomous Systems by Embryomorphic Engineering. In Organic Computing; Würtz, R.P., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 167–200. [Google Scholar]
- Doursat, R.; Sayama, H.; Michel, O. Morphogenetic Engineering: Toward Programmable Complex Systems; Springer: Berlin/Heidelberg, Germany, 2012; in press. [Google Scholar]
- MacLennan, B.J. Models and Mechanisms for Artificial Morphogenesis. In Natural Computing, Proceedings in Information and Communications Technology, Himeji, Japan, September 2009; Peper, F., Umeo, H., Matsui, N., Isokawa, T., Eds.; Springer: Tokyo, Japan, 2010; Volume 2, pp. 23–33. [Google Scholar]
- MacLennan, B.J. Artificial morphogenesis as an example of embodied computation. Int. J. Unconv. Comput. 2011, 7, 3–23. [Google Scholar]
- Tomita, K.; Murata, S.; Kurokawa, H. Self-description for construction and computation on graph-rewriting automata. Artif. Life 2007, 13, 383–396. [Google Scholar] [CrossRef] [PubMed]
- Harding, S.; Miller, J.F.; Banzhaf, W. Self-modifying Cartesian Genetic Programming. In Proceedings of the GECCO 2007, London, UK, 7–11 July 2007; Lipson, H., Ed.; ACM: New York, NY, USA, 2007; pp. 1021–1028. [Google Scholar]
- Harding, S.; Miller, J.F.; Banzhaf, W. Self-modifying Cartesian Genetic Programming. In Cartesian Genetic Programming; Miller, J.F., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; chapter 4; pp. 101–124. [Google Scholar]
- Rosen, R. Life Itself: A Comprehensive Enquiry Into the Nature, Origin, and Fabrication of Life; Columbia University Press: New York, NY, USA, 1991. [Google Scholar]
- Maturana, H.R.; Varela, F.J. Autopoeisis and Cognition: The Realization of the Living; D. Reidel Publishing Company: Boston, MA, USA, 1980. [Google Scholar]
- Mingers, J. Self-Producing Systems: Implications and Applications of Autopoiesis; Plenum: New York, NY, USA, 1995. [Google Scholar]
- Danchin, A. The Delphic Boat: What Genomes Tell Us; Harvard University Press: Cambridge, MA, USA, 2002. [Google Scholar]
- McMullin, B. Thirty years of computational autopoiesis: A review. Artif. Life 2004, 10, 277–295. [Google Scholar] [PubMed]
- Laughlin, R.B. A Different Universe: Reinventing Physics from the Bottom Down; Basic Books: New York, NY, USA, 2005. [Google Scholar]
- Kampis, G. Self-Modifying Systems. In Biology and Cognitive Science: A New Framework for Dynamics, Information, and Complexity; Pergamon Press: Oxford, UK, 1991. [Google Scholar]
- Stepney, S. Unconventional Computer Programming. In Proceedings of the Symposium on Natural/Unconventional Computing and Its Philosophical Significance, Birmingham, UK, 2–3 July 2012; Dodig-Crnkovic, G., Giovagnoli, R., Eds.; pp. 12–15.
© 2012 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Stepney, S. Programming Unconventional Computers: Dynamics, Development, Self-Reference. Entropy 2012, 14, 1939-1952. https://doi.org/10.3390/e14101939
Stepney S. Programming Unconventional Computers: Dynamics, Development, Self-Reference. Entropy. 2012; 14(10):1939-1952. https://doi.org/10.3390/e14101939
Chicago/Turabian StyleStepney, Susan. 2012. "Programming Unconventional Computers: Dynamics, Development, Self-Reference" Entropy 14, no. 10: 1939-1952. https://doi.org/10.3390/e14101939
APA StyleStepney, S. (2012). Programming Unconventional Computers: Dynamics, Development, Self-Reference. Entropy, 14(10), 1939-1952. https://doi.org/10.3390/e14101939



