Local Stability Analysis of a Thermo-Economic Model of a Chambadal-Novikov-Curzon-Ahlborn Heat Engine
Abstract
:1. Introduction
2. Thermo-Economic Analysis of the Steady-State Chambadal-Novikov-Curzon-Ahlborn Heat Engine
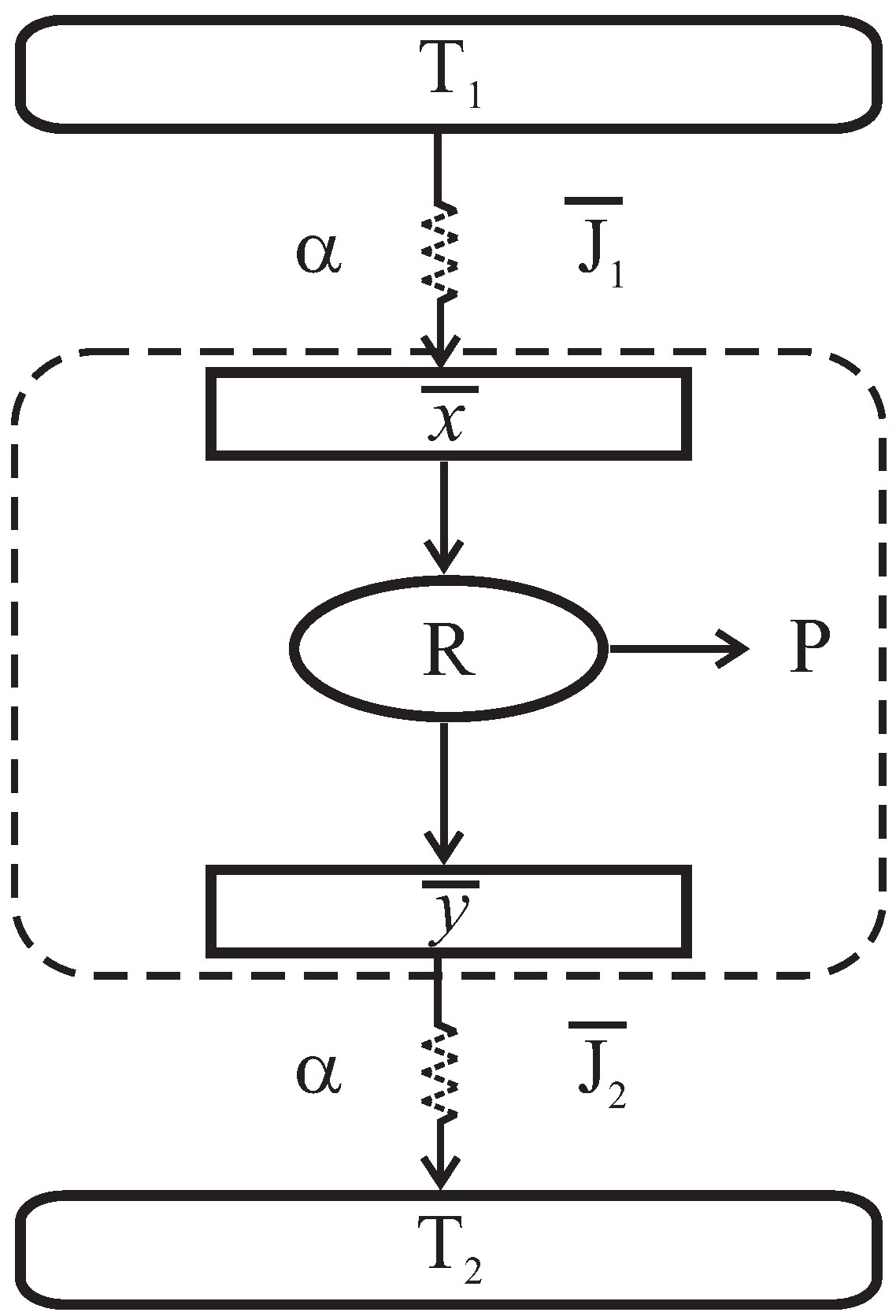
3. Linearization and Stability Analysis
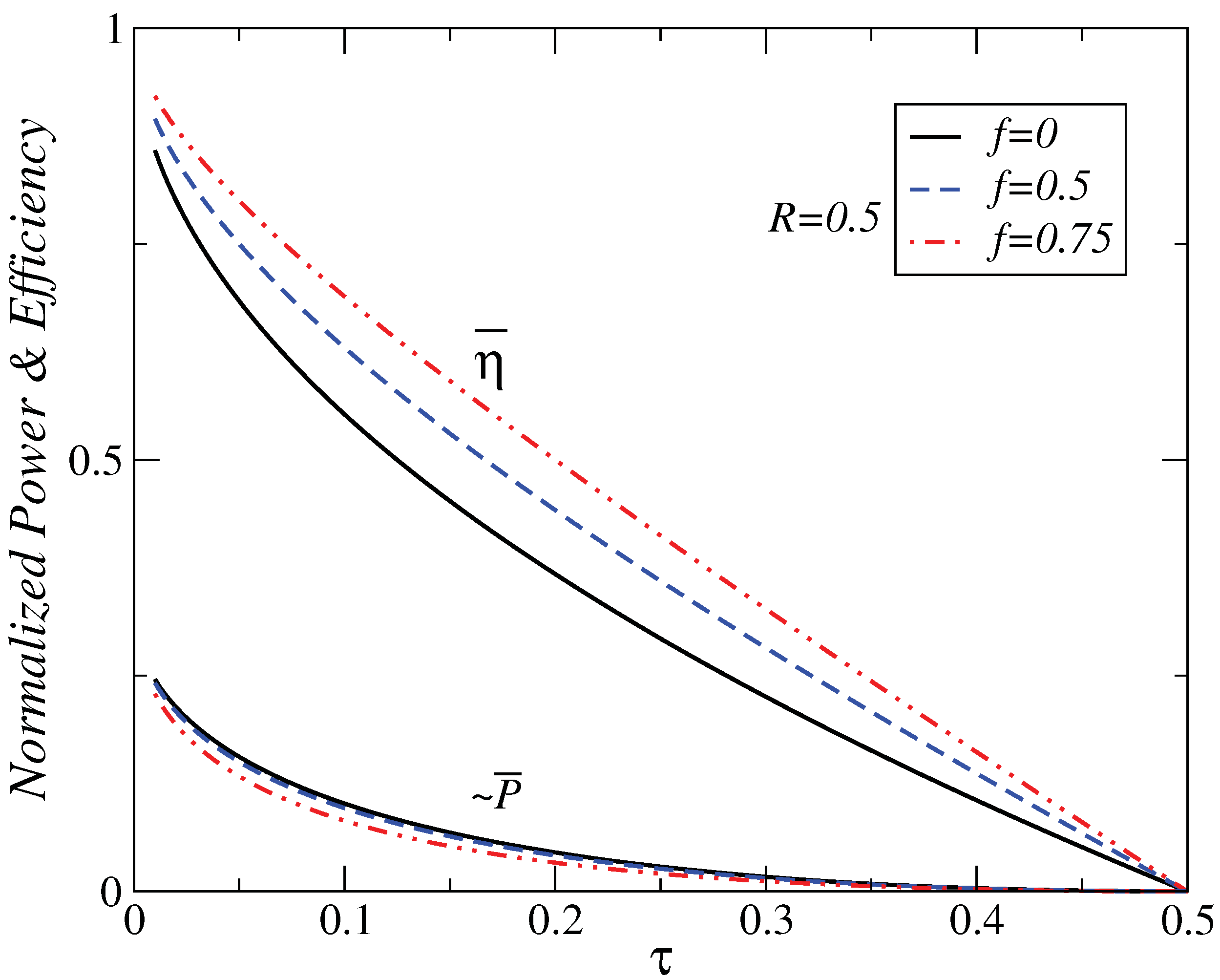
4. Local Stability Analysis
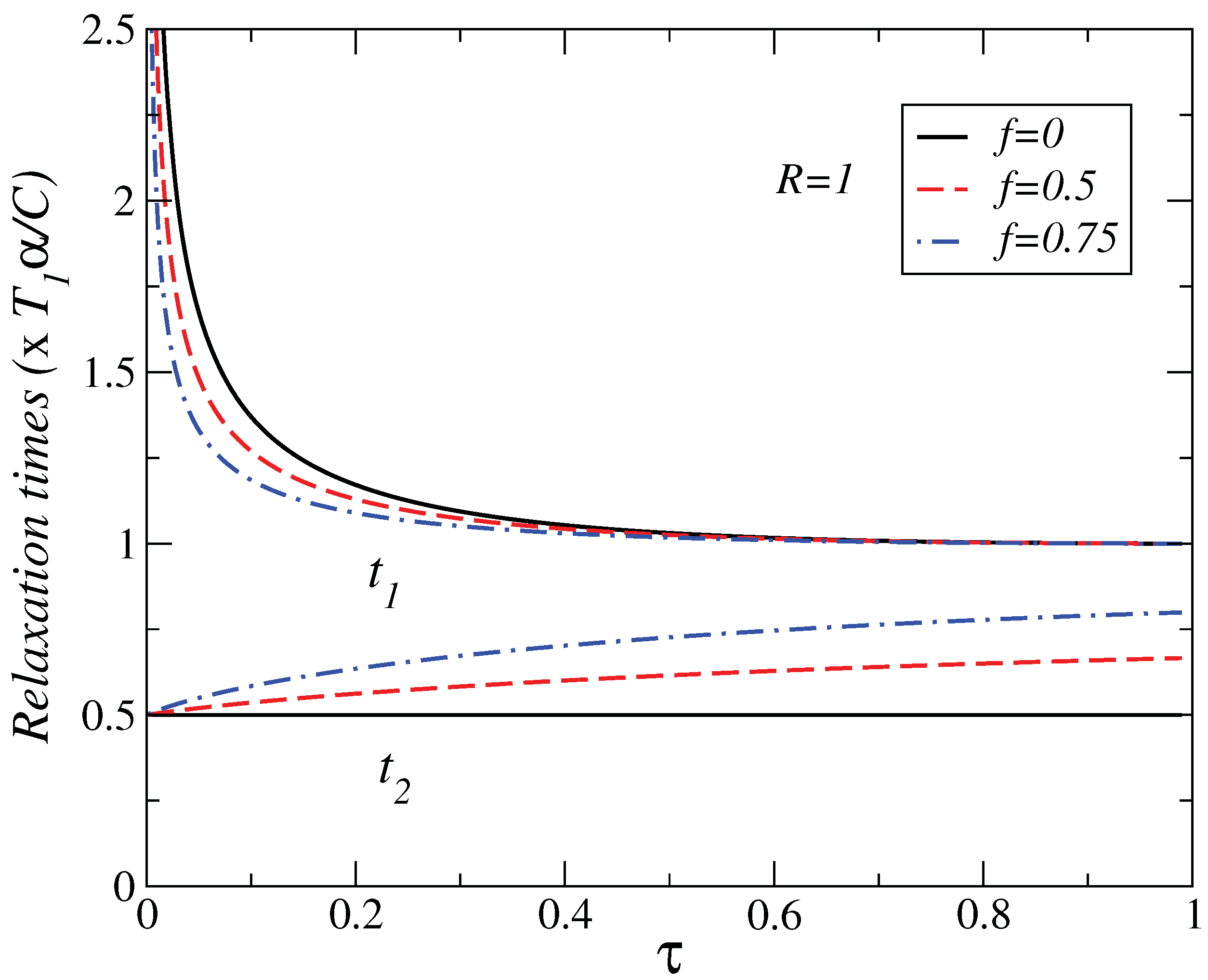
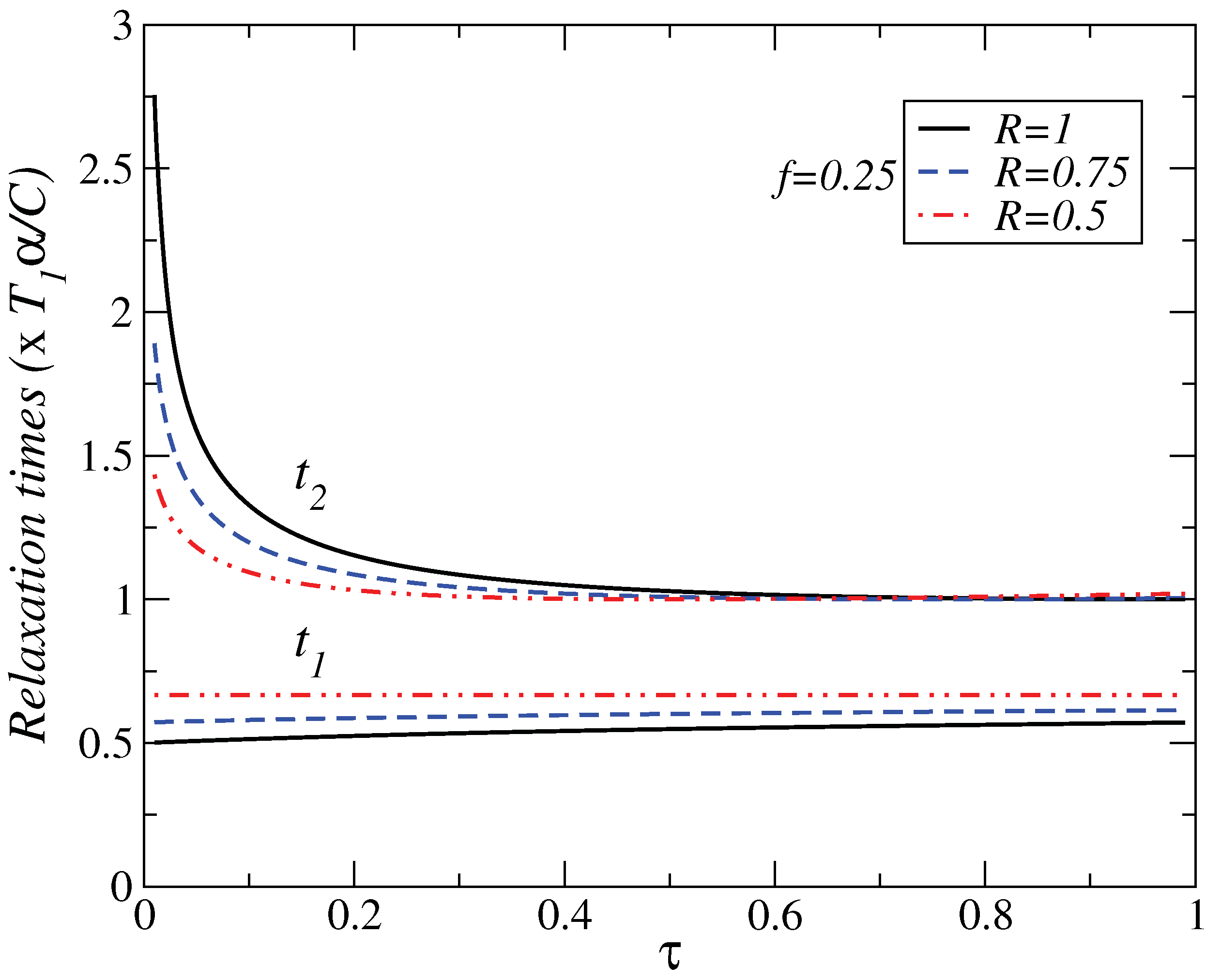
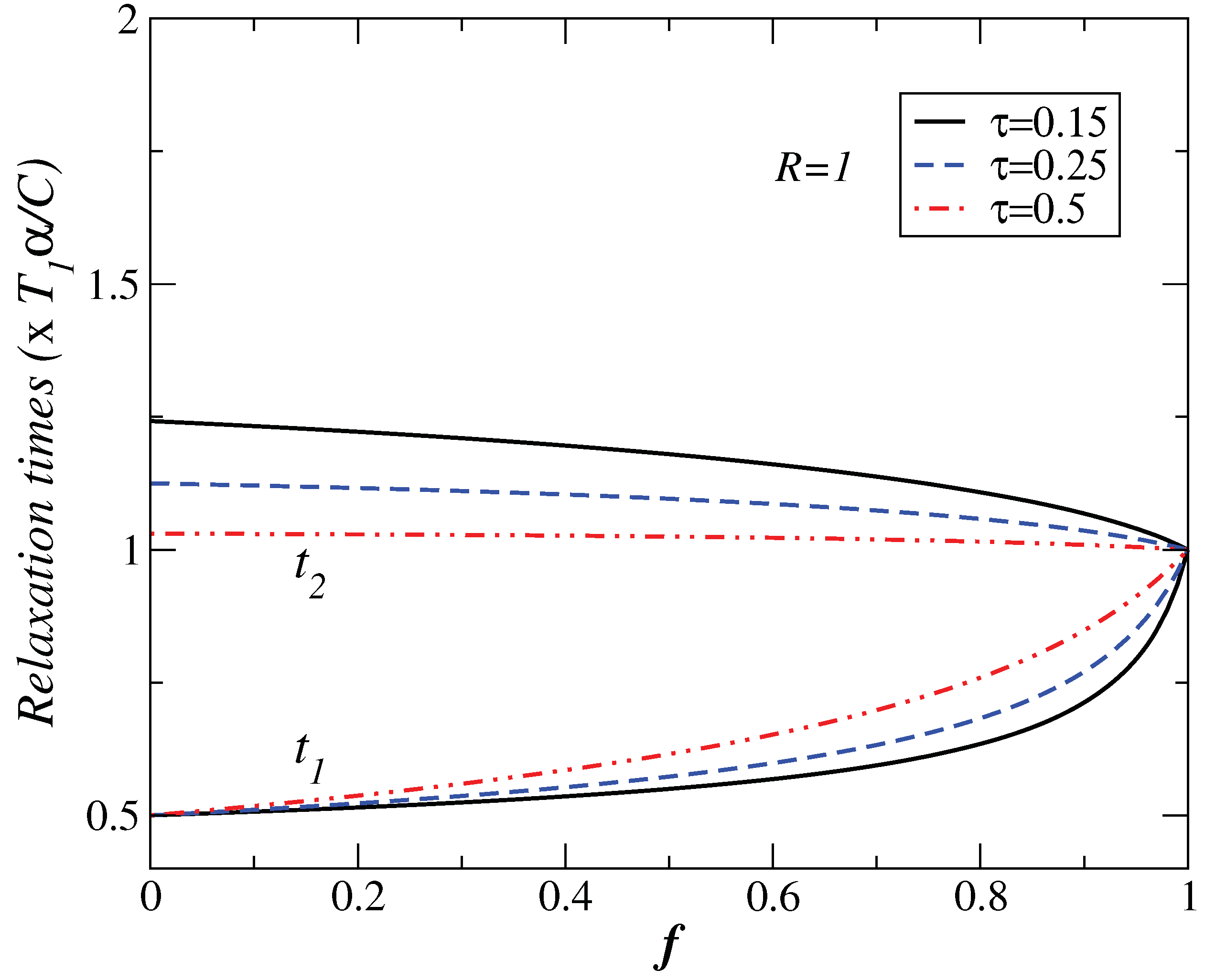
5. Conclusions
Acknowledgements
References
- Curzon, F.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Feidt, M.; Costea, M.; Petre, C.; Petrescu, S. Optimisation of the direct carnot cycle. Appl. Therm. Eng. 2007, 27, 829–839. [Google Scholar] [CrossRef]
- Feidt, M.L. Optimal use of energy system and processes. Int. J. Exergy 2008, 5, 500–531. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F. Advances in Finite Time Thermodynamics: Analysis and Optimization; Nova Science: New York, NY, USA, 2004. [Google Scholar]
- Sieniutycz, S.; Jezowski, J. Energy Optimization in Process Systems; Elsevier: Oxford, UK, 2009. [Google Scholar]
- De Vos, A. Endorreversible Thermodynamics of Solar Energy Conversion; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Andresen, B. Current trends in finite-time thermodynamics. Angew. Chem. Int. Ed. 2011, 50, 2690–2704. [Google Scholar] [CrossRef] [PubMed]
- Fisher, M.; Hoffmann, K.H. Can a quantitative simulation of an Otto engine be accurately rendered by a simple Novikov model with heat leak? J. Non-Equilib. Thermodyn. 2004, 29, 9–28. [Google Scholar] [CrossRef]
- Velasco, S.; Roco, J.M.M.; Medina, A.; White, J.A.; Calvo-Hernández, A. Optimization of heat engines including the saving of natural resources and the reduction of thermal pollution. J. Phys. D 2000, 33, 355–359. [Google Scholar] [CrossRef]
- Sieniutycs, S.; Salamon, P. Finite Time Thermodyancmis and Themoeconomics; Taylor and Francis: London, UK, 1990. [Google Scholar]
- Santillán, M.; Maya-Aranda, G.; Angulo-Brown, F. Local stability analysis of an endoreversible Curzon-Ahlborn-Novikov engine working in a maximum-power like regime. J. Phys. D 2001, 34, 2068–2072. [Google Scholar] [CrossRef]
- Guzmán-Vargas, L.; Reyes-Ramírez, I.; Sánchez-Salas, N. The efect of heat transfer laws and thermal conductances on the local stability of an endoreversible heat engine. J. Phys. D 2005, 38, 1282–1291. [Google Scholar] [CrossRef]
- Páez-Hernández, R.T.; Angulo-Brown, F.; Santillán, M. Dynamic robustness and thermodynamic optimization in a non-endoreversible curzonAhlborn engine. J. Non-Equilib. Thermodyn. 2006, 31, 173–188. [Google Scholar]
- De Vos, A. Endoreversible thermoeconomics. Energy Convers. Manage. 1995, 36, 1–5. [Google Scholar] [CrossRef]
- Novikov, I.I. The efficiency of atomic power stations (a review). At. Energ. 1957, 3, 409. [Google Scholar] [CrossRef]
- Qin, X.; Chen, L.; Sun, F.; Wu, C. Thermoeconomic optimization of an endoreversible four-heat-reservoir absorption-refrigerator. Appl. Energy 2005, 81, 420–433. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F.; Wu, C. Endoreversible thermoeconomics for heat engines. Appl. Energy 2005, 81, 388–396. [Google Scholar] [CrossRef]
- Sahin, B.; Kodal, A. Performance analysis of an endorreversible heat engine based on a new thermoeconomic optimization criterion. Energy Convers. Manage. 2001, 3, 1085–1093. [Google Scholar] [CrossRef]
- Wu, C.; Chen, L.; Chen, J. Recent Advances in Finite-Time Thermodynamics; Nova Science: New York, NY, USA, 1999. [Google Scholar]
- Barranco-Jiménez, M.A.; Sánchez-Salas, N.; Angulo-Brown, F. Finite-time themoeconomic optimization of a solar-driven heat engine model. Entropy 2011, 13, 171–183. [Google Scholar] [CrossRef]
- Wu, F.; Wu, C.; Guo, F.; Li, Q.; Chen, L. Optimization of a thermoacoustic engine with a complex heat transfer exponent. Entropy 2003, 5, 444–451. [Google Scholar] [CrossRef]
- Zheng, T.; Chen, L.; Sun, F.; Wu, C. Effect of heat leak and finite thermal capacity on the optimal configuration of a two-heat-reservoir heat engine for another linear heat transfer law. Entropy 2003, 5, 519–530. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, T.; Sun, F.; Wu, C. Optimal cooling load and COP relationship of a four-heat-reservoir endoreversible absorption refrigerator cycle. Entropy 2004, 6, 316–326. [Google Scholar] [CrossRef]
- Barranco-Jimenez, M.A.; Sanchez-Salas, N.; Rosales, M.A. Thermoeconomic optimum operation conditions of a solar-driven heat engine model. Entropy 2009, 11, 443–453. [Google Scholar] [CrossRef]
- Chambadal, P. Les Centrales Nucléaires; Armand Colin: Paris, France, 1957. [Google Scholar]
- Wu, C.; Kiang, R.L. Finite-time thermodynamic analysis of a Carnot engine with internal irreversibility. Energy 1992, 1, 1173–1178. [Google Scholar] [CrossRef]
- Chen, J. The maximum power output and maximum efficiency of an irreversible Carnot heat engine. J. Phys. D 1994, 27, 1144–1149. [Google Scholar] [CrossRef]
- Ozcaynak, S.; Goktan, S.; Yavuz, H. Finite-time thermodynamics analysis of a radiative heat engine with internal irreversibility. J. Phys. D 1994, 27, 1139–1143. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A. Finite-time thermodynamics optimization of a non endoreversible heat engine. Rev. Mex. Fis. 2009, 55, 211–220. [Google Scholar]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermo-economical optimization of an endoreversible power plant model. Rev. Mex. Fis. 2005, 51, 49–56. [Google Scholar]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermo-economic optimization of a Novikov power plant model under maximum ecological conditions. J. Energy Inst. 2007, 80, 96–104. [Google Scholar] [CrossRef]
- Arias-Hernández, L.A.; de Parga, G.A.; Angulo-Brown, F. On Some Nonendoreversible engine models with Nonlinear heat transfer laws. Open Sys. Inf. Dyn. 2003, 10, 351–375. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry and Engineering; Addison-Wesley Publising Company: Reading, MA, USA, 1994. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Barranco-Jiménez, M.A.; Páez-Hernández, R.T.; Reyes-Ramírez, I.; Guzmán-Vargas, L. Local Stability Analysis of a Thermo-Economic Model of a Chambadal-Novikov-Curzon-Ahlborn Heat Engine. Entropy 2011, 13, 1584-1594. https://doi.org/10.3390/e13091584
Barranco-Jiménez MA, Páez-Hernández RT, Reyes-Ramírez I, Guzmán-Vargas L. Local Stability Analysis of a Thermo-Economic Model of a Chambadal-Novikov-Curzon-Ahlborn Heat Engine. Entropy. 2011; 13(9):1584-1594. https://doi.org/10.3390/e13091584
Chicago/Turabian StyleBarranco-Jiménez, Marco A., Ricardo T. Páez-Hernández, Israel Reyes-Ramírez, and Lev Guzmán-Vargas. 2011. "Local Stability Analysis of a Thermo-Economic Model of a Chambadal-Novikov-Curzon-Ahlborn Heat Engine" Entropy 13, no. 9: 1584-1594. https://doi.org/10.3390/e13091584
APA StyleBarranco-Jiménez, M. A., Páez-Hernández, R. T., Reyes-Ramírez, I., & Guzmán-Vargas, L. (2011). Local Stability Analysis of a Thermo-Economic Model of a Chambadal-Novikov-Curzon-Ahlborn Heat Engine. Entropy, 13(9), 1584-1594. https://doi.org/10.3390/e13091584



