Phase-Controlled Atom-Photon Entanglement in a Three-Level V-Type Atomic System via Spontaneously Generated Coherence
Abstract
:1. Introduction
2. Model and Equations
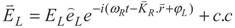 with frequency ωL and Rabi frequency ΩL drives the transition |1〉 →|3〉, and other right field,
with frequency ωL and Rabi frequency ΩL drives the transition |1〉 →|3〉, and other right field, 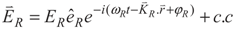 with frequency ωR and Rabi frequency ΩR is applied to the transition |1〉 → |2〉. Here, EL(ER) and
with frequency ωR and Rabi frequency ΩR is applied to the transition |1〉 → |2〉. Here, EL(ER) and 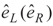 are the amplitude, and the polarization of the left (right) classical laser field, while ωL(ωR),
are the amplitude, and the polarization of the left (right) classical laser field, while ωL(ωR), 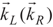 and ϕL(ϕR) are the frequency, wave vector, and initial phase of left (right) classical laser field. The parameters 2γ21 and 2γ31 denote the spontaneous decay rates from excited-states |2〉 and |3〉 to ground state, |1〉 respectively. Also ΔL = ωL − ω31, ΔR = ωR − ω21 are one-photon detuning of the two fields. Such a system, with a single ground state and a closely spaced excited doublet (e.g., two near-degenerate states), is damped by the usual vacuum interactions, so the two decay pathways from the excited doublet to the ground state are not independent. The system decays from the upper states doublet to a lower state via spontaneous emission leading to the quantum interference, i.e., spontaneously generated coherence (SGC) [24].
and ϕL(ϕR) are the frequency, wave vector, and initial phase of left (right) classical laser field. The parameters 2γ21 and 2γ31 denote the spontaneous decay rates from excited-states |2〉 and |3〉 to ground state, |1〉 respectively. Also ΔL = ωL − ω31, ΔR = ωR − ω21 are one-photon detuning of the two fields. Such a system, with a single ground state and a closely spaced excited doublet (e.g., two near-degenerate states), is damped by the usual vacuum interactions, so the two decay pathways from the excited doublet to the ground state are not independent. The system decays from the upper states doublet to a lower state via spontaneous emission leading to the quantum interference, i.e., spontaneously generated coherence (SGC) [24].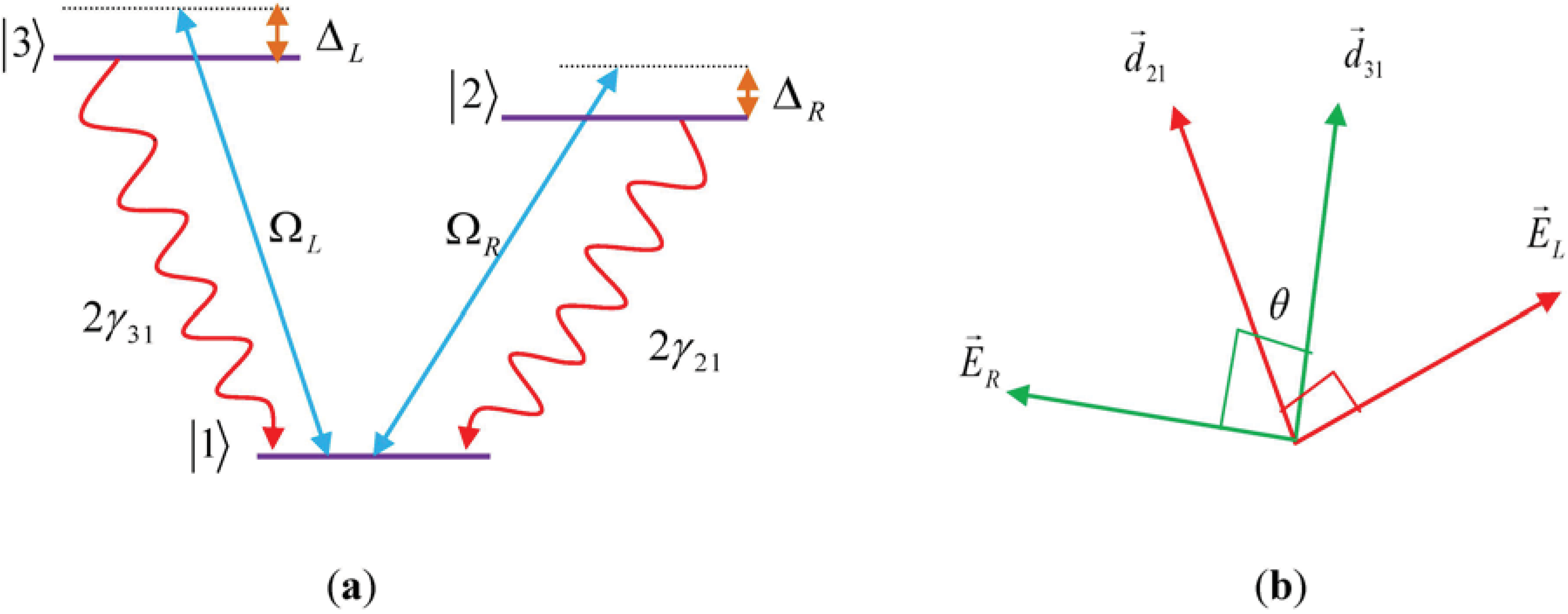
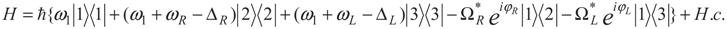
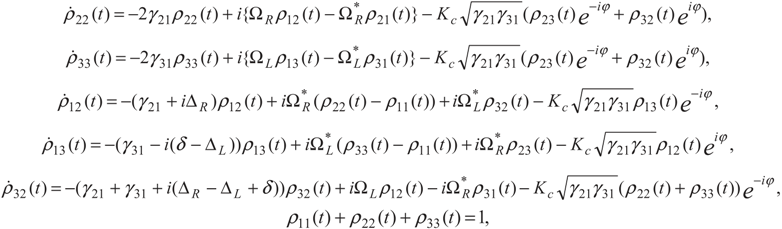
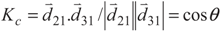 , where
, where 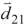 and
and 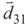 are the dipole moments of the corresponding transitions and θ is the angle between the two induced dipole moments as shown by Figure 1b. The effects of quantum interference are sensitive to the orientations of the atomic dipole moments. For parallel dipole moments, the interference effect is maximal and Kc = 1, while for perpendicular dipole moments, Kc = 0, and the quantum interference disappears. Note that the relative phase appears through equations via the parameter Kc. So, in Equation (2), the effect of relative phase of applied fields appear in all terms contain Kc. Then the solutions of these equations for Kc ≠ 0 are phase-dependent.
are the dipole moments of the corresponding transitions and θ is the angle between the two induced dipole moments as shown by Figure 1b. The effects of quantum interference are sensitive to the orientations of the atomic dipole moments. For parallel dipole moments, the interference effect is maximal and Kc = 1, while for perpendicular dipole moments, Kc = 0, and the quantum interference disappears. Note that the relative phase appears through equations via the parameter Kc. So, in Equation (2), the effect of relative phase of applied fields appear in all terms contain Kc. Then the solutions of these equations for Kc ≠ 0 are phase-dependent.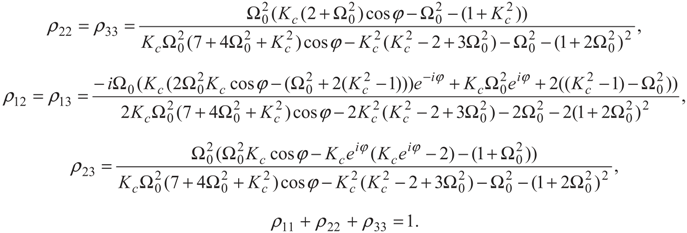
3. Entanglement and Entropy
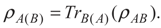
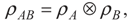
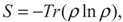
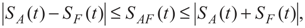
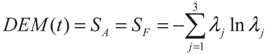
4. Results and Discussion
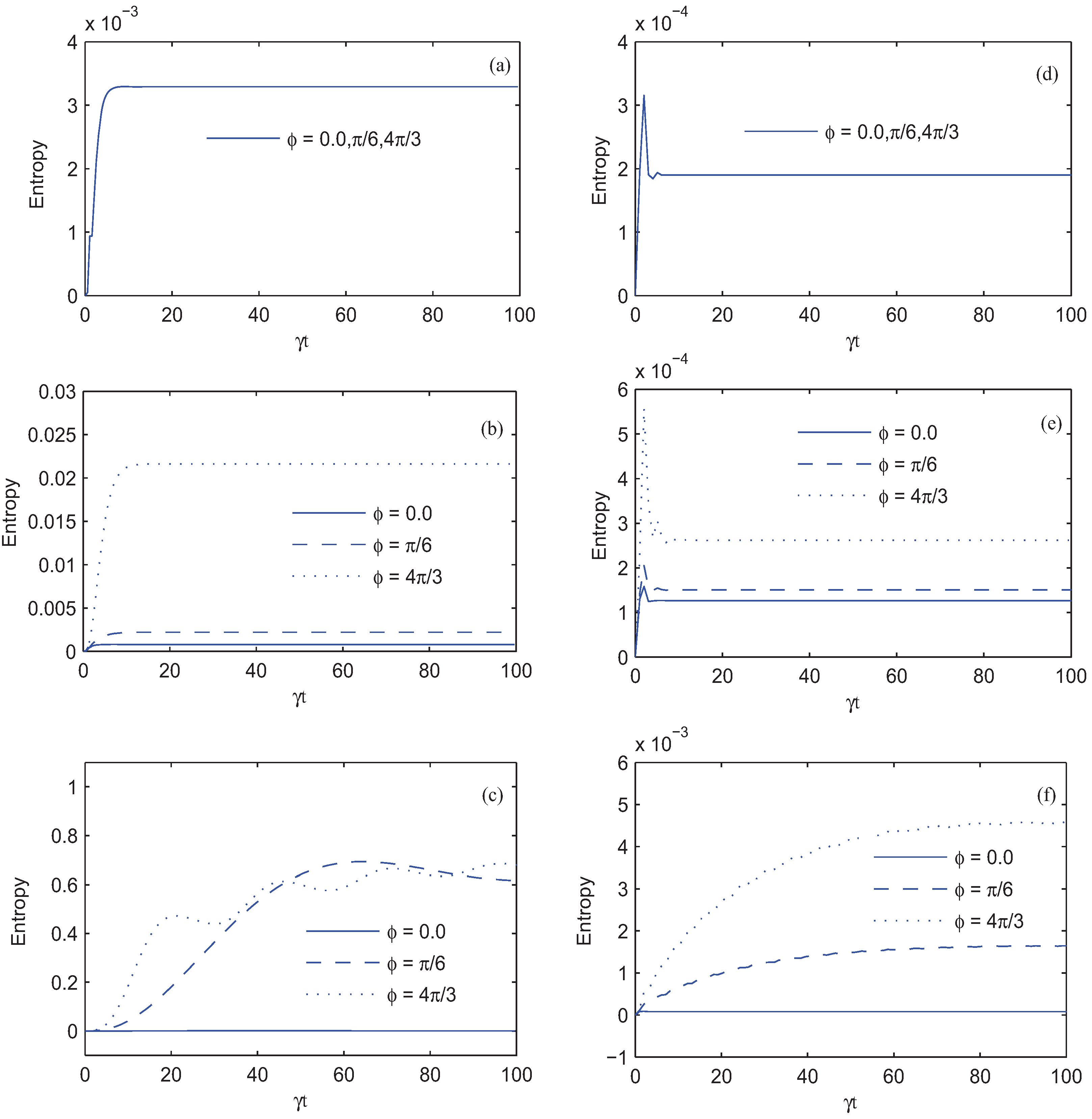
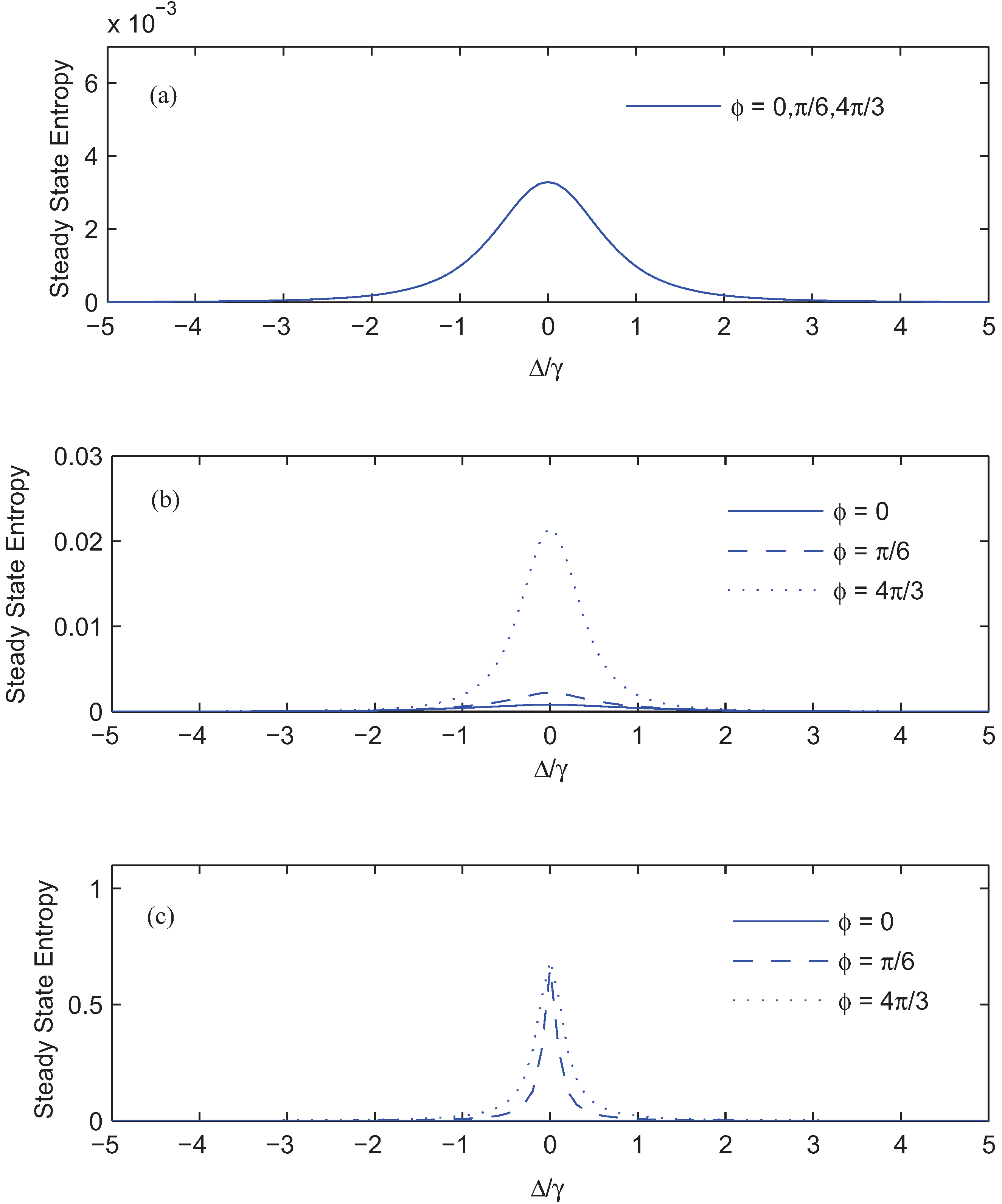
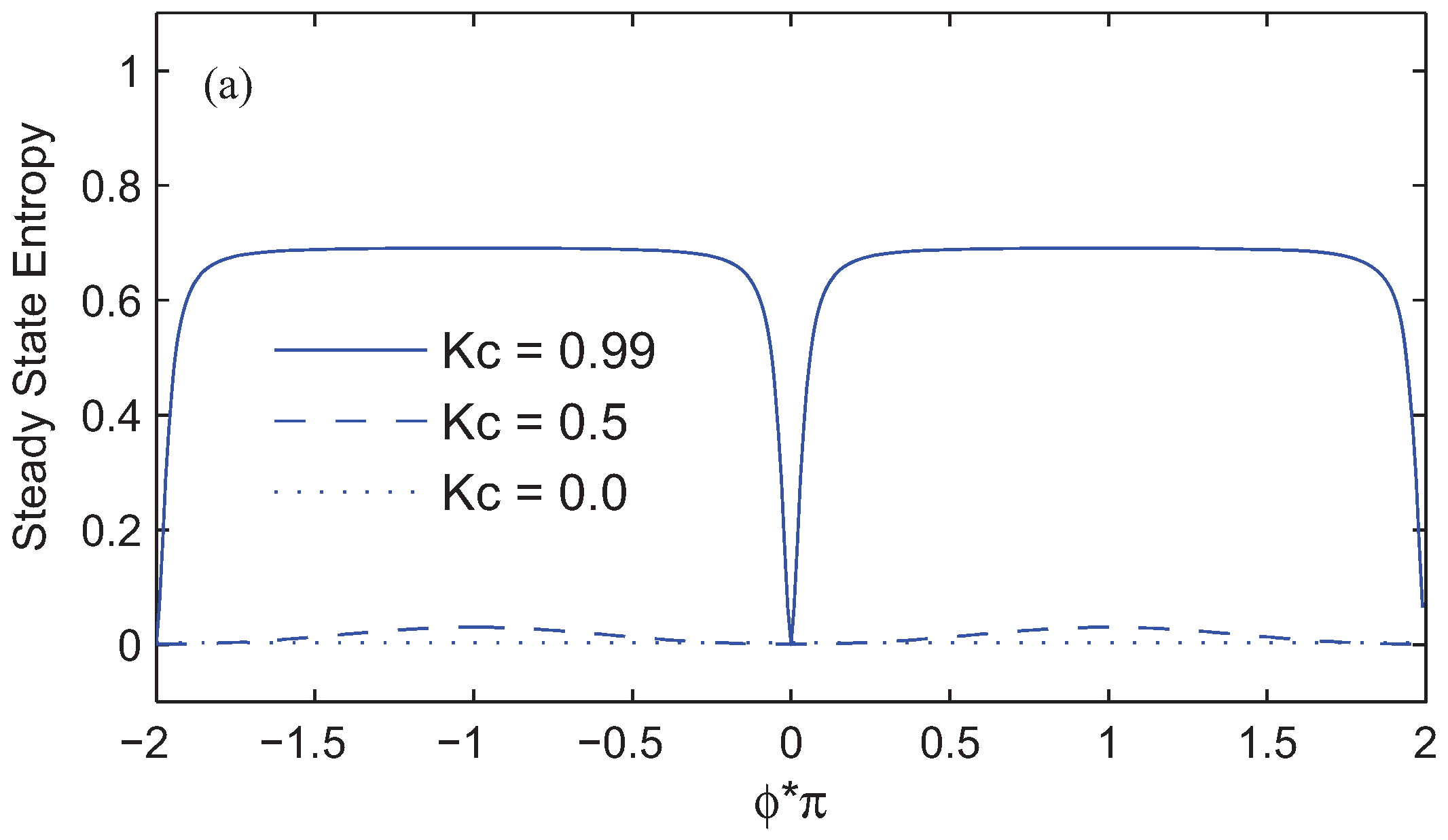
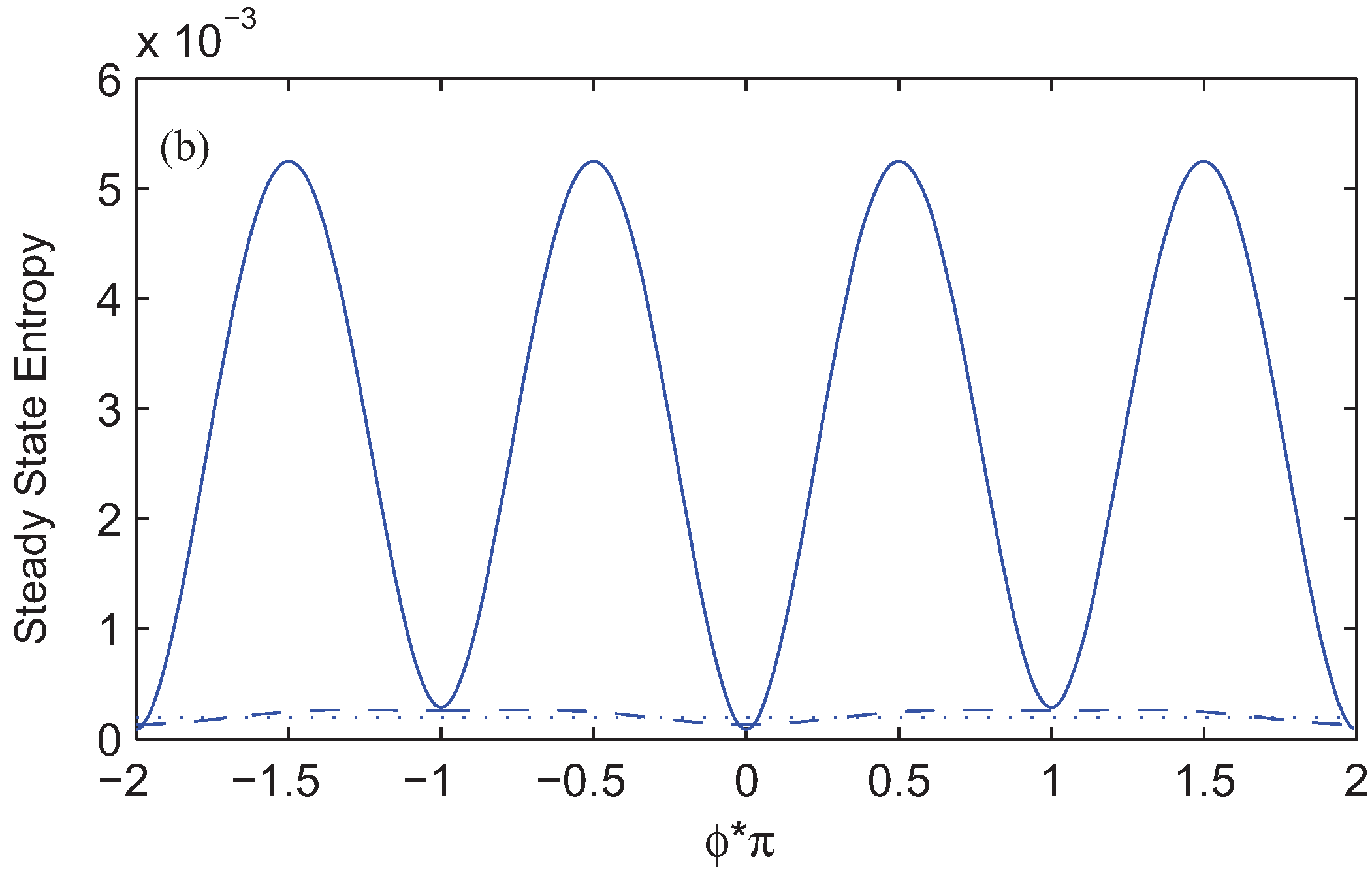
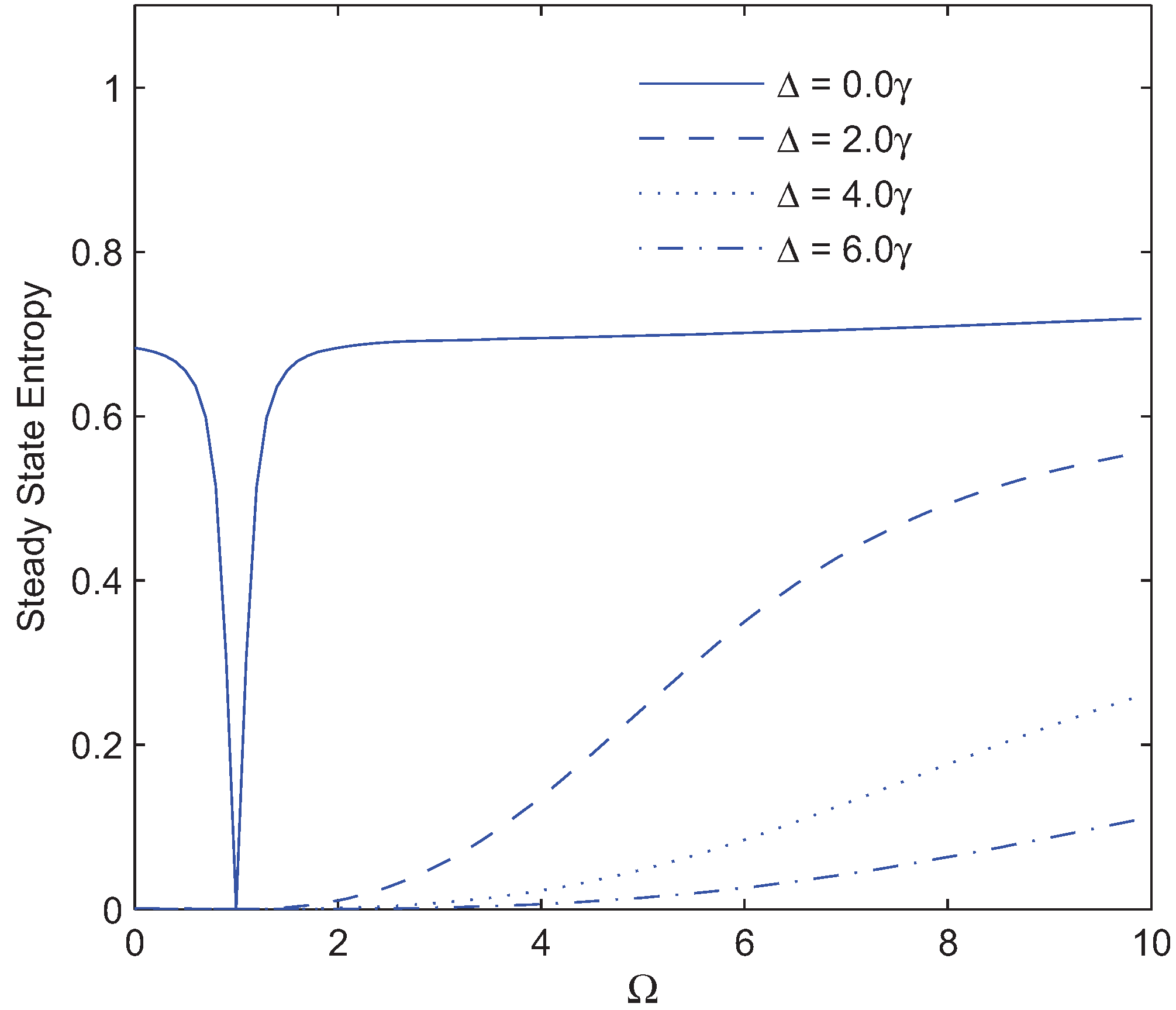
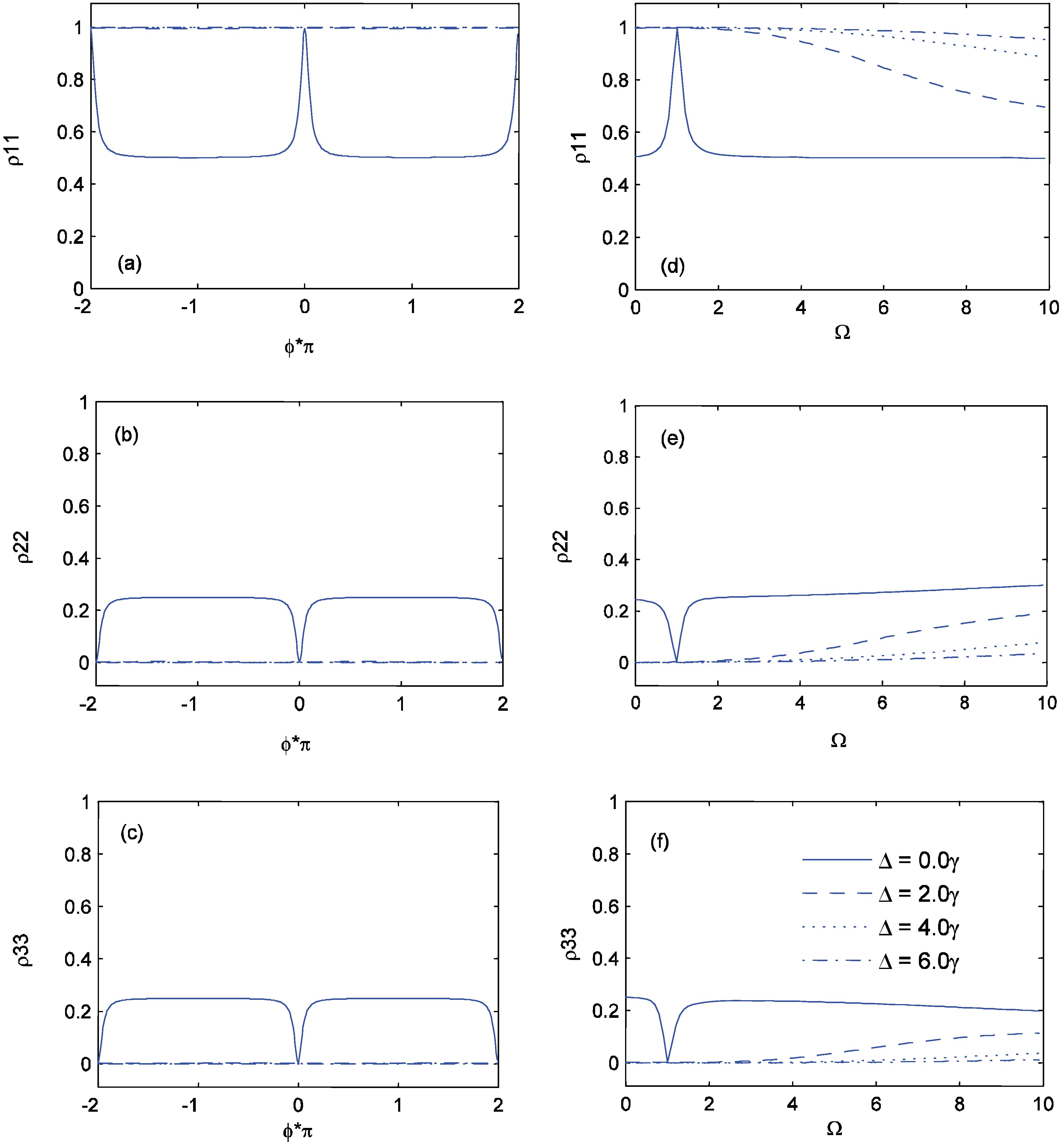
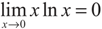 . To explain the physics of phenomena, let us introduce the new bases |1〉,
. To explain the physics of phenomena, let us introduce the new bases |1〉, 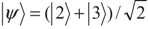 and
and 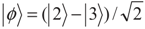 . The density matrix Equation (2) in these bases can be written as:
. The density matrix Equation (2) in these bases can be written as:
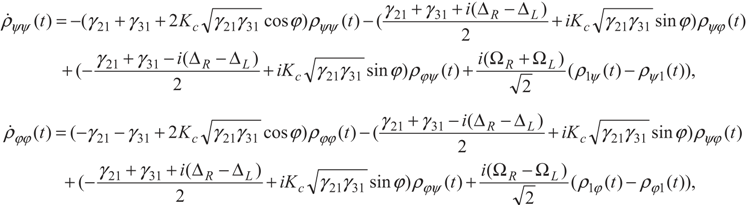
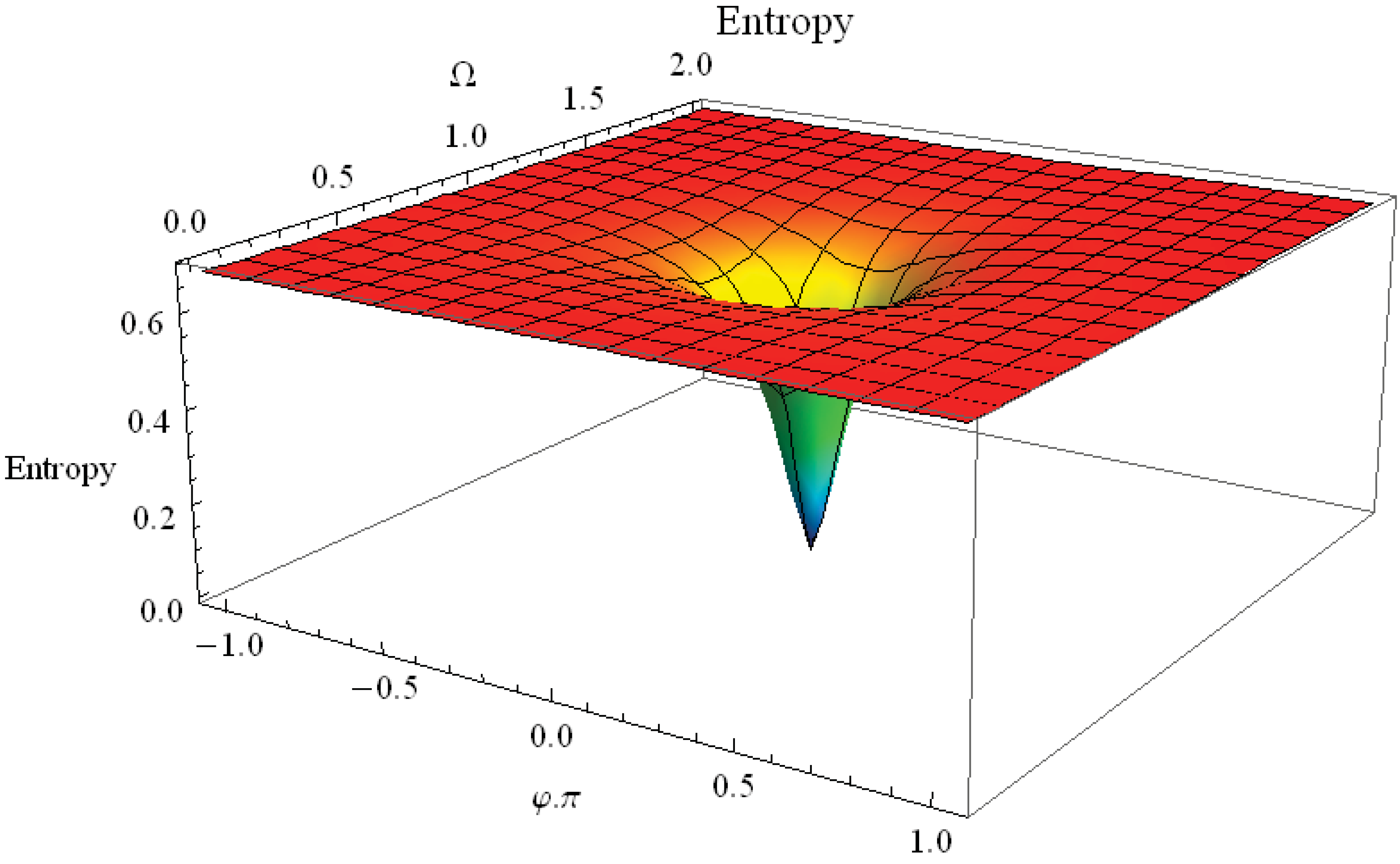
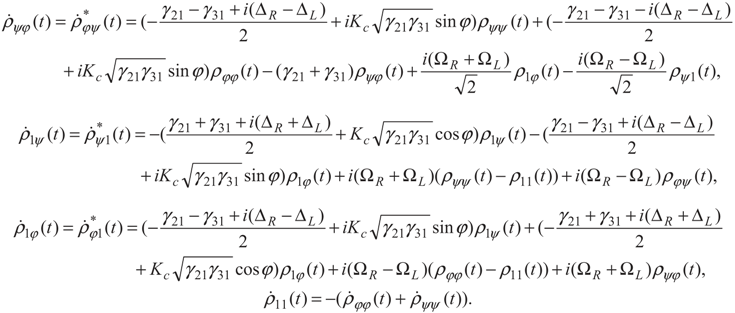
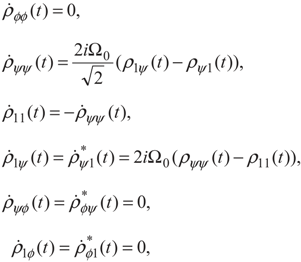
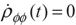
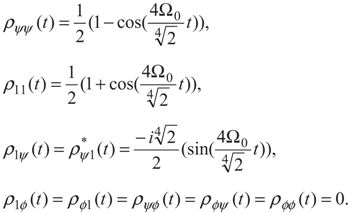
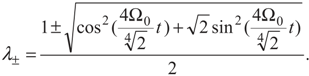
5. Conclusion and Perspectives
Acknowledgements
References
- Bennett, C.H.; DiVincenzo, D.P.; Smolin, J.A.; Wootters, W.K. Mixed state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824–3851. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Bernstein, H.J.; Popescu, S.; Schumacher, B. consecrating partial entanglement by local operations. Phys. Rev. A 1996, 53, 2046–2052. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A.; Podolsky, A.B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179.
- Fox, M. Quantum Optics: An Introduction, 1st ed.; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Benenti, G.; Casati, G.; Strini, G. Principles of Quantum Computation and Information; World Scientific Publishing Company: Singapore, 2004; Volume 1. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Bouwmeester, D.; Pan, J.-W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar]
- Freedman, S.J.; Clauser, J.F. Experimental test of local hidden-variable theories. Phys. Rev. Lett. 1972, 28, 938–941. [Google Scholar]
- Aspect, A.P.; Grangier, P.; Roger, G. experimental realization of einstein-podolsky-rosen-bohm gendankeexperiment: A new violation of Bell’s inequalities. Phys. Rev. Lett. 1982, 49, 91–94. [Google Scholar]
- Eichmann, U.C.; Bergquist, J.C.; Bollinger, J.J.; GilliganH, J.M.; Itano, W.E.; Winelandr, D.J. Yong interference experiment with light scattered from two atoms. Phys. Rev. Lett. 1993, 70, 2359–2362. [Google Scholar]
- DeVoe, R.G.; Brewer, R.G. Observation of superradiant and subradiant spontaneous emission of two trapped ions. Phys. Rev. Lett. 1996, 76, 2049–2052. [Google Scholar] [CrossRef] [PubMed]
- Volz, J.; Weber, M.; Schlenk, D.; Rosenfeld, W.; Vrana, J.; Saucke, K.; Kurtsiefer, C.; Weinfurter, H. Observation of entanglement of a single photon with a trapped atom. Phys. Rev. Lett. 2006, 96, 030404. [Google Scholar] [CrossRef] [PubMed]
- Abdalla, M.S.; Abdel-Aty, M.; Obada, A.-S.F. Entropy and entanglement of time dependent two-mode Jaynes-Cummings model. Phys. A 2003, 326, 203–219. [Google Scholar]
- Abdalla, M.S.; Abdel-Aty, M.; Obada, A.-S.F. Quantum entropy of isotropic coupled oscillators interacting with a single atom. Opt. Commun. 2002, 211, 225–234. [Google Scholar]
- Abdalla, M.; Abdel-Aty, M.; Obada, A.-S.F. Degree of entanglement for anisotropic coupled oscillators interacting with a single atom. J. Opt. B: Quant. Semiclass. Opt. 2002, 4, 396–401. [Google Scholar]
- Obada, A.-S.F.; Hessian, H.A.; Mohamed, A.-B.A. The effects of thermal photons on entanglement dynamics for dispersive Jaynes-Cummings model. Phys. Lett. A. 2008, 372, 3699–3706. [Google Scholar] [CrossRef]
- Mortezapour, A.; Abedi, M.; Mahmoudi, M.; Khajehpour, M.R.H. The effect of a coupling field on the entanglement dynamics of a three-level atom. J. Phys. B: At. Mol. Opt. Phys. 2011, 44, 085501. [Google Scholar]
- Malinovsky, V.S.; Sola, I.R. Quantum phase control of entanglement. Phys. Rev. Lett. 2004, 93, 190502. [Google Scholar]
- Roshan Entezar, S. Controllable atom-photon entanglement near a 3D anisotropic photonic band edge. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 085503. [Google Scholar]
- Boller, K.J.; Imamolu, A.; Harris, S.E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 1991, 66, 2593–2596. [Google Scholar] [CrossRef] [PubMed]
- Field, J.E.; Hahn, K.H.; Harris, S.E. Observation of electromagnetically induced transparency in collisionally broadened lead vapor. Phys. Rev. Lett. 1991, 67, 3062–3065. [Google Scholar] [CrossRef] [PubMed]
- Javanainen, J. Effect of state superpositions created by spontaneous emission on laser-driven transitions. Europhys. Lett. 1992, 17, 407–412. [Google Scholar]
- Mahmoudi, M.; Sahrai, M.; Tajalli, H. The effects of the incoherent pumping field on the phase control of group velocity. J. Phys. B: At. Mol. Opt. Phys. 2006, 39, 1825–1835. [Google Scholar]
- Mahmoudi, M.; Evers, J. Light propagation through closed-loop atomic media beyond the multiphoton resonance condition. Phys. Rev. A 2006, 74, 063827. [Google Scholar]
- Sahrai, M.; Mahmoudi, M.; Kheradmand, R. The impact of the relative phase on the transient optical properties of a four-level EIT medium. Phys. Lett. A 2007, 367, 408–414. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, G.; Wu, J.-H.; Wang, H.-H.; Gao, J.-Y.; Babin, S.A. HThe phase dependent double electromagnetically induced transparency in a four-level system with closed interaction contour. Phys. Lett. A. 2004, 324, 388–395. [Google Scholar] [CrossRef]
- Wu, J.-H.; Zhang, H.-F.; Gao, J.-Y. Phase dependence of the inversionless gain in a ∧ System with Near-Degenerate Levels. Chin. Phys. Lett. 2002, 19, 1103–1105. [Google Scholar]
- Wu, J.-H.; Yu, Z.-L.; Gao, J.-Y. Response of the probe gain with or without inversion to the relative phase of two coherent fields in a three-level V model. Opt. Commun. 2002, 211, 257–264. [Google Scholar] [CrossRef]
- Zhou, P.; Swain, S. HPhase-dependent spectra in a driven two-level atomh. Phys. Rev. Lett. 1999, 82, 2500–2503. [Google Scholar] [CrossRef]
- Sahrai, M.; Maleki, A.; Hemmati, R.; Mahmoudi, M. Transient dispersion and absorption in a V-shaped atomic system. Eur. Phys. J. D 2010, 56, 105–112. [Google Scholar] [CrossRef]
- Roshan Entezar, S. Disentanglement of atom-photon via quantum interference in driven three-level atoms. Opt. Commun. 2009, 282, 1171–1174. [Google Scholar] [CrossRef]
- Boukobza, E.; Tannor, D.J. HEntropy exchange and entanglement in the Jaynes-Cummings modelh. Phys. Rev. A 2005, 71, 063821. [Google Scholar] [CrossRef]
- Phoenix, S.J.D.; Knight, P.L. Fluctuations and entropy in models of quantum optical resonance. Ann. Phys. 1988, 186, 381–407. [Google Scholar] [CrossRef]
- Araki, A.; Lieb, E. Entropy Inequalities. Commun. Math. Phys. 1970, 18, 160–170. [Google Scholar] [CrossRef]
- Phoenix, S.J.D.; Knight, P.L. Establishment of an entangled atom-field state in the Jaynes-Cummings model. Phys. Rev. A 1991, 44, 6023–6029. [Google Scholar] [CrossRef] [PubMed]
- Phoenix, S.J.D.; Knight, P.L. Comment on “Collapse and revival of the state vector in Jaynes-Cummings model: An example of state preparation by a quantum apparatus”. Phys. Rev. Lett. 1991, 66, 2833–2833. [Google Scholar] [CrossRef] [PubMed]
- Obada, A.-S.F.; Hessian, H.A. Entanglement generation and entropy growth due to intrinsic decoherence in the Jaynes-Cummings model. J. Opt. Soc. Am. B 2004, 21, 1535–1542. [Google Scholar] [CrossRef]
© 2011 by the authors licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Abazari, M.; Mortezapour, A.; Mahmoudi, M.; Sahrai, M. Phase-Controlled Atom-Photon Entanglement in a Three-Level V-Type Atomic System via Spontaneously Generated Coherence. Entropy 2011, 13, 1541-1554. https://doi.org/10.3390/e13091541
Abazari M, Mortezapour A, Mahmoudi M, Sahrai M. Phase-Controlled Atom-Photon Entanglement in a Three-Level V-Type Atomic System via Spontaneously Generated Coherence. Entropy. 2011; 13(9):1541-1554. https://doi.org/10.3390/e13091541
Chicago/Turabian StyleAbazari, Mohammad, Ali Mortezapour, Mohammad Mahmoudi, and Mostafa Sahrai. 2011. "Phase-Controlled Atom-Photon Entanglement in a Three-Level V-Type Atomic System via Spontaneously Generated Coherence" Entropy 13, no. 9: 1541-1554. https://doi.org/10.3390/e13091541
APA StyleAbazari, M., Mortezapour, A., Mahmoudi, M., & Sahrai, M. (2011). Phase-Controlled Atom-Photon Entanglement in a Three-Level V-Type Atomic System via Spontaneously Generated Coherence. Entropy, 13(9), 1541-1554. https://doi.org/10.3390/e13091541



