On Accuracy of PDF Divergence Estimators and Their Applicability to Representative Data Sampling
Abstract
:1. Introduction
2. Estimation of the PDFs
2.1. Parzen Window Method
- Pseudo likelihood cross-validation [13], which attempts to select the bandwidth σ to maximize a pseudo-likelihood function of the density estimate using leave-one-out approximation to avoid a trivial maximum at . Interestingly, the pseudo-likelihood method minimizes the Kullback-Leibler divergence between the true density and the estimated density, but it tends to produce inconsistent estimates for heavy-tailed distributions [12].
- “Rule of Thumb” (RoT) minimisation [14] of the Asymptotic Mean Integrated Squared Error (AMISE) between the true distribution and its estimate. Calculation of bandwidth minimizing the AMISE criterion requires estimation of integral of squared second derivative of the unknown true density function (see [12]), which is a difficult task by itself. The RoT method thus replaces the unknown value with an estimate calculated with reference to a normal distribution. This makes the method computationally tractable at the risk of producing poor estimates for non-Gaussian PDFs.
- “Solve-the-equation plug-in method” [15], which also minimizes AMISE between the true distribution and its estimate, but without assuming any parametric form of the former. This method is currently considered as state-of-the-art [16], although it has a computational complexity which is quadratic in the dataset size. A fast approximate bandwidth selection algorithm of [17], which scales linearly in the size of data has been used in this study.
2.2. k-Nearest Neighbour Method
3. Divergence Measures
3.1. Kullback-Leibler Divergence
3.2. Jeffrey’s Divergence
3.3. Jensen-Shannon Divergence
3.4. Cauchy-Schwarz Divergence
3.5. Mean Integrated Squared Error
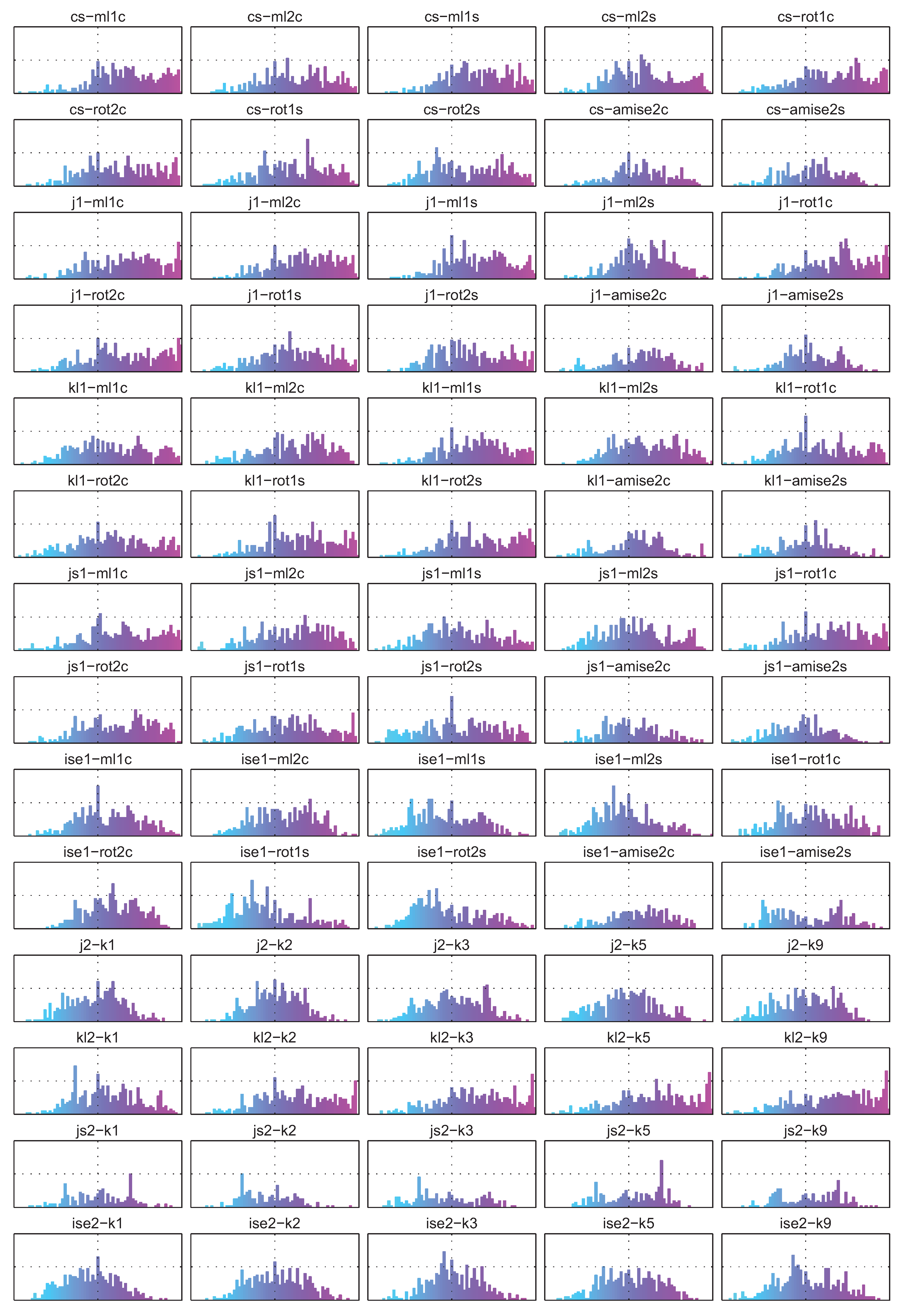
4. Empirical Convergence of the Divergence Estimators
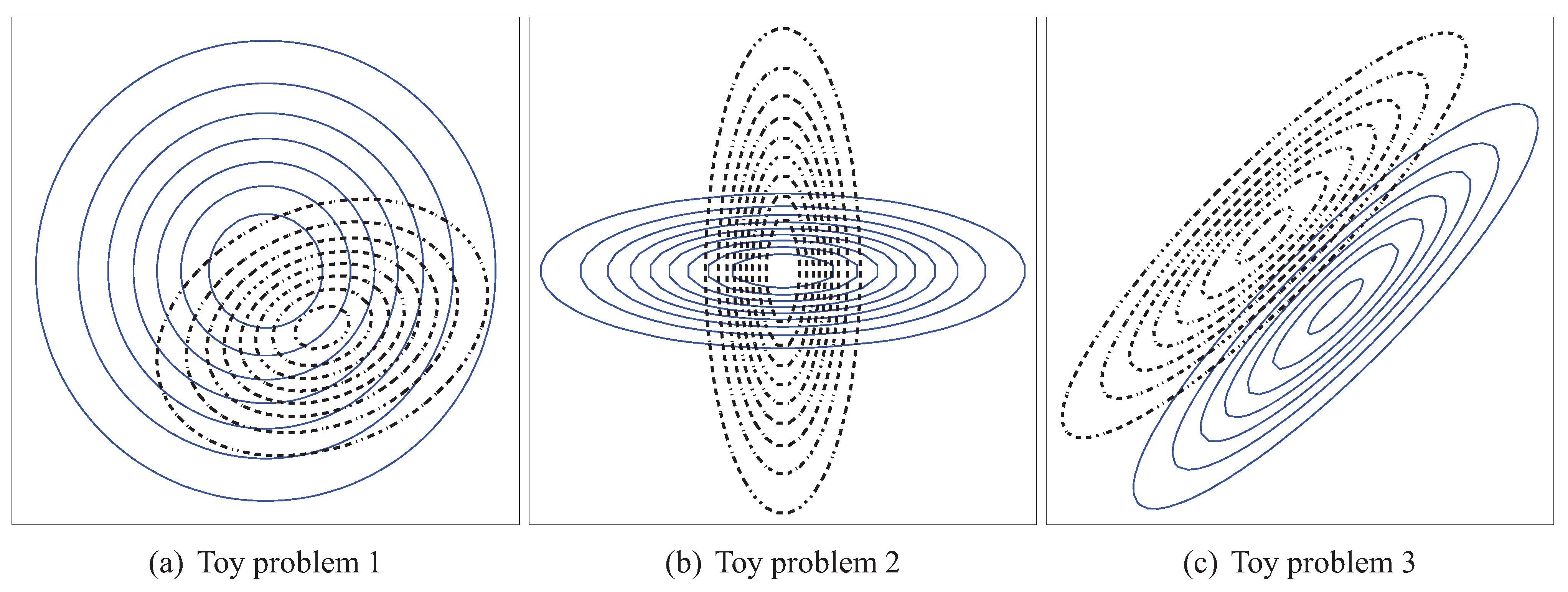
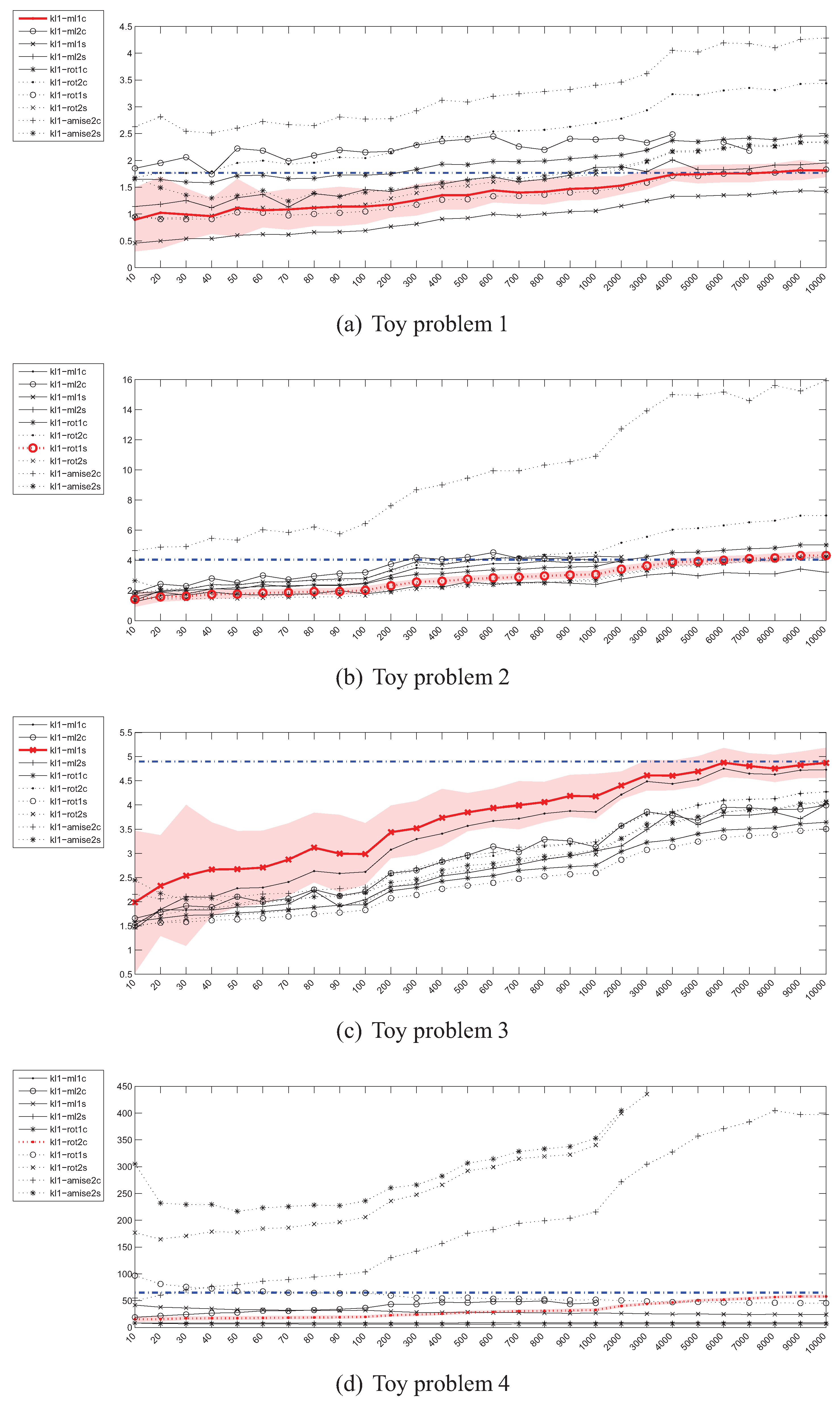
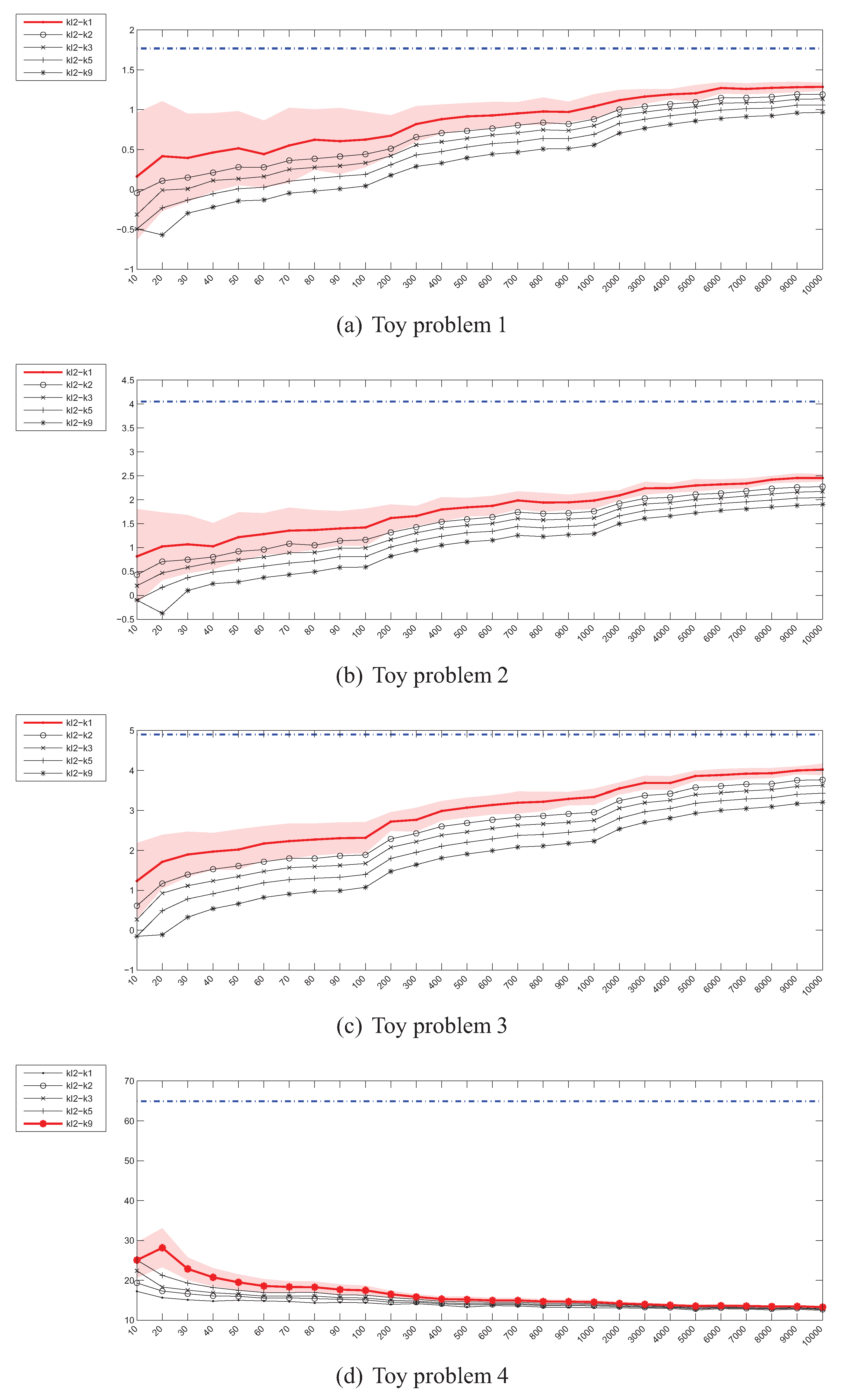
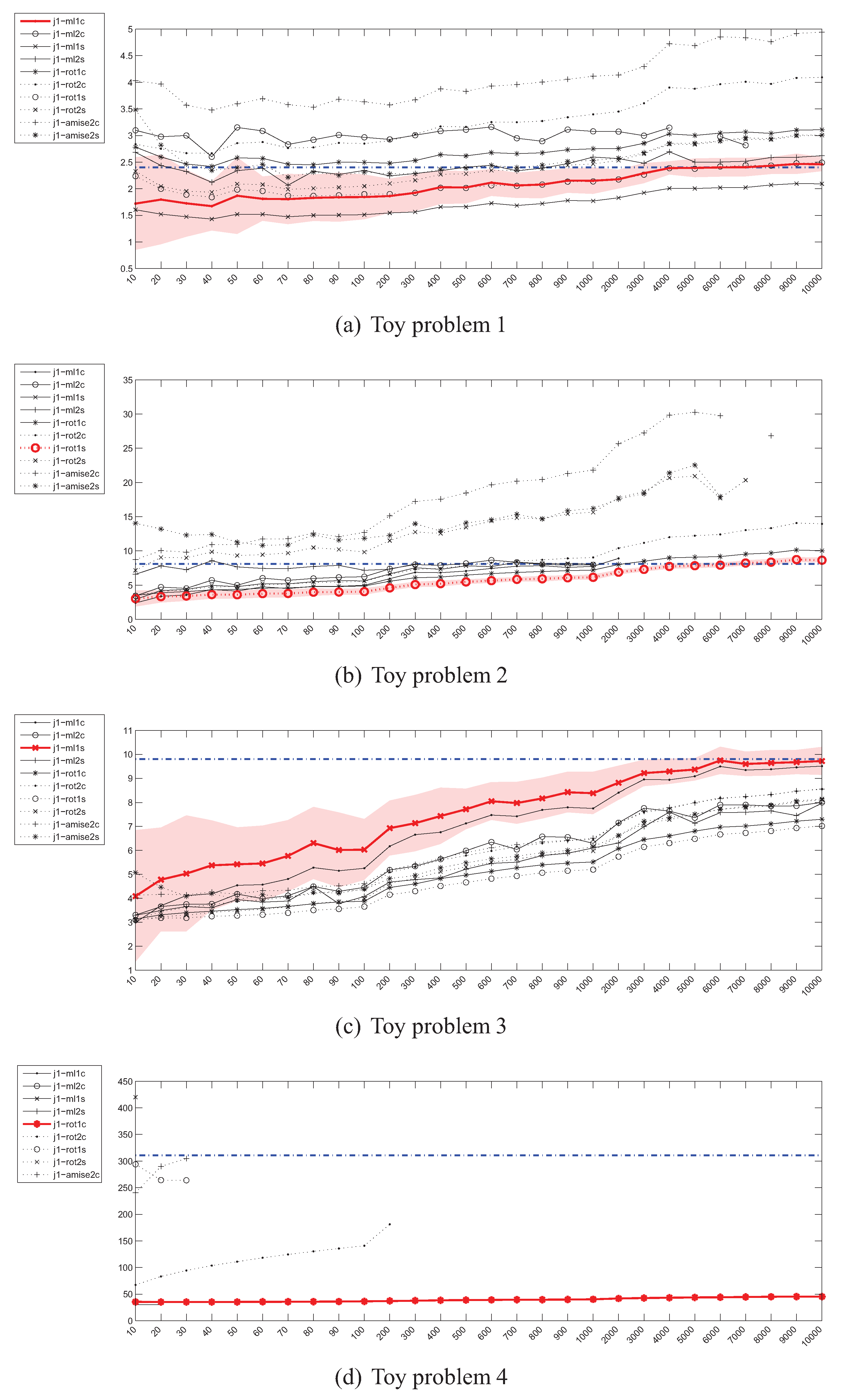
4.1. Experiment Setup
- Problem 1, which is the same as the one in [18]:
- Problem 2, where the means of both distributions are equal, but the covariance matrices are not:
- Problem 3, where the covariance matrices of both distributions are equal, but the means are not:
- Problem 4, where the Gaussians are 20-dimensional, , and , have been generated randomly from the and intervals respectively.
4.2. Estimation of the Kullback-Leibler (KL) Divergence
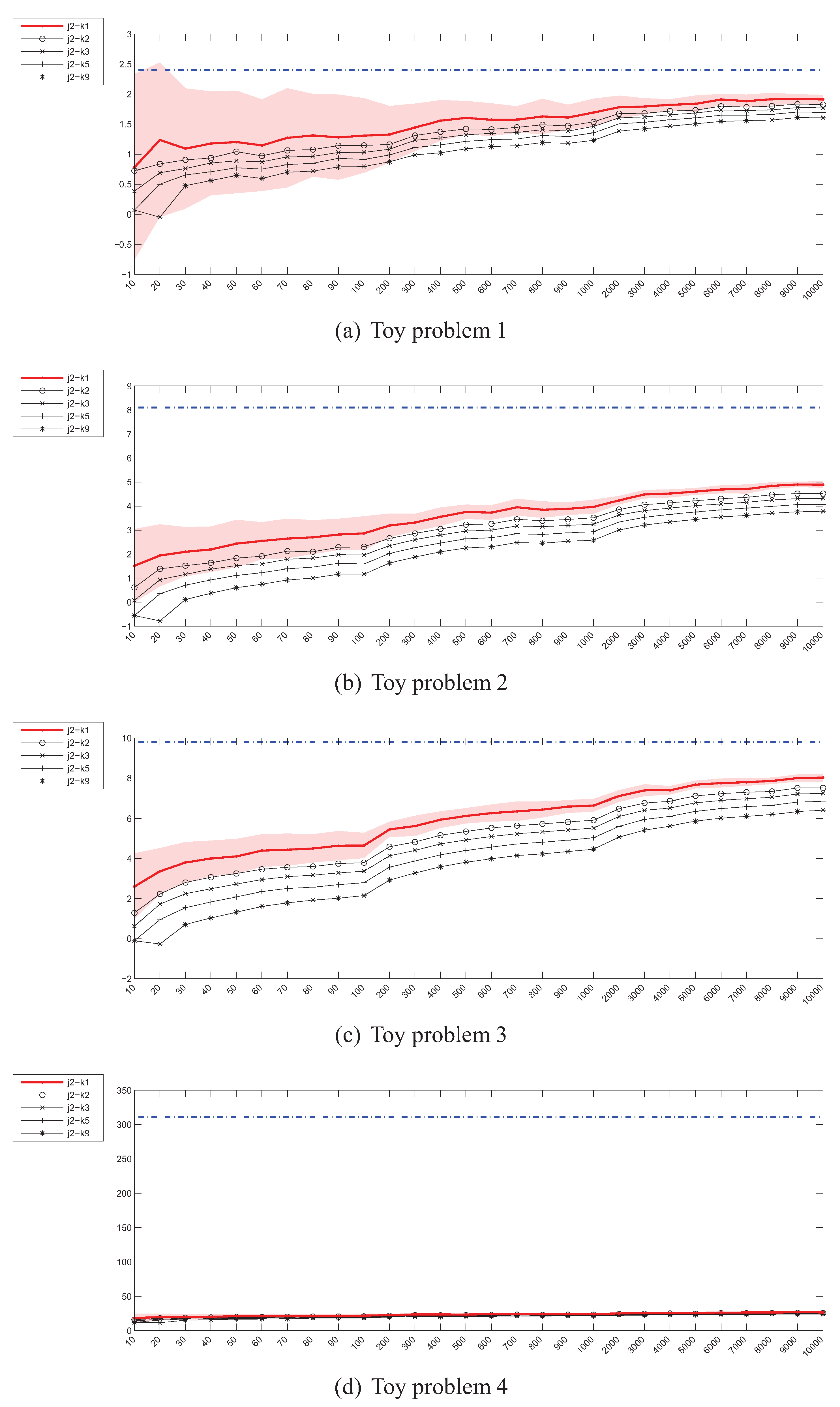
4.3. Estimation of the Jeffrey’s (J) Divergence
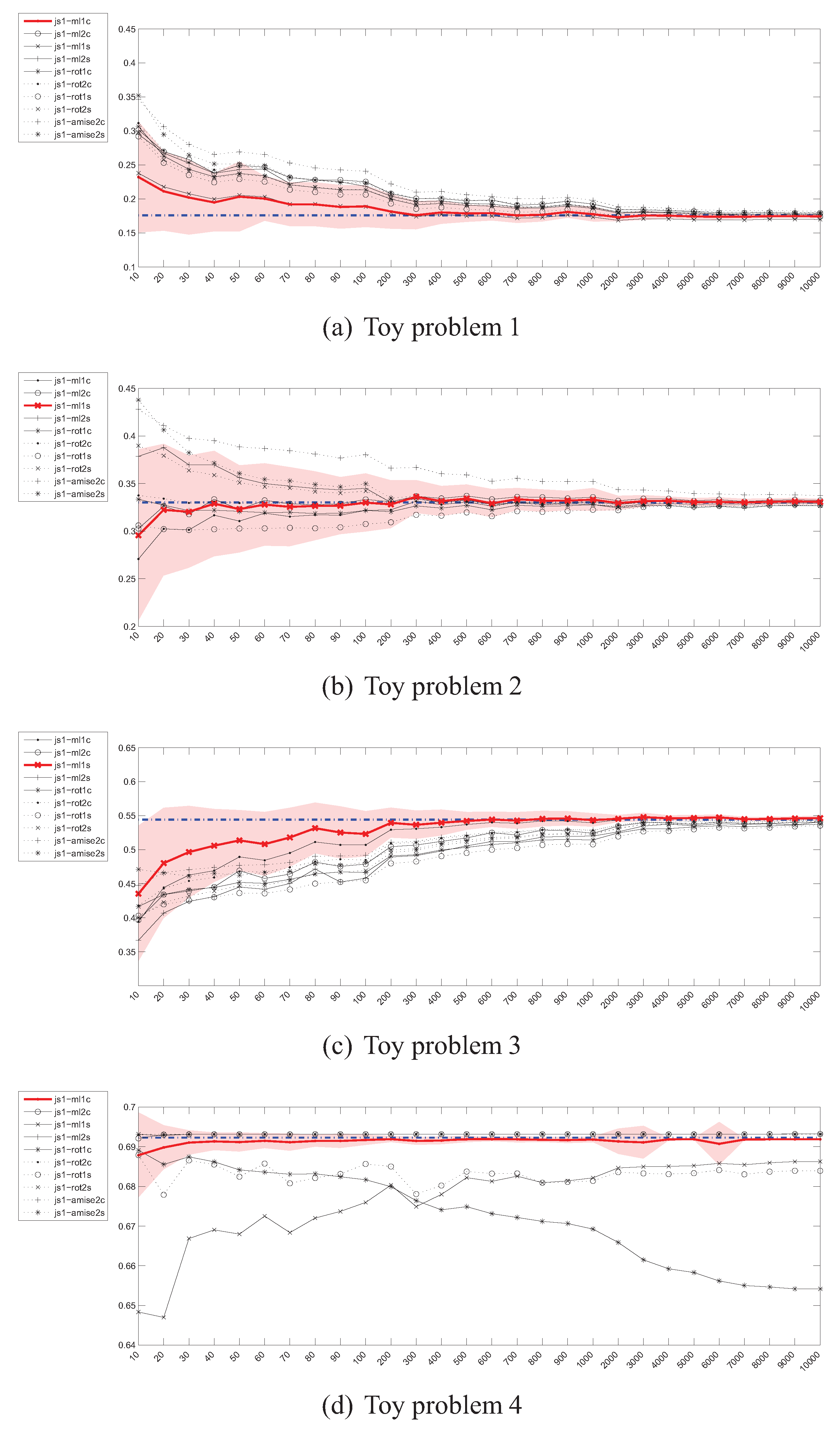
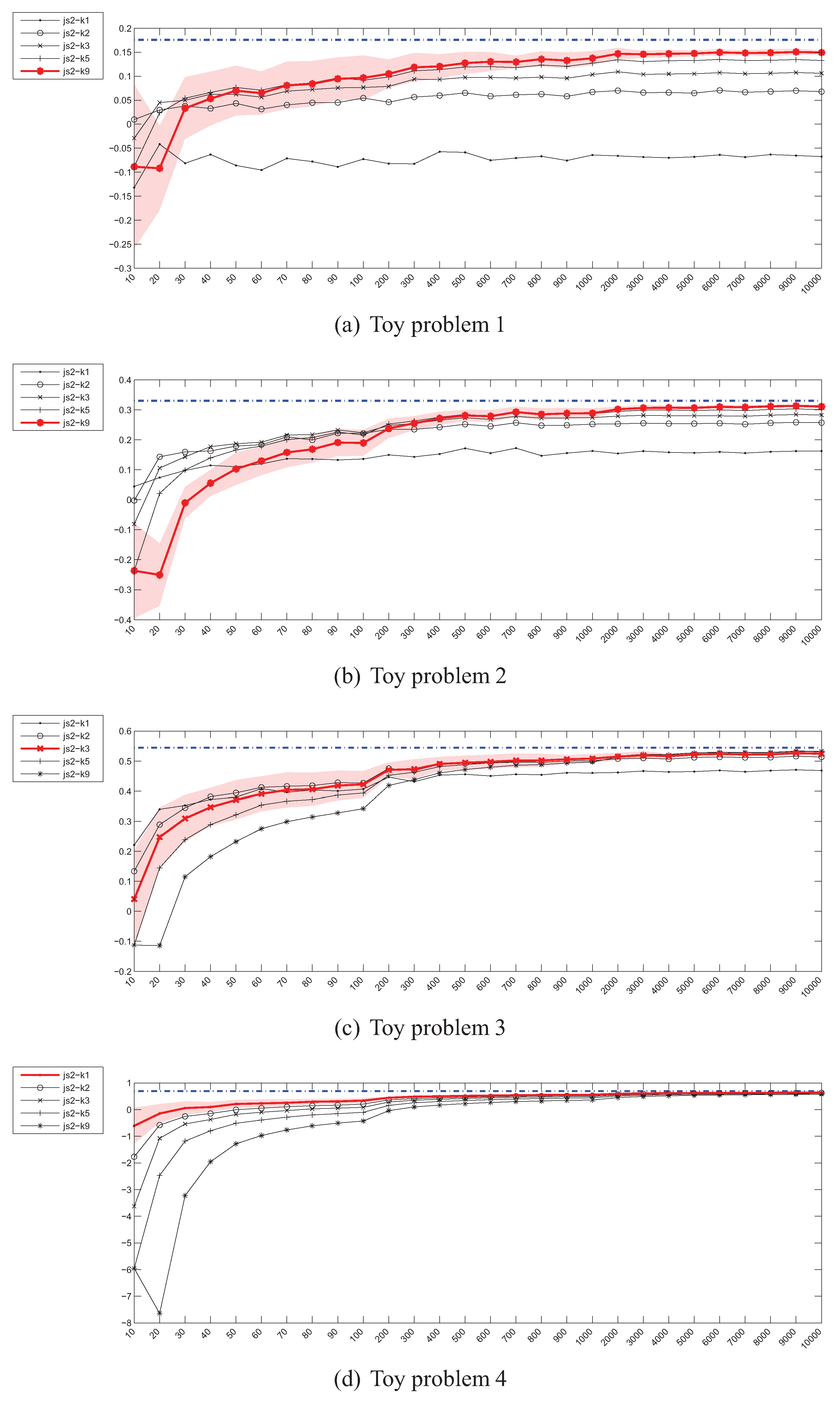
4.4. Estimation of the Jensen-Shannon’s (JS) divergence
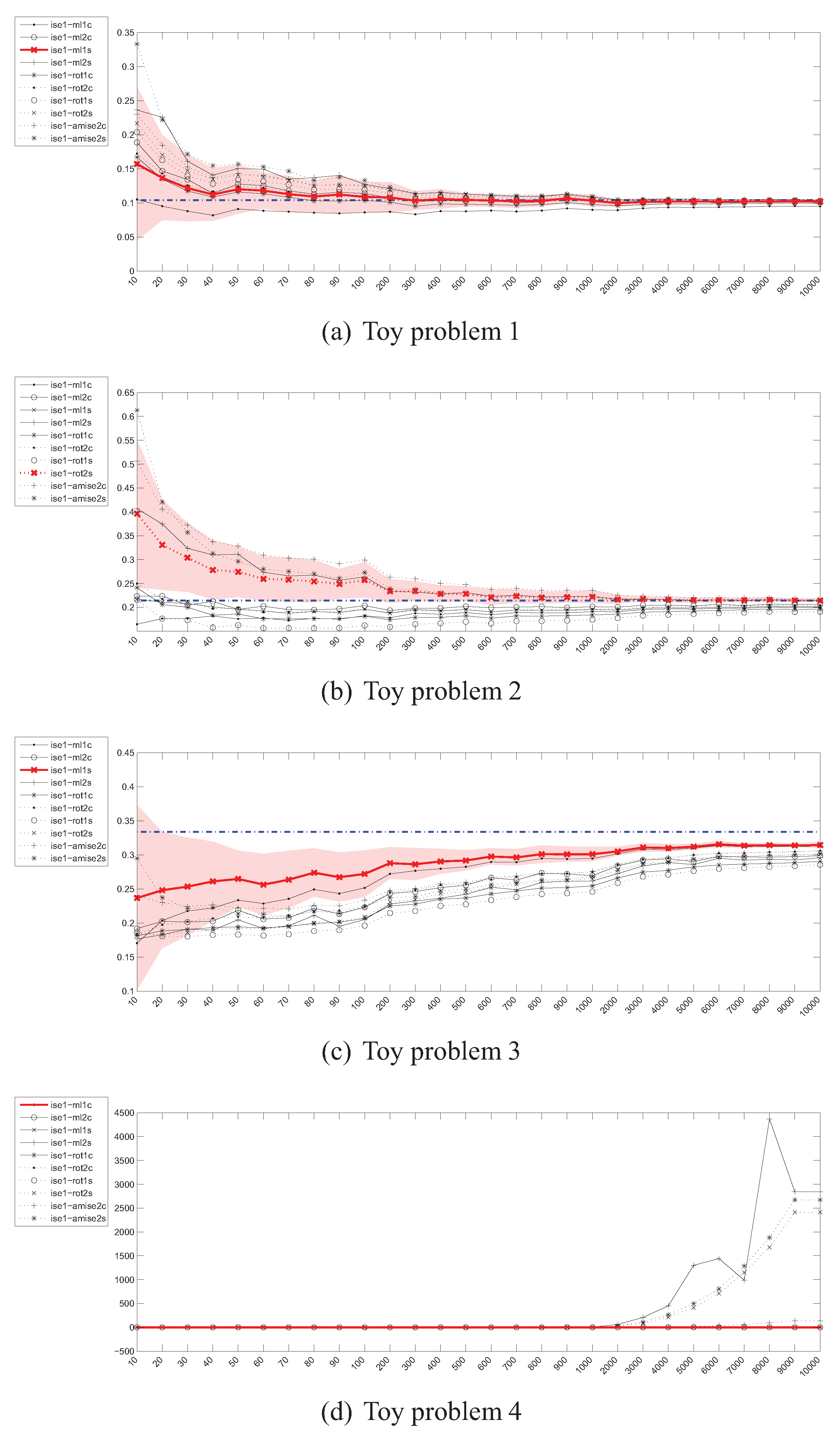
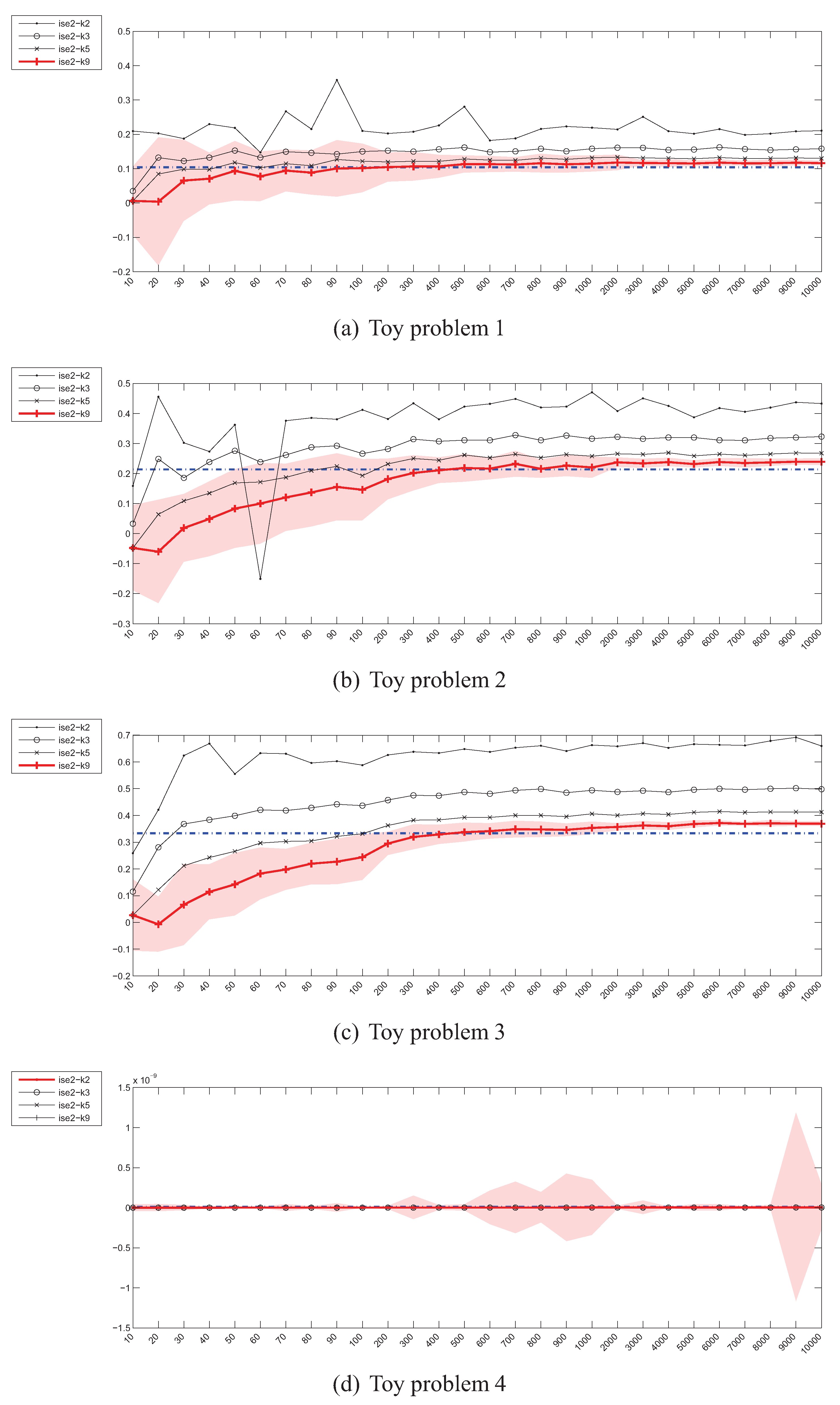
4.5. Estimation of the Integrated Squared Error (ISE)
4.6. Estimation of the Cauchy-Schwarz (CS) divergence
4.7. Summary
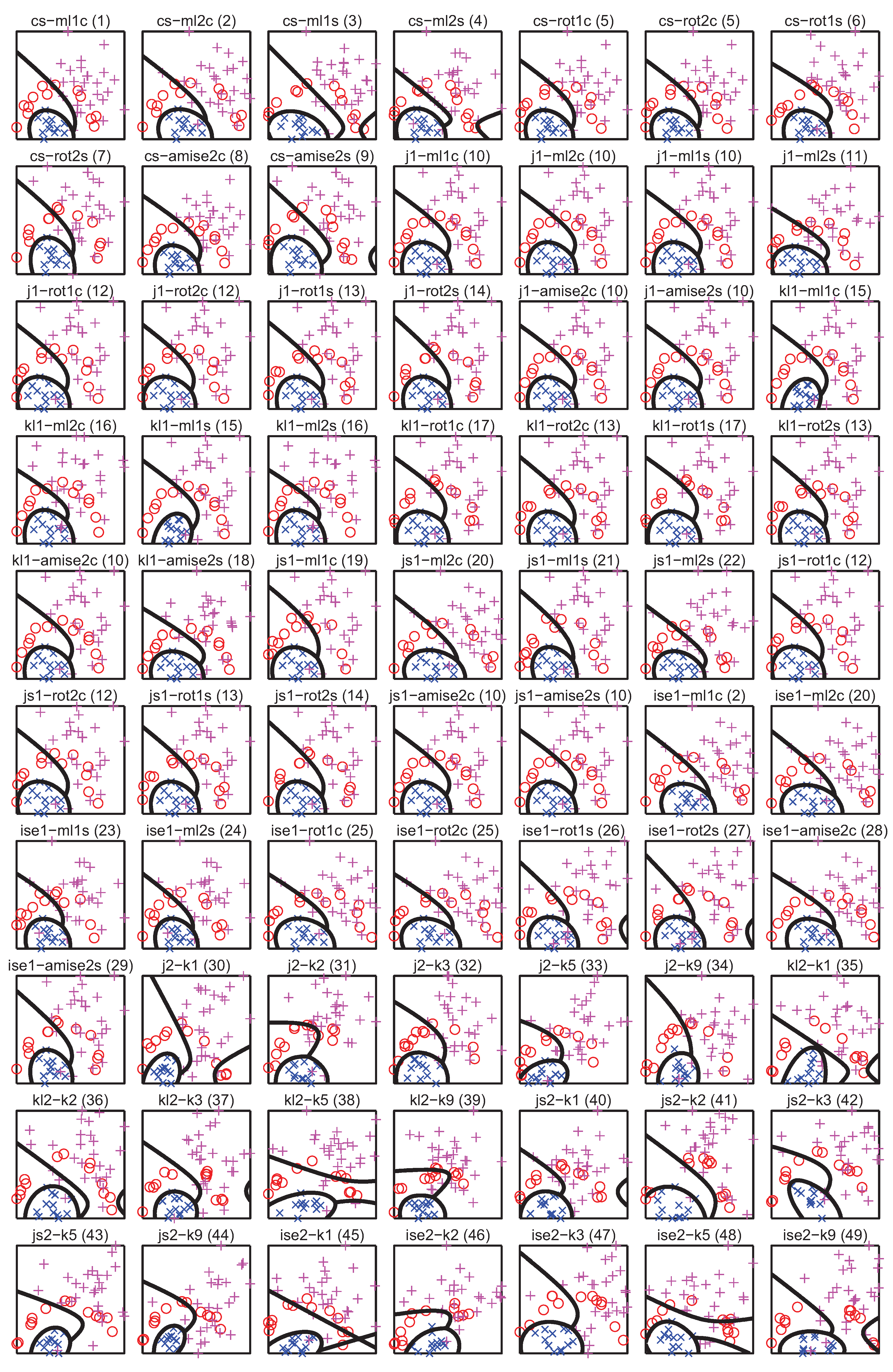
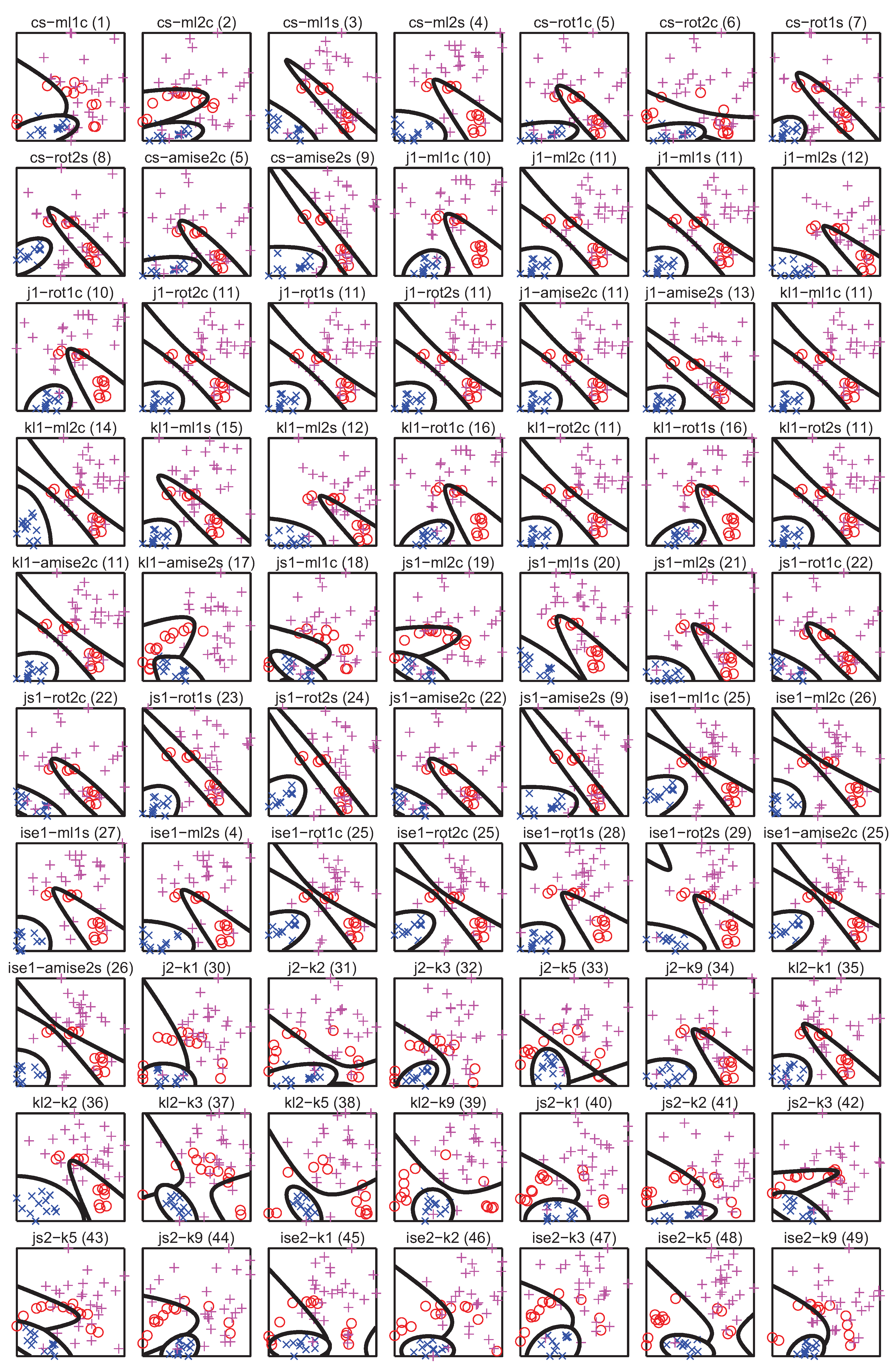
5. PDF Divergence Guided Sampling for Error Estimation
5.1. Experiment Setup
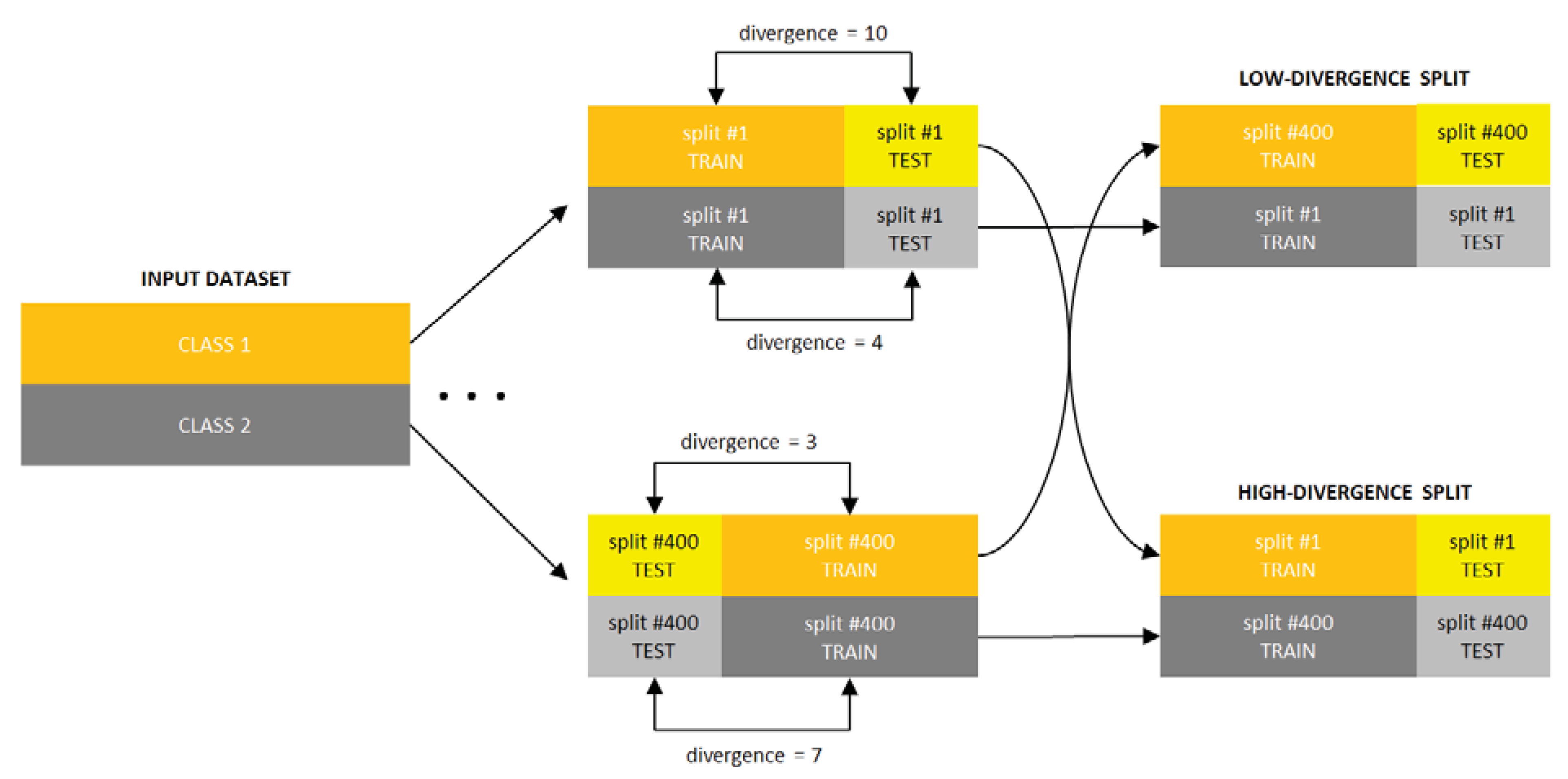
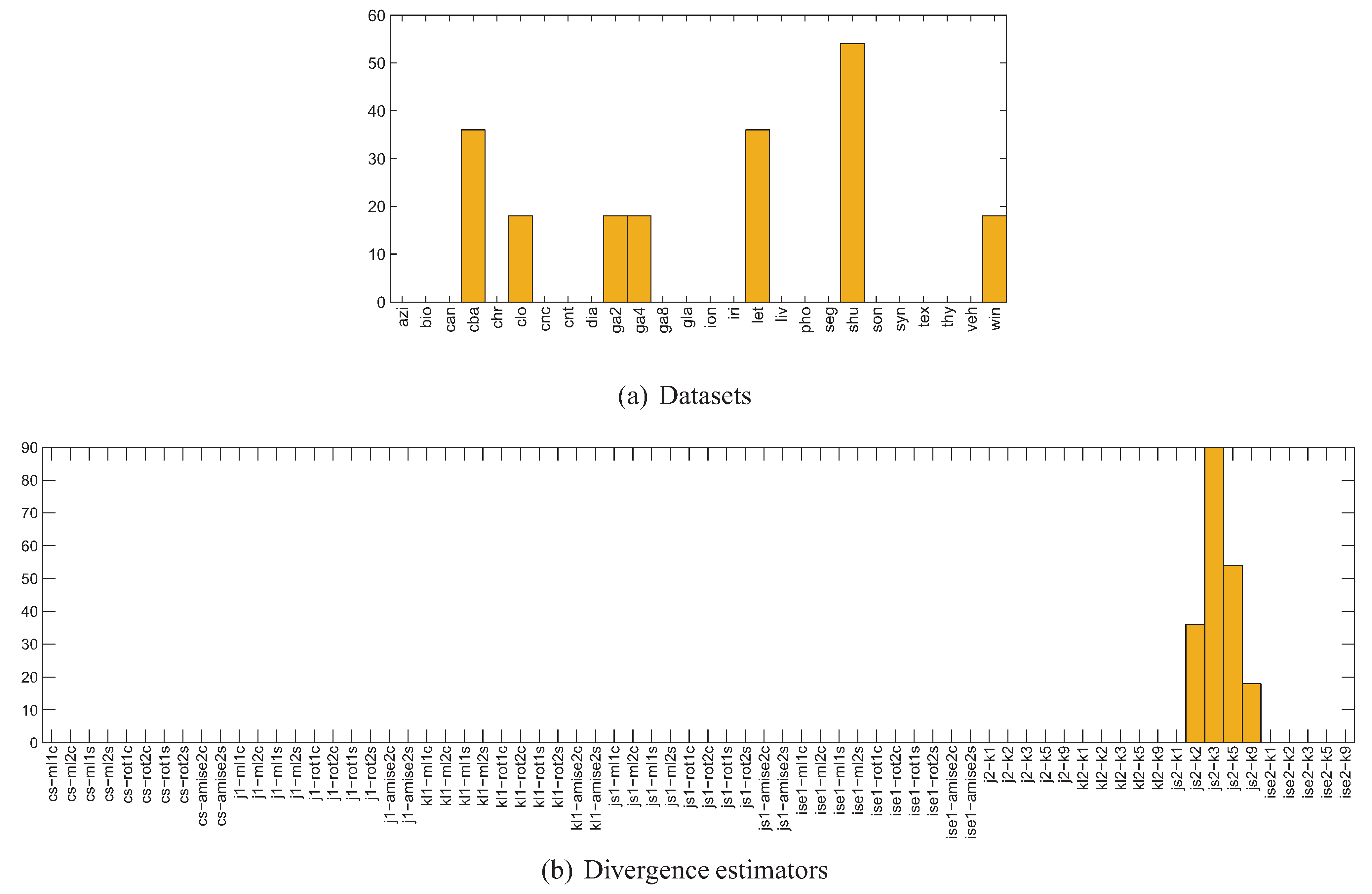
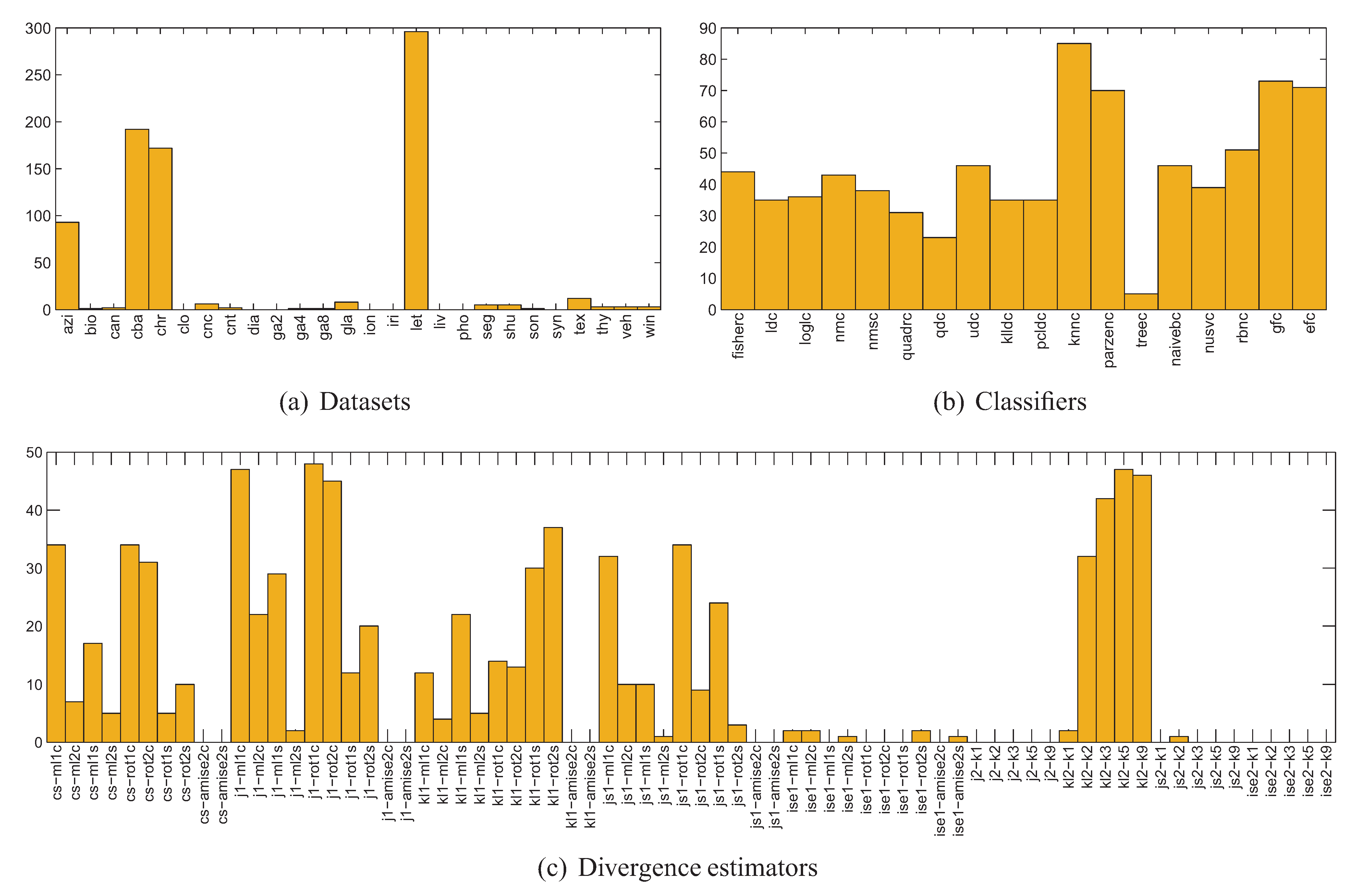
- for each of the 400 splits and each class of the dataset, 70 different estimators of divergence between the training and test parts were calculated, accounting for all possible combinations of techniques listed in Table 1, where in the case of kNN density based estimators were used; the rationale behind estimating the divergence for each class separately is that the dataset can only be representative of a classification problem if the same is true for its every class,
- for each divergence estimator the classes were sorted by the estimated value, forming 400 new splits per estimator (since for some splits some estimators produced negative values, these splits have been discarded),
- 11 splits were selected for each divergence estimator based on the estimated value averaged over all classes, including splits for the lowest and highest averaged estimate and 9 intermediate values,
- the classifiers were trained using the training part and tested using the test part for each split and each divergence estimator, producing error estimates sorted according to the divergence estimate.
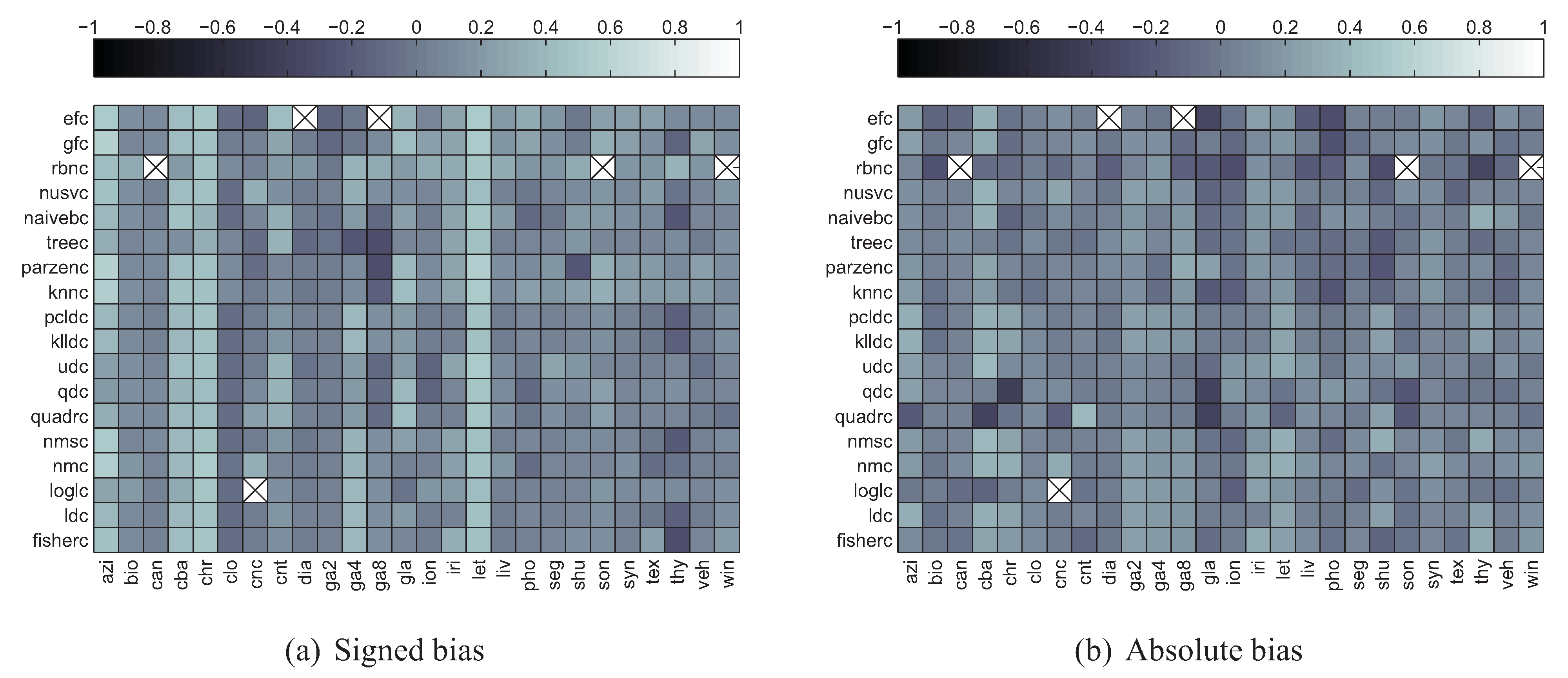
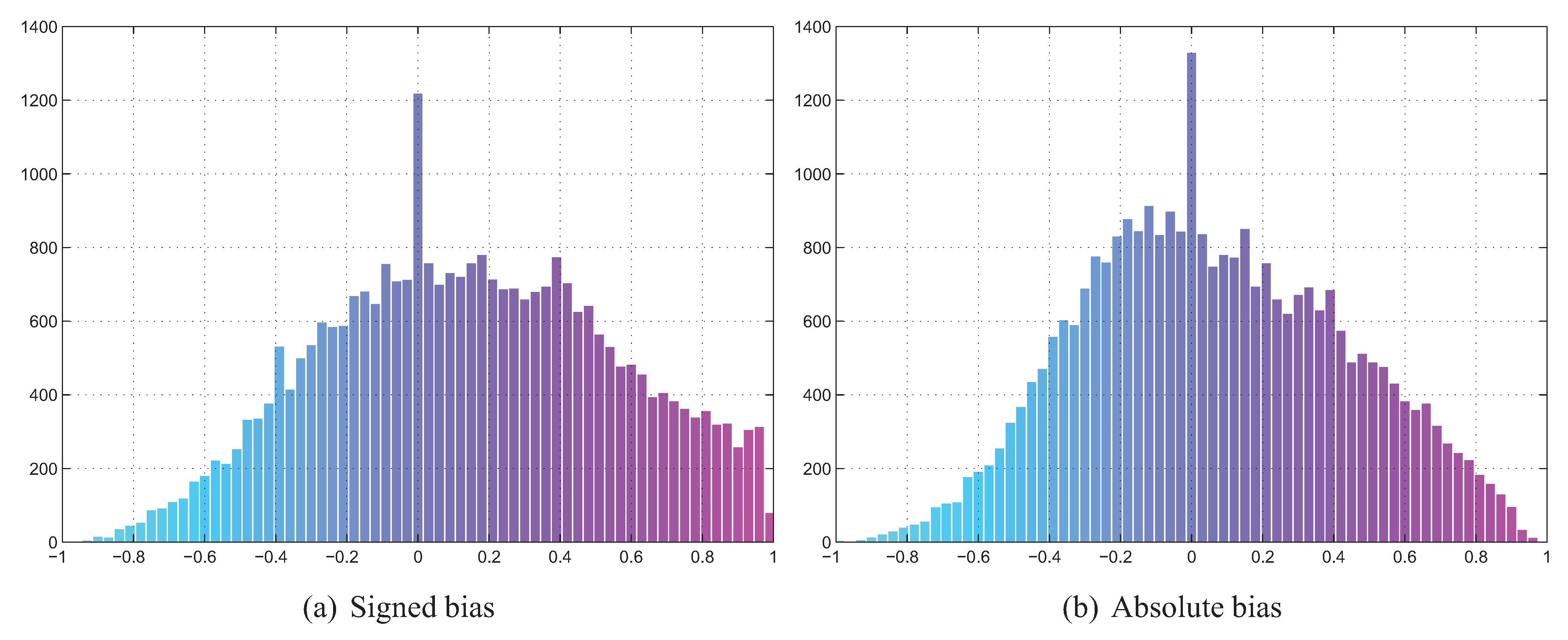
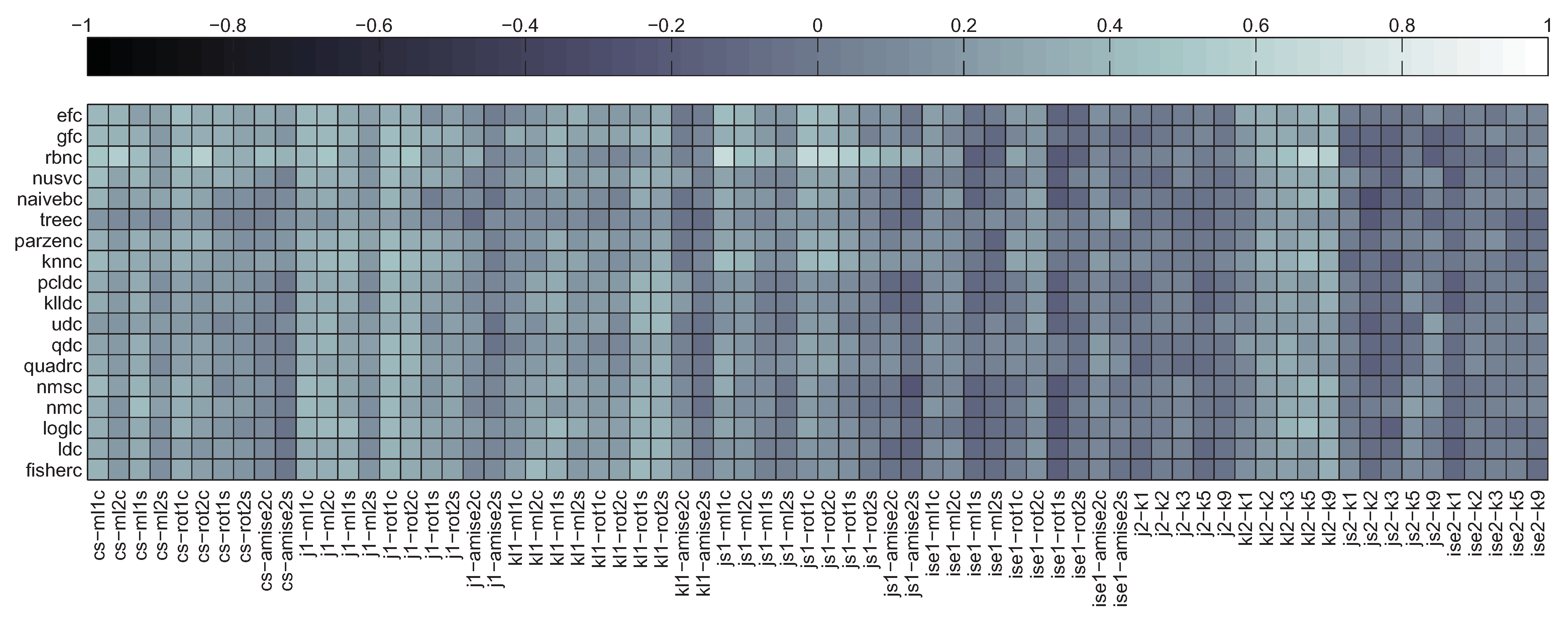
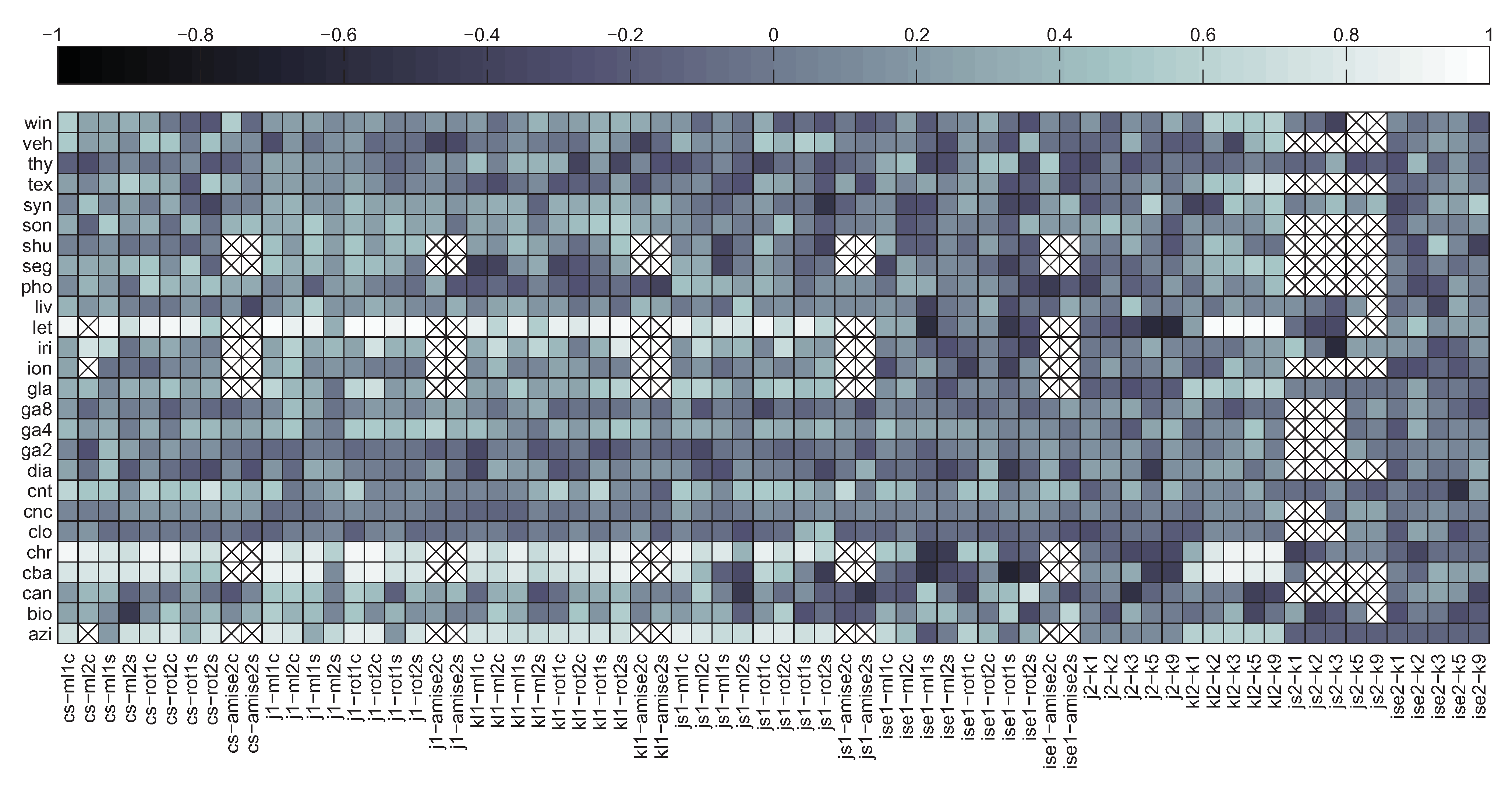
5.2. Correlation between Divergence Estimators and Bias
5.3. Summary
6. Discussion
- Experiments based on Gaussian distributions, with (1) three 8-dimensional datasets consisting of two normally distributed classes with various configurations of means and covariances, (2) 100 instances drawn randomly per class, used for selection of representative subsample and parameter tuning (for each class separately), and (3) 100 instances drawn randomly per class for testing.
- Experiments based on non-Gaussian distributions, with (1) one dataset of unknown dimensionality having two classes, each distributed according to a mixture of two Gaussians (two-modal distributions), (2) 75 instances drawn randomly per each mode (i.e., 150 instances per class) for selection of representative subsample and parameter tuning (for each class separately), and (3) instances drawn randomly per each class for testing.
- Greedy optimisation of the Kullback-Leibler divergence estimator in both cases.
7. Conclusions
Acknowledgements
References
- Budka, M.; Gabrys, B. Correntropy-based density-preserving data sampling as an alternative to standard cross-validation. In Proceedings of the International Joint Conference on Neural Networks, IJCNN 2010, part of the IEEE World Congress on Computational Intelligence, WCCI 2010, Barcelona, Spain, 18–23 July 2010; pp. 1437–1444.
- Budka, M.; Gabrys, B. Density Preserving Sampling (DPS) for error estimation and model selection. IEEE Trans. Pattern Anal. Mach. Intell. submitted for publication. 2011. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, Canada, 20–25 August 1995; Morgan Kaufmann: San Francisco, CA, USA, 1995; Volume 2, pp. 1137–1145. [Google Scholar]
- Liu, W.; Pokharel, P.; Principe, J. Correntropy: A Localized Similarity Measure. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, Canada, 16–21 July 2006; pp. 4919–4924.
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar]
- Duda, R.; Hart, P.; Stork, D. Pattern Classification, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Seghouane, A.; Bekara, M. A small sample model selection criterion based on Kullback’s symmetric divergence. IEEE Trans. Signal Process. 2004, 52, 3314–3323. [Google Scholar] [CrossRef]
- Stone, M. An asymptotic equivalence of choice of model by cross-validation and Akaike’s criterion. J. Roy. Stat. Soc. B 1977, 39, 44–47. [Google Scholar]
- Nguyen, X.; Wainwright, M.; Jordan, M. Estimating divergence functionals and the likelihood ratio by convex risk minimization. IEEE Trans. Inform. Theor. 2010, 56, 5847–5861. [Google Scholar] [CrossRef]
- Jenssen, R.; Principe, J.; Erdogmus, D.; Eltoft, T. The Cauchy-Schwarz divergence and Parzen windowing: Connections to graph theory and Mercer kernels. J. Franklin Inst. 2006, 343, 614–629. [Google Scholar]
- Turlach, B. Bandwidth selection in kernel density estimation: A review. CORE and Institut de Statistique 1993, 23–493. [Google Scholar]
- Duin, R. On the choice of smoothing parameters for Parzen estimators of probability density functions. IEEE Trans. Comput. 1976, 100, 1175–1179. [Google Scholar] [CrossRef]
- Silverman, B. Density Estimation for Statistics and Data Analysis; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Sheather, S.J.; Jones, M.C. A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation. J. Roy. Stat. Soc. B 1991, 53, 683–690. [Google Scholar]
- Jones, M.C.; Marron, J.S.; Sheather, S.J. A Brief Survey of Bandwidth Selection for Density Estimation. J. Am. Stat. Assoc. 1996, 91, 401–407. [Google Scholar] [CrossRef]
- Raykar, V.C.; Duraiswami, R. Fast optimal bandwidth selection for kernel density estimation. In Proceedings of the 6th SIAM International Conference on Data Mining, Bethesda, Maryland, USA, 20–22 April 2006; Ghosh, J., Lambert, D., Skillicorn, D., Srivastava, J., Eds.; SIAM: Philadelphia, PA, USA, 2006; pp. 524–528. [Google Scholar]
- Perez–Cruz, F. Kullback-Leibler divergence estimation of continuous distributions. In Proceedings of the IEEE International Symposium on Information Theory, Toronto, Canada, 6–11 July 2008; pp. 1666–1670.
- Cichocki, A.; Amari, S. Families of Alpha-Beta-and Gamma-Divergences: Flexible and Robust Measures of Similarities. Entropy 2010, 12, 1532–1568. [Google Scholar]
- Kullback, S. Information Theory and Statistics; Dover Publications Inc.: New York, NY, USA, 1997. [Google Scholar]
- Kullback, S.; Leibler, R. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar]
- Le Cam, L.; Yang, G. Asymptotics in Statistics: Some Basic Concepts; Springer Verlag: New York, NY, USA, 2000. [Google Scholar]
- Fukunaga, K.; Hayes, R. The reduced Parzen classifier. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 423–425. [Google Scholar]
- Cardoso, J. Infomax and maximum likelihood for blind source separation. IEEE Signal Process. Lett. 1997, 4, 112–114. [Google Scholar]
- Cardoso, J. Blind signal separation: statistical principles. Proc. IEEE 1998, 86, 2009–2025. [Google Scholar]
- Ojala, T.; Pietikäinen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distributions. Pattern Recogn. 1996, 29, 51–59. [Google Scholar]
- Hastie, T.; Tibshirani, R. Classification by pairwise coupling. Ann. Stat. 1998, 26, 451–471. [Google Scholar] [CrossRef]
- Buccigrossi, R.; Simoncelli, E. Image compression via joint statistical characterization in the wavelet domain. IEEE Trans. Image Process. 1999, 8, 1688–1701. [Google Scholar] [CrossRef] [PubMed]
- Moreno, P.; Ho, P.; Vasconcelos, N. A Kullback-Leibler divergence based kernel for SVM classification in multimedia applications. Adv. Neural Inform. Process. Syst. 2004, 16, 1385–1392. [Google Scholar]
- MacKay, D. Information Theory, Inference, and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wang, Q.; Kulkarni, S.; Verdu, S. A nearest-neighbor approach to estimating divergence between continuous random vectors. In Proceedings of the IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 242–246.
- Hershey, J.; Olsen, P. Approximating the Kullback-Leibler divergence between Gaussian mixture models. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, Hawaii, 15–20 April 2007; Volume 4, pp. 317–320.
- Seghouane, A.; Amari, S. The AIC criterion and symmetrizing the Kullback-Leibler divergence. IEEE Trans. Neural Network 2007, 18, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. Roy. Soc. Lond. Math. Phys. Sci. A 1946, 186, 453–461. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inform. Theor. 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Dhillon, I.; Mallela, S.; Kumar, R. A divisive information theoretic feature clustering algorithm for text classification. J. Mach. Learn. Res. 2003, 3, 1265–1287. [Google Scholar]
- Subramaniam, S.; Palpanas, T.; Papadopoulos, D.; Kalogeraki, V.; Gunopulos, D. Online outlier detection in sensor data using non-parametric models. In Proceedings of the 32nd international conference on Very large data bases, Seoul, Korea, 12–15 September 2006; VLDB Endowment: USA, 2006; pp. 187–198. [Google Scholar]
- Rao, S.; Liu, W.; Principe, J.; de Medeiros Martins, A. Information theoretic mean shift algorithm. In Proceedings of the 16th IEEE Signal Processing Society Workshop on Machine Learning for Signal Processing, Arlington, VA, USA, 6–8 September 2006; pp. 155–160.
- Principe, J.; Xu, D.; Fisher, J. Information theoretic learning. In Unsupervised Adaptive Filtering; Haykin, S., Ed.; John Wiley & Sons: Toronto, Canada, 2000; pp. 265–319. [Google Scholar]
- Jenssen, R.; Erdogmus, D.; Principe, J.; Eltoft, T. The Laplacian spectral classifier. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 18–23 March 2005; pp. 325–328.
- Jenssen, R.; Erdogmus, D.; Hild, K.; Principe, J.; Eltoft, T. Optimizing the Cauchy-Schwarz PDF distance for information theoretic, non-parametric clustering. In Energy Minimization Methods in Computer Vision and Pattern Recognition; Rangarajan, A., Vemurl, B., Yuille, A., Eds.; Springer: Berlin, Germany, Lect. Notes Comput. Sci., 2005, 3257, 34–45.
- Kapur, J. Measures of Information and Their Applications; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Zhou, S.; Chellappa, R. Kullback-Leibler distance between two Gaussian densities in reproducing kernel Hilbert space. In Proceedings of the IEEE International Symposium on Information Theory, Chicago, IL, USA, 27 June–2 July 2004.
- Kuncheva, L. Fuzzy Classifier Design; Physica Verlag: Heidelberg, Germany, 2000. [Google Scholar]
- Ripley, B. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Ruta, D.; Gabrys, B. A framework for machine learning based on dynamic physical fields. Nat. Comput. 2009, 8, 219–237. [Google Scholar] [CrossRef]
- Minka, T. A family of algorithms for approximate Bayesian inference. PhD thesis, MIT, Cambridge, MA, USA, January 2001. [Google Scholar]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Goldberger, J.; Gordon, S.; Greenspan, H. An efficient image similarity measure based on approximations of KL-divergence between two Gaussian mixtures. In Proceedings of the 9th IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 1, pp. 487–493.


| XX | Description |
|---|---|
| kl1 | Kullback-Leibler divergence estimator based on Parzen window density |
| kl2 | Kullback-Leibler divergence estimator based on kNN density |
| j1 | Jeffrey’s divergence estimator based on Parzen window density |
| j2 | Jeffrey’s divergence estimator based on kNN density |
| js1 | Jensen-Shannon divergence estimator based on Parzen window density |
| js2 | Jensen-Shannon divergence estimator based on kNN density |
| cs | Cauchy-Schwarz divergence estimator |
| ise1 | Integrated Squared Error estimator based on Parzen window density |
| ise2 | Integrated Squared Error estimator based on kNN density |
| YY | Description |
| ml | Pseudo-likelihood cross-validation |
| rot | Rule of Thumb |
| amise | AMISE minimisation |
| ZZ | Description |
| 1c | Identity covariance matrix multiplied by a scalar, common for both PDFs |
| 2c | Diagonal covariance matrix, common for both distributions |
| 1s | Identity covariance matrix multiplied by a scalar, separate for each PDF |
| 2s | Diagonal covariance matrix, separate for each distribution |
| Acronym | Name | Source | #obj | #attr | #class |
|---|---|---|---|---|---|
| azi | Azizah dataset | PRTools | 291 | 8 | 20 |
| bio | Biomedical diagnosis | PRTools | 194 | 5 | 2 |
| can | Breast cancer Wisconsin | UCI | 569 | 30 | 2 |
| cba | Chromosome bands | PRTools | 1000* | 30 | 24 |
| chr | Chromosome | PRTools | 1143 | 8 | 24 |
| clo | Clouds | ELENA | 1000* | 2 | 2 |
| cnc | Concentric | ELENA | 1000* | 2 | 2 |
| cnt | Cone-torus | [44] | 800 | 3 | 2 |
| dia | Pima Indians diabetes | UCI | 768 | 8 | 2 |
| ga2 | Gaussians 2d | ELENA | 1000* | 2 | 2 |
| ga4 | Gaussians 4d | ELENA | 1000* | 4 | 2 |
| ga8 | Gaussians 8d | ELENA | 1000* | 8 | 2 |
| gla | Glass identification data | UCI | 214 | 10 | 6 |
| ion | Ionosphere radar data | UCI | 351 | 34 | 2 |
| iri | Iris dataset | UCI | 150 | 4 | 3 |
| let | Letter images | UCI | 1000* | 16 | 26 |
| liv | Liver disorder | UCI | 345 | 6 | 2 |
| pho | Phoneme speech | ELENA | 1000* | 5 | 2 |
| seg | Image segmentation | UCI | 1000* | 19 | 7 |
| shu | Shuttle | UCI | 1000* | 9 | 7 |
| son | Sonar signal database | UCI | 208 | 60 | 2 |
| syn | Synth-mat | [45] | 1250 | 2 | 2 |
| tex | Texture | ELENA | 1000* | 40 | 11 |
| thy | Thyroid gland data | UCI | 215 | 5 | 3 |
| veh | Vehicle silhouettes | UCI | 846 | 18 | 4 |
| win | Wine recognition data | UCI | 178 | 13 | 3 |
| Acronym | Source | Description |
|---|---|---|
| fisherc | PRTools | Fisher’s Linear Classifier |
| ldc | PRTools | Linear Bayes Normal Classifier |
| loglc | PRTools | Logistic Linear Classifier |
| nmc | PRTools | Nearest Mean Classifier |
| nmsc | PRTools | Nearest Mean Scaled Classifier |
| quadrc | PRTools | Quadratic Discriminant Classifier |
| qdc | PRTools | Quadratic Bayes Normal Classifier |
| udc | PRTools | Uncorrelated Quadratic Bayes Normal Classifier |
| klldc | PRTools | Linear Classifier using Karhunen-Loeve expansion |
| pcldc | PRTools | Linear Classifier using Principal Component expansion |
| knnc | PRTools | k-Nearest Neighbor Classifier |
| parzenc | PRTools | Parzen Density Classifier |
| treec | PRTools | Decision Tree Classifier |
| naivebc | PRTools | Naive Bayes Classifier |
| perlc | PRTools | Linear Perceptron Classifier |
| rbnc | PRTools | RBF Neural Network Classifier |
| svc | PRTools | Support Vector Machine classifier (C-SVM) |
| nusvc | PRTools | Support Vector Machine classifier (ν-SVM) |
| gfc | [46] | Gravity Field Classifier |
| efc | [46] | Electrostatic Field Classifier |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Budka, M.; Gabrys, B.; Musial, K. On Accuracy of PDF Divergence Estimators and Their Applicability to Representative Data Sampling. Entropy 2011, 13, 1229-1266. https://doi.org/10.3390/e13071229
Budka M, Gabrys B, Musial K. On Accuracy of PDF Divergence Estimators and Their Applicability to Representative Data Sampling. Entropy. 2011; 13(7):1229-1266. https://doi.org/10.3390/e13071229
Chicago/Turabian StyleBudka, Marcin, Bogdan Gabrys, and Katarzyna Musial. 2011. "On Accuracy of PDF Divergence Estimators and Their Applicability to Representative Data Sampling" Entropy 13, no. 7: 1229-1266. https://doi.org/10.3390/e13071229
APA StyleBudka, M., Gabrys, B., & Musial, K. (2011). On Accuracy of PDF Divergence Estimators and Their Applicability to Representative Data Sampling. Entropy, 13(7), 1229-1266. https://doi.org/10.3390/e13071229




