1. Introduction
Spintronics is a generalization of electronics that takes into account the degrees of freedom related to the spins of the conduction electrons (or the spin of other electric carriers). Spintronics emerged with the discovery of giant magnetoresistance in the late 1980s [
1], and it today plays a crucial role in the development of new electronic devices and functionalities. A typical spintronic system is defined by a statistical ensemble of a plurality of electronic populations (discriminated by their internal degrees of freedom), that are put out of equilibrium in the presence of electric and magnetic forces. The consequence is the creation of coupled currents of different species of electric charges and spin carriers.
The goal of this report is to revisit spintronics in the framework of the theory of Non-Equilibrium Thermodynamics [
2,
3,
4,
5,
6,
7,
8]. More precisely, the objective is to establish a general definition of the basic concepts of spin pumping and spin transfer from the expression of the power dissipated through spin-dependent relaxation processes.
Spin transfer is the name given to the ferromagnetic excitations observed while injecting spin-dependent electric currents into a ferromagnetic nanostructure. In our context, “spin transfer” is not reduced to a given microscopic mechanism (often presented as a transverse “spin-torque” in the literature: see section 5 below). Instead, it is a consequence of both the “spin-pumping" effect (i.e., any spin-dependent relaxation mechanism that is maintained by the electric current) and the dynamic coupling between individual spins attached to the conduction electrons and the ferromagnetic degrees of freedom. Spin pumping is here a generalization of the well-known spin accumulation concept introduced for giant magnetoresistance. This is a change of paradigm in the sense that whatever the microscopic mechanism involved—and we propose three different mechanisms of spin pumping below—the effect is phenomenologically the same in terms of modification of the dynamics of the magnetization. The main result of this work, given in last section, is the equation of the dynamics of the magnetization (the so-called Landau-Lifshitz-Gilbert equation) generalized to spin-pumping effects. From the Generalized Landau-Lifshitz-Gilbert equation, the different spin-pumping contributions can be experimentally assessed and studied, e.g., with both ferromagnetic resonance-like experiments (measurement of the precession states) and magnetic hysteresis experiments (measurements of the quasi-static states).
The description holds at the mesoscopic scales, under the hypothesis of local equilibrium extended to internal degrees of freedom [
9,
10]. We have restricted the generality of this work to the simplest systems. Only classical or semi-classical systems are considered; the extension to quantum systems, especially for the definitions related to “permanent currents” (for which the second law of thermodynamics is inoperative), is beyond the scope of this report (see [
11,
12,
13]). The review is also restricted to spin and charge currents, without considering heat flows and corresponding cross coefficients (see e.g., the references [
14,
15,
16,
17,
18,
19,
20]). Finally, this work is restricted to uniform ferromagnets. It is worth noting that previous studies of spin pumping do not differentiate the spin of the conduction electrons and the ferromagnetic order parameters [
21,
22]. In those cases, the spin-pumping force can be directly defined from the space inhomogeneity of the magnetization. However, if both magnetic subsystems are differentiated, the pumping force has a different meaning, and a generalization of our model to non-uniform magnetization would be misleading in a first approach.
1.1. Longitudinal Spin Relaxation
The typical system to be investigated is a 1D wire (with x as coordinate) containing a Ferromagnetic/Non-Ferromagnetic metal junction (or a Ferromagnetic/Ferromagnetic metal junction). In the most simple cases it can be described by a statistical ensemble of independent electrons that are defined by an effective mass , an electric charge e, internal degrees of freedom reduced to the spin one half, and a quantization axis (fixed by the magnetization of the ferromagnetic layer). The system can then be reduced to two electronic populations locally represented by a reservoir of conduction electrons of spin up—defined by a chemical potential —and a reservoir of conduction electrons of spin down—defined by a chemical potential . This approach is called the two spin-channel model.
There are then two different ways to put the system out of equilibrium: (i) Applying an electric field will create spin-dependent electric currents through the wire (where is the conductivity). (ii) Applying an effective magnetic field will put the two spin populations out-of-equilibrium, creating in turn a flux of spins (noted here) in the spin configuration space.
However, the striking point is that the two generalized forces, electric and magnetic, are not independent. Applying a voltage difference through the junction also generates a stationary flux of spins because an electric field difference is maintained. The junction produces a non-zero chemical potential difference , that plays the role of an effective magnetic field, or spin-pumping force conjugated to the flux of spins . The spin flux can also be written , where is the spin-flip relaxation time and is the density of out-of-equilibrium spins.
As a consequence, applying a voltage difference through the junction generates not only the stationary spin-dependent electric currents but also the stationary spin flux .
If
is the energy density of the system (function of the entropy
and the density of charge carriers
and
), the following canonical definitions holds:
,
and
. The first relation defines the temperature, the second defines the chemical potential, and the last relation
defines the pumping force as the chemical affinity of the reaction that transforms a conduction electron of spin up into a conduction electron of spin down [
23,
24].
The power dissipated by the system at fixed temperature reads , where is the internal entropy production. The relation between the generalized force and the generalized flux is imposed by the second law of thermodynamics, , and is formally expressed by the Onsager relation.
This two-channel approach has first been proposed by Johnson and Silsbee [
25,
26], and the introduction of the pumping force
in the context of spin-dependent transport is due to Van Son
et al. [
27], with the description of longitudinal spin-accumulation and giant magnetoresistance at a Ferromagnetic/Non-Ferromagnetic interface. This approach was systematized by T. Valet and A. Fert in 1993, on the basis of the Boltzmann transport equations [
28]. The model is presented below (
Section 3) in the language of non-equilibrium thermodynamics.
Note that in the Spintronics literature, the term spin-current is devoted to the spin-dependent electric current that flows through the wire, and not to the spin-fluxÓ that flows though the spin-space (e.g., the so-called “Bloch sphere”).
1.2. Spin Precession
However, the description of spin dynamics in the spin-space is not restricted to spin-flip relaxation (
i.e., “longitudinal" spin relaxation) but it is also characterized by precession effects (“transverse spin relaxation") as observed in paramagnetic resonance or in the Spin-Hanle effect measured in semiconductors [
29]. In the framework of spintronics, the effect of the precession can be taken into account in terms of diffusion in space of the transverse components of the spin. This generalization was called transverse spin-accumulation [
30,
31,
32,
33,
34], and was introduced much later in the context of spin-transfer experiments (see below).
As a consequence, there is another way to drive the spins out-of-equilibrium with the use of the transverse spin pumping force
that generates the transverse spin flux
. Also in that case, the application of a potential difference trough the junction gives rise to non-zero
, and the transverse spin-polarized current
is produced at the interface. The transverse spin flux can also be expressed in terms of transverse relaxation time
with
. These recent developments are presented in
Section 4 on equal footing with the longitudinal spin-flip relaxation.
1.3. Band Structure and s-d Relaxation
Furthermore, beyond the spin internal degrees of freedom, it is important to push the description to a more realistic situation that takes into account the ferromagnetic specificity of the material (and not only the paramagnetic properties of the conduction electrons). Indeed, the out-of-equilibrium magnetization described within the two-channel model is given by
(where
is the Bohr magneton and
g the Landé factor). This system is paramagnetic. However, in
ferromagnets, the contribution
to the total magnetization is superimposed to the ferromagnetic collective variable
(which is essentially due to the
d band electrons [
35]). In terms of transport parameters, the quasi particles
s and
d are defined by effective masses
and
,
i.e., by supplementary internal degrees of freedom that takes into account the coupling to the periodic lattice.
In line with the pioneering works of Mott [
36], we will consider a simple generalization of the two channel model that takes into account the ferromagnetic nature of the
metals by enlarging the internal degrees of freedom to four electronic populations: the conduction electrons of the
s band for up and down spins, and the conduction electrons of the
d band for up and down spins. We have then a four-channel model, in which two kinds of spin flux
and
should be defined for both interband and intraband spin-dependent relaxation. A third kind of pumping force can then be introduced with the interband chemical potential difference
[
18]. This treatment is performed in
Section 5.
1.4. Ferromagnetic Collective Variable
An important observable is still missing in the above description of a ferromagnetic junction: the ferromagnetic collective variable
has not been introduced explicitly. Accordingly, the next section (
Section 2) presents a derivation of the equation of the dynamics for the ferromagnetic variable (
i.e., the Landau-Lifshitz-Gilbert equation) performed with the introduction of a generalized force
thermodynamically conjugated to the ferromagnetic degrees of freedom (
is the ferromagnetic chemical potential and Σ is the magnetic configuration space). The effective magnetic field
can also legitimately be called “spin-pumping force”. This generalized ferromagnetic force generates the current
in the magnetic configuration space.
Yet, many experiments have shown that it is possible to switch the magnetization [
37,
38,
39,
40] or to generate ferromagnetic entropy [
41] while injecting spin-polarized currents in Ferromagnetic/Non-Ferromagnetic junctions. The corresponding effect—called spin-transfer—shows that the spin-dependent electronic transport coefficients are coupled to the transport coefficient of the ferromagnet. In other terms, the ferromagnetic current generated by
and the spin-polarized current generated by
,
, or
are coupled.
The dynamicl coupling that occurs between the current of spins and the current of ferromagnetic moments is discussed in
Section 6. It leads to the definition of a spin-transfer effect for all the spin-pumping sources we have previously identified: longitudinal [
23,
24,
42], transverse [
43,
44], and s-d interband relaxation [
45,
46].
2. Introduction of the Ferromagnetic Degrees of Freedom
In this section, we focus on a uniform ferromagnetic moment
defined with radial unit vector
and the magnetization at saturation
. It is called macrospin, in opposition to the microscopic spins attached to atoms or electrons. In order to treat statistically the time dependence of ferromagnetic degrees of freedom
contacted to a heat bath, the ergodic property is used. It allows working with a statistical ensemble of a large number of ferromagnetic moments
that defines a surface
on the sphere Σ of radius
(see
Figure 1). The corresponding density
is then identified with the statistical distribution of ferromagnetic moments [
47]. The mean value of the magnetization is
. The introduction of the density is justified by the nanoscopic size of the magnetic single domain, for which the fluctuations plays a major role. With this point of view, the system is mesoscopic. Accordingly [
48,
49], the ferromagnetic chemical potential takes the general form
where
is the usual ferromagnetic potential (deduced e.g., from the quasi static hysteresis loops) and the first term accounts for diffusion. On the other hand, the current of ferromagnetic moments,
, is confined on the surface of the sphere.
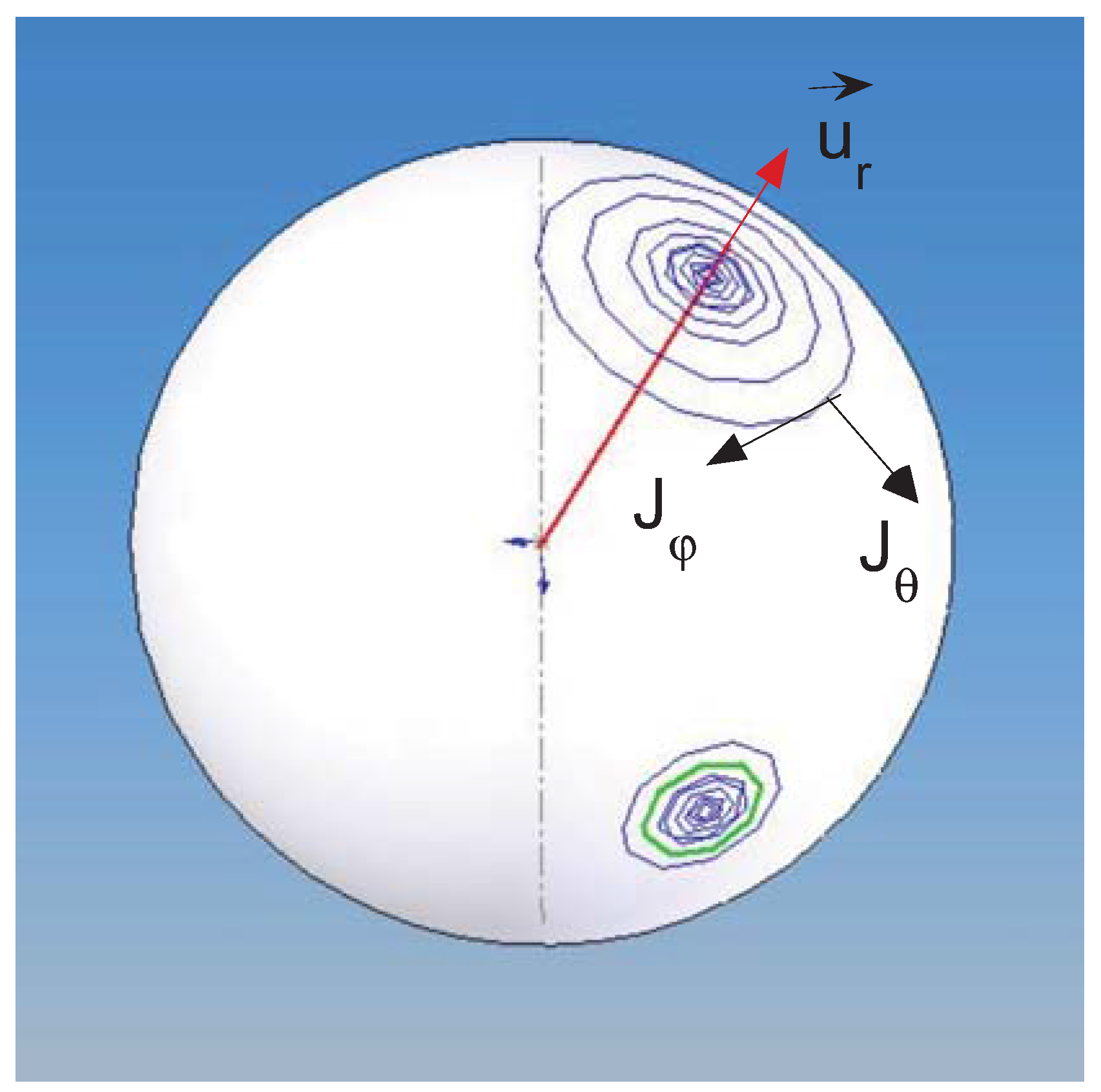
Figure 1.
Illustration of the Σ configuration space of the ferromagnetic variable. The two potential minima and the ferromagnetic currents are sketched.
Figure 1.
Illustration of the Σ configuration space of the ferromagnetic variable. The two potential minima and the ferromagnetic currents are sketched.
The power dissipated by the ferromagnetic system is given by the corresponding internal entropy production
, and is formed by the product of the generalized flux by the generalized force. Assuming a uniform temperature
T we have:
The application of the second law of thermodynamics
allows the transport equation to be deduced by writing the relation that links the generalized flux (the current
) of the extensive variables under consideration to the generalized force defined in the corresponding space Σ. Both quantities, flux and forces, are related by the Onsager matrix of the transport coefficients
:
This is the simplest form of the well-known Landau-Lifshitz equation (see below). We started from the hypothesis that the magnetic domain is uniform: the modulus of the magnetization is conserved. The trajectory of the magnetization is then confined on the surface of a sphere of radius
, and the flow is a two component vector defined with the unit vectors
of Σ. Accordingly, the Onsager matrix is a 2 × 2 matrix defined by four transport coefficients
. Furthermore, the Onsager-Casimir reciprocity relations impose that
. Assuming that the dissipation is isotropic, we have
. Let us now introduce a dimensionless coefficient
α, which is the ratio of the off-diagonal to the diagonal coefficients:
. Summarizing, the ferromagnetic kinetic equation is defined by two ferromagnetic transport coefficients
and
α:
On the other hand, the generalized force
, thermodynamically conjugated to the magnetization, is the effective magnetic field
. It is a generalization in the sense that this effective field includes the diffusive term [
50] that was first introduced by Brown in the rotational Fokker-Planck equation [
51].
Actually, it could be rather surprising to claim that Equation (
2) is the “well-known LL equation”. However, it is sufficient to rewrite Equation (
2) in 3D space with re-introducing the radial unit vector
of the reference frame
, and recalling that the current is the density multiplied by the velocity
, to recover the traditional LL equation from Equation (
2) and Equation (
3):
Furthermore, it is well-known that the LL equation is equivalent to the phenomenological Gilbert [
51,
52] equation, that defines the magnetic damping coefficient
η:
where
γ is the gyromagnetic ratio. The equivalence between the two equations defines the coefficients
α and
as a function of the coefficients
η and
γ:
is the dimensionless damping coefficient and
is defined by the relation:
The above approach can be applied to microscopic spins (e.g., for the derivation of the Bloch equation), but it should be generalized to the case in which the modulus of the magnetization is not constant (3 × 3 matrix) and the damping is not necessarily isotropic (
). Such generalizations are beyond the scope of this report (see however reference [
47]).
3. Two Spin-Channel Model
In this section we focus on the spin-dependent electric transport only and on the two-channel model sketched in the introduction. The corresponding electric wire is defined along the x axis, with a section unity. The relevant configuration space is the one-dimensional real space .
The conservation laws write:
where
and
are the densities of charge carriers in the channels
, and the spin-dependent relaxation is taken into account by the flux
. This is the velocity of the reaction (or relaxation of the spin-dependent internal variable) that transforms a conduction electron ↑ into a conduction electron ↓. This relaxation is formally equivalent to a chemical reaction, driven by the chemical affinity
[
23]. The power dissipated by the system then reads:
The corresponding kinetic equations are deduced from the second law of thermodynamics, after introducing a supplementary Onsager coefficient
L.
The set of equations Equation (
9) is sufficient in order to describe, in the stationary regime, spin-accumulation effects and any non-equilibrium contribution to the resistance due to relaxation (
) occurring at an interface [
18,
24]. Equation (
9) shows that the spin-dependent electric currents
and the spin flux
are not independent. Accordingly, it is more convenient to rewrite Equation (
9) as a function of the variables
and
. Let us define the conductivity asymmetry by the parameter
β such that
and the mean conductivity
. On the other hand, the spin-polarized electric current is
and the current of electric charges is
. The Onsager relation re-writes:
The current is called “spin current” or “pure spin-current” in the spintronics literature. The dynamical coupling between the "spin current" and the current of electric charges is described by the Onsager cross-coefficient .
The system of equations Equation (
10) allows the diffusion equation for
to be derived for the stationary conditions
and
:
where
. This diffusion process is called
spin-accumulation, and it can be considered as the archetype of the spin-pumping effects occurring at a ferromagnetic interface. The typical profile for a ferromagnetic layer of some tens of nanometer is depicted in
Figure 2.
Figure 2.
Spin-accumulation trough a Non-Ferromagnetic/Ferromagnetic/Non-Ferromagntic junction with typical size of the order of the spin diffusion length. The spin-diffusion length has been taken as equal for both materials.
Figure 2.
Spin-accumulation trough a Non-Ferromagnetic/Ferromagnetic/Non-Ferromagntic junction with typical size of the order of the spin diffusion length. The spin-diffusion length has been taken as equal for both materials.
The corresponding non-equilibrium magnetoresistance produced by the interface writes (see the details of the derivation in references [
18,
24,
46]):
where the measurement points
A and
B are located far enough in each side of the interface so that
.
The spin diffusion length is typically some tens of nanometers in ferromagnetic metals, so that the non-equilibrium magnetoresistance requires thin films (current-in-plane geometry) or nanostructured pillars (current-perpendicular-to-the-plane geometry).
4. Spin Precession
The description proposed above with a spin-dependent internal variable that takes the two spin values is not able to take into account the precession of the spins occurring in a magnetic field, and observed with electronic resonance or Hanle effects. In the case of the processes that lead to spin accumulation and giant magnetoresistance, the mean values are averaged out over the spin-diffusion length, so that the precession of the spin is not relevant. However, this is no longer the case in a quasi-ballistic regime close enough to the interface.
In order to take into account these quasi-ballistic effects (
i.e., sub-nanometric scales in metallic devices), the two-channel model has been recently generalized to transverse spin-accumulation in the context of spin-transfer-torque investigations [
30,
31,
32,
33,
34]. The transverse spin-accumulation is introduced with the corresponding current
and the corresponding chemical potential
. Transverse means here that the spin density is considered in the plan perpendicular to the quantification axis ↕ that defines the spin up and spin down in the two-channel model.
The conservation law writes:
The transverse spin flux
can be expressed with a transverse relaxation time
such that
, where
is the density of transverse spins.
Note that in metals the two potentials
and
are defined at very different length scales and it is necessary to refer to quantum approaches in order to understand the physical signification of the transverse parameters [
44,
53]. The corresponding transverse contribution to the dissipated power is
Putting all together, we have the following Onsager relations for the electric system:
5. The Role of the Electronic Subband
A justification of the spin-dependent conductivity asymmetry
in ferromagnetic metals has been proposed by N. Mott in 1936 [
36], on the bases of the band-structure approach. In the Mott description, the observed transport properties (e.g., the decreased resistivity of Ni below the Curie temperature) have been accounted for by the existence of four electronic populations: the conduction electrons of spin up and down (
and
) of the
s band and the conduction electrons of spin up and down (
and
) of the
d band. The argument is based on the fact that the contribution to the resistivity due to
interband scattering is higher than the contribution due to
s intraband scattering. In the ferromagnetic 3d metal, the
band is full so that the relaxation channel of
electrons to
band is blocked (according to the Fermi golden rule, the relaxation rate is proportional to the density of states in the final
band). Furthermore, the spin-flip interband relaxation is too energetic to be efficient (the relaxation
to
is negligible). As a consequence, the
are more scattered that the
, and the conductivities of the two channels is asymmetric:
. This mechanism is also responsible for the anisotropic magnetoresistance [
54]. The necessity of enlarging the internal degrees of freedom to the band structure enriches the concept of spin-currents and spin-pumping forces.
Using the notations introduced in the previous sections, the total current
is composed by the three currents for each channel :
(
because the band is full). The relaxation rate
is introduced to account for
spin-conserved scattering, and the relaxation rate
, is introduced in order to account for previously defined spin-flip scattering. Assuming that all channels are in steady states, the conservation laws write:
where
are respectively the total densities of particles and the density of particles in the
,
,
channels. The conjugate (intensive) variables are the chemical potentials
. The application of the first and second laws of thermodynamics allows us to deduce the Onsager relations of the system :
where the conductivity of each channel
has been introduced. The first three equations are Ohm’s laws applied to each channel, and the two last equations introduce new Onsager transport coefficients,
and
, that respectively describe the
relaxation for minority spins under the action of the chemical potential difference
and the spin-flip relaxation under spin pumping
. The Onsager coefficients are proportional to the corresponding relaxation times [
24].
In the same manner as performed in
Section 3, the equations of conservation Equation (
16) and the Onsager equations Equation (
17) lead to the two coupled diffusion equations:
where the four diffusion lengths
are given as a function of the transport coefficients in reference [
24]. The resolution of the coupled diffusion equations (the spin-accumulation processes) is discussed in the same reference.
The two spin pumping mechanisms gives rise to the corresponding contributions to the non-equilibrium magnetoresistance; these contributions can hence be assessed experimentally with electric measurements [
18]. Furthermore, as shown below, these contributions can also be observed through the measurements of the magnetization states under current injection.
6. Derivation of Spin Transfer due to Spin-Pumping Forces
In usual experimental configurations for spin-transfer, an electric current is injected in a ferromagnet through an interface (in series or in non-local configuration [
55]) and the magnetoresistance allows the magnetization states to be measured. The effect of strong electric currents on the magnetization states can then be observed. The two sub-systems Σ and the spin-polarized current described in the previous sections exchange magnetic moments at the junctions and both are open systems. In order to describe the dynamics of the ferromagnetic degrees of freedom, we have to deal with a closed system. The system of interest is now the ferromagnetic system that includes spin-accumulation effects at the junctions.
For the sake of simplicity, we treat in the following a unique spin-accumulation process and that takes into account both spin-flip and relaxation mechanisms. This total ferromagnetic system is such that the density of ferromagnetic moments and the total ferromagnetic flux are related by the conservation law: .
The initial configuration space of magnetic moments is then extended to 1D real space parametrized by the internal variable . The important point here is that the internal variable is spin dependent, and related to the ferromagnetic space Σ (e.g., through spin-flip or relaxation and the corresponding spin accumulation). This accounts for the coupling, i.e., the transfer, of magnetic moments between the two sub-systems.
The dissipation is given by the internal power dissipated in the total system
:
Where the first term in the right hand side is the power dissipated by the total ferromagnetic sub-system (including the ferromagnetic contribution due to spin-transfer), the two following terms are the power dissipated by spin-dependent electric transport, and the fourth term is the spin-independent Joule heating. The two last terms describe the power due to the various spin-dependent relaxation mechanisms occurring in the spin space.
In Equation (
19), the vectors are defined on the sphere Σ with the help of two angles
θ and
φ. The total ferromagnetic current
includes the contribution due to spin-accumulation mechanisms. The chemical potential
accounts for the energy of a ferromagnetic layer. On the other hand, the system is contacted to electric reservoirs with the electric currents and the corresponding chemical potentials. Applying the second law of thermodynamics, we obtain the general Onsager relations:
All coefficients were defined in the previous sections, except the two cross-coefficients
, introduced in this model as spin-transfer coefficients. The coefficients
are given by the Onsager reciprocity relations. We assumed that the other cross-coefficients are zero or negligible.
The total ferromagnetic current can be written after integrating over the volume
v of the ferromagnetic layer of section unity and the spin accumulation zone. This volume is such that
, where
and
are two sections close to the interface but far enough with respect to the diffusion lengths. We assume here that the diffusion lengths are much smaller than the width of the ferromagnetic layer in order to simplify the calculation: the volume of the ferromagnet is identified as
v. Let us define
as the correction due to the spin-transfer after integrating over the volume
v deduced from the two first equations of the matrix equation Equation (
20):
where
is the matrix defined in Equation (
3). The assumption of constant modulus of the magnetization imposes that
is confined on the surface of the sphere Σ. The Helmoltz decomposition theorem can then be applied: the vector
can be decomposed in a unique way with the introduction of two potentials
χ and Φ (
i.e., a potential vector) such that:
where the first term is divergenceless and the second term is curlless (i.e., non-conservative). The total correction to the Landau-Lifshitz-Gilbert equation writes
The generalized LLG takes the form:
where
is the usual effective ferromagnetic field.
Equation (
24) is a generalized LLG equation that includes the effect of spin-pumping
and
(the contribution of
has not been added to the Onsager relations Equation (
20) for the sake of simplicity). Qualitatively, the most important point is that the dynamics should now be described by the introduction of two potentials, or two magnetic fields
for the precession and
for the longitudinal relaxation, instead of a single field
in the usual case. Both fields appearing in the LLG equation contains the electric-current dependence and are related to the relevant spin-pumping mechanisms. The first contribution is measured, e.g., with ferromagnetic resonance experiments (the corresponding device is called “spin-transfer oscillator”): the field
is responsible for the shift of the resonance frequency (
i.e., the Larmor frequency). The second contribution can be assessed with the measurement of the magnetic hysteresis loop under current injection: the quasi-static states are defined by
: the spin-transfer effect shifts the hysteresis loop. Beyond, fluctuations and diffusion effects are described by the corresponding Fokker-Planck equation of the statistical distribution function
, obtained by inserting the expression of
into the conservation equation:
.
7. Conclusions
The fundamental concepts of Spintronics—spin-pumping force and spin currents—have been presented on the basis of the theory of Non-Equilibrium Thermodynamics. Spin pumping is defined as a generalized force associated to any kind of spin-dependent relaxation mechanisms that is maintained at stationary regime through an interface. It has been shown that different relaxation mechanisms can be invoked, each of which defines a specific spin-pumping force and a specific spin flux. Three mechanisms have been investigated within this formalism: spin-flip scattering, quasi-ballistic spin precession and scattering. The dynamics of the magnetization—i.e., the Landau-Lifshitz-Gilbert equation (with both longitudinal relaxation and precessional motion)—can also be described in this context as the flux produced by a spin-pumping force (i.e., the effective magnetic field ).
This approach shows that the application of a voltage difference through a Ferromagnetic/Non-Ferromagnetic junction leads to the creation of spin-pumping and spin-flux, which in turn leads to both non-equilibrium interface resistance and excitation of the ferromagnetic collective variable. The derivation proposed for the spin-accumulation formulae, magnetization dynamics and spin-transfer effects, are based on the expression of the entropy production and the second law of thermodynamics.
The dynamical equation of the magnetization (the Landau-Lifshitz-Gilbert equation) generalized to spin-pumping effects has been derived. From this generalized equation, the different spin-pumping contributions can be experimentally assessed and studied, e.g., with using ferromagnetic resonance-like experiments (precession states for the determination of the transverse field
) and magnetic hysteresis experiments (quasi-static states for the determination of the longitudinal field
). The spin-transfer transport cross-coefficients
can then be deduced. Equivalently, Equations (
20) show that the cross-coefficients can also be measured without electric currents (
spin-pumping experiments) through the dynamics of the magnetization:
.
Beyond the present phenomenological model, the explicit expressions of the spin-transfer transport cross-coefficients could be derived in principle in the framework of non-equilibrium statistical mechanics.